F# free monad recipe by Mark Seemann

How to create free monads in F#.

This is not a design pattern, but it's something related. Let's call it a recipe. A design pattern should, in my opinion, be fairly language-agnostic (although hardly universally applicable). This article, on the contrary, specifically addresses a problem in F#:

How do you create a free monad in F#?

By following the present recipe.

The recipe here is a step-by-step process, but be sure to first read the sections on motivation and when to use it. A free monads isn't a goal in itself.

This article doesn't attempt to explain the details of free monads, but instead serve as a reference. For an introduction to free monads, I think my article Pure times is a good place to start. See also the Motivating examples section, below.

Motivation #

A frequently asked question about F# is: what's the F# equivalent to an interface? There's no single answer to this question, because, as always, It Depends™. Why do you need an interface in the first place? What is its intended use?

Sometimes, in OOP, an interface can be used for a Strategy. This enables you to dynamically replace or select between different (sub)algorithms at run-time. If the algorithm is pure, then an idiomatic F# equivalent would be a function.

At other times, though, the person asking the question has Dependency Injection in mind. In OOP, dependencies are often modelled as interfaces with several members. Such dependencies are systematically impure, and thereby not part of functional design. If at all possible, prefer impure/pure/impure sandwiches over interactions. Sometimes, however, you'll need something that works like an interface or abstract base class. Free monads can address such situations.

In general, a free monad allows you to build a monad from any functor, but why would you want to do that? The most common reason I've encountered is exactly in order to model impure interactions in a pure manner; in other words: Dependency Injection.

Refactor interface to functor #

This recipe comes in three parts:

  1. A recipe for refactoring interfaces to a functor.
  2. The core recipe for creating a monad from any functor.
  3. A recipe for adding an interpreter.
The universal recipe for creating a monad from any functor follows in a later section. In this section, you'll see how to refactor an interface to a functor.

Imagine that you have an interface that you'd like to refactor. In C# it might look like this: 

public interface IFace
{
    Out1 Member1(In1 input);
    Out2 Member2(In2 input);
}

In F#, it'd look like this: 

type IFace =
    abstract member Member1 : input:In1 -> Out1
    abstract member Member2 : input:In2 -> Out2

I've deliberately kept the interface vague and abstract in order to showcase the recipe instead of a particular example. For realistic examples, refer to the examples section, further down.

To refactor such an interface to a functor, do the following:

  1. Create a discriminated union. Name it after the interface name, but append the word instruction as a suffix.
  2. Make the union type generic.
  3. For each member in the interface, add a case.
    1. Name the case after the name of the member.
    2. Declare the type of data contained in the case as a pair (a two-element tuple).
    3. Declare the type of the first element in that tuple as the type of the input argument(s) to the interface member. If the member has more than one input argument, declare it as a (nested) tuple.
    4. Declare the type of the second element in the tuple as a function. The input type of that function should be the output type of the original interface member, and the output type of the function should be the generic type argument for the union type.
  4. Add a map function for the union type. I'd recommend making this function private and avoid naming it map in order to prevent naming conflicts. I usually name this function mapI, where the I stands for instruction.
  5. The map function should take a function of the type 'a -> 'b as its first (curried) argument, and a value of the union type as its second argument. It should return a value of the union type, but with the generic type argument changed from 'a to 'b.
  6. For each case in the union type, map it to a value of the same case. Copy the (non-generic) first element of the pair over without modification, but compose the function in the second element with the input function to the map function.
Following that recipe, the above interface becomes this union type: 

type FaceInstruction<'a> =
| Member1 of (In1 * (Out1 -> 'a))
| Member2 of (In2 * (Out2 -> 'a))

The map function becomes: 

// ('a -> 'b) -> FaceInstruction<'a> -> FaceInstruction<'b>
let private mapI f = function
    | Member1 (x, next) -> Member1 (x, next >> f)
    | Member2 (x, next) -> Member2 (x, next >> f)

Such a combination of union type and map function satisfies the functor laws, so that's how you refactor an interface to a functor.

Free monad recipe #

Given any functor, you can create a monad. The monad will be a new type that contains the functor; you will not be turning the functor itself into a monad. (Some functors can be turned into monads themselves, but if that's the case, you don't need to create a free monad.)

The recipe for turning any functor into a monad is as follows:

  1. Create a generic discriminated union. You can name it after the underlying functor, but append a suffix such as Program. In the following, this is called the 'program' union type.
  2. Add two cases to the union: Free and Pure.
  3. The Free case should contain a single value of the contained functor, generically typed to the 'program' union type itself. This is a recursive type definition.
  4. The Pure case should contain a single value of the union's generic type.
  5. Add a bind function for the new union type. The function should take two arguments:
  6. The first argument to the bind function should be a function that takes the generic type argument as input, and returns a value of the 'program' union type as output. In the rest of this recipe, this function is called f.
  7. The second argument to the bind function should be a 'program' union type value.
  8. The return type of the bind function should be a 'program' union type value, with the same generic type as the return type of the first argument (f).
  9. Declare the bind function as recursive by adding the rec keyword.
  10. Implement the bind function by pattern-matching on the Free and Pure cases:
  11. In the Free case, pipe the contained functor value to the functor's map function, using bind f as the mapper function; then pipe the result of that to Free.
  12. In the Pure case, return f x, where x is the value contained in the Pure case.
  13. Add a computation expression builder, using bind for Bind and Pure for Return.
Continuing the above example, the 'program' union type becomes: 

type FaceProgram<'a> =
| Free of FaceInstruction<FaceProgram<'a>>
| Pure of 'a

It's worth noting that the Pure case always looks like that. While it doesn't take much effort to write it, you could copy and paste it from another free monad, and no changes would be required.

According to the recipe, the bind function should be implemented like this: 

// ('a -> FaceProgram<'b>) -> FaceProgram<'a> -> FaceProgram<'b>
let rec bind f = function
| Free x -> x |> mapI (bind f) |> Free
| Pure x -> f x

Apart from one small detail, the bind function always looks like that, so you can often copy and paste it from here and use it in your code, if you will. The only variation is that the underlying functor's map function isn't guaranteed to be called mapI - but if it is, you can use the above bind function as is. No modifications will be necessary.

In F#, a monad is rarely a goal in itself, but once you have a monad, you can add a computation expression builder: 

type FaceBuilder () =
    member this.Bind (x, f) = bind f x
    member this.Return x = Pure x
    member this.ReturnFrom x = x
    member this.Zero () = Pure ()

While you could add more members (such as Combine, For, TryFinally, and so on), I find that usually, those four methods are all I need.

Create an instance of the builder object, and you can start writing computation expressions: 

let face = FaceBuilder ()

Finally, as an optional step, if you've refactored an interface to an instruction set, you can add convenience functions that lift each instruction case to the free monad type:

  1. For each case, add a function of the same name, but camelCased instead of PascalCased.
  2. Each function should have input arguments that correspond to the first element of the case's contained tuple (i.e. the input argument for the original interface). I usually prefer the arguments in curried form, but that's not a requirement.
  3. Each function should return the corresponding instruction union case inside of the Free case. The case constructor must be invoked with the pair of data it requires. Populate the first element with values from the input arguments to the convenience function. The second element should be the Pure case constructor, passed as a function.
In the current example, that would be two functions, one for each case of FaceInstruction<'a>: 

// In1 -> FaceProgram<Out1>
let member1 in1 = Free (Member1 (in1, Pure))
 
// In2 -> FaceProgram<Out2>
let member2 in2 = Free (Member2 (in2, Pure))

Such functions are conveniences that make it easier to express what the underlying functor expresses, but in the context of the free monad.

Interpreters #

A free monad is a recursive type, and values are trees. The leafs are the Pure values. Often (if not always), the point of a free monad is to evaluate the tree in order to pull the leaf values out of it. In order to do that, you must add an interpreter. This is a function that recursively pattern-matches over the free monad value until it encounters a Pure case.

At least in the case where you've refactored an interface to a functor, writing an interpreter also follows a recipe. This is equivalent to writing a concrete class that implements an interface.

  1. For each case in the instruction-set functor, write an implementation function that takes the case's 'input' tuple element type as input, and returns a value of the type used in the case's second tuple element. Recall that the second element in the pair is a function; the output type of the implementation function should be the input type for that function.
  2. Add a function to implement the interpreter; I often call it interpret. Make it recursive by adding the rec keyword.
  3. Pattern-match on Pure and each case contained in Free.
  4. In the Pure case, simply return the value contained in the case.
  5. In the Free case, pattern-match the underlying pair out if each of the instruction-set functor's cases. The first element of that tuple is the 'input value'. Pipe that value to the corresponding implementation function, pipe the return value of that to the function contained in the second element of the tuple, and pipe the result of that recursively to the interpreter function.
Assume that two implementation functions imp1 and imp2 exist. According to the recipe, imp1 has the type In1 -> Out1, and imp2 has the type In2 -> Out2. Given these functions, the running example becomes: 

// FaceProgram<'a> -> 'a
let rec interpret = function
    | Pure x -> x
    | Free (Member1 (x, next)) -> x |> imp1 |> next |> interpret
    | Free (Member2 (x, next)) -> x |> imp2 |> next |> interpret

The Pure case always looks like that. Each of the Free cases use a different implementation function, but apart from that, they are, as you can tell, the spitting image of each other.

Interpreters like this are often impure because the implementation functions are impure. Nothing prevents you from defining pure interpreters, although they often have limited use. They do have their place in unit testing, though. 

// Out1 -> Out2 -> FaceProgram<'a> -> 'a
let rec interpretStub out1 out2 = function
    | Pure x -> x
    | Free (Member1 (_, next)) -> out1 |> next |> interpretStub out1 out2
    | Free (Member2 (_, next)) -> out2 |> next |> interpretStub out1 out2

This interpreter effectively ignores the input value contained within each Free case, and instead uses the pure values out1 and out2. This is essentially a Stub - an 'implementation' that always returns pre-defined values.

The point is that you can have more than a single interpreter, pure or impure, just like you can have more than one implementation of an interface.

When to use it #

Free monads are often used instead of Dependency Injection. Note, however, that while the free monad values themselves are pure, they imply impure behaviour. In my opinion, the main benefit of pure code is that, as a code reader and maintainer, I don't have to worry about side-effects if I know that the code is pure. With a free monad, I do have to worry about side-effects, because, although the ASTs are pure, an impure interpreter will cause side-effects to happen. At least, however, the side-effects are known; they're restricted to a small subset of operations. Haskell enforces this distinction, but F# doesn't. The question, then, is how valuable you find this sort of design.

I think it still has some value, because a free monad explicitly communicates an intent of doing something impure. This intent becomes encoded in the types in your code base, there for all to see. Just as I prefer that functions return 'a option values if they may fail to produce a value, I like that I can tell from a function's return type that a delimited set of impure operations may result.

Clearly, creating free monads in F# requires some boilerplate code. I hope that this article has demonstrated that writing that boilerplate code isn't difficult - just follow the recipe. You almost don't have to think. Since a monad is a universal abstraction, once you've written the code, it's unlikely that you'll need to deal with it much in the future. After all, mathematical abstractions don't change.

Perhaps a more significant concern is how familiar free monads are to developers of a particular code base. Depending on your position, you could argue that free monads come with high cognitive overhead, or that they specifically lower the cognitive overhead.

Insights are obscure until you grasp them; after that, they become clear.

This applies to free monads as well. You have to put effort into understanding them, but once you do, you realise that they are more than a pattern. They are universal abstractions, governed by laws. Once you grok free monads, their cognitive load wane.

Consider, then, the developers who will be interacting with the free monad. If they already know free monads, or have enough of a grasp of monads that this might be their next step, then using free monads could be beneficial. On the other hand, if most developers are new to F# or functional programming, free monads should probably be avoided for the time being.

This flowchart summarises the above reflections:

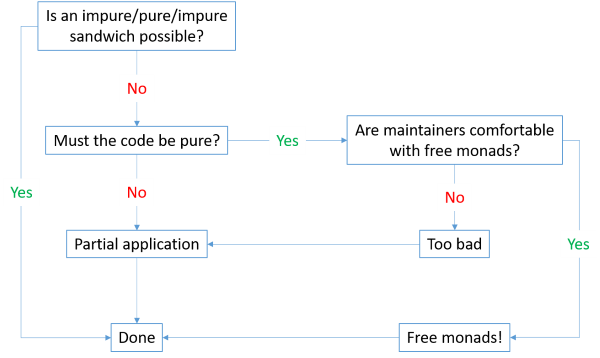
Decision flowchart for whether or not to choose free monads as a design principle.

Your first consideration should be whether your context enables an impure/pure/impure sandwich. If so, there's no reason to make things more complicated than they have to be. To use Fred Brooks' terminology, this should go a long way to avoid accidental complexity.

If you can't avoid long-running, impure interactions, then consider whether purity, or strictly functional design, is important to you. F# is a multi-paradigmatic language, and it's perfectly possible to write code that's impure, yet still well-structured. You can use partial application as an idiomatic alternative to Dependency Injection.

If you prefer to keep your code functional and explicit, you may consider using free monads. In this case, I still think you should consider the maintainers of the code base in question. If everyone involved are comfortable with free monads, or willing to learn, then I believe it's a viable option. Otherwise, I'd recommend falling back to partial application, even though Dependency Injection makes everything impure.

Motivating examples #

The strongest motivation, I believe, for introducing free monads into a code base is to model long-running, impure interactions in a functional style.

Like most other software design considerations, the overall purpose of application architecture is to deal with (essential) complexity. Thus, any example must be complex enough to warrant the design. There's little point in a Dependency Injection hello world example in C#. Likewise, a hello world example using free monads hardly seems justified. For that reason, examples are provided in separate articles.

A good place to start, I believe, is with the small Pure times article series. These articles show how to address a particular, authentic problem using strictly functional programming. The focus of these articles is on problem-solving, so they sometimes omit detailed explanations in order to keep the narrative moving.

If you need detailed explanations about all elements of free monads in F#, the present article series offers just that, particularly the Hello, pure command-line interaction article.

Variations #

The above recipes describe the regular scenario. Variations are possible. Obviously, you can choose different naming strategies and so on, but I'm not going to cover this in greater detail.

There are, however, various degenerate cases that deserve a few words. An interaction may return no data, or take no input. In F#, you can always model the lack of data as unit (()), so it's definitely possible to define an instruction case like Foo of (unit * Out1 -> 'a), or Bar of (In2 * unit -> 'a), but since unit doesn't contain any data, you can remove it without changing the abstraction.

The Hello, pure command-line interaction article contains a single type that exemplifies both degenerate cases. It defines this instruction set: 

type CommandLineInstruction<'a> =
| ReadLine of (string -> 'a)
| WriteLine of string * 'a

The ReadLine case takes no input, so instead of containing a pair of input and continuation, this case contains only the continuation function. Likewise, the WriteLine case is also degenerate, but here, there's no output. This case does contain a pair, but the second element isn't a function, but a value.

This has some superficial consequences for the implementation of functor and monad functions. For example, the mapI function becomes: 

// ('a -> 'b) -> CommandLineInstruction<'a> -> CommandLineInstruction<'b>
let private mapI f = function
    | ReadLine next -> ReadLine (next >> f)
    | WriteLine (x, next) -> WriteLine (x, next |> f)

Notice that in the ReadLine case, there's no tuple on which to pattern-match. Instead, you can directly access next.

In the WriteLine case, the return value changes from function composition (next >> f) to a regular function call (next |> f, which is equivalent to f next).

The lift functions also change: 

// CommandLineProgram<string>
let readLine = Free (ReadLine Pure)
 
// string -> CommandLineProgram<unit>
let writeLine s = Free (WriteLine (s, Pure ()))

Since there's no input, readLine degenerates to a value, instead of a function. On the other hand, while writeLine remains a function, you'll have to pass a value (Pure ()) as the second element of the pair, instead of the regular function (Pure).

Apart from such minor changes, the omission of unit values for input or output has little significance.

Another variation from the above recipe that you may see relates to interpreters. In the above recipe, I described how, for each instruction, you should create an implementation function. Sometimes, however, that function is only a few lines of code. When that happens, I occasionally inline the function directly in the interpreter. Once more, the CommandLineProgram API provides an example: 

// CommandLineProgram<'a> -> 'a
let rec interpret = function
    | Pure x -> x
    | Free (ReadLine  next) -> Console.ReadLine () |> next |> interpret
    | Free (WriteLine (s, next)) ->
        Console.WriteLine s
        next |> interpret

Here, no custom implementation functions are required, because Console.ReadLine and Console.WriteLine already exist and serve the desired purpose.

Summary #

This article describes a repeatable, and automatable, process for refactoring an interface to a free monad. I've done this enough times now that I believe that this process is always possible, but I have no formal proof for this.

I also strongly suspect that the reverse process is possible. For any instruction set elevated to a free monad, I think you should be able to define an object-oriented interface. If this is true, then object-oriented interfaces and AST-based free monads are isomorphic.

Comments

Yacoub Massad #

Hello Mark. I am trying to understand what is going on.
So basically the Free Moand allows us to separate pure code from impure code even when the impure/pure/impure sandwish idea is not possible to implement. Right?
We want to separate pure and impure code for these reasons: (1) Easier testing (2) Reasoning about pure code is easier than impure code (3) making impure code explicit makes it easier to understand programs. Is this correct?
What I am still trying to figure out is why we can't simply do this with Dependency Injection?
We can separate all units of behavior into pure ones and impure ones (e.g. functions), and then compose them all in the Composition Root. Pure units take no dependencies, they take in "direct input" and give back "direct output" as you describe in one of your blog posts.
To make the impure code explicit and clear, we can make the root method in the Composition Root construct all impure units of behavior first (e.g. adapters to the external world) and then inject them into a method that bakes these dependencies with the rest of pure code. E.g.: public static IApplication CreateApplication(IImpureDependency1 dependency1, IImpureDependency2 dependency2) => { //compose graph here}
If you have sub methods that the CreateApplication method uses for modularizing the Composition Root, they will also take any impurities they need as parameters.
So in summary, only the Composition Root knows about the impure parts of the application and they are explicitly stated as parameters in the Composition Root methods.
Doesn't this solve the impure/pure separation issue?
For example, to test, you can easilly call the CreateApplication method and pass the fake (pure) dependencies. This will make the whole graph pure in the test.
Also, the Composition Root would make it clear which impure dependencies each component in the system depends on.
Am I missing something?

2018-05-03 21:42 UTC
Mark Seemann #

Hello Yacoub, thank you for writing. Your summary of the motivations covers most of them. The reason that purity interests me is that it forces me (and everyone else) to consider decoupling. One day, I should write a more explicit article about this, but I believe that the general problem with programming today has little to do with writing code, but with reading it. Until I get such an article written, I can only refer to my Humane Code video, and perhaps my recent appearance on .NET Rocks!. What fundamentally interests me is how to break down code into small enough chunks that they fit in our brains at all levels of abstraction. Purity, and functional programming in general, attracts me because it offers a principled way of doing that.

If we forget about functional programming and free monads for a while, we could ask a question similar to yours about Dependency Injection (DI). Why should we use Dependency Injection? Can't we just, say, call a database when we need some data? Technically, we can, but we deliberately invert the control of our code so that it becomes easier to break apart into smaller chunks. You may find this observation trivial, but it wasn't ten years ago, and I made much effort in my book to explain the benefits of DI.

The problem with DI is that at detailed levels of abstractions, DI-based code may fit in our brains, but at higher levels of abstraction the complexity still increases. Put another way, understanding a single class that receives a few dependencies is easy. Getting a high-level, big-picture understanding of a DI-based code base can still be quite the challenge. At a high level of abstraction, the moving parts in underlying components are still too visible, you could say.

Strictly functional programming interests me because, by pushing impure behaviours to the boundaries of the application, the pure core of an application becomes easier to treat as a hierarchy of abstractions. (I really need to write an article with diagrams about this some day.)

What's strictly functional programming? It's code that obeys the rule that pure code can't call impure code. The reason I find Haskell so interesting is that the compiler enforces that rule. Code isn't pure if it calls impure functions, and in Haskell, the code simply will not compile if you attempt to do that.

F#, on the other hand, doesn't work like that. There's no compile-time check of whether the code is pure or impure. Thus, when you pass functions to other functions, your higher-order function could look pure, but since you don't know what an 'injected' function does, you really don't know if it's pure or not. In F#, all it takes is a single call to, say, DateTime.Now, Guid.NewGuid(), or similar, deep in your system, and that makes the entire code base impure!

The only way to prevent that in F# is by diligence.

That's a roundabout answer to your question. The gist of it, though, is that in F#, you rarely need free monads. If you find yourself in the situation where a free monad would be required in Haskell, you could just as well use DI, or rather, partial application. My article on that approach explains how this works in F#, but also why it doesn't work in Haskell. When you inject impure behaviour into an 'otherwise' pure function, then everything becomes impure.

This is where F# differs from Haskell. In Haskell, such an attempt simply doesn't compile. In F#, an otherwise pure function suddenly becomes impure. If you mostly care about that distinction because of, say, testability, then that's not a problem, because when you 'inject' pure behaviour, then the composed function is still pure, and thus trivial to unit test.

The entire system is still impure with that design, though, and that can make it difficult to fit the entire application behaviour in our brains.

I'm afraid this answer doesn't help. I'll have to write a more coherent article on this some day, but I wanted to leave this here because, realistically, a more coherent article isn't part of my immediate plans.

2018-05-06 12:41 UTC
Yacoub Massad #

Hello Mark. Thanks for the reply and for providing the links. I have already watched your Humane Code videos at clean coders before. Will listen to the podcast too.

I understand that with the free monad, you can maintain the rule that pure code will never call impure code.

This is one goal.

However, as you describe, this by itself is not the final goal. We want to achieve this goal as a mean to achieve other goals. For example, we want our code to be easier to reason about.

As you describe, we cannot achieve the first goal using DI (or partial application). And in Haskell, the compiler will prevent us from even trying.

However, I think you agree with me that there is still some great value in separating "pure" and impure code in different functions or classes, and then combining them in the Composition Root. This is basically Command Query Separation + DI. Although the graph as a whole is impure, some benefit (e.g. easier to reason about code) is still there as a result of the separation.

What I am trying to argue (or let me say think about and discuss) is that if one does the following:

  1. Separate impure and pure behavior at the level of individual units of behavior (e.g. functions or classes).
  2. Compose these units at the Composition Root (only the Composition Root knows about the impure units).
  3. In the Composition Root, first all impure units are created/prepared, and then injected into "pure" (now not pure) units.
  4. Make impure dependencies explicit as parameters in the "Create" methods of the Composition Root. (Basically "Create" methods are a way to modularize the Composition Root. I describe what I mean in more details here
then there is not much value in moving from what I just described to using Free monads just to make the Haskell compiler happy :).

Or is there something that I am missing?

Basically, if we forget for a moment about the first goal (since it is only a mean to other goals), what goals will we be not achieving?

In your reply, I can find the following that might answer these questions:
"Getting a high-level, big-picture understanding of a DI-based code base can still be quite the challenge. At a high level of abstraction, the moving parts in underlying components are still too visible"

But I can't understand what you mean here. What is the problem here? and how does the Free monad fix it?

I hope I was able to explain my ideas correctly.

2018-05-06 21:19 UTC
Yacoub Massad #

Reading my comment again, I would like to add/update a few things.

Regarding CQS, this is not exactly the same as separating impure and pure code. Still, a query can be impure (like one that reads from the database). Such query can be separated into a set of pure and impure queries. Also, a command can have some pure logic in it that can be extracted into a separate pure query (or queries). But, CQS is a step in the right direction towards this and it is a good example of how separation at some level has benefits of its own.

I would like to explain also that the steps I describe in my comment aim basically to delay the composition of pure and impure code to the last possible moment. So basically, all pure logic is composed first (parameterized with functions/delegates/interfaces representing possibly impure code). After that, impure code will be injected into such pure graph rendering it impure of course.

So basically, imagine an imaginary version of Haskell that would allow the root method of an application to allow “pure” code to call impure code.

2018-05-10 19:59 UTC
Yacoub Massad #

Here is a concrete example. Imagine these three pure functions:

(A, Func<C,D> dep1, Func<E,F> dep2) => B (1)

(C, Func<G,H> dep3) => D (2)

(G, Func<I,J> dep4) => H (3)

Now, in the Composition Root, we "compose" these together to get the following:

(A, Func<I,J> dep4, Func<E,F> dep2) =>B

So far, this is a pure function, we havn't injected any impurities in it. Thinking about this, this might be a special case of dependency injection. We might call it dependency replacing or something like that.
What I have done is "inject" function #2 as dep1 in function #1. But this is not fully injected. I replaced "dep1" with "dep3".
Then, I "inject" function #3 as dep3. Again, this is not full injection as I replace it with "dep4".

Now, after all "pure" functions have been baked together, I inject the impure "dep4" and "dep2" to get this:

A => B

I hope the code gets displayed correctly in the comment.

2018-05-14 07:30 UTC
Mark Seemann #

Yacoub, thank you for the pseudo-code. That makes it easier to discuss things.

Your premise is that functions 1, 2, and 3 are pure. The rest of the argument rests on whether or not they are. Just to be sure that we share the same terminology, I take pure to mean referentially transparent. Nothing you've written gives me any indication that this isn't your interpretation as well, so I mostly include this as an explicit definition for the benefit of other readers who may happen upon this discussion in the future.

It's clear that a function (or method) that adds two numbers together is pure. This also applies to any other first-order function with isolation. I use the word isolation as described by Jessica Kerr: A function has the property of isolation when the only information it has about the external word is passed into it via arguments.

You can write arbitrarily complex isolated functions in, say, C#: 

public static DateTime Foo(int year, string month)
{
    if (year < 1)
        return DateTime.MinValue;
    if (9999 < year)
        return DateTime.MaxValue;
 
    if (!int.TryParse(month, out int imonth))
        imonth = 7;
    if (imonth < 1)
        imonth = 1;
    if (12 < imonth)
        imonth = 12;
 
    var day = month.Length;
    if (day < 1)
        day = 10;
    if (28 < day)
        day = 20;
 
    return new DateTime(year, imonth, day);
}

To be clear, this Foo method makes no sense, but it is, as far as I can tell, pure; it operates entirely on its input.

Consider, however, this variation: 

public static DateTime Foo(int year, string month)
{
    if (year < 1)
        return DateTime.MinValue;
    if (9999 < year)
        return DateTime.MaxValue;
 
    if (!int.TryParse(month, out int imonth))
        imonth = 7;
    if (imonth < 1)
        imonth = 1;
    if (12 < imonth)
        imonth = 12;
 
    var day = month.Length;
    if (day < 1)
        day = 10;
    if (DateTime.DaysInMonth(year, imonth) < day)
        day = 20;
 
    return new DateTime(year, imonth, day);
}

Notice that DateTime.DaysInMonth(year, imonth) replaces the hard-coded value 28. Is this variation pure?

I don't know. In order to figure that out, we'd need to understand if DateTime.DaysInMonth is pure. Does it use a hard-coded table or algorithm of leap years, or does it use a call to the operating system (OS)? If the latter, does the OS base its functionality on a pure implementation, or does it look up the information in some resource (like the Windows Registry)?

With leap years, and for the Gregorian calendar, a pure algorithm exists, but imagine that we create a similar nonsense function that creates DateTimeOffset values, including time and time-zone offsets. In this case, figuring out if a value is valid relies on external data, since rules about daylight saving time are political and subject to change.

My point is that without a machine tool (such as a type system) to guide us, it's practically impossible to reason about the purity of code.

To make matters worse, as soon as you pass a function as an argument to another function, all bets are off. Even if you've diligently reviewed functions like 1, 2, and 3 above for purity, they're only pure if dep2 and dep4 are pure as well.

Haskell takes away all that angst related to purity by enforcing it via its type system. This liberates us to worry about other things, because the compiler has our backs regarding purity.

In C#, F#, Java, and most other languages, we get no such guarantees. As I've tried to demonstrate above, I'd regard all non-trivial code to be impure. All it takes is one system call, Guid.NewGuid(), random.Next(), DateTime.Now, log.Warning("foo"), etc. to make all code transitively calling such a statement impure. This is, realistically, impossible to prevent.

Do we care, then? What if the functions 1, 2, and 3 are 'pure enough'?

In an analogy to this discussion, in RESTful design, GET requests should be side-effect free. Almost all web servers, however, log HTTP requests, so GET requests are never side-effect free. The interpretation used in that context, therefore, is that GET requests should be free of side effects for which the client is responsible.

You can have a similar discussion about functional programming. What if a function logs debug information? Does that change the observable state of the system?

In any case, before even beginning to discuss whether dependency injection or partial application is functional, we need to make it clear why we care about purity.

I care about purity because it eliminates entire classes of bugs. It also means that I don't have to log what happens inside my pure code; as long as I log what happens at the impure boundary, I can always reproduce the result of a pure computation. All this makes the overall code simpler. Logging, caching, instrumentation. Many cross-cutting concerns either disappear or greatly simplify.

Returning to the overall discussion related to this article, free monads are one way to separate pure code from impure code. What you suggest, though, isn't pure, because all it takes to make the entire composition impure is that dep2 or dep4 are impure (or one of the 'pure' functions turning out to be impure after all). It's Dependency Injection, only you replace interfaces with delegates.

Does it matter? Probably not. Trying to keep things 'as pure as possible' in C# and similar languages could still provide benefits. That's how I approach F#. Ultimately, the goal is to make the code sustainable. If you can do that with Dependency Injection or partial application, then the mission is accomplished.

In Haskell, free monads are sometimes required, but in F#, it's a specialised design I'd only reach for in niche situations.

2018-05-15 8:36 UTC
Nikolay Terletskyi #

Hello! I just want to add my humble optinion to Mark and Yacoub disscussion. There is something that you could not achieve with partial application.

Imagine that you have pipeline that process some entity. And if some conditions are met you need another one. Id of second entity is the field of first.

So you can not just pass second entity as parameter. Because you do not sure if it is needed. You can pass function that give you an entity.

But what is return type of this function? SecondEntetyType or Async<SecondEntetyType> or Task<SecondEntetyType>? What if you use library with callback interface to load this entity?

Should you care about it to declare relations between first and second entities?

Without free monad answer is yes !!!

It is main achievement from free monads for me.

2019-06-06 5:30 UTC
Nick Dunets #

Hi, I had the same questions as Yacoub i.e. how is Free any better than raw Dependency Injection?

After some research I can see at least couple of advantages. Even if code is messy and pure/impure parts interleaved chaotically, and function doesn't reduce to a simple tree and therefore can't serve as a convincing test case without being further interpreted etc. - there are still at least two advantages over DI:

1. No need to pass extra parameters representing the abstraction of impure code all over the place

2. Async aspect doesn't leak: e.g. WriteLine case from the article's example could have been interpreted as Console.Out.WriteLineAsync() - why not? but the "pure" core would still be decopuled from async aspect.

2019-07-09 20:15 UTC
Romain Deneau @DeneauRomain #

Thank you Mark for these high quality articles. I was wondering if it wouldn't be more relevant to talk about Operations rather than Members in the interface: 

public interface IFace
{
    Out1 Operation1(In1 input);
    Out2 Operation2(In2 input);
}

Indeed, a dependency is needed in order to perform some (impure?) operations to be delegated to another object, in another layer or to follow the Single Responsibility Principle. Also it makes more sense to have operations rather than "members" in an instruction: 

type FaceInstruction<'a> =
		| Operation1 of (In1 * (Out1 -> 'a))
		| Operation2 of (In2 * (Out2 -> 'a))

On the other hand, being extreme in the application of another SOLID principle, the Segragation Principle Interface, each operation may be splitted in as many different interfaces to be injected into the object. I think it doesn't change your recipe: putting all operations in the same instruction set / union type. What do you think of about it?

2019-10-11 20:48 UTC
Mark Seemann #

Romain, thank you for writing. In addition to members, we could call them operations, or actions. I chose member because it's established C# terminology when you're talking about the united set of methods, properties, and events defined by a type such as an interface.

If you approach free monads from functional programming, we wouldn't call them members, but rather functions.

I chose to start with the term member because I surmised that this would be the term with which most readers would be familiar. Since the article starts with those names, I chose to keep the same terms all the way through so that the reader would be able to follow the various steps in the recipe.

With regards to the SOLID principles, the logical conclusion is to have lots of one-method interfaces. You can have one-function free monads as well, but combining them involves much plumbing work in F#. This is much easier in Haskell.

2019-10-12 23:20 UTC

Wish to comment?

You can add a comment to this post by sending me a pull request. Alternatively, you can discuss this post on Twitter or somewhere else with a permalink. Ping me with the link, and I may respond.

Published

Monday, 07 August 2017 08:11:00 UTC

Tags

Mark Seemann
Support the blog
Buy my book Code That Fits in Your Head
Buy my book about Dependency Injection
Watch my Pluralsight courses
Watch my Clean Coders videos
Public speaking schedule

"Our team wholeheartedly endorses Mark. His expert service provides tremendous value."
Hire me!
Published: Monday, 07 August 2017 08:11:00 UTC