Maybe monoids by Mark Seemann
You can combine Maybe objects in several ways. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
You can combine Maybe objects in various ways, thereby turning them into monoids. There's at least two unconstrained monoids over Maybe values, as well as some constrained monoids. By constrained I mean that the monoid only exists for Maybe objects that contain certain values. You'll see such an example first.
Combining Maybes over semigroups #
If you have two Maybe objects, and they both (potentially) contain values that form a semigroup, you can combine the Maybe values as well. Here's a few examples.
public static Maybe<int> CombineMinimum(Maybe<int> x, Maybe<int> y) { if (x.HasItem && y.HasItem) return new Maybe<int>(Math.Min(x.Item, y.Item)); if (x.HasItem) return x; return y; }
In this first example, the semigroup operation in question is the minimum operation. Since C# doesn't enable you to write generic code over mathematical operations, the above method just gives you an example implemented for Maybe<int> values. If you also want to support e.g. Maybe<decimal> or Maybe<long>, you'll have to add overloads for those types.
If both x and y have values, you get the minimum of those, still wrapped in a Maybe container:
var x = new Maybe<int>(42); var y = new Maybe<int>(1337); var m = Maybe.CombineMinimum(x, y);
Here, m is a new Maybe<int>(42).
It's possible to combine any two Maybe objects as long as you have a way to combine the contained values in the case where both Maybe objects contain values. In other words, you need a binary operation, so the contained values must form a semigroup, like, for example, the minimum operation. Another example is maximum:
public static Maybe<decimal> CombineMaximum(Maybe<decimal> x, Maybe<decimal> y) { if (x.HasItem && y.HasItem) return new Maybe<decimal>(Math.Max(x.Item, y.Item)); if (x.HasItem) return x; return y; }
In order to vary the examples, I chose to implement this operation for decimal instead of int, but you can see that the implementation code follows the same template. When both x and y contains values, you invoke the binary operation. If, on the other hand, y is empty, then right identity still holds:
var x = new Maybe<decimal>(42); var y = new Maybe<decimal>(); var m = Maybe.CombineMaximum(x, y);
Since y in the above example is empty, the resulting object m is a new Maybe<decimal>(42).
You don't have to constrain yourself to semigroups exclusively. You can use a monoid as well, such as the sum monoid:
public static Maybe<long> CombineSum(Maybe<long> x, Maybe<long> y) { if (x.HasItem && y.HasItem) return new Maybe<long>(x.Item + y.Item); if (x.HasItem) return x; return y; }
Again, notice how most of this code is boilerplate code that follows the same template as above. In C#, unfortunately, you have to write out all the combinations of operations and contained types, but in Haskell, with its stronger type system, it all comes in the base library:
Prelude Data.Semigroup> Option (Just (Min 42)) <> Option (Just (Min 1337))
Option {getOption = Just (Min {getMin = 42})}
Prelude Data.Semigroup> Option (Just (Max 42)) <> mempty
Option {getOption = Just (Max {getMax = 42})}
Prelude Data.Semigroup> mempty <> Option (Just (Sum 1337))
Option {getOption = Just (Sum {getSum = 1337})}
That particular monoid over Maybe, however, does require as a minimum that the contained values form a semigroup. There are other monoids over Maybe that don't have any such constraints.
First #
As you can read in the introductory article about semigroups, there's two semigroup operations called first and last. Similarly, there's two operations by the same name defined over monoids. They behave a little differently, although they're related.
The first monoid operation returns the left-most non-empty value among candidates. You can view nothing as being a type-safe equivalent to null, in which case this monoid is equivalent to a null coalescing operator.
public static Maybe<T> First<T>(Maybe<T> x, Maybe<T> y) { if (x.HasItem) return x; return y; }
As long as x contains a value, First returns it. The contained values don't have to form monoids or semigroups, as this example demonstrates:
var x = new Maybe<Guid>(new Guid("03C2ECDBEF1D46039DE94A9994BA3C1E")); var y = new Maybe<Guid>(new Guid("A1B7BC82928F4DA892D72567548A8826")); var m = Maybe.First(x, y);
While I'm not aware of any reasonable way to combine GUIDs, you can still pick the left-most non-empty value. In the above example, m contains 03C2ECDBEF1D46039DE94A9994BA3C1E. If, on the other hand, the first value is empty, you get a different result:
var x = new Maybe<Guid>(); var y = new Maybe<Guid>(new Guid("2A2D19DE89D84EFD9E5BEE7C4ADAFD90")); var m = Maybe.First(x, y);
In this case, m contains 2A2D19DE89D84EFD9E5BEE7C4ADAFD90, even though it comes from y.
Notice that there's no guarantee that First returns a non-empty value. If both x and y are empty, then the result is also empty. The First operation is an associative binary operation, and the identity is the empty value (often called nothing or none). It's a monoid.
Last #
Since you can define a binary operation called First, it's obvious that you can also define one called Last:
public static Maybe<T> Last<T>(Maybe<T> x, Maybe<T> y) { if (y.HasItem) return y; return x; }
This operation returns the right-most non-empty value:
var x = new Maybe<Guid>(new Guid("1D9326CDA0B3484AB495DFD280F990A3")); var y = new Maybe<Guid>(new Guid("FFFC6CE263C7490EA0290017FE02D9D4")); var m = Maybe.Last(x, y);
In this example, m contains FFFC6CE263C7490EA0290017FE02D9D4, but while Last favours y, it'll still return x if y is empty. Notice that, like First, there's no guarantee that you'll receive a populated Maybe. If both x and y are empty, the result will be empty as well.
Like First, Last is an associative binary operation with nothing as the identity.
Generalisation #
The first examples you saw in this article (CombineMinimum, CombineMaximum, and so on), came with the constraint that the contained values form a semigroup. The First and Last operations, on the other hand, seem unconstrained. They work even on GUIDs, which notoriously can't be combined.
If you recall, though, first and last are both associative binary operations. They are, in fact, unconstrained semigroups. Recall the Last semigroup:
public static T Last<T>(T x, T y) { return y; }
This binary operation operates on any unconstrained type T, including Guid. It unconditionally returns y.
You could implement the Last monoid over Maybe using the same template as above, utilising the underlying semigroup:
public static Maybe<T> Last<T>(Maybe<T> x, Maybe<T> y) { if (x.HasItem && y.HasItem) return new Maybe<T>(Last(x.Item, y.Item)); if (x.HasItem) return x; return y; }
This implementation has exactly the same behaviour as the previous implementation of Last shown earlier. You can implement First in the same way.
That's exactly how Haskell works:
Prelude Data.Semigroup Data.UUID.Types> x =
sequence $ Last $ fromString "03C2ECDB-EF1D-4603-9DE9-4A9994BA3C1E"
Prelude Data.Semigroup Data.UUID.Types> x
Just (Last {getLast = 03c2ecdb-ef1d-4603-9de9-4a9994ba3c1e})
Prelude Data.Semigroup Data.UUID.Types> y =
sequence $ Last $ fromString "A1B7BC82-928F-4DA8-92D7-2567548A8826"
Prelude Data.Semigroup Data.UUID.Types> y
Just (Last {getLast = a1b7bc82-928f-4da8-92d7-2567548a8826})
Prelude Data.Semigroup Data.UUID.Types> Option x <> Option y
Option {getOption = Just (Last {getLast = a1b7bc82-928f-4da8-92d7-2567548a8826})}
Prelude Data.Semigroup Data.UUID.Types> Option x <> mempty
Option {getOption = Just (Last {getLast = 03c2ecdb-ef1d-4603-9de9-4a9994ba3c1e})}
The <> operator is the generic binary operation, and the way Haskell works, it changes behaviour depending on the type upon which it operates. Option is a wrapper around Maybe, and Last represents the last semigroup. When you stack UUID values inside of Option Last, you get the behaviour of selecting the right-most non-empty value.
In fact,
Any semigroup S may be turned into a monoid simply by adjoining an element e not in S and defining e • s = s = s • e for all s ∈ S.
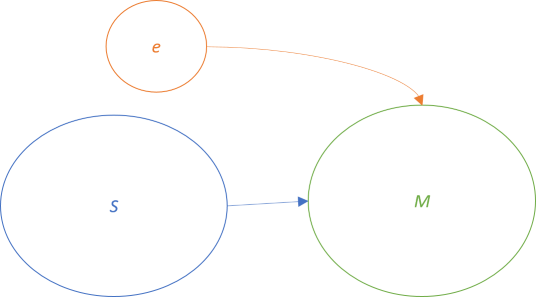
That's just a mathematical way of saying that if you have a semigroup, you can add an extra value e and make e behave like the identity for the monoid you're creating. That extra value is nothing. The way Haskell's Data.Semigroup module models a monoid over Maybe instances aligns with the underlying mathematics.
Conclusion #
Just as there's more than one monoid over numbers, and more than one monoid over Boolean values, there's more than one monoid over Maybe values. The most useful one may be the one that elevates any semigroup to a monoid by adding nothing as the identity, but others exist. While, at first glance, the first and last monoids over Maybes look like operations in their own right, they're just applications of the general rule. They elevate the first and last semigroups to monoids by 'wrapping' them in Maybes, and using nothing as the identity.
Next: Lazy monoids.
