Functional architecture: a definition by Mark Seemann
How do you know whether your software architecture follows good functional programming practices? Here's a way to tell.
Over the years, I've written articles on functional architecture, including Functional architecture is Ports and Adapters, given conference talks, and even produced a Pluralsight course on the topic. How should we define functional architecture, though?
People sometimes ask me about their F# code: How do I know that my F# code is functional?
Please permit me a little detour before I answer that question.
What's the definition of object-oriented design? #
Object-oriented design (OOD) has been around for decades; at least since the nineteen-sixties. Sometimes people get into discussions about whether or not a particular design is good object-oriented design. I know, since I've found myself in such discussions more than once.
These discussions usually die out without resolution, because it seems that no-one can provide a sufficiently rigorous definition of OOD that enables people to determine an outcome. One thing's certain, though, so I'd like to posit this corollary to Godwin's law:
As a discussion about OOD grows longer, the probability of a comparison involving Alan Kay approaches 1.Not that I, in any way, wish to suggest any logical relationship between Alan Kay and Hitler, but in a discussion about OOD, sooner or later someone states:
"That's not what Alan Kay had in mind!"That may be true, even.
My problem with that assertion is that I've never been able to figure out exactly what Alan Kay had in mind. It's something that involves message-passing and Smalltalk, and conceivably, the best modern example of this style of programming might be Erlang (often, ironically, touted as a functional programming language).
This doesn't seem to be a good basis for determining whether or not something is object-oriented.
In any case, despite what Alan Kay had in mind, that wasn't the object-oriented programming we got. While Eiffel is in many ways a strange programming language, the philosophy of OOD presented in Object-Oriented Software Construction feels, to me, like something from which Java could develop.
I'm not aware of the detailed history of Java, but the spirit of the language seems more compatible with Bertrand Meyer's vision than with Alan Kay's.
Subsequently, C# would hardly look the way it does had it not been for Java.
The OOD we got wasn't the OOD originally envisioned. To make matters worse, the OOD we did get seems to be driven by unclear principles. Yes, there's the idea about encapsulation, but while Meyer had some very specific ideas about design-by-contract, that was the distinguishing trait of his vision that didn't make the transition to Java or C#.
It's not clear what OOD is, but I think we can do better when it comes to functional programming (FP).
Referential transparency #
It's possible to pinpoint what FP is to a degree not possible with OOD. Some people may be uncomfortable with the following definition; I don't claim that this is a generally accepted definition. It does have, however, the advantage that it's precise and supports falsification.
The foundation of FP is referential transparency. It's the idea that, for an expression, the left- and right-hand sides of the equal sign are truly equal:
two = 1 + 1
In Haskell, this is enforced by the compiler. The = operator truly implies equality. To be clear, this isn't the case in C#:
var two = 1 + 1;
In C#, Java, and other imperative languages, the = implies assignment, not equality. Here, two can change, despite the absurdity of the claim.
When code is referentially transparent, then you can substitute the expression on the right-hand side with the symbol on the left-hand side. This seems obvious when we consider addition of two numbers, but becomes less clear when we consider function invocation:
i = findBestNumber [42, 1337, 2112, 90125]
In Haskell, functions are referentially transparent. You don't know exactly what findBestNumber does, but you do know that you can substitute i with findBestNumber [42, 1337, 2112, 90125], or vice versa.
In order for a function to be referentially transparent (also known as a pure function), it must have two properties:
- It must always return the same output for the same input. We call this quality determinism.
- It must have no side effects.
The reason I prefer this definition is that it supports falsification. You can assert that a function or value is pure; all it takes is a single counter-example to prove that it's not. A counter-example can be either an input value that doesn't always produce the same return value, or a function call that produces a side effect.
I'm not aware of any other definition that offers similar decision power.
IO #
All software produces side effects: Changing a pixel on a monitor is a side effect. Writing a byte to disk is a side effect. Transmitting a bit over a network is a side effect. It seems that it'd be impossible to interact with pure functions, and indeed, it is, without some sort of affordance for impurity.
Haskell resolves this problem with the IO monad, but the purpose of this article isn't to serve as an introduction to Haskell, monads, or IO. The point is only that in FP, you need some sort of 'wormhole' that will enable you to interact with the real world. There's no way around that, but logically, the rules still apply. Pure functions must stay deterministic and free of side effects.
It follows that you have two groups of operations: impure activities and pure functions.
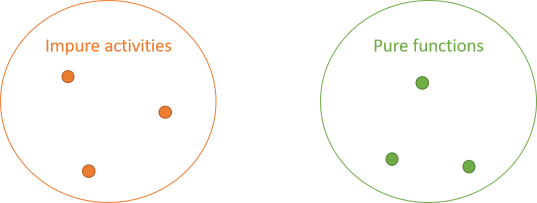
While there are rules for pure functions, those rules still allow for interaction. One pure function can call another pure function. Such an interaction doesn't change the properties of any of those functions. Both caller and callee remain side-effect-free and deterministic.
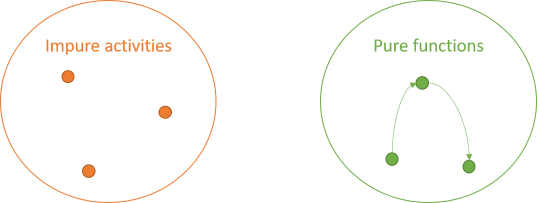
The impure activities can also interact. No rules apply to them:
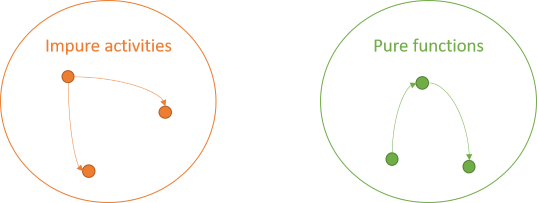
Finally, since no rules apply to impure activities, they can invoke pure functions:
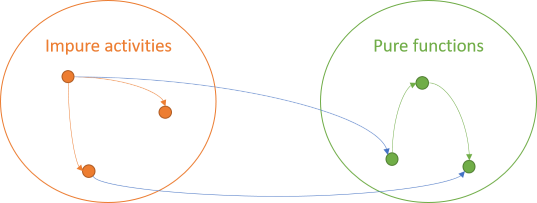
Impure activities are unbound by rules, so they can do anything they need to do, including painting pixels, writing to files, or calling pure functions. A pure function is deterministic and has no side effects. Those properties don't change just because the result is subsequently displayed on a screen.
The fourth combination of arrows is, however, illegal.
A pure function can't invoke an impure activity.If it did, it would either transitively produce a side effect or non-deterministic behaviour.
This is the rule of functional architecture. You can also explain it with a table:
| Callee | |||
|---|---|---|---|
| Impure | Pure | ||
| Caller | Impure | Valid | Valid |
| Pure | Invalid | Valid | |
Clearly, you can trivially obey the functional interaction law by writing exclusively impure code. In a sense, this is what you do by default in imperative programming languages. If you're familiar with Haskell, imagine writing an entire program in IO. That would be possible, but pointless.
Thus, we need to add the qualifier that a significant part of the code base should consist of pure code. How much? The more, the better. Subjectively, I'd say significantly more than half the code base should be pure. I'm concerned, though, that stating a hard limit is as useful here as it is for code coverage.
Tooling #
How do you verify that you obey the functional interaction law? Unfortunately, in most languages the answer is that this requires painstaking analysis. This can be surprisingly tricky to get right. Consider this realistic F# example:
let createEmailNotification templates msg (user : UserEmailData) = let { SubjectLine = subjectTemplate; Content = contentTemplate } = templates |> Map.tryFind user.Localization |> Option.defaultValue (Map.find Localizations.english templates) let r = Templating.append (Templating.replacementOfEnvelope msg) (Templating.replacementOfFlatRecord user) let subject = Templating.run subjectTemplate r let content = Templating.run contentTemplate r { RecipientUserId = user.UserId EmailAddress = user.EmailAddress NotificationSubjectLine = subject NotificationText = content CreatedDate = DateTime.UtcNow }
Is this a pure function?
You may protest that this isn't a fair question, because you don't know what, say, Templating.replacementOfFlatRecord does, but that turns out to be irrelevant. The presence of DateTime.UtcNow makes the entire function impure, because getting the current date and time is non-deterministic. This trait is transitive, which means that any code that calls createEmailNotification is also going to be impure.
That means that the purity of an expression like the following easily becomes obscure.
let emailMessages = specificUsers |> Seq.map (createEmailNotification templates msg)
Is this a pure expression? In this case, we've just established that createEmailNotification is impure, so that wasn't hard to answer. The problem, however, is that the burden is on you, the code reader, to remember which functions are pure, and which ones aren't. In a large code base, this soon becomes a formidable endeavour.
It'd be nice if there was a tool that could automatically check the functional interaction law.
This is where many people in the functional programming community become uncomfortable about this definition of functional architecture. The only tools that I'm aware of that enforce the functional interaction law are a few programming languages, most notably Haskell (others exist, too).
Haskell enforces the functional interaction law via its IO type. You can't use an IO value from within a pure function (a function that doesn't return IO). If you try, your code doesn't compile.
I've personally used Haskell repeatedly to understand the limits of functional architecture, for example to establish that Dependency Injection isn't functional because it makes everything impure.
The overall lack of tooling, however, may make people uncomfortable, because it means that most so-called functional languages (e.g. F#, Erlang, Elixir, and Clojure) offer no support for validating or enforcing functional architecture.
My own experience with writing entire applications in F# is that I frequently, inadvertently violate the functional interaction law somewhere deep in the bowels of my code.
Conclusion #
What's functional architecture? I propose that it's code that obeys the functional architecture law, and that is made up of a significant portion of pure functions.
This is a narrow definition. It excludes a lot of code bases that could easily be considered 'functional enough'. By the definition, I don't intend to denigrate fine programming languages like F#, Clojure, Erlang, etcetera. I personally find it a joy to write in F#, which is my default language choice for .NET programming.
My motivation for offering this definition, albeit restrictive, is to avoid the OOD situation where it seems entirely subjective whether or not something is object-oriented. With the functional interaction law, we may conclude that most (non-Haskell) programs are probably not 'really' functional, but at least we establish a falsifiable ideal to strive for.
This would enable us to look at, say, an F# code base and start discussing how close to the ideal is it?
Ultimately, functional architecture isn't a goal in itself. It's a means to achieve an objective, such as a sustainable code base. I find that FP helps me keep a code base sustainable, but often, 'functional enough' is sufficient to accomplish that.

Comments
Good idea of basing the definition on falsifiability!
The createEmailNotification example makes me wonder though. If it is not a functional design, then what design it actually is? I mean it has to be some design and it does not looks like object-oriented or procedural one.
Max, thank you for writing. I'm not sure whether the assertion that it has to be some design or other is axiomatically obvious, but I suppose that we humans have an innate need to categorise things.
Don Syme calls F# a functional-first language, and that epithet could easily apply to that style of programming as well. Other options could be near-functional, or perhaps, if we're in a slightly more academic mood, quasi-functional.
In daily use, we'd probably still call code like that functional, and I don't think it'll cause much confusion.
If I remember the history of programming correctly, the first attempts at functional programming didn't focus on referential transparency, but simply on the concept of functions as first-class language features, including lambda expressions and higher-order functions. The little I know of Lisp corroborates that view on the history of functional programming.
Only later (I think) did languages appear that make compile-time distinction between pure and impure code.
My purpose with this article wasn't to exclude a large number of languages or code bases from being functional, but just to offer a falsifiable test that we can use for evaluation purposes, if we're ever in doubt. This is something that I feel is sorely missing from the object-oriented debate, and while I can't think of a way to remedy the OOD situation, I hope that the present definition of functional architecture presents firmer ground upon which to have a debate.
Thank you for your definition that forms good grounds for reasoning about functional property of code. I remember some people say that even C# is functional as it allows for delegates. Several thoughts:
1. Remember [Pure] attribute and CodeContracts? It aided the purpose of defensive programming to hold pre/postconditions and invariants. I have this impression that both functional purity and defensive programming help us find ad-hoc quasi-mathematical proofs of code correctness after we load a codebase to our heads. It's way easier then to presume how it works and make changes. Of course it's not mathematical in the strict sense, but still - we tend to trust the code more (e.g. threading). I'm pretty sure unit tests belong to this family too.
2. Isn't the purity concept anywhere close to gateways (code that crosses the boundaries of program determinism control zone, e.g. IO, time, volatile memory)? It's especially evident while refactoring legacy code to make it unit testable. We often extract out infrastructure dependent parts (impure activities, e.g. DateTime.Now) for the other be deterministic (pure) and hence - testable.
3. Can the whole program/system be as pure as this:
I'm afraid not as it'd mean the pure code needed to know all the required input data upfront. That's impossible most of times. So, when it comes to measures, I'd argue that the number of pure code lines is enough to tell how pure the codebase is. I'd accompany this with e.g. percentile distribution of pure chunk length (functions/blocks of contingent im/purity etc.). E.g. I'd personally favour 1) over 2) in the following:4. I'd love to see such tools too :) I believe the purity concept does not pertain only to FP nor OO and is related to the early foundational days of computer programming with mathematical proofs they had.
Marcin, thank you for writing. To be clear, you can perform side effects or non-deterministic behaviour in C# delegates, so delegates aren't guaranteed to be referentially transparent. In fact, delegates, and particularly closures, are isomorphic to objects. In C#, they even compile to classes.
I'm aware that some people think that they're doing functional programming when they use lambda expressions in C#, but I disagree.
I'll see if I can address your other comments below.
Re: 1. #
Some functions are certainly ad-hoc, while others are grounded in mathematics. I agree that pure functions 'fit better in your brain', mostly because it's clear that the only stimuli that can affect the outcome of the function is the input. Granted, if we imagine a concrete, ad-hoc function that takes 23 function arguments, we might still consider it bad code. Small functions, though, tend to be easy to reason about.
I've previously written about the relationship between types and tests, and I believe that there's some sort of linearity in that relationship. The better the type system, the fewer tests you need. The weaker the type system, the more tests you need. It's no wonder that the unit testing culture related to languages like Ruby seems stronger than in the Haskell community.
Re: 2. #
In my experience, most people make legacy code more testable by introducing some variation of Dependency Injection. This may enable you to control some otherwise non-deterministic behaviour from tests, but it doesn't make the design more functional. Those types of dependencies (e.g. on
DateTime.Now) are inherently impure, and therefore they make everything that invokes them impure as well. The above functional interaction law excludes such a design from being considered functional.Functional code, on the other hand, is intrinsically testable. Watch out for a future series of articles that show how to move an object-oriented architecture towards something both more functional, more sustainable, and more testable.
Re: 3. #
A command-line utility could be as pure as you suggest, but most other programs will need to at least
- load some more data from impure sources, such as files, databases, or the current time,
- run some pure functions,
- output the results to some impure destinations, such as files, databases, UI, email, and so on.
I call this type of architecture a impure-pure-impure sandwich, and you can often, but not always, structure your application code in that way.Re: 4. #
I'm not sure I understand what you mean by that comment, but the mathematical proofs about computability pre-date computer programming. Gödel's work on recursive functions is from 1933, Church's work on lambda calculus is from 1936, and Turing's paper On Computable Numbers, with an Application to the Entscheidungsproblem is from later in 1936. Turing and Church later showed that all three definitions of computability are equivalent.
I don't know much about Gödel's work, but lambda calculus is defined entirely on the foundation of functions, while the Turing machines described in Turing's paper have nothing to do with functions in the mathematical sense.
Mathematical functions are, however, referentially transparent. They're also total, meaning that they always return a result for any input in the function's domain. Due to the halting problem, a Turing-complete language can't guarantee that all functions are total.
Mathematical functions are not always defined for all input, as seen with division (since it's only defined in ℝ ∖ {0}, real numbers without 0). We see for instance the term partial applied instead of total. You could say that the domain of division in ℝ is ℝ ∖ {0}.
Having total functions for some space S where the domain of the function is the same as S are nice to have, but not we are not always that fortunate.
Oskar, yes, you're right. I admit that what I wrote about totality above was a bit too sweeping. If we really start to dissect what I wrote, it's wrong on more levels. Clearly, mathematical functions (or, at least, algorithms) that never return exist; an algorithm to calculate all the decimals of π would be an example.
If I understand the results that both Church and Gödel arrived at, such algorithms can be encoded in such a way that we can also consider them mathematical functions. If so, then not all mathematical functions are total.
As you may be able to tell, it wasn't entirely clear to me what I was supposed to respond to, and it seems (now that I reread what I wrote) that I managed to write a few sentences that don't make clear sense. My main point, however, seems to have been that we can't write a general-purpose tool that'll be able to determine whether or not any arbitrary function is total or not. Does that part seem reasonable?
Thanks for this article. I feel there is a huge benefit of having a precise definition like that.
I want to point out that there is one more dimension in deciding how far a piece of code is from ‘the ideal functional architecture’. And that is developer's intention. I know, that sound stupid. And technically that code is not pure. But we are talking about how close to the ideal it is.
This is a problem I discovered some time ago. Especially in dynamic languages even the code that looks pure might not be strictly speaking pure because of some dynamic behaviour of the language and other quirks. There are some examples in JavaScript in this article: Do pure functions exist in JavaScript?.
Why is this a different dimention? For F# code there could exist a static analysis tool that would discover usage of impure function down in the code base. That is simply impossible in e.g. JavaScript. So I suggest that the intention the developer had and which is manifested in the code (assuming no harmful behaviour) should also play its role.
What do you and others think? Should such a soft view be considered?
Robin, thank you for writing. If I understand you correctly, you're asking whether we should consider code functional if the programmer intended it to be functional?
To be clear, I don't think that a static analysis tool like the one you suggest could be made for a language like F#. Not only do you need to analyse all of your own code, but if your code calls other libraries, you need to know whether or not these other libraries are pure as well. That's not a trivial undertaking.
My point is that even in F#, a programmer could intend to write pure code, yet still inadvertently fail to do so. Should we still consider it functional?
I admit that I haven't thought deeply about this, but I'd be inclined to say no. I'm sure that you can think of many examples, from other walks of life, where good intentions led to bad outcomes.
The goal of functional architecture is ultimately larger than just purity for the sake of purity. Why is functional programming valuable? I believe that it's valuable because a pure function holds few surprises. When you call a pure function, it doesn't have unintended side-effects. The lack of state mutation eradicates aliasing bugs.
If a programmer intends to write functional code, but nevertheless leaves behind many surprises in the code, the potential of functional programming remains unfulfilled.
Perhaps I misunderstood what you meant, so please elaborate if I missed your point.
You mention, that most languages provide no way to determine whatever or not, a function is pure. I agree, that this is an oversight in functional programming and while FSharp is my most favorite language, is there one that is, you could say, quite surprisingly well defined in this regard. Surprisingly because it is not a functional language per se. It supports nearly all the important concepts, while not something like an HMD type system and immutable data structures.
I am speaking about Nim. It has the keyword func for pure functions and opposite to this the keyword proc in order to perform procedures. In that context is it already obvious, what is the cause for all this confusion:
Calling one thing function, while it is actually something impure, has let to the acceptance that functions can be impure.
And this is the cause of all this trouble: Both in programming, and as well about this specific topic. Talking about implicit versus explicit as well.Matthias, thank you for writing. I didn't know about Nim.
I agree that it's confusing to call an impure procedure a function. These days, I try to stay away form that word in that context, and instead talk about impure actions or, as I did in this article, impure activities.