ploeh blog danish software design

If you don't clean up after yourself, at least enable others to do so.

I'm currently developing a software library that interacts with a third-party HTTP API to automate creation of various resources at that third party. While I use automated testing to verify that my code works, I still need to run my automation code against the real service once in while. After all, I'd like to verify that I've correctly interpreted the third party's documentation.

I run my tests against a staging environment. The entire purpose of the library is to create resources, so all successful tests leave behind new 'things' in that staging environment.

I'm not the only person who's testing against that environment, so all sorts of test entries accumulate.

Test data accretion #

More than one developer is working with the third-party staging environment. They create various records in the system for test purposes. Often, they forget about these items once the test is complete.

After a few weeks, you have various entries like these:

• Foo test Permit Client
• Fo Permit test client
• Paul Fo client from ..id
• Paul Verify Bar Test Client
• Pauls test
• SomeClient
• michael-template-client

Some of these may be used for sustained testing. Others look suspiciously like abandoned objects.

Does it matter that stuff like this builds up?

Perhaps not, but it bothers my sense of order. If enough stuff builds up, it may also make it harder to find the item you actually need, and rarely, there may be real storage costs associated with the jetsam. But realistically, it just offends my proclivity for tidiness.

Label ephemeral objects explicitly #

While I was testing my library's ability to create new resources, it dawned on me that I could use the records' display names to explicitly label them as temporary.

At first, I named the objects like this:

Test by Mark Seemann. Delete if older than 10 minutes.

While browsing the objects via a web UI (instead of the HTTP API), however, I realised that the creation date wasn't visible in the UI. That makes it hard to identify the actual age.

So, instead, I began labelling the items with a absolute time of safe deletion:

Test by Mark Seemann. Delete after 2021-11-23T13:13:00Z.

I chose to use ISO 8601 Zulu time because it's unambiguous.

Author name #

As you can tell from the above examples, I explicitly named the object Test by Mark Seemann. The word Test indicates to everyone else that this is a test resource. The reason I decided to include my own name was to make it clear to other readers who to contact in case of doubt.

While I find a message like Delete after 2021-11-23T13:13:00Z quite clear, you can never predict how other readers will interpret a text. Thus, I left my name in the title to give other people an opportunity to contact me if they have questions about the record.

Conclusion #

This is just a little pleasantry you can use to make life for a development team a little more agreeable.

You may not always be able to explicitly label a test item. Some records don't have display names, or the name field is too short to allow a detailed, explicit label.

You may also feel that this isn't worth the trouble, and perhaps it isn't.

I usually clean up after having added test data, but sometimes one forgets. When working in a shared environment, I find it considerate to clearly label test data to indicate to others when it's safe to delete it.

Or: How do I convince X to adopt Y in software development?

In January 2012 a customer asked for my help with software architecture. The CTO needed to formulate a strategy to deal with increasing demand for bring-your-own-device (BYOD) access to internal systems. Executives brought their iPhones and iPads to work and expected to be able to access and interact with custom-developed and bespoke internal line-of-business applications.

Quite a few of these were running on the Microsoft stack, which was the reason Microsoft Denmark had recommended me.

I had several meetings with the developers responsible for enabling BYOD. One guy, in particular, kept suggesting a Silverlight solution. I pointed out that Silverlight wouldn't run on Apple devices, but he wouldn't be dissuaded. He was certain that this was the correct solution, and I could tell that he became increasingly frustrated with me because he couldn't convince me.

We'll return to this story later in this essay.

Please convince my manager #

Sometimes people ask me questions like these:

• How do I convince my manager to let me use F#?
• How do I convince my team mates to adopt test-driven development?
• How do I convince the entire team that code quality matters?

Sometimes I receive such questions via email. Sometimes people ask me at conferences or user groups.

To quote Eric Lippert: Why are you even asking me?

To be fair, I do understand why people ask me, but I have few good answers.

Why ask me? #

I suppose people ask me because I've been writing about software improvement for decades. This blog dates back to January 2009, and my previous MSDN blog goes back to January 2006. These two resources alone contain more than 700 posts, the majority of which are about some kind of suggested improvement. Granted, there's also the occasional rant, by I think it's fair to say that my main motivation for writing is to share with readers what I think is right and good.

I do write a lot about potential improvements to software development.

As most readers have discovered, my book about Dependency Injection (with Steven van Deursen) is more than just a manual to a few Dependency Injection Containers, and my new book Code That Fits in Your Head is full of suggested improvements.

Add to that my Pluralsight courses, my Clean Coders videos, and my conference talks, and there's a clear pattern to most of my content.

Maven #

In The Tipping Point Malcolm Gladwell presents a model for information dissemination, containing three types of people required for an idea to take hold: Connectors, mavens, and salesmen.

In that model, a maven is an 'information specialist' - someone who accumulates knowledge and shares it with others. If I resemble any of these three types of people, I'm a maven. I like learning and discovering new ways of doing things, and obviously I like sharing that information. I wouldn't have blogged consistently for sixteen years if I didn't feel compelled to do so.

My role, as I see it, is to find and discover better ways of writing software. Much of what I write about is something that I've picked up somewhere else, but I try to present it in my own way, and I'm diligent about citing sources.

When people ask me concrete questions, like how do I refactor this piece of code? or how do write this in a more functional style?, I present an answer (if I can).

The suggestions I make are just that: It's a buffet of possible solutions to certain problems. If you encounter one of my articles and find the proposed technique useful, then that makes me happy and proud.

Notice the order of events: Someone has a problem, finds my content, and decides that it looks like a solution. Perhaps (s)he remembers my name. Perhaps (s)he feels that I helped solve a problem.

Audience members that come to my conference talks, or readers who buy my books, may not have a concrete problem to solve, but they still voluntarily seeks me out - perhaps because of previous exposure to my content.

To reiterate:

• You have a problem (concrete or vague)
• Perhaps you come across my content
• Perhaps you find it useful

Perhaps you think that I convinced you that 'my way' is best. I didn't. You were already looking for a solution. You were ready for a change. You were open.

Salesman #

When you ask me about how to convince your manager, or your team mates, you're no longer asking me a technical question. Now you're asking about how to win friends and influence people. You don't need a maven for that; you need a salesman. That's not me.

I've had some success applying changes to software organisations, but in all cases, the reason I was there in the first place was because the organisation itself (or members thereof) had asked me to come and help them. When people want your help changing things, convincing them to try something new isn't a hard sell.

When I consult development teams, I'm not there to sell them new processes; I'm there to help them use appropriate solutions at opportune moments.

I'm not a salesman. Just because I convinced you that, say, property-based testing is a good idea doesn't mean I can convince anyone else. Keep in mind that I probably convinced you because you were ready for a change.

Your manager or your team mates may not be.

Bide your time #

While I'm no salesman, I've managed to turn people around from time to time. The best strategy, I've found, is to wait for an opportunity.

As long as everything is going well, people aren't ready to change.

"Only a crisis - actual or perceived - produces real change. When that crisis occurs, the actions that are taken depend on the ideas that are lying around. That, I believe, is our basic function: to develop alternatives to existing policies, to keep them alive and available until the politically impossible becomes the politically inevitable"

If you have solutions at the ready, you may be able to convince your manager or your colleagues to try something new if a crisis occurs. Don't gloat - just present your suggestion: What if we did this instead?

Vocabulary #

Indeed, I'm not a salesman, and while I can't tell you how to sell an idea to an unwilling audience, I can tell you how you can weaken your position: Make it all about you.

Notice how questions like the above are often phrased: my manager will not let me... or how do I convince my colleagues?

I actually didn't much like How to Win Friends and Influence People, but it does present the insight that in order to sway people, you have to consider what's in it for them.

I had to be explicitly told this before I learned that lesson.

In the second half of the 2000s I was attached to a software development project at a large Danish company. After a code review, I realised that the architecture of the code was all wrong!

In order to make the project manager aware of the issue, I wrote an eight-page internal 'white paper' and emailed it to the project manager (let's call him Henk).

Nothing happened. No one addressed the problem.

A few weeks later, I had a scheduled one-on-one meeting with my own manager in Microsoft, and when asked if I had any issues, I started to complain about this problem I'd identified.

My manager looked at me for a moment and asked me: How do you think receiving that email made Henk feel?

It had never crossed my mind to think about that. It was my problem! I discovered it! I viewed myself as a great programmer and architect because I had perceived such a complex issue and was able to describe it clearly. It was all about me, me, me.

When we programmers ask how to convince our managers to 'let us' use TDD, or FP, or some other 'cool' practice, we're still focused on us. What's in it for the manager?

When we talk about code quality and lack thereof, 'ugly code', refactoring, and other such language, a non-coding manager is likely to see us as primadonnas out of touch with reality: We have features to ship, but the programmers only care about making the code 'pretty'.

I offer no silver bullet to convince other people that certain techniques are superior, but do consider introducing suggestions by describing the benefits they bring: Wouldn't it be cool if we could decrease our testing phase from three weeks to three days?, Wouldn't it be nice if we could deploy every week?, Wouldn't it be nice if we could decrease the number of errors our users encounter?

You could be wrong #

Have you ever felt frustrated that you couldn't convince other people to do it your way, despite knowing that you were right?

Recall the developer from the introduction, the one who kept insisting that Silverlight was the right solution to the organisation's BYOD problem. He was clearly convinced that he had the solution, and he was frustrated that I kept rejecting it.

We may scoff at such obvious ignorance of facts, but he had clearly drunk the Microsoft Kool-Aid. I could tell, because I'd been there myself. When you're a young programmer, you may easily buy into a compelling narrative. Microsoft evangelists were quite good at their game back then, as I suppose their Apple and Linux counterparts were and are. As an inexperienced developer, you can easily be convinced that a particular technology will solve all problems.

When you're young and inexperienced, you can easily feel that you're absolutely right and still be unequivocally wrong.

Consider this the next time you push your agenda. Perhaps your manager and colleagues reject your ideas because they're actually bad. A bit of metacognition is often appropriate.

Conclusion #

How do you convince your manager or team mates to do things better?

I don't know; I'm not a salesman, but in this essay, I've nonetheless tried to reflect on the question. I think it helps to consider what the other party gains from accepting a change, but I also think it's a waiting game. You have to be patient.

As an economist, I could also say much about incentives, but this essay is already long enough as it is. Still, when you consider how your counterparts react to your suggestions, reflect on how they are incentivised.

Even if you do everything right, make the best suggestions at the most opportune times, you may find yourself in a situation systemically rigged against doing the right thing. Ultimately, as Martin Fowler quipped, either change your organisation, or change your organisation.

In order to keep backwards compatibility, you can weaken preconditions or strengthen postconditions.

Like the previous articles on Postel's law as a profunctor and the Liskov Substitution Principle as a profunctor, this article is part of a series titled Some design patterns as universal abstractions. And like the previous articles, it's a bit of a stretch including the present article in that series, since backwards compatibility isn't a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.

Backwards compatibility is often (but not always) a desirable property of a system. Even in Zoo software, it pays to explicitly consider versioning. In order to support Continuous Delivery, you must be able to evolve a system in such a way that it's always in a working state.

When other systems depend on a system, it's important to maintain backwards compatibility. Evolve the system, but support legacy dependents as well.

Adding new test code #

In Code That Fits in Your Head, chapter 11 contains a subsection on adding new test code. Despite admonitions to the contrary, I often experience that programmers treat test code as a second-class citizen. They casually change test code in a more undisciplined way than they'd edit production code. Sometimes, that may be in order, but I wanted to show that you can approach the task of editing test code in a more disciplined way. After all, the more you edit tests, the less you can trust them.

After a preliminary discussion about adding entirely new test code, the book goes on to say:

You can also append test cases to a parametrised test. If, for example, you have the test cases shown in listing 11.1, you can add another line of code, as shown in listing 11.2. That’s hardly dangerous.

Listing 11.1 A parametrised test method with three test cases. Listing 11.2 shows the updated code after I added a new test case. (Restaurant/b789ef1/Restaurant.RestApi.Tests/ReservationsTests.cs)

[Theory]
[InlineData(null, "j@example.net", "Jay Xerxes", 1)]
[InlineData("not a date", "w@example.edu", "Wk Hd", 8)]
[InlineData("2023-11-30 20:01", null, "Thora", 19)]
public async Task PostInvalidReservation(

Listing 11.2 A test method with a new test case appended, compared to listing 11.1. The line added is highlighted. (Restaurant/745dbf5/Restaurant.RestApi.Tests/ReservationsTests.cs)

[Theory]
[InlineData(null, "j@example.net", "Jay Xerxes", 1)]
[InlineData("not a date", "w@example.edu", "Wk Hd", 8)]
[InlineData("2023-11-30 20:01", null, "Thora", 19)]
[InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)]
public async Task PostInvalidReservation(

You can also add assertions to existing tests. Listing 11.3 shows a single assertion in a unit test, while listing 11.4 shows the same test after I added two more assertions.

Listing 11.3 A single assertion in a test method. Listing 11.4 shows the updated code after I added more assertions. (Restaurant/36f8e0f/Restaurant.RestApi.Tests/ReservationsTests.cs)

Assert.Equal(
    HttpStatusCode.InternalServerError,
    response.StatusCode);

Listing 11.4 Verification phase after I added two more assertions, compared to listing 11.3. The lines added are highlighted. (Restaurant/0ab2792/Restaurant.RestApi.Tests/ReservationsTests.cs)

Assert.Equal(
    HttpStatusCode.InternalServerError,
    response.StatusCode);
Assert.NotNull(response.Content);
var content = await response.Content.ReadAsStringAsync();
Assert.Contains(
    "tables",
    content,
    StringComparison.OrdinalIgnoreCase);

These two examples are taken from a test case that verifies what happens if you try to overbook the restaurant. In listing 11.3, the test only verifies that the HTTP response is 500 Internal Server Error. The two new assertions verify that the HTTP response includes a clue to what might be wrong, such as the message No tables available.

I often run into programmers who’ve learned that a test method may only contain a single assertion; that having multiple assertions is called Assertion Roulette. I find that too simplistic. You can view appending new assertions as a strengthening of postconditions. With the assertion in listing 11.3 any 500 Internal Server Error response would pass the test. That would include a 'real' error, such as a missing connection string. This could lead to false negatives, since a general error could go unnoticed.

Adding more assertions strengthens the postconditions. Any old 500 Internal Server Error will no longer do. The HTTP response must also come with content, and that content must, at least, contain the string "tables".

This strikes me as reminiscent of the Liskov Substitution Principle. There are many ways to express it, but in one variation, we say that subtypes may weaken preconditions and strengthen postconditions, but not the other way around. You can think of of subtyping as an ordering, and you can think of time in the same way, as illustrated by figure 11.1. Just like a subtype depends on its supertype, a point in time 'depends' on previous points in time. Going forward in time, you’re allowed to strengthen the postconditions of a system, just like a subtype is allowed to strengthen the postcondition of a supertype.

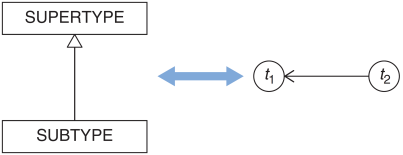
Figure 11.1 A type hierarchy forms a directed graph, as indicated by the arrow from subtype to supertype. Time, too, forms a directed graph, as indicated by the arrow from t₂ to t₁. Both present a way to order elements.

Think of it another way, adding new tests or assertions is fine; deleting tests or assertions would weaken the guarantees of the system. You probably don’t want that; herein lie regression bugs and breaking changes.

The book leaves it there, but I find it worthwhile to expand on that thought.

Function evolution over time #

As in the previous articles about x as a profunctor, let's first view 'a system' as a function. As I've repeatedly suggested, with sufficient imagination, every operation looks like a function. Even an HTTP POST request, as suggested in the above test snippets, can be considered a function, albeit one with the IO effect.

You can envision a function as a pipe. In previous articles, I've drawn horizontal pipes, with data flowing from left to right, but we can also rotate them 90° and place them on a timeline:

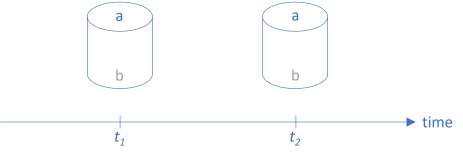
As usually depicted in Western culture, time moves from left to right. In a stable system, functions don't change: The function at t₁ is equal to the function at t₂.

The function in the illustration takes values belonging to the set a as input and returns values belonging to the set b as output. A bit more formally, we can denote the function as having the type a -> b.

We can view the passing of time as a translation of the function a -> b at t₁ to a -> b at t₂. If we just leave the function alone (as implied by the above figure), it corresponds to mapping the function with the identity function.

Clients that rely on the function are calling it by supplying input values from the set a. In return, they receive values from the set b. As already discussed in the article about Postel's law as a profunctor, we can illustrate such a fit between client and function as snugly fitting pipes:

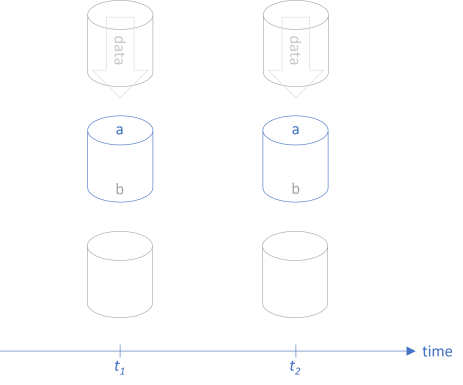
As long as the clients keep supplying elements from a and expecting elements from b in return, the function remains compatible.

If we have to change the function, which kind of change will preserve compatibility?

We can make the function accept a wider set of input, and let it return narrower set of output:

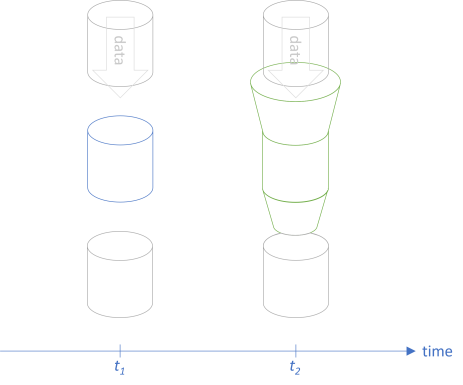
This will not break any existing clients, because they'll keep calling the function with a input and expecting b output values. The drawing is similar to the drawings from the articles on Postel's law as a profunctor and The Liskov Substitution Principle as a profunctor. It seems reasonable to consider backwards compatibility in the same light.

Profunctor #

Consider backwards compatible function evolution as a mapping of a function a -> b at t₁ to a' -> b' at t₂.

What rules should we institute for this mapping?

In order for this translation to be backwards compatible, we must be able to translate the larger input set a' to a; that is: a' -> a. That's the top flange in the above figure.

Likewise, we must be able to translate the original output set b to the smaller b': b -> b'. That's the bottom nozzle in the above figure.

Thus, armed with the two functions a' -> a and b -> b', we can translate a -> b at t₁ to a' -> b' at t₂ in a way that preserves backwards compatibility. More formally:

(a' -> a) -> (b -> b') -> (a -> b) -> (a' -> b')

This is exactly the definition of dimap for the Reader profunctor!

Arrow directions #

That's why I wrote as I did in Code That Fits in Your Head. The direction of the arrows in the book's figure 11.1 may seem counter-intuitive, but I had them point in that direction because that's how most readers are used to see supertypes and subtypes depicted.

When thinking of concepts such as Postel's law, it may be more intuitive to think of the profunctor as a mapping from a formal specification a -> b to the more robust implementation a' -> b'. That is, the arrow would point in the other direction.

Likewise, when we think of the Liskov Substitution Principle as rule about how to lawfully derive subtypes from supertypes, again we have a mapping from the supertype a -> b to the subtype a' -> b'. Again, the arrow direction goes from supertype to subtype - that is, in the opposite direction from the book's figure 11.1.

This now also better matches how we intuitively think about time, as flowing from left to right. The arrow, again, goes from t₁ to t₂.

Most of the time, the function doesn't change as time goes by. This corresponds to the mapping dimap id id - that is, applying the identity function to the mapping.

Implications for tests #

Consider the test snippets shown at the start of the article. When you add test cases to an existing test, you increase the size of the input set. Granted, unit test inputs are only samples of the entire input set, but it's still clear that adding a test case increases the input set. Thus, we can view such an edit as a mapping a -> a', where a ⊂ a'.

Likewise, when you add more assertions to an existing set of assertions, you add extra constraints. Adding an assertion implies that the test must pass all of the previous assertions, as well as the new one. That's a Boolean and, which implies a narrowing of the allowed result set (unless the new assertion is a tautological assertion). Thus, we can view adding an assertion as a mapping b -> b', where b' ⊂ b.

This is why it's okay to add more test cases, and more assertions, to an existing test, whereas you should be weary of the opposite: It may imply (or at least allow) a breaking change.

Conclusion #

As Michael Feathers observed, Postel's law seems universal. That's one way to put it.

Another way to view it is that Postel's law is a formulation of a kind of profunctor. And it certainly seems as though profunctors pop up here, there, and everywhere, once you start looking for that idea.

We can think of the Liskov Substitution Principle as a profunctor, and backwards compatibility as well. It seems reasonable enough: In order to stay backwards compatible, a function can become more tolerant of input, or more conservative in what it returns. Put another way: Contravariant in input, and covariant in output.

With a realistic example in C#.

Like the previous article on Postel's law as a profunctor, this article is part of a series titled Some design patterns as universal abstractions. And like the previous article, it's a bit of a stretch to include the present article in that series, since the Liskov Substitution Principle (LSP) isn't a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.

As was also the case for the previous article, I don't claim that any of this is new. Michael Feathers and Rúnar Bjarnason blazed that trail long before me.

LSP distilled #

In more or less natural language, the LSP states that subtypes must preserve correctness. A subtype isn't allowed to change behaviour in such a way that client code breaks.

Note that subtypes are allowed to change behaviour. That's often the point of subtyping. By providing a subtype, you can change the behaviour of a system. You can, for example, override how messages are sent, so that an SMS becomes a Slack notification or a Tweet.

If client code 'originally' supplied correct input for sending an SMS, this input should also be valid for posting a Tweet.

Specifically (paraphrasing the Wikipedia entry as of early November 2021):

• Subtypes must be contravariant in input
• Subtypes must be covariant in output
• Preconditions must not be strengthened in the subtype
• Postconditions must not be weakened in the subtype

There's a bit more, but in this article, I'll focus on those rules. The first two we already know. Since any function is already a profunctor, we know that functions are contravariant in input and covariant in output.

The LSP, however, isn't a rule about a single function. Rather, it's a rule about a family of functions. Think about a function a -> b as a pipe. You can replace the pipe segment with another pipe segment that has exactly the same shape, but replacing it with a flanged pipe also works, as long as the input flange is wider, and the nozzle narrower than the original pipe shape.

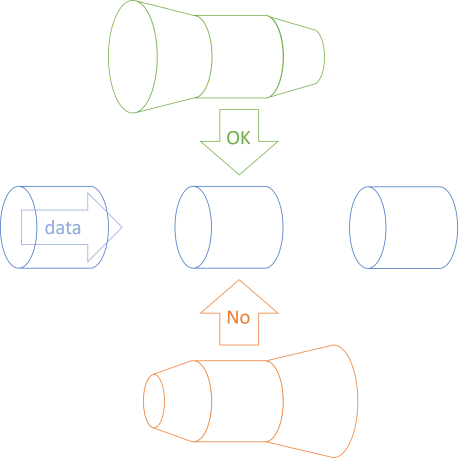
On the other hand, if you narrow the pipe at the input and widen it at the output, spillage will happen. That's essentially what the LSP states: The upper, green, flanged pipe is a good replacement for the supertype (the blue pipe in the middle), while the lower, orange, flanged pipe is not useful.

The previous article already described that visual metaphor when it comes to co- and contravariance, so this article will focus on pre- and postconditions. My conjecture is that this is just another take on co- and contravariance.

Supertype example #

When encountering statements about subtypes and supertypes, most people tend to think about object inheritance, but that's just one example. As I've previously outlined, anything that can 'act as' something else is a subtype of that something else. Specifically, an interface implementation is a subtype of the interface, and the interface itself the supertype.

Consider, as a supertype example, this interface from my book Code That Fits in Your Head:

public interface IReservationsRepository
{
    Task Create(int restaurantId, Reservation reservation);
 
    Task<IReadOnlyCollection<Reservation>> ReadReservations(
        int restaurantId, DateTime min, DateTime max);
 
    Task<Reservation?> ReadReservation(int restaurantId, Guid id);
 
    Task Update(int restaurantId, Reservation reservation);
 
    Task Delete(int restaurantId, Guid id);
}

Specifically, in this article, I'll focus exclusively on the ReadReservations method. You can imagine that there's an interface with only that method, or that when subtyping the interface in the following, we vary only that method and keep everything else fixed.

What might be the pre- and postconditions of the ReadReservations method?

ReadReservations preconditions #

The most basic kind of precondition is captured by the parameter types. In order to be able to call the method, you must supply an int and two DateTime instances. You can't omit any of them or replace one of the DateTime values with a Guid. In a statically typed language, this is obvious, and the compiler will take care of that.

Both int and DateTime are value types (structs), so they can't be null. Had one of the parameters been a reference type, it'd be appropriate to consider whether or not null constitutes valid input.

So far, we've only discussed static types. Of course a subtype must satisfy the compiler, but what other pre-conditions might be implied by ReadReservations?

The purpose of the method is to enable client code to query a data store and retrieve the reservations for a particular restaurant and in a particular time interval.

Is any restaurantId acceptable? 1? 0? -235?

It's probably a distraction that the restaurant ID is even an int. After all, you don't add IDs together, or multiply one with another one. That an ID is an integer is really just a leaky implementation detail - databases like it best when IDs are integers. I should actually have defined the restaurant ID as an opaque object with Value Object semantics, but I didn't (like other humans, I'm imperfect and lazy). The bottom line is that any number is as good as any other number. No precondition there.

What about the two DateTime parameters? Are DateTime.MinValue or DateTime.MaxValue valid values? Probably: If you'd like to retrieve all reservations in the past, you could ask for DateTime.MinValue as min and DateTime.Now as max. On the other hand, it'd be reasonable to require that min should be less than (or equal to?) max. That sounds like a proper precondition, and one that's difficult to express as a type.

We may also consider it a precondition that the object that implements the ReadReservations method is properly initialised, but I'll take that as a given. Making sure of that is the responsibility of the constructor, not the ReadReservations method.

To summarise, apart from the types and other things handled by the compiler, there's only one additional pre-condition: that min must be less than max.

Are there any postconditions?

ReadReservations postconditions #

The code base for the book obeys Command-Query Separation. Since ReadReservations returns data, it must be a Query. Thus, we can assume that calling it isn't supposed to change state. Thus, postconditions can only be statements about the return value.

Again, static typing takes care of the most fundamental postconditions. An implementation can't return a double or an UriBuilder. It must be a Task, and that task must compute an IReadOnlyCollection<Reservation>.

Why IReadOnlyCollection, by the way? That's my attempt at describing a particular postcondition as a type.

The IReadOnlyCollection<T> interface is a restriction of IEnumerable<T> that adds a Count. By adding the Count property, the interface strongly suggests that the collection is finite.

IEnumerable<T> implementations can be infinite sequences. These can be useful as functional alternatives to infinite loops, but are clearly not appropriate when retrieving reservations from a database.

The use of IReadOnlyCollection tells us about a postcondition: The collection of reservations is finite. This is, however, captured by the type. Any valid implementation of the interface ought to make that guarantee.

Is there anything else? Is it okay if the collection is empty? Yes, that could easily happen, if you have no reservations in the requested interval.

What else? Not much comes to mind, only that we'd expect the collection to be 'stable'. Technically, you could implement the GetEnumerator method so that it generates Count random Reservation objects every time you enumerate it, but none of the built-in implementations do that; that's quite a low bar, as postconditions go.

To summarise the postconditions: None, apart from a well-behaved implementation of IReadOnlyCollection<Reservation>.

SQL implementation #

According to the LSP, a subtype should be allowed to weaken preconditions. Keep in mind that I consider an interface implementation a subtype, so every implementation of ReadReservations constitutes a subtype. Consider the SQL Server-based implementation:

public async Task<IReadOnlyCollection<Reservation>> ReadReservations(
    int restaurantId,
    DateTime min,
    DateTime max)
{
    var result = new List<Reservation>();
 
    using var conn = new SqlConnection(ConnectionString);
    using var cmd = new SqlCommand(readByRangeSql, conn);
    cmd.Parameters.AddWithValue("@RestaurantId", restaurantId);
    cmd.Parameters.AddWithValue("@Min", min);
    cmd.Parameters.AddWithValue("@Max", max);
 
    await conn.OpenAsync().ConfigureAwait(false);
    using var rdr =
        await cmd.ExecuteReaderAsync().ConfigureAwait(false);
    while (await rdr.ReadAsync().ConfigureAwait(false))
        result.Add(ReadReservationRow(rdr));
 
    return result.AsReadOnly();
}
 
private const string readByRangeSql = @"
    SELECT [PublicId], [At], [Name], [Email], [Quantity]
    FROM [dbo].[Reservations]
    WHERE [RestaurantId] = @RestaurantId AND
          @Min <= [At] AND [At] <= @Max";

This implementation actually doesn't enforce the precondition that min ought to be less than max. It doesn't have to, since the code will run even if that's not the case - the result set, if min is greater than max, will always be empty.

While perhaps not useful, weakening this precondition doesn't adversely affect well-behaved clients, and buggy clients are always going to receive empty results. If this implementation also fulfils all postconditions, it's already LSP-compliant.

Still, could it weaken preconditions even more, or in a different way?

Weakening of preconditions #

As Postel's law suggests, a method should be liberal in what it accepts. If it understands 'what the caller meant', it should perform the desired operation instead of insisting on the letter of the law.

Imagine that you receive a call where min is midnight June 6 and max is midnight June 5. While wrong, what do you think that the caller 'meant'?

The caller probably wanted to retrieve the reservations for June 5.

You could weaken that precondition by swapping back min and max if you detect that they've been swapped.

Let's assume, for the sake of argument, that we make the above ReadReservations implementation virtual. This enables us to inherit from SqlReservationsRepository and override the method:

public override Task<IReadOnlyCollection<Reservation>> ReadReservations(
    int restaurantId,
    DateTime min,
    DateTime max)
{
    if (max < min)
        return base.ReadReservations(restaurantId, max, min);
 
    return base.ReadReservations(restaurantId, min, max);
}

While this weakens preconditions, it breaks no existing clients because they all 'know' that they must pass the lesser value before the greater value.

Strengthening of postconditions #

Postel's law also suggests that a method should be conservative in what it sends. What could that mean?

In the case of ReadReservations, you may notice that the result set isn't explicitly sorted. Perhaps we'd like to also sort it on the date and time:

public override async Task<IReadOnlyCollection<Reservation>> ReadReservations(
    int restaurantId,
    DateTime min,
    DateTime max)
{
    var query =
        min < max ?
            base.ReadReservations(restaurantId, min, max) :
            base.ReadReservations(restaurantId, max, min);
    var reservations = await query.ConfigureAwait(false);
    return reservations.OrderBy(r => r.At).ToList();
}

This implementation retains the weakened precondition from before, but now it also explicitly sorts the reservations on At.

Since no client code relies on sorting, this breaks no existing clients.

While the behaviour changes, it does so in a way that doesn't violate the original contract.

Profunctor #

While we've used terms such as weaken preconditions and strengthen postconditions, doesn't this look an awful lot like co- and contravariance?

I think it does, so let's rewrite the above implementation using the Reader profunctor.

First, we'll need to express the original method in the shape of a function like a -> b - that is: a function that takes a single input and returns a single output. While ReadReservations return a single value (a Task), it takes three input arguments. To make it fit the a -> b mould, we have to convert those three parameters to a Parameter Object.

This enables us to write the original implementation as a function:

Func<QueryParameters, Task<IReadOnlyCollection<Reservation>>> imp =
    q => base.ReadReservations(q.RestaurantId, q.Min, q.Max);

If we didn't want to weaken any preconditions or strengthen any postconditions, we could simply call imp and return its output.

The above weakened precondition can be expressed like this:

Func<QueryParameters, QueryParameters> pre =
    q => q.Min < q.Max ?
        new QueryParameters(q.RestaurantId, q.Min, q.Max) :
        new QueryParameters(q.RestaurantId, q.Max, q.Min);

Notice that this is a function from QueryParameters to QueryParameters. As above, it simply swaps Min and Max if required.

Likewise, we can express the strengthened postcondition as a function:

Func<Task<IReadOnlyCollection<Reservation>>, Task<IReadOnlyCollection<Reservation>>> post =
    t => t.Select(rs => rs.OrderBy(r => r.At).ToReadOnly());

The Select method exists because Task forms an asynchronous functor.

It's now possible to compose imp with pre and post using DiMap:

Func<QueryParameters, Task<IReadOnlyCollection<Reservation>>> composition = imp.DiMap(pre, post);

You can now call composition with the original arguments:

composition(new QueryParameters(restaurantId, min, max))

The output of such a function call is entirely equivalent to the above, subtyped ReadReservations implementation.

In case you've forgotten, the presence of a lawful DiMap function is what makes something a profunctor. We already knew that functions are profunctors, but now we've also seen that we can use this knowledge to weaken preconditions and strengthen postconditions.

It seems reasonable to conjecture that the LSP actually describes a profunctor.

It seems to me that the profunctor composition involved with the LSP always takes the specialised form where, for a function a -> b, the preprocessor (the contravariant mapping) always takes the form a -> a, and the postprocessor (the covariant mapping) always takes the form b -> b. This is because polymorphism must preserve the shape of the original function (a -> b).

Conclusion #

We already know that something contravariant in input and covariant in output is a profunctor candidate, but the Liskov Substitution Principle is usually expressed in terms of pre- and postconditions. Subtypes may weaken preconditions and strengthen postconditions, but not the other way around.

Evidence suggests that you can phrase these rules as a profunctor specialisation.

Next: Backwards compatibility as a profunctor.

Comments

Func<HttpStyleUriParser, MemberInfo> general = specific;

When viewing inputs and outputs as sets, Postel's law looks like a profunctor.

This article is part of a series titled Some design patterns as universal abstractions. Including the present article in that series is a bit of a stretch, since Postel's law isn't really a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.

This article is heavily inspired by Michael Feathers' article The Universality of Postel's Law, in which he writes:

[Postel's law] has been paraphrased over the years as “Be liberal in what you accept, and conservative in what you send” and for people who are mathematically inclined: “be contravariant in your inputs and covariant in your outputs.”

A thing contravariant in input and covariant in output sounds like a profunctor, but why does Michael Feathers write that about Postel's law?

In this article, I'll try to explain.

Perfect fit #

Postel's law is a statement about functions, methods, procedures, or whatever else you'd like to call them. As I've previously outlined, with sufficient squinting, we can think about methods and other operations as functions, so in this article I'll focus on functions.

Functions don't stand alone. Functions have callers. Some other entity, usually client code, passes some input data to the function, which then performs its work and returns output data. When viewed with a set-based perspective, we can depict a function as a pipe:

Client code often use the output of one function as input for another:

Int3 isEven = EncodeEven(number);
Int3 decremented = Decrement(isEven);

Even though this code example uses an explicit intermediary variable (isEven), it's equivalent to function composition:

var composition = EncodeEven.Compose(Decrement);

where Compose can be implemented as:

public static Func<A, C> Compose<A, B, C>(this Func<A, B> f, Func<B, C> g)
{
    return x => g(f(x));
}

Such a composition we can depict by appending one pipe after another:

This works, but is brittle. It's a close fit. The output set of the first function has to exactly fit the input set of the second function. What happens if the pipes don't perfectly align?

Misalignment #

Functions compose when they fit perfectly, but in the real world, that's rarely the case. For example, it may turn out that Decrement is defined like this:

static Int3 Decrement(Int3 i)
{
    if (i == 0)
        throw new ArgumentOutOfRangeException(
            nameof(i),
            "Can't decrement 0.");
 
    return i - (Int3)1;
}

This function is undefined for 0. If we wanted to peek at the set diagram 'inside' the pipe, we might depict the function like this:

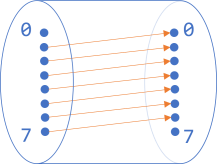
In a sense, it's still a mapping from our hypothetical 3-bit integer to 3-bit integer, but it's a partial function.

Another way to depict the mapping, however, is to constrain the domain to [1..7], and narrow the codomain to the function's image, producing a bijection:

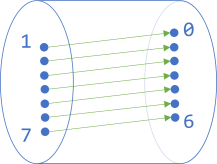
Such sets are a little harder to express in code, because how do you represent a set with seven elements? Often, you'd stick with an implementation like the above Decrement function.

This turns out to be unfortunate, however, because EncodeEven is defined like this:

static Int3 EncodeEven(Int3 i)
{
    return i.IsEven ? (Int3)1 : (Int3)0;
}

As a set diagram, we might depict it like this:

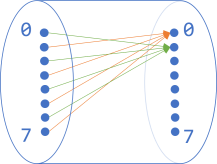
It turns out that half the inputs into the above composition don't work! It's almost as though the pipes are misaligned:

This can easily happen, also in the real world:

This is also why Michael Feathers writes:

We can see Postel in the physical world too. Every time you see a PVC pipe with a flanged end, you’re seeing something that serves as a decent visual metaphor for Postel’s Law. Those pipes fit well together because one end is more accepting.

In other words, there's nothing new in any of the above. I've just been supplying the illustrations.

Flanges #

How should we interpret the idea of flanges? How do we illustrate them? Here's a way:

Given our set-based interpretation of things, how should we interpret a flange? Let's isolate one of them. It doesn't matter which one, but lets consider the left flange. If we attempt to make it transparent, we could also draw it like this:

What does that look like? It looks like a mapping from one set to another.

The left-hand set is slightly larger than the right-hand set, but the illustration includes neither the elements of each set nor the arrows that connect them.

If we think of the 'original' function as a function from the set A to the set B we can also write it in pseudo-code as A -> B. In Haskell you'd exactly write A -> B if A and B were two concrete types. Polymorphically, though, you'd write any function as a -> b, or in C# as Func<A, B>.

Let's think of any function a -> b as the 'perfect fit' case. While such a function composes with, say, a function b -> c, the composition is brittle. It can easily become misaligned.

How do we add flanges to the function a -> b?

As the above illustration of the flange implies, we can think of the flange as another function. Perhaps we should call the slightly larger set to the left a+ (since it's 'like' a, just larger - that is, more liberal). With that nomenclature, the flange would be a function a+ -> a.

Likewise, the right flange would be a function b -> b-. Here, I've called the narrower set of the flange b- because it's smaller (more conservative) than b.

Thus, the flanged pipe is just the composition of these three functions: a+ -> a, a -> b, and b -> b-:

That's exactly how dimap is defined in Haskell:

dimap ab cd bc = cd . bc . ab

The implementation code uses other letters, and recall that Haskell is typically read from right to left. As its name implies, ab is a function a -> b, bc is a function b -> c, and cd is a function c -> d.

In other words, Postel's law is a description of the Reader profunctor, or, as Michael Feathers put it: Be contravariant in your inputs and covariant in your outputs.

Conclusion #

Postel's law is a useful design principle to keep in mind. Intuitively, it makes sense to think of it as making sure that pipes are flanged. The bigger the receiving flange is, and the smaller the nozzle is, the easier it is to compose the flanged pipe with other (flanged) pipes.

Using mostly visual metaphor, this article demonstrates that this is equivalent with being contravariant in input and covariant in output, and thus that the principle describes a profunctor.

Postel's law, however, isn't the only design principle describing a profunctor.

Next: The Liskov Substitution Principle as a profunctor.

A visual metaphor.

A recent article on types as sets briefly touched on functions as sets. For example, you can think of Boolean negation as a set of two arrows:

Here the arrows stay within the set, because the function is a function from the set of Boolean values to the set of Boolean values.

In general, however, functions aren't always endomorphisms. They often map one set of values to another set. How can we think of this as sets?

As was also the case with the article on types as sets, I'd like to point out that this article isn't necessarily mathematically rigorous. I'm neither a computer scientist nor a mathematician, and while I try to be as correct as possible, some hand-waving may occur. My purpose with this article isn't to prove a mathematical theorem, but rather to suggest what I, myself, find to be a useful metaphor.

Boolean negation visualised with domain and codomain #

Instead of visualising Boolean negation within a single set, we can also visualise it as a mapping of elements from an input set (the domain) to an output set (the codomain):

In this figure, the domain is to the left and the codomain is on the right.

How do we visualise more complex functions? What if the domain isn't the same as the codomain?

Boolean and #

Let's proceed slowly. Let's consider Boolean and next. While this function still involves only Boolean values, it combines two Boolean values into a single Boolean value. It'd seem, then, that in order to visualise this mapping, we'd need two sets to the left, and one to the right. But perhaps a better option is to visualise the domain as pairs of Boolean values:

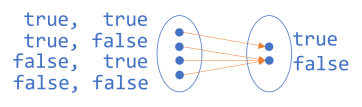
To the left, we have four pairs that each map to the Boolean values on the right.

Even numbers #

Perhaps using only Boolean values is misleading. Even when dealing with pairs, the above example may fail to illustrate that we can think of any function as a mapping from a domain to a codomain.

Imagine that there's such a thing as a 3-bit number. Such a data structure would be able to represent eight different numbers. To be clear, I'm only 'inventing' such a thing as a 3-bit number because it's still manageable to draw a set of eight elements.

How would we illustrate a function that returns true if the input is an even 3-bit number, and false otherwise? We could make a diagram like this:

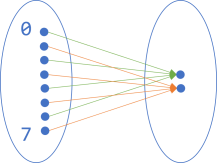
On the left-hand side, I've only labelled two of the numbers, but I'm sure you can imagine that the rest of the elements are ordered from top to bottom: 0, 1, 2, 3, 4, 5, 6, 7. To the right, the two elements are true (top) and false (bottom).

Given this illustration, I'm sure you can extrapolate to 32-bit integers and so on. It's impractical to draw, but the concept is the same.

Encoding #

So far, we've only looked at functions where the codomain is the set of Boolean values. How does it look with other codomains?

We could, for example, imagine a function that 'encodes' Boolean values as 3-bit numbers, false corresponding (arbitrarily) to 5 and true to 2. The diagram for that function looks like this:

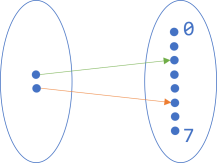
Now the set of Boolean values is on the left, with true on top.

A function as a pipe #

In all examples, we have the domain to the left and the codomain on the right, connected with arrows. Sometimes, however, we may want to think about a function as just a single thing, without all the details. After all, the diagrams in this article are simple only because the examples are toy examples. Even a simple function like this one would require a huge diagram:

public static bool IsPrime(int candidate)

An input type of int corresponds to a set with 4,294,967,296 elements. That's a big set to draw, and a lot of arrows, too!

So perhaps, instead, we'd like to have a way to illustrate a function without all the details, yet still retaining this set-based way of thinking.

Let's return to one of the earlier examples, but add a shape around it all:

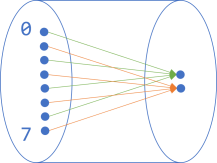
This seems like a fair addition to make. It starts to look like the function is enclosed in a pipe. Let's make the pipe opaque:

In architecture diagrams, a horizontal pipe is a common way to illustrate that some sort of data processing takes place, so this figure should hardly be surprising.

Composition #

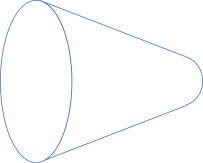
You may say that I've been cheating. After all, in a figure like the one that illustrates an isEven function, the domain is larger than the codomain, yet I've kept both ovals of the same size. Wouldn't the following be a fairer depiction?

If we try to enclose this diagram in an opaque pipe, it'd look like this:

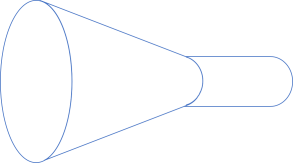
This mostly looks like a (bad) perspective drawing of a pipe, but it does start to suggest how functions fit together. For example, the output of this isEven function is the Boolean set, which is also the input of, for example the Boolean negation function (! or not). This means that if the shapes fit together, we can compose the pipes:

Continuing this line of thinking, we can keep on composing the shapes as long as the output fits the input of the next function. For example, the output of Boolean negation is still the Boolean set, which is also the domain of the above 'encoding' function:

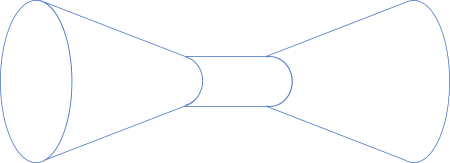
We can even, if we'd like to peek into the composition, make the pipes transparent again, to illustrate what's going on:

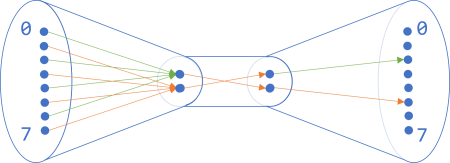
As long as the right-hand side of one pipe fits the left-hand side of another pipe, it indicates that you can compose these two functions.

Haskell translation #

For completeness' sake, let's try to express these three functions, as well as their composition, in a programming language. Since Haskell already comes with a composition operator (.), it fits nicely. It also already comes with two of the three functions we'll need:

even :: Integral a => a -> Bool
 
not :: Bool -> Bool

Thanks to Haskell's type-class feature, even works for any Integral instance, so if we imagine that our hypothetical 3-bit number is an Integral instance, it'll work for that type of input as well.

The remaining function is trivial to implement:

encode :: Num a => Bool -> a
encode  True = 2
encode False = 5

Since Integral is a supertype of Num, if our 3-bit number is an Integral instance, it's also a Num instance.

The composition implied by the above figure is this:

composition :: Integral a => a -> a
composition = encode . not . even

Haskell is typically read from right to left, so this composition starts with even, continues with not, and concludes with encode.

Let's call it:

> composition 3
2
> composition 4
5

composition 3 first passes through even, which returns False. False then passes through not, which returns True. Finally, True passes through encode, which returns 2.

I'll leave the exegesis of composition 4 as an exercise for the reader.

C# translation #

In C#, imagine that an Int3 data type exists. You can now define the three functions like this:

Func<Int3, bool> isEven = number => number.IsEven;
Func<bool, bool> not = b => !b;
Func<bool, Int3> encode = b => b ? (Int3)2 : (Int3)5;

Given a Compose extension method on Func<A, B>, you can now compose the functions like this:

Func<Int3, Int3> composition = isEven.Compose(not).Compose(encode);

This composition works just like the above Haskell example, and produces the same results.

Conclusion #

A function takes input and returns output. Even if the function takes multiple arguments, we can think of an argument as a single object: a tuple or Parameter Object.

Thus, we can think of a function as a mapping from one set to another. While we can illustrate a specific mapping (such as even, not, and encode), it's often useful to think of a function as a single abstract thing. When we think of functions as mappings from sets to sets, it makes intuitive sense to visualise the abstraction as a pipe.

This visual metaphor works for object-oriented programming as well. With sufficient mental gymnastics, functions are isomorphic to methods, so the pipe metaphor works beyond pure functions.

To a certain degree, you can think of static types as descriptions of sets.

If you've ever worked with C#, Java, F#, Haskell, or other compiled languages, you've encountered static types in programming. In school, you've probably encountered basic set theory. The two relate to each other in illuminating ways.

To be clear, I'm neither a mathematician nor a computer scientist, so I'm only basing this article on my layman's understanding of these topics. Still, I find some of the correspondences to be useful when thinking about certain programming topics.

Two elements #

What's the simplest possible set? For various definitions of simple, probably the empty set. After that? The singleton set. We'll skip these, and instead start with a set with two elements:

If you had to represent such a set in code, how would you do it?

First, you'd have to figure out how to distinguish the two elements from each other. Giving each a label seems appropriate. What do you call them? Yin and yang? Church and state? Alice and Bob?

And then, how do you represent the labels in code, keeping in mind that they somehow must 'belong to the same set'? Perhaps as an enum?

public enum Dualism
{
    Yin,
    Yang
}

As a data definition, though, an enum is a poor choise because the underlying data type is an integer (int by default). Thus, a method like this compiles and executes just fine:

public Dualism YinOrYang()
{
    return (Dualism)42;
}

The Dualism returned by the function is neither Yin nor Yang.

So, how do you represent a set with two elements in code? One option would be to Church encode it (try it! It's a good exercise), but perhaps you find something like the following simpler:

public sealed class Dualism
{
    public static readonly Dualism  Yin = new Dualism(false);
    public static readonly Dualism Yang = new Dualism( true);
 
    public Dualism(bool isYang)
    {
        IsYang = isYang;
    }
 
    public bool IsYang { get; }
 
    public bool IsYin => !IsYang;
}

With this design, a method like YinOrYang can't cheat, but must return either Yin or Yang:

public Dualism YinOrYang()
{
    return Dualism.Yin;
}

Notice that this variation is based entirely off a single member: IsYang, which is a Boolean value.

In fact, this implementation is isomorphic to bool. You can create a Dualism instance from a bool, and you can convert that instance back to a Boolean value via IsYang, without loss of information.

This holds for any two-element set: it's isomorphic to bool. You could say that the data type bool is equivalent to 'the' two-element set.

More, but still few, elements #

Is there a data type that corresponds to a three-element set? Again, you can always use Church encoding to describe a data type with three cases, but in C#, the easiest backing type would probably be bool? (Nullable<bool>). When viewed as a set, it's a set inhabited by the three values false, true, and null.

How about a set with four elements? A pair of Boolean values seems appropriate:

public sealed class Direction
{
    public readonly static Direction North = new Direction(false, false);
    public readonly static Direction South = new Direction(false,  true);
    public readonly static Direction  East = new Direction( true, false);
    public readonly static Direction  West = new Direction( true,  true);
 
    public Direction(bool isEastOrWest, bool isLatter)
    {
        IsEastOrWest = isEastOrWest;
        IsLatter = isLatter;
    }
 
    public bool IsEastOrWest { get; }
    public bool IsLatter { get; }
}

The Direction class is backed by two Boolean values. We can say that a four-element set is isomorphic to a pair of Boolean values.

How about a five-element set? If a four-element set corresponds to a pair of Boolean values, then perhaps a pair of one Boolean value and one Nullable<bool>?

Alas, that doesn't work. When combining types, the number of possible combinations is the product, not the sum, of individual types. So, a pair of bool and bool? would support 2 × 3 = 6 combinations: (false, null), (false, false), (false, true), (true, null), (true, false), and (true, true).

Again, a Church encoding (try it!) is an option, but you could also do something like this:

public sealed class Spice
{
    public readonly static Spice   Posh = new Spice(0);
    public readonly static Spice  Scary = new Spice(1);
    public readonly static Spice   Baby = new Spice(2);
    public readonly static Spice Sporty = new Spice(3);
    public readonly static Spice Ginger = new Spice(4);
 
    private readonly int id;
 
    private Spice(int id)
    {
        this.id = id;
    }
 
    public override bool Equals(object obj)
    {
        return obj is Spice spice &&
               id == spice.id;
    }
 
    public override int GetHashCode()
    {
        return HashCode.Combine(id);
    }
}

This seems like cheating, since it uses a much larger underlying data type (int), but it still captures the essence of a set with five elements. You can't add more elements, or initialise the class with an out-of-range id since the constructor is private.

The point isn't so much how to implement particular classes, but rather that if you can enumerate all possible values of a type, you can map a type to a set, and vice versa.

More elements #

Which type corresponds to this set?

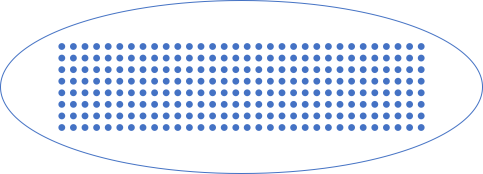
I hope that by now, it's clear that this set could correspond to infinitely many types. It's really only a matter of what we call the elements.

If we call the first element 0, the next one 1, and then 2, 3, and so on up to 255, the set corresponds to an unsigned byte. If we call the elements -128, -127, -126 up to 127, the set corresponds to a signed byte. They are, however, isomorphic.

Likewise, a set with 65,536 elements corresponds to a 16-bit integer, and so on. This also holds for 32-bit integers, 64-bit integers, and even floating point types like float and double. These sets are just too large to draw.

Infinite sets #

While most languages have built-in number types based on a fixed number of bytes, some languages also come with number types that support arbitrarily large numbers. .NET has BigInteger, Haskell comes with Integer, and so on. These numbers aren't truly infinite, but are limited by machine capacity rather than the data structure used to represent them in memory.

Another example of a type with arbitrary size is the ubiquitous string. There's no strict upper limit to how large strings you can create, although, again, your machine will ultimately run out of memory or disk space.

Theoretically, there are infinitely many strings, so, like BigInteger, string corresponds to an infinite set. This also implies that string and BigInteger are isomorphic, but that shouldn't really be that surprising, since everything that's happening on a computer is already encoded as (binary) numbers - including strings.

Any class that contains a string field is therefore also isomorphic to an (or the?) infinite set. Two string fields also correspond to infinity, as does a string field paired with a bool field, and so on. As soon as you have just one 'infinite type', the corresponding set is infinite.

Constrained types #

How about static types (classes) that use one or more built-in types as backing fields, but on top of that impose 'business rules'?

This one, for example, uses a byte as a backing field, but prohibits some values:

public sealed class DesByte
{
    private readonly byte b;
 
    public DesByte(byte b)
    {
        if (12 <= b && b <= 19)
            throw new ArgumentOutOfRangeException(nameof(b), "[12, 19] not allowed.");
 
        this.b = b;
    }
}

While this class doesn't correspond to the above 256-element set, you can still enumerate all possible values:

But then what about a class like this one?

public sealed class Gadsby
{
    private readonly string manuscript;
 
    public Gadsby(string manuscript)
    {
        if (manuscript.Contains('e', StringComparison.OrdinalIgnoreCase))
            throw new ArgumentException(
                "The manuscript may not contain the letter 'e'.",
                nameof(manuscript));
 
        this.manuscript = manuscript;
    }
}

While the constructor prohibits any string that contains the letter e, you can still create infinitely many string values even with that constraint.

You can, however, still conceivably enumerate all possible Gadsby values, although the corresponding set would be infinitely large.

Obviously, this isn't practical, but the point isn't one of practicality. The point is that you can think of types as sets.

Function types #

So far we've only covered 'values', even though it's trivial to create types that correspond to infinitely large sets.

In type systems, functions also have types. In Haskell, for example, the type Int -> Bool indicates a function that takes an Int as input and return a Bool. This might for example be a function that checks whether the number is even.

Likewise, we can write the type of not (Boolean negation) as Bool -> Bool. In a set diagram, we can illustrate it like this:

Each element points to the other one: true points to false, and vice versa. Together, the two arrows completely describe the not function (the ! operator in C#).

If we remove the original elements (true and false) of the set, it becomes clearer that these two arrows also form a set.

In general, we can think of functions as sets of arrows, but still sets. Many of these sets are infinite.

Conclusion #

Set theory is a branch of mathematics, and so is type theory. Having no formal education in either, I don't claim that types and sets are the same. A quick web search implies that while there are many similarities between types and sets, there are also differences. In this article, I've highlighted some similarities.

Thinking about types as sets can be helpful in everyday programming. In test-driven development, for example, equivalence partitioning provides insights into which test inputs to use. Being able to consider a system under test's inputs as sets (rather than types) makes this easier.

As future articles will cover, it also becomes easier to think about Postel's law and the Liskov substitution principle.

Comments

Any function gives rise to a profunctor. An article for object-oriented programmers.

This article is an instalment in a short article series about profunctors. It assumes that you've read the introduction.

Previous articles in the overall article series on functors and similar abstractions discussed Reader as both a covariant functor, as well as a contravariant functor. As the profunctor introduction intimated, if you combine the properties of both co- and contravariance, you'll have a profunctor.

There's a wide selection of well-known functors and a smaller selection of contravariant functors. Of all those that I've covered so far, only one appears in both lists: Reader.

Reader #

Consider, again, this IReader interface:

public interface IReader<R, A>
{
    A Run(R environment);
}

When discussing IReader as a covariant functor, we'd fix R and let A vary. When discussing the same interface as a contravariant functor, we'd fix A and let R vary. If you allow both to vary freely, you have a profunctor.

As the profunctor overview article asserted, you can implement ContraMap and Select with DiMap, or you can implement DiMap with ContraMap and Select. Since previous articles have supplied both Select and ContraMap for IReader, it's a natural opportunity to see how to implement DiMap:

public static IReader<R1, A1> DiMap<R, R1, A, A1>(
    this IReader<R, A> reader,
    Func<R1, R> contraSelector,
    Func<A, A1> coSelector)
{
    return reader.ContraMap(contraSelector).Select(coSelector);
}

You simply pass contraSelector to ContraMap and coSelector to Select, while chaining the two method calls. You can also flip the order in which you call these two functions - as long as they are both pure functions, it'll make no difference. You'll shortly see an example of flipping the order.

First, though, an example of using DiMap. Imagine that you have this IReader implementation:

public sealed class TotalSecondsReader : IReader<TimeSpan, double>
{
    public double Run(TimeSpan environment)
    {
        return environment.TotalSeconds;
    }
}

This class converts a TimeSpan value into the total number of seconds represented by that duration. You can project this Reader in both directions using DiMap:

[Fact]
public void ReaderDiMapExample()
{
    IReader<TimeSpan, double> reader = new TotalSecondsReader();
    IReader<DateTime, bool> projection =
        reader.DiMap((DateTime dt) => dt.TimeOfDay, d => d % 2 == 0);
    Assert.True(projection.Run(new DateTime(3271, 12, 11, 2, 3, 4)));
}

This example maps the Reader from TimeSpan to DateTime by mapping in the opposite direction: The lambda expression (DateTime dt) => dt.TimeOfDay returns the time of day of a given DateTime. This value is a TimeSpan value representing the time passed since midnight on that date.

The example also checks whether or not a double value is an even number.

When the resulting projection is executed, the expected result is true because the input date and time is first converted to a time of day (02:03:04) by the contraSelector. Then TotalSecondsReader converts that duration to the total number of seconds: 2 * 60 * 60 + 3 * 60 + 4 = 7,384. Finally, 7,384 is an even number, so the output is true.

Raw functions #

As already explained in the previous Reader articles, the IReader interface is mostly a teaching device. In a language where you can treat functions as values, you don't need the interface. In C#, for example, the standard function delegates suffice. You can implement DiMap directly on Func<A, B>:

public static Func<R1, A1> DiMap<R, R1, A, A1>(
    this Func<R, A> func,
    Func<R1, R> contraSelector,
    Func<A, A1> coSelector)
{
    return func.Select(coSelector).ContraMap(contraSelector);
}

As promised, I've here flipped the order of methods in the chain, so that the implementation first calls Select and then ContraMap. This is entirely arbitrary, and I only did it to demonstrate that the order doesn't matter.

Here's another usage example:

[Fact]
public void AreaOfDate()
{
    Func<Version, int> func = v => v.Major + v.Minor * v.Build;
    Func<DateTime, double> projection = func.DiMap(
        (DateTime dt) => new Version(dt.Year, dt.Month, dt.Day),
        i => i * i * Math.PI);
    Assert.Equal(
        expected: 16662407.390443427686297314140028,
        actual: projection(new DateTime(1991, 12, 26)));
}

This example starts with a nonsensical function that calculates a number from a Version value. Using DiMap the example then transforms func into a function that produces a Version from a DateTime and also calculates the area of a circle with the radius i.

Clearly, this isn't a useful piece of code - it only demonstrates how DiMap works.

Identity law #

As stated in the profunctor introduction, I don't intend to make much of the profunctor laws, since they are only reiterations of the (covariant) functor and contravariant functor laws. Still, an example (not a proof) of the profunctor identity law may be in order:

[Fact]
public void ProfunctorIdentityLaw()
{
    Func<Guid, int> byteRange = g => g.ToByteArray().Max() - g.ToByteArray().Min();
 
    T id<T>(T x) => x;
    Func<Guid, int> projected = byteRange.DiMap<Guid, Guid, int, int>(id, id);
 
    var guid = Guid.NewGuid();
    Assert.Equal(byteRange(guid), projected(guid));
}

This example uses another silly function. Given any Guid, the byteRange function calculates the difference between the largest and smallest byte in the value. Projecting this function with the identity function id along both axes should yield a function with the same behaviour. The assertion phase generates an arbitrary Guid and verifies that both byteRange and projected produce the same resulting value.

Haskell #

As usual, I've adopted many of the concepts and ideas from Haskell. The notion of a profunctor is so exotic that, unlike the Contravariant type class, it's not (to my knowledge) part of the base library. Not that I've ever felt the need to import it, but if I did, I would probably use Data.Profunctor. This module defines a Profunctor type class, of which a normal function (->) is an instance. The type class defines the dimap function.

We can replicate the above AreaOfDate example using the Profunctor type class, and the types and functions in the time library.

First, I'll implement func like this:

func :: Num a => (a, a, a) -> a
func (maj, min, bld) = maj + min * bld

Instead of using a Version type (which I'm not sure exists in the 'standard' Haskell libraries) this function just uses a triple (three-tuple).

The projection is a bit more involved:

projection :: Day -> Double
projection =
  dimap
    ((\(maj, min, bld) -> (fromInteger maj, min, bld)) . toGregorian)
    (\i -> toEnum (i * i) * pi)
    func

It basically does the same as the AreaOfDate, but the lambda expressions look more scary because of all the brackets and conversions. Haskell isn't always more succinct than C#.

> projection $ fromGregorian 1991 12 26
1.6662407390443427e7

Notice that GHCi returns the result in scientific notation, so while the decimal separator seems to be oddly placed, the result is the same as in the C# example.

Conclusion #

The Reader functor is not only a (covariant) functor and a contravariant functor. Since it's both, it's also a profunctor. And so what?

This knowledge doesn't seem immediately applicable, but shines an interesting light on the fabric of code. If you squint hard enough, most programming constructs look like functions, and functions are profunctors. I don't intent to go so far as to claim that 'everything is a profunctor', but the Reader profunctor is ubiquitous.

I'll return to this insight in a future article.

Next: Invariant functors.

Functors that are both co- and contravariant. An article for C# programmers.

This article series is part of a larger series of articles about functors, applicatives, and other mappable containers. Particularly, you've seen examples of both functors and contravariant functors.

What happens if you, so to speak, combine those two?

Mapping in both directions #

A profunctor is like a bifunctor, except that it's contravariant in one of its arguments (and covariant in the other). Usually, you'd list the contravariant argument first, and the covariant argument second. By that convention, a hypothetical Profunctor<A, B> would be contravariant in A and covariant in B.

In order to support such mapping, you could give the class a DiMap method:

public sealed class Profunctor<A, B>
{
    public Profunctor<A1, B1> DiMap<A1, B1>(Func<A1, A> contraSelector, Func<B, B1> coSelector)
 
    // ...

Contrary to (covariant) functors, where C# will light up some extra compiler features if you name the mapping method Select, there's no extra language support for profunctors. Thus, you can call the method whatever you like, but here I've chosen the name DiMap just because that's what the Haskell Profunctors package calls the corresponding function.

Notice that in order to map the contravariant type argument A to A1, you must supply a selector that moves in the contrary direction: from A1 to A. Mapping the covariant type argument B to B1, on the other hand, goes in the same direction: from B to B1.

An example might look like this:

Profunctor<TimeSpan, double> profunctor = CreateAProfunctor();
Profunctor<string, bool> projection =
    profunctor.DiMap<string, bool>(TimeSpan.Parse, d => d % 1 == 0);

This example starts with a profunctor where the contravariant type is TimeSpan and the covariant type is double. Using DiMap you can map it to a Profunctor<string, bool>. In order to map the profunctor value's TimeSpan to the projection value's string, the method call supplies TimeSpan.Parse: a (partial) function that maps string to TimeSpan.

The second argument maps the profunctor value's double to the projection value's bool by checking if d is an integer. The lambda expression d => d % 1 == 0 implements a function from double to bool. That is, the profunctor covaries with that function.

Covariant mapping #

Given DiMap you can implement the standard Select method for functors.

public Profunctor<A, B1> Select<B1>(Func<B, B1> selector)
{
    return DiMap<A, B1>(x => x, selector);
}

Equivalently to bifunctors, when you have a function that maps both dimensions, you can map one dimension by using the identity function for the dimension you don't need to map. Here I've used the lambda expression x => x as the identity function.

You can use this Select method with standard method-call syntax:

Profunctor<DateTime, string> profunctor = CreateAProfunctor();
Profunctor<DateTime, int> projection = profunctor.Select(s => s.Length);

or with query syntax:

Profunctor<DateTime, TimeSpan> profunctor = CreateAProfunctor();
Profunctor<DateTime, int> projection = from ts in profunctor
                                       select ts.Minutes;

All profunctors are also covariant functors.

Contravariant mapping #

Likewise, given DiMap you can implement a ContraMap method:

public Profunctor<A1, B> ContraMap<A1>(Func<A1, A> selector)
{
    return DiMap<A1, B>(selector, x => x);
}

Using ContraMap is only possible with normal method-call syntax, since C# has no special understanding of contravariant functors:

Profunctor<long, DateTime> profunctor = CreateAProfunctor();
Profunctor<string, DateTime> projection = profunctor.ContraMap<string>(long.Parse);

All profunctors are also contravariant functors.

While you can implement Select and ContraMap from DiMap, it's also possible to go the other way. If you have Select and ContraMap you can implement DiMap.

Laws #

In the overall article series, I've focused on the laws that govern various universal abstractions. In this article, I'm going to treat this topic lightly, since it'd mostly be a reiteration of the laws that govern co- and contravariant functors.

The only law I'll highlight is the profunctor identity law, which intuitively is a generalisation of the identity laws for co- and contravariant functors. If you map a profunctor in both dimensions, but use the identity function in both directions, nothing should change:

Profunctor<Guid, string> profunctor = CreateAProfunctor();
Profunctor<Guid, string> projection = profunctor.DiMap((Guid g) => g, s => s);

Here I've used two lambda expressions to implement the identity function. While they're two different lambda expressions, they both 'implement' the general identity function. If you aren't convinced, we can demonstrate the idea like this instead:

T id<T>(T x) => x;
Profunctor<Guid, string> profunctor = CreateAProfunctor();
Profunctor<Guid, string> projection = profunctor.DiMap<Guid, string>(id, id);

This alternative representation defines a local function called id. Since it's generic, you can use it as both arguments to DiMap.

The point of the identity law is that in both cases, projection should be equal to profunctor.

Usefulness #

Are profunctors useful in everyday programming? So far, I've found no particular use for them. This mirrors my experience with contravariant functors, which I also find little use for. Why should we care, then?

It turns out that, while we rarely work explicitly with profunctors, they're everywhere. Normal functions are profunctors.

• Reader as a profunctor

In addition to normal functions (which are both covariant and contravariant) other profunctors exist. At the time that I'm writing this article, I've no particular plans to add articles about any other profunctors, but if I do, I'll add them to the above list. Examples include Kleisli arrows and profunctor optics.

The reason I find it worthwhile to learn about profunctors is that this way of looking at well-behaved functions shines an interesting light on the fabric of computation, so to speak. In a future article, I'll expand on that topic.

Conclusion #

A profunctor is a functor that is covariant in one dimension and contravariant in another dimension. While various exotic examples exist, the only example that you'd tend to encounter in mainstream programming is the Reader profunctor, also known simply as functions.

Next: Reader as a profunctor.

Comments

A note on C# co- and contravariance, and how it relates to functors.

This article is an instalment in an article series about contravariant functors. It assumes that you've read the introduction, and a few of the examples.

If you know your way around C# you may know that the language has its own notion of co- and contravariance. Perhaps you're wondering how it fits with contravariant functors.

Quite well, fortunately.

Assignment compatibility #

For the C# perspective on co- and contravariance, the official documentation is already quite good. It starts with this example of assignment compatibility:

// Assignment compatibility.
string str = "test";
// An object of a more derived type is assigned to an object of a less derived type.
object obj = str;

This kind of assignment is always possible, because a string is also already an object. An upcast within the inheritance hierarchy is always possible, so C# automatically allows it.

F#, on the other hand, doesn't. If you try to do something similar in F#, it doesn't compile:

let str = "test"
let obj : obj = str // Doesn't compile

The compiler error is:

This expression was expected to have type 'obj' but here has type 'string'

You have to explicitly use the upcast operator:

let str = "test"
let obj = str :> obj

When you do that, the explicit type declaration of the value is redundant, so I removed it.

In this example, you can think of :> as a function from string to obj: string -> obj. In C#, the equivalent function would be Func<string, object>.

These functions always exist for types that are properly related to each other, upcast-wise. You can think of it as a generic function 'a -> 'b (or Func<A, B>), with the proviso that A must be 'upcastable' to B:

In my head, I'd usually think about this as A being a subtype of B, but unless I explain what I mean by subtyping, it usually confuses people. I consider anything that can 'act as' something else a subtype. So string is a subtype of object, but I also consider TimeSpan a subtype of IComparable, because that cast is also always possible:

TimeSpan twoMinutes = TimeSpan.FromMinutes(2);
IComparable comp = twoMinutes;

Once again, F# is only happy if you explicitly use the :> operator:

let twoMinutes = TimeSpan.FromMinutes 2.
let comp = twoMinutes :> IComparable

All this is surely old hat to any .NET developer with a few months of programming under his or her belt. All the same, I want to drive home one last point (that you already know): Automatic upcast conversions are transitive. Consider a class like HttpStyleUriParser, which is part of a small inheritance hierarchy: object -> UriParser -> HttpStyleUriParser (sic, that's how the documentation denotes the inheritance hierarchy; be careful about the arrow direction!). You can upcast an HttpStyleUriParser to both UriParser and object:

HttpStyleUriParser httParser = new HttpStyleUriParser();
UriParser parser = httParser;
object op = httParser;

Again, the same is true in F#, but you have to explicitly use the :> operator.

To recapitulate: C# has a built-in automatic conversion that upcasts. It's also built into F#, but here as an operator that you explicitly have to use. It's like an automatic function from subtype to supertype.

Covariance #

The C# documentation continues with an example of covariance:

// Covariance.
IEnumerable<string> strings = new List<string>();
// An object that is instantiated with a more derived type argument
// is assigned to an object instantiated with a less derived type argument.
// Assignment compatibility is preserved.
IEnumerable<object> objects = strings;

Since IEnumerable<T> forms a (covariant) functor you can lift a function Func<A, B> to a function from IEnumerable<A> to IEnumerable<B>. Consider the above example that goes from IEnumerable<string> to IEnumerable<object>. Let's modify the diagram from the functor article:

Since the C# compiler already knows that an automatic function (:>) exists that converts string to object, it can automatically convert IEnumerable<string> to IEnumerable<object>. You don't have to call Select to do this. The compiler does it for you.

How does it do that?

It looks for a little annotation on the generic type argument. For covariant types, the relevant keyword is out. And, as expected, the T in IEnumerable<T> is annotated with out:

public interface IEnumerable<out T>

The same is true for Func<T, TResult>, which is both covariant and contravariant:

public delegate TResult Func<in T, out TResult>(T arg);

The in keyword denotes contravariance, but we'll get to that shortly.

The reason that covariance is annotated with the out keyword is that covariant type arguments usually sit in the return-type position. The rule is actually a little more nuanced than that, but I'll again refer you to Sandy Maguire's excellent book Thinking with Types if you're interested in the details.

Contravariance #

So far, so good. What about contravariance? The C# documentation continues its example:

// Contravariance.
// Assume that the following method is in the class:
// static void SetObject(object o) { }
Action<object> actObject = SetObject;
// An object that is instantiated with a less derived type argument
// is assigned to an object instantiated with a more derived type argument.
// Assignment compatibility is reversed.
Action<string> actString = actObject;

The Action<T> delegate gives rise to a contravariant functor. The T is also annotated with the in keyword, since the type argument sits in the input position:

public delegate void Action<in T>(T obj)

Again, let's modify the diagram from the article about contravariant functors:

Again, since the C# compiler already knows that an automatic function exists that converts string to object, it can automatically convert Action<object> to Action<string>. You don't have to call Contramap to do this. The compiler does it for you.

It knows that Action<T> is contravariant because it's annotated with the in keyword. Thus, it allows contravariant assignment.

It all checks out.

Conclusion #

The C# compiler understands co- and contravariance, but while it automatically supports it, it only deals with automatic conversion from subtype to supertype. Thus, for those kinds of conversions, you don't need a Select or ContraMap method.

The functor notion of co- and contravariance is a generalisation of how the C# compiler works. Instead of relying on automatic conversions, the Select and ContraMap methods enable you to supply arbitrary conversion functions.

Next: Contravariant Dependency Injection.