Bifunctors by Mark Seemann
Bifunctors are like functors, only they vary in two dimensions instead of one. An article for object-oriented programmers.
This article is a continuation of the article series about functors and about applicative functors. In this article, you'll learn about a generalisation called a bifunctor. The prefix bi typically indicates that there's two of something, and that's also the case here.
As you've already seen in the functor articles, a functor is a mappable container of generic values, like Foo<T>, where the type of the contained value(s) can be any generic type T. A bifunctor is just a container with two independent generic types, like Bar<T, U>. If you can map each of the types independently of the other, you may have a bifunctor.
The two most common bifunctors are tuples and Either.
Maps #
A normal functor is based on a structure-preserving map of the contents within a container. You can, for example, translate an IEnumerable<int> to an IEnumerable<string>, or a Maybe<DateTime> to a Maybe<bool>. The axis of variability is the generic type argument T. You can translate T1 to T2 inside a container, but the type of the container remains the same: you can translate Tree<T1> to Tree<T2>, but it remains a Tree<>.

A bifunctor involves a pair of maps, one for each generic type. You can map a Bar<string, int> to a Bar<bool, int>, or to a Bar<string, DateTime>, or even to a Bar<bool, DateTime>. Notice that the last example, mapping from Bar<string, int> to Bar<bool, DateTime> could be viewed as translating both axes simultaneously.
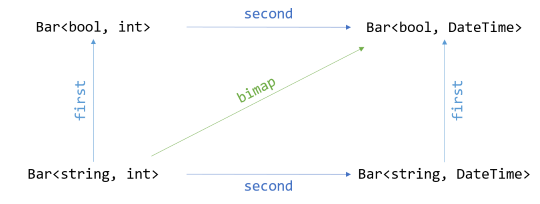
In Haskell, the two maps are called first and second, while the 'simultaneous' map is called bimap.
The first translation translates the first, or left-most, value in the container. You can use it to map Bar<string, int> to a Bar<bool, int>. In C#, we could decide to call the method SelectFirst, or SelectLeft, in order to align with the C# naming convention of calling the functor morphism Select.
Likewise, the second map translates the second, or right-most, value in the container. This is where you map Bar<string, int> to Bar<string, DateTime>. In C#, we could call the method SelectSecond, or SelectRight.
The bimap function maps both values in the container in one go. This corresponds to a translation from Bar<string, int> to Bar<bool, DateTime>. In C#, we could call the method SelectBoth. There's no established naming conventions for bifunctors in C# that I know of, so these names are just some that I made up.
You'll see examples of how to implement and use such functions in the next articles:
Other bifunctors exist, but the first two are the most common.Identity laws #
As is the case with functors, laws govern bifunctors. Some of the functor laws carry over, but are simply repeated over both axes, while other laws are generalisations of the functor laws. For example, the first functor law states that if you translate a container with the identity function, the result is the original input. This generalises to bifunctors as well:
bimap id id ≡ id
This just states that if you translate both axes using the endomorphic Identity, it's equivalent to applying the Identity.

Using C# syntax, you could express the law like this:
bf.SelectBoth(id, id) == bf;
Here, bf is some bifunctor, and id is the identity function. The point is that if you translate over both axes, but actually don't perform a real translation, nothing happens.
Likewise, if you consider a bifunctor a functor over two dimensions, the first functor law should hold for both:
first id ≡ id second id ≡ id
Both of those equalities only restate the first functor law for each dimension. If you map an axis with the identity function, nothing happens:
In C#, you can express both laws like this:
bf.SelectFirst(id) == bf; bf.SelectSecond(id) == bf;
When calling SelectFirst, you translate only the first axis while you keep the second axis constant. When calling SelectSecond it's the other way around: you translate only the second axis while keeping the first axis constant. In both cases, though, if you use the identity function for the translation, you effectively keep the mapped dimension constant as well. Therefore, one would expect the result to be the same as the input.
Consistency law #
As you'll see in the articles on tuple and Either bifunctors, you can derive bimap or SelectBoth from first/SelectFirst and second/SelectSecond, or the other way around. If, however, you decide to implement all three functions, they must act in a consistent manner. The name Consistency law, however, is entirely my own invention. If it has a more well-known name, I'm not aware of it.
In pseudo-Haskell syntax, you can express the law like this:
bimap f g ≡ first f . second g
This states that mapping (using the functions f and g) simultaneously should produce the same result as mapping using an intermediary step:
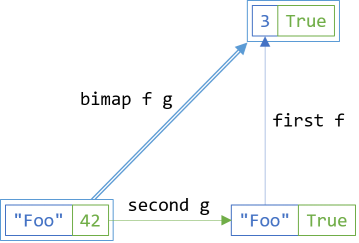
In C#, you could express it like this:
bf.SelectBoth(f, g) == bf.SelectSecond(g).SelectFirst(f);
You can project the input bifunctor bf using both f and g in a single step, or you can first translate the second dimension with g and then subsequently map that intermediary result along the first axis with f.
The above diagram ought to commute:
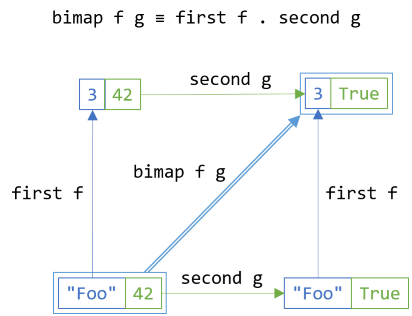
It shouldn't matter whether the intermediary step is applying f along the first axis or g along the second axis. In C#, we can write it like this:
bf.SelectFirst(f).SelectSecond(g) == bf.SelectSecond(g).SelectFirst(f);
On the left-hand side, you first translate the bifunctor bf along the first axis, using f, and then translate that intermediary result along the second axis, using g. On the right-hand side, you first project bf along the second axis, using g, and then map that intermediary result over the first dimension, using f.
Regardless of order of translation, the result should be the same.
Composition laws #
Similar to how the first functor law generalises to bifunctors, the second functor law generalises as well. For (mono)functors, the second functor law states that if you have two functions over the same dimension, it shouldn't matter whether you perform a projection in one, composed step, or in two steps with an intermediary result.
For bifunctors, you can generalise that law and state that you can project over both dimensions in one or two steps:
bimap (f . g) (h . i) ≡ bimap f h . bimap g i
If you have two functions, f and g, that compose, and two other functions, h and i, that also compose, you can translate in either one or two steps; the result should be the same.
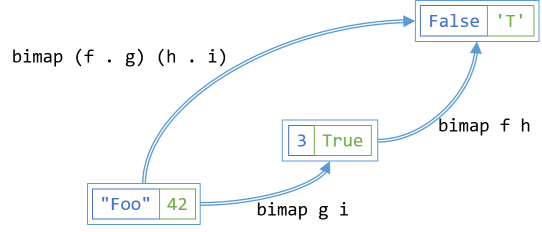
In C#, you can express the law like this:
bf.SelectBoth(x => f(g(x)), y => h(i(y))) == bf.SelectBoth(g, i).SelectBoth(f, h);
On the left-hand side, the first dimension is translated in one step. For each x contained in bf, the translation first invokes g(x), and then immediately calls f with the output of g(x). The second dimension also gets translated in one step. For each y contained in bf, the translation first invokes i(y), and then immediately calls h with the output of i(y).
On the right-hand side, you first translate bf along both axes using g and i. This produces an intermediary result that you can use as input for a second translation with f and h.
The translation on the left-hand side should produce the same output as the right-hand side.
Finally, if you keep one of the dimensions fixed, you essentially have a normal functor, and the second functor law should still hold. For example, if you hold the second dimension fixed, translating over the first dimension is equivalent to a normal functor projection, so the second functor law should hold:
first (f . g) ≡ first f . first g
If you replace first with fmap, you have the second functor law.
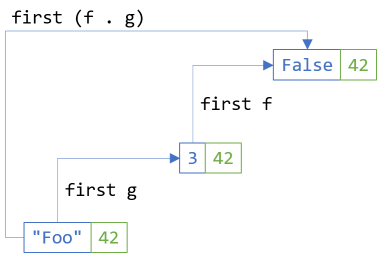
In C#, you can write it like this:
bf.SelectFirst(x => f(g(x))) == bf.SelectFirst(g).SelectFirst(f);
Likewise, you can keep the first dimension constant and apply the second functor law to projections along the second axis:
second (f . g) ≡ second f . second g
Again, if you replace second with fmap, you have the second functor law.
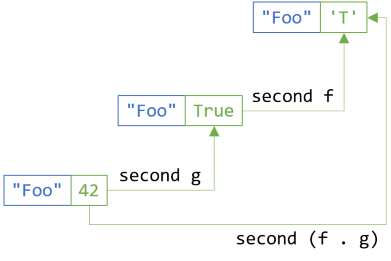
In C#, you express it like this:
bf.SelectSecond(x => f(g(x))) == bf.SelectSecond(g).SelectSecond(f);
The last two of these composition laws are specialisations of the general composition law, but where you fix either one or the other dimension.
Summary #
A bifunctor is a container that can be translated over two dimensions, instead of a (mono)functor, which is a container that can be translated over a single dimension. In reality, there isn't a multitude of different bifunctors. While others exist, tuples and Either are the two most common bifunctors. They share an abstraction, but are still fundamentally different. A tuple always contains values of both dimensions at the same time, whereas Either only contains one of the values.
Do trifunctors, quadfunctors, and so on, exist? Nothing prevents that, but they aren't particularly useful; in practice, you never run into them.
Next: Tuple bifunctor.
