ploeh blog danish software design
A restaurant sandwich
An Impureim Sandwich example in C#.
When learning functional programming (FP) people often struggle with how to organize code. How do you discern and maintain purity? How do you do Dependency Injection in FP? What does a functional architecture look like?
A common FP design pattern is the Impureim Sandwich. The entry point of an application is always impure, so you push all impure actions to the boundary of the system. This is also known as Functional Core, Imperative Shell. If you have a micro-operation-based architecture, which includes all web-based systems, you can often get by with a 'sandwich'. Perform impure actions to collect all the data you need. Pass all data to a pure function. Finally, use impure actions to handle the referentially transparent return value from the pure function.
No design pattern applies universally, and neither does this one. In my experience, however, it's surprisingly often possible to apply this architecture. We're far past the Pareto principle's 80 percent.
Examples may help illustrate the pattern, as well as explore its boundaries. In this article you'll see how I refactored an entry point of a REST API, specifically the PUT handler in the sample code base that accompanies Code That Fits in Your Head.
Starting point #
As discussed in the book, the architecture of the sample code base is, in fact, Functional Core, Imperative Shell. This isn't, however, the main theme of the book, and the code doesn't explicitly apply the Impureim Sandwich. In spirit, that's actually what's going on, but it isn't clear from looking at the code. This was a deliberate choice I made, because I wanted to highlight other software engineering practices. This does have the effect, though, that the Impureim Sandwich is invisible.
For example, the book follows the 80/24 rule closely. This was a didactic choice on my part. Most code bases I've seen in the wild have far too big methods, so I wanted to hammer home the message that it's possible to develop and maintain a non-trivial code base with small code blocks. This meant, however, that I had to split up HTTP request handlers (in ASP.NET known as action methods on Controllers).
The most complex HTTP handler is the one that handles PUT requests for reservations. Clients use this action when they want to make changes to a restaurant reservation.
The action method actually invoked by an HTTP request is this Put method:
[HttpPut("restaurants/{restaurantId}/reservations/{id}")] public async Task<ActionResult> Put( int restaurantId, string id, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); if (!Guid.TryParse(id, out var rid)) return new NotFoundResult(); Reservation? reservation = dto.Validate(rid); if (reservation is null) return new BadRequestResult(); var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); return await TryUpdate(restaurant, reservation).ConfigureAwait(false); }
Since I, for pedagogical reasons, wanted to fit each method inside an 80x24 box, I made a few somewhat unnatural design choices. The above code is one of them. While I don't consider it completely indefensible, this method does a bit of up-front input validation and verification, and then delegates execution to the TryUpdate method.
This may seem all fine and dandy until you realize that the only caller of TryUpdate is that Put method. A similar thing happens in TryUpdate: It calls a method that has only that one caller. We may try to inline those two methods to see if we can spot the Impureim Sandwich.
Inlined Transaction Script #
Inlining those two methods leave us with a larger, Transaction Script-like entry point:
[HttpPut("restaurants/{restaurantId}/reservations/{id}")] public async Task<ActionResult> Put( int restaurantId, string id, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); if (!Guid.TryParse(id, out var rid)) return new NotFoundResult(); Reservation? reservation = dto.Validate(rid); if (reservation is null) return new BadRequestResult(); var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); using var scope = new TransactionScope( TransactionScopeAsyncFlowOption.Enabled); var existing = await Repository .ReadReservation(restaurant.Id, reservation.Id) .ConfigureAwait(false); if (existing is null) return new NotFoundResult(); var reservations = await Repository .ReadReservations(restaurant.Id, reservation.At) .ConfigureAwait(false); reservations = reservations.Where(r => r.Id != reservation.Id).ToList(); var now = Clock.GetCurrentDateTime(); var ok = restaurant.MaitreD.WillAccept( now, reservations, reservation); if (!ok) return NoTables500InternalServerError(); await Repository.Update(restaurant.Id, reservation) .ConfigureAwait(false); scope.Complete(); return new OkObjectResult(reservation.ToDto()); }
While I've definitely seen longer methods in the wild, this variation is already so big that it no longer fits on my laptop screen. I have to scroll up and down to read the whole thing. When looking at the bottom of the method, I have to remember what was at the top, because I can no longer see it.
A major point of Code That Fits in Your Head is that what limits programmer productivity is human cognition. If you have to scroll your screen because you can't see the whole method at once, does that fit in your brain? Chances are, it doesn't.
Can you spot the Impureim Sandwich now?
If you can't, that's understandable. It's not really clear because there's quite a few small decisions being made in this code. You could argue, for example, that this decision is referentially transparent:
if (existing is null) return new NotFoundResult();
These two lines of code are deterministic and have no side effects. The branch only returns a NotFoundResult when existing is null. Additionally, these two lines of code are surrounded by impure actions both before and after. Is this the Sandwich, then?
No, it's not. This is how idiomatic imperative code looks. To borrow a diagram from another article, pure and impure code is interleaved without discipline:

Even so, the above Put method implements the Functional Core, Imperative Shell architecture. The Put method is the Imperative Shell, but where's the Functional Core?
Shell perspective #
One thing to be aware of is that when looking at the Imperative Shell code, the Functional Core is close to invisible. This is because it's typically only a single function call.
In the above Put method, this is the Functional Core:
var ok = restaurant.MaitreD.WillAccept( now, reservations, reservation); if (!ok) return NoTables500InternalServerError();
It's only a few lines of code, and had I not given myself the constraint of staying within an 80 character line width, I could have instead laid it out like this and inlined the ok flag:
if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError();
Now that I try this, in fact, it turns out that this actually still stays within 80 characters. To be honest, I don't know exactly why I had that former code instead of this, but perhaps I found the latter alternative too dense. Or perhaps I simply didn't think of it. Code is rarely perfect. Usually when I revisit a piece of code after having been away from it for some time, I find some thing that I want to change.
In any case, that's beside the point. What matters here is that when you're looking through the Imperative Shell code, the Functional Core looks insignificant. Blink and you'll miss it. Even if we ignore all the other small pure decisions (the if statements) and pretend that we already have an Impureim Sandwich, from this viewpoint, the architecture looks like this:

It's tempting to ask, then: What's all the fuss about? Why even bother?
This is a natural experience for a code reader. After all, if you don't know a code base well, you often start at the entry point to try to understand how the application handles a certain stimulus. Such as an HTTP PUT request. When you do that, you see all of the Imperative Shell code before you see the Functional Core code. This could give you the wrong impression about the balance of responsibility.
After all, code like the above Put method has inlined most of the impure code so that it's right in your face. Granted, there's still some code hiding behind, say, Repository.ReadReservations, but a substantial fraction of the imperative code is visible in the method.
On the other hand, the Functional Core is just a single function call. If we inlined all of that code, too, the picture might rather look like this:

This obviously depends on the de-facto ratio of pure to imperative code. In any case, inlining the pure code is a thought experiment only, because the whole point of functional architecture is that a referentially transparent function fits in your head. Regardless of the complexity and amount of code hiding behind that MaitreD.WillAccept function, the return value is equal to the function call. It's the ultimate abstraction.
Standard combinators #
As I've already suggested, the inlined Put method looks like a Transaction Script. The cyclomatic complexity fortunately hovers on the magical number seven, and branching is exclusively organized around Guard Clauses. Apart from that, there are no nested if statements or for loops.
Apart from the Guard Clauses, this mostly looks like a procedure that runs in a straight line from top to bottom. The exception is all those small conditionals that may cause the procedure to exit prematurely. Conditions like this:
if (!Guid.TryParse(id, out var rid)) return new NotFoundResult();
or
if (reservation is null) return new BadRequestResult();
Such checks occur throughout the method. Each of them are actually small pure islands amidst all the imperative code, but each is ad hoc. Each checks if it's possible for the procedure to continue, and returns a kind of error value if it decides that it's not.
Is there a way to model such 'derailments' from the main flow?
If you've ever encountered Scott Wlaschin's Railway Oriented Programming you may already see where this is going. Railway-oriented programming is a fantastic metaphor, because it gives you a way to visualize that you have, indeed, a main track, but then you have a side track that you may shuffle some trains too. And once the train is on the side track, it can't go back to the main track.
That's how the Either monad works. Instead of all those ad-hoc if statements, we should be able to replace them with what we may call standard combinators. The most important of these combinators is monadic bind. Composing a Transaction Script like Put with standard combinators will 'hide away' those small decisions, and make the Sandwich nature more apparent.
If we had had pure code, we could just have composed Either-valued functions. Unfortunately, most of what's going on in the Put method happens in a Task-based context. Thankfully, Either is one of those monads that nest well, implying that we can turn the combination into a composed TaskEither monad. The linked article shows the core TaskEither SelectMany implementations.
The way to encode all those small decisions between 'main track' or 'side track', then, is to wrap 'naked' values in the desired Task<Either<L, R>> container:
Task.FromResult(id.TryParseGuid().OnNull((ActionResult)new NotFoundResult()))
This little code snippet makes use of a few small building blocks that we also need to introduce. First, .NET's standard TryParse APIs don't, compose, but since they're isomorphic to Maybe-valued functions, you can write an adapter like this:
public static Guid? TryParseGuid(this string candidate) { if (Guid.TryParse(candidate, out var guid)) return guid; else return null; }
In this code base, I treat nullable reference types as equivalent to the Maybe monad, but if your language doesn't have that feature, you can use Maybe instead.
To implement the Put method, however, we don't want nullable (or Maybe) values. We need Either values, so we may introduce a natural transformation:
public static Either<L, R> OnNull<L, R>(this R? candidate, L left) where R : struct { if (candidate.HasValue) return Right<L, R>(candidate.Value); return Left<L, R>(left); }
In Haskell one might just make use of the built-in Maybe catamorphism:
ghci> maybe (Left "boo!") Right $ Just 123 Right 123 ghci> maybe (Left "boo!") Right $ Nothing Left "boo!"
Such conversions from Maybe to Either hover just around the Fairbairn threshold, but since we are going to need it more than once, it makes sense to add a specialized OnNull transformation to the C# code base. The one shown here handles nullable value types, but the code base also includes an overload that handles nullable reference types. It's almost identical.
Support for query syntax #
There's more than one way to consume monadic values in C#. While many C# developers like LINQ, most seem to prefer the familiar method call syntax; that is, just call the Select, SelectMany, and Where methods as the normal extension methods they are. Another option, however, is to use query syntax. This is what I'm aiming for here, since it'll make it easier to spot the Impureim Sandwich.
You'll see the entire sandwich later in the article. Before that, I'll highlight details and explain how to implement them. You can always scroll down to see the end result, and then scroll back here, if that's more to your liking.
The sandwich starts by parsing the id into a GUID using the above building blocks:
var sandwich = from rid in Task.FromResult(id.TryParseGuid().OnNull((ActionResult)new NotFoundResult()))
It then immediately proceeds to Validate (parse, really) the dto into a proper Domain Model:
from reservation in dto.Validate(rid).OnNull((ActionResult)new BadRequestResult())
Notice that the second from expression doesn't wrap the result with Task.FromResult. How does that work? Is the return value of dto.Validate already a Task? No, this works because I added 'degenerate' SelectMany overloads:
public static Task<Either<L, R1>> SelectMany<L, R, R1>( this Task<Either<L, R>> source, Func<R, Either<L, R1>> selector) { return source.SelectMany(x => Task.FromResult(selector(x))); } public static Task<Either<L, R1>> SelectMany<L, U, R, R1>( this Task<Either<L, R>> source, Func<R, Either<L, U>> k, Func<R, U, R1> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
Notice that the selector only produces an Either<L, R1> value, rather than Task<Either<L, R1>>. This allows query syntax to 'pick up' the previous value (rid, which is 'really' a Task<Either<ActionResult, Guid>>) and continue with a function that doesn't produce a Task, but rather just an Either value. The first of these two overloads then wraps that Either value and wraps it with Task.FromResult. The second overload is just the usual ceremony that enables query syntax.
Why, then, doesn't the sandwich use the same trick for rid? Why does it explicitly call Task.FromResult?
As far as I can tell, this is because of type inference. It looks as though the C# compiler infers the monad's type from the first expression. If I change the first expression to
from rid in id.TryParseGuid().OnNull((ActionResult)new NotFoundResult())
the compiler thinks that the query expression is based on Either<L, R>, rather than Task<Either<L, R>>. This means that once we run into the first Task value, the entire expression no longer works.
By explicitly wrapping the first expression in a Task, the compiler correctly infers the monad we'd like it to. If there's a more elegant way to do this, I'm not aware of it.
Values that don't fail #
The sandwich proceeds to query various databases, using the now-familiar OnNull combinators to transform nullable values to Either values.
from restaurant in RestaurantDatabase .GetRestaurant(restaurantId) .OnNull((ActionResult)new NotFoundResult()) from existing in Repository .ReadReservation(restaurant.Id, reservation.Id) .OnNull((ActionResult)new NotFoundResult())
This works like before because both GetRestaurant and ReadReservation are queries that may fail to return a value. Here's the interface definition of ReadReservation:
Task<Reservation?> ReadReservation(int restaurantId, Guid id);
Notice the question mark that indicates that the result may be null.
The GetRestaurant method is similar.
The next query that the sandwich has to perform, however, is different. The return type of the ReadReservations method is Task<IReadOnlyCollection<Reservation>>. Notice that the type contained in the Task is not nullable. Barring database connection errors, this query can't fail. If it finds no data, it returns an empty collection.
Since the value isn't nullable, we can't use OnNull to turn it into a Task<Either<L, R>> value. We could try to use the Right creation function for that.
public static Either<L, R> Right<L, R>(R right) { return Either<L, R>.Right(right); }
This works, but is awkward:
from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => Either.Right<ActionResult, IReadOnlyCollection<Reservation>>(rs))
The problem with calling Either.Right is that while the compiler can infer which type to use for R, it doesn't know what the L type is. Thus, we have to tell it, and we can't tell it what L is without also telling it what R is. Even though it already knows that.
In such scenarios, the F# compiler can usually figure it out, and GHC always can (unless you add some exotic language extensions to your code). C# doesn't have any syntax that enables you to tell the compiler about only the type that it doesn't know about, and let it infer the rest.
All is not lost, though, because there's a little trick you can use in cases such as this. You can let the C# compiler infer the R type so that you only have to tell it what L is. It's a two-stage process. First, define an extension method on R:
public static RightBuilder<R> ToRight<R>(this R right) { return new RightBuilder<R>(right); }
The only type argument on this ToRight method is R, and since the right parameter is of the type R, the C# compiler can always infer the type of R from the type of right.
What's RightBuilder<R>? It's this little auxiliary class:
public sealed class RightBuilder<R> { private readonly R right; public RightBuilder(R right) { this.right = right; } public Either<L, R> WithLeft<L>() { return Either.Right<L, R>(right); } }
The code base for Code That Fits in Your Head was written on .NET 3.1, but today you could have made this a record instead. The only purpose of this class is to break the type inference into two steps so that the R type can be automatically inferred. In this way, you only need to tell the compiler what the L type is.
from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => rs.ToRight().WithLeft<ActionResult>())
As indicated, this style of programming isn't language-neutral. Even if you find this little trick neat, I'd much rather have the compiler just figure it out for me. The entire sandwich query expression is already defined as working with Task<Either<ActionResult, R>>, and the L type can't change like the R type can. Functional compilers can figure this out, and while I intend this article to show object-oriented programmers how functional programming sometimes work, I don't wish to pretend that it's a good idea to write code like this in C#. I've covered that ground already.
Not surprisingly, there's a mirror-image ToLeft/WithRight combo, too.
Working with Commands #
The ultimate goal with the Put method is to modify a row in the database. The method to do that has this interface definition:
Task Update(int restaurantId, Reservation reservation);
I usually call that non-generic Task class for 'asynchronous void' when explaining it to non-C# programmers. The Update method is an asynchronous Command.
Task and void aren't legal values for use with LINQ query syntax, so you have to find a way to work around that limitation. In this case I defined a local helper method to make it look like a Query:
async Task<Reservation> RunUpdate(int restaurantId, Reservation reservation, TransactionScope scope) { await Repository.Update(restaurantId, reservation).ConfigureAwait(false); scope.Complete(); return reservation; }
It just echoes back the reservation parameter once the Update has completed. This makes it composable in the larger query expression.
You'll probably not be surprised when I tell you that both F# and Haskell handle this scenario gracefully, without requiring any hoop-jumping.
Full sandwich #
Those are all the building block. Here's the full sandwich definition, colour-coded like the examples in Impureim sandwich.
Task<Either<ActionResult, OkObjectResult>> sandwich = from rid in Task.FromResult( id.TryParseGuid().OnNull((ActionResult)new NotFoundResult())) from reservation in dto.Validate(rid).OnNull( (ActionResult)new BadRequestResult()) from restaurant in RestaurantDatabase .GetRestaurant(restaurantId) .OnNull((ActionResult)new NotFoundResult()) from existing in Repository .ReadReservation(restaurant.Id, reservation.Id) .OnNull((ActionResult)new NotFoundResult()) from reservations in Repository .ReadReservations(restaurant.Id, reservation.At) .Traverse(rs => rs.ToRight().WithLeft<ActionResult>()) let now = Clock.GetCurrentDateTime() let reservations2 = reservations.Where(r => r.Id != reservation.Id) let ok = restaurant.MaitreD.WillAccept( now, reservations2, reservation) from reservation2 in ok ? reservation.ToRight().WithLeft<ActionResult>() : NoTables500InternalServerError().ToLeft().WithRight<Reservation>() from reservation3 in RunUpdate(restaurant.Id, reservation2, scope) .Traverse(r => r.ToRight().WithLeft<ActionResult>()) select new OkObjectResult(reservation3.ToDto());
As is evident from the colour-coding, this isn't quite a sandwich. The structure is honestly more accurately depicted like this:

As I've previously argued, while the metaphor becomes strained, this still works well as a functional-programming architecture.
As defined here, the sandwich value is a Task that must be awaited.
Either<ActionResult, OkObjectResult> either = await sandwich.ConfigureAwait(false); return either.Match(x => x, x => x);
By awaiting the task, we get an Either value. The Put method, on the other hand, must return an ActionResult. How do you turn an Either object into a single object?
By pattern matching on it, as the code snippet shows. The L type is already an ActionResult, so we return it without changing it. If C# had had a built-in identity function, I'd used that, but idiomatically, we instead use the x => x lambda expression.
The same is the case for the R type, because OkObjectResult inherits from ActionResult. The identity expression automatically performs the type conversion for us.
This, by the way, is a recurring pattern with Either values that I run into in all languages. You've essentially computed an Either<T, T>, with the same type on both sides, and now you just want to return whichever T value is contained in the Either value. You'd think this is such a common pattern that Haskell has a nice abstraction for it, but even Hoogle fails to suggest a commonly-accepted function that does this. Apparently, either id id is considered below the Fairbairn threshold, too.
Conclusion #
This article presents an example of a non-trivial Impureim Sandwich. When I introduced the pattern, I gave a few examples. I'd deliberately chosen these examples to be simple so that they highlighted the structure of the idea. The downside of that didactic choice is that some commenters found the examples too simplistic. Therefore, I think that there's value in going through more complex examples.
The code base that accompanies Code That Fits in Your Head is complex enough that it borders on the realistic. It was deliberately written that way, and since I assume that the code base is familiar to readers of the book, I thought it'd be a good resource to show how an Impureim Sandwich might look. I explicitly chose to refactor the Put method, since it's easily the most complicated process in the code base.
The benefit of that code base is that it's written in a programming language that reach a large audience. Thus, for the reader curious about functional programming I thought that this could also be a useful introduction to some intermediate concepts.
As I've commented along the way, however, I wouldn't expect anyone to write production C# code like this. If you're able to do this, you're also able to do it in a language better suited for this programming paradigm.
Implementation and usage mindsets
A one-dimensional take on the enduring static-versus-dynamic debate.
It recently occurred to me that one possible explanation for the standing, and probably never-ending, debate about static versus dynamic types may be that each camp have disjoint perspectives on the kinds of problems their favourite languages help them solve. In short, my hypothesis is that perhaps lovers of dynamically-typed languages often approach a problem from an implementation mindset, whereas proponents of static types emphasize usage.

I'll expand on this idea here, and then provide examples in two subsequent articles.
Background #
For years I've struggled to understand 'the other side'. While I'm firmly in the statically typed camp, I realize that many highly skilled programmers and thought leaders enjoy, or get great use out of, dynamically typed languages. This worries me, because it might indicate that I'm stuck in a local maximum.
In other words, just because I, personally, prefer static types, it doesn't follow that static types are universally better than dynamic types.
In reality, it's probably rather the case that we're dealing with a false dichotomy, and that the problem is really multi-dimensional.
"Let me stop you right there: I don't think there is a real dynamic typing versus static typing debate.
"What such debates normally are is language X vs language Y debates (where X happens to be dynamic and Y happens to be static)."
Even so, I can't help thinking about such things. Am I missing something?
For the past few years, I've dabbled with Python to see what writing in a popular dynamically typed language is like. It's not a bad language, and I can clearly see how it's attractive. Even so, I'm still frustrated every time I return to some Python code after a few weeks or more. The lack of static types makes it hard for me to pick up, or revisit, old code.
A question of perspective? #
Whenever I run into a difference of opinion, I often interpret it as a difference in perspective. Perhaps it's my academic background as an economist, but I consider it a given that people have different motivations, and that incentives influence actions.
A related kind of analysis deals with problem definitions. Are we even trying to solve the same problem?
I've discussed such questions before, but in a different context. Here, it strikes me that perhaps programmers who gravitate toward dynamically typed languages are focused on another problem than the other group.
Again, I'd like to emphasize that I don't consider the world so black and white in reality. Some developers straddle the two camps, and as the above Kevlin Henney quote suggests, there really aren't only two kinds of languages. C and Haskell are both statically typed, but the similarities stop there. Likewise, I don't know if it's fair to put JavaScript and Clojure in the same bucket.
That said, I'd still like to offer the following hypothesis, in the spirit that although all models are wrong, some are useful.
The idea is that if you're trying to solve a problem related to implementation, dynamically typed languages may be more suitable. If you're trying to implement an algorithm, or even trying to invent one, a dynamic language seems useful. One year, I did a good chunk of Advent of Code in Python, and didn't find it harder than in Haskell. (I ultimately ran out of steam for reasons unrelated to Python.)
On the other hand, if your main focus may be usage of your code, perhaps you'll find a statically typed language more useful. At least, I do. I can use the static type system to communicate how my APIs work. How to instantiate my classes. How to call my functions. How return values are shaped. In other words, the preconditions, invariants, and postconditions of my reusable code: Encapsulation.
Examples #
Some examples may be in order. In the next two articles, I'll first examine how easy it is to implement an algorithm in various programming languages. Then I'll discuss how to encapsulate that algorithm.
The articles will both discuss the rod-cutting problem from Introduction to Algorithms, but I'll introduce the problem in the next article.
Conclusion #
I'd be naive if I believed that a single model can fully explain why some people prefer dynamically typed languages, and others rather like statically typed languages. Even so, suggesting a model helps me understand how to analyze problems.
My hypothesis is that dynamically typed languages may be suitable for implementing algorithms, whereas statically typed languages offer better encapsulation.
This may be used as a heuristic for 'picking the right tool for the job'. If I need to suss out an algorithm, perhaps I should do it in Python. If, on the other hand, I need to publish a reusable library, perhaps Haskell is a better choice.
Next: Implementing rod-cutting.
Short-circuiting an asynchronous traversal
Another C# example.
This article is a continuation of an earlier post about refactoring a piece of imperative code to a functional architecture. It all started with a Stack Overflow question, but read the previous article, and you'll be up to speed.
Imperative outset #
To begin, consider this mostly imperative code snippet:
var storedItems = new List<ShoppingListItem>(); var failedItems = new List<ShoppingListItem>(); var state = (storedItems, failedItems, hasError: false); foreach (var item in itemsToUpdate) { OneOf<ShoppingListItem, NotFound, Error> updateResult = await UpdateItem(item, dbContext); state = updateResult.Match<(List<ShoppingListItem>, List<ShoppingListItem>, bool)>( storedItem => { storedItems.Add(storedItem); return state; }, notFound => { failedItems.Add(item); return state; }, error => { state.hasError = true; return state; } ); if (state.hasError) return Results.BadRequest(); } await dbContext.SaveChangesAsync(); return Results.Ok(new BulkUpdateResult([.. storedItems], [.. failedItems]));
I'll recap a few points from the previous article. Apart from one crucial detail, it's similar to the other post. One has to infer most of the types and APIs, since the original post didn't show more code than that. If you're used to engaging with Stack Overflow questions, however, it's not too hard to figure out what most of the moving parts do.
The most non-obvious detail is that the code uses a library called OneOf, which supplies general-purpose, but rather abstract, sum types. Both the container type OneOf, as well as the two indicator types NotFound and Error are defined in that library.
The Match method implements standard Church encoding, which enables the code to pattern-match on the three alternative values that UpdateItem returns.
One more detail also warrants an explicit description: The itemsToUpdate object is an input argument of the type IEnumerable<ShoppingListItem>.
The major difference from before is that now the update process short-circuits on the first Error. If an error occurs, it stops processing the rest of the items. In that case, it now returns Results.BadRequest(), and it doesn't save the changes to dbContext.
The implementation makes use of mutable state and undisciplined I/O. How do you refactor it to a more functional design?
Short-circuiting traversal #
The standard Traverse function isn't lazy, or rather, it does consume the entire input sequence. Even various Haskell data structures I investigated do that. And yes, I even tried to traverse ListT. If there's a data structure that you can traverse with deferred execution of I/O-bound actions, I'm not aware of it.
That said, all is not lost, but you'll need to implement a more specialized traversal. While consuming the input sequence, the function needs to know when to stop. It can't do that on just any IEnumerable<T>, because it has no information about T.
If, on the other hand, you specialize the traversal to a sequence of items with more information, you can stop processing if it encounters a particular condition. You could generalize this to, say, IEnumerable<Either<L, R>>, but since I already have the OneOf library in scope, I'll use that, instead of implementing or pulling in a general-purpose Either data type.
In fact, I'll just use a three-way OneOf type compatible with the one that UpdateItem returns.
internal static async Task<IEnumerable<OneOf<T1, T2, Error>>> Sequence<T1, T2>( this IEnumerable<Task<OneOf<T1, T2, Error>>> tasks) { var results = new List<OneOf<T1, T2, Error>>(); foreach (var task in tasks) { var result = await task; results.Add(result); if (result.IsT2) break; } return results; }
This implementation doesn't care what T1 or T2 is, so they're free to be ShoppingListItem and NotFound. The third type argument, on the other hand, must be Error.
The if conditional looks a bit odd, but as I wrote, the types that ship with the OneOf library have rather abstract APIs. A three-way OneOf value comes with three case tests called IsT0, IsT1, and IsT2. Notice that the library uses a zero-indexed naming convention for its type parameters. IsT2 returns true if the value is the third kind, in this case Error. If a task turns out to produce an Error, the Sequence method adds that one error, but then stops processing any remaining items.
Some readers may complain that the entire implementation of Sequence is imperative. It hardly matters that much, since the mutation doesn't escape the method. The behaviour is as functional as it's possible to make it. It's fundamentally I/O-bound, so we can't consider it a pure function. That said, if we hypothetically imagine that all the tasks are deterministic and have no side effects, the Sequence function does become a pure function when viewed as a black box. From the outside, you can't tell that the implementation is imperative.
It is possible to implement Sequence in a proper functional style, and it might make a good exercise. I think, however, that it'll be difficult in C#. In F# or Haskell I'd use recursion, and while you can do that in C#, I admit that I've lost sight of whether or not tail recursion is supported by the C# compiler.
Be that as it may, the traversal implementation doesn't change.
internal static Task<IEnumerable<OneOf<TResult, T2, Error>>> Traverse<T1, T2, TResult>( this IEnumerable<T1> items, Func<T1, Task<OneOf<TResult, T2, Error>>> selector) { return items.Select(selector).Sequence(); }
You can now Traverse the itemsToUpdate:
// Impure IEnumerable<OneOf<ShoppingListItem, NotFound<ShoppingListItem>, Error>> results = await itemsToUpdate.Traverse(item => UpdateItem(item, dbContext));
As the // Impure comment may suggest, this constitutes the first impure layer of an Impureim Sandwich.
Aggregating the results #
Since the above statement awaits the traversal, the results object is a 'pure' object that can be passed to a pure function. This does, however, assume that ShoppingListItem is an immutable object.
The next step must collect results and NotFound-related failures, but contrary to the previous article, it must short-circuit if it encounters an Error. This again suggests an Either-like data structure, but again I'll repurpose a OneOf container. I'll start by defining a seed for an aggregation (a left fold).
var seed = OneOf<(IEnumerable<ShoppingListItem>, IEnumerable<ShoppingListItem>), Error> .FromT0(([], []));
This type can be either a tuple or an error. The .NET tendency is often to define an explicit Result<TSuccess, TFailure> type, where TSuccess is defined to the left of TFailure. This, for example, is how F# defines Result types, and other .NET libraries tend to emulate that design. That's also what I've done here, although I admit that I'm regularly confused when going back and forth between F# and Haskell, where the Right case is idiomatically considered to indicate success.
As already discussed, OneOf follows a zero-indexed naming convention for type parameters, so FromT0 indicates the first (or leftmost) case. The seed is thus initialized with a tuple that contains two empty sequences.
As in the previous article, you can now use the Aggregate method to collect the result you want.
OneOf<BulkUpdateResult, Error> result = results .Aggregate( seed, (state, result) => result.Match( storedItem => state.MapT0( t => (t.Item1.Append(storedItem), t.Item2)), notFound => state.MapT0( t => (t.Item1, t.Item2.Append(notFound.Item))), e => e)) .MapT0(t => new BulkUpdateResult(t.Item1.ToArray(), t.Item2.ToArray()));
This expression is a two-step composition. I'll get back to the concluding MapT0 in a moment, but let's first discuss what happens in the Aggregate step. Since the state is now a discriminated union, the big lambda expression not only has to Match on the result, but it also has to deal with the two mutually exclusive cases in which state can be.
Although it comes third in the code listing, it may be easiest to explain if we start with the error case. Keep in mind that the seed starts with the optimistic assumption that the operation is going to succeed. If, however, we encounter an error e, we now switch the state to the Error case. Once in that state, it stays there.
The two other result cases map over the first (i.e. the success) case, appending the result to the appropriate sequence in the tuple t. Since these expressions map over the first (zero-indexed) case, these updates only run as long as the state is in the success case. If the state is in the error state, these lambda expressions don't run, and the state doesn't change.
After having collected the tuple of sequences, the final step is to map over the success case, turning the tuple t into a BulkUpdateResult. That's what MapT0 does: It maps over the first (zero-indexed) case, which contains the tuple of sequences. It's a standard functor projection.
Saving the changes and returning the results #
The final, impure step in the sandwich is to save the changes and return the results:
// Impure return await result.Match( async bulkUpdateResult => { await dbContext.SaveChangesAsync(); return Results.Ok(bulkUpdateResult); }, _ => Task.FromResult(Results.BadRequest()));
Note that it only calls dbContext.SaveChangesAsync() in case the result is a success.
Accumulating the bulk-update result #
So far, I've assumed that the final BulkUpdateResult class is just a simple immutable container without much functionality. If, however, we add some copy-and-update functions to it, we can use that to aggregate the result, instead of an anonymous tuple.
internal BulkUpdateResult Store(ShoppingListItem item) => new([.. StoredItems, item], FailedItems); internal BulkUpdateResult Fail(ShoppingListItem item) => new(StoredItems, [.. FailedItems, item]);
I would have personally preferred the name NotFound instead of Fail, but I was going with the original post's failedItems terminology, and I thought that it made more sense to call a method Fail when it adds to a collection called FailedItems.
Adding these two instance methods to BulkUpdateResult simplifies the composing code:
// Pure OneOf<BulkUpdateResult, Error> result = results .Aggregate( OneOf<BulkUpdateResult, Error>.FromT0(new([], [])), (state, result) => result.Match( storedItem => state.MapT0(bur => bur.Store(storedItem)), notFound => state.MapT0(bur => bur.Fail(notFound.Item)), e => e));
This variation starts with an empty BulkUpdateResult and then uses Store or Fail as appropriate to update the state. The final, impure step of the sandwich remains the same.
Conclusion #
It's a bit more tricky to implement a short-circuiting traversal than the standard traversal. You can, still, implement a specialized Sequence or Traverse method, but it requires that the input stream carries enough information to decide when to stop processing more items. In this article, I used a specialized three-way union, but you could generalize this to use a standard Either or Result type.
Nested monads
You can stack some monads in such a way that the composition is also a monad.
This article is part of a series of articles about functor relationships. In a previous article you learned that nested functors form a functor. You may have wondered if monads compose in the same way. Does a monad nested in a monad form a monad?
As far as I know, there's no universal rule like that, but some monads compose well. Fortunately, it's been my experience that the combinations that you need in practice are among those that exist and are well-known. In a Haskell context, it's often the case that you need to run some kind of 'effect' inside IO. Perhaps you want to use Maybe or Either nested within IO.
In .NET, you may run into a similar need to compose task-based programming with an effect. This happens more often in F# than in C#, since F# comes with other native monads (option and Result, to name the most common).
Abstract shape #
You'll see some real examples in a moment, but as usual it helps to outline what it is that we're looking for. Imagine that you have a monad. We'll call it F in keeping with tradition. In this article series, you've seen how two or more functors compose. When discussing the abstract shapes of things, we've typically called our two abstract functors F and G. I'll stick to that naming scheme here, because monads are functors (that you can flatten).
Now imagine that you have a value that stacks two monads: F<G<T>>. If the inner monad G is the 'right' kind of monad, that configuration itself forms a monad.
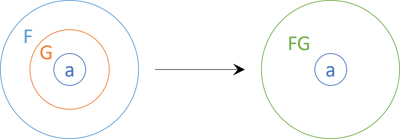
In the diagram, I've simply named the combined monad FG, which is a naming strategy I've seen in the real world, too: TaskResult, etc.
As I've already mentioned, if there's a general theorem that says that this is always possible, I'm not aware of it. To the contrary, I seem to recall reading that this is distinctly not the case, but the source escapes me at the moment. One hint, though, is offered in the documentation of Data.Functor.Compose:
"The composition of applicative functors is always applicative, but the composition of monads is not always a monad."
Thankfully, the monads that you mostly need to compose do, in fact, compose. They include Maybe, Either, State, Reader, and Identity (okay, that one maybe isn't that useful). In other words, any monad F that composes with e.g. Maybe, that is, F<Maybe<T>>, also forms a monad.
Notice that it's the 'inner' monad that determines whether composition is possible. Not the 'outer' monad.
For what it's worth, I'm basing much of this on my personal experience, which was again helpfully guided by Control.Monad.Trans.Class. I don't, however, wish to turn this article into an article about monad transformers, because if you already know Haskell, you can read the documentation and look at examples. And if you don't know Haskell, the specifics of monad transformers don't readily translate to languages like C# or F#.
The conclusions do translate, but the specific language mechanics don't.
Let's look at some common examples.
TaskMaybe monad #
We'll start with a simple, yet realistic example. The article Asynchronous Injection shows a simple operation that involves reading from a database, making a decision, and potentially writing to the database. The final composition, repeated here for your convenience, is an asynchronous (that is, Task-based) process.
return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok);
The problem here is that TryAccept returns Maybe<Reservation>, but since the overall workflow already 'runs in' an asynchronous monad (Task), the monads are now nested as Task<Maybe<T>>.
The way I dealt with that issue in the above code snippet was to rely on a traversal, but it's actually an inelegant solution. The way that the SelectMany invocation maps over the Maybe<Reservation> m is awkward. Instead of composing a business process, the scaffolding is on display, so to speak. Sometimes this is unavoidable, but at other times, there may be a better way.
In my defence, when I wrote that article in 2019 I had another pedagogical goal than teaching nested monads. It turns out, however, that you can rewrite the business process using the Task<Maybe<T>> stack as a monad in its own right.
A monad needs two functions: return and either bind or join. In C# or F#, you can often treat return as 'implied', in the sense that you can always wrap new Maybe<T> in a call to Task.FromResult. You'll see that in a moment.
While you can be cavalier about monadic return, you'll need to explicitly implement either bind or join. In this case, it turns out that the sample code base already had a SelectMany implementation:
public static async Task<Maybe<TResult>> SelectMany<T, TResult>( this Task<Maybe<T>> source, Func<T, Task<Maybe<TResult>>> selector) { Maybe<T> m = await source; return await m.Match( nothing: Task.FromResult(new Maybe<TResult>()), just: x => selector(x)); }
The method first awaits the Maybe value, and then proceeds to Match on it. In the nothing case, you see the implicit return being used. In the just case, the SelectMany method calls selector with whatever x value was contained in the Maybe object. The result of calling selector already has the desired type Task<Maybe<TResult>>, so the implementation simply returns that value without further ado.
This enables you to rewrite the SelectMany call in the business process so that it instead looks like this:
return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(r => Repository.Create(r).Select(i => new Maybe<int>(i))) .Match(InternalServerError("Table unavailable"), Ok);
At first glance, it doesn't look like much of an improvement. To be sure, the lambda expression within the SelectMany method no longer operates on a Maybe value, but rather on the Reservation Domain Model r. On the other hand, we're now saddled with that graceless Select(i => new Maybe<int>(i)).
Had this been Haskell, we could have made this more succinct by eta reducing the Maybe case constructor and used the <$> infix operator instead of fmap; something like Just <$> create r. In C#, on the other hand, we can do something that Haskell doesn't allow. We can overload the SelectMany method:
public static Task<Maybe<TResult>> SelectMany<T, TResult>( this Task<Maybe<T>> source, Func<T, Task<TResult>> selector) { return source.SelectMany(x => selector(x).Select(y => new Maybe<TResult>(y))); }
This overload generalizes the 'pattern' exemplified by the above business process composition. Instead of a specific method call, it now works with any selector function that returns Task<TResult>. Since selector only returns a Task<TResult> value, and not a Task<Maybe<TResult>> value, as actually required in this nested monad, the overload has to map (that is, Select) the result by wrapping it in a new Maybe<TResult>.
This now enables you to improve the business process composition to something more readable.
return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(Repository.Create) .Match(InternalServerError("Table unavailable"), Ok);
It even turned out to be possible to eta reduce the lambda expression instead of the (also valid, but more verbose) r => Repository.Create(r).
If you're interested in the sample code, I've pushed a branch named use-monad-stack to the GitHub repository.
Not surprisingly, the F# bind function is much terser:
let bind f x = async { match! x with | Some x' -> return! f x' | None -> return None }
You can find that particular snippet in the code base that accompanies the article Refactoring registration flow to functional architecture, although as far as I can tell, it's not actually in use in that code base. I probably just added it because I could.
You can find Haskell examples of combining MaybeT with IO in various articles on this blog. One of them is Dependency rejection.
TaskResult monad #
A similar, but slightly more complex, example involves nesting Either values in asynchronous workflows. In some languages, such as F#, Either is rather called Result, and asynchronous workflows are modelled by a Task container, as already demonstrated above. Thus, on .NET at least, this nested monad is often called TaskResult, but you may also see AsyncResult, AsyncEither, or other combinations. Depending on the programming language, such names may be used only for modules, and not for the container type itself. In C# or F# code, for example, you may look in vain after a class called TaskResult<T>, but rather find a TaskResult static class or module.
In C# you can define monadic bind like this:
public static async Task<Either<L, R1>> SelectMany<L, R, R1>( this Task<Either<L, R>> source, Func<R, Task<Either<L, R1>>> selector) { if (source is null) throw new ArgumentNullException(nameof(source)); Either<L, R> x = await source.ConfigureAwait(false); return await x.Match( l => Task.FromResult(Either.Left<L, R1>(l)), selector).ConfigureAwait(false); }
Here I've again passed the eta-reduced selector straight to the right case of the Either value, but r => selector(r) works, too.
The left case shows another example of 'implicit monadic return'. I didn't bother defining an explicit Return function, but rather use Task.FromResult(Either.Left<L, R1>(l)) to return a Task<Either<L, R1>> value.
As is the case with C#, you'll also need to add a special overload to enable the syntactic sugar of query expressions:
public static Task<Either<L, R1>> SelectMany<L, U, R, R1>( this Task<Either<L, R>> source, Func<R, Task<Either<L, U>>> k, Func<R, U, R1> s) { return source.SelectMany(x => k(x).Select(y => s(x, y))); }
You'll see a comprehensive example using these functions in a future article.
In F# I'd often first define a module with a few functions including bind, and then use those implementations to define a computation expression, but in one article, I jumped straight to the expression builder:
type AsyncEitherBuilder () = // Async<Result<'a,'c>> * ('a -> Async<Result<'b,'c>>) // -> Async<Result<'b,'c>> member this.Bind(x, f) = async { let! x' = x match x' with | Success s -> return! f s | Failure f -> return Failure f } // 'a -> 'a member this.ReturnFrom x = x let asyncEither = AsyncEitherBuilder ()
That article also shows usage examples. Another article, A conditional sandwich example, shows more examples of using this nested monad, although there, the computation expression is named taskResult.
Stateful computations that may fail #
To be honest, you mostly run into a scenario where nested monads are useful when some kind of 'effect' (errors, mostly) is embedded in an I/O-bound computation. In Haskell, this means IO, in C# Task, and in F# either Task or Async.
Other combinations are possible, however, but I've rarely encountered a need for additional nested monads outside of Haskell. In multi-paradigmatic languages, you can usually find other good designs that address issues that you may occasionally run into in a purely functional language. The following example is a Haskell-only example. You can skip it if you don't know or care about Haskell.
Imagine that you want to keep track of some statistics related to a software service you offer. If the variance of some number (say, response time) exceeds 10 then you want to issue an alert that the SLA was violated. Apparently, in your system, reliability means staying consistent.
You have millions of observations, and they keep arriving, so you need an online algorithm. For average and variance we'll use Welford's algorithm.
The following code uses these imports:
import Control.Monad import Control.Monad.Trans.State.Strict import Control.Monad.Trans.Maybe
First, you can define a data structure to hold the aggregate values required for the algorithm, as well as an initial, empty value:
data Aggregate = Aggregate { count :: Int, meanA :: Double, m2 :: Double } deriving (Eq, Show) emptyA :: Aggregate emptyA = Aggregate 0 0 0
You can also define a function to update the aggregate values with a new observation:
update :: Aggregate -> Double -> Aggregate update (Aggregate count mean m2) x = let count' = count + 1 delta = x - mean mean' = mean + delta / fromIntegral count' delta2 = x - mean' m2' = m2 + delta * delta2 in Aggregate count' mean' m2'
Given an existing Aggregate record and a new observation, this function implements the algorithm to calculate a new Aggregate record.
The values in an Aggregate record, however, are only intermediary values that you can use to calculate statistics such as mean, variance, and sample variance. You'll need a data type and function to do that, as well:
data Statistics = Statistics { mean :: Double, variance :: Double, sampleVariance :: Maybe Double } deriving (Eq, Show) extractStatistics :: Aggregate -> Maybe Statistics extractStatistics (Aggregate count mean m2) = if count < 1 then Nothing else let variance = m2 / fromIntegral count sampleVariance = if count < 2 then Nothing else Just $ m2 / fromIntegral (count - 1) in Just $ Statistics mean variance sampleVariance
This is where the computation becomes 'failure-prone'. Granted, we only have a real problem when we have zero observations, but this still means that we need to return a Maybe Statistics value in order to avoid division by zero.
(There might be other designs that avoid that problem, or you might simply decide to tolerate that edge case and code around it in other ways. I've decided to design the extractStatistics function in this particular way in order to furnish an example. Work with me here.)
Let's say that as the next step, you'd like to compose these two functions into a single function that both adds a new observation, computes the statistics, but also returns the updated Aggregate.
You could write it like this:
addAndCompute :: Double -> Aggregate -> Maybe (Statistics, Aggregate) addAndCompute x agg = do let agg' = update agg x stats <- extractStatistics agg' return (stats, agg')
This implementation uses do notation to automate handling of Nothing values. Still, it's a bit inelegant with its two agg values only distinguishable by the prime sign after one of them, and the need to explicitly return a tuple of the value and the new state.
This is the kind of problem that the State monad addresses. You could instead write the function like this:
addAndCompute :: Double -> State Aggregate (Maybe Statistics) addAndCompute x = do modify $ flip update x gets extractStatistics
You could actually also write it as a one-liner, but that's already a bit too terse to my liking:
addAndCompute :: Double -> State Aggregate (Maybe Statistics) addAndCompute x = modify (`update` x) >> gets extractStatistics
And if you really hate your co-workers, you can always visit pointfree.io to entirely obscure that expression, but I digress.
The point is that the State monad amplifies the essential and eliminates the irrelevant.
Now you'd like to add a function that issues an alert if the variance is greater than 10. Again, you could write it like this:
monitor :: Double -> State Aggregate (Maybe String) monitor x = do stats <- addAndCompute x case stats of Just Statistics { variance } -> return $ if 10 < variance then Just "SLA violation" else Nothing Nothing -> return Nothing
But again, the code is graceless with its explicit handling of Maybe cases. Whenever you see code that matches Maybe cases and maps Nothing to Nothing, your spider sense should be tingling. Could you abstract that away with a functor or monad?
Yes you can! You can use the MaybeT monad transformer, which nests Maybe computations inside another monad. In this case State:
monitor :: Double -> State Aggregate (Maybe String) monitor x = runMaybeT $ do Statistics { variance } <- MaybeT $ addAndCompute x guard (10 < variance) return "SLA Violation"
The function type is the same, but the implementation is much simpler. First, the code lifts the Maybe-valued addAndCompute result into MaybeT and pattern-matches on the variance. Since the code is now 'running in' a Maybe-like context, this line of code only executes if there's a Statistics value to extract. If, on the other hand, addAndCompute returns Nothing, the function already short-circuits there.
The guard works just like imperative Guard Clauses. The third line of code only runs if the variance is greater than 10. In that case, it returns an alert message.
The entire do workflow gets unwrapped with runMaybeT so that we return back to a normal stateful computation that may fail.
Let's try it out:
ghci> (evalState $ monitor 1 >> monitor 7) emptyA Nothing ghci> (evalState $ monitor 1 >> monitor 8) emptyA Just "SLA Violation"
Good, rigorous testing suggests that it's working.
Conclusion #
You sometimes run into situations where monads are nested. This mostly happens in I/O-bound computations, where you may have a Maybe or Either value embedded inside Task or IO. This can sometimes make working with the 'inner' monad awkward, but in many cases there's a good solution at hand.
Some monads, like Maybe, Either, State, Reader, and Identity, nest nicely inside other monads. Thus, if your 'inner' monad is one of those, you can turn the nested arrangement into a monad in its own right. This may help simplify your code base.
In addition to the common monads listed here, there are few more exotic ones that also play well in a nested configuration. Additionally, if your 'inner' monad is a custom data structure of your own creation, it's up to you to investigate if it nests nicely in another monad. As far as I can tell, though, if you can make it nest in one monad (e.g Task, Async, or IO) you can probably make it nest in any monad.
Next: Software design isomorphisms.
Collecting and handling result values
The answer is traverse. It's always traverse.
I recently came across a Stack Overflow question about collecting and handling sum types (AKA discriminated unions or, in this case, result types). While the question was tagged functional-programming, the overall structure of the code was so imperative, with so much interleaved I/O, that it hardly qualified as functional architecture.
Instead, I gave an answer which involved a minimal change to the code. Subsequently, the original poster asked to see a more functional version of the code. That's a bit too large a task for a Stack Overflow answer, I think, so I'll do it here on the blog instead.
Further comments and discussion on the original post reveal that the poster is interested in two alternatives. I'll start with the alternative that's only discussed, but not shown, in the question. The motivation for this ordering is that this variation is easier to implement than the other one, and I consider it pedagogical to start with the simplest case.
I'll do that in this article, and then follow up with another article that covers the short-circuiting case.
Imperative outset #
To begin, consider this mostly imperative code snippet:
var storedItems = new List<ShoppingListItem>(); var failedItems = new List<ShoppingListItem>(); var errors = new List<Error>(); var state = (storedItems, failedItems, errors); foreach (var item in itemsToUpdate) { OneOf<ShoppingListItem, NotFound, Error> updateResult = await UpdateItem(item, dbContext); state = updateResult.Match<(List<ShoppingListItem>, List<ShoppingListItem>, List<Error>)>( storedItem => { storedItems.Add(storedItem); return state; }, notFound => { failedItems.Add(item); return state; }, error => { errors.Add(error); return state; } ); } await dbContext.SaveChangesAsync(); return Results.Ok(new BulkUpdateResult([.. storedItems], [.. failedItems], [.. errors]));
There's quite a few things to take in, and one has to infer most of the types and APIs, since the original post didn't show more code than that. If you're used to engaging with Stack Overflow questions, however, it's not too hard to figure out what most of the moving parts do.
The most non-obvious detail is that the code uses a library called OneOf, which supplies general-purpose, but rather abstract, sum types. Both the container type OneOf, as well as the two indicator types NotFound and Error are defined in that library.
The Match method implements standard Church encoding, which enables the code to pattern-match on the three alternative values that UpdateItem returns.
One more detail also warrants an explicit description: The itemsToUpdate object is an input argument of the type IEnumerable<ShoppingListItem>.
The implementation makes use of mutable state and undisciplined I/O. How do you refactor it to a more functional design?
Standard traversal #
I'll pretend that we only need to turn the above code snippet into a functional design. Thus, I'm ignoring that the code is most likely part of a larger code base. Because of the implied database interaction, the method isn't a pure function. Unless it's a top-level method (that is, at the boundary of the application), it doesn't exemplify larger-scale functional architecture.
That said, my goal is to refactor the code to an Impureim Sandwich: Impure actions first, then the meat of the functionality as a pure function, and then some more impure actions to complete the functionality. This strongly suggests that the first step should be to map over itemsToUpdate and call UpdateItem for each.
If, however, you do that, you get this:
IEnumerable<Task<OneOf<ShoppingListItem, NotFound, Error>>> results = itemsToUpdate.Select(item => UpdateItem(item, dbContext));
The results object is a sequence of tasks. If we consider Task as a surrogate for IO, each task should be considered impure, as it's either non-deterministic, has side effects, or both. This means that we can't pass results to a pure function, and that frustrates the ambition to structure the code as an Impureim Sandwich.
This is one of the most common problems in functional programming, and the answer is usually: Use a traversal.
IEnumerable<OneOf<ShoppingListItem, NotFound<ShoppingListItem>, Error>> results = await itemsToUpdate.Traverse(item => UpdateItem(item, dbContext));
Because this first, impure layer of the sandwich awaits the task, results is now an immutable value that can be passed to the pure step. This, by the way, assumes that ShoppingListItem is immutable, too.
Notice that I adjusted one of the cases of the discriminated union to NotFound<ShoppingListItem> rather than just NotFound. While the OneOf library ships with a NotFound type, it doesn't have a generic container of that name, so I defined it myself:
internal sealed record NotFound<T>(T Item);
I added it to make the next step simpler.
Aggregating the results #
The next step is to sort the results into three 'buckets', as it were.
// Pure var seed = ( Enumerable.Empty<ShoppingListItem>(), Enumerable.Empty<ShoppingListItem>(), Enumerable.Empty<Error>() ); var result = results.Aggregate( seed, (state, result) => result.Match( storedItem => (state.Item1.Append(storedItem), state.Item2, state.Item3), notFound => (state.Item1, state.Item2.Append(notFound.Item), state.Item3), error => (state.Item1, state.Item2, state.Item3.Append(error))));
It's also possible to inline the seed value, but here I defined it in a separate expression in an attempt at making the code a little more readable. I don't know if I succeeded, because regardless of where it goes, it's hardly idiomatic to break tuple initialization over multiple lines. I had to, though, because otherwise the code would run too far to the right.
The lambda expression handles each result in results and uses Match to append the value to its proper 'bucket'. The outer result is a tuple of the three collections.
Saving the changes and returning the results #
The final, impure step in the sandwich is to save the changes and return the results:
// Impure await dbContext.SaveChangesAsync(); return new OkResult( new BulkUpdateResult([.. result.Item1], [.. result.Item2], [.. result.Item3]));
To be honest, the last line of code is pure, but that's not unusual when it comes to Impureim Sandwiches.
Accumulating the bulk-update result #
So far, I've assumed that the final BulkUpdateResult class is just a simple immutable container without much functionality. If, however, we add some copy-and-update functions to it, we can use them to aggregate the result, instead of an anonymous tuple.
internal BulkUpdateResult Store(ShoppingListItem item) => new([.. StoredItems, item], FailedItems, Errors); internal BulkUpdateResult Fail(ShoppingListItem item) => new(StoredItems, [.. FailedItems, item], Errors); internal BulkUpdateResult Error(Error error) => new(StoredItems, FailedItems, [.. Errors, error]);
I would have personally preferred the name NotFound instead of Fail, but I was going with the original post's failedItems terminology, and I thought that it made more sense to call a method Fail when it adds to a collection called FailedItems.
Adding these three instance methods to BulkUpdateResult simplifies the composing code:
// Impure IEnumerable<OneOf<ShoppingListItem, NotFound<ShoppingListItem>, Error>> results = await itemsToUpdate.Traverse(item => UpdateItem(item, dbContext)); // Pure var result = results.Aggregate( new BulkUpdateResult([], [], []), (state, result) => result.Match( storedItem => state.Store(storedItem), notFound => state.Fail(notFound.Item), error => state.Error(error))); // Impure await dbContext.SaveChangesAsync(); return new OkResult(result);
This variation starts with an empty BulkUpdateResult and then uses Store, Fail, or Error as appropriate to update the state.
Parallel Sequence #
If the tasks you want to traverse are thread-safe, you might consider making the traversal concurrent. You can use Task.WhenAll for that. It has the same type as Sequence, so if you can live with the extra non-determinism that comes with parallel execution, you can use that instead:
internal static async Task<IEnumerable<T>> Sequence<T>(this IEnumerable<Task<T>> tasks) { return await Task.WhenAll(tasks); }
Since the method signature doesn't change, the rest of the code remains unchanged.
Conclusion #
One of the most common stumbling blocks in functional programming is when you have a collection of values, and you need to perform an impure action (typically I/O) for each. This leaves you with a collection of impure values (Task in C#, Task or Async in F#, IO in Haskell, etc.). What you actually need is a single impure value that contains the collection of results.
The solution to this kind of problem is to traverse the collection, rather than mapping over it (with Select, map, fmap, or similar). Note that computer scientists often talk about traversing a data structure like a tree. This is a less well-defined use of the word, and not directly related. That said, you can also write Traverse and Sequence functions for trees.
This article used a Stack Overflow question as the starting point for an example showing how to refactor imperative code to an Impureim Sandwich.
This completes the first variation requested in the Stack Overflow question.
Traversals
How to convert a list of tasks into an asynchronous list, and similar problems.
This article is part of a series of articles about functor relationships. In a previous article you learned about natural transformations, and then how functors compose. You can skip several of them if you like, but you might find the one about functor compositions relevant. Still, this article can be read independently of the rest of the series.
You can go a long way with just a single functor or monad. Consider how useful C#'s LINQ API is, or similar kinds of APIs in other languages - typically map and flatMap methods. These APIs work exclusively with the List monad (which is also a functor). Working with lists, sequences, or collections is so useful that many languages have other kinds of special syntax specifically aimed at working with multiple values: List comprehension.
Asynchronous monads like Task<T> or F#'s Async<'T> are another kind of functor so useful in their own right that languages have special async and await keywords to compose them.
Sooner or later, though, you run into situations where you'd like to combine two different functors.
Lists and tasks #
It's not unusual to combine collections and asynchrony. If you make an asynchronous database query, you could easily receive something like Task<IEnumerable<Reservation>>. This, in isolation, hardly causes problems, but things get more interesting when you need to compose multiple reads.
Consider a query like this:
public static Task<Foo> Read(int id)
What happens if you have a collection of IDs that you'd like to read? This happens:
var ids = new[] { 42, 1337, 2112 }; IEnumerable<Task<Foo>> fooTasks = ids.Select(id => Foo.Read(id));
You get a collection of Tasks, which may be awkward because you can't await it. Perhaps you'd rather prefer a single Task that contains a collection: Task<IEnumerable<Foo>>. In other words, you'd like to flip the functors:
IEnumerable<Task<Foo>> Task<IEnumerable<Foo>>
The top type is what you have. The bottom type is what you'd like to have.
The combination of asynchrony and collections is so common that .NET has special methods to do that. I'll briefly mention one of these later, but what's the general solution to this problem?
Whenever you need to flip two functors, you need a traversal.
Sequence #
As is almost always the case, we can look to Haskell for a canonical definition of traversals - or, as the type class is called: Traversable.
A traversable functor is a functor that enables you to flip that functor and another functor, like the above C# example. In more succinct syntax:
t (f a) -> f (t a)
Here, t symbolises any traversable functor (like IEnumerable<T> in the above C# example), and f is another functor (like Task<T>, above). By flipping the functors I mean making t and f change places; just like IEnumerable and Task, above.
Thinking of functors as containers we might depict the function like this:
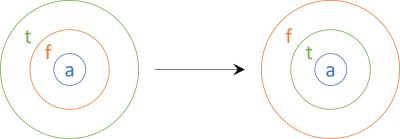
To the left, we have an outer functor t (e.g. IEnumerable) that contains another functor f (e.g. Task) that again 'contains' values of type a (in C# typically called T). We'd like to flip how the containers are nested so that f contains t.
Contrary to what you might expect, the function that does that isn't called traverse; it's called sequence. (For those readers who are interested in Haskell specifics, the function I'm going to be talking about is actually called sequenceA. There's also a function called sequence, but it's not as general. The reason for the odd names are related to the evolution of various Haskell type classes.)
The sequence function doesn't work for any old functor. First, t has to be a traversable functor. We'll get back to that later. Second, f has to be an applicative functor. (To be honest, I'm not sure if this is always required, or if it's possible to produce an example of a specific functor that isn't applicative, but where it's still possible to implement a sequence function. The Haskell sequenceA function has Applicative f as a constraint, but as far as I can tell, this only means that this is a sufficient requirement - not that it's necessary.)
Since tasks (e.g. Task<T>) are applicative functors (they are, because they are monads, and all monads are applicative functors), that second requirement is fulfilled for the above example. I'll show you how to implement a Sequence function in C# and how to use it, and then we'll return to the general discussion of what a traversable functor is:
public static Task<IEnumerable<T>> Sequence<T>( this IEnumerable<Task<T>> source) { return source.Aggregate( Task.FromResult(Enumerable.Empty<T>()), async (acc, t) => { var xs = await acc; var x = await t; return xs.Concat(new[] { x }); }); }
This Sequence function enables you to flip any IEnumerable<Task<T>> to a Task<IEnumerable<T>>, including the above fooTasks:
Task<IEnumerable<Foo>> foosTask = fooTasks.Sequence();
You can also implement sequence in F#:
// Async<'a> list -> Async<'a list> let sequence asyncs = let go acc t = async { let! xs = acc let! x = t return List.append xs [x] } List.fold go (fromValue []) asyncs
and use it like this:
let fooTasks = ids |> List.map Foo.Read let foosTask = fooTasks |> Async.sequence
For this example, I put the sequence function in a local Async module; it's not part of any published Async module.
These C# and F# examples are specific translations: From lists of tasks to a task of list. If you need another translation, you'll have to write a new function for that particular combination of functors. Haskell has more general capabilities, so that you don't have to write functions for all combinations. I'm not assuming that you know Haskell, however, so I'll proceed with the description.
Traversable functor #
The sequence function requires that the 'other' functor (the one that's not the traversable functor) is an applicative functor, but what about the traversable functor itself? What does it take to be a traversable functor?
I have to admit that I have to rely on Haskell specifics to a greater extent than normal. For most other concepts and abstractions in the overall article series, I've been able to draw on various sources, chief of which are Category Theory for Programmers. In various articles, I've cited my sources whenever possible. While I've relied on Haskell libraries for 'canonical' ways to represent concepts in a programming language, I've tried to present ideas as having a more universal origin than just Haskell.
When it comes to traversable functors, I haven't come across universal reasoning like that which gives rise to concepts like monoids, functors, Church encodings, or catamorphisms. This is most likely a failing on my part.
Traversals of the Haskell kind are, however, so useful that I find it appropriate to describe them. When consulting, it's a common solution to a lot of problems that people are having with functional programming.
Thus, based on Haskell's Data.Traversable, a traversable functor must:
- be a functor
- be a 'foldable' functor
- define a sequence or traverse function
Haskell comes with a Foldable type class. It defines a class of data that has a particular type of catamorphism. As I've outlined in my article on catamorphisms, Haskell's notion of a fold sometimes coincides with a (or 'the') catamorphism for a type, and sometimes not. For Maybe and List they do coincide, while they don't for Either or Tree. It's not that you can't define Foldable for Either or Tree, it's just that it's not 'the' general catamorphism for that type.
I can't tell whether Foldable is a universal abstraction, or if it's just an ad-hoc API that turns out to be useful in practice. It looks like the latter to me, but my knowledge is only limited. Perhaps I'll be wiser in a year or two.
I will, however, take it as licence to treat this topic a little less formally than I've done with other articles. While there are laws associated with Traversable, they are rather complex, so I'm going to skip them.
The above requirements will enable you to define traversable functors if you run into some more exotic ones, but in practice, the common functors List, Maybe, Either, Tree, and Identity are all traversable. That it useful to know. If any of those functors is the outer functor in a composition of functors, then you can flip them to the inner position as long as the other functor is an applicative functor.
Since IEnumerable<T> is traversable, and Task<T> (or Async<'T>) is an applicative functor, it's possible to use Sequence to convert IEnumerable<Task<Foo>> to Task<IEnumerable<Foo>>.
Traverse #
The C# and F# examples you've seen so far arrive at the desired type in a two-step process. First they produce the 'wrong' type with ids.Select(Foo.Read) or ids |> List.map Foo.Read, and then they use Sequence to arrive at the desired type.
When you use two expressions, you need two lines of code, and you also need to come up with a name for the intermediary value. It might be easier to chain the two function calls into a single expression:
Task<IEnumerable<Foo>> foosTask = ids.Select(Foo.Read).Sequence();
Or, in F#:
let foosTask = ids |> List.map Foo.Read |> Async.sequence
Chaining Select/map with Sequence/sequence is so common that it's a named function: traverse. In C#:
public static Task<IEnumerable<TResult>> Traverse<T, TResult>( this IEnumerable<T> source, Func<T, Task<TResult>> selector) { return source.Select(selector).Sequence(); }
This makes usage a little easier:
Task<IEnumerable<Foo>> foosTask = ids.Traverse(Foo.Read);
In F# the implementation might be similar:
// ('a -> Async<'b>) -> 'a list -> Async<'b list> let traverse f xs = xs |> List.map f |> sequence
Usage then looks like this:
let foosTask = ids |> Async.traverse Foo.Read
As you can tell, if you've already implemented sequence you can always implement traverse. The converse is also true: If you've already implemented traverse, you can always implement sequence. You'll see an example of that later.
A reusable idea #
If you know the .NET Task Parallel Library (TPL), you may demur that my implementation of Sequence seems like an inefficient version of Task.WhenAll, and that Traverse could be written like this:
public static async Task<IEnumerable<TResult>> Traverse<T, TResult>( this IEnumerable<T> source, Func<T, Task<TResult>> selector) { return await Task.WhenAll(source.Select(selector)); }
This alternative is certainly possible. Whether it's more efficient I don't know; I haven't measured. As foreshadowed in the beginning of the article, the combination of collections and asynchrony is so common that .NET has special APIs to handle that. You may ask, then: What's the point?
The point of is that a traversable functor is a reusable idea.
You may be able to find existing APIs like Task.WhenAll to deal with combinations of collections and asynchrony, but what if you need to deal with asynchronous Maybe or Either? Or a List of Maybes?
There may be no existing API to flip things around - before you add it. Now you know that there's a (dare I say it?) design pattern you can implement.
Asynchronous Maybe #
Once people go beyond collections they often run into problems. You may, for example, decide to use the Maybe monad in order to model the presence or absence of a value. Then, once you combine Maybe-based decision values with asynchronous processesing, you may run into problems.
For example, in my article Asynchronous Injection I modelled the core domaim logic as returning Maybe<Reservation>. When handling an HTTP request, the application should use that value to determine what to do next. If the return value is empty it should do nothing, but when the Maybe value is populated, it should save the reservation in a data store using this method:
Task<int> Create(Reservation reservation)
Finally, if accepting the reservation, the HTTP handler (ReservationsController) should return the resevation ID, which is the int returned by Create. Please refer to the article for details. It also links to the sample code on GitHub.
The entire expression is, however, Task-based:
public async Task<IActionResult> Post(Reservation reservation) { return await Repository.ReadReservations(reservation.Date) .Select(rs => maîtreD.TryAccept(rs, reservation)) .SelectMany(m => m.Traverse(Repository.Create)) .Match(InternalServerError("Table unavailable"), Ok); }
The Select and SelectMany methods are defined on the Task monad. The m in the SelectMany lambda expression is the Maybe<Reservation> returned by TryAccept. What would happen if you didn't have a Traverse method?
Task<Maybe<Task<int>>> whatIsThis = Repository.ReadReservations(reservation.Date)
.Select(rs => maîtreD.TryAccept(rs, reservation))
.Select(m => m.Select(Repository.Create));
Notice that whatIsThis (so named because it's a temporary variable used to investigate the type of the expression so far) has an awkward type: Task<Maybe<Task<int>>>. That's a Task within a Maybe within a Task.
This makes it difficult to continue the composition and return an HTTP result.
Instead, use Traverse:
Task<Task<Maybe<int>>> whatIsThis = Repository.ReadReservations(reservation.Date)
.Select(rs => maîtreD.TryAccept(rs, reservation))
.Select(m => m.Traverse(Repository.Create));
This flips the inner Maybe<Task<int>> to Task<Maybe<int>>. Now you have a Maybe within a Task within a Task. The outer two Tasks are now nicely nested, and it's a job for a monad to remove one level of nesting. That's the reason that the final composition uses SelectMany instead of Select.
The Traverse function is implemented like this:
public static Task<Maybe<TResult>> Traverse<T, TResult>( this Maybe<T> source, Func<T, Task<TResult>> selector) { return source.Match( nothing: Task.FromResult(new Maybe<TResult>()), just: async x => new Maybe<TResult>(await selector(x))); }
The idea is reusable. You can also implement a similar traversal in F#:
// ('a -> Async<'b>) -> 'a option -> Async<'b option> let traverse f = function | Some x -> async { let! x' = f x return Some x' } | None -> async { return None }
You can see the F# function as well as a usage example in the article Refactoring registration flow to functional architecture.
Sequence from traverse #
You've already seen that if you have a sequence function, you can implement traverse. I also claimed that the reverse is true: If you have traverse you can implement sequence.
When you've encountered these kinds of dual definitions a couple of times, you start to expect the ubiquitous identity function to make an appearance, and indeed it does:
let sequence x = traverse id x
That's the F# version where the identity function is built in as id. In C# you'd use a lambda expression:
public static Task<Maybe<T>> Sequence<T>(this Maybe<Task<T>> source) { return source.Traverse(x => x); }
Since C# doesn't come with a predefined identity function, it's idiomatic to use x => x instead.
Conclusion #
Traversals are useful when you need to 'flip' the order of two different, nested functors. The outer one must be a traversable functor, and the inner an applicative functor.
Common traversable functors are List, Maybe, Either, Tree, and Identity, but there are more than those. In .NET you often need them when combining them with Tasks. In Haskell, they are useful when combined with IO.
Next: Nested monads.
Pendulum swing: no Haskell type annotation by default
Are Haskell IDE plugins now good enough that you don't need explicit type annotations?
More than three years ago, I published a small article series to document that I'd changed my mind on various small practices. Belatedly, here comes a fourth article, which, frankly, is a cousin rather than a sibling. Still, it fits the overall theme well enough to become another instalment in the series.
Here, I consider using fewer Haskell type annotations, following a practice that I've always followed in F#.
To be honest, though, it's not that I've already applied the following practice for a long time, and only now write about it. It's rather that I feel the need to write this article to kick an old habit and start a new.
Inertia #
As I write in the dedication in Code That Fits in Your Head,
"To my parents:
"My mother, Ulla Seemann, to whom I owe my attention to detail.
"My father, Leif Seemann, from whom I inherited my contrarian streak."
One should always be careful simplifying one's personality to a simple, easy-to-understand model, but a major point here is that I have two traits that pull in almost the opposite direction.

Despite much work, I only make slow progress. My desire to make things neat and proper almost cancel out my tendency to go against the norms. I tend to automatically toe whatever line that exists until the cognitive dissonance becomes so great that I can no longer ignore it.
I then write an article for the blog to clarify my thoughts.
You may read what comes next and ask, what took you so long?!
I can only refer to the above. I may look calm on the surface, but underneath I'm paddling like the dickens. Despite much work, though, only limited progress is visible.
Nudge #
Haskell is a statically typed language with the most powerful type system I know my way around. The types carry so much information that one can often infer a function's contract from the type alone. This is also fortunate, since many Haskell libraries tend to have, shall we say, minimal documentation. Even so, I've often found myself able to figure out how to use an unfamiliar Haskell API by examining the various types that a library exports.
In fact, the type system is so powerful that it drives a specialized search engine. If you need a function with the type (String -> IO Int) -> [String] -> IO [Int] you can search for it. Hoogle will list all functions that match that type, including functions that are more abstract than your specialized need. You don't even have to imagine what the name might be.
Since the type system is so powerful, it's a major means of communication. Thus, it makes sense that GHC regularly issues a warning if a function lacks a type annotation.
While the compiler enables you to control which warnings are turned on, the missing-signatures warning is included in the popular all flag that most people, I take it, use. I do, at least.
If you forget to declare the type of a function, the compiler will complain:
src\SecurityManager.hs:15:1: warning: [GHC-38417] [-Wmissing-signatures] Top-level binding with no type signature: createUser :: (Monad m, Text.Printf.PrintfArg b, Text.Printf.PrintfArg (t a), Foldable t, Eq (t a)) => (String -> m ()) -> m (t a) -> (t a -> b) -> m () | 15 | createUser writeLine readLine encrypt = do | ^^^^^^^^^^
This is a strong nudge that you're supposed to give each function a type declaration, so I've been doing that for years. Neat and proper.
Of course, if you treat warnings as errors, as I recommend, the nudge becomes a law.
Learning from F# #
While I try to adopt the style and idioms of any language I work in, it's always annoyed me that I had to add a type annotation to a Haskell function. After all, the compiler can usually infer the type. Frankly, adding a type signature feels like redundant ceremony. It's like having to declare a function in a header file before being able to implement it in another file.
This particularly bothers me because I've long since abandoned type annotations in F#. As far as I can tell, most of the F# community has, too.
When you implement an F# function, you just write the implementation and let the compiler infer the type. (Code example from Zone of Ceremony.)
let inline consume quantity = let go (acc, xs) x = if quantity <= acc then (acc, Seq.append xs (Seq.singleton x)) else (acc + x, xs) Seq.fold go (LanguagePrimitives.GenericZero, Seq.empty) >> snd
Since F# often has to interact with .NET code written in C#, you regularly have to add some type annotations to help the compiler along:
let average (timeSpans : NonEmpty<TimeSpan>) = [ timeSpans.Head ] @ List.ofSeq timeSpans.Tail |> List.averageBy (_.Ticks >> double) |> int64 |> TimeSpan.FromTicks
Even so, I follow the rule of minimal annotations: Only add the type information required to compile, and let the compiler infer the rest. For example, the above average function has the inferred type NonEmpty<TimeSpan> -> TimeSpan. While I had to specify the input type in order to be able to use the Ticks property, I didn't have to specify the return type. So I didn't.
My impression from reading other people's F# code is that this is a common, albeit not universal, approach to type annotation.
This minimizes ceremony, since you only need to declare and maintain the types that the compiler can't infer. There's no reason to repeat the work that the compiler can already do, and in practice, if you do, it just gets in the way.
Motivation for explicit type definitions #
When I extol the merits of static types, proponents of dynamically typed languages often argue that the types are in the way. Granted, this is a discussion that I still struggle with, but based on my understanding of the argument, it seems entirely reasonable. After all, if you have to spend time declaring the type of each and every parameter, as well as a function's return type, it does seem to be in the way. This is only exacerbated if you later change your mind.
Programming is, to a large extend, an explorative activity. You start with one notion of how your code should be structured, but as you progress, you learn. You'll often have to go back and change existing code. This, as far as I can tell, is much easier in, say, Python or Clojure than in C# or Java.
If, however, one extrapolates from the experience with Java or C# to all statically typed languages, that would be a logical fallacy. My point with Zone of Ceremony was exactly that there's a group of languages 'to the right' of high-ceremony languages with low levels of ceremony. Even though they're statically typed.
I have to admit, however, that in that article I cheated a little in order to drive home a point. While you can write Haskell code in a low-ceremony style, the tooling (in the form of the all warning set, at least) encourages a high-ceremony style. Add those type definitions, even thought they're redundant.
It's not that I don't understand some of the underlying motivation behind that rule. Daniel Wagner enumerated several reasons in a 2013 Stack Overflow answer. Some of the reasons still apply, but on the other hand, the world has also moved on in the intervening decade.
To be honest, the Haskell IDE situation has always been precarious. One day, it works really well; the next day, I struggle with it. Over the years, though, things have improved.
There was a time when an explicit type definition was a indisputable help, because you couldn't rely on tools to light up and tell you what the inferred type was.
Today, on the other hand, the Haskell extension for Visual Studio Code automatically displays the inferred type above a function implementation:

To be clear, the top line that shows the type definition is not part of the source code. It's just shown by Visual Studio Code as a code lens (I think it's called), and it automatically changes if I edit the code in such a way that the type changes.
If you can rely on such automatic type information, it seems that an explicit type declaration is less useful. It's at least one less reason to add type annotations to the source code.
Ceremony example #
In order to explain what I mean by the types being in the way, I'll give an example. Consider the code example from the article Legacy Security Manager in Haskell. In it, I described how every time I made a change to the createUser action, I had to effectively remove and re-add the type declaration.
It doesn't have to be like that. If instead I'd started without type annotations, I could have moved forward without being slowed down by having to edit type definitions. Take the first edit, breaking the dependency on the console, as an example. Without type annotations, the createUser action would look exactly as before, just without the type declaration. Its type would still be IO ().
After the first edit, the first lines of the action now look like this:
createUser writeLine readLine = do () <- writeLine "Enter a username" -- ...
Even without a type definition, the action still has a type. The compiler infers it to be (Monad m, Eq a, IsChar a) => (String -> m ()) -> m [a] -> m (), which is certainly a bit of a mouthful, but exactly what I had explicitly added in the other article.
The code doesn't compile until I also change the main method to pass the new parameters:
main = createUser putStrLn getLine
You'd have to make a similar edit in, say, Python, although there'd be no compiler to remind you. My point isn't that this is better than a dynamically typed language, but rather that it's on par. The types aren't in the way.
We see the similar lack of required ceremony when the createUser action finally pulls in the comparePasswords and validatePassword functions:
createUser writeLine readLine encrypt = do () <- writeLine "Enter a username" username <- readLine writeLine "Enter your full name" fullName <- readLine writeLine "Enter your password" password <- readLine writeLine "Re-enter your password" confirmPassword <- readLine writeLine $ either id (printf "Saving Details for User (%s, %s, %s)" username fullName . encrypt) (validatePassword =<< comparePasswords password confirmPassword)
Again, there's no type annotation, and while the type actually does change to
(Monad m, PrintfArg b, PrintfArg (t a), Foldable t, Eq (t a)) => (String -> m ()) -> m (t a) -> (t a -> b) -> m ()
it impacts none of the existing code. Again, the types aren't in the way, and no ceremony is required.
Compare that inferred type signature with the explicit final type annotation in the previous article. The inferred type is much more abstract and permissive than the explicit declaration, although I also grant that Daniel Wagner had a point that you can make explicit type definitions more reader-friendly.
Flies in the ointment #
Do the inferred types communicate intent? That's debatable. For example, it's not immediately clear that the above t a allows String.
Another thing that annoys me is that I had to add that unit binding on the first line:
createUser writeLine readLine encrypt = do () <- writeLine "Enter a username" -- ...
The reason for that is that if I don't do that (that is, if I just write writeLine "Xyz" all the way), the compiler infers the type of writeLine to be String -> m b2, rather than just String -> m (). In effect, I want b2 ~ (), but because the compiler thinks that b2 may be anything, it issues an unused-do-bind warning.
The idiomatic way to resolve that situation is to add a type definition, but that's the situation I'm trying to avoid. Thus, my desire to do without annotations pushes me to write unnatural implementation code. This reminds me of the notion of test-induced damage. This is at best a disagreeable compromise.
It also annoys me that implementation details leak out to the inferred type, witnessed by the PrintfArg type constraint. What happens if I change the implementation to use list concatenation?
createUser writeLine readLine encrypt = do () <- writeLine "Enter a username" username <- readLine writeLine "Enter your full name" fullName <- readLine writeLine "Enter your password" password <- readLine writeLine "Re-enter your password" confirmPassword <- readLine let createMsg pwd = "Saving Details for User (" ++ username ++", " ++ fullName ++ ", " ++ pwd ++")" writeLine $ either id (createMsg . encrypt) (validatePassword =<< comparePasswords password confirmPassword)
If I do that, the type also changes:
Monad m => (String -> m ()) -> m [Char] -> ([Char] -> [Char]) -> m ()
While we get rid of the PrintfArg type constraint, the type becomes otherwise more concrete, now operating on String values (keeping in mind that String is a type synonym for [Char]).
The code still compiles, and all tests still pass, because the abstraction I've had in mind all along is essentially this last type.
The writeLine action should take a String and have some side effect, but return no data. The type String -> m () nicely models that, striking a fine balance between being sufficiently concrete to capture intent, but still abstract enough to be testable.
The readLine action should provide input String values, and again m String nicely models that concern.
Finally, encrypt is indeed a naked String endomorphism: String -> String.
With my decades of experience with object-oriented design, it still strikes me as odd that implementation details can make a type more abstract, but once you think it over, it may be okay.
More liberal abstractions #
The inferred types are consistently more liberal than the abstraction I have in mind, which is
Monad m => (String -> m ()) -> m String -> (String -> String) -> m ()
In all cases, the inferred types include that type as a subset.

I hope that I've created the above diagram so that it makes sense, but the point I'm trying to get across is that the two type definitions in the lower middle are equivalent, and are the most specific types. That's the intended abstraction. Thinking of types as sets, all the other inferred types are supersets of that type, in various ways. Even though implementation details leak out in the shape of PrintfArg and IsChar, these are effectually larger sets.
This takes some getting used to: The implementation details are more liberal than the abstraction. This seems to be at odds with the Dependency Inversion Principle (DIP), which suggests that abstractions shouldn't depend on implementation details. I'm not yet sure what to make of this, but I suspect that this is more of problem of overlapping linguistic semantics than software design. What I mean is that I have a feeling that 'implementation detail' have more than one meaning. At least, in the perspective of the DIP, an implementation detail limits your options. For example, depending on a particular database technology is more constraining than depending on some abstract notion of what the persistence mechanism might be. Contrast this with an implementation detail such as the PrintfArg type constraint. It doesn't narrow your options; on the contrary, it makes the implementation more liberal.
Still, while an implementation should be liberal in what it accepts, it's probably not a good idea to publish such a capability to the wider world. After all, if you do, someone will eventually rely on it.
For internal use only #
Going through all these considerations, I think I'll revise my position as the following.
I'll forgo type annotations as long as I explore a problem space. For internal application use, this may effectively mean forever, in the sense that how you compose an application from smaller building blocks is likely to be in permanent flux. Here I have in mind your average web asset or other public-facing service that's in constant development. You keep adding new features, or changing domain logic as the overall business evolves.
As I've also recently discussed, Haskell is a great scripting language, and I think that here, too, I'll dial down the type definitions.
If I ever do another Advent of Code in Haskell, I think I'll also eschew explicit type annotations.
On the other hand, I can see that once an API stabilizes, you may want to lock it down. This may also apply to internal abstractions if you're working in a team and you explicitly want to communicate what a contract is.
If the code is a reusable library, I think that explicit type definitions are still required. Both for the reasons outlined by Daniel Wagner, and also to avoid being the victim of Hyrum's law.
That's why I phrase this pendulum swing as a new default. I'll begin programming without type definitions, but add them as needed. The point is rather that there may be parts of a code base where they're never needed, and then it's okay to keep going without them.
You can use a language pragma to opt out of the missing-signatures compiler warning on a module-by-module basis:
{-# OPTIONS_GHC -Wno-missing-signatures #-}
This will enable me to rely on type inference in parts of the code base, while keeping the build clean of compiler warnings.
Conclusion #
I've always appreciated the F# compiler's ability to infer types and just let type changes automatically ripple through the code base. For that reason, the Haskell norm of explicitly adding a (redundant) type annotation has always vexed me.
It often takes me a long time to reach seemingly obvious conclusions, such as: Don't always add type definitions to Haskell functions. Let the type inference engine do its job.
The reason it takes me so long to take such a small step is that I want to follow 'best practice'; I want to write idiomatic code. When the standard compiler-warning set complains about missing type definitions, it takes me significant deliberation to discard such advice. I could imagine other programmers being in the same situation, which is one reason I wrote this article.
The point isn't that type definitions are a universally bad idea. They aren't. Rather, the point is only that it's also okay to do without them in parts of a code base. Perhaps only temporarily, but in some cases maybe permanently.
The missing-signatures warning shouldn't, I now believe, be considered an absolute law, but rather a contextual rule.
Functor compositions
A functor nested within another functor forms a functor. With examples in C# and another language.
This article is part of a series of articles about functor relationships. In this one you'll learn about a universal composition of functors. In short, if you have one functor nested within another functor, then this composition itself gives rise to a functor.
Together with other articles in this series, this result can help you answer questions such as: Does this data structure form a functor?
Since functors tend to be quite common, and since they're useful enough that many programming languages have special support or syntax for them, the ability to recognize a potential functor can be useful. Given a type like Foo<T> (C# syntax) or Bar<T1, T2>, being able to recognize it as a functor can come in handy. One scenario is if you yourself have just defined this data type. Recognizing that it's a functor strongly suggests that you should give it a Select method in C#, a map function in F#, and so on.
Not all generic types give rise to a (covariant) functor. Some are rather contravariant functors, and some are invariant.
If, on the other hand, you have a data type where one functor is nested within another functor, then the data type itself gives rise to a functor. You'll see some examples in this article.
Abstract shape #
Before we look at some examples found in other code, it helps if we know what we're looking for. Imagine that you have two functors F and G, and you're now considering a data structure that contains a value where G is nested inside of F.
public sealed class GInF<T> { private readonly F<G<T>> ginf; public GInF(F<G<T>> ginf) { this.ginf = ginf; } // Methods go here...
The GInF<T> class has a single class field. The type of this field is an F container, but 'inside' F there's a G functor.
This kind of data structure gives rise to a functor. Knowing that, you can give it a Select method:
public GInF<TResult> Select<TResult>(Func<T, TResult> selector) { return new GInF<TResult>(ginf.Select(g => g.Select(selector))); }
The composed Select method calls Select on the F functor, passing it a lambda expression that calls Select on the G functor. That nested Select call produces an F<G<TResult>> that the composed Select method finally wraps in a new GInF<TResult> object that it returns.
I'll have more to say about how this generalizes to a nested composition of more than two functors, but first, let's consider some examples.
Priority list #
A common configuration is when the 'outer' functor is a collection, and the 'inner' functor is some other kind of container. The article An immutable priority collection shows a straightforward example. The PriorityCollection<T> class composes a single class field:
private readonly Prioritized<T>[] priorities;
The priorities field is an array (a collection) of Prioritized<T> objects. That type is a simple record type:
public sealed record Prioritized<T>(T Item, byte Priority);
If we squint a little and consider only the parameter list, we may realize that this is fundamentally an 'embellished' tuple: (T Item, byte Priority). A pair forms a bifunctor, but in the Haskell Prelude a tuple is also a Functor instance over its rightmost element. In other words, if we'd swapped the Prioritized<T> constructor parameters, it might have naturally looked like something we could fmap:
ghci> fmap (elem 'r') (55, "foo") (55,False)
Here we have a tuple of an integer and a string. Imagine that the number 55 is the priority that we give to the label "foo". This little ad-hoc example demonstrates how to map that tuple to another tuple with a priority, but now it instead holds a Boolean value indicating whether or not the string contained the character 'r' (which it didn't).
You can easily swap the elements:
ghci> import Data.Tuple
ghci> swap (55, "foo")
("foo",55)
This looks just like the Prioritized<T> parameter list. This also implies that if you originally have the parameter list in that order, you could swap it, map it, and swap it again:
ghci> swap $ fmap (elem 'r') $ swap ("foo", 55)
(False,55)
My point is only that Prioritized<T> is isomorphic to a known functor. In reality you rarely need to analyze things that thoroughly to come to that realization, but the bottom line is that you can give Prioritized<T> a lawful Select method:
public sealed record Prioritized<T>(T Item, byte Priority) { public Prioritized<TResult> Select<TResult>(Func<T, TResult> selector) { return new(selector(Item), Priority); } }
Hardly surprising, but since this article postulates that a functor of a functor is a functor, and since we already know that collections give rise to a functor, we should deduce that we can give PriorityCollection<T> a Select method. And we can:
public PriorityCollection<TResult> Select<TResult>(Func<T, TResult> selector) { return new PriorityCollection<TResult>( priorities.Select(p => p.Select(selector)).ToArray()); }
Notice how much this implementation looks like the above GInF<T> 'shape' implementation.
Tree #
An example only marginally more complicated than the above is shown in A Tree functor. The Tree<T> class shown in that article contains two constituents:
private readonly IReadOnlyCollection<Tree<T>> children; public T Item { get; }
Just like PriorityCollection<T> there's a collection, as well as a 'naked' T value. The main difference is that here, the collection is of the same type as the object itself: Tree<T>.
You've seen a similar example in the previous article, which also had a recursive data structure. If you assume, however, that Tree<T> gives rise to a functor, then so does the nested composition of putting it in a collection. This means, from the 'theorem' put forth in this article, that IReadOnlyCollection<Tree<T>> composes as a functor. Finally you have a product of a T (which is isomorphic to the Identity functor) and that composed functor. From Functor products it follows that that's a functor too, which explains why Tree<T> forms a functor. The article shows the Select implementation.
Binary tree Zipper #
In both previous articles you've seen pieces of the puzzle explaining why the binary tree Zipper gives rise to functor. There's one missing piece, however, that we can now finally address.
Recall that BinaryTreeZipper<T> composes these two objects:
public BinaryTree<T> Tree { get; } public IEnumerable<Crumb<T>> Breadcrumbs { get; }
We've already established that both BinaryTree<T> and Crumb<T> form functors. In this article you've learned that a functor in a functor is a functor, which applies to IEnumerable<Crumb<T>>. Both of the above read-only properties are functors, then, which means that the entire class is a product of functors. The Select method follows:
public BinaryTreeZipper<TResult> Select<TResult>(Func<T, TResult> selector) { return new BinaryTreeZipper<TResult>( Tree.Select(selector), Breadcrumbs.Select(c => c.Select(selector))); }
Notice that this Select implementation calls Select on the 'outer' Breadcrumbs by calling Select on each Crumb<T>. This is similar to the previous examples in this article.
Other nested containers #
There are plenty of other examples of functors that contains other functor values. Asynchronous programming supplies its own family of examples.
The way that C# and many other languages model asynchronous or I/O-bound actions is to wrap them in a Task container. If the value inside the Task<T> container is itself a functor, you can make that a functor, too. Examples include Task<IEnumerable<T>>, Task<Maybe<T>> (or its close cousin Task<T?>; notice the question mark), Task<Result<T1, T2>>, etc. You'll run into such types every time you have an I/O-bound or concurrent operation that returns IEnumerable<T>, Maybe<T> etc. as an asynchronous result.
While you can make such nested task functors a functor in its own right, you rarely need that in languages with native async and await features, since those languages nudge you in other directions.
You can, however, run into other issues with task-based programming, but you'll see examples and solutions in a future article.
You'll run into other examples of nested containers with many property-based testing libraries. They typically define Test Data Generators, often called Gen<T>. For .NET, both FsCheck, Hedgehog, and CsCheck does this. For Haskell, QuickCheck, too, defines Gen a.
You often need to generate random collections, in which case you'd work with Gen<IEnumerable<T>> or a similar collection type. If you need random Maybe values, you'll work with Gen<Maybe<T>>, and so on.
On the other hand, sometimes you need to work with a collection of generators, such as seq<Gen<'a>>.
These are all examples of functors within functors. It's not a given that you must treat such a combination as a functor in its own right. To be honest, typically, you don't. On the other hand, if you find yourself writing Select within Select, or map within map, depending on your language, it might make your code more succinct and readable if you give that combination a specialized functor affordance.
Higher arities #
Like the previous two articles, the 'theorem' presented here generalizes to more than two functors. If you have a third H functor, then F<G<H<T>>> also gives rise to a functor. You can easily prove this by simple induction. We may first consider the base case. With a single functor (n = 1) any functor (say, F) is trivially a functor.
In the induction step (n > 1), you then assume that the n - 1 'stack' of functors already gives rise to a functor, and then proceed to prove that the configuration where all those nested functors are wrapped by yet another functor also forms a functor. Since the 'inner stack' of functors forms a functor (by assumption), you only need to prove that a configuration of the outer functor, and that 'inner stack', gives rise to a functor. You've seen how this works in this article, but I admit that a few examples constitute no proof. I'll leave you with only a sketch of this step, but you may consider using equational reasoning as demonstrated by Bartosz Milewski and then prove the functor laws for such a composition.
The Haskell Data.Functor.Compose module defines a general-purpose data type to compose functors. You may, for example, compose a tuple inside a Maybe inside a list:
thriceNested :: Compose [] (Compose Maybe ((,) Integer)) String thriceNested = Compose [Compose (Just (42, "foo")), Compose Nothing, Compose (Just (89, "ba"))]
You can easily fmap that data structure, for example by evaluating whether the number of characters in each string is an odd number (if it's there at all):
ghci> fmap (odd . length) thriceNested Compose [Compose (Just (42,True)),Compose Nothing,Compose (Just (89,False))]
The first element now has True as the second tuple element, since "foo" has an odd number of characters (3). The next element is Nothing, because Nothing maps to Nothing. The third element has False in the rightmost tuple element, since "ba" doesn't have an odd number of characters (it has 2).
Relations to monads #
A nested 'stack' of functors may remind you of the way that I prefer to teach monads: A monad is a functor your can flatten. In short, the definition is the ability to 'flatten' F<F<T>> to F<T>. A function that can do that is often called join or Flatten.
So far in this article, we've been looking at stacks of different functors, abstractly denoted F<G<T>>. There's no rule, however, that says that F and G may not be the same. If F = G then F<G<T>> is really F<F<T>>. This starts to look like the antecedent of the monad definition.
While the starting point may be the same, these notions are not equivalent. Yes, F<F<T>> may form a monad (if you can flatten it), but it does, universally, give rise to a functor. On the other hand, we can hardly talk about flattening F<G<T>>, because that would imply that you'd have to somehow 'throw away' either F or G. There may be specific functors (e.g. Identity) for which this is possible, but there's no universal law to that effect.
Not all 'stacks' of functors are monads. All monads, on the other hand, are functors.
Conclusion #
A data structure that configures one type of functor inside of another functor itself forms a functor. The examples shown in this article are mostly constrained to two functors, but if you have a 'stack' of three, four, or more functors, that arrangement still gives rise to a functor.
This is useful to know, particularly if you're working in a language with only partial support for functors. Mainstream languages aren't going to automatically turn such stacks into functors, in the way that Haskell's Compose container almost does. Thus, knowing when you can safely give your generic types a Select method or map function may come in handy.
To be honest, though, this result is hardly the most important 'theorem' concerning stacks of functors. In reality, you often run into situations where you do have a stack of functors, but they're in the wrong order. You may have a collection of asynchronous tasks, but you really need an asynchronous task that contains a collection of values. The next article addresses that problem.
Next: Traversals.
Legacy Security Manager in Haskell
A translation of the kata, and my first attempt at it.
In early 2013 Richard Dalton published an article about legacy code katas. The idea is to present a piece of 'legacy code' that you have to somehow refactor or improve. Of course, in order to make the exercise manageable, it's necessary to reduce it to some essence of what we might regard as legacy code. It'll only be one aspect of true legacy code. For the legacy Security Manager exercise, the main problem is that the code is difficult to unit test.
The original kata presents the 'legacy code' in C#, which may exclude programmers who aren't familiar with that language and platform. Since I find the exercise useful, I've previous published a port to Python. In this article, I'll port the exercise to Haskell, as well as walk through one attempt at achieving the goals of the kata.
The legacy code #
The original C# code is a static procedure that uses the Console API to ask a user a few simple questions, do some basic input validation, and print a message to the standard output stream. That's easy enough to port to Haskell:
module SecurityManager (createUser) where import Text.Printf (printf) createUser :: IO () createUser = do putStrLn "Enter a username" username <- getLine putStrLn "Enter your full name" fullName <- getLine putStrLn "Enter your password" password <- getLine putStrLn "Re-enter your password" confirmPassword <- getLine if password /= confirmPassword then putStrLn "The passwords don't match" else if length password < 8 then putStrLn "Password must be at least 8 characters in length" else do -- Encrypt the password (just reverse it, should be secure) let array = reverse password putStrLn $ printf "Saving Details for User (%s, %s, %s)" username fullName array
Notice how the Haskell code seems to suffer slightly from the Arrow code smell, which is a problem that the C# code actually doesn't exhibit. The reason is that when using Haskell in an 'imperative style' (which you can, after a fashion, with do notation), you can't 'exit early' from a an if check. The problem is that you can't have if-then without else.
Haskell has other language features that enable you to get rid of Arrow code, but in the spirit of the exercise, this would take us too far away from the original C# code. Making the code prettier should be a task for the refactoring exercise, rather than the starting point.
I've published the code to GitHub, if you want a leg up.
Combined with Richard Dalton's original article, that's all you need to try your hand at the exercise. In the rest of this article, I'll go through my own attempt at the exercise. That said, while this was my first attempt at the Haskell version of it, I've done it multiple times in C#, and once in Python. In other words, this isn't my first rodeo.
Break the dependency on the Console #
As warned, the rest of the article is a walkthrough of the exercise, so if you'd like to try it yourself, stop reading now. On the other hand, if you want to read on, but follow along in the GitHub repository, I've pushed the rest of the code to a branch called first-pass.
The first part of the exercise is to break the dependency on the console. In a language like Haskell where functions are first-class citizens, this part is trivial. I removed the type declaration, moved putStrLn and getLine to parameters and renamed them. Finally, I asked the compiler what the new type is, and added the new type signature.
import Text.Printf (printf, IsChar) createUser :: (Monad m, Eq a, IsChar a) => (String -> m ()) -> m [a] -> m () createUser writeLine readLine = do writeLine "Enter a username" username <- readLine writeLine "Enter your full name" fullName <- readLine writeLine "Enter your password" password <- readLine writeLine "Re-enter your password" confirmPassword <- readLine if password /= confirmPassword then writeLine "The passwords don't match" else if length password < 8 then writeLine "Password must be at least 8 characters in length" else do -- Encrypt the password (just reverse it, should be secure) let array = reverse password writeLine $ printf "Saving Details for User (%s, %s, %s)" username fullName array
I also changed the main action of the program to pass putStrLn and getLine as arguments:
import SecurityManager (createUser) main :: IO () main = createUser putStrLn getLine
Manual testing indicates that I didn't break any functionality.
Get the password comparison feature under test #
The next task is to get the password comparison feature under test. Over a small series of Git commits, I added these inlined, parametrized HUnit tests:
"Matching passwords" ~: do pw <- ["password", "12345678", "abcdefgh"] let actual = comparePasswords pw pw return $ Right pw ~=? actual , "Non-matching passwords" ~: do (pw1, pw2) <- [ ("password", "PASSWORD"), ("12345678", "12345677"), ("abcdefgh", "bacdefgh"), ("aaa", "bbb") ] let actual = comparePasswords pw1 pw2 return $ Left "The passwords don't match" ~=? actual
The resulting implementation is this comparePasswords function:
comparePasswords :: String -> String -> Either String String comparePasswords pw1 pw2 = if pw1 == pw2 then Right pw1 else Left "The passwords don't match"
You'll notice that I chose to implement it as an Either-valued function. While I consider validation a solved problem, the usual solution involves some applicative validation container. In this exercise, validation is already short-circuiting, which means that we can use the standard monadic composition that Either affords.
At this point in the exercise, I just left the comparePasswords function there, without trying to use it within createUser. The reason for that is that Either-based composition is sufficiently different from if-then-else code that I wanted to get the entire system under test before I attempted that.
Get the password validation feature under test #
The third task of the exercise is to get the password validation feature under test. That's similar to the previous task. Once more, I'll show the tests first, and then the function driven by those tests, but I want to point out that both code artefacts came iteratively into existence through the usual red-green-refactor cycle.
"Validate short password" ~: do pw <- ["", "1", "12", "abc", "1234", "gtrex", "123456", "1234567"] let actual = validatePassword pw return $ Left "Password must be at least 8 characters in length" ~=? actual , "Validate long password" ~: do pw <- ["12345678", "123456789", "abcdefghij", "elevenchars"] let actual = validatePassword pw return $ Right pw ~=? actual
The resulting function is hardly surprising.
validatePassword :: String -> Either String String validatePassword pw = if length pw < 8 then Left "Password must be at least 8 characters in length" else Right pw
As in the previous step, I chose to postpone using this function from within createUser until I had a set of characterization tests. That may not be entirely in the spirit of the four subtasks of the exercise, but on the other hand, I intended to do more than just those four activities. The code here is actually simple enough that I could easily refactor without full test coverage, but recalling that this is a legacy code exercise, I find it warranted to pretend that it's complicated.
To be fair to the exercise, there'd also be a valuable exercise in attempting to extract each feature piecemeal, because it's not alway possible to add complete characterization test coverage to a piece of gnarly legacy code. Be that as it may, I've already done that kind of exercise in C# a few times, and I had a different agenda for the Haskell exercise. In short, I was curious about what sort of inferred type createUser would have, once I'd gone through all four subtasks. I'll return to that topic in a moment. First, I want to address the fourth subtask.
Allow different encryption algorithms to be used #
The final part of the exercise is to add a feature to allow different encryption algorithms to be used. Once again, when you're working in a language where functions are first-class citizens, and higher-order functions are idiomatic, one solution is easily at hand:
createUser :: (Monad m, Foldable t, Eq (t a), PrintfArg (t a), PrintfArg b) => (String -> m ()) -> m (t a) -> (t a -> b) -> m () createUser writeLine readLine encrypt = do writeLine "Enter a username" username <- readLine writeLine "Enter your full name" fullName <- readLine writeLine "Enter your password" password <- readLine writeLine "Re-enter your password" confirmPassword <- readLine if password /= confirmPassword then writeLine "The passwords don't match" else if length password < 8 then writeLine "Password must be at least 8 characters in length" else do let array = encrypt password writeLine $ printf "Saving Details for User (%s, %s, %s)" username fullName array
The only change I've made is to promote encrypt to a parameter. This, of course, ripples through the code that calls the action, but currently, that's only the main action, where I had to add reverse as a third argument:
main :: IO () main = createUser putStrLn getLine reverse
Before I made the change, I removed the type annotation from createUser, because adding a parameter causes the type to change. Keeping the type annotation would have caused a compilation error. Eschewing type annotations makes it easier to make changes. Once I'd made the change, I added the new annotation, inferred by the Haskell Visual Studio Code extension.
I was curious what kind of abstraction would arise. Would it be testable in some way?
Testability #
Consider the inferred type of createUser above. It's quite abstract, and I was curious if it was flexible enough to allow testability without adding test-induced damage. In short, in object-oriented programming, you often need to add Dependency Injection to make code testable, and the valid criticism is that this makes code more complicated than it would otherwise have been. I consider such reproval justified, although I disagree with the conclusion. It's not the desire for testability that causes the damage, but rather that object-oriented design is at odds with testability.
That's my conjecture, anyway, so I'm always curious when working with other paradigms like functional programming. Is idiomatic code already testable, or do you need to 'do damage to it' in order to make it testable?
As a Haskell action goes, I would consider its type fairly idiomatic. The code, too, is straightforward, although perhaps rather naive. It looks like beginner Haskell, and as we'll see later, we can rewrite it to be more elegant.
Before I started the exercise, I wondered whether it'd be necessary to use free monads to model pure command-line interactions. Since createUser returns m (), where m is any Monad instance, using a free monad would be possible, but turns out to be overkill. After having thought about it a bit, I recalled that in many languages and platforms, you can redirect standard in and standard out for testing purposes. The way you do that is typically by replacing each with some kind of text stream. Based on that knowledge, I thought I could use the State monad for characterization testing, with a list of strings for each text stream.
In other words, the code is already testable as it is. No test-induced damage here.
Characterization tests #
To use the State monad, I started by importing Control.Monad.Trans.State.Lazy into my test code. This enabled me to write the first characterization test:
"Happy path" ~: flip evalState (["just.inhale", "Justin Hale", "12345678", "12345678"], []) $ do let writeLine x = modify (second (++ [x])) let readLine = state (\(i, o) -> (head i, (tail i, o))) let encrypt = reverse createUser writeLine readLine encrypt actual <- gets snd let expected = [ "Enter a username", "Enter your full name", "Enter your password", "Re-enter your password", "Saving Details for User (just.inhale, Justin Hale, 87654321)"] return $ expected ~=? actual
I consulted my earlier code from An example of state-based testing in Haskell instead of reinventing the wheel, so if you want a more detailed walkthrough, you may want to consult that article as well as this one.
The type of the state that the test makes use of is ([String], [String]). As the lambda expression suggests by naming the elements i and o, the two string lists are used for respectively input and output. The test starts with an 'input stream' populated by 'user input' values, corresponding to each of the four answers a user might give to the questions asked.
The readLine function works by pulling the head off the input list i, while on the other hand not touching the output list o. Its type is State ([a], b) a, compatible with createUser, which requires its readLine parameter to have the type m (t a), where m is a Monad instance, and t a Foldable instance. The effective type turns out to be t a ~ [Char] = String, so that readLine effectively has the type State ([String], b) String. Since State ([String], b) is a Monad instance, it fits the m type argument of the requirement.
The same kind of reasoning applies to writeLine, which appends the input value to the 'output stream', which is the second list in the I/O tuple.
The test runs the createUser action and then checks that the output list contains the expected values.
A similar test verifies the behaviour when the passwords don't match:
"Mismatched passwords" ~: flip evalState (["i.lean.right", "Ilene Wright", "password", "Password"], []) $ do let writeLine x = modify (second (++ [x])) let readLine = state (\(i, o) -> (head i, (tail i, o))) let encrypt = reverse createUser writeLine readLine encrypt actual <- gets snd let expected = [ "Enter a username", "Enter your full name", "Enter your password", "Re-enter your password", "The passwords don't match"] return $ expected ~=? actual
You can see the third and final characterization test in the GitHub repository.
Refactored action #
With full test coverage I could proceed to refactor the createUser action, pulling in the two functions I'd test-driven into existence earlier:
createUser :: (Monad m, PrintfArg a) => (String -> m ()) -> m String -> (String -> a) -> m () createUser writeLine readLine encrypt = do writeLine "Enter a username" username <- readLine writeLine "Enter your full name" fullName <- readLine writeLine "Enter your password" password <- readLine writeLine "Re-enter your password" confirmPassword <- readLine writeLine $ either id (printf "Saving Details for User (%s, %s, %s)" username fullName . encrypt) (validatePassword =<< comparePasswords password confirmPassword)
Because createUser now calls comparePasswords and validatePassword, the type of the overall composition is also more concrete. That's really just an artefact of my (misguided?) decision to give each of the two helper functions types that are more concrete than necessary.
As you can see, I left the initial call-and-response sequence intact, since I didn't feel that it needed improvement.
Conclusion #
I ported the Legacy Security Manager kata to Haskell because I thought it'd be easy enough to port the code itself, and I also found the exercise compelling enough in its own right.
The most interesting point, I think, is that the createUser action remains testable without making any other concession to testability than turning it into a higher-order function. For pure functions, we would expect this to be the case, since pure functions are intrinsically testable, but for impure actions like createUser, this isn't a given. Interacting exclusively with the command-line API is, however, sufficiently simple that we can get by with the State monad. No free monad is needed, and so test-induced damage is kept at a minimum.
Functor sums
A choice of two or more functors gives rise to a functor. An article for object-oriented programmers.
This article is part of a series of articles about functor relationships. In this one you'll learn about a universal composition of functors. In short, if you have a sum type of functors, that data structure itself gives rise to a functor.
Together with other articles in this series, this result can help you answer questions such as: Does this data structure form a functor?
Since functors tend to be quite common, and since they're useful enough that many programming languages have special support or syntax for them, the ability to recognize a potential functor can be useful. Given a type like Foo<T> (C# syntax) or Bar<T1, T2>, being able to recognize it as a functor can come in handy. One scenario is if you yourself have just defined this data type. Recognizing that it's a functor strongly suggests that you should give it a Select method in C#, a map function in F#, and so on.
Not all generic types give rise to a (covariant) functor. Some are rather contravariant functors, and some are invariant.
If, on the other hand, you have a data type which is a sum of two or more (covariant) functors with the same type parameter, then the data type itself gives rise to a functor. You'll see some examples in this article.
Abstract shape in F# #
Before we look at some examples found in other code, it helps if we know what we're looking for. You'll see a C# example in a minute, but since sum types require so much ceremony in C#, we'll make a brief detour around F#.
Imagine that you have two lawful functors, F and G. Also imagine that you have a data structure that holds either an F<'a> value or a G<'a> value:
type FOrG<'a> = FOrGF of F<'a> | FOrGG of G<'a>
The name of the type is FOrG. In the FOrGF case, it holds an F<'a> value, and in the FOrGG case it holds a G<'a> value.
The point of this article is that since both F and G are (lawful) functors, then FOrG also gives rise to a functor. The composed map function can pattern-match on each case and call the respective map function that belongs to each of the two functors.
let map f forg = match forg with | FOrGF fa -> FOrGF (F.map f fa) | FOrGG ga -> FOrGG (G.map f ga)
For clarity I've named the values fa indicating f of a and ga indicating g of a.
Notice that it's an essential requirement that the individual functors (here F and G) are parametrized by the same type parameter (here 'a). If your data structure contains F<'a> and G<'b>, the 'theorem' doesn't apply.
Abstract shape in C# #
The same kind of abstract shape requires much more boilerplate in C#. When defining a sum type in a language that doesn't support them, we may instead either turn to the Visitor design pattern or alternatively use Church encoding. While the two are isomorphic, Church encoding is a bit simpler while the Visitor pattern seems more object-oriented. In this example I've chosen the simplicity of Church encoding.
Like in the above F# code, I've named the data structure the same, but it's now a class:
public sealed class FOrG<T>
Two constructors enable you to initialize it with either an F<T> or a G<T> value.
public FOrG(F<T> f) public FOrG(G<T> g)
Notice that F<T> and G<T> share the same type parameter T. If a class had, instead, composed either F<T1> or G<T2>, the 'theorem' doesn't apply.
Finally, a Match method completes the Church encoding.
public TResult Match<TResult>( Func<F<T>, TResult> whenF, Func<G<T>, TResult> whenG)
Regardless of exactly what F and G are, you can add a Select method to FOrG<T> like this:
public FOrG<TResult> Select<TResult>(Func<T, TResult> selector) { return Match( whenF: f => new FOrG<TResult>(f.Select(selector)), whenG: g => new FOrG<TResult>(g.Select(selector))); }
Since we assume that F and G are functors, which in C# idiomatically have a Select method, we pass the selector to their respective Select methods. f.Select returns a new F value, while g.Select returns a new G value, but there's a constructor for each case, so the composed Select method repackages those return values in new FOrG<TResult> objects.
I'll have more to say about how this generalizes to a sum of more than two alternatives, but first, let's consider some examples.
Open or closed endpoints #
The simplest example that I can think of is that of range endpoints. A range may be open, closed, or a mix thereof. Some mathematical notations use (1, 6] to indicate the range between 1 and 6, where 1 is excluded from the range, but 6 is included. An alternative notation is ]1, 6].
A given endpoint (1 and 6, above) is either open or closed, which implies a sum type. In F# I defined it like this:
type Endpoint<'a> = Open of 'a | Closed of 'a
If you're at all familiar with F#, this is clearly a discriminated union, which is just what the F# documentation calls sum types.
The article Range as a functor goes through examples in both Haskell, F#, and C#, demonstrating, among other points, how an endpoint sum type forms a functor.
Binary tree #
The next example we'll consider is the binary tree from A Binary Tree Zipper in C#. In the original Haskell Zippers article, the data type is defined like this:
data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)
Even if you're not familiar with Haskell syntax, the vertical bar (|) indicates a choice between the left-hand side and the right-hand side. Many programming languages use the | character for Boolean disjunction (or), so the syntax should be intuitive. In this definition, a binary tree is either empty or a node with a value and two subtrees. What interests us here is that it's a sum type.
One way this manifests in C# is in the choice of two alternative constructors:
public BinaryTree() : this(Empty.Instance) { } public BinaryTree(T value, BinaryTree<T> left, BinaryTree<T> right) : this(new Node(value, left.root, right.root)) { }
BinaryTree<T> clearly has a generic type parameter. Does the class give rise to a functor?
It does if it's composed from a sum of two functors. Is that the case?
On the 'left' side, it seems that we have nothing. In the Haskell code, it's called Empty. In the C# code, this case is represented by the parameterless constructor (also known as the default constructor). There's no T there, so that doesn't look much like a functor.
All is, however, not lost. We may view this lack of data as a particular value ('nothing') wrapped in the Const functor. In Haskell and F# a value without data is called unit and written (). In C# or Java you may think of it as void, although unit is a value that you can pass around, which isn't the case for void.
In Haskell, we could instead represent Empty as Const (), which is a bona-fide Functor instance that you can fmap:
ghci> emptyNode = Const () ghci> fmap (+1) emptyNode Const ()
This examples pretends to 'increment' a number that isn't there. Not that you'd need to do this. I'm only showing you this to make the argument that the empty node forms a functor.
The 'right' side of the sum type is most succinctly summarized by the Haskell code:
Node a (Tree a) (Tree a)
It's a 'naked' generic value and two generic trees. In C# it's the parameter list
(T value, BinaryTree<T> left, BinaryTree<T> right)
Does that make a functor? Yes, it's a triple of a 'naked' generic value and two recursive subtrees, all sharing the same T. Just like in the previous article we can view a 'naked' generic value as equivalent to the Identity functor, so that parameter is a functor. The other ones are recursive types: They are of the same type as the type we're trying to evaluate, BinaryTree<T>. If we assume that that forms a functor, that triple is a product type of functors. From the previous article, we know that that gives rise to a functor.
This means that in C#, for example, you can add the idiomatic Select method:
public BinaryTree<TResult> Select<TResult>(Func<T, TResult> selector) { return Aggregate( whenEmpty: () => new BinaryTree<TResult>(), whenNode: (value, left, right) => new BinaryTree<TResult>(selector(value), left, right)); }
In languages that support pattern-matching on sum types (such as F#), you'd have to match on each case and explicitly deal with the recursive mapping. Notice, however, that here I've used the Aggregate method to implement Select. The Aggregate method is the BinaryTree<T> class' catamorphism, and it already handles the recursion for us. In other words, left and right are already BinaryTree<TResult> objects.
What remains is only to tell Aggregate what to do when the tree is empty, and how to transform the 'naked' node value. The Select implementation handles the former by returning a new empty tree, and the latter by invoking selector(value).
Not only does the binary tree form a functor, but it turns out that the Zipper does as well, because the breadcrumbs also give rise to a functor.
Breadcrumbs #
The original Haskell Zippers article defines a breadcrumb for the binary tree Zipper like this:
data Crumb a = LeftCrumb a (Tree a) | RightCrumb a (Tree a) deriving (Show)
That's another sum type with generics on the left as well as the right. In C# the two options may be best illustrated by these two creation methods:
public static Crumb<T> Left<T>(T value, BinaryTree<T> right) { return Crumb<T>.Left(value, right); } public static Crumb<T> Right<T>(T value, BinaryTree<T> left) { return Crumb<T>.Right(value, left); }
Notice that the Left and Right choices have the same structure: A 'naked' generic T value, and a BinaryTree<T> object. Only the names differ. This suggests that we only need to think about one of them, and then we can reuse our conclusion for the other.
As we've already done once, we consider a T value equivalent with Identity<T>, which is a functor. We've also, just above, established that BinaryTree<T> forms a functor. We have a product (argument list, or tuple) of functors, so that combination forms a functor.
Since this is true for both alternatives, this sum type, too, gives rise to a functor. This enables you to implement a Select method:
public Crumb<TResult> Select<TResult>(Func<T, TResult> selector) { return Match( (v, r) => Crumb.Left(selector(v), r.Select(selector)), (v, l) => Crumb.Right(selector(v), l.Select(selector))); }
By now the pattern should be familiar. Call selector(v) directly on the 'naked' values, and pass selector to any other functors' Select method.
That's almost all the building blocks we have to declare BinaryTreeZipper<T> a functor as well, but we need one last theorem before we can do that. We'll conclude this work in the next article.
Higher arities #
Although we finally saw a 'real' triple product, all the sum types have involved binary choices between a 'left side' and a 'right side'. As was the case with functor products, the result generalizes to higher arities. A sum type with any number of cases forms a functor if all the cases give rise to a functor.
We can, again, use canonicalized forms to argue the case. (See Thinking with Types for a clear explanation of canonicalization of types.) A two-way choice is isomorphic to Either, and a three-way choice is isomorphic to Either a (Either b c). Just like it's possible to build triples, quadruples, etc. by nesting pairs, we can construct n-ary choices by nesting Eithers. It's the same kind of inductive reasoning.
This is relevant because just as Haskell's base library provides Data.Functor.Product for composing two (and thereby any number of) functors, it also provides Data.Functor.Sum for composing functor sums.
The Sum type defines two case constructors: InL and InR, but it's isomorphic with Either:
canonizeSum :: Sum f g a -> Either (f a) (g a) canonizeSum (InL x) = Left x canonizeSum (InR y) = Right y summarizeEither :: Either (f a) (g a) -> Sum f g a summarizeEither (Left x) = InL x summarizeEither (Right y) = InR y
The point is that we can compose not only a choice of two, but of any number of functors, to a single functor type. A simple example is this choice between Maybe, list, or Tree:
maybeOrListOrTree :: Sum (Sum Maybe []) Tree String maybeOrListOrTree = InL (InL (Just "foo"))
If we rather wanted to embed a list in that type, we can do that as well:
maybeOrListOrTree' :: Sum (Sum Maybe []) Tree String maybeOrListOrTree' = InL (InR ["bar", "baz"])
Both values have the same type, and since it's a Functor instance, you can fmap over it:
ghci> fmap (elem 'r') maybeOrListOrTree InL (InL (Just False)) ghci> fmap (elem 'r') maybeOrListOrTree' InL (InR [True,False])
These queries examine each String to determine whether or not they contain the letter 'r', which only "bar" does.
The point, anyway, is that sum types of any arity form a functor if all the cases do.
Conclusion #
In the previous article, you learned that a functor product gives rise to a functor. In this article, you learned that a functor sum does, too. If a data structure contains a choice of two or more functors, then that data type itself forms a functor.
As the previous article argues, this is useful to know, particularly if you're working in a language with only partial support for functors. Mainstream languages aren't going to automatically turn such sums into functors, in the way that Haskell's Sum container almost does. Thus, knowing when you can safely give your generic types a Select method or map function may come in handy.
There's one more rule like this one.
Next: Functor compositions.

Comments
Thanks for this one. You might be interested in Andrew Lock's take on the whole subject as well.