ploeh blog danish software design
The end of trust?
Software development in a globalized, hostile world.
Imagine that you're perusing the thriller section in an airport book store and come across a book with the following back cover blurb:
Programmers are dying.
Holly-Ann Kerr works as a data scientist for an NGO that fights workplace discrimination. While scrubbing input, she discovers an unusual pattern in the data. Some employees seem to have an unusually high fatal accident rate. Programmers are dying in traffic accidents, falling on stairs, defect electrical wiring, smoking in bed. They work for a variety of companies. Some for Big Tech, others for specialized component vendors, some for IT-related NGOs, others again for utility companies. The deaths seem to have nothing in common, until H-A uncovers a disturbing pattern.
All victims had recently started in a new position. And all were of Iranian descent.
Is a racist killer on the loose? But if so, why is he only targeting new hires? And why only software developers?
When H-A shares her discovery with the wrong people, she soon discovers that she'll be the next victim.
Okay, I'm not a professional editor, so this could probably do with a bit of polish. Does it sound like an exiting piece of fiction, though?

I'm going to spoil the plot, since the book doesn't exist anyway.
An international plot #
(Apologies to Iranian readers. I have nothing against Iranians, but find the regime despicable. In any case, nothing in the following hinges on the ICC. You can replace it with another adversarial intelligence agency that you don't like, including, but not limited to RGB, FSB, or a clandestine Chinese intelligence organization. You could probably even swap the roles and make CIA, MI5, or Mossad be the bad guys, if your loyalties lie elsewhere.)
In the story, it turns out that clandestine Iranian special operations are attempting to recruit moles in software organizations that constitute the supply chain of Western digital infrastructure.
Intelligence bureaus and software organizations that directly develop sensitive software tend to have good security measures. Planting a mole in such an organization is difficult. The entire supply chain of software dependencies, on the other hand, is much more vulnerable. If you can get an employee to install a backdoor in left-pad, chances are that you may attain remote execution capabilities on an ostensibly secure system.
In my hypothetical thriller, the Iranians kill those software developers that they fail to recruit. After all, one can't run a clandestine operation if people notify the police that they've been approached by a foreign power.
Long game #
Does that plot sound far-fetched?
I admit that I did turn to 11 some plot elements. This is, after all, supposed to be a thriller.
The story is, however, 'loosely based on real events'. Earlier this year, a Microsoft developer revealed a backdoor that someone had intentionally planted in xz Utils. That version of the software was close to being merged into Debian and Red Hat Linux distributions. It would have enabled an attacker to execute arbitrary code on an infected machine.
The attack was singularly sophisticated. It also looks as though it was initiated years ago by one or more persons who contributed real, useful work to an open-source project, apparently (in hindsight) with the sole intention of gaining the trust of the rest of the community.
This is such a long game that it reeks of an adversarial state actor. The linked article speculates on which foreign power may be behind the attack. No, not the Iranians, after all.
If you think about it, it's an entirely rational gambit for a foreign intelligence agency to make. It's not that the NSA hasn't already tried something comparable. If anything, the xz hack mostly seems far-fetched because it's so unnecessarily sophisticated.
Usually, the most effective hacking techniques utilize human trust or gullibility. Why spend enormous effort developing sophisticated buffer overrun exploits if you can get a (perhaps unwitting) insider to run arbitrary code for you?
It'd be much cheaper, and much more reliable, to recruit moles on the inside of software companies, and get them to add the backdoors you need. It doesn't necessary have to be new hires, but perhaps (I'm speculating) it's easier to recruit people before they've developed any loyalty to their new team mates.
The soft underbelly #
Which software organizations are the most promising targets? If it were me, I'd particularly try to go after various component vendors. One category may be companies that produce RAD tools such as grid GUIs, but also service providers that offer free SDKs to, say, send email, generate invoices, send SMS, charge credit cards, etc.
I'm not implying that any such company has ill intent, but since such software run on many machines, it's a juicy target if you can sneak a backdoor into one.
Why not open-source software (OSS)? Many OSS libraries run on even more machines, so wouldn't that be an even more attractive target for an adversary? Yes, but on the other hand, most popular open-source code is also scrutinized by many independent agents, so it's harder to sneak in a backdoor. As the attempted xz hack demonstrates, even a year-long sophisticated attack is at risk of being discovered.
Doesn't commercial or closed-source code receive the same level of scrutiny?
In my experience, not always. Of course, some development organizations use proper shared-code-ownership techniques like code reviews or pair programming, but others rely on siloed solo development. Programmers just check in code that no-one else ever looks at.
In such an organization, imagine how easy it'd be for a mole to add a backdoor to a widely-distributed library. He or she wouldn't even have to resort to sophisticated ways to obscure the backdoor, because no colleague would be likely to look at the code. Particularly not if you bury it in seven levels of nested for loops and call the class MonitorManager or similar. As long as the reusable library ships as compiled code, it's unlikely that customers will discover the backdoor before its too late.
Trust #
Last year I published an article on trust in software development. The point of that piece wasn't that you should suspect your colleagues of ill intent, but rather that you can trust neither yourself nor your co-workers for the simple reason that people make mistakes.
Since then, I've been doing some work in the digital security space, and I've been forced to think about concerns like supply-chain attacks. The implications are, unfortunately, that you can't automatically trust that your colleague has benign intentions.
This, obviously, will vary with context. If you're only writing a small web site for your HR department to use, it's hard to imagine how an adversarial state actor could take advantage of a backdoor in your code. If so, it's unlikely that anyone will go to the trouble of planting a mole in your organization.
On the other hand, if you're writing any kind of reusable library or framework, you just might be an interesting target. If so, you can no longer entirely trust your team mates.
As a Dane, that bothers me deeply. Denmark, along with the other Nordic countries, exhibit the highest levels of inter-societal trust in the world. I was raised to trust strangers, and so far, it's worked well enough for me. A business transaction in Denmark is often just a short email exchange. It's a great benefit to the business environment, and the economy in general, that we don't have to waste a lot of resources filling out formulas, contracts, agreements, etc. Trust is grease that makes society run smoother.
Even so, Scandinavians aren't naive. We don't believe that we can trust everyone. To a large degree, we rely on a lot of subtle social cues to assess a given situation. Some people shouldn't be trusted, and we're able to identify those situations, too.
What remains is that insisting that you can trust your colleague, just because he or she is your colleague, would be descending into teleology. I'm not a proponent of wishful thinking if good arguments suggest the contrary.
Shared code ownership #
Perhaps you shouldn't trust your colleagues. How does that impact software development?
The good news is that this is yet another argument to practice the beneficial practices of shared code ownership. Crucially, what this should entail is not just that everyone is allowed to edit any line of code, but rather that all team members take responsibility for the entire code base. No-one should be allowed to write code in splendid isolation.
There are several ways to address this concern. I often phrase it as follows: There should be at least two pair of eyes on every line of code before a merge to master.
As I describe in Code That Fits in Your Head, you can achieve that goal with pair programming, ensemble programming, or code reviews (including agile pull request reviews). That's a broad enough palette that it should be possible for every developer in every organization to find a modus vivendi that fits any personality and context.
Just looking at each others' code could significantly raise the bar for a would-be mole to add a backdoor to the code base. As an added benefit, it might also raise the general code quality.
What this does suggest to me, however, is that a too simplistic notion of running on trunk may be dangerous. Letting everyone commit to master and trusting that everyone means well no longer strikes me as a good idea (again, given the context, and all that).
Or, if you do, you should consider having some sort of systematic posterior post mortem review process. I've read of organizations that do that, but specific sources escape me at the moment. With Git, however, it's absolutely within the realms of the possible to make a diff of all change since the last ex-post review, and then go through those changes.
Conclusion #
The world is changed. I feel it in the OWASP top 10. I sense it in the shifting geopolitical climate. I smell it on the code I review.
Much that once was, is lost. The dream of a global computer network with boundless trust is no more. There are countries whose interests no longer align with ours. Who pay full-time salaries to people whose job it is to wage 'cyber warfare' against us. We can't rule out that parts of such campaigns include planting moles in our midsts. Moles whose task it is to weaken the foundations of our digital infrastructure.
In that light, should you always trust your colleagues?
Despite the depressing thought that I probably shouldn't, I'm likely to bounce back to my usual Danish most-people-are-to-be-trusted attitude tomorrow. On the other hand, I'll still insist that more than one person is involved with every line of code. Not only because every other person may be a foreign agent, but mostly, still, because humans are fallible, and two brains think better than one.
Should interfaces be asynchronous?
Async and await are notorious for being contagious. Must all interfaces be Task-based, just in case?
I recently came across this question on Mastodon:
"To async or not to async?
"How would you define a library interface for a service that probably will be implemented with an in memory procedure - let's say returning a mapped value to a key you registered programmatically - and a user of your API might want to implement a decorator that needs a 'long running task' - for example you want to log a msg into your db or load additional mapping from a file?
"Would you define the interface to return a Task<string> or just a string?"
While seemingly a simple question, it's both fundamental and turns out to have deeper implications than you may at first realize.
Interpretation #
Before I proceed, I'll make my interpretation of the question more concrete. This is just how I interpret the question, so doesn't necessarily reflect the original poster's views.
The post itself doesn't explicitly mention a particular language, and since several languages now have async and await features, the question may be of more general interest that a question constrained to a single language. On the other hand, in order to have something concrete to discuss, it'll be useful with some real code examples. From perusing the discussion surrounding the original post, I get the impression that the language in question may be C#. That suits me well, since it's one of the languages with which I'm most familiar, and is also a language where programmers of other C-based languages should still be able to follow along.
My interpretation of the implementation, then, is this:
public sealed class NameMap { private readonly Dictionary<Guid, string> knownIds = new() { { new Guid("4778CA3D-FB1B-4665-AAC1-6649CEFA4F05"), "Bob" }, { new Guid("8D3B9093-7D43-4DD2-B317-DCEE4C72D845"), "Alice" } }; public string GetName(Guid guid) { return knownIds.TryGetValue(guid, out var name) ? name : "Trudy"; } }
Nothing fancy, but, as Fandermill writes in a follow-up post:
"Used examples that first came into mind, but it could be anything really."
The point, as I understand it, is that the intended implementation doesn't require asynchrony. A Decorator, on the other hand, may.
Should we, then, declare an interface like the following?
public interface INameMap { Task<string> GetName(Guid guid); }
If we do, the NameMap class can't automatically implement that interface because the return types of the two GetName methods don't match. What are the options?
Conform #
While the following may not be the 'best' answer, let's get the obvious solution out of the way first. Let the implementation conform to the interface:
public sealed class NameMap : INameMap { private readonly Dictionary<Guid, string> knownIds = new() { { new Guid("4778CA3D-FB1B-4665-AAC1-6649CEFA4F05"), "Bob" }, { new Guid("8D3B9093-7D43-4DD2-B317-DCEE4C72D845"), "Alice" } }; public Task<string> GetName(Guid guid) { return Task.FromResult( knownIds.TryGetValue(guid, out var name) ? name : "Trudy"); } }
This variation of the NameMap class conforms to the interface by making the GetName method look asynchronous.
We may even keep the synchronous implementation around as a public method if some client code might need it:
public sealed class NameMap : INameMap { private readonly Dictionary<Guid, string> knownIds = new() { { new Guid("4778CA3D-FB1B-4665-AAC1-6649CEFA4F05"), "Bob" }, { new Guid("8D3B9093-7D43-4DD2-B317-DCEE4C72D845"), "Alice" } }; public Task<string> GetName(Guid guid) { return Task.FromResult(GetNameSync(guid)); } public string GetNameSync(Guid guid) { return knownIds.TryGetValue(guid, out var name) ? name : "Trudy"; } }
Since C# doesn't support return-type-based overloading, we need to distinguish these two methods by giving them different names. In C# it might be more idiomatic to name the asynchronous method GetNameAsync and the synchronous method just GetName, but for reasons that would be too much of a digression now, I've never much liked that naming convention. In any case, I'm not going to go in this direction for much longer, so it hardly matters how we name these two methods.
Kinds of interfaces #
Another digression is, however, quite important. Before we can look at some more code, I'm afraid that we have to perform a bit of practical ontology, as it were. It starts with the question: Why do we even need interfaces?
I should also make clear, as a digression within a digression, that by 'interface' in this context, I'm really interested in any kind of mechanism that enables you to achieve polymorphism. In languages like C# or Java, we may in fact avail ourselves of the interface keyword, as in the above INameMap example, but we may equally well use a base class or perhaps just what C# calls a delegate. In other languages, we may use function or action types, or even function pointers.
Regardless of specific language constructs, there are, as far as I can tell, two kinds of interfaces:
- Interfaces that enable variability or extensibility in behaviour.
- Interfaces that mostly or exclusively exist to support automated testing.
While there may be some overlap between these two kinds, in my experience, the intersection between the two tends to be surprisingly small. Interfaces tend to mostly belong to one of those two categories.
Strategies and higher-order functions #
In design-patterns parlance, examples of the first kind are Builder, State, Chain of Responsibility, Template Method, and perhaps most starkly represented by the Strategy pattern. A Strategy is an encapsulated piece of behaviour that you pass around as a single 'thing' (an object).
And granted, you could also use a Strategy to access a database or make a web-service call, but that's not how the pattern was originally described. We'll return to that use case in the next section.
Rather, the first kind of interface exists to enable extensibility or variability in algorithms. Typical examples (from Design Patterns) include page layout, user interface component rendering, building a maze, finding the most appropriate help topic for a given application context, and so on. If we wish to relate this kind of interface to the SOLID principles, it mostly exists to support the Open-closed principle.
A good heuristics for identifying such interfaces is to consider the Reused Abstractions Principle (Jason Gorman, 2010, I'd link to it, but the page has fallen off the internet. Use your favourite web archive to read it.). If your code base contains multiple production-ready implementations of the same interface, you're reusing the interface, most likely to vary the behaviour of a general-purpose data structure.
And before the functional-programming (FP) crowd becomes too smug: FP uses this kind of interface all the time. In the FP jargon, however, we rather talk about higher-order functions and the interfaces we use to modify behaviour are typically modelled as functions and passed as lambda expressions. So when you write Cata((_, xs) => xs.Sum(), _ => 1) (as one does), you might as well just have passed a Visitor implementation to an Accept method.
This hints at a more quantifiable distinction: If the interface models something that's intended to be a pure function, it'd typically be part of a higher-order API in FP, while we in object-oriented design (once again) lack the terminology to distinguish these interfaces from the other kind.
These days, in C# I mostly use these kinds of interfaces for the Visitor pattern.
Seams #
The other kind of interface exists to afford automated testing. In Working Effectively with Legacy Code, Michael Feathers calls such interfaces Seams. Modern object-oriented code bases often use Dependency Injection (DI) to control which Strategies are in use in a given context. The production system may use an object that communicates with a relational database, while an automated test environment might replace that with a Test Double.
Yes, I wrote Strategies. As I suggested above, a Strategy is really a replaceable object in its purest form. When you use DI you may call all those interfaces IUserRepository, ICommandHandler, IEmailGateway, and so on, but they're really all Strategies.
Contrary to the first kind of interface, you typically only find a single production implementation of each of these interfaces. If you find more that one, the rest are usually Decorators (one that logs, one that caches, one that works as a Circuit Breaker, etc.). All other implementations will be defined in the test code as dynamic mocks or Fakes.
Code bases that rely heavily on DI in order to support testing rub many people the wrong way. In 2014 David Heinemeier Hansson published a serious criticism of such test-induced damage. For the record, I agree with the criticism, but not with the conclusion. While I still practice test-driven development, I only define interfaces for true architectural dependencies. So, yes, my code bases may have an IReservationsRepository or IEmailGateway, but no ICommandHandler or IUserManager.
The bottom line, though, is that some interfaces exist to support testing. If there's a better way to make inherently non-deterministic systems behave deterministically in a test context, I've yet to discover it.
(As an aside, it's worth looking into tests that adopt non-deterministic behaviour as a driving principle, or at least an unavoidable state of affairs. Property-based testing is one such approach, but I also found the article When I'm done, I don't clean up by Arialdo Martini interesting. You may also want to refer to my article Waiting to happen for a discussion of how to make tests independent of system time.)
Where to define interfaces #
The reason the above distinction is important is that it fundamentally determines where interfaces should be defined. In short, the first kind of interface is part of an object model's API, and should be defined together with that API. The second kind, on the other hand, is part of a particular application's architecture, and should be defined by the client code that talks to the interface.
As an example of the first kind, consider this recent example, where the IPriorityEditor<T> interface is part of the PriorityCollection<T> API. You must ship the interface together with the class, because the Edit method takes an interface implementation as an argument. It's how client code interacts with the API.
Another example is this Table class that comes with an ITableVisitor<T> interface. In both cases, we'd expect interface implementations to be deterministic. These interfaces don't exist to support automated testing, but rather to afford a flexible programming model.
For the sake of argument, imagine that you package such APIs in reusable libraries that you publish via a package manager. In that case, it's obvious that the interface is as much part of the package as the class.
Contrast this with the other kind of interface, as described in the article Decomposing CTFiYH's sample code base or showcased in the article An example of state-based testing in C#. In the latter example, the interfaces IUserReader and IUserRepository are not part of any pre-packaged library. Rather, they are defined by the application code to support application-specific needs.
This may be even more evident if you contemplate the diagram in Decomposing CTFiYH's sample code base. Interfaces like IPostOffice and IReservationsRepository only exist to support the application. Following the Dependency Inversion Principle
"clients [...] own the abstract interfaces"
In these code bases, only the Controllers (or rather the tests that exercise them) need these interfaces, so the Controllers get to define them.
Should it be asynchronous, then? #
Okay, so should INameMap.GetName return string or Task<string>, then?
Hopefully, at this point, it should be clear that the answer depends on what kind of interface it is.
If it's the first kind, the return type should support the requirements of the API. If the object model doesn't need the return type to be asynchronous, it shouldn't be.
If it's the second kind of interface, the application code decides what it needs, and defines the interface accordingly.
In neither case, however, is it the concrete class' responsibility to second-guess what client code might need.
But client code may need the method to be asynchronous. What's the harm of returning Task<string>, just in case?
The problem, as you may well be aware, is that the asynchronous programming model is contagious. Once you've made an API asynchronous, you can't easily make it synchronous, whereas if you have a synchronous API, you can easily make it asynchronous. This follows from Postel's law, in this case: Be conservative with what you send.
Library API #
Imagine, for the sake of argument, that the NameMap class is defined in a reusable library, wrapped in a package and imported into your code base via a package manager (NuGet, Maven, pip, NPM, Hackage, RubyGems, etc.).
Clearly it shouldn't implement any interface in order to 'support unit testing', since such interfaces should be defined by application code.
It could implement one or more 'extensibility' interfaces, if such interfaces are part of the wider API offered by the library. In the case of the NameMap class, we don't really know if that's the case. To complete this part of the argument, then, I'd just leave it as shown in the first code example, shown above. It doesn't need to implement any interface, and GetName can just return string.
Domain Model #
What if, instead of an external library, the NameMap class is part of an application's Domain Model?
In that case, you could define application-level interfaces as part of the Domain Model. In fact, most people do. Even so, I'd recommend that you don't, at least if you're aiming for a Functional Core, Imperative Shell architecture, a functional architecture, or even a Ports and Adapters or, if you will, Clean Architecture. The interfaces that exist only to support testing are application concerns, so keep them out of the Domain Model and instead define them in the Application Model.
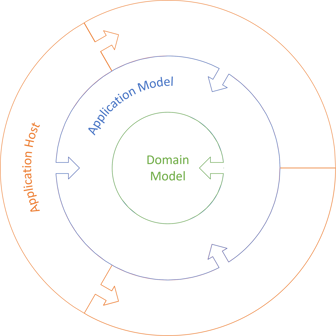
You don't have to follow my advice. If you want to define interfaces in the Domain Model, I can't stop you. But what if, as I recommend, you define application-specific interfaces in the Application Model? If you do that, your NameMap Domain Model can't implement your INameMap interface, because the dependencies point the other way, and most languages will not allow circular dependencies.
In that case, what do you do if, as the original toot suggested, you need to Decorate the GetName method with some asynchronous behaviour?
You can always introduce an Adapter:
public sealed class NameMapAdapter : INameMap { private readonly NameMap imp; public NameMapAdapter(NameMap imp) { this.imp = imp; } public Task<string> GetName(Guid guid) { return Task.FromResult(imp.GetName(guid)); } }
Now any NameMap object can look like an INameMap. This is exactly the kind of problem that the Adapter pattern addresses.
But, you say, that's too much trouble! I don't want to have to maintain two classes that are almost identical.
I understand the concern, and it may even be appropriate. Maybe you're right. As usual, I don't really intend this article to be prescriptive. Rather, I'm offering ideas for your consideration, and you can choose to adopt them or ignore them as it best fits your context.
When it comes to whether or not an Adapter is an unwarranted extra complication, I'll return to that topic later in this article.
Application Model #
The final architectural option is when the concrete NameMap class is part of the Application Model, where you'd also define the application-specific INameMap interface. In that case, we must assume that the NameMap class implements some application-specific concern. If you want it to implement an interface so that you can wrap it in a Decorator, then do that. This means that the GetName method must conform to the interface, and if that means that it must be asynchronous, then so be it.
As Kent Beck wrote in a Facebook article that used to be accessible without a Facebook account (but isn't any longer):
"Things that change at the same rate belong together. Things that change at different rates belong apart."
If the concrete NameMap class and the INameMap interface are both part of the application model, it's not unreasonable to guess that they may change together. (Do be mindful of Shotgun Surgery, though. If you expect the interface and the concrete class to frequently change, then perhaps another design might be more appropriate.)
Easier Adapters #
Before concluding this article, let's revisit the topic of introducing an Adapter for the sole purpose of 'architectural purity'. Should you really go to such lengths only to 'do it right'? You decide, but
You can only be pragmatic if you know how to be dogmatic.
I'm presenting a dogmatic solution for your consideration, so that you know what it might look like. Would I follow my own 'dogmatic' advice? Yes, I usually do, but then, I wouldn't log the return value of a pure function, so I wouldn't introduce an interface for that purpose, at least. To be fair to Fandermill, he or she also wrote: "or load additional mapping from a file", which could be an appropriate motivation for introducing an interface. I'd probably go with an Adapter in that case.
Whether or not an Adapter is an unwarranted complication depends, however, on language specifics. In high-ceremony languages like C#, Java, or C++, adding an Adapter involves at least one new file, and dozens of lines of code.
Consider, on the other hand, a low-ceremony language like Haskell. The corresponding getName function might close over a statically defined map and have the type getName :: UUID -> String.
How do you adapt such a pure function to an API that returns IO (which is roughly comparable to task-based programming)? Trivially:
getNameM :: Monad m => UUID -> m String getNameM = return . getName
For didactic purposes I have here shown the 'Adapter' as an explicit function, but in idiomatic Haskell I'd consider this below the Fairbairn threshold; I'd usually just inline the composition return . getName if I needed to adapt the getName function to the Kleisli category.
You can do the same in F#, where the composition would be getName >> Task.FromResult. F# compositions usually go in the (for Westerners) intuitive left-to-right directions, whereas Haskell compositions follow the mathematical right-to-left convention.
The point, however, is that there's nothing conceptually complicated about an Adapter. Unfortunately, however, some languages require substantial ceremony to implement them.
Conclusion #
Should an API return a Task-based (asynchronous) value 'just in case'? In general: No.
You can't predict all possible use cases, so don't make an API more complicated than it has to be. If you need to implement an application-specific interface, use the Adapter design pattern.
A possible exception to this rule is if the entire API (the concrete implementation and the interface) only exists to support a specific application. If the interface and its concrete implementation are both part of the Application Model, you may as well skip the Adapter step and consider the concrete implementation as its own Adapter.
An immutable priority collection
With examples in C# and F#.
This article is part of a series about encapsulation and immutability. After two attempts at an object-oriented, mutable implementation, I now turn toward immutability. As already suggested in the introductory article, immutability makes it easier to maintain invariants.
In the introductory article, I described the example problem in more details, but in short, the exercise is to develop a class that holds a collection of prioritized items, with the invariant that the priorities must always sum to 100. It should be impossible to leave the object in a state where that's not true. It's quite an illuminating exercise, so if you have the time, you should try it for yourself before reading on.
Initialization #
Once again, I begin by figuring out how to initialize the object, and how to model it. Since it's a kind of collection, and since I now plan to keep it immutable, it seems natural to implement IReadOnlyCollection<T>.
In this, the third attempt, I'll reintroduce Prioritized<T>, with one important difference. It's now an immutable record:
public sealed record Prioritized<T>(T Item, byte Priority);
If you're not on a version of C# that supports records (which is also trivially true if you're not using C# at all), you can always define an immutable class by hand. It just requires more boilerplate code.
Prioritized<T> is going to be the T in the IReadOnlyCollection<T> implementation:
public sealed class PriorityCollection<T> : IReadOnlyCollection<Prioritized<T>>
Since an invariant should always hold, it should also hold at initialization, so the PriorityCollection<T> constructor must check that all is as it should be:
private readonly Prioritized<T>[] priorities; public PriorityCollection(params Prioritized<T>[] priorities) { if (priorities.Sum(p => p.Priority) != 100) throw new ArgumentException( "The sum of all priorities must be 100.", nameof(priorities)); this.priorities = priorities; }
The rest of the class is just the IReadOnlyCollection<T> implementation, which just delegates to the priorities field.
That's it, really. That's the API. We're done.
Projection #
But, you may ask, how does one edit such a collection?

(Comic originally by John Muellerleile.)
Humour aside, you don't edit an immutable object, but rather make a new object from a previous one. Most modern languages now come with built-in collection-projection APIs; in .NET, it's called LINQ. Here's an example. You begin with a collection with two items:
var pc = new PriorityCollection<string>( new Prioritized<string>("foo", 60), new Prioritized<string>("bar", 40));
You'd now like to add a third item with priority 20:
var newPriority = new Prioritized<string>("baz", 20);
How should you make room for this new item? One option is to evenly reduce each of the existing priorities:
var reduction = newPriority.Priority / pc.Count; IEnumerable<Prioritized<string>> reduced = pc .Select(p => p with { Priority = (byte)(p.Priority - reduction) });
Notice that while the sum of priorities in reduced no longer sum to 100, it's okay, because reduced isn't a PriorityCollection object. It's just an IEnumerable<Prioritized<string>>.
You can now Append the newPriority to the reduced sequence and repackage that in a PriorityCollection:
var adjusted = new PriorityCollection<string>(reduced.Append(newPriority).ToArray());
Like the original pc object, the adjusted object is valid upon construction, and since its immutable, it'll remain valid.
Edit #
If you think this process of unwrapping and rewrapping seems cumbersome, we can make it a bit more palatable by defining a wrapping Edit function, similar to the one in the previous article:
public PriorityCollection<T> Edit( Func<IReadOnlyCollection<Prioritized<T>>, IEnumerable<Prioritized<T>>> edit) { return new PriorityCollection<T>(edit(this).ToArray()); }
You can now write code equivalent to the above example like this:
var adjusted = pc.Edit(col => { var reduced = col.Select(p => p with { Priority = (byte)(p.Priority - reduction) }); return reduced.Append(newPriority); });
I'm not sure it's much of an improvement, though.
Using the right tool for the job #
While C# over the years has gained some functional-programming features, it's originally an object-oriented language, and working with immutable values may still seem a bit cumbersome. If so, consider using a language natively designed for this style of programming. On .NET, F# is the obvious choice.
First, you define the required types:
type Prioritized<'a> = { Item: 'a; Priority: byte } type PriorityList = private PriorityList of Prioritized<string> list
Notice that PriorityList has a private constructor, so that client code can't just create any value. The type should protect its invariants, since encapsulation is also relevant in functional programming. Since client code can't directly create PriorityList objects, you instead supply a function for that purpose:
module PriorityList = let tryCreate priorities = if priorities |> List.sumBy (_.Priority) = 100uy then Some (PriorityList priorities) else None
That's really it, although you also need a way to work with the data. We supply two alternatives that correspond to the above C#:
let edit f (PriorityList priorities) = f priorities |> tryCreate let toList (PriorityList priorities) = priorities
These functions are also defined on the PriorityList module.
Here's the same adjustment example as shown above in C#:
let pl = [ { Item = "foo"; Priority = 60uy }; { Item = "bar"; Priority = 40uy } ] |> PriorityList.tryCreate let newPriority = { Item = "baz"; Priority = 20uy } let adjusted = pl |> Option.bind (PriorityList.edit (fun l -> l |> List.map (fun p -> { p with Priority = p.Priority - (newPriority.Priority / byte l.Length) }) |> List.append [ newPriority ]))
The entire F# definition is 15 lines of code, including namespace declaration and blank lines.
Conclusion #
With an immutable data structure, you only need to check the invariants upon creation. Invariants therefore become preconditions. Once a value is created in a valid state, it stays valid because it never changes state.
If you're having trouble maintaining invariants in an object-oriented design, try making the object immutable. It's likely to make it easier to attain good encapsulation.
Comments
First, it's a nice series of articles.
I see that nowadays C# has a generic projection, which is a sort of wither in Java parlance. I should be usable instead of having to define the `Edit` one.
A way to make it more palatable would be to have a `tryAddAndRedistrube(Prioritized
But, it's usually not possible to anticipate all the ways the clients wants to add elements to something, so I think I prefer the open-ended way this API lets clients choose.
Thank you for writing. Whether or not a wither works in this case depends on language implementation details. For example, the F# example code doesn't allow copy-and-update expressions because the record constructor is private. This is as it should be, since otherwise, client code would be able to circumvent the encapsulation.
I haven't tried to refactor the C# class to a record, and I don't recall whether C# with expressions respect custom constructors. That's a good exercise for any reader to try out; unfortunately, I don't have time for that at the moment.
As to your other point, it's definitely conceivable that a library developer could add more convenient methods to the PriorityCollection<T> class, including one that uses a simple formula to redistribute existing priorities to make way for the new one. As far as I can tell, though, you'd be able to implement such more convenient APIs as extension methods that are implemented using the basic affordances already on display here. If so, we may consider the constructor and the IReadOnlyCollection<Prioritized<T>> interface as the fundamental API. Everything else, including the Edit method, could build off that.
A mutable priority collection
An encapsulated, albeit overly complicated, implementation.
This is the second in a series of articles about encapsulation and immutability. In the next article, you'll see how immutability makes encapsulation easier, but in order to appreciate that, you should see the alternative. This article, then, shows a working, albeit overly complicated, implementation that does maintain its invariants.
In the introductory article, I described the example problem in more details, but in short, the exercise is to develop a class that holds a collection of prioritized items, with the invariant that the priorities must always sum to 100. It should be impossible to leave the object in a state where that's not true. It's quite an illuminating exercise, so if you have the time, you should try it for yourself before reading on.
Initialization #
As the previous article demonstrated, inheriting directly from a base class seems like a dead end. Once you see the direction that I go in this article, you may argue that it'd be possible to also make that design work with an inherited collection. It may be, but I'm not convinced that it would improve anything. Thus, for this iteration, I decided to eschew inheritance.
On the other hand, we need an API to query the object about its state, and I found that it made sense to implement the IReadOnlyDictionary interface.
As before, invariants are statements that are always true about an object, and that includes a newly initialized object. Thus, the PriorityCollection<T> class should require enough information to safely initialize.
public sealed class PriorityCollection<T> : IReadOnlyDictionary<T, byte> where T : notnull { private readonly Dictionary<T, byte> dict; public PriorityCollection(T initial) { dict = new Dictionary<T, byte> { { initial, 100 } }; } // IReadOnlyDictionary implemented by delegating to dict field... }
Several design decisions are different from the previous article. This design has no Prioritized<T> class. Instead it treats the item (of type T) as a dictionary key, and the priority as the value. The most important motivation for this design decision was that this enables me to avoid the 'leaf node mutation' problem that I demonstrated in the previous article. Notice how, while the general design in this iteration will be object-oriented and mutable, I already take advantage of a bit of immutability to make the design simpler and safer.
Another difference is that you can't initialize a PriorityCollection<T> object with a list. Instead, you only need to tell the constructor what the initial item is. The constructor will then infer that, since this is the only item so far, its priority must be 100. It can't be anything else, because that would violate the invariant. Thus, no assertion is required in the constructor.
Mutation API #
So far, the code only implements the IReadOnlyDictionary API, so we need to add some methods that will enable us to add new items and so on. As a start, we can add methods to add, remove, or update items:
public void Add(T key, byte value) { AssertInvariants(dict.Append(KeyValuePair.Create(key, value))); dict.Add(key, value); } public void Remove(T key) { AssertInvariants(dict.Where(kvp => !kvp.Key.Equals(key))); dict.Remove(key); } public byte this[T key] { get { return dict[key]; } set { var l = dict.ToDictionary(kvp => kvp.Key, kvp => kvp.Value); l[key] = value; AssertInvariants(l); dict[key] = value; } }
I'm not going to show the AssertInvariants helper method yet, since it's going to change anyway.
At this point, the implementation suffers from the same problem as the example in the previous article. While you can add new items, you can only add an item with priority 0. You can only remove items if they have priority 0. And you can only 'update' an item if you set the priority to the same value as it already had.
We need to be able to add new items, change their priorities, and so on. How do we get around the above problem, without breaking the invariant?
Edit mode #
One way out of this conundrum is introduce a kind of 'edit mode'. The idea is to temporarily turn off the maintenance of the invariant for long enough to allow edits.
Af first glance, such an idea seems to go against the very definition of an invariant. After all, an invariant is a statement about the object that is always true. If you allow a client developer to turn off that guarantee, then, clearly, the guarantee is gone. Guarantees only work if you can trust them, and you can't trust them if they can be cancelled.
That idea in itself doesn't work, but if we can somehow encapsulate such an 'edit action' in an isolated scope that either succeeds or fails in its entirety, we may be getting somewhere. It's an idea similar to Unit of Work, although here we're not involving an actual database. Still, an 'edit action' is a kind of in-memory transaction.
For didactic reasons, I'll move toward that design in a series of step, where the intermediate steps fail to maintain the invariant. We'll get there eventually. The first step is to introduce 'edit mode'.
private bool isEditing;
While I could have made that flag public, I found it more natural to wrap access to it in two methods:
public void BeginEdit() { isEditing = true; } public void EndEdit() { isEditing = false; }
This still doesn't accomplishes anything in itself, but the final change in this step is to change the assertion so that it respects the flag:
private void AssertInvariants(IEnumerable<KeyValuePair<T, byte>> candidate) { if (!isEditing && candidate.Sum(kvp => kvp.Value) != 100) throw new InvalidOperationException( "The sum of all values must be 100."); }
Finally, you can add or change priorities, as this little F# example shows:
sut.BeginEdit () sut["foo"] <- 50uy sut["bar"] <- 50uy sut.EndEdit ()
Even if you nominally 'don't read F#', this little example is almost like C# without semicolons. The <- arrow is F#'s mutation or assignment operator, which in C# would be =, and the uy suffix is the F# way of stating that the literal is a byte.
The above example is well-behaved because the final state of the object is valid. The priorities sum to 100. Even so, no code in PriorityCollection<T> actually checks that, so we could trivially leave the object in an invalid state.
Assert invariant at end of edit #
The first step toward remedying that problem is to add a check to the EndEdit method:
public void EndEdit() { isEditing = false; AssertInvariants(dict); }
The class is still not effectively protecting its invariants, because a client developer could forget to call EndEdit, or client code might pass around a collection in edit mode. Other code, receiving such an object as an argument, may not know whether or not it's in edit mode, so again, doesn't know if it can trust it.
We'll return to that problem shortly, but first, there's another, perhaps more pressing issue that we should attend to.
Edit dictionary #
The current implementation directly edits the collection, and even if a client developer remembers to call EndEdit, other code, higher up in the call stack could circumvent the check and leave the object in an invalid state. Not that I expect client developers to be deliberately malicious, but the notion that someone might wrap a method call in a try-catch block seems realistic.
The following F# unit test demonstrates the issue:
[<Fact>] let ``Attempt to circumvent`` () = let sut = PriorityCollection<string> "foo" try sut.BeginEdit () sut["foo"] <- 50uy sut["bar"] <- 48uy sut.EndEdit () with _ -> () 100uy =! sut["foo"] test <@ sut.ContainsKey "bar" |> not @>
Again, let me walk you through it in case you're unfamiliar with F#.
The try-with block works just like C# try-catch blocks. Inside of that try-with block, the test enters edit mode, changes the values in such a way that the sum of them is 98, and then calls EndEdit. While EndEdit throws an exception, those four lines of code are wrapped in a try-with block that suppresses all exceptions.
The test attempts to verify that, since the edit failed, the "foo" value should be 100, and there should be no "bar" value. This turns out not to be the case. The test fails. The edits persist, even though EndEdit throws an exception, because there's no roll-back.
You could probably resolve that defect in various ways, but I chose to address it by introducing two, instead of one, backing dictionaries. One holds the data that always maintains the invariant, and the other is a temporary dictionary for editing.
private Dictionary<T, byte> current; private readonly Dictionary<T, byte> encapsulated; private readonly Dictionary<T, byte> editable; private bool isEditing; public PriorityCollection(T initial) { encapsulated = new Dictionary<T, byte> { { initial, 100 } }; editable = []; current = encapsulated; }
There are two dictionaries: encapsulated holds the always-valid list of priorities, while editable is the dictionary that client code will be editing when in edit mode. Finally, current is either of these: editable when the object is in edit mode, and encapsulated when it's not. Most of the existing code shown so far now uses current, which before was called dict. The important changes are in BeginEdit and EndEdit.
public void BeginEdit() { isEditing = true; editable.Clear(); foreach (var kvp in current) editable.Add(kvp.Key, kvp.Value); current = editable; }
Besides setting the isEditing flag, BeginEdit now copies all data from current to editable, and then sets current to editable. Keep in mind that encapsulated still holds the original, valid values.
Now that I'm writing this, I'm not even sure if this method is re-entrant, in the following sense: What happens if client code calls BeginEdit, makes some changes, and then calls BeginEdit again? It's questions like these that I don't feel intelligent enough to feel safe that I always answer correctly. That's why I like functional programming better. I don't have to think so hard.
Anyway, this will soon become irrelevant, since BeginEdit and EndEdit will eventually become private methods.
The EndEdit method performs the inverse manoeuvre:
public void EndEdit() { isEditing = false; try { AssertInvariants(current); encapsulated.Clear(); foreach (var kvp in current) encapsulated.Add(kvp.Key, kvp.Value); current = encapsulated; } catch { current = encapsulated; throw; } }
It first checks the invariant, and only copies the edited values to the encapsulated dictionary if the invariant still holds. Otherwise, it restores the original encapsulated values and rethrows the exception.
This helps to make the nature of editing 'transactional' in nature, but it doesn't address the issue that the collection is in an invalid state during editing, or that a client developer may forget to call EndEdit.
Edit action #
As the next step towards addressing that problem, we may now introduce a 'wrapper method' for that little object protocol:
public void Edit(Action<PriorityCollection<T>> editAction) { BeginEdit(); editAction(this); EndEdit(); }
As you can see, it just wraps that little call sequence so that you don't have to remember to call BeginEdit and EndEdit. My F# test code comes with this example:
sut.Edit (fun col -> col["bar"] <- 55uy col["baz"] <- 45uy col.Remove "foo" )
The fun col -> part is just F# syntax for a lambda expression. In C#, you'd write it as col =>.
We're close to a solution. What remains is to make BeginEdit and EndEdit private. This means that client code can only edit a PriorityCollection<T> object through the Edit method.
Replace action with interface #
You may complain that this solution isn't properly object-oriented, since it makes use of Action<T> and requires that client code uses lambda expressions.
We can easily fix that.
Instead of the action, you can introduce a Command interface with the same signature:
public interface IPriorityEditor<T> where T : notnull { void EditPriorities(PriorityCollection<T> priorities); }
Next, change the Edit method:
public void Edit(IPriorityEditor<T> editor) { BeginEdit(); editor.EditPriorities(this); EndEdit(); }
Now you have a nice, object-oriented design, with no lambda expressions in sight.
Full code dump #
The final code is complex enough that it's easy to lose track of what it looks like, as I walk through my process. To make it easer, here's the full code for the collection class:
public sealed class PriorityCollection<T> : IReadOnlyDictionary<T, byte> where T : notnull { private Dictionary<T, byte> current; private readonly Dictionary<T, byte> encapsulated; private readonly Dictionary<T, byte> editable; private bool isEditing; public PriorityCollection(T initial) { encapsulated = new Dictionary<T, byte> { { initial, 100 } }; editable = []; current = encapsulated; } public void Add(T key, byte value) { AssertInvariants(current.Append(KeyValuePair.Create(key, value))); current.Add(key, value); } public void Remove(T key) { AssertInvariants(current.Where(kvp => !kvp.Key.Equals(key))); current.Remove(key); } public byte this[T key] { get { return current[key]; } set { var l = current.ToDictionary(kvp => kvp.Key, kvp => kvp.Value); l[key] = value; AssertInvariants(l); current[key] = value; } } public void Edit(IPriorityEditor<T> editor) { BeginEdit(); editor.EditPriorities(this); EndEdit(); } private void BeginEdit() { isEditing = true; editable.Clear(); foreach (var kvp in current) editable.Add(kvp.Key, kvp.Value); current = editable; } private void EndEdit() { isEditing = false; try { AssertInvariants(current); encapsulated.Clear(); foreach (var kvp in current) encapsulated.Add(kvp.Key, kvp.Value); current = encapsulated; } catch { current = encapsulated; throw; } } private void AssertInvariants(IEnumerable<KeyValuePair<T, byte>> candidate) { if (!isEditing && candidate.Sum(kvp => kvp.Value) != 100) throw new InvalidOperationException( "The sum of all values must be 100."); } public IEnumerable<T> Keys { get { return current.Keys; } } public IEnumerable<byte> Values { get { return current.Values; } } public int Count { get { return current.Count; } } public bool ContainsKey(T key) { return current.ContainsKey(key); } public IEnumerator<KeyValuePair<T, byte>> GetEnumerator() { return current.GetEnumerator(); } public bool TryGetValue(T key, [MaybeNullWhen(false)] out byte value) { return current.TryGetValue(key, out value); } IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } }
The IPriorityEditor<T> interface remains as shown above.
Conclusion #
Given how simple the problem is, this solution is surprisingly complicated, and I'm fairly sure that it's not even thread-safe.
At least it does, as far as I can tell, protect the invariant that the sum of priorities must always be exactly 100. Even so, it's just complicated enough that I wouldn't be surprised if a bug is lurking somewhere. It'd be nice if a simpler design existed.
Comments
Where does the notion come that a data structure invariant has to be true at all times? I am fairly certain that it's only required to be true at "quiescent" points of executions. That is, just as the loop invariant is only required to hold before and after each loop step but not inside the loop step, so is the data structure invariant is only required to hold before and after each invocation of its public methods.
This definition actually has an interesting quirk which is absent in the loop invariant: a data structure's method can't, generally speaking, call other public methods of the very same data structure because the invariant might not hold at this particular point of execution! I've been personally bitten by this a couple of times, and I've seen others tripping over this subtle point as well. You yourself notice it when you muse about the re-entrancy of the BeginEdit method.
Now, this particular problem is quite similar to the problem with inner iteration, and can be solved the same way, with the outer editor, as you've done, although I would have probably provided each editor with its own, separate editable dictionary because right now, the editors cannot nest/compose... but that'd complicate implementation even further.
Thank you for writing. As so many other areas of knowledge, the wider field of software development suffers from the problem of overlapping or overloaded terminology. The word invariant is just one of them. In this context, invariant doesn't refer to loop invariants, or any other kind of invariants used in algorithmic analysis.
As outlined in the introduction article, when discussing encapsulation, I follow Object-Oriented Software Construction (OOSC). In that seminal work, Bertrand Meyer proposes the notion of design-by-contract, and specifically decomposes a contract into three parts: preconditions, invariants, and postconditions.
Having actually read the book, I'm well aware that it uses Eiffel as an exemplar of the concept. This has led many readers to conflate design-by-contract with Eiffel, and (in yet another logical derailment) conclude that it doesn't apply to, say, Java or C# programming.
It turns out, however, to transfer easily to other languages, and it's a concept with much practical potential.
A major problem with object-oriented design is that most ideas about good design are too 'fluffy' to be of immediate use to most developers. Take the Single Responsibility Principle (SRP) as an example. It's seductively easy to grasp the overall idea, but turns out to be hard to apply. Being able to identify reasons to change requires more programming experience than most people have. Or rather, the SRP is mostly useful to programmers who already have that experience. Being too 'fluffy', it's not a good learning tool.
I've spent quite some time with development organizations and individual programmers eager to learn, but struggling to find useful, concrete design rules. The decomposition of encapsulation into preconditions, invariants, and postconditions works well as a concrete, almost quantifiable heuristic.
Does it encompass everything that encapsulation means? Probably not, but it's by far the most effective heuristic that I've found so far.
Since I'm currently travelling, I don't have my copy of OOSC with me, but as far as I remember, the notion that an invariant should be true at all times originates there.
In any case, if an invariant doesn't always hold, then of what value is it? The whole idea behind encapsulation (as I read Meyer) is that client developers should be able to use 'objects' without having intimate knowledge of their implementation details. The use of contracts proposes to achieve that ideal by decoupling affordances from implementation details by condensing the legal protocol between object and client code into a contract. This means that a client developer, when making programming decisions, should be able to trust that certain guarantees stipulated by a contract always hold. If a client developer can't trust those guarantees, they aren't really guarantees.
"the data structure invariant is only required to hold before and after each invocation of its public methods"
I can see how a literal reading of OOSC may leave one with that impression. One must keep in mind, however, that the book was written in the eighties, at a time when multithreading wasn't much of a concern. (Incidentally, this is an omission that also mars a much later book on API design, the first edition of the .NET Framework Design Guidelines.)
In modern code, concurrent execution is a real possibility, so is at least worth keeping in mind. I'm still most familiar with the .NET ecosystem, and in it, there are plenty of classes that are documented as not being thread-safe. You could say that such a statement is part of the contract, in which case what you wrote is true: The invariant is only required to hold before and after each method invocation.
If, on the other hand, you want to make the code thread-safe, you must be more rigorous than that. Then an invariant must truly always hold.
This is, of course, a design decision one may take. Just don't bother with thread-safety if it's not important.
Still, the overall thrust of this article series is that immutability makes encapsulation much simpler. This is also true when it comes to concurrency. Immutable data structures are automatically thread-safe.
A failed attempt at priority collection with inheritance
An instructive dead end.
This article is part of a short series on encapsulation and immutability. As the introductory article claims, object mutation makes it difficult to maintain invariants. In order to demonstrate the problem, I deliberately set out to do it wrong, and report on the result.
In subsequent articles in this series I will then show one way you can maintain the invariants in the face of mutation, as well as how much easier everything becomes if you choose an immutable design.
For now, however, I'll pretend to be naive and see how far I can get with that.
In the first article, I described the example problem in more details, but in short, the exercise is to develop a class that holds a collection of prioritized items, with the invariant that the priorities must always sum to 100. It should be impossible to leave the object in a state where that's not true. It's quite an illuminating exercise, so if you have the time, you should try it for yourself before reading on.
Initialization #
In object-oriented design it's common to inherit from a base class. Since I'll try to implement a collection of prioritized items, it seems natural to inherit from Collection<T>:
public sealed class PriorityCollection<T> : Collection<Prioritized<T>>
Of course, I also had to define Prioritized<T>:
public sealed class Prioritized<T> { public Prioritized(T item, byte priority) { Item = item; Priority = priority; } public T Item { get; set; } public byte Priority { get; set; } }
Since Prioritized<T> is generic, it can be used to prioritize any kind of object. In the tests I wrote, however, I exclusively used strings.
A priority is a number between 0 and 100, so I chose to represent that with a byte. Not that this strongly protects invariants, because values can still exceed 100, but on the other hand, there's no reason to use a 32-bit integer to model a number between 0 and 100.
Now that I write this text, I realize that I could have added a Guard Clause to the Prioritized<T> constructor to enforce that precondition, but as you can tell, I didn't think of doing that. This omission, however, doesn't change the conclusion, because the problems that we'll run into stems from another source.
In any case, just inheriting from Collection<Prioritized<T>> isn't enough to guarantee the invariant that the sum of priorities must be 100. An invariant must always hold, even for a newly initialized object. Thus, we need something like this ensure that this is the case:
public sealed class PriorityCollection<T> : Collection<Prioritized<T>> { public PriorityCollection(params Prioritized<T>[] priorities) : base(priorities) { AssertSumIsOneHundred(); } private void AssertSumIsOneHundred() { if (this.Sum(p => p.Priority) != 100) throw new InvalidOperationException( "The sum of all priorities must be 100."); } }
So far, there's no real need to have a separate AssertSumIsOneHundred helper method; I could have kept that check in the constructor, and that would have been simpler. I did, however, anticipate that I'd need the helper method in other parts of the code base. As it turned out, I did, but not without having to change it.
Protecting overrides #
The Collection<T> base class offers normal collection methods like Add, Insert, Remove and so on. The default implementation allows client code to make arbitrary changes to the collection, including clearing it. The PriorityCollection<T> class can't allow that, because such edits could easily violate the invariants.
Collection<T> is explicitly designed to be a base class, so it offers various virtual methods that inheritors can override to change the behaviour. In this case, this is necessary.
As it turned out, I quickly realized that I had to change my assertion helper method to check the invariant in various cases:
private static void AssertSumIsOneHundred(IEnumerable<Prioritized<T>> priorities) { if (priorities.Sum(p => p.Priority) != 100) throw new InvalidOperationException( "The sum of all priorities must be 100."); }
By taking the sequence of priorities as an input argument, this enables me to simulate what would happen if I make a change to the actual collection, for example when adding an item to the collection:
protected override void InsertItem(int index, Prioritized<T> item) { AssertSumIsOneHundred(this.Append(item)); base.InsertItem(index, item); }
By using Append, the InsertItem method creates a sequence of values that simulates what the collection would look like if we add the candidate item. The Append function returns a new collection, so this operation doesn't change the actual PriorityCollection<T>. This only happens if we get past the assertion and call InsertItem.
Likewise, I can protect the invariant in the other overrides:
protected override void RemoveItem(int index) { var l = this.ToList(); l.RemoveAt(index); AssertSumIsOneHundred(l); base.RemoveItem(index); } protected override void SetItem(int index, Prioritized<T> item) { var l = this.ToList(); l[index] = item; AssertSumIsOneHundred(l); base.SetItem(index, item); }
I can even use it in the implementation of ClearItems, although that may seem a tad redundant:
protected override void ClearItems() { AssertSumIsOneHundred([]); }
I could also just have thrown an exception directly from this method, since it's never okay to clear the collection. This would violate the invariant, because the sum of an empty collection of priorities is zero.
As far as I recall, the entire API of Collection<T> is (transitively) based on those four virtual methods, so now that I've protected the invariant in all four, the PriorityCollection<T> class maintains the invariant, right?
Not yet. See if you can spot the problem.
There are, in fact, at least two remaining problems. One that we can recover from, and one that is insurmountable with this design. I'll get back to the serious problem later, but see if you can spot it already.
Leaf mutation #
In the introductory article I wrote:
"If the mutation happens on a leaf node in an object graph, the leaf may have to notify its parent, so that the parent can recheck the invariants."
I realize that this may sound abstract, but the current code presents a simple example. What happens if you change the Priority of an item after you've initialized the collection?
Consider the following example. For various reasons, I wrote the examples (that is, the unit tests) for this exercise in F#, but even if you're not an F# developer, you can probably understand what's going on. First, we create a Prioritized<string> object and use it to initialize a PriorityCollection<string> object named sut:
let item = Prioritized<string> ("foo", 40uy) let sut = PriorityCollection<string> (item, Prioritized<string> ("bar", 60uy))
The item has a priority of 40 (the uy suffix is the F# way of stating that the literal is a byte), and the other unnamed value has a priority of 60, so all is good so far; the sum is 100.
Since, however, item is a mutable object, we can now change its Priority:
item.Priority <- 50uy
This changes item.Priority to 50, but since none of the four virtual base class methods of Collection<T> are involved, the sut never notices, the assertion never runs, and the object is now in an invalid state.
That's what I meant when I discussed mutations in leaf nodes. You can think of a collection as a rather flat and boring tree. The collection object itself is the root, and each of the items are leaves, and no further nesting is allowed.
When you edit a leaf, the root isn't automatically aware of such an event. You explicitly have to wire the object graph up so that this happens.
Event propagation #
One possible way to address this issue is to take advantage of .NET's event system. If you're reading along, but you normally write in another language, you can also use the Observer pattern, or even ReactiveX.
We need to have Prioritized<T> raise events, and one option is to let it implement INotifyPropertyChanging:
public sealed class Prioritized<T> : INotifyPropertyChanging
A Prioritized<T> object can now raise its PropertyChanging event before accepting an edit:
public byte Priority { get => priority; set { if (PropertyChanging is { }) PropertyChanging( this, new PriorityChangingEventArgs(value)); priority = value; } }
where PriorityChangingEventArgs is a little helper class that carries the proposed value around:
public class PriorityChangingEventArgs(byte proposal) : PropertyChangingEventArgs(nameof(Priority)) { public byte Proposal { get; } = proposal; }
A PriorityCollection<T> object can now subscribe to that event on each of the values it keeps track of, so that it can protect the invariant against leaf node mutations.
private void Priority_PropertyChanging(object? sender, PropertyChangingEventArgs e) { if (sender is Prioritized<T> p && e is Prioritized<T>.PriorityChangingEventArgs pcea) { var l = this.ToList(); l[l.IndexOf(p)] = new Prioritized<T>(p.Item, pcea.Proposal); AssertSumIsOneHundred(l); } }
Such a solution comes with its own built-in complexity, because the PriorityCollection<T> class must be careful to subscribe to the PropertyChanging event in various different places. A new Prioritized<T> object may be added to the collection during initialization, or via the InsertItem or SetItem methods. Furthermore, the collection should make sure to unsubscribe from the event if an item is removed from the collection.
To be honest, I didn't bother to implement these extra checks, because the point is moot anyway.
Fatal flaw #
The design shown here comes with a fatal flaw. Can you tell what it is?
Since the invariant is that the priorities must always sum to exactly 100, it's impossible to add, remove, or change any items after initialization.
Or, rather, you can add new Prioritized<T> objects as long as their Priority is 0. Any other value breaks the invariant.
Likewise, the only item you can remove is one with a Priority of 0. Again, if you remove an item with any other Priority, you'd be violating the invariant.
A similar situation arises with editing an existing item. While you can change the Priority of an item, you can only 'change' it to the same value. So you can change 0 to 0, 42 to 42, or 100 to 100, but that's it.
But, I can hear you say, I'll only change 60 to 40 because I intend to add a new item with a 20 priority! In the end, the sum will be 100!
Yes, but this design doesn't know that, and you have no way of telling it.
While we may be able to rectify the situation, I consider this design so compromised that I think it better to start afresh with this realization. Thus, I'll abandon this version of PriorityCollection<T> in favour of a fresh start in the next article.
Conclusion #
While I've titled this article "A failed attempt", the actual purpose was to demonstrate how 'aggregate' requirements make it difficult to maintain class invariants.
I've seen many code bases with poor encapsulation. As far as I can tell, a major reason for that is that the usual 'small-scale' object-oriented design techniques like Guard Clauses fall short when an invariant involves the interplay of multiple objects. And in real business logic, that's the rule rather than the exception.
Not all is lost, however. In the next article, I'll develop an alternative object-oriented solution to the priority collection problem.
Comments
2 things.
I had a difficult time getting this to work with as a mutable type and the only two things I could come with (i spent some hours on it, it was in fact hard!) was
1. To throw an exception when the items in the collection didn't sum up to the budget. That violates the variant because you can add and remove items all you want.
2. Another try, which I didn't finish, is to add some kind of result-object that could tell about the validity of the collection and not expose the collection items before the result is valid.
I haven't tried this and it doesn't resemble a collection but it could perhaps be a way to go.
I am also leaning towards a wrapper around the item type, making it immutable, so the items cannot change afterwards. Cheating ?
I tried with the events approach but it is as you put yourself not a very friendly type you end up with.
Daniel, thank you for writing. You'll be interested in the next articles in the series, then.
Simpler encapsulation with immutability
A worked example.
I've noticed that many software organizations struggle with encapsulation with 'bigger' problems. It may be understandable and easily applicable to define a NaturalNumber type or ensure that a minimum value is less than a maximum value, and so on. How do you, however, guarantee invariants once the scope of the problem becomes bigger and more complex?
In this series of articles, I'll attempt to illustrate how and why this worthy design goal seems elusive, and what you can do to achieve it.
Contracts #
As usual, when I discuss encapsulation, I first need to establish what I mean by the term. It is, after all, one of the most misunderstood concepts in software development. As regular readers will know, I follow the lead of Object-Oriented Software Construction. In that perspective, encapsulation is the appropriate modelling and application of preconditions, invariants, and postconditions.
Particularly when it comes to invariants, things seem to fall apart as the problem being modelled grows in complexity. Teams eventually give up guaranteeing any invariants, leaving client developers with no recourse but defensive coding, which again leads to code duplication, bugs, and maintenance problems.
If you need a reminder, an invariant is an assertion about an object that is always true. The more invariants an object has, the better guarantees it gives, and the more you can trust it. The more you can trust it, the less defensive coding you have to write. You don't have to check if return values are null, strings empty, numbers negative, collections empty, or so on.
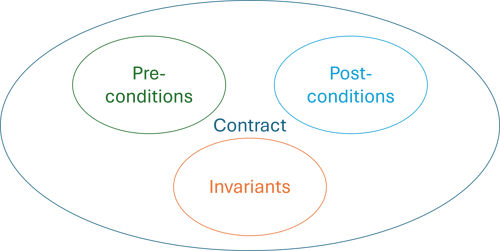
All together, I usually denote the collection of invariants, pre-, and postconditions as a type's contract.
For a simple example like modelling a natural number, or a range, or a user name, most people are able to produce sensible and coherent designs. Once, however, the problem becomes more complex, and the invariants involve multiple interacting values, maintaining the contract becomes harder.
Immutability to the rescue #
I'm not going to bury the lede any longer. It strikes me that mutation is a major source of complexity. It's not that hard to check a set of conditions when you create a value (or object or record). What makes it hard to maintain invariants is when objects are allowed to change. This implies that for every possible change to the object, it needs to examine its current state in order to decide whether or not it should allow the operation.
If the mutation happens on a leaf node in an object graph, the leaf may have to notify its parent, so that the parent can recheck the invariants. If the graph has cycles it becomes more complicated still, and if you want to make the problem truly formidable, try making the object thread-safe.
Making the object immutable makes most of these problems go away. You don't have to worry about thread-safety, because immutable values are automatically thread-safe; there's no state for any thread to change.
Even better, though, is that an immutable object's contract is smaller and simpler. It still has preconditions, because there are rules that govern what has to be true before you can create such an object. Furthermore, there may also be rules that stipulate what must be true before you can call a method on it.
Likewise, postconditions are still relevant. If you call a method on the object, it may give you guarantees about what it returns.
There are, however, no independent invariants.
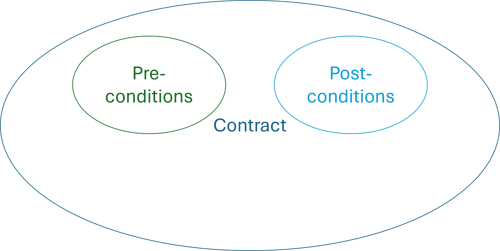
Or rather, the invariants for an immutable object entirely coincide with its preconditions. If it was valid at creation, it remains valid.
Priority collection #
As promised, I'll work through a problem to demonstrate what I mean. I'll first showcase how mutation makes the problem hard, and then how trivial it becomes with an immutable design.
The problem is this: Design and implement a class (or just a data structure if you don't want to do Object-Oriented programming) that models a priority list (not a Priority Queue) as you sometimes run into in surveys. You know, one of these survey questions that asks you to distribute 100 points on various different options:
- Option F: 30%
- Option A: 25%
- Option C: 25%
- Option E: 20%
- Option B: 0%
- Option D: 0%
If you have the time, I suggest that you treat this problem as a kata. Try to do the exercise before reading the next articles in this series. You can assume the following, which is what I did.
- The budget is 100. (You could make it configurable, but the problem is gnarly enough even with a hard-coded value.)
- You don't need to include items with priority value 0, but you should allow it.
- The sum of priorities must be exactly 100. This is the invariant.
The difficult part is that last invariant. Let me stress this requirement: At any time, the object should be in a consistent state; i.e. at any time should the sum of priorities be exactly 100. Not 101 or 99, but 100. Good luck with that.
The object should also be valid at initialization.
Of course, having read this far, you understand that all you have to do is to make the object immutable, but just for the sake of argument, try designing a mutable object with this invariant. Once you've tried your hand with that, read on.
Attempts #
There's educational value going through even failed attempts. When I thought of this example, I fairly quickly outlined in my head one approach that was unlikely to ever work, one that could work, and the nice immutable solution that trivially works.
I'll cover each in turn:
- A failed attempt at priority collection with inheritance
- A mutable priority collection
- An immutable priority collection
It's surprising how hard even a simple exercise like this one turns out to be, if you try to do it the object-oriented way.
In reality, business rules are much more involved than what's on display here. For only a taste of how bad it might get, read Hillel Wayne's suggestions regarding a similar kind of problem.
Conclusion #
If you've lived all your programming life with mutation as an ever-present possibility, you may not realize how much easier immutability makes everything. This includes invariants.
When you have immutable data, object graphs tend to be simpler. You can't easily define cyclic graphs (although Haskell, due to its laziness, surprisingly does enable this), and invariants essentially coincide with preconditions.
In the following articles, I'll show how mutability makes even simple invariants difficult to implement, and how immutability easily addresses the issue.
Next: A failed attempt at priority collection with inheritance.
Comments
I've been enjoying going through your articles in the past couple months, and I really like the very pedagogic treatment of functional programming and adjacent topics.
The kata here is an interesting one, but I don't think I'd link it with the concept of immutability/mutability. My immediate thought was a naïve struct that can represent illegal values and whose validity is managed through functions containing some tricky logic, but that didn't seem promising whether it was done immutably or not.
Instead, the phrase "distribute 100 points" triggered an association with the stars and bars method for similar problems. The idea is that we have N=100 points in a row, and inserting dividers to break it into (numOptions) groups. Concretely, our data structure is (dividers: int array), which is a sorted array of length (numOptions + 1) where the first element is 0 and the last element is N=100. The priorities are then exactly the differences between adjacent elements of the array. The example in the kata (A=25, B=0, C=25, D=0, E=20, F=30) is then represented by the array [| 0; 25; 25; 50; 50; 70; 100|].
This solution seems to respect the invariant, has a configurable budget, can work with other numerical types, and works well whether immutable or not (if mutable, just ensure the array remains sorted, has min 0, and max N). The invariant is encoded in the representation of the data, which seems to me to be the more relevant point than mutability.
And a somewhat disjoint thought, the kata reminded me of a WinForms TableLayoutPanel (or MS Word table) whose column widths all must fit within the container's width...
Thank you for writing. The danger of writing these article series is always that as soon as I've published the first one, someone comes by and puts a big hole through my premise. Well, I write this blog for a couple of independent reasons, and one of them is to learn.
And you just taught me something. Thank you. That is, at least, an elegant implementation.
How would you design the API encapsulating that implementation?
Clearly, arrays already have APIs, so you could obviously define an array-like API that performs the appropriate boundary checks. That, however, doesn't seem to model the given problem. Rather, it reveals the implementation, and forces a client developer to think in terms of the data structure, rather the problem (s)he has to solve.
Ideally, again channelling Bertrand Meyer, an object should present as an Abstract Data Structure (ADT) that doesn't require client developers to understand the implementation details. I'm curious what such an API would look like.
You've already surprised me once, and please do so once again. I'm always happy to learn something new, and that little stars-and-bars concept I've now added to my tool belt.
All that said, this article makes a more general claim, although its possible that the example it showcases is a tad too simple and naive to be a truly revealing one. The claim is that this kind of 'aggregate constraint' often causes so much trouble in the face of arbitrary state mutation that most programmers give up on encapsulation.
What happens if we instead expand the requirements a bit? Let's say that we will require the user to spend at least 90% of the budget, but no more than 100%. Also, there must be at least three prioritized items, and no individual item can receive more than a third of the budget.
Thank you for the response. Here's my thoughts - it's a bit of a wall of text, I might be wrong in any of the following, and the conclusion may be disappointing. When you ask how I'd design the API, I'd say it depends on how the priority list is going to be used. The implementation trick with stars and bars might just be a one-off trick that happens to work here, but it doesn't (shouldn't) affect the contract with the outside world.
If we're considering survey questions or budgets, the interest is in the priority values. So I think the problem then is about a list of priorities with an aggregate constraint. So I would define... an array-like API that performs the appropriate boundary checks (wow), but for the item priorities. My approach would be to go for "private data, public functions", and rely on a legal starting state and preserving the legality through the public API. In pseudocode:
type PriorityList = { budget: int; dividers: int list }
create :: numItems: int -> budget: int -> PriorityList
// Returns priorities.
getAll :: plist: PriorityList -> int list
get :: itemIdx: int -> plist: PriorityList -> int
// *Sets the priority for an item (taking the priority from other items, starting from the back).
set :: itemIdx: int -> priority: int -> plist: PriorityList -> PriorityList
// *Adds a new item to (the end of) the PriorityList (with priority zero).
addItem :: plist: PriorityList -> PriorityList
// *Removes an item from the PriorityList (and assigns its priority to the last item).
removeItem :: itemIdx: int -> plist PriorityList -> PriorityList
// Utility functions: see text
_toPriorities :: dividers: int list -> int list
_toDividers :: priorities: int list -> int list
Crucially: since set, addItem, and removeItem must maintain the invariants, they must have "side effects" of altering other priorities. I think this is unavoidable here because we have aggregate/global constraints, rather than just elementwise/local constraints. (Is this why resizing rows and columns in WinForms tableLayoutPanels and MS Word tables is so tedious?) This will manifest in the API - the client needs to know what "side effects" there are (suggested behaviour in parentheses in the pseudocode comments above). See my crude attempt at implementation.
You may already see where this is going. If I accept that boundary checks are needed, then my secondary goal in encapsulation is to express the constraints as clearly as possible, and hopefully not spread the checking logic all over the code.
Whence the utility functions: it turned out to be useful to convert from a list of dividers to priorities, and vice versa. This is because the elementwise operations/invariants like the individual priority values are easier to express in terms of raw priorities, while the aggregate ones like the total budget are easier in terms of "dividers" (the cumulative priorities). There is a runtime cost to the conversion, but the code becomes clearer. This smells similar to feature envy...
So why not just have the underlying implementation hold a list of priorities in the first place?! Almost everything in the implementation needs translation back to that anyway. D'oh! I refactored myself back to the naïve approach. The original representation seemed elegant, but I couldn't find a way to manipulate it that clients would find intuitive and useful in the given problem.
But... if I approach the design from the angle "what advantages does the cumulative priority model offer?", I might come up with the following candidate API functions, which could be implemented cleanly in the "divider" space:
// (same type, create, get, getAll, addItem as above)
// Removes the item and merges its priority with the item before it.
merge :: ItemIdx: int -> PriorityList
// Sets the priority of an item to zero and gives it to the item after it.
collapse :: itemIdx: int -> PriorityList
// Swaps the priority of an item and the one after it (e.g. to "bubble" a priority value forwards or backwards, although this is easier in the "priority" space)
swap :: itemIdx: int -> PriorityList
// Sets (alternative: adds to) the priority of an item, taking the priority from the items after it in sequence ("consuming" them in the forward direction)
consume :: itemIdx: int -> priority: int -> PriorityList
// Splits the item into 2 smaller items each with half the priority (could be generalised to n items)
split :: ItemIdx: int -> PriorityList
// etc.
And this seems like a more fitting API for that table column width example I keep bringing up. What's interesting to me is that despite the data structures of the budget/survey question and the table column widths being isomorphic, we can come up with rather different APIs depending on which view we consider. I think this is my main takeaway from this exploration, actually.
As for the additional requirements, individually each constraint is easy to handle, but their composition is tricky. If it's easy to transform an illegal PriorityList to make it respect the invariants, we can just apply the transformation after every create/set/add/remove. Something like:
type PriorityList =
{ budget: int
dividers: int list
budgetCondition: int -> bool
maxPriority: int
minChoices: int }
let _enforceBudget (predicate: int -> bool) (defaultBudget: int) (dividers: int list) : int list =
if (List.last dividers |> predicate) then
dividers
else
List.take (dividers.Length - 1) dividers @ [ defaultBudget ]
let _enforceMaxPriority (maxPriority: int) (dividers: int list) : int list =
_toPriorities dividers |> List.map (fun p -> min p maxPriority) |> _toDividers
The problem is those transforms may not preserve each others' invariant. Life would be easy if we could write a single transform to preserve everything (I haven't found one - notice that the two above are operating on different int lists so it's tricky). Otherwise, we could write validations instead of transformations, then let create/set/add/remove fail by returning Option.None (explicitly fail) or the original list (silently fail). This comes at the cost of making the API less friendly.
Ultimately with this approach I can't see a way to make all illegal states unrepresentable without sprinkling ad-hoc checks everywhere in the code. The advantages of the "cumulative priorities" representation I can think of are (a) it makes the total budget invariant obvious, and (b) it maps nicely to a UI where you click and drag segments around. Since you might have gone down a different path in the series, I'm curious to see how that shapes up.
Hello and thank you for your blog. It is really informative and provides great food for thought.
What if it will be impossible to compile and run program which would lead to illegal (list) state?
I've tried to implement priority collection in Rust, and what I've ended up with is a heterogenous priority list with compile-time priority validation. Idea behind this implementation is simple: you declare recursive generic struct, which holds current element and tail (another list or unit type).
struct PriorityList<const B: usize, const P: usize, H, T> {
head: H,
tail: T,
}
If, for example, we need list of two Strings with budget 100, and 30/70 priority split, it will have the following type:
PriorityList<100, 30, String, PriorityList<100, 70, String, ()>>
Note that information about list budget and current element priority is contained in generic arguments B and P respectively.
These are compile-time "variables", and will be replaced be their values in compiled program.
Since each element of such list is a list itself, and budget is the same for each element, all elements except the first are invalid priority lists. So, in order to make it possible to create lists other than containing one element, or only one element with >0 priority, validity check should be targeted and deferred. In order to target invariant validation on the first element of the list, I've included validation into list methods (except set_priority method). Every time list method is called, compiler does recursive computation of priority sum, and compares it with list budget, giving compile-time error if there is mismatch. Consider the following example, which will compile and run:
let list = ListBuilder::new::<10, 10>("Hello");
let list = list.set_priority::<5>();
Seems like invariants have been violated and sum of priorities is less than the budget. But if we try to manipulate this list in any other way except to add element or change priority, program won't compile
// Won't compile
let _ = list.pop();
// Won't compile
let list = list.push::<4>("Hi");
// Will do
let list = list.push::<5>("Hello there");
This implementation may not be as practical as it could be due to verbose compilation error messages, but is a good showcase and exercise I've also uploaded full source code at GitLab: https://gitlab.com/studiedlist/priority-collection
Marken, thank you for writing. It's always interesting to learn new techniques, and, as I previously mentioned, the array-based implementation certainly seems to make illegal states unrepresentable. And then, as we'll see in the last (yet unpublished) article in this little series, if we also make the data structure immutable, we'll have a truly simple and easy-to-understand API to work with.
I've tried experimenting with the F# script you linked, but I must admit that I'm having trouble understanding how to use it. You did write that it was a crude attempt, so I'm not complaining, but on the other hand, it doesn't work well as an example of good encapsulation. The following may seem as though I'm moving the goalpost, so apologies for that in advance.
Usually, when I consult development organizations about software architecture, the failure to maintain invariants is so fundamental that I usually have to start with that problem. That's the reason that this article series is so narrow-mindedly focused on contract, and seemingly not much else. We must not, though, lose sight of what ultimately motivates us to consider encapsulation beneficial. This is what I've tried to outline in Code That Fits in Your Head: That the human brain is ill-suited to keep all implementation details in mind at the same time. One way we may attempt to address this problem is to hide implementation details behind an API which, additionally, comes with some guarantees. Thus (and this is where you may, reasonably, accuse me of moving the goal post), not only should an object fulfil its contract, it should also be possible to interact with its API without understanding implementation details.
The API you propose seem to have problems, some of which may be rectifiable:
- At a fundamental level, it's not really clear to me how to use the various functions in the script file.
- The API doesn't keep track of what is being prioritized. This could probably be fixed.
- It's not clear whether it's possible to transition from one arbitrary valid distribution to another arbitrary valid distribution.
I'll briefly expand on each.
As an example of the API being less that clear to me, I can't say that I understand what's going on here:
> create 1 100 |> set 1 50 |> addItem |> set 1 30;;
val it: PriorityList = { budget = 100
dividers = [0; 50; 100] }
As for what's being prioritized, you could probably mend that shortcoming by letting the array be an array of tuples.
The last part I'm not sure of, but you write:
"Crucially: since
set,addItem, andremoveItemmust maintain the invariants, they must have "side effects" of altering other priorities."
As the most recent article in this series demonstrates, this isn't an overall limitation imposed by the invariant, but rather by your chosen API design. Specifically, assuming that you initially have a 23, 31, 46 distribution, how do you transition to a 19, 29, 43, 7, 2 distribution?
Aliaksei, thank you for writing. I've never programmed in Rust, so I didn't know it had that capability. At first I though it was dependent typing, but after reading up on it, it seems as though it's not quite that.
An exercise like the one in this article series is useful because it can help shed light on options and their various combinations of benefits and drawbacks. Thus, there are no entirely right or wrong solutions to such an exercise.
Since I don't know Rust, I can't easily distinguish what might be possible drawbacks here. I usually regard making illegal states unrepresentable as a benefit, but we must always be careful not to go too far in that direction. One thing is to reject invalid states, but can we still represent all valid states? What if priority distributions are run-time values?
You'll regret using natural keys
Beating another dead horse.
Although I live in Copenhagen and mostly walk or ride my bicycle in order to get around town, I do own an old car for getting around the rest of the country. In Denmark, cars go through mandatory official inspection every other year, and I've been through a few of these in my life. A few years ago, the mechanic doing the inspection informed me that my car's chassis number was incorrect.
This did make me a bit nervous, because I'd bought the car used, and I was suddenly concerned that things weren't really as I thought. Had I unwittingly bought a stolen car?
But the mechanic just walked over to his computer in order to correct the error. That's when a different kind of unease hit me. When you've programmed for some decades, you learn to foresee various typical failure modes. Since a chassis number is an obvious candidate for a natural key, I already predicted that changing the number would prove to be either impossible, or have all sorts of cascading effects, ultimately terminating in official records no longer recognizing that the car is mine.
As it turned out, though, whoever made that piece of software knew what they were doing, because the mechanic just changed the chassis number, and that was that. This is now five or six years ago, and I still own the same car, and I've never had any problems with the official ownership records.
Uniqueness #
The reason I related this story is that I'm currently following an undergraduate course in databases and information systems. Since this course is aimed at students with no real-world experience, it wisely moves forward in a pedagogical progression. In order to teach database keys, it starts with natural keys. From a didactic perspective, this makes sense, but the result, so far, is that the young people I work with now propose database designs with natural keys.
I'm not blaming anyone. You have to learn to crawl before you can walk.
Still, this situation made me reflect on the following question: Are natural keys ever a good idea?
Let's consider an example. For a little project we're doing, we've created a database of the World's 50 best restaurants. My fellow students suggest a table design like this:
CREATE TABLE Restaurants ( year TEXT NOT NULL, rank TEXT NOT NULL, restaurantName TEXT NOT NULL, cityName TEXT NOT NULL );
Granted, at this point, this table definition defines no key at all. I'm not complaining about that. After all, a month ago, the students probably hadn't seen a database table.
From following the course curriculum, it'd be natural, however, to define a key for the Restaurants table as the combination of restaurantName, cityName, and year. The assumption is that name and city uniquely identifies a restaurant.
In this particular example, this assumption may actually turn out to hold. So far. After all, the data set isn't that big, and it's important for restaurants in that league to have recognizable names. If I had to guess, I'd say that there's probably only one Nobelhart & Schmutzig in the world.
Still, a good software architect should challenge the underlying assumptions. Is name and city a natural key? It's easy to imagine that it's not. What if we expand the key to include the country as well? Okay, but what if we had a restaurant named China Wok in Springfield, USA? Hardly unique. Add the state, you say? Probably still not unique.
Identity #
Ensuring uniqueness is only the first of many problems with natural keys. You may quickly reach the conclusion that for a restaurant database, a synthetic key is probably the best choice.
But what about 'natural' natural keys, so to speak? An example may be a car's chassis number. This is already an opaque number, and it probably originates from a database somewhere. Or how about a personal identification number? In Denmark we have the CPR number, and I understand that the US Social Security Number is vaguely analogous.
If you're designing a database that already includes such a personal identification number, you might be tempted to use it as a natural key. After all, it's already a key somewhere else, so it's guaranteed to be unique, right?
Yes, the number may uniquely identify a person, but the converse may not be true. A person may have more than one identification number. At least when time is a factor.
As an example, for technical-historical reasons, the Danish CPR number carries information (which keys shouldn't do), such as a person's date of birth and sex. Since 2014 a new law enables transsexual citizens to get a new CPR number that reflects their perceived gender. The consequence is that the same person may have more than one CPR number. Perhaps not more than one at the same time, but definitely two during a lifetime.
Even if existing keys are guaranteed to be unique, you can't assume that the uniqueness gives rise to a bijection. If you use an external unique key, you may lose track of the entities that you're trying to keep track of.
This is true not only for people, but cars, bicycles (which also have chassis numbers), network cards, etc.
Clerical errors #
Finally, even if you've found a natural key that is guaranteed to be unique and track the actual entity that you want to keep track of, there's a final argument against using an externally defined key in your system: Data-entry errors.
Take the story about my car's chassis number. The mechanic who spotted the discrepancy clearly interpreted it as a clerical error.
After a few decades of programming, I've learned that sooner or later, there will be errors in your data. Either it's a clerical error, or the end-user mistyped, or there was a data conversion error when importing from an external system. Or even data conversion errors within the same system, as it goes through upgrades and migrations.
Your system should be designed to allow corrections to data. This includes corrections of external keys, such as chassis numbers, government IDs, etc. This means that you can't use such keys as database keys in your own system.
Heuristic #
Many were the times, earlier in my career, when I decided to use a 'natural key' as a key in my own database. As far as I recall, I've regretted it every single time.
These days I follow a hard heuristic: Always use synthetic keys for database tables.
Conclusion #
Is it ever a good idea to use natural keys in a database design? My experience tells me that it's not. Ultimately, regardless of how certain you can be that the natural key is stable and correctly tracks the entity that it's supposed to keep track of, data errors will occur. This includes errors in those natural keys.
You should be able to correct such errors without losing track of the involved entities. You'll regret using natural keys. Use synthetic keys.
Comments
There are lots of different types of keys. I agree that using natural keys as physical primary keys is a bad idea but you really should be modelling your data logically with natural keys. Thinking about uniqueness and identity is a part of your data design. Natural keys often end up as constraints, indexes and query plans. When natural keys are not unique enough then you need to consider additional attributes in your design to ensure access to a specific record.
Considering natural keys during design can help elicit additional requirements and business rules. "Does a social security number uniquely identify a person? If not why?" In the UK they recycle them so the natural key is a combination of national insurance number and birth year. You have to ask questions.

I largely agree with James Snape, but wanted to throw in a few other thoughts on top. Surrogates don't defend you from duplicate data, in fact they facilitate it, because the routine generating the surrogate key isn't influenced by any of the other data in the record. The concept of being unable to correct a natural key is also odd, why can't you? Start a transaction, insert a new record with the correct key, update the related records to point to the new record, then delete the old record, done. Want some crucial information about a related record but only have the surrogate to it? I guess you have to join it every time in order to get the columns the user actually wants to see. A foreign key that uses a natural key often often prevents the join entirely, because it tells the user what they wanted to know.
I find the problem with natural keys usually comes from another source entirely. Developers write code and don't tend to prefer using SQL. They typically interact with databases through ORM libraries. ORMs are complicated and rely on conventions to uniformly deal with data. It's not uncommon for ORMs to dictate the structure of tables to some degree, or what datatypes to prefer. It's usually easier in an ORM to have a single datatype for keys (BIGINT?) and use it uniformly across all the tables.
James, Nicholas, thank you for writing. I realize that there are some unstated assumptions and implied concerns that I should have made more explicit. I certainly have no problem with adding constraints and other rules to model data. For the Danish CPR number, for example, while I wouldn't make it a primary key (for the reasons outlined in the article), I'd definitely put a UNIQUE constraint on it.
Another unspoken context that I had in mind is that systems often exist in a wider context where ACID guarantees fall apart. I suppose it's true that if you look at a database in isolation, you may be able to update a foreign key with the help of some cascading changes rippling through the database, but if you've ever shared the old key outside of the database, you now have orphaned data.
A simple example could be sending out an email with a link that embeds the old key. If you change the key after sending out the email, but before the user clicks, the link no longer works.
That's just a simple and easy-to-explain example. The more integration (particularly system-to-system integration) you have, the worse this kind of problem becomes. I briefly discussed the CPR number example with my doctor wife, and she immediately confirmed that this is a real problem in the Danish health sector, where many independent software systems need to exchange patient data.
You can probably work around such problems in various ways, but if you had avoided using natural keys, you wouldn't have had to change the key in the first place.
I think it is best to have two separate generated keys for each row:
- A key used only for relationships between tables. I like to call this relid, and make it serialised, so it is just an increasing number. This key is the primary key and should never be exposed outside the database.
- A key used only outside the database as a unique reference to which row to update. I like to call this id, and make it a uuid, since it is well accepted to uniquely identify rows by a uuid, and to expose them to the outside world - many public APIs do this. Theoretically, the same uuid should never be generated twice, so this key doesn't necessarily have to be declared as unique.
The relid can be used in simple foreign keys, and in bridging/join tables - tables that contain primary keys of multiple tables. Generally speaking, the relid is far more readable than a uuid - it is easier to hold in your head a simple integer, which usually is not that large, than a 36 character sequence that looks similar to other 36 character sequences. UUIDs generally look like a jumble.
A relid can be 32-bits for tables you're confident will never need more than 2.1 billion rows, which really is 99.99% of all tables ever created by 99.99% of applications. If this turns out to be wrong, it is possible to upgrade the relids to 64-bit for a given table. It's a bit of a pain, especially if there are lots of references to it, but it can be done.
The relid doesn't always have to be a serialised value, and you don't always have to call the column relid. Since the primary key is never exposed publicly, it doesn't matter if different column types or names are used for different use cases. For example, code tables might use one of the codes as the primary key.
I don't think it makes sense to be religious on key usage; just like everything else, there are valid reasons for periodically varying how they work. I'm sure somebody has a valid case where a single key is better than two. I just think it generally makes sense to have a pair of internal and external keys for most cases.
The thing with databases keys is you really need to be precise on what you mean by a key. Any combination of attributes is a candidate key. There are also logical and physical representations of keys. For example, a SQL Server primary key is a physical record locator but logically a unique key constraint. Yes, these behave poorly when you use natural keys as the primary key for all the reasons you mention. They are a complete implementation detail. Users should never see these attributes though and you shouldn't share the values outside of your implementation. Sharing integer surrogate keys in urls is a classic issue allowing enumeration attacks on your data if not secured properly.
Foreign keys are another logical and physical dual use concept. In SQL Server a physical foreign key constrain must reference the primary key from a parent table but logically that doesn't need to happen for relational theory to work.
Alternate keys are combinations of attributes that identify a record (or many records); these are often the natural keys you use in your user interface and where clauses etc. Alternate keys are also how systems communicate. Take your CPR number example, you cannot exchange patient data unless both systems agree on a common key. This can't be an internally generated surrogate value.
Natural keys also serve another purpose in parent-child relationships. By sharing natural key attributes with a parent you can ensure a child is not accidentally moved to a new parent plus you can query a child table without needing to join to the parent table.
There isn't a one-size-fits all when it comes to databases and keys. Joe Celko has written extensively on the subject so maybe its better to read the following than my small commentary:
Greg, thank you for writing. I agree with everything you wrote, and I've been using that kind of design for... wow, at least a decade, it looks! for a slightly different reason. This kind of design seems, even if motivated by a different concern, congruent with what you describe.
Like you also imply, only a sith speaks in absolutes. The irony of the article is that I originally intended it to be more open-ended, in the sense that I was curious if there were genuinely good reasons to use natural keys. As I wrote, the article turned out more unconditional than I originally had in mind.
I am, in reality, quite ready to consider arguments to the contrary. But really, I was curious: Is it ever a good idea to use natural keys as primary keys? It sounds like a rhetorical question, but I don't mind if someone furnishes a counter-example.
As Nicholas Peterson intimated, it's probably not a real problem if those keys never 'leave' the database. What I failed to make explicit in this article is that the problems I've consistently run into occur when a system has shared keys with external systems or users.
James, thank you for writing. I think we're discussing issues at different levels of abstraction. This just underscores how difficult technical writing is. I should have made my context and assumptions more explicit. The error is mine.
Everything you write sounds correct to me. I am aware of both relational calculus and relational algebra, so I'm familiar with the claims you make, and I don't dispute them.
My focus is rather on systems architecture. Even an 'internal' system may actually be composed from multiple independent systems, and my concern is that using natural keys to exchange data between such systems ultimately turns out to make things more difficult than they could have been. The only statement of yours with which I think I disagree is that you can't exchange data between systems unless you use natural keys. You definitely can, although you need to appoint one of the systems to be a 'master key issuer'.
In practice, like Greg Hall, I'd prefer using GUIDs for that purpose, rather than sequential numbers. That also addresses the concern about enumeration attacks. (Somewhat tangentially, I also recommend signing URLs with a private key in order to prevent reverse-engineering, or 'URL-hacking'.)
I think we are basically agreeing here because I would never use natural keys nor externally visible synthetic keys for physical primary keys. (I think this statement is even more restrictive than the article's main premise). Well, with a rule exception for configurable enum type tables because the overhead of joining to resolve a single column value is inefficient. I would however always use a natural key for a logical primary key.
The only reason why I'm slightly pedantic about this is due the the number of clients why have used surrogate keys in a logical model and then gone on to create databases where the concept of entity identity doesn't exist. This creates many of the issues Nicholas Peterson mentioned above: duplicates, historical change tracking, etc. Frankly, it doesn't help that lots of code examples for ORMs just start with an entity that has an ID attribute.
One final comment on sharing data based on a golden master synthetic key. The moment you do I would argue that you have now committed to maintaining that key through all types of data mergers and acquisitions. It must never collide, and always point to exactly the same record and only that record. Since users can use it to refer to an entity and it makes up part of your external API, it now meets the definition of a natural key. Whether you agree or not on my stretching the definition a little, you still should not use this attribute as the physical primary key (record locator) because we should not expose implementation details in our APIs. The first Celko article I linked to explains some of the difficulties for externally visible synthetic keys.
I'd like to comment with an example where using a synthetic key came back to bite me. My system had posts and users with synthetic IDs. Now I wanted to track an unread state across them. Naively, I designed just another entity:
public int ID { get; set; }
public int PostID { get; set; }
public int UserID { get; set; }
And it worked flawlessly for years. One day, however, a user complained that he always got an exception "Sequence contains more than one element". Of course I used SingleOrDefault() in application code because I expected 0 or 1 record per user and post. The quick solution was deleting the spurious table row. As a permanant solution I removed the ID field (and column) so the unread state had its natural key as primary key (both columns). So if it happens again in the future, the app will error on insertin rather than querying.
Since my application is in control of the IDs and it's just a very simple join table I think it was the best solution. If the future requirements hold different kinds of unread state, I can always add the key again.
Julius, thank you for writing. I see what you mean, and would also tend to model this as just a table with two foreign keys. From the perspective of entity-relationship modelling, such a table isn't even an entity, but rather a relationship. For that reason, it doesn't need its own key; not because the combination is 'natural', but rather because it's not really an independent 'thing'.
Continuous delivery without a CI server
An illustrative example.
More than a decade ago, I worked on a small project. It was a small single-page application (SPA) with a REST API backend, deployed to Azure. As far as I recall, the REST API used blob storage, so all in all it wasn't a complex system.
We were two developers, and although we wanted to do continuous delivery (CD), we didn't have much development infrastructure. This was a little startup, and back then, there weren't a lot of free build services available. We were using GitHub, but it was before it had any free services to compile your code and run tests.
Given those constraints, we figured out a simple way to do CD, even though we didn't have a continuous integration (CI) server.
I'll tell you how we did this.
Shining an extraordinary light on the mundane #
The reason I'm relating this little story isn't to convince you that you, too, should do it that way. Rather, it's a didactic device. By doing something extreme, we can sometimes learn about the ordinary.
You can only be pragmatic if you know how to be dogmatic.
From what I hear and read, it seems that there's a lot of organizations that believe that they're doing CI (or perhaps even CD) because they have a CI server. What the following tale will hopefully highlight is that, while build servers are useful, they aren't a requirement for CI or CD.
Distributed CD #
Dramatis personae: My colleague and me. Scene: One small SPA project with a REST API and blob storage, to be deployed to Azure. Code base in GitHub. Two laptops. Remote work.
One of us (let's say me) would start on implementing a feature, or fixing a bug. I'd use test-driven development (TDD) to get feedback on API ideas, as well as to accumulate a suite of regression tests. After a few hours of effective work, I'd send a pull request to my colleague.
Since we were only two people on the team, the responsibility was clear. It was the other person's job to review the pull request. It was also clear that the longer the reviewer dawdled, the less efficient the process would be. For that reason, we'd typically have agile pull requests with a good turnaround time.
While we were taking advantage of GitHub as a central coordination hub for pull requests, Git itself is famously distributed. Thus, we wondered whether it'd be possible to make the CD process distributed as well.
Yes, apart from GitHub, what we did was already distributed.
A little more automation #
Since we were both doing TDD, we already had automated tests. Due to the simple setup of the system, we'd already automated more than 80% of our process. It wasn't much of a stretch to automate whatever else needed automation. Such as deployment.
We agreed on a few simple rules:
- Every part of our process should be automated.
- Reviewing a pull request included running all tests.
When people review pull requests, they often just go to GitHub and look around before issuing an LGTM.
But, you do realize that this is Git, right? You can pull down the proposed changes and run them.
What if you're already in the middle of something, working on the same code base? Stash your changes and pull down the code.
The consequence of this process was that every time a pull request was accepted, we already knew that it passed all automated tests on two physical machines. We actually didn't need a server to run the tests a third time.
After a merge, the final part of the development process mandated that the original author should deploy to production. We had Bash script that did that.
Simplicity #
This process came with some built-in advantages. First of all, it was simple. There wasn't a lot of moving parts, so there weren't many steps that could break.
Have you ever had the pleasure of troubleshooting a build? The code works on your machine, but not on the build server.
It sometimes turns out that there's a configuration mismatch with the compiler or test tools. Thus, the problem with the build server doesn't mean that you prevented a dangerous defect from being deployed to production. No, the code just didn't compile on the build server, but would actually have run fine on the production system.
It's much easier troubleshooting issues on your own machine than on some remote server.
I've also seen build servers that were set up to run tests, but along the way, something had failed and the tests didn't run. And no-one was looking at logs or warning emails from the build system because that system would already be sending hundreds of warnings a day.
By agreeing to manually(!) run the automated tests as part of the review process, we were sure that they were exercised.
Finally, by keeping the process simple, we could focus on what mattered: Delivering value to our customer. We didn't have to waste time learning how a proprietary build system worked.
Does it scale? #
I know what you're going to say: This may have worked because the overall requirements were so simple. This will never work in a 'real' development organization, with a 'real' code base.
I understand. I never claimed that it would.
The point of this story is to highlight what CI and CD is. It's a way of working where you continuously integrate your code with everyone else's code, and where you continuously deploy changes to production.
In reality, having a dedicated build system for that can be useful. These days, such systems tend to be services that integrate with GitHub or other sites, rather than an actual server that you have to care for. Even so, having such a system doesn't mean that your organization makes use of CI or CD.
(Oh, and for the mathematically inclined: In this context continuous doesn't mean actually continuous. It just means arbitrarily often.)
Conclusion #
CI and CD are processes that describe how we work with code, and how we work together.
Continuous integration means that you often integrate your code with everyone else's code. How often? More than once a day.
Continuous deployment means that you often deploy code changes to production. How often? Every time new code is integrated.
A build system can be convenient to help along such processes, but it's strictly speaking not required.
Fundamentals
How to stay current with technology progress.
A long time ago, I landed my dream job. My new employer was a consulting company, and my role was to be the resident Azure expert. Cloud computing was still in its infancy, and there was a good chance that I might be able to establish myself as a leading regional authority on the topic.
As part of the role, I was supposed to write articles and give presentations showing how to solve various problems with Azure. I dug in with fervour, writing sample code bases and even an MSDN Magazine article. To my surprise, after half a year I realized that I was bored.
At that time I'd already spent more than a decade learning new technology, and I knew that I was good at it. For instance, I worked five years for Microsoft Consulting Services, and a dirty little secret of that kind of role is that, although you're sold as an expert in some new technology, you're often only a few weeks ahead of your customer. For example, I was once engaged as a Windows Workflow Foundation expert at a time when it was still in beta. No-one had years of experience with that technology, but I was still expected to know much more about it than my customer.
I had lots of engagements like that, and they usually went well. I've always been good at cramming, and as a consultant you're also unencumbered by all the daily responsibilities and politics that often occupy the time and energy of regular employees. The point being that while I'm decent at learning new stuff, the role of being a consultant also facilitates that sort of activity.
After more then a decade of learning new frameworks, new software libraries, new programming languages, new tools, new online services, it turned out that I was ready for something else. After spending a few months learning Azure, I realized that I'd lost interest in that kind of learning. When investigating a new Azure SDK, I'd quickly come to the conclusion that, oh, this is just another object-oriented library. There are these objects, and you call this method to do that, etc. That's not to say that learning a specific technology is a trivial undertaking. The worse the design, the more difficult it is to learn.
Still, after years of learning new technologies, I'd started recognizing certain patterns. Perhaps, I thought, well-designed technologies are based on some fundamental ideas that may be worth learning instead.
Staying current #
A common lament among software developers is that the pace of technology is so overwhelming that they can't keep up. This is true. You can't keep up.
There will always be something that you don't know. In fact, most things you don't know. This isn't a condition isolated only to technology. The sum total of all human knowledge is so vast that you can't know it all. What you will learn, even after a lifetime of diligent study, will be a nanoscopic fraction of all human knowledge - even of everything related to software development. You can't stay current. Get used to it.
A more appropriate question is: How do I keep my skill set relevant?
Assuming that you wish to stay employable in some capacity, it's natural to be concerned with how your mad Flash skillz will land you the next gig.
Trying to keep abreast of all new technologies in your field is likely to lead to burnout. Rather, put yourself in a position so that you can quickly learn necessary skills, just in time.
Study fundamentals, rather than specifics #
Those many years ago, I realized that it'd be a better investment of my time to study fundamentals. Often, once you have some foundational knowledge, you can apply it in many circumstances. Your general knowledge will enable you to get quickly up to speed with specific technologies.
Success isn't guaranteed, but knowing fundamentals increases your chances.
This may still seem too abstract. Which fundamentals should you learn?
In the remainder of this article, I'll give you some examples. The following collection of general programmer knowledge spans software engineering, computer science, broad ideas, but also specific tools. I only intend this set of examples to serve as inspiration. The list isn't complete, nor does it constitute a minimum of what you should learn.
If you have other interests, you may put together your own research programme. What follows here are just some examples of fundamentals that I've found useful during my career.
A criterion, however, for constituting foundational knowledge is that you should be able to apply that knowledge in a wide variety of contexts. The fundamental should not be tied to a particular programming language, platform, or operating system.
Design patterns #
Perhaps the first foundational notion that I personally encountered was that of design patterns. As the Gang of Four (GoF) wrote in the book, a design pattern is an abstract description of a solution that has been observed 'in the wild', more than once, independently evolved.
Please pay attention to the causality. A design pattern isn't prescriptive, but descriptive. It's an observation that a particular code organisation tends to solve a particular problem.
There are lots of misconceptions related to design patterns. One of them is that the 'library of patterns' is finite, and more or less constrained to the patterns included in the original book.
There are, however, many more patterns. To illustrate how much wider this area is, here's a list of some patterns books in my personal library:
- Design Patterns
- Pattern Languages of Program Design 3
- Patterns of Enterprise Application Architecture
- Enterprise Integration Patterns
- xUnit Test Patterns
- Service Design Patterns
- Implementation Patterns
- RESTful Web Services Cookbook
- AntiPatterns
In addition to these, there are many more books in my library that are patterns-adjacent, including one of my own. The point is that software design patterns is a vast topic, and it pays to know at least the most important ones.
A design pattern fits the criterion that you can apply the knowledge independently of technology. The original GoF book has examples in C++ and Smalltalk, but I've found that they apply well to C#. Other people employ them in their Java code.
Knowing design patterns not only helps you design solutions. That knowledge also enables you to recognize patterns in existing libraries and frameworks. It's this fundamental knowledge that makes it easier to learn new technologies.
Often (although not always) successful software libraries and frameworks tend to follow known patterns, so if you're aware of these patterns, it becomes easier to learn such technologies. Again, be aware of the causality involved. I'm not claiming that successful libraries are explicitly designed according to published design patterns. Rather, some libraries become successful because they offer good solutions to certain problems. It's not surprising if such a good solution falls into a pattern that other people have already observed and recorded. It's like parallel evolution.
This was my experience when I started to learn the details of Azure. Many of those SDKs and APIs manifested various design patterns, and once I'd recognized a pattern it became much easier to learn the rest.
The idea of design patterns, particularly object-oriented design patterns, have its detractors, too. Let's visit that as the next set of fundamental ideas.
Functional programming abstractions #
As I'm writing this, yet another Twitter thread pokes fun at object-oriented design (OOD) patterns as being nothing but a published collection of workarounds for the shortcomings of object orientation. The people who most zealously pursue that agenda tends to be functional programmers.
Well, I certainly like functional programming (FP) better than OOD too, but rather than poking fun at OOD, I'm more interested in how design patterns relate to universal abstractions. I also believe that FP has shortcomings of its own, but I'll have more to say about that in a future article.
Should you learn about monoids, functors, monads, catamorphisms, and so on?
Yes you should, because these ideas also fit the criterion that the knowledge is technology-independent. I've used my knowledge of these topics in Haskell (hardly surprising) and F#, but also in C# and Python. The various LINQ methods are really just well-known APIs associated with, you guessed it, functors, monads, monoids, and catamorphisms.
Once you've learned these fundamental ideas, it becomes easier to learn new technologies. This has happened to me multiple times, for example in contexts as diverse as property-based testing and asynchronous message-passing architectures. Once I realize that an API gives rise to a monad, say, I know that certain functions must be available. I also know how I should best compose larger code blocks from smaller ones.
Must you know all of these concepts before learning, say, F#? No, not at all. Rather, a language like F# is a great vehicle for learning such fundamentals. There's a first time for learning anything, and you need to start somewhere. Rather, the point is that once you know these concepts, it becomes easier to learn the next thing.
If, for example, you already know what a monad is when learning F#, picking up the idea behind computation expressions is easy once you realize that it's just a compiler-specific way to enable syntactic sugaring of monadic expressions. You can learn how computation expressions work without that knowledge, too; it's just harder.
This is a recurring theme with many of these examples. You can learn a particular technology without knowing the fundamentals, but you'll have to put in more time to do that.
On to the next example.
SQL #
Which object-relational mapper (ORM) should you learn? Hibernate? Entity Framework?
How about learning SQL? I learned SQL in 1999, I believe, and it's served me well ever since. I consider raw SQL to be more productive than using an ORM. Once more, SQL is largely technology-independent. While each database typically has its own SQL dialect, the fundamentals are the same. I'm most well-versed in the SQL Server dialect, but I've also used my SQL knowledge to interact with Oracle and PostgreSQL. Once you know one SQL dialect, you can quickly solve data problems in one of the other dialects.
It doesn't matter much whether you're interacting with a database from .NET, Haskell, Python, Ruby, or another language. SQL is not only universal, the core of the language is stable. What I learned in 1999 is still useful today. Can you say the same about your current ORM?
Most programmers prefer learning the newest, most cutting-edge technology, but that's a risky gamble. Once upon a time Silverlight was a cutting-edge technology, and more than one of my contemporaries went all-in on it.
On the contrary, most programmers find old stuff boring. It turns out, though, that it may be worthwhile learning some old technologies like SQL. Be aware of the Lindy effect. If it's been around for a long time, it's likely to still be around for a long time. This is true for the next example as well.
HTTP #
The HTTP protocol has been around since 1991. It's an effectively text-based protocol, and you can easily engage with a web server on a near-protocol level. This is true for other older protocols as well.
In my first IT job in the late 1990s, one of my tasks was to set up and maintain Exchange Servers. It was also my responsibility to make sure that email could flow not only within the organization, but that we could exchange email with the rest of the internet. In order to test my mail servers, I would often just telnet into them on port 25 and type in the correct, text-based instructions to send a test email.
Granted, it's not that easy to telnet into a modern web server on port 80, but a ubiquitous tool like curl accomplishes the same goal. I recently wrote how knowing curl is better than knowing Postman. While this wasn't meant as an attack on Postman specifically, neither was it meant as a facile claim that curl is the only tool useful for ad-hoc interaction with HTTP-based APIs. Sometimes you only realize an underlying truth when you write about a thing and then other people find fault with your argument. The underlying truth, I think, is that it pays to understand HTTP and being able to engage with an HTTP-based web service at that level of abstraction.
Preferably in an automatable way.
Shells and scripting #
The reason I favour curl over other tools to interact with HTTP is that I already spend quite a bit of time at the command line. I typically have a little handful of terminal windows open on my laptop. If I need to test an HTTP server, curl is already available.
Many years ago, an employer introduced me to Git. Back then, there were no good graphical tools to interact with Git, so I had to learn to use it from the command line. I'm eternally grateful that it turned out that way. I still use Git from the command line.
When you install Git, by default you also install Git Bash. Since I was already using that shell to interact with Git, it began to dawn on me that it's a full-fledged shell, and that I could do all sorts of other things with it. It also struck me that learning Bash would be a better investment of my time than learning PowerShell. At the time, there was no indication that PowerShell would ever be relevant outside of Windows, while Bash was already available on most systems. Even today, knowing Bash strikes me as more useful than knowing PowerShell.
It's not that I do much Bash-scripting, but I could. Since I'm a programmer, if I need to automate something, I naturally reach for something more robust than shell scripting. Still, it gives me confidence to know that, since I already know Bash, Git, curl, etc., I could automate some tasks if I needed to.
Many a reader will probably complain that the Git CLI has horrible developer experience, but I will, again, postulate that it's not that bad. It helps if you understand some fundamentals.
Algorithms and data structures #
Git really isn't that difficult to understand once you realize that a Git repository is just a directed acyclic graph (DAG), and that branches are just labels that point to nodes in the graph. There are basic data structures that it's just useful to know. DAGs, trees, graphs in general, adjacency lists or adjacency matrices.
Knowing that such data structures exist is, however, not that useful if you don't know what you can do with them. If you have a graph, you can find a minimum spanning tree or a shortest-path tree, which sometimes turn out to be useful. Adjacency lists or matrices give you ways to represent graphs in code, which is why they are useful.
Contrary to certain infamous interview practices, you don't need to know these algorithms by heart. It's usually enough to know that they exist. I can't remember Dijkstra's algorithm off the top of my head, but if I encounter a problem where I need to find the shortest path, I can look it up.
Or, if presented with the problem of constructing current state from an Event Store, you may realize that it's just a left fold over a linked list. (This isn't my own realization; I first heard it from Greg Young in 2011.)
Now we're back at one of the first examples, that of FP knowledge. A list fold is its catamorphism. Again, these things are much easier to learn if you already know some fundamentals.
What to learn #
These examples may seems overwhelming. Do you really need to know all of that before things become easier?
No, that's not the point. I didn't start out knowing all these things, and some of them, I'm still not very good at. The point is rather that if you're wondering how to invest your limited time so that you can remain up to date, consider pursuing general-purpose knowledge rather than learning a specific technology.
Of course, if your employer asks you to use a particular library or programming language, you need to study that, if you're not already good at it. If, on the other hand, you decide to better yourself, you can choose what to learn next.
Ultimately, if your're learning for your own sake, the most important criterion may be: Choose something that interests you. If no-one forces you to study, it's too easy to give up if you lose interest.
If, however, you have the choice between learning Noun.js or design patterns, may I suggest the latter?
For life #
When are you done, you ask?
Never. There's more stuff than you can learn in a lifetime. I've met a lot of programmers who finally give up on the grind to keep up, and instead become managers.
As if there's nothing to learn when you're a manager. I'm fortunate that, before I went solo, I mainly had good managers. I'm under no illusion that they automatically became good managers. All I've heard said about management is that there's a lot to learn in that field, too. Really, it'd be surprising if that wasn't the case.
I can understand, however, how just keep learning the next library, the next framework, the next tool becomes tiring. As I've already outlined, I hit that wall more than a decade ago.
On the other hand, there are so many wonderful fundamentals that you can learn. You can do self-study, or you can enrol in a more formal programme if you have the opportunity. I'm currently following a course on compiler design. It's not that I expect to pivot to writing compilers for the rest of my career, but rather,
- "It is considered a topic that you should know in order to be "well-cultured" in computer science.
- "A good craftsman should know his tools, and compilers are important tools for programmers and computer scientists.
- "The techniques used for constructing a compiler are useful for other purposes as well.
- "There is a good chance that a programmer or computer scientist will need to write a compiler or interpreter for a domain-specific language."
That's good enough for me, and so far, I'm enjoying the course (although it's also hard work).
You may not find this particular topic interesting, but then hopefully you can find something else that you fancy. 3D rendering? Machine learning? Distributed systems architecture?
Conclusion #
Technology moves at a pace with which it's impossible to keep up. It's not just you who's falling behind. Everyone is. Even the best-paid GAMMA programmer knows next to nothing of all there is to know in the field. They may have superior skills in certain areas, but there will be so much other stuff that they don't know.
You may think of me as a thought leader if you will. If nothing else, I tend to be a prolific writer. Perhaps you even think I'm a good programmer. I should hope so. Who fancies themselves bad at something?
You should, however, have seen me struggle with C programming during a course on computer systems programming. There's a thing I'm happy if I never have to revisit.
You can't know it all. You can't keep up. But you can focus on learning the fundamentals. That tends to make it easier to learn specific technologies that build on those foundations.
Gratification
Some thoughts on developer experience.
Years ago, I was introduced to a concept called developer ergonomics. Despite the name, it's not about good chairs, standing desks, or multiple monitors. Rather, the concept was related to how easy it'd be for a developer to achieve a certain outcome. How easy is it to set up a new code base in a particular language? How much work is required to save a row in a database? How hard is it to read rows from a database and display the data on a web page? And so on.
These days, we tend to discuss developer experience rather than ergonomics, and that's probably a good thing. This term more immediately conveys what it's about.
I've recently had some discussions about developer experience (DevEx, DX) with one of my customers, and this has lead me to reflect more explicitly on this topic than previously. Most of what I'm going to write here are opinions and beliefs that go back a long time, but apparently, it's only recently that these notions have congealed in my mind under the category name developer experience.
This article may look like your usual old-man-yells-at-cloud article, but I hope that I can avoid that. It's not the case that I yearn for some lost past where 'we' wrote Plankalkül in Edlin. That, in fact, sounds like a horrible developer experience.
The point, rather, is that most attractive things come with consequences. For anyone who have been reading this blog even once in a while, this should come as no surprise.
Instant gratification #
Fat foods, cakes, and wine can be wonderful, but can be detrimental to your health if you overindulge. It can, however, be hard to resist a piece of chocolate, and even if we think that we shouldn't, we often fail to restrain ourselves. The temptation of instant gratification is simply too great.
There are other examples like this. The most obvious are the use of narcotics, lack of exercise, smoking, and dropping out of school. It may feel good in the moment, but can have long-term consequences.
Small children are notoriously bad at delaying gratification, and we often associate the ability to delay gratification with maturity. We all, however, fall in from time to time. Food and wine are my weak spots, while I don't do drugs, and I didn't drop out of school.
It strikes me that we often talk about ideas related to developer experience in a way where we treat developers as children. To be fair, many developers also act like children. I don't know how many times I've heard something like, "I don't want to write tests/go through a code review/refactor! I just want to ship working code now!"
Fine, so do I.
Even if wine is bad for me, it makes life worth living. As the saying goes, even if you don't smoke, don't drink, exercise rigorously, eat healthily, don't do drugs, and don't engage in dangerous activities, you're not guaranteed to live until ninety, but you're guaranteed that it's going to feel that long.
Likewise, I'm aware that doing everything right can sometimes take so long that by the time we've deployed the software, it's too late. The point isn't to always or never do certain things, but rather to be aware of the consequences of our choices.
Developer experience #
I've no problem with aiming to make the experience of writing software as good as possible. Some developer-experience thought leaders talk about the importance of documentation, predictability, and timeliness. Neither do I mind that a development environment looks good, completes my words, or helps me refactor.
To return to the analogy of human vices, not everything that feels good is ultimately bad for you. While I do like wine and chocolate, I also love sushi, white asparagus, turbot, chanterelles, lumpfish roe caviar, true morels, Norway lobster, and various other foods that tend to be categorized as healthy.
A good IDE with refactoring support, statement completion, type information, test runner, etc. is certainly preferable to writing all code in Notepad.
That said, there's a certain kind of developer tooling and language features that strikes me as more akin to candy. These are typically tools and technologies that tend to demo well. Recent examples include OpenAPI, GitHub Copilot, C# top-level statements, code generation, and Postman. Not all of these are unequivocally bad, but they strike me as mostly aiming at immature developers.
The point of this article isn't to single out these particular products, standards, or language features, but on the other hand, in order to make a point, I do have to at least outline why I find them problematic. They're just examples, and I hope that by explaining what is on my mind, you can see the pattern and apply it elsewhere.
OpenAPI #
A standard like OpenAPI, for example, looks attractive because it automates or standardizes much work related to developing and maintaining REST APIs. Frameworks and tools that leverage that standard automatically creates machine-readable schema and contract, which can be used to generate client code. Furthermore, an OpenAPI-aware framework can also autogenerate an entire web-based graphical user interface, which developers can use for ad-hoc testing.
I've worked with clients who also published these OpenAPI user interfaces to their customers, so that it was easy to get started with the APIs. Easy onboarding.
Instant gratification.
What's the problem with this? There are clearly enough apparent benefits that I usually have a hard time talking my clients out of pursuing this strategy. What are the disadvantages? Essentially, OpenAPI locks you into level 2 APIs. No hypermedia controls, no smooth conneg-based versioning, no HATEOAS. In fact, most of what makes REST flexible is lost. What remains is an ad-hoc, informally-specified, bug-ridden, slow implementation of half of SOAP.
I've previously described my misgivings about Copilot, and while I actually still use it, I don't want to repeat all of that here. Let's move on to another example.
Top-level statements #
Among many other language features, C# 9 got top-level-statements. This means that you don't need to write a Main method in a static class. Rather, you can have a single C# code file where you can immediately start executing code.
It's not that I consider this language feature particularly harmful, but it also solves what seems to me a non-problem. It demos well, though. If I understand the motivation right, the feature exists because 'modern' developers are used to languages like Python where you can, indeed, just create a .py file and start adding code statements.
In an attempt to make C# more attractive to such an audience, it, too, got that kind of developer experience enabled.
You may argue that this is a bid to remove some of the ceremony from the language, but I'm not convinced that this moves that needle much. The level of ceremony that a language like C# has is much deeper than that. That's not to target C# in particular. Java is similar, and don't even get me started on C or C++! Did anyone say header files?
Do 'modern' developers choose Python over C# because they can't be arsed to write a Main method? If that's the only reason, it strikes me as incredibly immature. I want instant gratification, and writing a Main method is just too much trouble!
If developers do, indeed, choose Python or JavaScript over C# and Java, I hope and believe that it's for other reasons.
This particular C# feature doesn't bother me, but I find it symptomatic of a kind of 'innovation' where language designers target instant gratification.
Postman #
Let's consider one more example. You may think that I'm now attacking a company that, for all I know, makes a decent product. I don't really care about that, though. What I do care about is the developer mentality that makes a particular tool so ubiquitous.
I've met web service developers who would be unable to interact with the HTTP APIs that they are themselves developing if they didn't have Postman. Likewise, there are innumerable questions on Stack Overflow where people ask questions about HTTP APIs and post screen shots of Postman sessions.
It's okay if you don't know how to interact with an HTTP API. After all, there's a first time for everything, and there was a time when I didn't know how to do this either. Apparently, however, it's easier to install an application with a graphical user interface than it is to use curl.
Do yourself a favour and learn curl instead of using Postman. Curl is a command-line tool, which means that you can use it for both ad-hoc experimentation and automation. It takes five to ten minutes to learn the basics. It's also free.
It still seems to me that many people are of a mind that it's easier to use Postman than to learn curl. Ultimately, I'd wager that for any task you do with some regularity, it's more productive to learn the text-based tool than the point-and-click tool. In a situation like this, I'd suggest that delayed gratification beats instant gratification.
CV-driven development #
It is, perhaps, easy to get the wrong impression from the above examples. I'm not pointing fingers at just any 'cool' new technology. There are techniques, languages, frameworks, and so on, which people pick up because they're exciting for other reasons. Often, such technologies solve real problems in their niches, but are then applied for the sole reason that people want to get on the bandwagon. Examples include Kubernetes, mocks, DI Containers, reflection, AOP, and microservices. All of these have legitimate applications, but we also hear about many examples where people use them just to use them.
That's a different problem from the one I'm discussing in this article. Usually, learning about such advanced techniques requires delaying gratification. There's nothing wrong with learning new skills, but part of that process is also gaining the understanding of when to apply the skill, and when not to. That's a different discussion.
Innovation is fine #
The point of this article isn't that every innovation is bad. Contrary to Charles Petzold, I don't really believe that Visual Studio rots the mind, although I once did publish an article that navigated the same waters.
Despite my misgivings, I haven't uninstalled GitHub Copilot, and I do enjoy many of the features in both Visual Studio (VS) and Visual Studio Code (VS Code). I also welcome and use many new language features in various languages.
I can certainly appreciate how an IDE makes many things easier. Every time I have to begin a new Haskell code base, I long for the hand-holding offered by Visual Studio when creating a new C# project.
And although I don't use the debugger much, the built-in debuggers in VS and VS Code sure beat GDB. It even works in Python!
There's even tooling that I wish for, but apparently never will get.
Simple made easy #
In Simple Made Easy Rich Hickey follows his usual look-up-a-word-in-the-dictionary-and-build-a-talk-around-the-definition style to contrast simple with easy. I find his distinction useful. A tool or technique that's close at hand is easy. This certainly includes many of the above instant-gratification examples.
An easy technique is not, however, necessarily simple. It may or may not be. Rich Hickey defines simple as the opposite of complex. Something that is complex is assembled from parts, whereas a simple thing is, ideally, single and undivisible. In practice, truly simple ideas and tools may not be available, and instead we may have to settle with things that are less complex than their alternatives.
Once you start looking for things that make simple things easy, you see them in many places. A big category that I personally favour contains all the language features and tools that make functional programming (FP) easier. FP tends to be simpler than object-oriented or procedural programming, because it explicitly distinguishes between and separates predictable code from unpredictable code. This does, however, in itself tend to make some programming tasks harder. How do you generate a random number? Look up the system time? Write a record to a database?
Several FP languages have special features that make even those difficult tasks easy. F# has computation expressions and Haskell has do notation.
Let's say you want to call a function that consumes a random number generator. In Haskell (as in .NET) random number generators are actually deterministic, as long as you give them the same seed. Generating a random seed, on the other hand, is non-deterministic, so has to happen in IO.
Without do notation, you could write the action like this:
rndSelect :: Integral i => [a] -> i -> IO [a] rndSelect xs count = (\rnd -> rndGenSelect rnd xs count) <$> newStdGen
(The type annotation is optional.) While terse, this is hardly readable, and the developer experience also leaves something to be desired. Fortunately, however, you can rewrite this action with do notation, like this:
rndSelect :: Integral i => [a] -> i -> IO [a] rndSelect xs count = do rnd <- newStdGen return $ rndGenSelect rnd xs count
Now we can clearly see that the action first creates the rnd random number generator and then passes it to rndGenSelect. That's what happened before, but it was buried in a lambda expression and Haskell's right-to-left causality. Most people would find the first version (without do notation) less readable, and more difficult to write.
Related to developer ergonomics, though, do notation makes the simple code (i.e. code that separates predictable code from unpredictable code) easy (that is; at hand).
F# computation expressions offer the same kind of syntactic sugar, making it easy to write simple code.
Delay gratification #
While it's possible to set up a development context in such a way that it nudges you to work in a way that's ultimately good for you, temptation is everywhere.
Not only may new language features, IDE functionality, or frameworks entice you to do something that may be disadvantageous in the long run. There may also be actions you don't take because it just feels better to move on.
Do you take the time to write good commit messages? Not just a single-line heading, but a proper message that explains your context and reasoning?
Most people I've observed working with source control 'just want to move on', and can't be bothered to write a useful commit message.
I hear about the same mindset when it comes to code reviews, particularly pull request reviews. Everyone 'just wants to write code', and no-one want to review other people's code. Yet, in a shared code base, you have to live with the code that other people write. Why not review it so that you have a chance to decide what that shared code base should look like?
Delay your own gratification a bit, and reap the awards later.
Conclusion #
The only goal I have with this article is to make you think about the consequences of new and innovative tools and frameworks. Particularly if they are immediately compelling, they may be empty calories. Consider if there may be disadvantages to adopting a new way of doing things.
Some tools and technologies give you instant gratification, but may be unhealthy in the long run. This is, like most other things, context-dependent. In the long run your company may no longer be around. Sometimes, it pays to deliberately do something that you know is bad, in order to reach a goal before your competition. That was the original technical debt metaphor.
Often, however, it pays to delay gratification. Learn curl instead of Postman. Learn to design proper REST APIs instead of relying on OpenAI. If you need to write ad-hoc scripts, use a language suitable for that.
Comments
Regarding Postman vs. curl, I have to disagree. Sure, curl is pretty easy to use. But while it's good for one-off tests, it sucks when you need to maintain a collection of requests that you can re-execute whevenever you want. In a testing session, you either need to re-type whole command, or reuse a previous command from the shell's history. Or have a file with all your commands and copy-paste to the shell. Either way, it's not a good experience.
That being said, I'm not very fond of Postman either. It's too heavyweight for what it does, IMHO, and the import/export mechanism is terrible for sharing collections with the team. These days, I tend to use VSCode extensions like httpYac or REST Client, or the equivalent that is now built into Visual Studio and Rider. It's much easier to work with than Postman (it's just text), while still being interactive. And since it's just a text file, you can just add it to the Git to share it with the team.
@Thomas Levesque: I agree with you, yet VSCode or Rider's extensions lock you into an editor quite quickly.
But you can have the best of both worlds: a cli tool first, with editor extensions. Just like Hurl.
Note that you can run a curl command from a file with curl --config [curl_request.file],
it makes chaining requests (like with login and secrets) rather cumbersome very quickly.
Thank you, both, for writing. In the end, it's up to every team to settle on technical solutions that work for them, in that context. Likewise, it's up to each developer to identify methodology and tools that work for her or him, as long as it doesn't impact the rest of the team.
The reason I suggest curl over other alternatives is that not only is it free, it also tends to be ubiquitous. Most systems come with curl baked in - perhaps not a consumer installation of Windows, but if you have developer tools installed, it's highly likely that you have curl on your machine. It's a fundamental skill that may serve you well if you know it.
In addition to that, since curl is a CLI you can always script it if you need a kind of semi-automation. What prevents you from maintaining a collection of script files? They could even take command-line arguments, if you'd like.
That said, personally, if I realize that I need to maintain a collection of requests that I can re-execute whenever I want, I'd prefer writing a 'real' program. On the other hand, I find a tool like curl useful for ad-hoc testing.
... maintain a collection of requests that you can re-execute whevenever you want.
@Thomas Levesque: that sounds like a proper collection of automatically executable tests would be a better fit. But yeah, it's just easier to write those simple commands than to set up a test project - instant gratification 😉

Comments
My company has a Google Docs template for postmortem analysis that we use when something goes especially wrong. The primary focus is stating what went wrong according to the "five whys technique". Our template links to this post by Eric Ries. There is alsothis Wikipedia article on the subject. The section heading are "What happened" (one sentence), "Impact on Customers" (duration and severity), "What went wrong (5 Whys)", "What went right (optional)", "Corrective Actions" (and all of the content so far should be short enough to fit on one page), "Timeline" (a bulleted list asking for "Event beginning", "Time to Detect (monitoring)", "Time to Notify (alerting)", "Time to Respond (devops)", "Time to Troubleshoot (devops)", "Time to Mitigate (devops)", "Event end"), "Logs (optional)".
Tyson, thank you for writing. I now realize that 'post mortem' was a poor choice of words on my part, since it implies that something went wrong. I should have written 'posterior' instead. I'll update the article.
I've been digging around a bit to see if I can find the article that originally made me aware of that option. I'm fairly sure that it wasn't Optimizing the Software development process for continuous integration and flow of work, but that article, on the other hand, seems to be the source that other articles cite. It's fairly long, and also discusses other concepts; the relevant section here is the one called Non-blocking reviews.
An shorter overview of this kind of process can be found in Non-Blocking, Continuous Code Reviews - a case study.
In change management/risk control, your There should be at least two pair of eyes on every line of code is called four eye principle, and is a standard practice in my industry (IT services provider for the travel industry).
It goes further, and requires 2 more pair of eyes for any changes from the code review, to the load of a specific software in production.
I has a nice side-effect during code reviews: it's an automatic way to dessiminate knowledge in the team, so the bus factor is never 1.
I think that real people can mostly be trusted. But, software is not always run by people. Even when it is, a single non-trust-worthy person's action is amplified by software being run by mindless computers. It's like one rotten apple is enough to poison the full bag.
In the end, and a bit counter-intuitively, trusting people less now is leading to being able to trust more soon: people are forced to say "you can trust me, and here are the proofs". (Eg: the recently announced Apple's Private Cloud Compute).
Jiehong, thank you for writing. Indeed, in Code That Fits in Your Head I discuss how shared code ownership reduces the bus factor.
From this article and previous discussions I've had, I can see that the term trust is highly charged. People really don't like the notion that trust may be misplaced, or that mistrust, even, might be appropriate. I can't tell if it's a cultural bias of which I'm not aware. While English isn't my native language, I believe that I'm sufficiently acquainted with anglo-saxon culture to know of its most obvious quirks. Still, I'm sometimes surprised.
I admit that I, too, first consider whether I'm dealing with a deliberate adversary if I'm asked whether I trust someone, but soon after, there's a secondary interpretation that originates from normal human fallibility. I've already written about that: No, I don't trust my colleagues to be infallible, as I don't trust myself to be so.
Fortunately, it seems to me that the remedies that may address such concerns are the same, regardless of the underlying reasons.