ploeh blog danish software design
Refactoring a saga from the State pattern to the State monad
A slightly less unrealistic example in C#.
This article is one of the examples that I promised in the earlier article The State pattern and the State monad. That article examines the relationship between the State design pattern and the State monad. It's deliberately abstract, so one or more examples are in order.
In the previous example you saw how to refactor Design Patterns' TCP connection example. That example is, unfortunately, hardly illuminating due to its nature, so a second example is warranted.
This second example shows how to refactor a stateful asynchronous message handler from the State pattern to the State monad.
Shipping policy #
Instead of inventing an example from scratch, I decided to use an NServiceBus saga tutorial as a foundation. Read on even if you don't know NServiceBus. You don't have to know anything about NServiceBus in order to follow along. I just thought that I'd embed the example code in a context that actually executes and does something, instead of faking it with a bunch of unit tests. Hopefully this will help make the example a bit more realistic and relatable.
The example is a simple demo of asynchronous message handling. In a web store shipping department, you should only ship an item once you've received the order and a billing confirmation. When working with asynchronous messaging, you can't, however, rely on message ordering, so perhaps the OrderBilled message arrives before the OrderPlaced message, and sometimes it's the other way around.
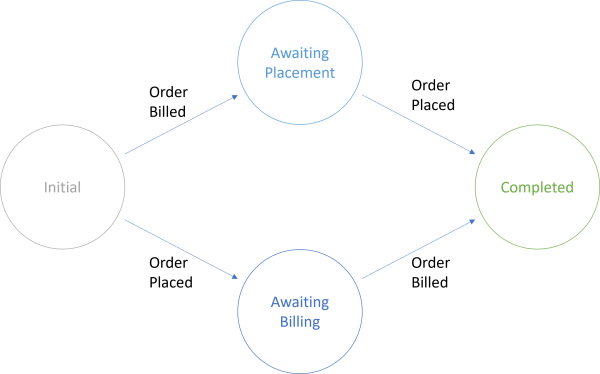
Only when you've received both messages may you ship the item.
It's a simple workflow, and you don't really need the State pattern. So much is clear from the sample code implementation:
public class ShippingPolicy : Saga<ShippingPolicyData>, IAmStartedByMessages<OrderBilled>, IAmStartedByMessages<OrderPlaced> { static ILog log = LogManager.GetLogger<ShippingPolicy>(); protected override void ConfigureHowToFindSaga(SagaPropertyMapper<ShippingPolicyData> mapper) { mapper.MapSaga(sagaData => sagaData.OrderId) .ToMessage<OrderPlaced>(message => message.OrderId) .ToMessage<OrderBilled>(message => message.OrderId); } public Task Handle(OrderPlaced message, IMessageHandlerContext context) { log.Info($"OrderPlaced message received."); Data.IsOrderPlaced = true; return ProcessOrder(context); } public Task Handle(OrderBilled message, IMessageHandlerContext context) { log.Info($"OrderBilled message received."); Data.IsOrderBilled = true; return ProcessOrder(context); } private async Task ProcessOrder(IMessageHandlerContext context) { if (Data.IsOrderPlaced && Data.IsOrderBilled) { await context.SendLocal(new ShipOrder() { OrderId = Data.OrderId }); MarkAsComplete(); } } }
I don't expect you to be familiar with the NServiceBus API, so don't worry about the base class, the interfaces, or the ConfigureHowToFindSaga method. What you need to know is that this class handles two types of messages: OrderPlaced and OrderBilled. What the base class and the framework does is handling message correlation, hydration and dehydration, and so on.
For the purposes of this demo, all you need to know about the context object is that it enables you to send and publish messages. The code sample uses context.SendLocal to send a new ShipOrder Command.
Messages arrive asynchronously and conceptually with long wait times between them. You can't just rely on in-memory object state because a ShippingPolicy instance may receive one message and then risk that the server it's running on shuts down before the next message arrives. The NServiceBus framework handles message correlation and hydration and dehydration of state data. The latter is modelled by the ShippingPolicyData class:
public class ShippingPolicyData : ContainSagaData { public string OrderId { get; set; } public bool IsOrderPlaced { get; set; } public bool IsOrderBilled { get; set; } }
Notice that the above sample code inspects and manipulates the Data property defined by the Saga<ShippingPolicyData> base class.
When the ShippingPolicy methods are called by the NServiceBus framework, the Data is automatically populated. When you modify the Data, the state data is automatically persisted when the message handler shuts down to wait for the next message.
Characterisation tests #
While you can draw an explicit state diagram like the one above, the sample code doesn't explicitly model the various states as objects. Instead, it relies on reading and writing two Boolean values.
There's nothing wrong with this implementation. It's the simplest thing that could possibly work, so why make it more complicated?
In this article, I am going to make it more complicated. First, I'm going to refactor the above sample code to use the State design pattern, and then I'm going to refactor that code to use the State monad. From a perspective of maintainability, this isn't warranted, but on the other hand, I hope it's educational. The sample code is just complex enough to showcase the structures of the State pattern and the State monad, yet simple enough that the implementation logic doesn't get in the way.
Simplicity can be deceiving, however, and no refactoring is without risk.
"to refactor, the essential precondition is [...] solid tests"
I found it safest to first add a few Characterisation Tests to make sure I didn't introduce any errors as I changed the code. It did catch a few copy-paste goofs that I made, so adding tests turned out to be a good idea.
Testing NServiceBus message handlers isn't too hard. All the tests I wrote look similar, so one should be enough to give you an idea.
[Theory] [InlineData("1337")] [InlineData("baz")] public async Task OrderPlacedAndBilled(string orderId) { var sut = new ShippingPolicy { Data = new ShippingPolicyData { OrderId = orderId } }; var ctx = new TestableMessageHandlerContext(); await sut.Handle(new OrderPlaced { OrderId = orderId }, ctx); await sut.Handle(new OrderBilled { OrderId = orderId }, ctx); Assert.True(sut.Completed); var msg = Assert.Single(ctx.SentMessages.Containing<ShipOrder>()); Assert.Equal(orderId, msg.Message.OrderId); }
The tests use xUnit.net 2.4.2. When I downloaded the NServiceBus saga sample code it targeted .NET Framework 4.8, and I didn't bother to change the version.
While the NServiceBus framework will automatically hydrate and populate Data, in a unit test you have to remember to explicitly populate it. The TestableMessageHandlerContext class is a Test Spy that is part of NServiceBus testing API.
You'd think I was paid by Particular Software to write this article, but I'm not. All this is really just the introduction. You're excused if you've forgotten the topic of this article, but my goal is to show a State pattern example. Only now can we begin in earnest.
State pattern implementation #
Refactoring to the State pattern, I chose to let the ShippingPolicy class fill the role of the pattern's Context. Instead of a base class with virtual method, I used an interface to define the State object, as that's more Idiomatic in C#:
public interface IShippingState { Task OrderPlaced(OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy); Task OrderBilled(OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy); }
The State pattern only shows examples where the State methods take a single argument: The Context. In this case, that's the ShippingPolicy. Careful! There's also a parameter called context! That's the NServiceBus context, and is an artefact of the original example. The two other parameters, message and context, are run-time values passed on from the ShippingPolicy's Handle methods:
public IShippingState State { get; internal set; } public async Task Handle(OrderPlaced message, IMessageHandlerContext context) { log.Info($"OrderPlaced message received."); Hydrate(); await State.OrderPlaced(message, context, this); Dehydrate(); } public async Task Handle(OrderBilled message, IMessageHandlerContext context) { log.Info($"OrderBilled message received."); Hydrate(); await State.OrderBilled(message, context, this); Dehydrate(); }
The Hydrate method isn't part of the State pattern, but finds an appropriate state based on Data:
private void Hydrate() { if (!Data.IsOrderPlaced && !Data.IsOrderBilled) State = InitialShippingState.Instance; else if (Data.IsOrderPlaced && !Data.IsOrderBilled) State = AwaitingBillingState.Instance; else if (!Data.IsOrderPlaced && Data.IsOrderBilled) State = AwaitingPlacementState.Instance; else State = CompletedShippingState.Instance; }
In more recent versions of C# you'd be able to use more succinct pattern matching, but since this code base is on .NET Framework 4.8 I'm constrained to C# 7.3 and this is as good as I cared to make it. It's not important to the topic of the State pattern, but I'm showing it in case you where wondering. It's typical that you need to translate between data that exists in the 'external world' and your object-oriented, polymorphic code, since at the boundaries, applications aren't object-oriented.
Likewise, the Dehydrate method translates the other way:
private void Dehydrate() { if (State is AwaitingBillingState) { Data.IsOrderPlaced = true; Data.IsOrderBilled = false; return; } if (State is AwaitingPlacementState) { Data.IsOrderPlaced = false; Data.IsOrderBilled = true; return; } if (State is CompletedShippingState) { Data.IsOrderPlaced = true; Data.IsOrderBilled = true; return; } Data.IsOrderPlaced = false; Data.IsOrderBilled = false; }
In any case, Hydrate and Dehydrate are distractions. The important part is that the ShippingPolicy (the State Context) now delegates execution to its State, which performs the actual work and updates the State.
Initial state #
The first time the saga runs, both Data.IsOrderPlaced and Data.IsOrderBilled are false, which means that the State is InitialShippingState:
public sealed class InitialShippingState : IShippingState { public readonly static InitialShippingState Instance = new InitialShippingState(); private InitialShippingState() { } public Task OrderPlaced( OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy) { policy.State = AwaitingBillingState.Instance; return Task.CompletedTask; } public Task OrderBilled( OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy) { policy.State = AwaitingPlacementState.Instance; return Task.CompletedTask; } }
As the above state transition diagram indicates, the only thing that each of the methods do is that they transition to the next appropriate state: AwaitingBillingState if the first event was OrderPlaced, and AwaitingPlacementState when the event was OrderBilled.
"State object are often Singletons"
Like in the previous example I've made all the State objects Singletons. It's not that important, but since they are all stateless, we might as well. At least, it's in the spirit of the book.
Awaiting billing #
AwaitingBillingState is another IShippingState implementation:
public sealed class AwaitingBillingState : IShippingState { public readonly static IShippingState Instance = new AwaitingBillingState(); private AwaitingBillingState() { } public Task OrderPlaced( OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy) { return Task.CompletedTask; } public async Task OrderBilled( OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy) { await context.SendLocal( new ShipOrder() { OrderId = policy.Data.OrderId }); policy.Complete(); policy.State = CompletedShippingState.Instance; } }
This State doesn't react to OrderPlaced because it assumes that an order has already been placed. It only reacts to an OrderBilled event. When that happens, all requirements have been fulfilled to ship the item, so it sends a ShipOrder Command, marks the saga as completed, and changes the State to CompletedShippingState.
The Complete method is a little wrapper method I had to add to the ShippingPolicy class, since MarkAsComplete is a protected method:
internal void Complete() { MarkAsComplete(); }
The AwaitingPlacementState class is similar to AwaitingBillingState, except that it reacts to OrderPlaced rather than OrderBilled.
Terminal state #
The fourth and final state is the CompletedShippingState:
public sealed class CompletedShippingState : IShippingState { public readonly static IShippingState Instance = new CompletedShippingState(); private CompletedShippingState() { } public Task OrderPlaced( OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy) { return Task.CompletedTask; } public Task OrderBilled( OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy) { return Task.CompletedTask; } }
In this state, the saga is completed, so it ignores both events.
Move Commands to output #
The saga now uses the State pattern to manage state-specific behaviour as well as state transitions. To be clear, this complexity isn't warranted for the simple requirements. This is, after all, an example. All tests still pass, and smoke testing also indicates that everything still works as it's supposed to.
The goal of this article is now to refactor the State pattern implementation to pure functions. When the saga runs it has an observable side effect: It eventually sends a ShipOrder Command. During processing it also updates its internal state. Both of these are sources of impurity that we have to decouple from the decision logic.
I'll do this in several steps. The first impure action I'll address is the externally observable message transmission. A common functional-programming trick is to turn a side effect into a return value. So far, the IShippingState methods don't return anything. (This is strictly not true; they each return Task, but we can regard Task as 'asynchronous void'.) Thus, return values are still available as a communications channel.
Refactor the IShippingState methods to return Commands instead of actually sending them. Each method may send an arbitrary number of Commands, including none, so the return type has to be a collection:
public interface IShippingState { IReadOnlyCollection<ICommand> OrderPlaced( OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy); IReadOnlyCollection<ICommand> OrderBilled( OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy); }
When you change the interface you also have to change all the implementing classes, including AwaitingBillingState:
public sealed class AwaitingBillingState : IShippingState { public readonly static IShippingState Instance = new AwaitingBillingState(); private AwaitingBillingState() { } public IReadOnlyCollection<ICommand> OrderPlaced( OrderPlaced message, IMessageHandlerContext context, ShippingPolicy policy) { return Array.Empty<ICommand>(); } public IReadOnlyCollection<ICommand> OrderBilled( OrderBilled message, IMessageHandlerContext context, ShippingPolicy policy) { policy.Complete(); policy.State = CompletedShippingState.Instance; return new[] { new ShipOrder() { OrderId = policy.Data.OrderId } }; } }
In order to do nothing a method like OrderPlaced now has to return an empty collection of Commands. In order to 'send' a Command, OrderBilled now returns it instead of using the context to send it. The context is already redundant, but since I prefer to move in small steps, I'll remove it in a separate step.
It's now the responsibility of the ShippingPolicy class to do something with the Commands returned by the State:
public async Task Handle(OrderBilled message, IMessageHandlerContext context) { log.Info($"OrderBilled message received."); Hydrate(); var result = State.OrderBilled(message, context, this); await Interpret(result, context); Dehydrate(); } private async Task Interpret( IReadOnlyCollection<ICommand> commands, IMessageHandlerContext context) { foreach (var cmd in commands) await context.SendLocal(cmd); }
In functional programming, you often run an interpreter over the instructions returned by a pure function. Here the interpreter is just a private helper method.
The IShippingState methods are no longer asynchronous. Now they just return collections. I consider that a simplification.
Remove context parameter #
The context parameter is now redundant, so remove it from the IShippingState interface:
public interface IShippingState { IReadOnlyCollection<ICommand> OrderPlaced(OrderPlaced message, ShippingPolicy policy); IReadOnlyCollection<ICommand> OrderBilled(OrderBilled message, ShippingPolicy policy); }
I used Visual Studio's built-in refactoring tools to remove the parameter, which automatically removed it from all the call sites and implementations.
This takes us part of the way towards implementing the states as pure functions, but there's still work to be done.
public IReadOnlyCollection<ICommand> OrderBilled(OrderBilled message, ShippingPolicy policy) { policy.Complete(); policy.State = CompletedShippingState.Instance; return new[] { new ShipOrder() { OrderId = policy.Data.OrderId } }; }
The above OrderBilled implementation calls policy.Complete to indicate that the saga has completed. That's another state mutation that must be eliminated to make this a pure function.
Return complex result #
How do you refactor from state mutation to pure function? You turn the mutation statement into an instruction, which is a value that you return. In this case you might want to return a Boolean value: True to complete the saga. False otherwise.
There seems to be a problem, though. The IShippingState methods already return data: They return a collection of Commands. How do we get around this conundrum?
Introduce a complex object:
public sealed class ShippingStateResult { public ShippingStateResult( IReadOnlyCollection<ICommand> commands, bool completeSaga) { Commands = commands; CompleteSaga = completeSaga; } public IReadOnlyCollection<ICommand> Commands { get; } public bool CompleteSaga { get; } public override bool Equals(object obj) { return obj is ShippingStateResult result && EqualityComparer<IReadOnlyCollection<ICommand>>.Default .Equals(Commands, result.Commands) && CompleteSaga == result.CompleteSaga; } public override int GetHashCode() { int hashCode = -1668187231; hashCode = hashCode * -1521134295 + EqualityComparer<IReadOnlyCollection<ICommand>> .Default.GetHashCode(Commands); hashCode = hashCode * -1521134295 + CompleteSaga.GetHashCode(); return hashCode; } }
That looks rather horrible, but most of the code is generated by Visual Studio. The only thing I wrote myself was the class declaration and the two read-only properties. I then used Visual Studio's Generate constructor and Generate Equals and GetHashCode Quick Actions to produce the rest of the code.
With more modern versions of C# I could have used a record, but as I've already mentioned, I'm on C# 7.3 here.
The IShippingState interface can now define its methods with this new return type:
public interface IShippingState { ShippingStateResult OrderPlaced(OrderPlaced message, ShippingPolicy policy); ShippingStateResult OrderBilled(OrderBilled message, ShippingPolicy policy); }
This change reminds me of the Introduce Parameter Object refactoring, but instead applied to the return value instead of input.
Implementers now have to return values of this new type:
public sealed class AwaitingBillingState : IShippingState { public readonly static IShippingState Instance = new AwaitingBillingState(); private AwaitingBillingState() { } public ShippingStateResult OrderPlaced(OrderPlaced message, ShippingPolicy policy) { return new ShippingStateResult(Array.Empty<ICommand>(), false); } public ShippingStateResult OrderBilled(OrderBilled message, ShippingPolicy policy) { policy.State = CompletedShippingState.Instance; return new ShippingStateResult( new[] { new ShipOrder() { OrderId = policy.Data.OrderId } }, true); } }
Moving a statement to an output value implies that the effect must happen somewhere else. It seems natural to put it in the ShippingPolicy class' Interpret method:
public async Task Handle(OrderBilled message, IMessageHandlerContext context) { log.Info($"OrderBilled message received."); Hydrate(); var result = State.OrderBilled(message, this); await Interpret(result, context); Dehydrate(); } private async Task Interpret(ShippingStateResult result, IMessageHandlerContext context) { foreach (var cmd in result.Commands) await context.SendLocal(cmd); if (result.CompleteSaga) MarkAsComplete(); }
Since Interpret is an instance method on the ShippingPolicy class I can now also delete the internal Complete method, since MarkAsComplete is already callable (it's a protected method defined by the Saga base class).
Use message data #
Have you noticed an odd thing about the code so far? It doesn't use any of the message data!
This is an artefact of the original code example. Refer back to the original ProcessOrder helper method. It uses neither OrderPlaced nor OrderBilled for anything. Instead, it pulls the OrderId from the saga's Data property. It can do that because NServiceBus makes sure that all OrderId values are correlated. It'll only instantiate a saga for which Data.OrderId matches OrderPlaced.OrderId or OrderBilled.OrderId. Thus, these values are guaranteed to be the same, and that's why ProcessOrder can get away with using Data.OrderId instead of the message data.
So far, through all refactorings, I've retained this detail, but it seems odd. It also couples the implementation methods to the ShippingPolicy class rather than the message classes. For these reasons, refactor the methods to use the message data instead. Here's the AwaitingBillingState implementation:
public ShippingStateResult OrderBilled(OrderBilled message, ShippingPolicy policy) { policy.State = CompletedShippingState.Instance; return new ShippingStateResult( new[] { new ShipOrder() { OrderId = message.OrderId } }, true); }
Compare this version with the previous iteration, where it used policy.Data.OrderId instead of message.OrderId.
Now, the only reason to pass ShippingPolicy as a method parameter is to mutate policy.State. We'll get to that in due time, but first, there's another issue I'd like to address.
Immutable arguments #
Keep in mind that the overall goal of the exercise is to refactor the state machine to pure functions. For good measure, method parameters should be immutable as well. Consider a method like OrderBilled shown above in its most recent iteration. It mutates policy by setting policy.State. The long-term goal is to get rid of that statement.
The method doesn't mutate the other argument, message, but the OrderBilled class is actually mutable:
public class OrderBilled : IEvent { public string OrderId { get; set; } }
The same is true for the other message type, OrderPlaced.
For good measure, pure functions shouldn't take mutable arguments. You could argue that, since none of the implementation methods actually mutate the messages, it doesn't really matter. I am, however, enough of a neat freak that I don't like to leave such a loose strand dangling. I'd like to refactor the IShippingState API so that only immutable message data is passed as arguments.
In a situation like this, there are (at least) three options:
-
Make the message types immutable. This would mean making
OrderBilledandOrderPlacedimmutable. These message types are by default mutable Data Transfer Objects (DTO), because NServiceBus needs to serialise and deserialise them to transmit them over durable queues. There are ways you can configure NServiceBus to use serialisation mechanisms that enable immutable records as messages, but for an example code base like this, I might be inclined to reach for an easier solution if one presents itself. -
Add an immutable 'mirror' class. This may often be a good idea if you have a rich domain model that you'd like to represent. You can see an example of that in Code That Fits in Your Head, where there's both a mutable
ReservationDtoclass and an immutableReservationValue Object. This makes sense if the invariants of the domain model are sufficiently stronger than the DTO. That hardly seems to be the case here, since both messages only contain anOrderId. -
Dissolve the DTO into its constituents and pass each as an argument. This doesn't work if the DTO is complex and nested, but here there's only a single constituent element, and that's the
OrderIdproperty.
The third option seems like the simplest solution, so refactor the IShippingState methods to take an orderId parameter instead of a message:
public interface IShippingState { ShippingStateResult OrderPlaced(string orderId, ShippingPolicy policy); ShippingStateResult OrderBilled(string orderId, ShippingPolicy policy); }
While this is the easiest of the three options given above, the refactoring doesn't hinge on this. It would work just as well with one of the two other options.
Implementations now look like this:
public ShippingStateResult OrderBilled(string orderId, ShippingPolicy policy) { policy.State = CompletedShippingState.Instance; return new ShippingStateResult( new[] { new ShipOrder() { OrderId = orderId } }, true); }
The only impure action still lingering is the mutation of policy.State. Once we're rid of that, the API consists of pure functions.
Return state #
As outlined by the parent article, instead of mutating the caller's state, you can return the state as part of a tuple. This means that you no longer need to pass ShippingPolicy as a parameter:
public interface IShippingState { Tuple<ShippingStateResult, IShippingState> OrderPlaced(string orderId); Tuple<ShippingStateResult, IShippingState> OrderBilled(string orderId); }
Why not expand the ShippingStateResult class, or conversely, dissolve that class and instead return a triple (a three-tuple)? All of these are possible as alternatives, as they'd be isomorphic to this particular design. The reason I've chosen this particular return type is that it's the idiomatic implementation of the State monad: The result is the first element of a tuple, and the state is the second element. This means that you can use a standard, reusable State monad library to manipulate the values, as you'll see later.
An implementation now looks like this:
public sealed class AwaitingBillingState : IShippingState { public readonly static IShippingState Instance = new AwaitingBillingState(); private AwaitingBillingState() { } public Tuple<ShippingStateResult, IShippingState> OrderPlaced(string orderId) { return Tuple.Create( new ShippingStateResult(Array.Empty<ICommand>(), false), (IShippingState)this); } public Tuple<ShippingStateResult, IShippingState> OrderBilled(string orderId) { return Tuple.Create( new ShippingStateResult( new[] { new ShipOrder() { OrderId = orderId } }, true), CompletedShippingState.Instance); } }
Since the ShippingPolicy class that calls these methods now directly receives the state as part of the output, it no longer needs a mutable State property. Instead, it immediately handles the return value:
public async Task Handle(OrderPlaced message, IMessageHandlerContext context) { log.Info($"OrderPlaced message received."); var state = Hydrate(); var result = state.OrderPlaced(message.OrderId); await Interpret(result.Item1, context); Dehydrate(result.Item2); } public async Task Handle(OrderBilled message, IMessageHandlerContext context) { log.Info($"OrderBilled message received."); var state = Hydrate(); var result = state.OrderBilled(message.OrderId); await Interpret(result.Item1, context); Dehydrate(result.Item2); }
Each Handle method is now an impureim sandwich.
Since the result is now a tuple, the Handle methods now have to pass the first element (result.Item1) to the Interpret helper method, and the second element (result.Item2) - the state - to Dehydrate. It's also possible to pattern match (or destructure) each of the elements directly; you'll see an example of that later.
Since the mutable State property is now gone, the Hydrate method returns the hydrated state:
private IShippingState Hydrate() { if (!Data.IsOrderPlaced && !Data.IsOrderBilled) return InitialShippingState.Instance; else if (Data.IsOrderPlaced && !Data.IsOrderBilled) return AwaitingBillingState.Instance; else if (!Data.IsOrderPlaced && Data.IsOrderBilled) return AwaitingPlacementState.Instance; else return CompletedShippingState.Instance; }
Likewise, the Dehydrate method takes the new state as an input parameter:
private void Dehydrate(IShippingState state) { if (state is AwaitingBillingState) { Data.IsOrderPlaced = true; Data.IsOrderBilled = false; return; } if (state is AwaitingPlacementState) { Data.IsOrderPlaced = false; Data.IsOrderBilled = true; return; } if (state is CompletedShippingState) { Data.IsOrderPlaced = true; Data.IsOrderBilled = true; return; } Data.IsOrderPlaced = false; Data.IsOrderBilled = false; }
Since each Handle method only calls a single State-valued method, they don't need the State monad machinery. This only becomes useful when you need to compose multiple State-based operations.
This might be useful in unit tests, so let's examine that next.
State monad #
In previous articles about the State monad you've seen it implemented based on an IState interface. I've also dropped hints here and there that you don't need the interface. Instead, you can implement the monad functions directly on State-valued functions. That's what I'm going to do here:
public static Func<S, Tuple<T1, S>> SelectMany<S, T, T1>( this Func<S, Tuple<T, S>> source, Func<T, Func<S, Tuple<T1, S>>> selector) { return s => { var tuple = source(s); var f = selector(tuple.Item1); return f(tuple.Item2); }; }
This SelectMany implementation works directly on another function, source. This function takes a state of type S as input and returns a tuple as a result. The first element is the result of type T, and the second element is the new state, still of type S. Compare that to the IState interface to convince yourself that these are just two representations of the same idea.
The return value is a new function with the same shape, but where the result type is T1 rather than T.
You can implement the special SelectMany overload that enables query syntax in the standard way.
The return function also mirrors the previous interface-based implementation:
public static Func<S, Tuple<T, S>> Return<S, T>(T x) { return s => Tuple.Create(x, s); }
You can also implement the standard Get, Put, and Modify functions, but we are not going to need them here. Try it as an exercise.
State-valued event handlers #
The IShippingState methods almost look like State values, but the arguments are in the wrong order. A State value is a function that takes state as input and returns a tuple. The methods on IShippingState, however, take orderId as input and return a tuple. The state is also present, but as the instance that exposes the methods. We have to flip the arguments:
public static Func<IShippingState, Tuple<ShippingStateResult, IShippingState>> Billed( this string orderId) { return s => s.OrderBilled(orderId); } public static Func<IShippingState, Tuple<ShippingStateResult, IShippingState>> Placed( this string orderId) { return s => s.OrderPlaced(orderId); }
This is a typical example of how you have to turn things on their heads in functional programming, compared to object-oriented programming. These two methods convert OrderBilled and OrderPlaced to State monad values.
Testing state results #
A unit test demonstrates how this enables you to compose multiple stateful operations using query syntax:
[Theory] [InlineData("90125")] [InlineData("quux")] public void StateResultExample(string orderId) { var sf = from x in orderId.Placed() from y in orderId.Billed() select new[] { x, y }; var (results, finalState) = sf(InitialShippingState.Instance); Assert.Equal( new[] { false, true }, results.Select(r => r.CompleteSaga)); Assert.Single( results .SelectMany(r => r.Commands) .OfType<ShipOrder>() .Select(msg => msg.OrderId), orderId); Assert.Equal(CompletedShippingState.Instance, finalState); }
Keep in mind that a State monad value is a function. That's the reason I called the composition sf - for State Function. When you execute it with InitialShippingState as input it returns a tuple that the test immediately pattern matches (destructures) into its constituent elements.
The test then asserts that the results and finalState are as expected. The assertions against results are a bit awkward, since C# collections don't have structural equality. These assertions would have been simpler in F# or Haskell.
Testing with an interpreter #
While the Arrange and Act phases of the above test are simple, the Assertion phase seems awkward. Another testing strategy is to run a test-specific interpreter over the instructions returned as the State computation result:
[Theory] [InlineData("1984")] [InlineData("quuz")] public void StateInterpretationExample(string orderId) { var sf = from x in orderId.Placed() from y in orderId.Billed() select new[] { x, y }; var (results, finalState) = sf(InitialShippingState.Instance); Assert.Equal(CompletedShippingState.Instance, finalState); var result = Interpret(results); Assert.True(result.CompleteSaga); Assert.Single( result.Commands.OfType<ShipOrder>().Select(msg => msg.OrderId), orderId); }
It helps a little, but the assertions still have to work around the lack of structural equality of result.Commands.
Monoid #
The test-specific Interpret helper method is interesting in its own right, though:
private ShippingStateResult Interpret(IEnumerable<ShippingStateResult> results) { var identity = new ShippingStateResult(Array.Empty<ICommand>(), false); ShippingStateResult Combine(ShippingStateResult x, ShippingStateResult y) { return new ShippingStateResult( x.Commands.Concat(y.Commands).ToArray(), x.CompleteSaga || y.CompleteSaga); } return results.Aggregate(identity, Combine); }
It wasn't until I started implementing this helper method that I realised that ShippingStateResult gives rise to a monoid! Since monoids accumulate, you can start with the identity and use the binary operation (here called Combine) to Aggregate an arbitrary number of ShippingStateResult values into one.
The ShippingStateResult class is composed of two constituent values (a collection and a Boolean value), and since both of these give rise to one or more monoids, a tuple of those monoids itself gives rise to one or more monoids. The ShippingStateResult is isomorphic to a tuple, so this result carries over.
Should you move the Combine method and the identity value to the ShippingStateResult class itself. After all, putting them in a test-specific helper method smells a bit of Feature Envy.
This seems compelling, but it's not clear that arbitrary client code might need this particular monoid. After all, there are four monoids over Boolean values, and at least two over collections. That's eight possible combinations. Which one should ShippingStateResult expose as members?
The monoid used in Interpret combines the normal collection monoid with the any monoid. That seems appropriate in this case, but other clients might rather need the all monoid.
Without more usage examples, I decided to leave the code as an Interpret implementation detail for now.
In any case, I find it worth noting that by decoupling the state logic from the NServiceBus framework, it's possible to test it without running asynchronous workflows.
Conclusion #
In this article you saw how to implement an asynchronous messaging saga in three different ways. First, as a simple ad-hoc solution, second using the State pattern, and third implemented with the State monad. Both the State pattern and State monad implementations are meant exclusively to showcase these two techniques. The first solution using two Boolean flags is by far the simplest solution, and the one I'd use in a production system.
The point is that you can use the State monad if you need to write stateful computations. This may include finite state machines, as otherwise addressed by the State design pattern, but could also include other algorithms where you need to keep track of state.
Next: Postel's law as a profunctor.
Some thoughts on the economics of programming
On the net value of process and code quality.
Once upon a time there was a software company that had a special way of doing things. No other company had ever done things quite like that before, but the company had much success. In short time it rose to dominance in the market, outcompeting all serious competition. Some people disliked the company because of its business tactics and sheer size, but others admired it.
Even more wanted to be like it.
How did the company achieve its indisputable success? It looked as though it was really, really good at making software. How did they write such good software?
It turned out that the company had a special software development process.
Other software organisations, hoping to be able to be as successful, tried to copy the special process. The company was willing to share. Its employees wrote about the process. They gave conference presentations on their special sauce.
Which company do I have in mind, and what was the trick that made it so much better than its competition? Was it microservices? Monorepos? Kubernetes? DevOps? Serverless?
No, the company was Microsoft and the development process was called Microsoft Solutions Framework (MSF).
What?! do you say.
You've never heard of MSF?
That's hardly surprising. I doubt that MSF was in any way related to Microsoft's success.
Net profits #
These days, many people in technology consider Microsoft an embarrassing dinosaur. While you know that it's still around, does it really matter, these days?
You can't deny, however, that Microsoft made a lot of money in the Nineties. They still do.
What's the key to making a lot of money? Have a revenue larger than your costs.
I'm too lazy to look up the actual numbers, but clearly Microsoft had (and still has) a revenue vastly larger than its costs:
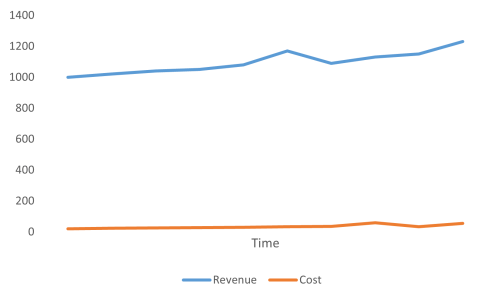
Compared to real, historic numbers, this may be exaggerated, but I'm trying to make a general point - not one that hinges on actual profit numbers of Microsoft, Apple, Amazon, Google, or any other tremendously profitable company. I'm also aware that real companies have costs that aren't directly related to software development: Marketing, operations, buildings, sales, etcetera. They also make money in other ways than from their software, mainly from investments of the profits.
The difference between the revenue and the cost is the profit or net value.
If the graph looks like the above, is managing cost the main cause of success? Hardly. The cost is almost a rounding error on the profits.
If so, is the technology or process key to such a company's success? Was it MSF that made Microsoft the wealthiest company in the world? Are two-pizza teams the only explanation of Amazon's success? Is Google the dominant search engine because the source code is organised in a monorepo?
I'd be surprised were that the case. Rather, I think that these companies were at the right place at the right time. While there were search engines before Google, Google was so much better that users quickly migrated. Google was also better at making money than earlier search engines like AltaVista or Yahoo! Likewise, Microsoft made more successful PC operating systems than the competition (which in the early Windows era consisted exclusively of OS/2) and better professional software (word processor, spreadsheet, etcetera). Amazon made a large-scale international web shop before anyone else. Apple made affordable computers with graphical user interfaces before other companies. Later, they introduced a smartphone at the right time.
All of this is simplified. For example, it's not really true that Apple made the first smartphone. When the iPhone was introduced, I already carried a Pocket PC Phone Edition device that could browse the internet, had email, phone, SMS, and so on. There were other precursors even earlier.
I'm not trying to explain away excellence of execution. These companies succeeded for a variety of reasons, including that they were good at what they were doing. Lots of companies, however, are good at what they are doing, and still they fail. Being at the right place at the right time matters. Once in a while, a company finds itself in such favourable circumstances that success is served on a silver platter. While good execution is important, it doesn't explain the magnitude of the success.
Bad execution is likely to eliminate you in the long run, but it doesn't follow logically that good execution guarantees success.
Perhaps the successful companies succeeded because of circumstances, and despite mediocre execution. As usual, you should be wary not to mistake correlation for causation.
Legacy code #
You should be sceptical of adopting processes or technology just because a Big Tech company uses it. Still, if that was all I had in mind, I could probably had said that shorter. I have another point to make.
I often encounter resistance to ideas about better software development on the grounds that the status quo is good enough. Put bluntly,
""legacy," [...] is condescending-engineer-speak for "actually makes money.""
To be clear, I have nothing against the author or the cited article, which discusses something (right-sizing VMs) that I know nothing about. The phrase, or variations thereof, however, is such a fit meme that it spreads. It strongly indicates that people who discuss code quality are wankers, while 'real programmers' produce code that makes money. I consider that a false dichotomy.
Most software organisations aren't in the fortunate situation that revenues are orders of magnitude greater than costs. Most software organisations can make a decent profit if they find a market and execute on a good idea. Perhaps the revenue starts at 'only' double the cost.
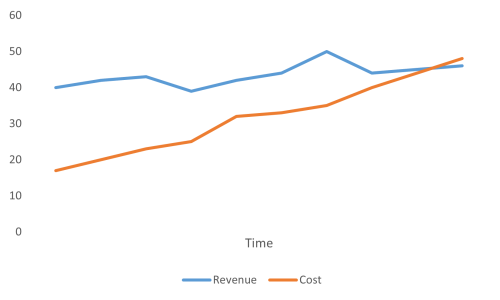
If you can consistently make the double of your costs, you'll be in business for a long time. As the above line chart indicates, however, is that if the costs rise faster than the revenue, you'll eventually hit a point when you start losing money.
The Big Tech companies aren't likely to run into that situation because their profit margins are so great, but normal companies are very much at risk.
The area between the revenue and the cost represents the profit. Thus, looking back, it may be true that a software system has been making money. This doesn't mean, however, that it will keep making money.
In the above chart, the cost eventually exceeds the revenue. If this cost is mainly driven by rising software development costs, then the company is in deep trouble.
I've worked with such a company. When I started with it, it was a thriving company with many employees, most of them developers or IT professionals. In the previous decade, it had turned a nice profit every year.
This all started to change around the time that I arrived. (I will, again, remind the reader that correlation does not imply causation.) One reason I was engaged was that the developers were stuck. Due to external market pressures they had to deliver a tremendous amount of new features, and they were stuck in analysis paralysis.
I helped them get unstuck, but as we started working on the new features, we discovered the size of the mess of the legacy code base.
I recall a conversation I later had with the CEO. He told me, after having discussed the situation with several key people: "I knew that we had a legacy code base... but I didn't know it was this bad!"
Revenue remained constant, but costs kept rising. Today, the company is no longer around.
This was a 100% digital service company. All revenue was ultimately based on software. The business idea was good, but the company couldn't keep up with competitors. As far as I can tell, it was undone by its legacy code base.
Conclusion #
Software should provide some kind of value. Usually profits, but sometimes savings, and occasionally wider concerns are in scope. It's reasonable and professional to consider value as you produce software. You should, however, be aware of a too myopic focus on immediate and past value.
Finding safety in past value is indulging in complacency. Legacy software can make money from day one, but that doesn't mean that it'll keep making money. The main problem with legacy code is that costs keep rising. When non-technical business stakeholders start to notice this, it may be too late.
The is one of many reasons I believe that we, software developers, have a responsibility to combat the mess. I don't think there's anything condescending about that attitude.
Refactoring the TCP State pattern example to pure functions
A C# example.
This article is one of the examples that I promised in the earlier article The State pattern and the State monad. That article examines the relationship between the State design pattern and the State monad. That article is deliberately abstract, so one or more examples are in order.
In this article, I show you how to start with the example from Design Patterns and refactor it to an immutable solution using pure functions.
The code shown here is available on GitHub.
TCP connection #
The example is a class that handles TCP connections. The book's example is in C++, while I'll show my C# interpretation.
A TCP connection can be in one of several states, so the TcpConnection class keeps an instance of the polymorphic TcpState, which implements the state and transitions between them.
TcpConnection plays the role of the State pattern's Context, and TcpState of the State.
public class TcpConnection { public TcpState State { get; internal set; } public TcpConnection() { State = TcpClosed.Instance; } public void ActiveOpen() { State.ActiveOpen(this); } public void PassiveOpen() { State.PassiveOpen(this); } // More members that delegate to State follows...
The TcpConnection class' methods delegate to a corresponding method on TcpState, passing itself an argument. This gives the TcpState implementation an opportunity to change the TcpConnection's State property, which has an internal setter.
State #
This is the TcpState class:
public class TcpState { public virtual void Transmit(TcpConnection connection, TcpOctetStream stream) { } public virtual void ActiveOpen(TcpConnection connection) { } public virtual void PassiveOpen(TcpConnection connection) { } public virtual void Close(TcpConnection connection) { } public virtual void Synchronize(TcpConnection connection) { } public virtual void Acknowledge(TcpConnection connection) { } public virtual void Send(TcpConnection connection) { } }
I don't consider this entirely idiomatic C# code, but it seems closer to the book's C++ example. (It's been a couple of decades since I wrote C++, so I could be mistaken.) It doesn't matter in practice, but instead of a concrete class with no-op virtual methods, I would usually define an interface. I'll do that in the next example article.
The methods have the same names as the methods on TcpConnection, but the signatures are different. All the TcpState methods take a TcpConnection parameter, whereas the TcpConnection methods take no arguments.
While the TcpState methods don't do anything, various classes can inherit from the class and override some or all of them.
Connection closed #
The book shows implementations of three classes that inherit from TcpState, starting with TcpClosed. Here's my translation to C#:
public class TcpClosed : TcpState { public static TcpState Instance = new TcpClosed(); private TcpClosed() { } public override void ActiveOpen(TcpConnection connection) { // Send SYN, receive SYN, Ack, etc. connection.State = TcpEstablished.Instance; } public override void PassiveOpen(TcpConnection connection) { connection.State = TcpListen.Instance; } }
This implementation overrides ActiveOpen and PassiveOpen. In both cases, after performing some work, they change connection.State.
"
TCPStatesubclasses maintain no local state, so they can be shared, and only one instance of each is required. The unique instance ofTCPStatesubclass is obtained by the staticInstanceoperation. [...]"This make each
TCPStatesubclass a Singleton [...]."
I've maintained that property of each subclass in my C# code, even though it has no impact on the structure of the State pattern.
The other subclasses #
The next subclass, TcpEstablished, is cast in the same mould:
public class TcpEstablished : TcpState { public static TcpState Instance = new TcpEstablished(); private TcpEstablished() { } public override void Close(TcpConnection connection) { // send FIN, receive ACK of FIN connection.State = TcpListen.Instance; } public override void Transmit( TcpConnection connection, TcpOctetStream stream) { connection.ProcessOctet(stream); } }
As is TcpListen:
public class TcpListen : TcpState { public static TcpState Instance = new TcpListen(); private TcpListen() { } public override void Send(TcpConnection connection) { // Send SYN, receive SYN, ACK, etc. connection.State = TcpEstablished.Instance; } }
I admit that I find these examples a bit anaemic, since there's really no logic going on. None of the overrides change state conditionally, which would be possible and make the examples a little more interesting. If you're interested in an example where this happens, see my article Tennis kata using the State pattern.
Refactor to pure functions #
There's only one obvious source of impurity in the example: The literal State mutation of TcpConnection:
public TcpState State { get; internal set; }
While client code can't set the State property, subclasses can, and they do. After all, it's how the State pattern works.
It's quite a stretch to claim that if we can only get rid of that property setter then all else will be pure. After all, who knows what all those comments actually imply:
// Send SYN, receive SYN, ACK, etc.
To be honest, we must imagine that I/O takes place here. This means that even though it's possible to refactor away from mutating the State property, these implementations are not really going to be pure functions.
I could try to imagine what that SYN and ACK would look like, but it would be unfounded and hypothetical. I'm not going to do that here. Instead, that's the reason I'm going to publish a second article with a more realistic and complex example. When it comes to the present example, I'm going to proceed with the unreasonable assumption that the comments hide no nondeterministic behaviour or side effects.
As outlined in the article that compares the State pattern and the State monad, you can refactor state mutation to a pure function by instead returning the new state. Usually, you'd have to return a tuple, because you'd also need to return the 'original' return value. Here, however, the 'return type' of all methods is void, so this isn't necessary.
void is isomorphic to unit, so strictly speaking you could refactor to a return type like Tuple<Unit, TcpConnection>, but that is isomorphic to TcpConnection. (If you need to understand why that is, try writing two functions: One that converts a Tuple<Unit, TcpConnection> to a TcpConnection, and another that converts a TcpConnection to a Tuple<Unit, TcpConnection>.)
There's no reason to make things more complicated than they have to be, so I'm going to use the simplest representation: TcpConnection. Thus, you can get rid of the State mutation by instead returning a new TcpConnection from all methods:
public class TcpConnection { public TcpState State { get; } public TcpConnection() { State = TcpClosed.Instance; } private TcpConnection(TcpState state) { State = state; } public TcpConnection ActiveOpen() { return new TcpConnection(State.ActiveOpen(this)); } public TcpConnection PassiveOpen() { return new TcpConnection(State.PassiveOpen(this)); } // More members that delegate to State follows...
The State property no longer has a setter; there's only a public getter. In order to 'change' the state, code must return a new TcpConnection object with the new state. To facilitate that, you'll need to add a constructor overload that takes the new state as an input. Here I made it private, but making it more accessible is not prohibited.
This implies, however, that the TcpState methods also return values instead of mutating state. The base class now looks like this:
public class TcpState { public virtual TcpState Transmit(TcpConnection connection, TcpOctetStream stream) { return this; } public virtual TcpState ActiveOpen(TcpConnection connection) { return this; } public virtual TcpState PassiveOpen(TcpConnection connection) { return this; } // And so on...
Again, all the methods previously 'returned' void, so while, according to the State monad, you should strictly speaking return Tuple<Unit, TcpState>, this simplifies to TcpState.
Individual subclasses now do their work and return other TcpState implementations. I'm not going to tire you with all the example subclasses, so here's just TcpEstablished:
public class TcpEstablished : TcpState { public static TcpState Instance = new TcpEstablished(); private TcpEstablished() { } public override TcpState Close(TcpConnection connection) { // send FIN, receive ACK of FIN return TcpListen.Instance; } public override TcpState Transmit( TcpConnection connection, TcpOctetStream stream) { TcpConnection newConnection = connection.ProcessOctet(stream); return newConnection.State; } }
The trickiest implementation is Transmit, since ProcessOctet returns a TcpConnection while the Transmit method has to return a TcpState. Fortunately, the Transmit method can achieve that goal by returning newConnection.State. It feels a bit roundabout, but highlights a point I made in the previous article: The TcpConnection and TcpState classes are isomorphic - or, they would be if we made the TcpConnection constructor overload public. Thus, the TcpConnection class is redundant and might be deleted.
Conclusion #
This article shows how to refactor the TCP connection sample code from Design Patterns to pure functions.
If it feels as though something's missing there's a good reason for that. The example, as given, is degenerate because all methods 'return' void, and we don't really know what the actual implementation code (all that Send SYN, receive SYN, ACK, etc.) looks like. This means that we actually don't have to make use of the State monad, because we can get away with endomorphisms. All methods on TcpConnection are really functions that take TcpConnection as input (the instance itself) and return TcpConnection. If you want to see a more realistic example showcasing that perspective, see my article From State tennis to endomorphism.
Even though the example is degenerate, I wanted to show it because otherwise you might wonder how the book's example code fares when exposed to the State monad. To be clear, because of the nature of the example, the State monad never becomes necessary. Thus, we need a second example.
Next: Refactoring a saga from the State pattern to the State monad.
When to refactor
FAQ: How do I convince my manager to let me refactor?
This question frequently comes up. Developers want to refactor, but are under the impression that managers or other stakeholders will not let them.
Sometimes people ask me how to convince their managers to get permission to refactor. I can't answer that. I don't know how to convince other people. That's not my métier.
I also believe that professional programmers should make their own decisions. You don't ask permission to add three lines to a file, or create a new class. Why do you feel that you have to ask permission to refactor?
Does refactoring take time? #
In Code That Fits in Your Head I tell the following story:
"I once led an effort to refactor towards deeper insight. My colleague and I had identified that the key to implementing a new feature would require changing a fundamental class in our code base.
"While such an insight rarely arrives at an opportune time, we wanted to make the change, and our manager allowed it.
"A week later, our code still didn’t compile.
"I’d hoped that I could make the change to the class in question and then lean on the compiler to identify the call sites that needed modification. The problem was that there was an abundance of compilation errors, and fixing them wasn’t a simple question of search-and-replace.
"My manager finally took me aside to let me know that he wasn’t satisfied with the situation. I could only concur.
"After a mild dressing down, he allowed me to continue the work, and a few more days of heroic effort saw the work completed.
"That’s a failure I don’t intend to repeat."
There's a couple of points to this story. Yes, I did ask for permission before refactoring. I expected the process to take time, and I felt that making such a choice of prioritisation should involve my manager. While this manager trusted me, I felt a moral obligation to be transparent about the work I was doing. I didn't consider it professional to take a week out of the calendar and work on one thing while the rest of the organisation was expecting me to be working on something else.
So I can understand why developers feel that they have to ask permission to refactor. After all, refactoring takes time... Doesn't it?
Small steps #
This may unearth the underlying assumption that prevents developers from refactoring: The notion that refactoring takes time.
As I wrote in Code That Fits in Your Head, that was a failure I didn't intend to repeat. I've never again asked permission to refactor, because I've never since allowed myself to be in a situation where refactoring would take significant time.
The reason I tell the story in the book is that I use it to motivate using the Strangler pattern at the code level. The book proceeds to show an example of that.
Migrating code to a new API by allowing the old and the new to coexist for a while is only one of many techniques for taking smaller steps. Another is the use of feature flags, a technique that I also show in the book. Martin Fowler's Refactoring is literally an entire book about how to improve code bases in small, controlled steps.
Follow the red-green-refactor checklist and commit after each green and refactor step. Move in small steps and use Git tactically.
I'm beginning to realise, though, that moving in small steps is a skill that must be explicitly learned. This may seem obvious once posited, but it may also be helpful to explicitly state it.
Whenever I've had a chance to talk to other software professionals and thought leaders, they agree. As far as I can tell, universities and coding boot camps don't teach this skill, and if (like me) you're autodidact, you probably haven't learned it either. After all, few people insist that this is an important skill. It may, however, be one of the most important programming skills you can learn.
Make it work, then make it right #
When should you refactor? As the boy scout rule suggests: All the time.
You can, specifically, do it after implementing a new feature. As Kent Beck perhaps said or wrote: Make it work, then make it right.
How long does it take to make it right?
Perhaps you think that it takes as much time as it does to make it work.

Perhaps you think that making it right takes even more time.

If this is how much time making the code right takes, I can understand why you feel that you need to ask your manager. That's what I did, those many years ago. But what if the proportions are more like this?
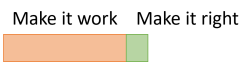
Do you still feel that you need to ask for permission to refactor?
Writing code so that the team can keep a sustainable pace is your job. It's not something you should have to ask for permission to do.
"Any fool can write code that a computer can understand. Good programmers write code that humans can understand."
Making the code right is not always a huge endeavour. It can be, if you've already made a mess of it, but if it's in good condition, keeping it that way doesn't have to take much extra effort. It's part of the ongoing design process that programming is.
How do you know what right is? Doesn't this make-it-work-make-it-right mentality lead to speculative generality?
No-one expects you to be able to predict the future, so don't try. Making it right means making the code good in the current context. Use good names, remove duplication, get rid of code smells, keep methods small and complexity low. Refactor if you exceed a threshold.
Make code easy to change #
The purpose of keeping code in a good condition is to make future changes as easy as possible. If you can't predict the future, however, then how do you know how to factor the code?
Another Kent Beck aphorism suggests a tactic:
"for each desired change, make the change easy (warning: this may be hard), then make the easy change"
In other words, when you know what you need to accomplish, first refactor the code so that it becomes easier to achieve the goal, and only then write the code to do that.

Should you ask permission to refactor in such a case? Only if you sincerely believe that you can complete the entire task significantly faster without first improving the code. How likely is that? If the code base is already a mess, how easy is it to make changes? Not easy, and granted: That will also be true for refactoring. The difference between first refactoring and not refactoring, however, is that if you refactor, you leave the code in a better state. If you don't, you leave it in a worse state.
These decisions compound.
But what if, as Kent Beck implies, refactoring is hard? Then the situation might look like this:

Should you ask for permission to refactor? I don't think so. While refactoring in this diagram is most of the work, it makes the change easy. Thus, once you're done refactoring, you make the easy change. The total amount of time this takes may turn out to be quicker than if you hadn't refactored (compare this figure to the previous figure: they're to scale). You also leave the code base in a better state so that future changes may be easier.
Conclusion #
There are lots of opportunities for refactoring. Every time you see something that could be improved, why not improve it? The fact that you're already looking at a piece of code suggests that it's somehow relevant to your current task. If it takes ten, fifteen minutes to improve it, why not do it? What if it takes an hour?
Most people think nothing of spending hours in meetings without asking their managers. If this is true, you can also decide to use a couple of hours improving code. They're likely as well spent as the meeting hours.
The key, however, is to be able to perform opportunistic refactoring. You can't do that if you can only move in day-long iterations; if hours, or days, go by when you can't compile, or when most tests fail.
On the other hand, if you're able to incrementally improve the code base in one-minute, or fifteen-minute, steps, then you can improve the code base every time an occasion arrives.
This is a skill that you need to learn. You're not born with the ability to improve in small steps. You'll have to practice - for example by doing katas. One customer of mine told me that they found Kent Beck's TCR a great way to teach that skill.
You can refactor in small steps. It's part of software engineering. Usually, you don't need to ask for permission.
Coalescing DTOs
Refactoring to a universal abstraction.
Despite my best efforts, no code base I write is perfect. This is also true for the code base that accompanies Code That Fits in Your Head.
One (among several) warts that has annoyed me for long is this:
[HttpPost("restaurants/{restaurantId}/reservations")] public async Task<ActionResult> Post( int restaurantId, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); var id = dto.ParseId() ?? Guid.NewGuid(); Reservation? reservation = dto.Validate(id); if (reservation is null) return new BadRequestResult(); // More code follows...
Passing id to Validate annoys me. Why does Validate need an id?
When you see it in context, it may makes some sort of sense, but in isolation, it seems arbitrary:
internal Reservation? Validate(Guid id)
Why does the method need an id? Doesn't ReservationDto have an Id?
Abstraction, broken #
Yes, indeed, ReservationDto has an Id property:
public string? Id { get; set; }
Then why do callers have to pass an id argument? Doesn't Validate use the Id property? It's almost as though the Validate method begs you to read the implementing code:
internal Reservation? Validate(Guid id) { if (!DateTime.TryParse(At, out var d)) return null; if (Email is null) return null; if (Quantity < 1) return null; return new Reservation( id, d, new Email(Email), new Name(Name ?? ""), Quantity); }
Indeed, the method doesn't use the Id property. Reading the code may not be of much help, but at least we learn that id is passed to the Reservation constructor. It's still not clear why the method isn't trying to parse the Id property, like it's doing with At.
I'll return to the motivation in a moment, but first I'd like to dwell on the problems of this design.
It's a typical example of ad-hoc design. I had a set of behaviours I needed to implement, and in order to avoid code duplication, I came up with a method that seemed to solve the problem.
And indeed, the Validate method does solve the problem of code duplication. It also passes all tests. It could be worse.
It could also be better.
The problem with an ad-hoc design like this is that the motivation is unclear. As a reader, you feel that you're missing the full picture. Perhaps you feel compelled to read the implementation code to gain a better understanding. Perhaps you look for other call sites. Perhaps you search the Git history to find a helpful comment. Perhaps you ask a colleague.
It slows you down. Worst of all, it may leave you apprehensive of refactoring. If you feel that there's something you don't fully understand, you may decide to leave the API alone, instead of improving it.
It's one of the many ways that code slowly rots.
What's missing here is a proper abstraction.
Motivation #
I recently hit upon a design that I like better. Before I describe it, however, you need to understand the problem I was trying to solve.
The code base for the book is a restaurant reservation REST API, and I was evolving the code as I wrote it. I wanted the code base (and its Git history) to be as realistic as possible. In a real-world situation, you don't always know all requirements up front, or even if you do, they may change.
At one point I decided that a REST client could supply a GUID when making a new reservation. On the other hand, I had lots of existing tests (and a deployed system) that accepted reservations without IDs. In order to not break compatibility, I decided to use the ID if it was supplied with the DTO, and otherwise create one. (I later explored an API without explicit IDs, but that's a different story.)
The id is a JSON property, however, so there's no guarantee that it's properly formatted. Thus, the need to first parse it:
var id = dto.ParseId() ?? Guid.NewGuid();
To make matters even more complicated, when you PUT a reservation, the ID is actually part of the resource address, which means that even if it's present in the JSON document, that value should be ignored:
[HttpPut("restaurants/{restaurantId}/reservations/{id}")] public async Task<ActionResult> Put( int restaurantId, string id, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); if (!Guid.TryParse(id, out var rid)) return new NotFoundResult(); Reservation? reservation = dto.Validate(rid); if (reservation is null) return new BadRequestResult(); // More code follows...
Notice that this Put implementation exclusively considers the resource address id parameter. Recall that the Validate method ignores the dto's Id property.
This is knowledge about implementation details that leaks through to the calling code. As a client developer, you need to know and keep this knowledge in your head while you write your own code. That's not really code that fits in your head.
As I usually put it: If you have to read the code, it implies that encapsulation is broken.
At the time, however, I couldn't think of a better alternative, and since the problem is still fairly small and localised, I decided to move on. After all, perfect is the enemy of good.
Why don't you just..? #
Is there a better way? Perhaps you think that you've spotted an obvious improvement. Why don't I just try to parse dto.Id and then create a Guid.NewGuid() if parsing fails? Like this:
internal Reservation? Validate() { if (!Guid.TryParse(Id, out var id)) id = Guid.NewGuid(); if (!DateTime.TryParse(At, out var d)) return null; if (Email is null) return null; if (Quantity < 1) return null; return new Reservation( id, d, new Email(Email), new Name(Name ?? ""), Quantity); }
The short answer is: Because it doesn't work.
It may work for Get, but then Put doesn't have a way to tell the Validate method which ID to use.
Or rather: That's not entirely true, because this is possible:
dto.Id = id;
Reservation? reservation = dto.Validate();
This does suggest an even better way. Before we go there, however, there's another reason I don't like this particular variation: It makes Validate impure.
Why care? you may ask.
I always end up regretting making an otherwise potentially pure function non-deterministic. Sooner or later, it turns out to have been a bad decision, regardless of how alluring it initially looked. I recently gave an example of that.
When weighing the advantages and disadvantages, I preferred passing id explicitly rather than relying on Guid.NewGuid() inside Validate.
First monoid #
One of the reasons I find universal abstractions beneficial is that you only have to learn them once. As Felienne Hermans writes in The Programmer's Brain our working memory juggles a combination of ephemeral data and knowledge from our long-term memory. The better you can leverage existing knowledge, the easier it is to read code.
Which universal abstraction enables you to choose from a prioritised list of candidates? The First monoid!
In C# with nullable reference types the null-coalescing operator ?? already implements the desired functionality. (If you're using another language or an older version of C#, you can instead use Maybe.)
Once I got that idea I was able to simplify the API.
Parsing and coalescing DTOs #
Instead of that odd Validate method which isn't quite a validator and not quite a parser, this insight suggests to parse, don't validate:
internal Reservation? TryParse() { if (!Guid.TryParse(Id, out var id)) return null; if (!DateTime.TryParse(At, out var d)) return null; if (Email is null) return null; if (Quantity < 1) return null; return new Reservation( id, d, new Email(Email), new Name(Name ?? ""), Quantity); }
This function only returns a parsed Reservation object when the Id is present and well-formed. What about the cases where the Id is absent?
The calling ReservationsController can deal with that:
Reservation? candidate1 = dto.TryParse(); dto.Id = Guid.NewGuid().ToString("N"); Reservation? candidate2 = dto.TryParse(); Reservation? reservation = candidate1 ?? candidate2; if (reservation is null) return new BadRequestResult();
First try to parse the dto, then explicitly overwrite its Id property with a new Guid, and then try to parse it again. Finally, pick the first of these that aren't null, using the null-coalescing ?? operator.
This API also works consistently in the Put method:
dto.Id = id; Reservation? reservation = dto.TryParse(); if (reservation is null) return new BadRequestResult();
Why is this better? I consider it better because the TryParse function should be a familiar abstraction. Once you've seen a couple of those, you know that a well-behaved parser either returns a valid object, or nothing. You don't have to go and read the implementation of TryParse to (correctly) guess that. Thus, encapsulation is maintained.
Where does mutation go? #
The ReservationsController mutates the dto and relies on the impure Guid.NewGuid() method. Why is that okay when it wasn't okay to do this inside of Validate?
This is because the code base follows the functional core, imperative shell architecture. Specifically, Controllers make up the imperative shell, so I consider it appropriate to put impure actions there. After all, they have to go somewhere.
This means that the TryParse function remains pure.
Conclusion #
Sometimes a good API design can elude you for a long time. When that happens, I move on with the best solution I can think of in the moment. As it often happens, though, ad-hoc abstractions leave me unsatisfied, so I'm always happy to improve such code later, if possible.
In this article, you saw an example of an ad-hoc API design that represented the best I could produce at the time. Later, it dawned on me that an implementation based on a universal abstraction would be possible. In this case, the universal abstraction was null coalescing (which is a specialisation of the monoid abstraction).
I like universal abstractions because, once you know them, you can trust that they work in well-understood ways. You don't have to waste time reading implementation code in order to learn whether it's safe to call a method in a particular way.
This saves time when you have to work with the code, because, after all, we spend more time reading code than writing it.
Comments
After the refactor in this article, is the entirety of your Post method (including the part you didn't show in this article) an impureim sandwich?
Not yet. There's a lot of (preliminary) interleaving of impure actions and pure functions remaining in the controller, even after this refactoring.
A future article will tackle that question. One of the reasons I even started writing about monads, functor relationships, etcetera was to establish the foundations for what this requires. If it can be done without monads and traversals I don't know how.
Even though the Post method isn't an impureim sandwich, I still consider the architecture functional core, imperative shell, since I've kept all impure actions in the controllers.
The reason I didn't go all the way to impureim sandwiches with the book's code is didactic. For complex logic, you'll need traversals, monads, sum types, and so on, and none of those things were in scope for the book.
The State pattern and the State monad
The names are the same. Is there a connection? An article for object-oriented programmers.
This article is part of a series of articles about specific design patterns and their category theory counterparts. In this article I compare the State design pattern to the State monad.
Since the design pattern and the monad share the name State you'd think that they might be isomorphic, but it's not quite that easy. I find it more likely that the name is an example of parallel evolution. Monads were discovered by Eugenio Moggi in the early nineties, and Design Patterns is from 1994. That's close enough in time that I find it more likely that whoever came up with the names found them independently. State, after all, is hardly an exotic word.
Thus, it's possible that the choice of the same name is coincidental. If this is true (which is only my conjecture), does the State pattern have anything in common with the State monad? I find that the answer is a tentative yes. The State design pattern describes an open polymorphic stateful computation. That kind of computation can also be described with the State monad.
This article contains a significant amount of code, and it's all quite abstract. It examines the abstract shape of the pattern, so there's little prior intuition on which to build an understanding. While later articles will show more concrete examples, if you want to follow along, you can use the GitHub repository.
Shape #
Design Patterns is a little vague when it comes to representing the essential form of the pattern. What one can deduce from the diagram in the Structure section describing the pattern, you have an abstract State class with a Handle method like this:
public virtual void Handle(Context context) { }
This, however, doesn't capture all scenarios. What if you need to pass more arguments to the method? What if the method returns a result? What if there's more than one method?
Taking into account all those concerns, you might arrive at a more generalised description of the State pattern where an abstract State class might define methods like these:
public abstract Out1 Handle1(Context context, In1 in1); public abstract Out2 Handle2(Context context, In2 in2);
There might be an arbitrary number of Handle methods, from Handle1 to HandleN, each with their own input and return types.
The idea behind the State pattern is that clients don't interact directly with State objects. Instead, they interact with a Context object that delegates operations to a State object, passing itself as an argument:
public Out1 Request1(In1 in1) { return State.Handle1(this, in1); } public Out2 Request2(In2 in2) { return State.Handle2(this, in2); }
Classes that derive from the abstract State may then mutate context.State.
public override Out2 Handle2(Context context, In2 in2) { if (in2 == In2.Epsilon) context.State = new ConcreteStateB(); return Out2.Eta; }
Clients interact with the Context object and aren't aware of this internal machinery:
var actual = ctx.Request2(in2);
With such state mutation going on, is it possible to refactor to a design that uses immutable data and pure functions?
State pair #
When you have a void method that mutates state, you can refactor it to a pure function by leaving the existing state unchanged and instead returning the new state. What do you do, however, when the method in question already returns a value?
This is the case with the generalised HandleN methods, above.
One way to resolve this problem is to introduce a more complex type to return. To avoid too much duplication or boilerplate code, you could make it a generic type:
public sealed class StatePair<T> { public StatePair(T value, State state) { Value = value; State = state; } public T Value { get; } public State State { get; } public override bool Equals(object obj) { return obj is StatePair<T> result && EqualityComparer<T>.Default.Equals(Value, result.Value) && EqualityComparer<State>.Default.Equals(State, result.State); } public override int GetHashCode() { return HashCode.Combine(Value, State); } }
This enables you to change the signatures of the Handle methods:
public abstract StatePair<Out1> Handle1(Context context, In1 in1); public abstract StatePair<Out2> Handle2(Context context, In2 in2);
This refactoring is always possible. Even if the original return type of a method was void, you can use a unit type as a replacement for void. While redundant but consistent, a method could return StatePair<Unit>.
Generic pair #
The above StatePair type is so coupled to a particular State class that it's not reusable. If you had more than one implementation of the State pattern in your code base, you'd have to duplicate that effort. That seems wasteful, so why not make the type generic in the state dimension as well?
public sealed class StatePair<TState, T> { public StatePair(T value, TState state) { Value = value; State = state; } public T Value { get; } public TState State { get; } public override bool Equals(object obj) { return obj is StatePair<TState, T> pair && EqualityComparer<T>.Default.Equals(Value, pair.Value) && EqualityComparer<TState>.Default.Equals(State, pair.State); } public override int GetHashCode() { return HashCode.Combine(Value, State); } }
When you do that then clearly you'd also need to modify the Handle methods accordingly:
public abstract StatePair<State, Out1> Handle1(Context context, In1 in1); public abstract StatePair<State, Out2> Handle2(Context context, In2 in2);
Notice that, as is the case with the State functor, the type declares the type with TState before T, while the constructor takes T before TState. While odd and potentially confusing, I've done this to stay consistent with my previous articles, which again do this to stay consistent with prior art (mainly Haskell).
With StatePair you can make the methods pure.
Pure functions #
Since Handle methods can now return a new state instead of mutating objects, they can be pure functions. Here's an example:
public override StatePair<State, Out2> Handle2(Context context, In2 in2) { if (in2 == In2.Epsilon) return new StatePair<State, Out2>(Out2.Eta, new ConcreteStateB()); return new StatePair<State, Out2>(Out2.Eta, this); }
The same is true for Context:
public StatePair<Context, Out1> Request1(In1 in1) { var pair = State.Handle1(this, in1); return new StatePair<Context, Out1>(pair.Value, new Context(pair.State)); } public StatePair<Context, Out2> Request2(In2 in2) { var pair = State.Handle2(this, in2); return new StatePair<Context, Out2>(pair.Value, new Context(pair.State)); }
Does this begin to look familiar?
Monad #
The StatePair class is nothing but a glorified tuple. Armed with that knowledge, you can introduce a variation of the IState interface I used to introduce the State functor:
public interface IState<TState, T> { StatePair<TState, T> Run(TState state); }
This variation uses the explicit StatePair class as the return type of Run, rather than a more anonymous tuple. These representations are isomorphic. (That might be a good exercise: Write functions that convert from one to the other, and vice versa.)
You can write the usual Select and SelectMany implementations to make IState a functor and monad. Since I have already shown these in previous articles, I'm also going to skip those. (Again, it might be a good exercise to implement them if you're in doubt of how they work.)
You can now, for example, use C# query syntax to run the same computation multiple times:
IState<Context, (Out1 a, Out1 b)> s = from a in in1.Request1() from b in in1.Request1() select (a, b); StatePair<Context, (Out1 a, Out1 b)> t = s.Run(ctx);
This example calls Request1 twice, and collects both return values in a tuple. Running the computation with a Context will produce both a result (the two outputs a and b) as well as the 'current' Context (state).
Request1 is a State-valued extension method on In1:
public static IState<Context, Out1> Request1(this In1 in1) { return from ctx in Get<Context>() let p = ctx.Request1(in1) from _ in Put(p.State) select p.Value; }
Notice the abstraction level in play. This extension method doesn't return a StatePair, but rather an IState computation, defined by using the State monad's Get and Put functions. Since the computation is running with a Context state, the computation can Get a ctx object and call its Request1 method. This method returns a pair p. The computation can then Put the pair's State (here, a Context object) and return the pair's Value.
This stateful computation is composed from the building blocks of the State monad, including query syntax supported by SelectMany, Get, and Put.
This does, however, still feel unsatisfactory. After all, you have to know enough of the details of the State monad to know that ctx.Request1 returns a pair of which you must remember to Put the State. Would it be possible to also express the underlying Handle methods as stateful computations?
StatePair bifunctor #
The StatePair class is isomorphic to a pair (a two-tuple), and we know that a pair gives rise to a bifunctor:
public StatePair<TState1, T1> SelectBoth<TState1, T1>( Func<T, T1> selectValue, Func<TState, TState1> selectState) { return new StatePair<TState1, T1>( selectValue(Value), selectState(State)); }
You can use SelectBoth to implement both Select and SelectState. In the following we're only going to need SelectState:
public StatePair<TState1, T> SelectState<TState1>(Func<TState, TState1> selectState) { return SelectBoth(x => x, selectState); }
This enables us to slightly simplify the Context methods:
public StatePair<Context, Out1> Request1(In1 in1) { return State.Handle1(this, in1).SelectState(s => new Context(s)); } public StatePair<Context, Out2> Request2(In2 in2) { return State.Handle2(this, in2).SelectState(s => new Context(s)); }
Keep in mind that Handle1 returns a StatePair<State, Out1>, Handle2 returns StatePair<State, Out2>, and so on. While Request1 calls Handle1, it must return a StatePair<Context, Out1> rather than a StatePair<State, Out1>. Since StatePair is a bifunctor, the Request1 method can use SelectState to map the State to a Context.
Unfortunately, this doesn't seem to move us much closer to being able to express the underlying functions as stateful computations. It does, however, set up the code so that the next change is a little easier to follow.
State computations #
Is it possible to express the Handle methods on State as IState computations? One option is to write another extension method:
public static IState<State, Out1> Request1S(this In1 in1) { return from s in Get<State>() let ctx = new Context(s) let p = s.Handle1(ctx, in1) from _ in Put(p.State) select p.Value; }
I had to add an S suffix to the name, since it only differs from the above Request1 extension method on its return type, and C# doesn't allow method overloading on return types.
You can add a similar Request2S extension method. It feels like boilerplate code, but enables us to express the Context methods in terms of running stateful computations:
public StatePair<Context, Out1> Request1(In1 in1) { return in1.Request1S().Run(State).SelectState(s => new Context(s)); } public StatePair<Context, Out2> Request2(In2 in2) { return in2.Request2S().Run(State).SelectState(s => new Context(s)); }
This still isn't entirely satisfactory, since the return types of these Request methods are state pairs, and not IState values. The above Request1S function, however, contains a clue about how to proceed. Notice how it can create a Context object from the underlying State, and convert that Context object back to a State object. That's a generalizable idea.
Invariant functor #
While it's possible to map the TState dimension of the state pair, it seems harder to do it on IState<TState, T>. A tuple, after all, is covariant in both dimensions. The State monad, on the other hand, is neither co- nor contravariant in the state dimension. You can deduce this with positional variance analysis (which I've learned from Thinking with Types). In short, this is because TState appears as both input and output in StatePair<TState, T> Run(TState state) - it's neither co- nor contravariant, but rather invariant.
What little option is left us, then, is to make IState an invariant functor in the state dimension:
public static IState<TState1, T> SelectState<TState, TState1, T>( this IState<TState, T> state, Func<TState, TState1> forward, Func<TState1, TState> back) { return from s1 in Get<TState1>() let s = back(s1) let p = state.Run(s) from _ in Put(forward(p.State)) select p.Value; }
Given an IState<TState, T> the SelectState function enables us to turn it into a IState<TState1, T>. This is, however, only possible if you can translate both forward and back between two representations. When we have two such translations, we can produce a new computation that runs in TState1 by first using Get to retrieve a TState1 value from the new environment, translate it back to TState, which enables the expression to Run the state. Then translate the resulting p.State forward and Put it. Finally, return the Value.
As Sandy Maguire explains:
"... an invariant type
Tallows you to map fromatobif and only ifaandbare isomorphic. [...] an isomorphism betweenaandbmeans they're already the same thing to begin with."
This may seem limiting, but is enough in this case. The Context class is only a wrapper of a State object:
public Context(State state) { State = state; } public State State { get; }
If you have a State object, you can create a Context object via the Context constructor. On the other hand, if you have a Context object, you can get the wrapped State object by reading the State property.
The first improvement this offers is simplification of the Request1 extension method:
public static IState<Context, Out1> Request1(this In1 in1) { return in1.Request1S().SelectState(s => new Context(s), ctx => ctx.State); }
Recall that Request1S returns a IState<State, Out1>. Since a two-way translation between State and Context exists, SelectState can translate IState<State, Out1> to IState<Context, Out1>.
The same applies to the equivalent Request2 extension method.
This, again, enables us to rewrite the Context methods:
public StatePair<Context, Out1> Request1(In1 in1) { return in1.Request1().Run(this); } public StatePair<Context, Out2> Request2(In2 in2) { return in2.Request2().Run(this); }
While this may seem like an insignificant change, one result has been gained: This last refactoring pushed the Run call to the right. It's now clear that each expression is a stateful computation, and that the only role that the Request methods play is to Run the computations.
This illustrates that the Request methods can be decomposed into two decoupled steps:
- A stateful computation expression
- Running the expression
Context wrapper class now?
Eliminating the Context #
A reasonable next refactoring might be to remove the context parameter from each of the Handle methods. After all, this parameter is a remnant of the State design pattern. Its original purpose was to enable State implementers to mutate the context by changing its State.
After refactoring to immutable functions, the context parameter no longer needs to be there - for that reason. Do we need it for other reasons? Does it carry other information that a State implementer might need?
In the form that the code now has, it doesn't. Even if it did, we could consider moving that data to the other input parameter: In1, In2, etcetera.
Therefore, it seems sensible to remove the context parameter from the State methods:
public abstract StatePair<State, Out1> Handle1(In1 in1); public abstract StatePair<State, Out2> Handle2(In2 in2);
This also means that a function like Request1S becomes simpler:
public static IState<State, Out1> Request1S(this In1 in1) { return from s in Get<State>() let p = s.Handle1(in1) from _ in Put(p.State) select p.Value; }
Since Context and State are isomorphic, you can rewrite all callers of Context to instead use State, like the above example:
IState<State, (Out1 a, Out1 b)> s = from a in in1.Request1() from b in in1.Request1() select (a, b); var t = s.Run(csa);
Do this consistently, and you can eventually delete the Context class.
Further possible refactorings #
With the Context class gone, you're left with the abstract State class and its implementers:
public abstract class State { public abstract StatePair<State, Out1> Handle1(In1 in1); public abstract StatePair<State, Out2> Handle2(In2 in2); }
One further change worth considering might be to change the abstract base class to an interface.
In this article, I've considered the general case where the State class supports an arbitrary number of independent state transitions, symbolised by the methods Handle1 and Handle2. With an arbitrary number of such state transitions, you would have additional methods up to HandleN for N independent state transitions.
At the other extreme, you may have just a single polymorphic state transition function. My intuition tells me that that's more likely to be the case than one would think at first.
Relationship between pattern and monad #
You can view the State design pattern as a combination of two common practices in object-oriented programming: Mutation and polymorphism.
The patterns in Design Patterns rely heavily on mutation of object state. Most other 'good' object-oriented code tends to do likewise.
Proper object-oriented code also makes good use of polymorphism. Again, refer to Design Patterns or a book like Refactoring for copious examples.
I view the State pattern as the intersection of these two common practices. The problem to solve is this:
"Allow an object to alter its behavior when its internal state changes."
The State pattern achieves that goal by having an inner polymorphic object (State) wrapped by an container object (Context). The State objects can mutate the Context, which enables them to replace themselves with other states.
While functional programming also has notions of polymorphism, a pure function can't mutate state. Instead, a pure function must return a new state, leaving the old state unmodified. If there's nothing else to return, you can model such state-changing behaviour as an endomorphism. The article From State tennis to endomorphism gives a quite literal example of that.
Sometimes, however, an object-oriented method does more than one thing: It both mutates state and returns a value. (This, by the way, violates the Command Query Separation principle.) The State monad is the functional way of doing that: Return both the result and the new state.
Essentially, you replace mutation with the State monad.
From a functional perspective, then, we can view the State pattern as the intersection of polymorphism and the State monad.
Examples #
This article is both long and abstract. Some examples might be helpful, so I'll give a few in separate articles:
- Refactoring the TCP State pattern example to pure functions
- Refactoring a saga from the State pattern to the State monad
Conclusion #
You can view the State design pattern as the intersection of polymorphism and mutation. Both are object-oriented staples. The pattern uses polymorphism to model state, and mutation to change from one polymorphic state to another.
In functional programming pure functions can't mutate state. You can often design around that problem, but if all else fails, the State monad offers a general-purpose alternative to both return a value and change object state. Thus, you can view the functional equivalent of the State pattern as the intersection of polymorphism and the State monad.
Next: Refactoring the TCP State pattern example to pure functions.
Natural transformations as invariant functors
An article (also) for object-oriented programmers.
Update 2022-09-04: This article is most likely partially incorrect. What it describes works, but may not be a natural transformation. See the below comment for more details.
This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details. The previous article described how you can view an endomorphism as an invariant functor. This article generalises that result.
Endomorphism as a natural transformation #
An endomorphism is a function whose domain and codomain is the same. In C# you'd denote the type as Func<T, T>, in F# as 'a -> 'a, and in Haskell as a -> a. T, 'a, and a all symbolise generic types - the notation is just different, depending on the language.
A 'naked' value is isomorphic to the Identity functor. You can wrap a value of the type a in Identity a, and if you have an Identity a, you can extract the a value.
An endomorphism is thus isomorphic to a function from Identity to Identity. In C#, you might denote that as Func<Identity<T>, Identity<T>>, and in Haskell as Identity a -> Identity a.
In fact, you can lift any function to an Identity-valued function:
Prelude Data.Functor.Identity> :t \f -> Identity . f . runIdentity \f -> Identity . f . runIdentity :: (b -> a) -> Identity b -> Identity a
While this is a general result that allows a and b to differ, when a ~ b this describes an endomorphism.
Since Identity is a functor, a function Identity a -> Identity a is a natural transformation.
The identity function (id in F# and Haskell; x => x in C#) is the only one possible entirely general endomorphism. You can use the natural-transformation package to make it explicit that this is a natural transformation:
idNT :: Identity :~> Identity idNT = NT $ Identity . id . runIdentity
The point, so far, is that you can view an endomorphism as a natural transformation.
Since an endomorphism forms an invariant functor, this suggests a promising line of inquiry.
Natural transformations as invariant functors #
Are all natural transformations invariant functors?
Yes, they are. In Haskell, you can implement it like this:
instance (Functor f, Functor g) => Invariant (NT f g) where invmap f g (NT h) = NT $ fmap f . h . fmap g
Here, I chose to define NT from scratch, rather than relying on the natural-transformation package.
newtype NT f g a = NT { unNT :: f a -> g a }
Notice how the implementation (fmap f . h . fmap g) looks like a generalisation of the endomorphism implementation of invmap (f . h . g). Instead of pre-composing with g, the generalisation pre-composes with fmap g, and instead of post-composing with f, it post-composes with fmap f.
Using the same kind of diagram as in the previous article, this composition now looks like this:
I've used thicker arrows to indicate that each one potentially involves 'more work'. Each is a mapping from a functor to a functor. For the List functor, for example, the arrow implies zero to many values being mapped. Thus, 'more data' moves 'through' each arrow, and for that reason I thought it made sense to depict them as being thicker. This 'more data' view is not always correct. For example, for the Maybe functor, the amount of data transported though each arrow is zero or one, which rather suggests a thinner arrow. For something like the State functor or the Reader functor, there's really no data in the strictest sense moving through the arrows, but rather functions (which are also, however, a kind of data). Thus, don't take this metaphor of the thicker arrows literally. I did, however, wish to highlight that there's something 'more' going on.
The diagram shows a natural transformation h from some functor F to another functor G. It transports objects of the type a. If a and b are isomorphic, you can map that natural transformation to one that transports objects of the type b.
Compared to endomorphisms, where you need to, say, map b to a, you now need to map F b to F a. If g maps b to a, then fmap g maps F b to F a. The same line of argument applies to fmap f.
In C# you can implement the same behaviour as follows. Assume that you have a natural transformation H from the functor F to the functor G:
public Func<F<A>, G<A>> H { get; }
You can now implement a non-standard Select overload (as described in the introductory article) that maps a natural transformation FToG<A> to a natural transformation FToG<B>:
public FToG<B> Select<B>(Func<A, B> aToB, Func<B, A> bToA) { return new FToG<B>(fb => H(fb.Select(bToA)).Select(aToB)); }
The implementation looks more imperative than in Haskell, but the idea is the same. First it uses Select on F in order to translate fb (of the type F<B>) to an F<A>. It then uses H to transform the F<A> to an G<A>. Finally, now that it has a G<A>, it can use Select on that functor to map to a G<B>.
Note that there's two different functors (F and G) in play, so the two Select methods are different. This is also true in the Haskell code. fmap g need not be the same as fmap f.
Identity law #
As in the previous article, I'll set out to prove the two laws for invariant functors, starting with the identity law. Again, I'll use equational reasoning with the notation that Bartosz Milewski uses. Here's the proof that the invmap instance obeys the identity law:
invmap id id (NT h)
= { definition of invmap }
NT $ fmap id . h . fmap id
= { first functor law }
NT $ id . h . id
= { eta expansion }
NT $ (\x -> (id . h . id) x)
= { definition of (.) }
NT $ (\x -> id(h(id(x))))
= { defintion of id }
NT $ (\x -> h(x))
= { eta reduction }
NT h
= { definition of id }
id (NT h)
I'll leave it here without further comment. The Haskell type system is so expressive and abstract that it makes little sense to try to translate these findings to C# or F# in the abstract. Instead, you'll see some more concrete examples later.
Composition law #
As with the identity law, I'll offer a proof for the composition law for the Haskell instance:
invmap f2 f2' $ invmap f1 f1' (NT h)
= { definition of invmap }
invmap f2 f2' $ NT $ fmap f1 . h . fmap f1'
= { defintion of ($) }
invmap f2 f2' (NT (fmap f1 . h . fmap f1'))
= { definition of invmap }
NT $ fmap f2 . (fmap f1 . h . fmap f1') . fmap f2'
= { associativity of composition (.) }
NT $ (fmap f2 . fmap f1) . h . (fmap f1' . fmap f2')
= { second functor law }
NT $ fmap (f2 . f1) . h . fmap (f1' . f2')
= { definition of invmap }
invmap (f2 . f1) (f1' . f2') (NT h)
Unless I've made a mistake, these two proofs should demonstrate that all natural transformations can be turned into an invariant functor - in Haskell, at least, but I'll conjecture that that result carries over to other languages like F# and C# as long as one stays within the confines of pure functions.
The State functor as a natural transformation #
I'll be honest and admit that my motivation for embarking on this exegesis was because I'd come to the realisation that you can think about the State functor as a natural transformation. Recall that State is usually defined like this:
newtype State s a = State { runState :: s -> (a, s) }
You can easily establish that this definition of State is isomorphic with a natural transformation from the Identity functor to the tuple functor:
stateToNT :: State s a -> NT Identity ((,) a) s stateToNT (State h) = NT $ h . runIdentity ntToState :: NT Identity ((,) a) s -> State s a ntToState (NT h) = State $ h . Identity
Notice that this is a natural transformation in s - not in a.
Since I've already established that natural transformations form invariant functors, this also applies to the State monad.
State mapping #
My point with all of this isn't really to insist that anyone makes actual use of all this machinery, but rather that this line of reasoning helps to identify a capability. We now know that it's possible to translate a State s a value to a State t a value if s is isomorphic to t.
As an example, imagine that you have some State-valued function that attempts to find the maximum value based on various criteria. Such a pickMax function may have the type State (Max Integer) String where the state type (Max Integer) is used to keep track of the maximum value found while examining candidates.
You could conceivably turn such a function around to instead look for the minimum by mapping the state to a Min value instead:
pickMin :: State (Min Integer) String pickMin = ntToState $ invmap (Min . getMax) (Max . getMin) $ stateToNT pickMax
You can use getMax to extract the underlying Integer from the Max Integer and then Min to turn it into a Min Integer value, and vice versa. Max Integer and Min Integer are isomorphic.
In C#, you can implement a similar method. The code shown here extends the code shown in The State functor. I chose to call the method SelectState so as to not make things too confusing. The State functor already comes with a Select method that maps T to T1 - that's the 'normal', covariant functor implementation. The new method is the invariant functor implementation that maps the state S to S1:
public static IState<S1, T> SelectState<T, S, S1>( this IState<S, T> state, Func<S, S1> sToS1, Func<S1, S> s1ToS) { return new InvariantStateMapper<T, S, S1>(state, sToS1, s1ToS); } private class InvariantStateMapper<T, S, S1> : IState<S1, T> { private readonly IState<S, T> state; private readonly Func<S, S1> sToS1; private readonly Func<S1, S> s1ToS; public InvariantStateMapper( IState<S, T> state, Func<S, S1> sToS1, Func<S1, S> s1ToS) { this.state = state; this.sToS1 = sToS1; this.s1ToS = s1ToS; } public Tuple<T, S1> Run(S1 s1) { return state.Run(s1ToS(s1)).Select(sToS1); } }
As usual when working in C# with interfaces instead of higher-order functions, there's some ceremony to be expected. The only interesting line of code is the Run implementation.
It starts by calling s1ToS in order to translate the s1 parameter into an S value. This enables it to call Run on state. The result is a tuple with the type Tuple<T, S>. It's necessary to translate the S to S1 with sToS1. You could do that by extracting the value from the tuple, mapping it, and returning a new tuple. Since a tuple gives rise to a functor (two, actually) I instead used the Select method I'd already defined on it.
Notice how similar the implementation is to the implementation of the endomorphism invariant functor. The only difference is that when translating back from S to S1, this happens inside a Select mapping. This is as predicted by the general implementation of invariant functors for natural transformations.
In a future article, you'll see an example of SelectState in action.
Other natural transformations #
As the natural transformations article outlines, there are infinitely many natural transformations. Each one gives rise to an invariant functor.
It might be a good exercise to try to implement a few of them as invariant functors. If you want to do it in C#, you could, for example, start with the safe head natural transformation.
If you want to stick to interfaces, you could define one like this:
public interface ISafeHead<T> { Maybe<T> TryFirst(IEnumerable<T> ts); }
The exercise is now to define and implement a method like this:
public static ISafeHead<T1> Select<T, T1>( this ISafeHead<T> source, Func<T, T1> tToT1, Func<T1, T> t1ToT) { // Implementation goes here... }
The implementation, once you get the handle of it, is entirely automatable. After all, in Haskell it's possible to do it once and for all, as shown above.
Conclusion #
A natural transformation forms an invariant functor. This may not be the most exciting result ever, because invariant functors are limited in use. They only work when translating between types that are already isomorphic. Still, I did find a use for this result when I was working with the relationship between the State design pattern and the State monad.
Comments
Due to feedback that I've received, I have to face evidence that this article may be partially incorrect. While I've added that proviso at the top of the article, I've decided to use a comment to expand on the issue.
On Twitter, the user @Savlambda (borar) argued that my newtype isn't a natural transformation:
"The newtype 'NT' in the article is not a natural transformation though. Quantification over 'a' is at the "wrong place": it is not allowed for a client module to instantiate the container element type of a natural transformation."
While I engaged with the tweet, I have to admit that it took me a while to understand the core of the criticism. Of course I'm not happy about being wrong, but initially I genuinely didn't understand what was the problem. On the other hand, it's not the first time @Savlambda has provided valuable insights, so I knew it'd behove me to pay attention.
After a few tweets back and forth, @Savlambda finally supplied a counter-argument that I understood.
"This is not being overly pedantic. Here is one practical implication:"
The practical implication shown in the tweet is a screen shot (in order to get around Twitter's character limitation), but I'll reproduce it as code here in order to not show images of code.
type (~>) f g = forall a. f a -> g a -- Use the natural transformation twice, for different types convertLists :: ([] ~> g) -> (g Int, g Bool) convertLists nt = (nt [1,2], nt [True]) newtype NT f g a = NT (f a -> g a) -- Does not type check, does not work; not a natural transformation convertLists2 :: NT [] g a -> (g Int, g Bool) convertLists2 (NT f) = (f [1,2], f [True])
I've moved the code comments to prevent horizontal scrolling, but otherwise tried to stay faithful to @Savlambda's screen shot.
This was the example that finally hit the nail on the head for me. A natural transformation is a mapping from one functor (f) to another functor (g). I knew that already, but hadn't realised the implications. In Haskell (and other languages with parametric polymorphism) a Functor is defined for all a.
A natural transformation is a higher level of abstraction, mapping one functor to another. That mapping must be defined for all a, and it must be reusable. The second example provided by @Savlambda demonstrates that the function wrapped by NT isn't reusable for different contained types.
If you try to compile that example, GHC emits this compiler error:
* Couldn't match type `a' with `Int'
`a' is a rigid type variable bound by
the type signature for:
convertLists2 :: forall (g :: * -> *) a.
NT [] g a -> (g Int, g Bool)
Expected type: g Int
Actual type: g a
* In the expression: f [1, 2]
In the expression: (f [1, 2], f [True])
In an equation for `convertLists2':
convertLists2 (NT f) = (f [1, 2], f [True])
Even though it's never fun to be proven wrong, I want to thank @Savlambda for educating me. One reason I write blog posts like this one is that writing is a way to learn. By writing about topics like these, I educate myself. Occasionally, it turns out that I make a mistake, and this isn't the first time that's happened. I also wish to apologise if this article has now left any readers more confused.
A remaining question is what practical implications this has? Only rarely do you need a programming construct like convertLists2. On the other hand, had I wanted a function with the type NT [] g Int -> (g Int, g Int), it would have type-checked just fine.
I'm not claiming that this is generally useful either, but I actually wrote this article because I did have use for the result that NT (whatever it is) is an invariant functor. As far as I can tell, that result still holds.
I could be wrong about that, too. If you think so, please leave a comment.
Can types replace validation?
With some examples in C#.
In a comment to my article on ASP.NET validation revisited Maurice Johnson asks:
"I was just wondering, is it possible to use the type system to do the validation instead ?
"What I mean is, for example, to make all the ReservationDto's field a type with validation in the constructor (like a class name, a class email, and so on). Normally, when the framework will build ReservationDto, it will try to construct the fields using the type constructor, and if there is an explicit error thrown during the construction, the framework will send us back the error with the provided message.
"Plus, I think types like "email", "name" and "at" are reusable. And I feel like we have more possibilities for validation with that way of doing than with the validation attributes.
"What do you think ?"
I started writing a response below the question, but it grew and grew so I decided to turn it into a separate article. I think the question is of general interest.
The halting problem #
I'm all in favour of using the type system for encapsulation, but there are limits to what it can do. We know this because it follows from the halting problem.
I'm basing my understanding of the halting problem on my reading of The Annotated Turing. In short, given an arbitrary computer program in a Turing-complete language, there's no general algorithm that will determine whether or not the program will finish running.
A compiler that performs type-checking is a program, but typical type systems aren't Turing-complete. It's possible to write type checkers that always finish, because the 'programming language' they are running on - the type system - isn't Turing-complete.
Normal type systems (like C#'s) aren't Turing-complete. You expect the C# compiler to always arrive at a result (either compiled code or error) in finite time. As a counter-example, consider Haskell's type system. By default it, too, isn't Turing-complete, but with sufficient language extensions, you can make it Turing-complete. Here's a fun example: Typing the technical interview by Kyle Kingsbury (Aphyr). When you make the type system Turing-complete, however, termination is no longer guaranteed. A program may now compile forever or, practically, until it times out or runs out of memory. That's what happened to me when I tried to compile Kyle Kingsbury's code example.
How is this relevant?
This matters because understanding that a normal type system is not Turing-complete means that there are truths it can't express. Thus, we shouldn't be surprised if we run into rules or policies that we can't express with the type system we're given. What exactly is inexpressible depends on the type system. There are policies you can express in Haskell that are impossible to express in C#, and so on. Let's stick with C#, though. Here are some examples of rules that are practically inexpressible:
- An integer must be positive.
- A string must be at most 100 characters long.
- A maximum value must be greater than a minimum value.
- A value must be a valid email address.
Hillel Wayne provides more compelling examples in the article Making Illegal States Unrepresentable.
Encapsulation #
Depending on how many times you've been around the block, you may find the above list naive. You may, for example, say that it's possible to express that an integer is positive like this:
public struct NaturalNumber : IEquatable<NaturalNumber> { private readonly int i; public NaturalNumber(int candidate) { if (candidate < 1) throw new ArgumentOutOfRangeException( nameof(candidate), $"The value must be a positive (non-zero) number, but was: {candidate}."); this.i = candidate; } // Various other members follow...
I like introducing wrapper types like this. To the inexperienced developer this may seem redundant, but using a wrapper like this has several advantages. For one, it makes preconditions explicit. Consider a constructor like this:
public Reservation( Guid id, DateTime at, Email email, Name name, NaturalNumber quantity)
What are the preconditions that you, as a client developer, has to fulfil before you can create a valid Reservation object? First, you must supply five arguments: id, at, email, name, and quantity. There is, however, more information than that.
Consider, as an alternative, a constructor like this:
public Reservation( Guid id, DateTime at, Email email, Name name, int quantity)
This constructor requires you to supply the same five arguments. There is, however, less explicit information available. If that was the only available constructor, you might be wondering: Can I pass zero as quantity? Can I pass -1?
When the only constructor available is the first of these two alternatives, you already have the answer: No, the quantity must be a natural number.
Another advantage of creating wrapper types like NaturalNumber is that you centralise run-time checks in one place. Instead of sprinkling defensive code all over the code base, you have it in one place. Any code that receives a NaturalNumber object knows that the check has already been performed.
There's a word for this: Encapsulation.
You gather a coherent set of invariants and collect it in a single type, making sure that the type always guarantees its invariants. Note that this is an important design technique in functional programming too. While you may not have to worry about state mutation preserving invariants, it's still important to guarantee that all values of a type are valid.
Predicative and constructive data #
It's debatable whether the above NaturalNumber class really uses the type system to model what constitutes valid data. Since it relies on a run-time predicate, it falls in the category of types Hillel Wayne calls predicative. Such types are easy to create and compose well, but on the other hand fail to take full advantage of the type system.
It's often worthwhile considering if a constructive design is possible and practical. In other words, is it possible to make illegal states unrepresentable (MISU)?
What's wrong with NaturalNumber? Doesn't it do that? No, it doesn't, because this compiles:
new NaturalNumber(-1)
Surely it will fail at run time, but it compiles. Thus, it's representable.
The compiler gives you feedback faster than tests. Considering MISU is worthwhile.
Can we model natural numbers in a constructive way? Yes, with Peano numbers. This is even possible in C#, but I wouldn't consider it practical. On the other hand, while it's possible to represent any natural number, there is no way to express -1 as a Peano number.
As Hillel Wayne describes, constructive data types are much harder and requires a considerable measure of creativity. Often, a constructive model can seem impossible until you get a good idea.
"a list can only be of even length. Most languages will not be able to express such a thing in a reasonable way in the data type."
Such a requirement may look difficult until inspiration hits. Then one day you may realise that it'd be as simple as a list of pairs (two-tuples). In Haskell, it could be as simple as this:
newtype EvenList a = EvenList [(a,a)] deriving (Eq, Show)
With such a constructive data model, lists of uneven length are unrepresentable. This is a simple example of the kind of creative thinking you may need to engage in with constructive data modelling.
If you feel the need to object that Haskell isn't 'most languages', then here's the same idea expressed in C#:
public sealed class EvenCollection<T> : IEnumerable<T> { private readonly IEnumerable<Tuple<T, T>> values; public EvenCollection(IEnumerable<Tuple<T, T>> values) { this.values = values; } public IEnumerator<T> GetEnumerator() { foreach (var x in values) { yield return x.Item1; yield return x.Item2; } } IEnumerator IEnumerable.GetEnumerator() { return GetEnumerator(); } }
You can create such a list like this:
var list = new EvenCollection<string>(new[] { Tuple.Create("foo", "bar"), Tuple.Create("baz", "qux") });
On the other hand, this doesn't compile:
var list = new EvenCollection<string>(new[] { Tuple.Create("foo", "bar"), Tuple.Create("baz", "qux", "quux") });
Despite this digression, the point remains: Constructive data modelling may be impossible, unimagined, or impractical.
Often, in languages like C# we resort to predicative data modelling. That's also what I did in the article ASP.NET validation revisited.
Validation as functions #
That was a long rambling detour inspired by a simple question: Is it possible to use types instead of validation?
In order to address that question, it's only proper to explicitly state assumptions and definitions. What's the definition of validation?
I'm not aware of a ubiquitous definition. While I could draw from the Wikipedia article on the topic, at the time of writing it doesn't cite any sources when it sets out to define what it is. So I may as well paraphrase. It seems fair, though, to consider the stem of the word: Valid.
Validation is the process of examining input to determine whether or not it's valid. I consider this a (mostly) self-contained operation: Given the data, is it well-formed and according to specification? If you have to query a database before making a decision, you're not validating the input. In that case, you're applying a business rule. As a rule of thumb I expect validations to be pure functions.
Validation, then, seems to imply a process. Before you execute the process, you don't know if data is valid. After executing the process, you do know.
Data types, whether predicative like NaturalNumber or constructive like EvenCollection<T>, aren't processes or functions. They are results.

Sometimes an algorithm can use a type to infer the validation function. This is common in statically typed languages, from C# over F# to Haskell (which are the languages with which I'm most familiar).
Data Transfer Object as a validation DSL #
In a way you can think of the type system as a domain-specific language (DSL) for defining validation functions. It's not perfectly suited for that task, but often good enough that many developers reach for it.
Consider the ReservationDto class from the ASP.NET validation revisited article where I eventually gave up on it:
public sealed class ReservationDto { public LinkDto[]? Links { get; set; } public Guid? Id { get; set; } [Required, NotNull] public DateTime? At { get; set; } [Required, NotNull] public string? Email { get; set; } public string? Name { get; set; } [NaturalNumber] public int Quantity { get; set; } }
It actually tries to do what Maurice Johnson suggests. Particularly, it defines At as a DateTime? value.
> var json = "{ \"At\": \"2022-10-11T19:30\", \"Email\": \"z@example.com\", \"Quantity\": 1}"; > JsonSerializer.Deserialize<ReservationDto>(json) ReservationDto { At=[11.10.2022 19:30:00], Email="z@example.com", Id=null, Name=null, Quantity=1 }
A JSON deserializer like this one uses run-time reflection to examine the type in question and then maps the incoming data onto an instance. Many XML deserializers work the same way.
What happens if you supply malformed input?
> var json = "{ \"At\": \"foo\", \"Email\": \"z@example.com\", \"Quantity\": 1}"; > JsonSerializer.Deserialize<ReservationDto>(json) System.Text.Json.JsonException:↩ The JSON value could not be converted to System.Nullable`1[System.DateTime].↩ Path: $.At | LineNumber: 0 | BytePositionInLine: 26.↩ [...]
(I've wrapped the result over multiple lines for readability. The ↩ symbol indicates where I've wrapped the text. I've also omitted a stack trace, indicated by [...]. I'll do that repeatedly throughout this article.)
What happens if we try to define ReservationDto.Quantity with NaturalNumber?
> var json = "{ \"At\": \"2022-10-11T19:30\", \"Email\": \"z@example.com\", \"Quantity\": 1}";
> JsonSerializer.Deserialize<ReservationDto>(json)
System.Text.Json.JsonException:↩
The JSON value could not be converted to NaturalNumber.↩
Path: $.Quantity | LineNumber: 0 | BytePositionInLine: 67.↩
[...]
While JsonSerializer is a sophisticated piece of software, it's not so sophisticated that it can automatically map 1 to a NaturalNumber value.
I'm sure that you can configure the behaviour with one or more JsonConverter objects, but this is exactly the kind of framework Whack-a-mole that I consider costly. It also suggests a wider problem.
Error handling #
What happens if input to a validation function is malformed? You may want to report the errors to the caller, and you may want to report all errors in one go. Consider the user experience if you don't: A user types in a big form and submits it. The system informs him or her that there's an error in the third field. Okay, correct the error and submit again. Now there's an error in the fifth field, and so on.
It's often better to return all errors as one collection.
The problem is that type-based validation doesn't compose well. What do I mean by that?
It's fairly clear that if you take a simple (i.e. non-complex) type like NaturalNumber, if you fail to initialize a value it's because the input is at fault:
> new NaturalNumber(-1) System.ArgumentOutOfRangeException: The value must be a positive (non-zero) number, but was: -1.↩ (Parameter 'candidate') + NaturalNumber..ctor(int)
The problem is that for complex types (i.e. types made from other types), exceptions short-circuit. As soon as one exception is thrown, further data validation stops. The ASP.NET validation revisited article shows examples of that particular problem.
This happens when validation functions have no composable way to communicate errors. When throwing exceptions, you can return an exception message, but exceptions short-circuit rather than compose. The same is true for the Either monad: It short-circuits. Once you're on the failure track you stay there and no further processing takes place. Errors don't compose.
Monoidal versus applicative validation #
The naive take on validation is to answer the question: Is that data valid or invalid? Notice the binary nature of the question. It's either-or.
This is true for both predicative data and constructive data.
For constructive data, the question is: Is a candidate value representable? For example, can you represent -1 as a Peano number? The answer is either yes or no; true or false.
This is even clearer for predicative data, which is defined by a predicate. (Here's another example of a natural number specification.) A predicate is a function that returns a Boolean value: True or false.
It's possible to compose Boolean values. The composition that we need in this case is Boolean and, which is also known as the all monoid: If all values are true, the composed value is true; if just one value is false, the composed value is false.
The problem is that during composition, we lose information. While a single false value causes the entire aggregated value to be false, we don't know why. And we don't know if there was only a single false value, or if there were more than one. Boolean all short-circuits on the first false value it encounters, and stops processing subsequent predicates.
In logic, that's all you need, but in data validation you often want to know what's wrong with the data.
Fortunately, this is a solved problem. Use applicative validation, an example of which I supplied in the article An applicative reservation validation example in C#.
This changes focus on validation. No longer is validation a true/false question. Validation is a function from less-structured data to more-structured data. Parse, don't validate.
Conclusion #
Can types replace validation?
In some cases they can, but I think that the general answer is no. Granted, this answer is partially based on capabilities of current deserialisers. JsonSerializer.Deserialize short-circuits on the first error it encounters, and the same does aeson's eitherDecode.
While that's the current state of affairs, it may not have to stay like that forever. One might be able to derive an applicative parser from a desired destination type, but I haven't seen that done yet.
It sounds like a worthwhile research project.
Comments
This slightly reminds me of Zod which is described as "TypeScript-first schema validation with static type inference".
The library automatically infers a type that matches the validation - in a way it blurs this line between types and validation by making them become one.
Of course, once you have that infered type there is nothing stopping you using it without the library, but that's something code reviews could catch. It's quite interesting though.
import { z } from 'zod';
const User = z.object({
username: z.string(),
age: z.number().positive({
message: 'Your age must be positive!',
}),
});
User.parse({ username: 'Ludwig', age: -1 });
// extract the inferred type
type User = z.infer<typeof User>;
// { username: string, age: number }
ASP.NET validation revisited
Is the built-in validation framework better than applicative validation?
I recently published an article called An applicative reservation validation example in C# in which I describe how to use the universal abstractions of applicative functors and semigroups to implement reusable, composable validation.
One reader reaction made me stop and think:
"An exercise on how to reject 90% of the framework's existing services (*Validation) only to re implement them more poorly, by renouncing standardization, interoperability and globalization all for the glory of FP."
(At the time of posting, the PopCatalin Twitter account's display name was Prime minister of truth™ カタリンポップ🇺🇦, which I find unhelpful. The linked GitHub account locates the user in Cluj-Napoca, a city I've repeatedly visited for conferences - the last time as recent as June 2022. I wouldn't be surprised if we've interacted, but if so, I'm sorry to say that I can't connect these accounts with one of the many wonderful people I've met there. In general, I'm getting a strong sarcastic vibe from that account, and I'm not sure whether or not to take Pronouns kucf/fof seriously. As the possibly clueless 51-year white male that I am, I will proceed with good intentions and to the best of my abilities.)
That reply is an important reminder that I should once in a while check my assumptions. I'm aware that the ASP.NET framework comes with validation features, but I many years ago dismissed them because I found them inadequate. Perhaps, in the meantime, these built-in services have improved to the point that they are to be preferred over applicative validation.
I decided to attempt to refactor the code to take advantage of the built-in ASP.NET validation to be able to compare the two approaches. This article is an experience report.
Requirements #
In order to compare the two approaches, the ASP.NET-based validation should support the same validation features as the applicative validation example:
- The
Atproperty is required and should be a valid date and time. If it isn't, the validation message should report the problem and the offending input. - The
Emailproperty should be required. If it's missing, the validation message should state so. - The
Quantityproperty is required and should be a natural number. If it isn't, the validation message should report the problem and the offending input.
The previous article includes an interaction example that I'll repeat here for convenience:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
Content-Type: application/json
{ "at": "large", "name": "Kerry Onn", "quantity": -1 }
HTTP/1.1 400 Bad Request
Invalid date or time: large.
Email address is missing.
Quantity must be a positive integer, but was: -1.
ASP.NET validation formats the errors differently, as you'll see later in this article. That's not much of a concern, though: Error messages are for other developers. They don't really have to be machine-readable or have a strict shape (as opposed to error types, which should be machine-readable).
Reporting the offending values, as in "Quantity must be a positive integer, but was: -1." is part of the requirements. A REST API can make no assumptions about its clients. Perhaps one client is an unattended batch job that only logs errors. Logging offending values may be helpful to maintenance developers of such a batch job.
Framework API #
The first observation to make about the ASP.NET validation API is that it's specific to ASP.NET. It's not a general-purpose API that you can use for other purposes.
If, instead, you need to validate input to a console application, a background message handler, a batch job, or a desktop or phone app, you can't use that API.
Perhaps each of these styles of software come with their own validation APIs, but even if so, that's a different API you'll have to learn. And in cases where there's no built-in validation API, then what do you do?
The beauty and practicality of applicative validation is that it's universal. Since it's based on mathematical foundations, it's not tied to a particular framework, platform, or language. These concepts exist independently of technology. Once you understand the concepts, they're always there for you.
The code example from the previous article, as well as here, build upon the code base that accompanies Code That Fits in Your Head. An example code base has to be written in some language, and I chose C# because I'm more familiar with it than I am with Java, C++, or TypeScript. While I wanted the code base to be realistic, I tried hard to include only coding techniques and patterns that you could use in more than one language.
As I wrote the book, I ran into many interesting problems and solutions that were specific to C# and ASP.NET. While I found them too specific to include in the book, I wrote a series of blog posts about them. This article is now becoming one of those.
The point about the previous article on applicative reservation validation in C# was to demonstrate how the general technique works. Not specifically in ASP.NET, or even C#, but in general.
It just so happens that this example is situated in a context where an alternative solution presents itself. This is not always the case. Sometimes you have to solve this problem yourself, and when this happens, it's useful to know that validation is a solved problem. Even so, while a universal solution exists, it doesn't follow that the universal solution is the best. Perhaps there are specialised solutions that are better, each within their constrained contexts.
Perhaps ASP.NET validation is an example of that.
Email validation #
The following is a report on my experience refactoring validation to use the built-in ASP.NET validation API.
I decided to start with the Email property, since the only requirement is that this value should be present. That seemed like an easy way to get started.
I added the [Required] attribute to the ReservationDto class' Email property. Since this code base also uses nullable reference types, it was necessary to also annotate the property with the [NotNull] attribute:
[Required, NotNull] public string? Email { get; set; }
That's not too difficult, and seems to be working satisfactorily:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
> content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 1
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|552ab5ff-494e1d1a9d4c6355.",
"errors": { "Email": [ "The Email field is required." ] }
}
As discussed above, the response body is formatted differently than in the applicative validation example, but I consider that inconsequential for the reasons I gave.
So far, so good.
Quantity validation #
The next property I decided to migrate was Quantity. This must be a natural number; that is, an integer greater than zero.
Disappointingly, no such built-in validation attribute seems to exist. One highly voted Stack Overflow answer suggested using the [Range] attribute, so I tried that:
[Range(1, int.MaxValue, ErrorMessage = "Quantity must be a natural number.")] public int Quantity { get; set; }
As a declarative approach to validation goes, I don't think this is off to a good start. I like declarative programming, but I'd prefer to be able to declare that Quantity must be a natural number, rather than in the range of 1 and int.MaxValue.
Does it work, though?
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|d9a6be38-4be82ede7c525913.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a natural number." ]
}
}
While it does capture the intent that Quantity must be one or greater, it fails to echo back the offending value.
In order to address that concern, I tried reading the documentation to find a way forward. Instead I found this:
"Internally, the attributes call String.Format with a placeholder for the field name and sometimes additional placeholders. [...]"
"To find out which parameters are passed to
String.Formatfor a particular attribute's error message, see the DataAnnotations source code."
Really?!
If you have to read implementation code, encapsulation is broken.
Hardly impressed, I nonetheless found the RangeAttribute source code. Alas, it only passes the property name, Minimum, and Maximum to string.Format, but not the offending value:
return string.Format(CultureInfo.CurrentCulture, ErrorMessageString, name, Minimum, Maximum);
This looked like a dead end, but at least it's possible to extend the ASP.NET validation API:
public sealed class NaturalNumberAttribute : ValidationAttribute { protected override ValidationResult IsValid( object value, ValidationContext validationContext) { if (validationContext is null) throw new ArgumentNullException(nameof(validationContext)); var i = value as int?; if (i.HasValue && 0 < i) return ValidationResult.Success; return new ValidationResult( $"{validationContext.MemberName} must be a positive integer, but was: {value}."); } }
Adding this NaturalNumberAttribute class enabled me to change the annotation of the Quantity property:
[NaturalNumber] public int Quantity { get; set; }
This seems to get the job done:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|bb45b60d-4bd255194871157d.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
The [NaturalNumber] attribute now correctly reports the offending value together with a useful error message.
Compare, however, the above NaturalNumberAttribute class to the TryParseQuantity function, repeated here for convenience:
private Validated<string, int> TryParseQuantity() { if (Quantity < 1) return Validated.Fail<string, int>( $"Quantity must be a positive integer, but was: {Quantity}."); return Validated.Succeed<string, int>(Quantity); }
TryParseQuantity is shorter and has half the cyclomatic complexity of NaturalNumberAttribute. In isolation, at least, I'd prefer the shorter, simpler alternative.
Date and time validation #
Remaining is validation of the At property. As a first step, I converted the property to a DateTime value and added attributes:
[Required, NotNull] public DateTime? At { get; set; }
I'd been a little apprehensive doing that, fearing that it'd break a lot of code (particularly tests), but that turned out not to be the case. In fact, it actually simplified a few of the tests.
On the other hand, this doesn't really work as required:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|1e1d600e-4098fb36635642f6.",
"errors": {
"dto": [ "The dto field is required." ],
"$.at": [ "The JSON value could not be converted to System.Nullable`1[System.DateTime].↩
Path: $.at | LineNumber: 0 | BytePositionInLine: 26." ]
}
}
(I've wrapped the last error message over two lines for readability. The ↩ symbol indicates where I've wrapped the text.)
There are several problems with this response. First, in addition to complaining about the missing at property, it should also have reported that there are problems with the Quantity and that the Email property is missing. Instead, the response implies that the dto field is missing. That's likely confusing to client developers, because dto is an implementation detail; it's the name of the C# parameter of the method that handles the request. Client developers can't and shouldn't know this. Instead, it looks as though the REST API somehow failed to receive the JSON document that the client posted.
Second, the error message exposes other implementation details, here that the at field has the type System.Nullable`1[System.DateTime]. This is, at best, irrelevant. At worst, it could be a security issue, because it reveals to a would-be attacker that the system is implemented on .NET.
Third, the framework rejects what looks like a perfectly good date and time: 2022-11-21 19:00. This is a breaking change, since the API used to accept such values.
What's wrong with 2022-11-21 19:00? It's not a valid ISO 8601 string. According to the ISO 8601 standard, the date and time must be separated by T:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21T19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|1e1d600f-4098fb36635642f6.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
Posting a valid ISO 8601 string does, indeed, enable the client to proceed - only to receive a new set of error messages. After I converted At to DateTime?, the ASP.NET validation framework fails to collect and report all errors. Instead it stops if it can't parse the At property. It doesn't report any other errors that might also be present.
That is exactly the requirement that applicative validation so elegantly solves.
Tolerant Reader #
While it's true that 2022-11-21 19:00 isn't valid ISO 8601, it's unambiguous. According to Postel's law an API should be a Tolerant Reader. It's not.
This problem, however, is solvable. First, add the Tolerant Reader:
public sealed class DateTimeConverter : JsonConverter<DateTime> { public override DateTime Read( ref Utf8JsonReader reader, Type typeToConvert, JsonSerializerOptions options) { return DateTime.Parse( reader.GetString(), CultureInfo.InvariantCulture); } public override void Write( Utf8JsonWriter writer, DateTime value, JsonSerializerOptions options) { if (writer is null) throw new ArgumentNullException(nameof(writer)); writer.WriteStringValue(value.ToString("s")); } }
Then add it to the JSON serialiser's Converters:
opts.JsonSerializerOptions.Converters.Add(new DateTimeConverter());
This, at least, addresses the Tolerant Reader concern:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "2022-11-21 19:00",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576943-400dafd4b489c282.",
"errors": {
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
The API now accepts the slightly malformed at field. It also correctly handles if the field is entirely missing:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576944-400dafd4b489c282.",
"errors": {
"At": [ "The At field is required." ],
"Email": [ "The Email field is required." ],
"Quantity": [ "Quantity must be a positive integer, but was: 0." ]
}
}
On the other hand, it still doesn't gracefully handle the case when the at field is unrecoverably malformed:
POST /restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D HTTP/1.1
content-type: application/json
{
"at": "foo",
"name": "Kerry Onn",
"quantity": 0
}
HTTP/1.1 400 Bad Request
Content-Type: application/problem+json; charset=utf-8
{
"type": "https://tools.ietf.org/html/rfc7231#section-6.5.1",
"title": "One or more validation errors occurred.",
"status": 400,
"traceId": "|11576945-400dafd4b489c282.",
"errors": {
"": [ "The supplied value is invalid." ],
"dto": [ "The dto field is required." ]
}
}
The supplied value is invalid. and The dto field is required.? That's not really helpful. And what happened to The Email field is required. and Quantity must be a positive integer, but was: 0.?
If there's a way to address this problem, I don't know how. I've tried adding another custom attribute, similar to the above NaturalNumberAttribute class, but that doesn't solve it - probably because the model binder (that deserialises the JSON document to a ReservationDto instance) runs before the validation.
Perhaps there's a way to address this problem with yet another class that derives from a base class, but I think that I've already played enough Whack-a-mole to arrive at a conclusion.
Conclusion #
Your context may differ from mine, so the conclusion that I arrive at may not apply in your situation. For example, I'm given to understand that one benefit that the ASP.NET validation framework provides is that when used with ASP.NET MVC (instead of as a Web API), (some of) the validation logic can also run in JavaScript in browsers. This, ostensibly, reduces code duplication.
"Yet in the case of validation, a Declarative model is far superior to a FP one. The declarative model allows various environments to implement validation as they need it (IE: Client side validation) while the FP one is strictly limited to the environment executing the code."
On the other hand, using the ASP.NET validation framework requires more code, and more complex code, than with applicative validation. It's a particular set of APIs that you have to learn, and that knowledge doesn't transfer to other frameworks, platforms, or languages.
Apart from client-side validation, I fail to see how applicative validation "re implement[s validation] more poorly, by renouncing standardization, interoperability and globalization".
I'm not aware that there's any standard for validation as such, so I think that @PopCatalin has the 'standard' ASP.NET validation API in mind. If so, I consider applicative validation a much more standardised solution than a specialised API.
If by interoperability @PopCatalin means the transfer of logic from server side to client side, then it's true that the applicative validation I showed in the previous article runs exclusively on the server. I wonder, however, how much of such custom validation as NaturalNumberAttribute automatically transfers to the client side.
When it comes to globalisation, I fail to see how applicative validation is less globalisable than the ASP.NET validation framework. One could easily replace the hard-coded strings in my examples with resource strings.
It would seem, again, that any sufficiently complicated custom validation framework contains an ad-hoc, informally-specified, bug-ridden, slow implementation of half of applicative validation.
"I must admit I really liked the declarative OOP model using annotations when I first saw it in Java (EJB3.0, almost 20yrs ago) until I saw FP way of doing things. FP way is so much simpler and powerful, because it's just function composition, nothing more, no hidden "magic"."
I still find myself in the same camp as Witold Szczerba. It's easy to get started using validation annotations, but it doesn't follow that it's simpler or better in the long run. As Rich Hickey points out in Simple Made Easy, simple and easy isn't the same. If I have to maintain code, I'll usually choose the simple solution over the easy solution. That means choosing applicative validation over a framework-specific validation API.
Comments
Hello Mark. I was just wondering, is it possible to use the type system to do the validation instead ?
What I mean is, for example, to make all the ReservationDto's field a type with validation in the constructor (like a class name, a class email, and so on). Normally, when the framework will build ReservationDto, it will try to construct the fields using the type constructor, and if there is an explicit error thrown during the construction, the framework will send us back the error with the provided message.
Plus, I think types like "email", "name" and "at" are reusable. And I feel like we have more possibilities for validation with that way of doing than with the validation attributes.
What do you think ?
Regards.
Maurice, thank you for writing. I started writing a reply, but it grew, so I'm going to turn it into a blog post. I'll post an update here once I've published it, but expect it to take a few weeks.
I've published the article: Can types replace validation?.
Endomorphism as an invariant functor
An article (also) for object-oriented programmers.
This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details.
An endomorphism is a function where the return type is the same as the input type.
In Haskell we denote an endomorphism as a -> a, in F# we have to add an apostrophe: 'a -> 'a, while in C# such a function corresponds to the delegate Func<T, T> or, alternatively, to a method that has the same return type as input type.
In Haskell you can treat an endomorphism like a monoid by wrapping it in a container called Endo: Endo a. In C#, we might model it as an interface called IEndomorphism<T>.
That looks enough like a functor that you might wonder if it is one, but it turns out that it's neither co- nor contravariant. You can deduce this with positional variance analysis (which I've learned from Thinking with Types). In short, this is because T appears as both input and output - it's neither co- nor contravariant, but rather invariant.
Explicit endomorphism interface in C# #
Consider an IEndomorphism<T> interface in C#:
public interface IEndomorphism<T> { T Run(T x); }
I've borrowed this interface from the article From State tennis to endomorphism. In that article I explain that I only introduce this interface for educational reasons. I don't expect you to use something like this in production code bases. On the other hand, everything that applies to IEndomorphism<T> also applies to 'naked' functions, as you'll see later in the article.
As outlined in the introduction, you can make a container an invariant functor by implementing a non-standard version of Select:
public static IEndomorphism<B> Select<A, B>( this IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { return new SelectEndomorphism<A, B>(endomorphism, aToB, bToA); } private class SelectEndomorphism<A, B> : IEndomorphism<B> { private readonly IEndomorphism<A> endomorphism; private readonly Func<A, B> aToB; private readonly Func<B, A> bToA; public SelectEndomorphism( IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { this.endomorphism = endomorphism; this.aToB = aToB; this.bToA = bToA; } public B Run(B x) { return aToB(endomorphism.Run(bToA(x))); } }
Since the Select method has to return an IEndomorphism<B> implementation, one option is to use a private, nested class. Most of this is ceremony required because it's working with interfaces. The interesting part is the nested class' Run implementation.
In order to translate an IEndomorphism<A> to an IEndomorphism<B>, the Run method first uses bToA to translate x to an A value. Once it has the A value, it can Run the endomorphism, which returns another A value. Finally, the method can use aToB to convert the returned A value to a B value that it can return.
Here's a simple example. Imagine that you have an endomorphism like this one:
public sealed class Incrementer : IEndomorphism<BigInteger> { public BigInteger Run(BigInteger x) { return x + 1; } }
This one simply increments a BigInteger value. Since BigInteger is isomorphic to a byte array, it's possible to transform this BigInteger endomorphism to a byte array endomorphism:
[Theory] [InlineData(new byte[0], new byte[] { 1 })] [InlineData(new byte[] { 1 }, new byte[] { 2 })] [InlineData(new byte[] { 255, 0 }, new byte[] { 0, 1 })] public void InvariantSelection(byte[] bs, byte[] expected) { IEndomorphism<BigInteger> source = new Incrementer(); IEndomorphism<byte[]> destination = source.Select(bi => bi.ToByteArray(), arr => new BigInteger(arr)); Assert.Equal(expected, destination.Run(bs)); }
You can convert a BigInteger to a byte array with the ToByteArray method, and convert such a byte array back to a BigInteger using one of its constructor overloads. Since this is possible, the example test can convert this IEndomorphism<BigInteger> to an IEndomorphism<byte[]> and later Run it.
Mapping functions in F# #
You don't need an interface in order to turn an endomorphism into an invariant functor. An endomorphism is just a function that has the same input and output type. In C# such a function has the type Func<T, T>, while in F# it's written 'a -> 'a.
You could write an F# module that defines an invmap function, which would be equivalent to the above Select method:
module Endo = // ('a -> 'b) -> ('b -> 'a) -> ('a -> 'a) -> ('b -> 'b) let invmap (f : 'a -> 'b) (g : 'b -> 'a) (h : 'a -> 'a) = g >> h >> f
Since this function doesn't have to deal with the ceremony of interfaces, the implementation is simple function composition: For any input, first apply it to the g function, then apply the output to the h function, and again apply the output of that function to the f function.
Here's the same example as above:
let increment (bi : BigInteger) = bi + BigInteger.One // byte [] -> byte [] let bArrInc = Endo.invmap (fun (bi : BigInteger) -> bi.ToByteArray ()) BigInteger increment
Here's a simple sanity check of the bArrInc function executed in F# Interactive:
> let bArr = bArrInc [| 255uy; 255uy; 0uy |];; val bArr : byte [] = [|0uy; 0uy; 1uy|]
If you are wondering about that particular output value, I'll refer you to the BigInteger documentation.
Function composition #
The F# implementation of invmap (g >> h >> f) makes it apparent that an endomorphism is an invariant functor via function composition. In F#, though, that fact almost disappears in all the type declaration ceremony. In the Haskell instance from the invariant package it's even clearer:
instance Invariant Endo where invmap f g (Endo h) = Endo (f . h . g)
Perhaps a diagram is helpful:
If you have a function h from the type a to a and you need a function b -> b, you can produce it by putting g in front of h, and f after. That's also what the above C# implementation does. In F#, you can express such a composition as g >> h >> f, which seems natural to most westerners, since it goes from left to right. In Haskell, most expressions are instead expressed from right to left, so it becomes: f . h . g. In any case, the result is the desired function that takes a b value as input and returns a b value as output. That composed function is indicated by a dashed arrow in the above diagram.
Identity law #
Contrary to my usual habit, I'm going to prove that both invariant functor laws hold for this implementation. I'll use equational reasoning with the notation that Bartosz Milewski uses. Here's the proof that the invmap instance obeys the identity law:
invmap id id (Endo h)
= { definition of invmap }
Endo (id . h . id)
= { eta expansion }
Endo (\x -> (id . h . id) x)
= { defintion of composition (.) }
Endo (\x -> id (h (id x)))
= { defintion of id }
Endo (\x -> h x)
= { eta reduction }
Endo h
= { definition of id }
id (Endo h)
While I'm not going to comment further on that, I can show you what the identity law looks like in C#:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(9)] public void IdentityLaw(long l) { IEndomorphism<BigInteger> e = new Incrementer(); IEndomorphism<BigInteger> actual = e.Select(x => x, x => x); Assert.Equal(e.Run(l), actual.Run(l)); }
In C#, you typically write the identity function (id in F# and Haskell) as the lambda expression x => x, since the identity function isn't 'built in' for C# like it is for F# and Haskell. (You can define it yourself, but it's not as idiomatic.)
Composition law #
As with the identity law, I'll start by suggesting a proof for the composition law for the Haskell instance:
invmap f2 f2' $ invmap f1 f1' (Endo h)
= { definition of invmap }
invmap f2 f2' $ Endo (f1 . h . f1')
= { defintion of ($) }
invmap f2 f2' (Endo (f1 . h . f1'))
= { definition of invmap }
Endo (f2 . (f1 . h . f1') . f2')
= { associativity of composition (.) }
Endo ((f2 . f1) . h . (f1' . f2'))
= { definition of invmap }
invmap (f2 . f1) (f1' . f2') (Endo h)
As above, a C# example may also help. First, assume that you have some endomorphism like this:
public sealed class SecondIncrementer : IEndomorphism<TimeSpan> { public TimeSpan Run(TimeSpan x) { return x + TimeSpan.FromSeconds(1); } }
A test then demonstrates the composition law in action:
[Theory] [InlineData(-3)] [InlineData(0)] [InlineData(11)] public void CompositionLaw(long x) { IEndomorphism<TimeSpan> i = new SecondIncrementer(); Func<TimeSpan, long> f1 = ts => ts.Ticks; Func<long, TimeSpan> f1p = l => new TimeSpan(l); Func<long, IntPtr> f2 = l => new IntPtr(l); Func<IntPtr, long> f2p = ip => ip.ToInt64(); IEndomorphism<IntPtr> left = i.Select(f1, f1p).Select(f2, f2p); IEndomorphism<IntPtr> right = i.Select(ts => f2(f1(ts)), ip => f1p(f2p(ip))); Assert.Equal(left.Run(new IntPtr(x)), right.Run(new IntPtr(x))); }
Don't try to make any sense of this. As outlined in the introductory article, in order to use an invariant functor, you're going to need an isomorphism. In order to demonstrate the composition law, you need three types that are isomorphic. Since you can convert back and forth between TimeSpan and IntPtr via long, this requirement is formally fulfilled. It doesn't make any sense to add a second to a value and then turn it into a function that changes a pointer. It sounds more like a security problem waiting to happen... Don't try this at home, kids.
Conclusion #
Since an endomorphism can be modelled as a 'generic type', it may look like a candidate for a functor or contravariant functor, but alas, neither is possible. The best we can get (apart from a monoid instance) is an invariant functor.
The invariant functor instance for an endomorphism turns out to be simple function composition. That's not how all invariant functors, work, though.

Comments
I've always had a problem with the notion of "red, green, refactor" and "first get it working, then make it right." I think the order is completely wrong.
As an explanation, I refer you to the first chapter of the first edition of Martin Fowler's Refactoring book. In that chapter is an example of a working system and we are presented with a change request.
In the example, the first thing that Fowler points out and does is the refactoring. And one of the highlighted ideas in the chapter says:
In other words, the refactoring comes first. You refactor as part of adding the feature, not as a separate thing that is done after you have working code. It may not trip off the tongue as nicely, but the saying should be "refactor, red, green."
Once you have working code, you are done, and when you are estimating the time it will take to add the feature, you include the refactoring time. Lastly, you never refactor "just because," you refactor in order to make a new feature easy to add.
This mode of working makes much more sense to me. I feel that refactoring with no clear goal in mind ("improve the design" is not a clear goal) just leads to an over-designed/unnecessarily complex system. What do you think of this idea?
Daniel, thank you for writing. You make some good points.
The red-green-refactor cycle is useful as a feedback cycle for new development work. It's not the only way to work. Particularly, as you point out, when you have existing code, first refactoring and then adding new code is a useful order.
Typically, though, when you're adding a new feature, you can rarely implement a new feature only by refactoring existing code. Normally you also need to add some new code. I still find the red-green-refactor cycle useful for that kind of work. I don't view it as an either-or proposition, but rather as a both-this-and-that way of working.
Never say never. I don't agree with that point of view. There are more than one reason for refactoring, and making room for a new feature is certainly one of them. This does not, however, rule out other reasons. I can easily think of a handful of other reasons that I consider warranted, but I don't want to derail the discussion by listing all of them. The list is not going to be complete anyway. I'll just outline one:
Sometimes, you read existing code because you need to understand what's going on. If the code is badly structured, it can take significant time and effort to reach such understanding. If, at that point you can see a simpler way to achieve the same behaviour, why not refactor the code? In that way, you make it easier for future readers of the code to understand what's going on. If you've already spent (wasted) significant time understanding something, why let other readers suffer and waste time if you can simplify the code?
This is essentially the boy scout rule, but as I claimed, there are other reasons to refactor as well.
Finally, thank you for the quote from Refactoring. I've usually been using this Kent Beck quote:
but that's from 2012, and Refactoring is from 1999. It's such a Kent Beck thing to say, though, and Kent is a coauthor of Refactoring, so who knows who came up with that. I'm happy to know of the earlier quote, though.
I think it is worth elaborating on this. I think am correct in saying that Mark believes that type-driven development and test-driven development are a both-this-and-that way of working instead of an either-or way of working. He did exactly this in his Pluralsight course titled Type-Driven Development with F# by first obtaining an implementation using type-driven development and then deleting his implementation but keeping his types and obtaining a second implementation using test-driven development.
When implementing a new feature, it is important to as quickly as possible derisk by discovering any surprises (aka unknown unknowns) and analyze all challenges (aka known unknowns). The reason for this is to make sure the intended approach is feasible. During this phase of work, we are in the "green" step of test-driven development. Anything goes. There are no rules. The code can horribly ugly or unmaintainable. Just get the failing test to pass.
After the test passes, you have proved that the approach is sound. Now you need to share your solution with others. Here is where refactoring first occurs. Just like in Mark's course, I often find it helpful to start over. Now that I know where I am going, I can first refactor the code to make the functional change, which I know will make the test pass. In this way, I know that all my refactors have a clear goal.
I agree that refactoring should be done as part of the feature, but I disagree that it should (always) be done before you have working code. It is often done after you have working code.
I agree that estimating should include the refactoring time, but I disagree that you are done when you have working code. When you have working code, you are approximately halfway done. Your code is currently optimized for writing. You still need to optimize it for reading.