Fractal trees with PureScript by Mark Seemann
A fractal tree drawn with PureScript
Last week, I attended Mathias Brandewinder's F# (and Clojure) dojo in Copenhagen, and had great fun drawing a fractal tree in F# together with other attendees. Afterwards, I started thinking that it'd be fairly easy to port the F# code to Haskell, but then I reconsidered. The combination of Haskell, Windows, and drawing sounded intimidating. This seemed a good opportunity to take PureScript for a spin, because that would enable me to draw the tree on an HTML canvas.
In case you're wondering, a fractal tree is simply a tree that branches infinitely in (I suppose) a deterministic fashion. Here's an example of the output of the code of this article:
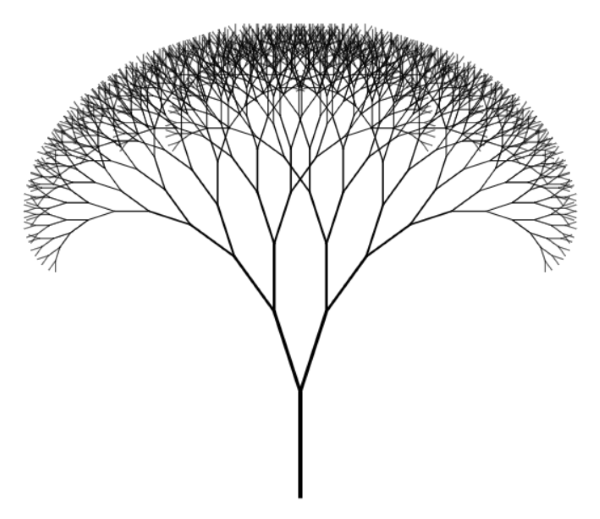
This is my first attempt at PureScript, and I think I spent between five and ten hours in total. Most of them I used to figure out how to install PureScript, how to set up a development environment, and so on. All in all I found the process pleasing.
While it's a separate, independent language, PureScript is clearly a descendant of Haskell, and the syntax is similar.
Separating data from effects #
In functional programming, you routinely separate data from effects. Instead of trying to both draw and calculate branches of a tree in a single operation, you figure out how to first define a fractal tree as data, and then subsequently you can draw it.
A generic binary tree is a staple of functional programming. Here's one way to do it:
data Tree a = Leaf a | Node a (Tree a) (Tree a)
Such a tree is either a leaf node with a generically typed value, or an (intermediate) node with a value and two branches, which are themselves (sub)trees.
In a sense, this definition is an approximation, because a 'real' fractal tree has no leafs. In Haskell you can easily define infinite trees, because Haskell is lazily evaluated. PureScript, on the other hand, is eagerly evaluated, so infinite recursion would require jumping through some hoops, and I don't think it's important in this exercise.
While the above tree type can contain values of any type, in this exercise, it should contain line segments. One way to do this is to define a Line record type:
data Line = Line { x :: Number, y :: Number, angle :: Number, length :: Number, width :: Number }
This is a type with five labelled values, all of them numbers. x and y are coordinates for the origin of the line, angle defines the angle (measured in radians) from the origin, and length the length of the line. In a similarly obvious vein, width denotes the width of the line, although this data element has no impact on the calculation of the tree. It's purely a display concern.
Given the first four numbers in a Line value, you can calculate the endpoint of a line:
endpoint :: forall r. { x :: Number , y :: Number , angle :: Number , length :: Number | r } -> Tuple Number Number endpoint line = -- Flip the y value because Canvas coordinate system points down from upper -- left corner Tuple (line.x + line.length * cos line.angle) (-(-line.y + line.length * sin line.angle))
This may look more intimidating than it really is. The first seven lines are simply the (optional) type declaration; ignore that for a minute. The function itself is a one-liner, although I've formatted it on several lines in order to stay within an 80 characters line width. It simply performs a bit of trigonometry in order to find the endpoint of a line with an origin, angle, and length. As the code comment states, it negates the y value because the HTML canvas coordinate system points down instead of up (larger y values are further towards the bottom of the screen than smaller values).
The function calculates a new set of coordinates for the endpoint, and returns them as a tuple. In PureScript, tuples are explicit and created with the Tuple data constructor.
In general, as far as I can tell, you have less need of tuples in PureScript, because instead, you have row type polymorphism. This is still a new concept to me, but as far as I can tell, it's a sort of static duck typing. You can see it in the type declaration of the endpoint function. The function takes a line argument, the type of which is any record type that contains x, y, angle, and length labels of the Number type. For instance, as you'll soon see, you can pass a Line value to the endpoint function.
Creating branches #
In a fractal tree, you calculate two branches for any given branch. Typically, in order to draw a pretty picture, you make the sub-branches smaller than the parent branch. You also incline each branch an angle from the parent branch. While you can hard-code the values for these operations, you can also pass them as arguments. In order to prevent an explosion of primitive function arguments, I collected all such parameters in a single data type:
data FractalParameters = FractalParameters { leftAngle :: Number, rightAngle :: Number, shrinkFactor :: Number }
This is a record type similar to the Line type you've already seen.
When you have a FractalParameters value and a (parent) line, you can calculate its branches:
createBranches :: FractalParameters -> Line -> Tuple Line Line createBranches (FractalParameters p) (Line line) = Tuple left right where Tuple x y = endpoint line left = Line { x: x, y: y, angle: pi * (line.angle / pi + p.leftAngle), length: (line.length * p.shrinkFactor), width: (line.width * p.shrinkFactor) } right = Line { x: x, y: y, angle: pi * (line.angle / pi - p.rightAngle), length: (line.length * p.shrinkFactor), width: (line.width * p.shrinkFactor) }
The createBranches function returns a tuple of Line values, one for the left branch, and one for the right branch. First, it calls endpoint with line. Notice that line is a Line value, and because Line defines x, y, angle, and length labels, it can be used as an input argument. This type-checks because of row type polymorphism.
Given the endpoint of the parent line, createBranches then creates two new Line values (left and right) with that endpoint as their origins. Both of these values are modified with the FractalParameters argument, so that they branch off to the left and the right, and also shrink in an aesthetically pleasing manner.
Creating a tree #
Now that you can calculate the branches of a line, you can create a tree using recursion:
createTree :: Int -> FractalParameters -> Line -> Tree Line createTree depth p line = if depth <= 0 then Leaf line else let Tuple leftLine rightLine = createBranches p line left = createTree (depth - 1) p leftLine right = createTree (depth - 1) p rightLine in Node line left right
The createTree function takes a depth argument, which specifies the depth (or is it the height?) of the tree. The reason I called it depth is because createTree is recursive, and depth controls the depth of the recursion. If depth is zero or less, the function returns a Leaf node containing the input line.
Otherwise, it calls createBranches with the input line, and recursively calls createTree for each of these branches, but with a decremented depth. It then returns a Node containing the input line and the two sub-trees left and right.
This implementation isn't tail-recursive, but the above image was generated with a recursion depth of only 10, so running out of stack space wasn't my biggest concern.
Drawing the tree #
With the createTree function you can create a fractal tree, but it's no fun if you can't draw it. You can use the Graphics.Canvas module in order to draw on an HTML canvas. First, here's how to draw a single line:
drawLine :: Context2D -> Line -> Eff (canvas :: CANVAS) Unit drawLine ctx (Line line) = do let Tuple x' y' = endpoint line void $ strokePath ctx $ do void $ moveTo ctx line.x line.y void $ setLineWidth line.width ctx void $ lineTo ctx x' y' closePath ctx
While hardly unmanageable, I was surprised that I wasn't able to find a pre-defined function that would let me draw a line. Perhaps I was looking in the wrong place.
With this helper function, you can now draw a tree using pattern matching:
drawTree :: Context2D -> Tree Line -> Eff (canvas :: CANVAS) Unit drawTree ctx (Leaf line) = drawLine ctx line drawTree ctx (Node line left right) = do drawLine ctx line drawTree ctx left drawTree ctx right
If the input tree is a Leaf value, the first line matches and the function simply draws the line, using the drawLine function.
When the input tree is a Node value, the function first draws the line associated with that node, and then recursively calls itself with the left and right sub-trees.
Execution #
The drawTree function enables you to draw using a Context2D value, which you can create from an HTML canvas:
mcanvas <- getCanvasElementById "canvas" let canvas = unsafePartial (fromJust mcanvas) ctx <- getContext2D canvas
From where does the "canvas" element come? Ultimately, PureScript compiles to JavaScript, and you can put the compiled script in an HTML file together with a canvas element:
<body> <canvas id="canvas" width="800" height="800"></canvas> <script src="index.js" type="text/javascript"></script> </body>
Once you have a Context2D value, you can draw a tree. Here's the whole entry point, including the above canvas-finding code:
main :: Eff (canvas :: CANVAS) Unit main = do mcanvas <- getCanvasElementById "canvas" let canvas = unsafePartial (fromJust mcanvas) ctx <- getContext2D canvas let trunk = Line { x: 300.0, y: 600.0, angle: (pi / 2.0), length: 100.0, width: 4.0 } let p = FractalParameters { leftAngle: 0.1, rightAngle: 0.1, shrinkFactor: 0.8 } let tree = createTree 10 p trunk drawTree ctx tree
After it finds the Context2D value, it hard-codes a trunk Line and a set of FractalParameters. From these, it creates a tree of size 10 and draws the tree in the beginning of this article.
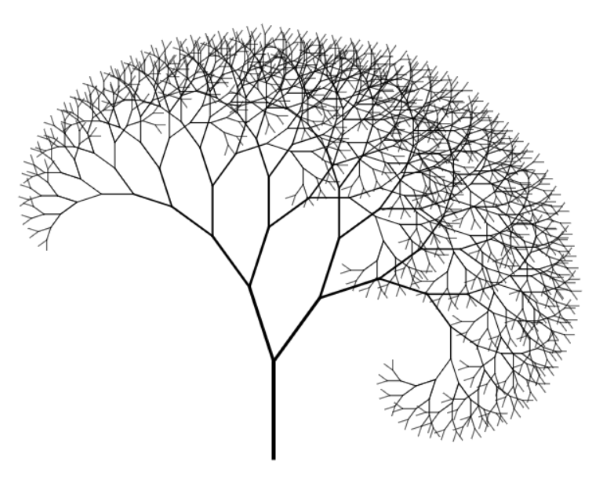
You can fiddle with the parameters to your liking. For example, you can make the right angle wider than the left angle:
let p = FractalParameters { leftAngle: 0.1, rightAngle: 0.2, shrinkFactor: 0.8 }
This produces an asymmetric tree:
In order to compile the code, I used this command:
$ pulp browserify -t html/index.js
This compiles the PureScript code to a single index.js file, which is output to the html directory. This directory also contains the HTML file with the canvas.
You can find the entire PureScript file in this Gist.
Summary #
It was fun to try PureScript. I've been staying away from JavaScript-based development for many years now, but if I ever have to do some client-side development, I may consider it. So far, I've found that PureScript seems viable for drawing. How good it is if you need to interact with 'normal' web-pages or SPAs, I don't know (yet).
If you have some experience with Haskell, it looks like it's easy to get started with PureScript.
