ploeh blog danish software design
Song recommendations from Haskell combinators
Traversing lists of IO. A refactoring.
This article is part of a series named Alternative ways to design with functional programming. In the previous article, you saw how to refactor the example code base to a composition of standard F# combinators. It's a pragmatic solution to the problem of dealing with lots of data in a piecemeal fashion, but although it uses concepts and programming constructs from functional programming, I don't consider it a proper functional architecture.
You'd expect the Haskell version to be the most idiomatic of the three language variations, but ironically, I had more trouble making the code in this article look nice than I had with the F# variation. You'll see what the problem is later, but it boils down to a combination of Haskell's right-to-left default composition order, and precedence rules of some of the operators.
Please consult the previous articles for context about the example code base. The code shown in this article is from the combinators Git branch. It refactors the code shown in the article Porting song recommendations to Haskell.
The goal is to extract pure functions from the overall recommendations algorithm and compose them using standard combinators, such as =<<, <$>, and traverse.
Getting rid of local mutation #
My first goal was to get rid of the IORef-based local mutation shown in the 'baseline' code base. That wasn't too difficult. If you're interested in the micro-commits I made to get to that milestone, you can consult the Git repository. The interim result looked like this:
getRecommendations srvc un = do -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations -- Impure scrobbles <- getTopScrobbles srvc un -- Pure let scrobblesSnapshot = take 100 $ sortOn (Down . scrobbleCount) scrobbles -- Impure recommendations <- join <$> traverse (\scrobble -> fmap join $ traverse (\otherListener -> fmap scrobbledSong . take 10 . sortOn (Down . songRating . scrobbledSong) . filter (songHasVerifiedArtist . scrobbledSong) <$> getTopScrobbles srvc (userName otherListener)) . take 20 <$> sortOn (Down . userScrobbleCount) . filter ((10_000 <=) . userScrobbleCount) =<< getTopListeners srvc (songId $ scrobbledSong scrobble)) scrobblesSnapshot -- Pure return $ take 200 $ sortOn (Down . songRating) recommendations
Granted, it's not the most readable way to present the algorithm, but it is, after all, only an intermediate step. As usual, I'll remind the reader that Haskell code should, by default, be read from right to left. When split over multiple lines, this also means that an expression should be read from the bottom to the top. Armed with that knowledge (and general knowledge of Haskell), combined with some helpful indentation, it's not altogether unreadable, but not something I'd like to come back to after half a year. And definitely not something I would foist upon (hypothetical) colleagues.
The careful reader may notice that I've decided to use the reverse bind operator =<<, rather than the standard >>= operator. I usually do that with Haskell, because most of Haskell is composed from right to left, and =<< is consistent with that direction. The standard >>= operator, on the other hand, composes monadic actions from left to right. You could argue that that's more natural (to Western audiences), but since everything else stays right-to-left biased, using >>= confuses the reading direction.
As a Westerner, I prefer left-to-right reading order, but in general I've found it hard to fight Haskell's bias in the other direction.
As the -- Pure and -- Impure comments indicate, interleaving the pure functions with impure actions makes the entire expression impure. The more I do that, the less pure code remains.
Single expression #
Going from from the above snapshot to a single impure expression doesn't require many more steps.
getRecommendations srvc un = -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations take 200 . sortOn (Down . songRating) <$> ((\scrobbles -> join <$> traverse (\scrobble -> fmap join $ traverse (\otherListener -> fmap scrobbledSong . take 10 . sortOn (Down . songRating . scrobbledSong) . filter (songHasVerifiedArtist . scrobbledSong) <$> getTopScrobbles srvc (userName otherListener)) . take 20 <$> sortOn (Down . userScrobbleCount) . filter ((10_000 <=) . userScrobbleCount) =<< getTopListeners srvc (songId $ scrobbledSong scrobble)) (take 100 $ sortOn (Down . scrobbleCount) scrobbles)) =<< getTopScrobbles srvc un)
Neither did it improve readability.
Helper functions #
As in previous incarnations of this exercise, it helps if you extract some well-named helper functions, like this one:
getUsersOwnTopScrobbles :: [Scrobble] -> [Scrobble] getUsersOwnTopScrobbles = take 100 . sortOn (Down . scrobbleCount)
As a one-liner, that one perhaps isn't that impressive, but none of them are particularly complicated. The biggest function is this:
getTopScrobblesOfOtherUsers :: [Scrobble] -> [Song] getTopScrobblesOfOtherUsers = fmap scrobbledSong . take 10 . sortOn (Down . songRating . scrobbledSong) . filter (songHasVerifiedArtist . scrobbledSong)
You can see the rest in the Git repository. None of them are exported by the module, which makes them implementation details that you may decide to change or remove at a later date.
You can now compose the overall action.
getRecommendations srvc un = -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations (aggregateTheSongsIntoRecommendations . getTopScrobblesOfOtherUsers) . join <$> ((traverse (getTopScrobbles srvc . userName) . getOtherUsersWhoListenedToTheSameSongs) . join =<< (traverse (getTopListeners srvc . (songId . scrobbledSong)) . getUsersOwnTopScrobbles =<< getTopScrobbles srvc un))
Some of the parentheses break over multiple lines in a non-conventional way. This is my best effort to format the code in a way that emphasises the four steps comprising the algorithm, while still staying within the bounds of the language, and keeping hlint silent.
I could try to argue that if you squint a bit, the operators and other glue like join should fade into the background, but in this case, I don't even buy that argument myself.
It bothers me that it's so hard to compose the code in a way that approaches being self-documenting. I find that the F# composition in the previous article does a better job of that.
Syntactic sugar #
The stated goal in this article is to demonstrate how it's possible to use standard combinators to glue the algorithm together. I've been complaining throughout this article that, while possible, it leaves the code less readable than desired.
That one reader who actually knows Haskell is likely frustrated with me. After all, the language does offer a way out. Using the syntactic sugar of do notation, you can instead write the composition like this:
getRecommendations srvc un = do -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations userTops <- getTopScrobbles srvc un <&> getUsersOwnTopScrobbles otherListeners <- traverse (getTopListeners srvc . (songId . scrobbledSong)) userTops <&> getOtherUsersWhoListenedToTheSameSongs . join songs <- traverse (getTopScrobbles srvc . userName) otherListeners <&> getTopScrobblesOfOtherUsers . join return $ aggregateTheSongsIntoRecommendations songs
By splitting the process up into steps with named variables, you can achieve the much-yearned-for top-to-bottom reading order. Taking advantage of the <&> operator from Data.Functor we also get left-to-right reading order on each line.
That's the best I've been able to achieve under the constraint that the IO-bound operations stay interleaved with pure functions.
Conclusion #
Mixing pure functions with impure actions like this is necessary when composing whole programs (usually at the entry point; i.e. main), but shouldn't be considered good functional-programming style in general. The entire getRecommendations action is impure, being non-deterministic.
Still, even Haskell code eventually needs to compose code in this way. Therefore, it's relevant covering how this may be done. Even so, alternative architectures exist.
Next: Song recommendations with pipes and filters.
Song recommendations from F# combinators
Traversing sequences of tasks. A refactoring.
This article is part of a series named Alternative ways to design with functional programming. In the previous article, you saw how to refactor the example code base to a composition of standard combinators. It's a pragmatic solution to the problem of dealing with lots of data in a piecemeal fashion, but although it uses concepts and programming constructs from functional programming, I don't consider it a proper functional architecture.
Porting the C# code to F# doesn't change that part, but most F# developers will probably agree that this style of programming is more idiomatic in F# than in C#.
Please consult the previous articles for context about the example code base. The code shown in this article is from the fsharp-combinators Git branch. It refactors the code shown in the article Porting song recommendations to F#.
The goal is to extract pure functions from the overall recommendations algorithm and compose them using standard combinators, such as bind, map, and traverse.
Composition from combinators #
Let's start with the completed composition, and subsequently look at the most interesting parts.
type RecommendationsProvider (songService : SongService) = member _.GetRecommendationsAsync = // 1. Get user's own top scrobbles // 2. Get other users who listened to the same songs // 3. Get top scrobbles of those users // 4. Aggregate the songs into recommendations songService.GetTopScrobblesAsync >> Task.bind ( getOwnTopScrobbles >> TaskSeq.traverse ( _.Song.Id >> songService.GetTopListenersAsync >> Task.bind ( getTopScrobbles >> TaskSeq.traverse ( _.UserName >> songService.GetTopScrobblesAsync >> Task.map aggregateRecommendations))) >> Task.map (Seq.flatten >> Seq.flatten >> takeTopRecommendations))
This is a single expression with nested subexpressions, and you may notice that it's completely point-free. This may be a little hardcore even for most F# programmers, since F# idiomatically favours explicit lambda expressions and the pipeline operator |>.
Although I'm personally fascinated by point-free programming, I might consider a more fun alternative if working in a team. You can see such a variation in the Git repository in an intermediary commit. The reason that I've pulled so heavily in this direction here is that it more clearly demonstrate why we call such functions combinators: They provide the glue that enable us to compose functions together.
If you're wondering, >> is also a combinator. In Haskell it's more common with 'unpronounceable' operators such as >>=, ., &, etc., and I'd argue that such terse operators can make code more readable.
The functions getOwnTopScrobbles, getTopScrobbles, aggregateRecommendations, and takeTopRecommendations are helper functions. Here's one of them:
let private getOwnTopScrobbles scrobbles = scrobbles |> Seq.sortByDescending (fun s -> s.ScrobbleCount) |> Seq.truncate 100
The other helpers are also simple, single-expression functions like this one.
As Oleksii Holub implies, you could make each of these small functions public if you wished to test them individually.
Let's now look at the various building blocks that enable this composition.
Combinators #
The F# base library comes with more standard combinators than are generally available for C#, not only for lists, but also Option and Result values. On the other hand, when it comes to asynchronous monads, the F# base library offers task and async computation expressions, but no Task module. You'll need to add Task.bind and Task.map yourself, or import a library that exports those combinators. The article Asynchronous monads shows the implementation used here.
The traverse implementation shouldn't be too surprising, either, but here I implemented it directly, instead of via sequence.
let traverse f xs = let go acc x = task { let! x' = x let! acc' = acc return Seq.append acc' [x'] } xs |> Seq.map f |> Seq.fold go (task { return [] })
Finally, the flatten function is the standard implementation that goes via monadic bind. In F#'s Seq module, bind is called collect.
let flatten xs = Seq.collect id xs
That all there is to it.
Conclusion #
In this article, you saw how to port the C# code from the previous article to F#. Since this style of programming is more idiomatic in F#, more building blocks and language features are available, and hence this kind of refactoring is better suited to F#.
I still don't consider this proper functional architecture, but it's pragmatic and I could see myself writing code like this in a professional setting.
Song recommendations from C# combinators
LINQ-style composition, including SelectMany and Traverse.
This article is part of a larger series titled Alternative ways to design with functional programming. In the previous article, I described, in general terms, a pragmatic small-scale architecture that may look functional, although it really isn't.
Please consult the previous articles for context about the example code base. The code shown in this article is from the combinators Git branch.
The goal is to extract pure functions from the overall recommendations algorithm and compose them using standard combinators, such as SelectMany (monadic bind), Select, and Traverse.
Composition from combinators #
Let's start with the completed composition, and subsequently look at the most interesting parts.
public Task<IReadOnlyList<Song>> GetRecommendationsAsync(string userName) { // 1. Get user's own top scrobbles // 2. Get other users who listened to the same songs // 3. Get top scrobbles of those users // 4. Aggregate the songs into recommendations return _songService.GetTopScrobblesAsync(userName) .SelectMany(scrobbles => UserTopScrobbles(scrobbles) .Traverse(scrobble => _songService .GetTopListenersAsync(scrobble.Song.Id) .Select(TopListeners) .SelectMany(users => users .Traverse(user => _songService .GetTopScrobblesAsync(user.UserName) .Select(TopScrobbles)) .Select(Songs))) .Select(TakeTopRecommendations)); }
This is a single expression with nested subexpressions.
The functions UserTopScrobbles, TopListeners, TopScrobbles, Songs, and TakeTopRecommendations are private helper functions. Here's one of them:
private static IEnumerable<Scrobble> UserTopScrobbles(IEnumerable<Scrobble> scrobbles) { return scrobbles.OrderByDescending(scrobble => scrobble.ScrobbleCount).Take(100); }
The other helpers are also simple, single-expression functions like this one.
As Oleksii Holub implies, you could make each of these small functions public if you wished to test them individually.
Let's now look at the various building blocks that enable this composition.
Asynchronous monad #
C# (or .NET) in general only comes with standard combinators for IEnumerable<T>, so whenever you need them for other monads, you have to define them yourself (or pull in a reusable library that defines them). For the above composition, you'll need SelectMany and Select for Task computations. You can see implementations in the article Asynchronous monads, so I'll not repeat the code here.
One exception is this extension method, which is a variant monadic return, which I'm not sure if I've published before:
internal static Task<T> AsTask<T>(this T source) { return Task.FromResult(source); }
Nothing much is going on here, since it's just a wrapper of Task.FromResult. The this keyword, however, makes AsTask an extension method, which makes usage marginally prettier. It's not used in the above composition, but, as you'll see below, in the implementation of Traverse.
Traversal #
The traversal could be implemented from a hypothetical Sequence action, but you can also implement it directly, which is what I chose to do here.
internal static Task<IEnumerable<TResult>> Traverse<T, TResult>( this IEnumerable<T> source, Func<T, Task<TResult>> selector) { return source .Select(selector) .Aggregate( Enumerable.Empty<TResult>().AsTask(), async (acc, x) => (await acc).Append(await x)); }
Mapping selector over source produces a sequence of tasks. The Aggregate expression subsequently inverts the containers to a single task that contains a sequence of result values.
That's really all there is to it.
Conclusion #
In the previous article, I made no secret of my position on this refactoring. For the example at hand, the benefit is at best marginal. The purpose of this article isn't to insist that you must write code like this. Rather, it's a demonstration of what's possible.
If you have a problem which is similar, but more complicated, refactoring to standard combinators may be a good idea. After all, a standard combinator like SelectMany, Traverse, etc. is well-understood and lawful. You should expect combinators to be defect-free, so using them instead of ad-hoc code constructs like nested loops with conditionals could help eliminate some trivial bugs.
Additionally, if you're working with a team comfortable with these few abstractions, code assembled from standard combinators may actually turn out to be more readable that code buried in ad-hoc imperative control flow. And if not everyone on the team is on board with this style, perhaps it's an opportunity to push the envelope a bit.
Of course, if you use a language where such constructs are already idiomatic, colleagues should already be used to this style of programming.
Song recommendations from combinators
Interleaving impure actions with pure functions. Not really functional programming.
This article is part of a larger article series about alternative ways to design with functional programming, particularly when faced with massive data loads. In the previous few articles, you saw functional architecture at its apparent limit. With sufficiently large data sizes, the Impureim Sandwich pattern starts to buckle. That's really not an indictment of that pattern; only an observation that no design pattern applies universally.
In this and the next few articles, we'll instead look at a more pragmatic option. In this article I'll discuss the general idea, and follow up in other articles with examples in three different languages.
In this overall article series, I'm using Oleksii Holub's inspiring article Pure-Impure Segregation Principle as an outset for the code example. Previous articles in this article series have already covered the basics, but the gist of it is a song recommendation service that uses past play information ('scrobbles') to suggest new songs to a user.
Separating pure functions from impure composition #
In the original article, Oleksii Holub suggests a way to separate pure functions from impure actions: We may extract as much pure code from the overall algorithm as possible, but we're still left with pure functions and impure actions mixed together.
Here's my reproduction of that suggestion, with trivial modifications:
// Pure public static IReadOnlyList<int> HandleOwnScrobbles(IReadOnlyCollection<Scrobble> scrobbles) => scrobbles .OrderByDescending(s => s.ScrobbleCount) .Take(100) .Select(s => s.Song.Id) .ToArray(); // Pure public static IReadOnlyList<string> HandleOtherListeners(IReadOnlyCollection<User> users) => users .Where(u => u.TotalScrobbleCount >= 10_000) .OrderByDescending(u => u.TotalScrobbleCount) .Take(20) .Select(u => u.UserName) .ToArray(); // Pure public static IReadOnlyList<Song> HandleOtherScrobbles(IReadOnlyCollection<Scrobble> scrobbles) => scrobbles .Where(s => s.Song.IsVerifiedArtist) .OrderByDescending(s => s.Song.Rating) .Take(10) .Select(s => s.Song) .ToArray(); // Pure public static IReadOnlyList<Song> FinalizeRecommendations(IReadOnlyList<Song> songs) => songs .OrderByDescending(s => s.Rating) .Take(200) .ToArray(); public async Task<IReadOnlyList<Song>> GetRecommendationsAsync(string userName) { // Impure var scrobbles = await _songService.GetTopScrobblesAsync(userName); // Pure var songIds = HandleOwnScrobbles(scrobbles); var recommendationCandidates = new List<Song>(); foreach (var songId in songIds) { // Impure var otherListeners = await _songService .GetTopListenersAsync(songId); // Pure var otherUserNames = HandleOtherListeners(otherListeners); foreach (var otherUserName in otherUserNames) { // Impure var otherScrobbles = await _songService .GetTopScrobblesAsync(otherUserName); // Pure var songsToRecommend = HandleOtherScrobbles(otherScrobbles); recommendationCandidates.AddRange(songsToRecommend); } } // Pure return FinalizeRecommendations(recommendationCandidates); }
As Oleksii Holub writes,
"However, instead of having one cohesive element to reason about, we ended up with multiple fragments, each having no meaning or value of their own. While unit testing of individual parts may have become easier, the benefit is very questionable, as it provides no confidence in the correctness of the algorithm as a whole."
I agree with that assessment, but still find it warranted to pursue the idea a little further. After all, my goal with this overall article series isn't to be prescriptive, but rather descriptive. By presenting and comparing alternatives, we become aware of more options. This, hopefully, helps us choose the 'right tool for the job'.
Triple-decker sandwich? #
If we look closer at this alternative, however, we find that we only need to deal with three impure actions. We might, then, postulate that this is an expanded sandwich - a triple-decker sandwich, if you will.
To be clear, I don't find this a reasonable argument. Even if you accept expanding the sandwich metaphor to add a pure validation step, the number of layers, and the structure of the sandwich would still be known at compile time. You may start at the impure boundary, then phase into pure validation, return to another impure step to gather data, call your 'main' pure function, and finally write the result to some kind of output. To borrow a figure from the What's a sandwich? article:

On the other hand, this isn't what the above code suggestion does. The problem with the song recommendation algorithm is that the impure actions cascade. While we start with a single impure out-of-process query, we then use the result of that to loop over, and perform n more queries. This, in fact, happens again, nested in the outer loop, so in terms of network calls, we're looking at an O(n2) algorithm.
We can actually be more precise than that, because the 'outer' queries actually limit their result sets. The first query only considers the top 100 results, so we know that GetTopListenersAsync is going to be called at most 100 times. The result of this call is again limited to the top 20, so that the inner calls to GetTopScrobblesAsync run at most 20 * 100 = 2,000 times. In all, the upper limit is 1 + 100 + 2,000 = 2,101 network calls. (Okay, so really, this is just an O(1) algorithm, although 1 ~ 2,101.)
Not that that isn't going to take a bit of time.
All that said, it's not execution time that concerns me in this context. Assume that the algorithm is already as optimal as possible, and that those 2,101 network calls are necessary. What rather concerns me here is how to organize the code in a way that's as maintainable as possible. As usual, when that's the main concern, I'll remind the reader to consider the example problem as a stand-in for a more complicated problem. Even Oleksii Holub's original code example is only some fifty-odd lines of code, which in itself hardly warrants all the hand-wringing we're currently subjecting it to.
Rather, what I'd like to address is the dynamic back-and-forth between pure function and impure action. Each of these thousands of out-of-process calls are non-deterministic. If you're tasked with maintaining or editing this algorithm, your brain will be taxed by all that unpredictable behaviour. Many subtle bugs lurk there.
The more we can pull the code towards pure functions the better, because referential transparency fits in your head.
So, to be explicit, I don't consider this kind of composition as an expanded Impureim Sandwich.
Standard combinators #
Is it possible to somehow improve, even just a little, on the above suggestion? Can we somehow make it look a little 'more functional'?
We could use some standard combinators, like monadic bind, traversals, and so on.
To be honest, for the specific song-recommendations example, the benefit is marginal at best, but doing it would still demonstrate a particular technique. We'd be able to get rid of the local mutation of recommendationCandidates, but that's about it.
Even so, refactoring to self-contained expressions makes other refactoring easier. As a counter-example, imagine that you'd like to extract the inner foreach loop in the above code example to a helper method.
private async Task CollectOtherUserTopScrobbles( List<Song> recommendationCandidates, IReadOnlyList<string> otherUserNames) { foreach (var otherUserName in otherUserNames) { // Impure var otherScrobbles = await _songService .GetTopScrobblesAsync(otherUserName); // Pure var songsToRecommend = HandleOtherScrobbles(otherScrobbles); recommendationCandidates.AddRange(songsToRecommend); } }
The call site would then look like this:
// Pure var otherUserNames = HandleOtherListeners(otherListeners); // Impure await CollectOtherUserTopScrobbles(recommendationCandidates, otherUserNames);
In this specific example, such a refactoring isn't too difficult, but it's more complicated than it could be. Because of state mutation, we have to pass the object to be modified, in this case recommendationCandidates, along as a method argument. Here, there's only one, but if you have code where you change the state of two objects, you'd have to pass two extra parameters, and so on.
You've most likely worked in a real code base where you have tried to extract a helper method, only to discover that it's so incredibly tangled with the objects that it modifies that you need a long parameter list. What should have been a simplification is in danger of making everything worse.
On the other hand, self-contained expressions, even if, as in this case, they're non-deterministic, don't mutate state. In general, this tends to make it easier to extract subexpressions as helper methods, if only because they are less coupled to the rest of the code. They may required inputs as parameters, but at least you don't have to pass around objects to be modified.
Thus, the reason I find it worthwhile to include articles about this kind of refactoring is that, since it demonstrates how to refactor to a more expression-based style, you may be able to extrapolate to your own context. And who knows, you may encounter a context where more substantial improvements can be made by moving in this direction.
As usual in this article series, you'll see how to apply this technique in three different languages.
- Song recommendations from C# combinators
- Song recommendations from F# combinators
- Song recommendations from Haskell combinators
All that said, it's important to underscore that I don't consider this proper functional architecture. Even the Haskell example is too non-deterministic to my tastes.
Conclusion #
Perhaps the most pragmatic approach to a problem like the song-recommendations example is to allow the impure actions and pure functions to interleave. I don't mean to insist that functional programming is the only way to make code maintainable. You can organize code according to other principles, and some of them may also leave you with a code base that can serve its mission well, now and in the future.
Another factor to take into account is the skill level of the team tasked with maintaining a code base. What are they comfortable with?
Not that I think you should settle for status quo. Progress can only be made if you push the envelop a little, but you can also come up with a code base so alien to your colleagues that they can't work with it at all.
I could easily imagine a team where the solution in the next three articles is the only style they'd be able to maintain.
Testing races with a slow Decorator
Delaying database interactions for test purposes.
In chapter 12 in Code That Fits in Your Head, I cover a typical race condition and how to test for it. The book comes with a pedagogical explanation of the problem, including a diagram in the style of Designing Data-Intensive Applications. In short, the problem occurs when two or more clients are competing for the last remaining seats in a particular time slot.
In my two-day workshop based on the book, I also cover this scenario. The goal is to show how to write automated tests for this kind of non-deterministic behaviour. In the book, and in the workshop, my approach is to rely on the law of large numbers. An automated test attempts to trigger the race condition by trying 'enough' times. A timeout on the test assumes that if the test does not trigger the condition in the allotted time window, then the bug is addressed.
At one of my workshops, one participant told me of a more efficient and elegant way to test for this. I wish I could remember exactly at which workshop it was, and who the gentleman was, but alas, it escapes me.
Reproducing the condition #
How do you deterministically reproduce non-deterministic behaviour? The default answer is almost tautological. You can't, since it's non-deterministic.
The irony, however, is that in the workshop, I deterministically demonstrate the problem. The problem, in short, is that in order to decide whether or not to accept a reservation request, the system first reads data from its database, runs a fairly complex piece of decision logic, and finally writes the reservation to the database - if it decides to accept it, based on what it read. When competing processes vie for the last remaining seats, a race may occur where both (or all) base their decision on the same data, so they all come to the conclusion that they still have enough remaining capacity. Again, refer to the book, and its accompanying code base, for the details.
How do I demonstrate this condition in the workshop? I go into the Controller code and insert a temporary, human-scale delay after reading from the database, but before making the decision:
var reservations = await Repository.ReadReservations(r.At); await Task.Delay(TimeSpan.FromSeconds(10)); if (!MaitreD.WillAccept(DateTime.Now, reservations, r)) return NoTables500InternalServerError(); await Repository.Create(restaurant.Id, reservation);
Then I open two windows, from which I, within a couple of seconds of each other, try to make competing reservations. When the bug is present, both reservations are accepted, although, according to business rules, only one should be.
So that's how to deterministically demonstrate the problem. Just insert a long enough delay.
We can't, however, leave such delays in the production code, so I never even considered that this simple technique could be used for automated testing.
Slowing things down with a Decorator #
That's until my workshop participant told me his trick: Why don't you slow down the database interactions for test-purposes only? At first, I thought he had in mind some nasty compiler pragmas or environment hacks, but no. Why don't you use a Decorator to slow things down?
Indeed, why not?
Fortunately, all database interaction already takes place behind an IReservationsRepository interface. Adding a test-only, delaying Decorator is straightforward.
public sealed class SlowReservationsRepository : IReservationsRepository { private readonly TimeSpan halfDelay; public SlowReservationsRepository( TimeSpan delay, IReservationsRepository inner) { Delay = delay; halfDelay = delay / 2; Inner = inner; } public TimeSpan Delay { get; } public IReservationsRepository Inner { get; } public async Task Create(int restaurantId, Reservation reservation) { await Task.Delay(halfDelay); await Inner.Create(restaurantId, reservation); await Task.Delay(halfDelay); } public async Task Delete(int restaurantId, Guid id) { await Task.Delay(halfDelay); await Inner.Delete(restaurantId, id); await Task.Delay(halfDelay); } public async Task<Reservation?> ReadReservation( int restaurantId, Guid id) { await Task.Delay(halfDelay); var result = await Inner.ReadReservation(restaurantId, id); await Task.Delay(halfDelay); return result; } public async Task<IReadOnlyCollection<Reservation>> ReadReservations( int restaurantId, DateTime min, DateTime max) { await Task.Delay(halfDelay); var result = await Inner.ReadReservations(restaurantId, min, max); await Task.Delay(halfDelay); return result; } public async Task Update(int restaurantId, Reservation reservation) { await Task.Delay(halfDelay); await Inner.Update(restaurantId, reservation); await Task.Delay(halfDelay); } }
This one uniformly slows down all operations. I arbitrarily decided to split the Delay in half, in order to apply half of it before each action, and the other half after. Honestly, I didn't mull this over too much; I just thought that if I did it that way, I wouldn't have to speculate whether it would make a difference if the delay happened before or after the action in question.
Slowing down tests #
I added a few helper methods to the RestaurantService class that inherits from WebApplicationFactory<Startup>, mainly to enable decoration of the injected Repository. With those changes, I could now rewrite my test like this:
[Fact] public async Task NoOverbookingRace() { var date = DateTime.Now.Date.AddDays(1).AddHours(18.5); using var service = RestaurantService.CreateWith(repo => new SlowReservationsRepository( TimeSpan.FromMilliseconds(100), repo)); var task1 = service.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var task2 = service.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var actual = await Task.WhenAll(task1, task2); Assert.Single( actual, msg => msg.StatusCode == HttpStatusCode.InternalServerError); var ok = Assert.Single(actual, msg => msg.IsSuccessStatusCode); // Check that the reservation was actually created: var resp = await service.GetReservation(ok.Headers.Location); resp.EnsureSuccessStatusCode(); var reservation = await resp.ParseJsonContent<ReservationDto>(); Assert.Equal(10, reservation.Quantity); }
The restaurant being tested has a maximum capacity of ten guests, so while it can accommodate either of the two requests, it can't make room for both.
For this example, I arbitrarily chose to configure the Decorator with a 100-millisecond delay. Every interaction with the database caused by that test gets a built-in 100-millisecond delay. 50 ms before each action, and 50 ms after.
The test starts both tasks, task1 and task2, without awaiting them. This allows them to run concurrently. After starting both tasks, the test awaits both of them with Task.WhenAll.
The assertion phase of the test is more involved than you may be used to see. The reason is that it deals with more than one possible failure scenario.
The first two assertions (Assert.Single) deal with the complete absence of transaction control in the application. In that case, both POST requests succeed, which they aren't supposed to. If the system works properly, it should accept one request and reject the other.
The rest of the assertions check that the successful reservation was actually created. That's another failure scenario.
The way I chose to deal with the race condition is standard in .NET. I used a TransactionScope. This is peculiar and, in my opinion, questionable API that enables you to start a transaction anywhere in your code, and then complete when you you're done. In the code base that accompanies Code That Fits in Your Head, it looks like this:
private async Task<ActionResult> TryCreate(Restaurant restaurant, Reservation reservation) { using var scope = new TransactionScope(TransactionScopeAsyncFlowOption.Enabled); var reservations = await Repository .ReadReservations(restaurant.Id, reservation.At) .ConfigureAwait(false); var now = Clock.GetCurrentDateTime(); if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError(); await Repository.Create(restaurant.Id, reservation).ConfigureAwait(false); scope.Complete(); return Reservation201Created(restaurant.Id, reservation); }
Notice the scope.Complete() statement towards the end.
What happens if someone forgets to call scope.Complete()?
In that case, the thread that wins the race returns 201 Created, but when the scope goes out of scope, it's disposed of. If Complete() wasn't called, the transaction is rolled back, but the HTTP response code remains 201. Thus, the two assertions that inspect the response codes aren't enough to catch this particular kind of defect.
Instead, the test subsequently queries the System Under Test to verify that the resource was, indeed, created.
Wait time #
The original test shown in the book times out after 30 seconds if it can't produce the race condition. Compared to that, the refactored test shown here is fast. Even so, we may fear that it spends too much time doing nothing. How much time might that be?
The TryCreate helper method shown above is the only part of a POST request that interacts with the Repository. As you can see, it calls it twice: Once to read, and once to write, if it decides to do that. With a 100 ms delay, that's 200 ms.
And while the test issues two POST requests, they run in parallel. That's the whole point. It means that they'll still run in approximately 200 ms.
The test then issues a GET request to verify that the resource was created. That triggers another database read, which takes another 100 ms.
That's 300 ms in all. Given that these tests are part of a second-level test suite, and not your default developer test suite, that may be good enough.
Still, that's the POST scenario. I also wrote a test that checks for a race condition when doing PUT requests, and it performs more work.
[Fact] public async Task NoOverbookingPutRace() { var date = DateTime.Now.Date.AddDays(1).AddHours(18.5); using var service = RestaurantService.CreateWith(repo => new SlowReservationsRepository( TimeSpan.FromMilliseconds(100), repo)); var (address1, dto1) = await service.PostReservation(date, 4); var (address2, dto2) = await service.PostReservation(date, 4); dto1.Quantity += 2; dto2.Quantity += 2; var task1 = service.PutReservation(address1, dto1); var task2 = service.PutReservation(address2, dto2); var actual = await Task.WhenAll(task1, task2); Assert.Single( actual, msg => msg.StatusCode == HttpStatusCode.InternalServerError); var ok = Assert.Single(actual, msg => msg.IsSuccessStatusCode); // Check that the reservations now have consistent values: var client = service.CreateClient(); var resp1 = await client.GetAsync(address1); var resp2 = await client.GetAsync(address2); resp1.EnsureSuccessStatusCode(); resp2.EnsureSuccessStatusCode(); var body1 = await resp1.ParseJsonContent<ReservationDto>(); var body2 = await resp2.ParseJsonContent<ReservationDto>(); Assert.Single(new[] { body1.Quantity, body2.Quantity }, 6); Assert.Single(new[] { body1.Quantity, body2.Quantity }, 4); }
This test first has to create two reservations in a nice, sequential manner. Then it attempts to perform two concurrent updates, and finally it tests that all is as it should be: That both reservations still exist, but only one had its Quantity increased to 6.
This test first makes two POST requests, nicely serialized so as to avoid a race condition. That's 400 ms.
Each PUT request triggers three Repository actions, for a total of 300 ms (since they run in parallel).
Finally, the test issues two GET requests for verification, for another 2 times 100 ms. Now that I'm writing this, I realize that I could also have parallelized these two calls, but as you read on, you'll see why that's not necessary.
In all, this test waits for 900 ms. That's almost a second.
Can we improve on that?
Decreasing unnecessary wait time #
In the latter example, the 300 ms wait time for the parallel PUT requests are necessary to trigger the race condition, but the rest of the test's actions don't need slowing down. We can remove the unwarranted wait time by setting up two services: One slow, and one normal.
To be honest, I could have modelled this by just instantiating two service objects, but why do something as pedestrian as that when you can turn RestaurantService into a monomorphic functor?
internal RestaurantService Select(Func<IReservationsRepository, IReservationsRepository> selector) { if (selector is null) throw new ArgumentNullException(nameof(selector)); return new RestaurantService(selector(repository)); }
Granted, this is verging on the frivolous, but when writing code for a blog post, I think I'm allowed a little fun.
In any case, this now enables me to rewrite the test like this:
[Fact] public async Task NoOverbookingRace() { var date = DateTime.Now.Date.AddDays(1).AddHours(18.5); using var service = new RestaurantService(); using var slowService = from repo in service select new SlowReservationsRepository(TimeSpan.FromMilliseconds(100), repo); var task1 = slowService.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var task2 = slowService.PostReservation(new ReservationDtoBuilder() .WithDate(date) .WithQuantity(10) .Build()); var actual = await Task.WhenAll(task1, task2); Assert.Single( actual, msg => msg.StatusCode == HttpStatusCode.InternalServerError); var ok = Assert.Single(actual, msg => msg.IsSuccessStatusCode); // Check that the reservation was actually created: var resp = await service.GetReservation(ok.Headers.Location); resp.EnsureSuccessStatusCode(); var reservation = await resp.ParseJsonContent<ReservationDto>(); Assert.Equal(10, reservation.Quantity); }
Notice how only the parallel execution of task1 and task2 run on the slow system. The rest runs as fast as it can. It's as if the client was hitting two different servers that just happen to connect to the same database. Now the test only waits for the 200 ms described above. The PUT test, likewise, only idles for 300 ms instead of 900 ms.
Near-deterministic tests #
Does this deterministically reproduce the race condition? In practice, it may move us close enough, but theoretically the race is still on. With the increased wait time, it's now much more unlikely that the race condition does not happen, but it still could.
Imagine that task1 queries the Repository. Just as it's received a response, but before task2 starts its query, execution is paused, perhaps because of garbage collection. Once the program resumes, task1 runs to completion before task2 reads from the database. In that case, task2 ends up making the right decision, rejecting the reservation. Even if no transaction control were in place.
This may not be a particularly realistic scenario, but I suppose it could happen if the computer is stressed in general. Even so, you might decide to make such false-negative scenarios even more unlikely by increasing the delay time. Of course, the downside is that tests take even longer to run.
Another potential problem is that there's no guarantee that task1 and task2 run in parallel. Even if the test doesn't await any of the tasks, both start executing immediately. There's an (unlikely) chance that task1 completes before task2 starts. Again, I don't consider this likely, but I suppose it could happen because of thread starvation, generation 2 garbage collection, the disk running full, etc. The point is that the test shown here is still playing the odds, even if the odds are really good.
Conclusion #
Instead of running a scenario 'enough' times that reproducing a race condition is likely, you can increase the odds to near-certainty by slowing down the race. In this example, the race involves a database, but you might also encounter race conditions internally in multi-threaded code. I'm not insisting that the technique described in this article applies universally, but if you can slow down certain interactions in the right way, you may be able reproduce problems as automated tests.
If you've ever troubleshot a race condition, you've probably tried inserting sleeps into the code in various places to understand the problem. As described above, a single, strategically-placed Task.Delay may be all you need to reproduce a problem. What escaped me for a long time, however, was that I didn't realize that I could cleanly insert such pauses into production code. Until my workshop participant suggested using a Decorator.
A delaying Decorator slows interactions with the database down sufficiently to reproduce the race condition as an automated test.
Song recommendations as a Haskell Impureim Sandwich
A pure function on potentially massive data.
This article is part of a larger article series called Alternative ways to design with functional programming. As the title suggests, these articles discuss various ways to apply functional-programming principles to a particular problem. All the articles engage with the same problem. In short, the task is to calculate song recommendations for a user, based on massive data sets. Earlier articles in this series give you detailed explanation of the problem.
In the previous article, you saw how to refactor the 'base' F# code base to a pure function. In this article, you'll see the same refactoring applied to the 'base' Haskell code base shown in Porting song recommendations to Haskell.
The Git branch discussed in this article is the pure-function branch in the Haskell Git repository.
Collecting all the data #
Like in the previous articles, we may start by adding two more methods to the SongService type class, which will enable us to enumerate all songs and all users. The full type class, with all four methods, then looks like this:
class SongService a where getAllSongs :: a -> IO [Song] getAllUsers :: a -> IO [User] getTopListeners :: a -> Int -> IO [User] getTopScrobbles :: a -> String -> IO [Scrobble]
If you compare with the type class definition shown in the article Porting song recommendations to Haskell, you'll see that getAllSongs and getAllUsers are the new methods.
They enable you to collect all top listeners, and all top scrobbles, even though it may take some time. To gather all the top listeners, we may add this collectAllTopListeners action:
collectAllTopListeners srvc = do songs <- getAllSongs srvc listeners <- newIORef Map.empty forM_ songs $ \song -> do topListeners <- getTopListeners srvc $ songId song modifyIORef listeners (Map.insert (songId song) topListeners) readIORef listeners
Likewise, you can amass all the top scrobbles with a similar action:
collectAllTopScrobbles srvc = do users <- getAllUsers srvc scrobbles <- newIORef Map.empty forM_ users $ \user -> do topScrobbles <- getTopScrobbles srvc $ userName user modifyIORef scrobbles (Map.insert (userName user) topScrobbles) readIORef scrobbles
As you may have noticed, they're so similar that, had there been more than two, we might consider extracting the similar parts to a reusable operation.
In both cases, we start with the action that enables us to enumerate all the resources (songs or scrobbles) that we're interested in. For each of these, we then invoke the action to get the 'top' resources for that song or scrobble. There's a massive n+1 problem here, but you could conceivably parallelize all these queries, as they're independent. Still, it's bound to take much time, possibly hours.
You may be wondering why I chose to use IORef values for both actions, instead of more idiomatic combinator-based expressions. Indeed, that is what I would usually do, but in this case, these two actions are heavily IO-bound already, and it makes the Haskell code more similar to the F# code. Not that that is normally a goal, but here I thought it might help you, the reader, to compare the different code bases.
All the data is kept in a Map per action, so two massive maps in all. Once these two actions return, we're done with the read phase of the Recawr Sandwich.
Referentially transparent function with local mutation #
As a first step, we may wish to turn the getRecommendations action into a referentially transparent function. If you look through the commits in the Git repository, you can see that I actually did this through a series of micro-commits, but here I only present a more coarse-grained version of the changes I made.
In this version, I've removed the srvc (SongService) parameter, and instead added the two maps topScrobbles and topListeners.
getRecommendations :: Map String [Scrobble] -> Map Int [User] -> String -> IO [Song] getRecommendations topScrobbles topListeners un = do -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations let scrobbles = Map.findWithDefault [] un topScrobbles let scrobblesSnapshot = take 100 $ sortOn (Down . scrobbleCount) scrobbles recommendationCandidates <- newIORef [] forM_ scrobblesSnapshot $ \scrobble -> do let otherListeners = Map.findWithDefault [] (songId $ scrobbledSong scrobble) topListeners let otherListenersSnapshot = take 20 $ sortOn (Down . userScrobbleCount) $ filter ((10_000 <=) . userScrobbleCount) otherListeners forM_ otherListenersSnapshot $ \otherListener -> do let otherScrobbles = Map.findWithDefault [] (userName otherListener) topScrobbles let otherScrobblesSnapshot = take 10 $ sortOn (Down . songRating . scrobbledSong) $ filter (songHasVerifiedArtist . scrobbledSong) otherScrobbles forM_ otherScrobblesSnapshot $ \otherScrobble -> do let song = scrobbledSong otherScrobble modifyIORef recommendationCandidates (song :) recommendations <- readIORef recommendationCandidates return $ take 200 $ sortOn (Down . songRating) recommendations
You've probably noticed that this action still looks impure, since it returns IO [Song]. Even so, it's referentially transparent, since it's fully deterministic and without side effects.
The way I refactored the action, this order of changes was what made most sense to me. Getting rid of the SongService parameter was more important to me than getting rid of the IO wrapper.
In any case, this is only an interim state towards a more idiomatic pure Haskell function.
A single expression #
A curious property of expression-based languages is that you can conceivably write functions in 'one line of code'. Granted, it would often be a terribly wide line, not at all readable, a beast to maintain, and often with poor performance, so not something you'd want to alway do.
In this case, however, we can do that, although in order to stay within an 80x24 box, we break the expression over multiple lines.
getRecommendations :: Map String [Scrobble] -> Map Int [User] -> String -> [Song] getRecommendations topScrobbles topListeners un = -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations take 200 $ sortOn (Down . songRating) $ fmap scrobbledSong $ (\otherListener -> take 10 $ sortOn (Down . songRating . scrobbledSong) $ filter (songHasVerifiedArtist . scrobbledSong) $ Map.findWithDefault [] (userName otherListener) topScrobbles) =<< (\scrobble -> take 20 $ sortOn (Down . userScrobbleCount) $ filter ((10_000 <=) . userScrobbleCount) $ Map.findWithDefault [] (songId $ scrobbledSong scrobble) topListeners) =<< take 100 (sortOn (Down . scrobbleCount) $ Map.findWithDefault [] un topScrobbles)
This snapshot also got rid of the IORef value, and IO in general. The function is still referentially transparent, but now Haskell can also see that.
Even so, this looks dense and confusing. It doesn't help that Haskell should usually be read right-to-left, and bottom-to-top. Is it possible to improve the readability of this function?
Composition from smaller functions #
To improve readability and maintainability, we may now extract helper functions. The first one easily suggests itself.
getUsersOwnTopScrobbles :: Ord k => Map k [Scrobble] -> k -> [Scrobble] getUsersOwnTopScrobbles topScrobbles un = take 100 $ sortOn (Down . scrobbleCount) $ Map.findWithDefault [] un topScrobbles
Each of the subexpressions in the above code listing are candidates for the same kind of treatment, like this one:
getOtherUsersWhoListenedToTheSameSongs :: Map Int [User] -> Scrobble -> [User] getOtherUsersWhoListenedToTheSameSongs topListeners scrobble = take 20 $ sortOn (Down . userScrobbleCount) $ filter ((10_000 <=) . userScrobbleCount) $ Map.findWithDefault [] (songId $ scrobbledSong scrobble) topListeners
You can't see it from the code listings themselves, but the module doesn't export these functions. They remain implementation details.
With a few more helper functions, you can now implement the getRecommendations function by composing the helpers.
getRecommendations :: Map String [Scrobble] -> Map Int [User] -> String -> [Song] getRecommendations topScrobbles topListeners un = -- 1. Get user's own top scrobbles -- 2. Get other users who listened to the same songs -- 3. Get top scrobbles of those users -- 4. Aggregate the songs into recommendations aggregateSongsIntoRecommendations $ getTopSongsOfOtherUser topScrobbles =<< getOtherUsersWhoListenedToTheSameSongs topListeners =<< getUsersOwnTopScrobbles topScrobbles un
Since Haskell by default composes from right to left, when you break such a composition over multiple lines (in order to stay within a 80x24 box), it should be read bottom-up.
You can remedy this situation by importing the & operator from Data.Function:
getRecommendations :: Map String [Scrobble] -> Map Int [User] -> String -> [Song] getRecommendations topScrobbles topListeners un = getUsersOwnTopScrobbles topScrobbles un >>= getOtherUsersWhoListenedToTheSameSongs topListeners >>= getTopSongsOfOtherUser topScrobbles & aggregateSongsIntoRecommendations
Notice that I've named each of the helper functions after the code comments that accompanied the previous incarnations of this function. If we consider code comments apologies for not properly organizing the code, we've now managed to structure it in such a way that those apologies are no longer required.
Conclusion #
If you accept the (perhaps preposterous) assumption that it's possible to fit the required data in persistent data structures, refactoring the recommendation algorithm to a pure function isn't that difficult. That's the pure part of a Recawr Sandwich. While I haven't shown the actual sandwich here, it's quite straightforward. You can find it in the tests in the Haskell Git repository. Also, once you've moved all the data collection to the boundary of the application, you may no longer need the SongService type class.
I find the final incarnation of the code shown here to be quite attractive. While I've kept the helper functions private to the module, it's always an option to export them if you find that warranted. This could improve testability of the overall code base, albeit at the risk of increasing the surface area of the API that you have to maintain and secure.
There are always trade-offs to be considered. Even if you, eventually, find that for this particular example, the input data size is just too big to make this alternative viable, there are, in my experience, many other situations when this kind of architecture is a good solution. Even if the input size is a decent amount of megabytes, the simplification offered by an Impureim Sandwich may trump the larger memory footprint. As always, if you're concerned about performance, measure it.
This article concludes the overview of using an Recawr Sandwich to address the problem. Since it's, admittedly, a bit of a stretch to imagine running a program that uses terabytes (or more) of memory, we now turn to alternative architectures.
Song recommendations as an F# Impureim Sandwich
A pure function on potentially massive data.
This article is part of a larger article series titled Alternative ways to design with functional programming. In the previous article, you saw an example of applying the Impureim Sandwich pattern to the problem at hand: A song recommendation engine that sifts through much historical data.
As already covered in Song recommendations as an Impureim Sandwich, the drawback, if you will, of a Recawr Sandwich is that you need to collect all data from impure sources before you can pass it to a pure function. It may happen that you need so much data that this strategy becomes untenable. This may be the case here, but surprisingly often, what strikes us humans as being vast amounts are peanuts for computers.
So even if you don't find this particular example realistic, I'll forge ahead and show how to apply the Recawr Sandwich pattern to this problem. This is essentially a port to F# of the C# code from the previous article. If you rather want to see some more realistic architectures to deal with the overall problem, you can always go back to the table of contents in the first article of the series.
In this article, I'm working with the fsharp-pure-function branch of the Git repository.
Collecting all the data #
Like in the previous article, we may start by adding two more members to the SongService interface, which will enable us to enumerate all songs and all users. The full interface, with all four methods, then looks like this:
type SongService = abstract GetAllSongs : unit -> Task<IEnumerable<Song>> abstract GetAllUsers : unit -> Task<IEnumerable<User>> abstract GetTopListenersAsync : songId : int -> Task<IReadOnlyCollection<User>> abstract GetTopScrobblesAsync : userName : string -> Task<IReadOnlyCollection<Scrobble>>
If you compare with the interface definition shown in the article Porting song recommendations to F#, you'll see that GetAllSongs and GetAllUsers are the new methods.
They enable you to collect all top listeners, and all top scrobbles, even though it may take some time. To gather all the top listeners, we may add this collectAllTopListeners action:
let collectAllTopListeners (songService : SongService) = task { let d = Dictionary<int, IReadOnlyCollection<User>> () let! songs = songService.GetAllSongs () do! songs |> TaskSeq.iter (fun s -> task { let! topListeners = songService.GetTopListenersAsync s.Id d.Add (s.Id, topListeners) } ) return d :> IReadOnlyDictionary<_, _> }
Likewise, you can amass all the top scrobbles with a similar action:
let collectAllTopScrobbles (songService : SongService) = task { let d = Dictionary<string, IReadOnlyCollection<Scrobble>> () let! users = songService.GetAllUsers () do! users |> TaskSeq.iter (fun u -> task { let! topScrobbles = songService.GetTopScrobblesAsync u.UserName d.Add (u.UserName, topScrobbles) } ) return d :> IReadOnlyDictionary<_, _> }
As you may have noticed, they're so similar that, had there been more than two, we might consider extracting the similar parts to a reusable operation.
In both cases, we start with the action that enables us to enumerate all the resources (songs or scrobbles) that we're interested in. For each of these, we then invoke the action to get the 'top' resources for that song or scrobble. There's a massive n+1 problem here, but you could conceivably parallelize all these queries, as they're independent. Still, it's bound to take much time, possibly hours.
All the data is kept in a dictionary per action, so two massive dictionaries in all. Once these two actions return, we're done with the read phase of the Recawr Sandwich.
Traversals #
You may have wondered about the above TaskSeq.iter action. That's not part of the standard library. What is it, and where does it come from?
It's a specialized traversal, designed to make asynchronous Commands more streamlined.
let iter f xs = task { let! units = traverse f xs Seq.iter id units }
If you've ever wondered why the identity function (id) is useful, here's an example. In the first line of code, units is a unit seq value; i.e. a sequence of unit values. To make TaskSeq.iter as easy to use as possible, it should turn that multitude of unit values into a single unit value. There's more than one way to do that, but I found that using Seq.iter was about the most succinct option I could think of. Be that as it may, Seq.iter requires as an argument a function that returns unit, and since we already have unit values, id does the job.
The iter action uses the TaskSeq module's traverse function, which is defined like this:
let traverse f xs = let go acc x = task { let! x' = x let! acc' = acc return Seq.append acc' [x'] } xs |> Seq.map f |> Seq.fold go (task { return [] })
The type of traverse is ('a -> #Task<'c>) -> 'a seq -> Task<'c seq>; that is, it applies an asynchronous action to each of a sequence of 'a values, and returns an asynchronous workflow that contains a sequence of 'c values.
Dictionary lookups #
In .NET, queries that may fail are idiomatically modelled with methods that take out parameters. This is also true for dictionary lookups. Since that kind of design doesn't compose well, it's useful to add a little helper function that instead may return an empty value. While you'd generally do that by returning an option value, in this case, an empty collection is more appropriate.
let findOrEmpty key (d : IReadOnlyDictionary<_, IReadOnlyCollection<_>>) = match d.TryGetValue key with | true, v -> v | _ -> List.empty
You may have noticed that I also added a similar helper function in the C# example, although there I called it GetOrEmpty.
Pure function with local mutation #
As a first step, we may wish to turn the GetRecommendationsAsync method into a pure function. If you look through the commits in the Git repository, you can see that I actually did this through a series of micro-commits, but here I only present a more coarse-grained version of the changes I made.
Instead of a method on a class, we now have a self-contained function that takes, as arguments, two dictionaries, but no SongService dependency.
let getRecommendations topScrobbles topListeners userName = // 1. Get user's own top scrobbles // 2. Get other users who listened to the same songs // 3. Get top scrobbles of those users // 4. Aggregate the songs into recommendations let scrobbles = topScrobbles |> Dict.findOrEmpty userName let scrobblesSnapshot = scrobbles |> Seq.sortByDescending (fun s -> s.ScrobbleCount) |> Seq.truncate 100 |> Seq.toList let recommendationCandidates = ResizeArray () for scrobble in scrobblesSnapshot do let otherListeners = topListeners |> Dict.findOrEmpty scrobble.Song.Id let otherListenersSnapshot = otherListeners |> Seq.filter (fun u -> u.TotalScrobbleCount >= 10_000) |> Seq.sortByDescending (fun u -> u.TotalScrobbleCount) |> Seq.truncate 20 |> Seq.toList for otherListener in otherListenersSnapshot do let otherScrobbles = topScrobbles |> Dict.findOrEmpty otherListener.UserName let otherScrobblesSnapshot = otherScrobbles |> Seq.filter (fun s -> s.Song.IsVerifiedArtist) |> Seq.sortByDescending (fun s -> s.Song.Rating) |> Seq.truncate 10 |> Seq.toList otherScrobblesSnapshot |> List.map (fun s -> s.Song) |> recommendationCandidates.AddRange let recommendations = recommendationCandidates |> Seq.sortByDescending (fun s -> s.Rating) |> Seq.truncate 200 |> Seq.toList :> IReadOnlyCollection<_> recommendations
Since this is now a pure function, there's no need to run as an asynchronous workflow. The function no longer returns a Task, and I've also dispensed with the Async suffix.
The implementation still has imperative remnants. It initializes an empty ResizeArray (AKA List<T>), and loops through nested loops to repeatedly call AddRange.
Even though the function contains local state mutation, none of it escapes the function's scope. The function is referentially transparent because it always returns the same result when given the same input, and it has no side effects.
You might still wish that it was 'more functional', which is certainly possible.
A single expression #
A curious property of expression-based languages is that you can conceivably write functions in 'one line of code'. Granted, it would often be a terribly wide line, not at all readable, a beast to maintain, and often with poor performance, so not something you'd want to alway do.
In this case, however, we can do that, although in order to stay within an 80x24 box, we break the expression over multiple lines.
let getRecommendations topScrobbles topListeners userName = // 1. Get user's own top scrobbles // 2. Get other users who listened to the same songs // 3. Get top scrobbles of those users // 4. Aggregate the songs into recommendations topScrobbles |> Dict.findOrEmpty userName |> Seq.sortByDescending (fun s -> s.ScrobbleCount) |> Seq.truncate 100 |> Seq.collect (fun scrobble -> topListeners |> Dict.findOrEmpty scrobble.Song.Id |> Seq.filter (fun u -> u.TotalScrobbleCount >= 10_000) |> Seq.sortByDescending (fun u -> u.TotalScrobbleCount) |> Seq.truncate 20 |> Seq.collect (fun otherListener -> topScrobbles |> Dict.findOrEmpty otherListener.UserName |> Seq.filter (fun s -> s.Song.IsVerifiedArtist) |> Seq.sortByDescending (fun s -> s.Song.Rating) |> Seq.truncate 10 |> Seq.map (fun s -> s.Song))) |> Seq.sortByDescending (fun s -> s.Rating) |> Seq.truncate 200 |> Seq.toList :> IReadOnlyCollection<_>
To be honest, the four lines of comments push the function definition over the edge of 24 lines of code, but without them, this variation actually does fit an 80x24 box. Even so, I'm not arguing that this is the best possible way to organize and lay out this function.
You may rightly complain that it's too dense. Perhaps you're also concerned about the arrow code tendency.
I'm not disagreeing, but at least this represents a milestone where the function is not only referentially transparent, but also implemented without local mutation. Not that that really should be the most important criterion, but once you have an entirely expression-based implementation, it's usually easier to break it up into smaller building blocks.
Composition from smaller functions #
To improve readability and maintainability, we may now extract helper functions. The first one easily suggests itself.
let private getUsersOwnTopScrobbles topScrobbles userName = topScrobbles |> Dict.findOrEmpty userName |> Seq.sortByDescending (fun s -> s.ScrobbleCount) |> Seq.truncate 100
Each of the subexpressions in the above code listing are candidates for the same kind of treatment, like this one:
let private getOtherUsersWhoListenedToTheSameSongs topListeners scrobble = topListeners |> Dict.findOrEmpty scrobble.Song.Id |> Seq.filter (fun u -> u.TotalScrobbleCount >= 10_000) |> Seq.sortByDescending (fun u -> u.TotalScrobbleCount) |> Seq.truncate 20
Notice that these helper methods are marked private so that they remain implementation details within the module that exports the getRecommendations function.
With a few more helper functions, you can now implement the getRecommendations function by composing the helpers.
let getRecommendations topScrobbles topListeners = getUsersOwnTopScrobbles topScrobbles >> Seq.collect ( getOtherUsersWhoListenedToTheSameSongs topListeners >> Seq.collect (getTopSongsOfOtherUser topScrobbles)) >> aggregateSongsIntoRecommendations
Notice that I've named each of the helper functions after the code comments that accompanied the previous incarnations of this function. If we consider code comments apologies for not properly organizing the code, we've now managed to structure it in such a way that those apologies are no longer required.
Conclusion #
If you accept the (perhaps preposterous) assumption that it's possible to fit the required data in persistent data structures, refactoring the recommendation algorithm to a pure function isn't that difficult. That's the pure part of a Recawr Sandwich. While I haven't shown the actual sandwich here, it's identical to the example shown in Song recommendations as a C# Impureim Sandwich.
I find the final incarnation of the code shown here to be quite attractive. While I've kept the helper functions private, it's always an option to promote them to public functions if you find that warranted. This could improve testability of the overall code base, albeit at the risk of increasing the surface area of the API that you have to maintain and secure.
There are always trade-offs to be considered. Even if you, eventually, find that for this particular example, the input data size is just too big to make this alternative viable, there are, in my experience, many other situations when this kind of architecture is a good solution. Even if the input size is a decent amount of megabytes, the simplification offered by an Impureim Sandwich may trump the larger memory footprint. As always, if you're concerned about performance, measure it.
Before we turn to alternative architectures, we'll survey how this variation looks in Haskell. As is generally the case in this article series, if you don't care about Haskell, you can always go back to the table of contents in the first article in the series and instead navigate to the next article that interests you.
Song recommendations proof-of-concept memory measurements
An attempt at measurement, and some results.
This is an article in a larger series about functional programming design alternatives, and a direct continuation of the previous article. The question lingering after the Impureim Sandwich proof of concept is: What are the memory requirements of front-loading all users, songs, and scrobbles?
One can guess, as I've already done, but it's safer to measure. In this article, you'll find a description of the experiment, as well as some results.
Test program #
Since I don't measure application memory profiles that often, I searched the web to learn how, and found this answer by Jon Skeet. That's a reputable source, so I'm assuming that the described approach is appropriate.
I added a new command-line executable to the source code and made this the entry point:
const int size = 100_000; static async Task Main() { var before = GC.GetTotalMemory(true); var (listeners, scrobbles) = await Populate(); var after = GC.GetTotalMemory(true); var diff = after - before; Console.WriteLine("Total memory: {0:N0}B.", diff); GC.KeepAlive(listeners); GC.KeepAlive(scrobbles); }
listeners and scrobbles are two dictionaries of data, as described in the previous article. Together, they contain the data that we measure. Both are populated by this method:
private static async Task<( IReadOnlyDictionary<int, IReadOnlyCollection<User>>, IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>>)> Populate() { var service = PopulateService(); var listeners = await service.CollectAllTopListeners(); var scrobbles = await service.CollectAllTopScrobbles(); return (listeners, scrobbles); }
The service variable is a FakeSongService object populated with randomly generated data. The CollectAllTopListeners and CollectAllTopScrobbles methods are the same as described in the previous article. When the method returns the two dictionaries, the service object goes out of scope and can be garbage-collected. When the program measures the memory load, it measures the size of the two dictionaries, but not service.
I've reused the FsCheck generators for random data generation:
private static SongService PopulateService() { var users = RecommendationsProviderTests.Gen.UserName.Sample(size); var songs = RecommendationsProviderTests.Gen.Song.Sample(size); var scrobbleGen = from user in Gen.Elements(users) from song in Gen.Elements(songs) from scrobbleCount in Gen.Choose(1, 10) select (user, song, scrobbleCount); var service = new FakeSongService(); foreach (var (user, song, scrobbleCount) in scrobbleGen.Sample(size)) service.Scrobble(user, song, scrobbleCount); return service; }
A Gen<T> object comes with a Sample method you can use to request a specified number of randomly generated values.
In order to keep the code simple, I used the size value for both the number of songs, number of users, and number of scrobbles. This probably creates too few scrobbles; a topic that requires further discussion later.
Measurements #
I ran the above program with various size values; 100,000 up to 1,000,000 in 100,000 increments, and from there up to 1,000,000 (one million) in 500,000 increments. At the higher values, it took a good ten minutes to run the program.
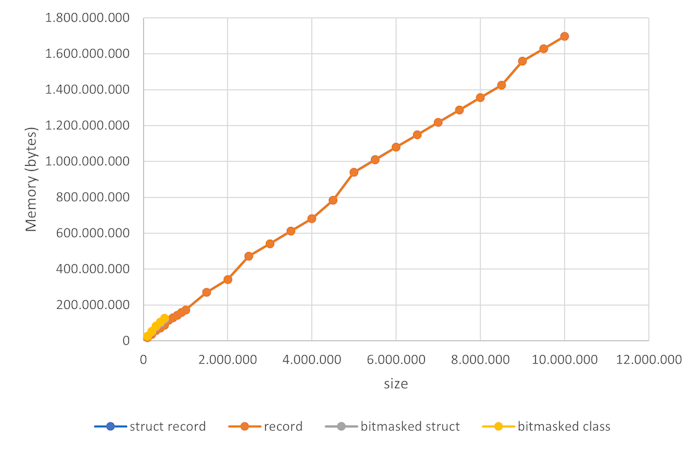
As the chart indicates, I ran the program with various data representations (more on that below). While there are four distinct data series, they overlap pairwise so perfectly that the graph doesn't show the difference. The record and struct record data series are so identical that you can't visibly see the difference. The same is true for the bitmasked class and the bitmasked struct data series, which only go to size 500,000.
There are small, but noticeable jumps from 4,500,000 to 5,000,000 and again from 8,500,000 to 9,000,000, but the overall impression is that the relationship is linear. It seems safe to conclude that the solution scales linearly with the data size.
The number of bytes per size is almost constant and averages to 178 bytes. How does that compare to my previous memory size estimates? There, I estimated a song and a scrobble to require 8 bytes each, and a user less than 32 bytes. The way the above simulation runs, it generates one song, one user, and one scrobble per size unit. Therefore, I'd expect the average memory cost per experiment size to be around 8 + 8 + 32 = 48, plus some overhead from the dictionaries.
Given that the number I measure is 178, that's 130 bytes of overhead. Honestly, that's more than I expected. I expect a dictionary to maintain an array of keys, perhaps hashed with a bucket per hash value. Perhaps, had I picked another data structure than a plain old Dictionary, it's possible that the overhead would be different. Or perhaps I just don't understand .NET's memory model, when push comes to shove.
I then tried to split the single size parameter into three that would control the number of users, songs, and scrobbles independently. Setting both the number of users and songs to ten million, I then ran a series of simulations with increasing scrobble counts.
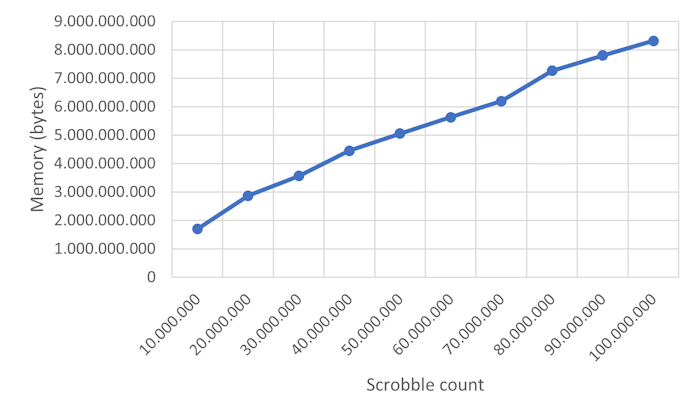
The relationship still looks linear, and at a hundred million scrobbles (and ten million users and ten million songs), the simulation uses 8.3 GB of memory.
I admit that I'm still a bit puzzled by the measurements, compared to my previous estimates. I would have expected those sizes to require about 1,2 GB, plus overhead, so the actual measurements are off by a factor of 7. Not quite an order of magnitude, but close.
Realism #
How useful are these measurements? How realistic are the experiments' parameters? Most streaming audio services report having catalogues with around 100 million songs, which is ten times more than what I've measured here. Such services may also have significantly more users than ten million, but what is going to make or break this architecture option (keeping all data in memory) is how many scrobbles users have, and how many times they listen to each song.
Even if we naively still believe that a scrobble only takes up 8 bytes, it doesn't follow automatically that 100 scrobbles take up 800 bytes. It depends on how many repeats there are. Recall how we may model a scrobble:
public sealed record Scrobble(Song Song, int ScrobbleCount);
If a user listens to the same song ten times, we don't have to create ten Scrobble objects; we can create one and set the ScrobbleCount to 10.
The memory requirement to store users' scrobbles depend on the average listening pattern. Even with millions of users, we may be able to store scrobbles in memory if users listen to relatively few songs. On the other hand, if they only listen to each song once, it's probably not going to fit in memory.
Still, we're dangerously close to the edge of what we can fit in memory. Shouldn't I just declare bankruptcy on that idea and move on?
The purpose of this overall article series is to demonstrate alternatives to the Impureim Sandwich pattern, so I'm ultimately going to do exactly that: Move on.
But not yet.
Sharding #
Some applications are truly global in nature, and when that's the case, keeping everything in memory may not be 'web scale'.
Still, I've seen more than one international company treat geographic areas as separate entities. This may be for legal reasons, or other business concerns that are unrelated to technology constraints.
As a programmer, you may think that a song recommendations service ought to be truly global. After all, more data produces more accurate results, right?
Your business owners may not think so. They may be concerned that regional music tastes may 'bleed over' market boundaries, and that this could ultimately scare customers away.
Even if you can technically prove that this isn't a relevant concern, because you can write an algorithm that takes this into account, you may get a direct order that, say, Southeast Asian scrobbles may not be used in North America, or vice verse.
It's worth investigating whether such business or legal constraints are already in place, because if they are, this may mean that you can shard the data, and that each shard still fits in memory.
You may still think that I'm trying to salvage a bad idea, but that's not my agenda. I discuss these topics because in my experience, many programmers don't consider them. Understanding the wider context of a problem may suggest solutions that you might otherwise dismiss.
But what if the business constraints change in the future? Shouldn't we be ready for that?
Yes and no. You should consider how such changes would impact the architecture. Then you discuss the advantages and disadvantages with other stakeholders.
Keep in mind that the reason to consider an Impureim Sandwich is because it's simple and easy to implement and maintain. Other alternatives may be more 'scalable', but also riskier to implement. You should involve other stakeholders in such decisions.
Song representations #
The first of the above charts draws graphs for four data series:
- struct record
- record
- bitmasked struct
- bitmasked class
These measure four different ways to model data; here more specifically a song.
My initial model of a song was a record:
public sealed record Song(int Id, bool IsVerifiedArtist, byte Rating);
Then I thought that perhaps, since the type only contains value types, it might be better to turn the above record into a record struct:
public record struct Song(int Id, bool IsVerifiedArtist, byte Rating);
It turns out that it makes no visible difference. In the chart, the two data series are so close to each other that you can't distinguish them.
Then I thought that instead of an int, a bool, and a byte, I could use a single bitmask to model all three values.
After all, I was only guessing when it came to data types anyway. It's likely that Rating is only a five-point or ten-point scale, but I still used a byte to model it. This suggests that I'm not using 96% of the data type's range. Perhaps I could use one of those redundant bits for IsVerifiedArtist, instead of an entire bool.
Taking this further, modelling the Id as an int suggests that you may have 4,294,967,295 unique songs. That's 4.3 billion songs - at least an order of magnitude more than those 100 million songs that we hear about. In reality though, most systems that use int for IDs only do so because int is CLS-compliant, and uint is not. In other words, most systems that use int for IDs most likely only use the positive half, which means there are 16 bytes to use for other purposes. Enter the bitmasked song:
public readonly struct Song { private const uint idMask = 0b0000_0111_1111_1111_1111_1111_1111_1111; private const uint isVerifiedArtistMask = 0b1000_0000_0000_0000_0000_0000_0000_0000; private const uint ratingMask = 0b0111_1000_0000_0000_0000_0000_0000_0000; private readonly uint bits; public Song(int id, bool isVerifiedArtist, byte rating) { var idBits = (uint)id & idMask; var isVerifiedArtistBits = isVerifiedArtist ? isVerifiedArtistMask : 0u; var ratingBits = ((uint)rating << 27) & ratingMask; bits = idBits | isVerifiedArtistBits | ratingBits; } public int Id => (int)(bits & idMask); public bool IsVerifiedArtist => (bits & isVerifiedArtistMask) == isVerifiedArtistMask; public byte Rating => (byte)((bits & ratingMask) >> 27); }
In this representation, I've set aside the lower 27 bits for the ID, enabling IDs to range between 0 and 134,217,727. The top bit is used for IsVerifiedArtist, and the remaining four bits for Rating.
This data structure only holds a single uint, and since I made it a struct, I thought it'd have minimal overhead.
As you can see in the above chart, that's not the case. When I run the experiment, this representation requires more memory.
Just to make sure I wasn't missing anything obvious, I tried making the bitmasked Song a class instead. No visible difference.
If you're wondering why the bitmasked data series only go to 500,000, it's because this change made the experiments glacial. It took somewhere between 12 and 24 hours to run the experiment with a size of 500,000.
For what it's worth, I don't think the slowdown is directly related to the data representation, but rather to the change I had to make to the FsCheck-based data generator:
let songParams = gen { let maxId = 0b0111_1111_1111_1111_1111_1111_1111 let! songId = Gen.choose (1, maxId) let! isVerified = ArbMap.generate ArbMap.defaults let! rating = Gen.choose (0, 10) |> Gen.map byte return songId, isVerified, rating } [<CompiledName "Song">] let song = gen { let! (id, isVerifiedArtist, rating) = songParams return Song (id, isVerifiedArtist, rating) }
I can't explain why the bitmasked representation requires more memory, but I'm increasingly having a nagging feeling that I've made a mistake somewhere. If you can spot a mistake, please let me know by leaving a comment.
Other data representations #
I also considered whether it'd make sense to represent the entire data set as a huge matrix. One could, for example, let rows represent users, and columns songs, and let each element represent the number of times a user has listened to a particular song:
| User | Song 1 | Song 2 | Song 3 | ... |
| 123 | 0 | 0 | 4 | ... |
| 456 | 2 | 0 | 4 | ... |
| ... | ||||
Let's say that you may expect some users to listen to a song more than 255 times, but probably not more than 65,535 times. Thus, you could store each play count as a ushort. Still, you would need users x songs values, so if you have 100 million songs and 10 million users, that implies 2 PB of memory. That doesn't sound useful.
On the other hand, most of those elements are going to be 0, so perhaps one could use an adjacency list instead. That is, however, essentially what an IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>> is, so we're now back where we started.
Conclusion #
This article reports on some measurements I've made of memory requirements, assuming that we keep all scrobble data in memory. While I suspect that I've made a mistake, it still seems reasonable to conclude that the song recommendations scenario is on the edge of what's possible with the Impureim Sandwich pattern.
That's okay. I'm interested in understanding the limitations of solutions.
I do think, however, that it's worth taking note of just how massive amounts of data are required before the Impureim Sandwich pattern becomes untenable.
When I describe the pattern, the most common reaction is that it doesn't scale. And, as this article has explored, it's true that it doesn't scale. But it scales much, much better than you think. You may have billions of entities in your system, and they may still fit in a few gigabytes. Don't dismiss the Impureim Sandwich before you've made a real effort to understand the memory implications of it. Your intuition is likely to work against you.
I'll round off this part of the article series by showing how the Impureim Sandwich looks in other, more functional languages.
Song recommendations as a C# Impureim Sandwich
A refactoring example.
This is an article in a larger series about functional programming design alternatives. I'm assuming that you've read the previous articles, but briefly told, I'm considering an example presented by Oleksii Holub in the article Pure-Impure Segregation Principle. The example gathers song recommendations for a user in a long-running process.
In the previous article I argued that while the memory requirements for this problem seem so vast that an Impureim Sandwich appears out of the question, it's nonetheless worthwhile to at least try it out. The refactoring isn't that difficult, and it turns out that it does simplify the code.
Enumeration API #
The data access API is a web service:
"I don't own the database, those are requests to an external API service (think Spotify API) that provides the data."
In order to read all data, we'll have to assume that there's a way to enumerate all songs and all users. With that assumption, I add the GetAllSongs and GetAllUsers methods to the SongService interface:
public interface SongService { Task<IEnumerable<Song>> GetAllSongs(); Task<IEnumerable<User>> GetAllUsers(); Task<IReadOnlyCollection<User>> GetTopListenersAsync(int songId); Task<IReadOnlyCollection<Scrobble>> GetTopScrobblesAsync(string userName); }
It is, of course, a crucial assumption, and it's possible that no such API exists. On the other hand, a REST API could expose such functionality as a paged feed. Leafing through potentially hundreds (or thousands) such pages is bound to take some time, so it's good to know that this is a background process. As I briefly mentioned in the previous article, we could imagine that we have a dedicated indexing server for this kind purpose. While we may rightly expect the initial data load to take some time (hours, even), once it's in memory, we should be able to reuse it to calculate song recommendations for all users, instead of just one user.
In the previous article I estimated that it should be possible to keep all songs in memory with less than a gigabyte. Users, without scrobbles, also take up surprisingly little space, to the degree that a million users fit in a few dozen megabytes. Even if, eventually, we may be concerned about memory, we don't have to be concerned about this part.
In any case, the addition of these two new methods doesn't break the existing example code, although I did have to implement the method in the FakeSongService class that I introduced in the article Characterising song recommendations:
public Task<IEnumerable<Song>> GetAllSongs() { return Task.FromResult<IEnumerable<Song>>(songs.Values); } public Task<IEnumerable<User>> GetAllUsers() { return Task.FromResult(users.Select(kvp => new User(kvp.Key, kvp.Value.Values.Sum()))); }
With those additions, we can load all data as the first layer (phase, really) of the sandwich.
Front-loading the data #
Loading all the data is the responsibility of this DataCollector module:
public static class DataCollector { public static async Task<IReadOnlyDictionary<int, IReadOnlyCollection<User>>> CollectAllTopListeners(this SongService songService) { var dict = new Dictionary<int, IReadOnlyCollection<User>>(); foreach (var song in await songService.GetAllSongs()) { var topListeners = await songService.GetTopListenersAsync(song.Id); dict.Add(song.Id, topListeners); } return dict; } public static async Task<IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>>> CollectAllTopScrobbles(this SongService songService) { var dict = new Dictionary<string, IReadOnlyCollection<Scrobble>>(); foreach (var user in await songService.GetAllUsers()) { var topScrobbles = await songService.GetTopScrobblesAsync(user.UserName); dict.Add(user.UserName, topScrobbles); } return dict; } }
These two methods work with any SongService implementation, so while the code base will work with FakeSongService, real 'production code' might as well use an HTTP-based implementation that pages through the implied web API.
The dictionaries returned by the methods are likely to be huge. That's a major point of this exercise. Once the change is implemented and Characterisation Tests show that it still works, it makes sense to generate data to get a sense of the memory footprint.
Table-driven methods #
Perhaps you wonder why the above CollectAllTopListeners and CollectAllTopScrobbles methods return dictionaries of exactly that shape.
Code Complete describes a programming technique called table-driven methods. The idea is to replace branching instructions such as if, else, and switch with a lookup table. The overall point, however, is that you can replace function calls with table lookups.
Consider the GetTopListenersAsync method. It takes an int as input, and returns a Task<IReadOnlyCollection<User>>
as output. If you ignore the Task, that's an IReadOnlyCollection<User>. In other words, you can exchange an int for an IReadOnlyCollection<User>.
If you have an IReadOnlyDictionary<int, IReadOnlyCollection<User>> you can also exchange an int for an IReadOnlyCollection<User>. These two APIs are functionally equivalent - although, of course, they have very different memory and run-time profiles.
The same goes for the GetTopScrobblesAsync method: It takes a string as input and returns an IReadOnlyCollection<Scrobble> as output (if you ignore the Task). An IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>> is equivalent.
To make it practical, it turns out that we also need a little helper method to deal with the case where the dictionary has no entry for a given key:
internal static IReadOnlyCollection<T> GetOrEmpty<T, TKey>( this IReadOnlyDictionary<TKey, IReadOnlyCollection<T>> dict, TKey key) { if (dict.TryGetValue(key, out var result)) return result; return Array.Empty<T>(); }
If there's no entry for a key, this function instead returns an empty array.
That should make it as easy as possible to replace calls to GetTopListenersAsync and GetTopScrobblesAsync with dictionary lookups.
Adding method parameters #
When refactoring, it's a good idea to proceed in small, controlled steps. You can see each of my micro-commits in the Git repository's refactor-to-function branch. Here, I'll give an overview.
First, I added two dictionaries as parameters to the GetRecommendationsAsync method. You may recall that the method used to look like this:
public async Task<IReadOnlyList<Song>> GetRecommendationsAsync(string userName)
After I added the two dictionaries, it looks like this:
public async Task<IReadOnlyList<Song>> GetRecommendationsAsync( string userName, IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>> topScrobbles, IReadOnlyDictionary<int, IReadOnlyCollection<User>> topListeners)
At this point, the GetRecommendationsAsync method uses neither the topScrobbles nor the topListeners parameter. Still, I consider this a distinct checkpoint that I commit to Git. As I've outlined in my book Code That Fits in Your Head, it's safest to either refactor production code while keeping test code untouched, or refactor test code without editing the production code. An API change like the current is an example of a situation where that separation is impossible. This is the reason I want to keep it small and isolated. While the change does touch both production code and test code, I'm not editing the behaviour of the System Under Test.
Tests now look like this:
[<Property>] let ``No data`` () = Gen.userName |> Arb.fromGen |> Prop.forAll <| fun userName -> task { let srvc = FakeSongService () let sut = RecommendationsProvider srvc let! topScrobbles = DataCollector.CollectAllTopScrobbles srvc let! topListeners = DataCollector.CollectAllTopListeners srvc let! actual = sut.GetRecommendationsAsync (userName, topScrobbles, topListeners) Assert.Empty actual } :> Task
The test now uses the DataCollector to front-load data into dictionaries that it then passes to GetRecommendationsAsync. Keep in mind that GetRecommendationsAsync doesn't yet use that data, but it's available to it once I make a change to that effect.
You may wish to compare this version of the No data test with the previous version shown in the article Characterising song recommendations.
Refactoring to function #
The code is now ready for refactoring from dependency injection to dependency rejection. It's even possible to do it one method call at a time, because the data in the FakeSongService is the same as the data in the two dictionaries. It's just two different representations of the same data.
Since, as described above, the dictionaries are equivalent to the SongService queries, each is easily replaced with the other. The first impure action in GetRecommendationsAsync, for example, is this one:
var scrobbles = await _songService.GetTopScrobblesAsync(userName);
The equivalent dictionary lookup enables us to change that line of code to this:
var scrobbles = topScrobbles.GetOrEmpty(userName);
Notice that the dictionary lookup is a pure function that the method need not await.
Even though the rest of GetRecommendationsAsync still queries the injected SongService, all tests pass, and I can commit this small, isolated change to Git.
Proceeding in a similar fashion enables us to eliminate the SongService queries one by one. There are only three method calls, so this can be done in three controlled steps. Once the last impure query has been replaced, the C# compiler complains about the async keyword in the declaration of the GetRecommendationsAsync method.
Not only is the async keyword no longer required, the method is no longer asynchronous. There's no reason to return a Task, and the Async method name suffix is also misleading.
public IReadOnlyList<Song> GetRecommendations( string userName, IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>> topScrobbles, IReadOnlyDictionary<int, IReadOnlyCollection<User>> topListeners)
The GetRecommendations method no longer uses the injected SongService, and since it's is the only method of the RecommendationsProvider class, we can now (r)eject the dependency.
This furthermore means that the class no longer has any class fields; we might as well make it (and the GetRecommendations function) static. Here's the final function in its entirety:
public static IReadOnlyList<Song> GetRecommendations( string userName, IReadOnlyDictionary<string, IReadOnlyCollection<Scrobble>> topScrobbles, IReadOnlyDictionary<int, IReadOnlyCollection<User>> topListeners) { // 1. Get user's own top scrobbles // 2. Get other users who listened to the same songs // 3. Get top scrobbles of those users // 4. Aggregate the songs into recommendations var scrobbles = topScrobbles.GetOrEmpty(userName); var scrobblesSnapshot = scrobbles .OrderByDescending(s => s.ScrobbleCount) .Take(100) .ToArray(); var recommendationCandidates = new List<Song>(); foreach (var scrobble in scrobblesSnapshot) { var otherListeners = topListeners.GetOrEmpty(scrobble.Song.Id); var otherListenersSnapshot = otherListeners .Where(u => u.TotalScrobbleCount >= 10_000) .OrderByDescending(u => u.TotalScrobbleCount) .Take(20) .ToArray(); foreach (var otherListener in otherListenersSnapshot) { var otherScrobbles = topScrobbles.GetOrEmpty(otherListener.UserName); var otherScrobblesSnapshot = otherScrobbles .Where(s => s.Song.IsVerifiedArtist) .OrderByDescending(s => s.Song.Rating) .Take(10) .ToArray(); recommendationCandidates.AddRange( otherScrobblesSnapshot.Select(s => s.Song) ); } } var recommendations = recommendationCandidates .OrderByDescending(s => s.Rating) .Take(200) .ToArray(); return recommendations; }
The overall structure is similar to the original version. Now that the code is simpler (because there's no longer any asynchrony) you could keep refactoring. With this C# code example, I'm going to stop here, but when I port it to F# I'm going to refactor more aggressively.
Sandwich #
One point of the whole exercise is to demonstrate how to refactor to an Impureim Sandwich. The GetRecommendations method shown above constitutes the pure filling of the sandwich, but what does the entire sandwich look like?
In this code base, the sandwiches only exist as unit tests, the simplest of which is still the No data test:
[<Property>] let ``No data`` () = Gen.userName |> Arb.fromGen |> Prop.forAll <| fun user -> task { let srvc = FakeSongService () let! topScrobbles = DataCollector.CollectAllTopScrobbles srvc let! topListeners = DataCollector.CollectAllTopListeners srvc let actual = RecommendationsProvider.GetRecommendations (user, topScrobbles, topListeners) Assert.Empty actual } :> Task
In the above code snippet, I've coloured in the relevant part of the test. I admit that it's a stretch to colour the last line red, since Assert.Empty is, at least, deterministic. One could argue that since it throws an exception on failure, it's not strictly free of side effects, but that's really a weak argument. It would be easy to refactor assertions to pure functions.
Instead, you may consider the bottom layer of the sandwich as a placeholder where something impure might happen. The background service that updates the song recommendations may, for example, save the result as a (CQRS-style) materialised view.
The above test snippet, then, is more of a sketch of how the Impureim Sandwich may look: First, front-load data using the DataCollector methods; second, call GetRecommendations; third, do something with the result.
Conclusion #
The changes demonstrated in this article serve two purposes. One is to show how to refactor an impure action to a pure function, pursuing the notion of an Impureim Sandwich. The second is to evaluate a proof-of-concept: If we do, indeed, front-load all of the data, is it realistic that all data fits in RAM?
We have yet to address that question, but since the present article is already substantial, I'll address that in a separate article.
Next: Song recommendations proof-of-concept memory measurements.Song recommendations as an Impureim Sandwich
Does your data fit in RAM?
This article is part of a series on functional programming design alternatives. In a previous article you saw how to add enough Characterisation Tests to capture the intended behaviour of the example song recommendations system originally presented by Oleksii Holub in the article Pure-Impure Segregation Principle.
Problem statement #
After showing how one problem can be refactored to pure functions, Oleksii Holub writes:
"Although very useful, the type of "lossless" refactoring shown earlier only works if the data required by the function can be easily encapsulated within its input parameters. Unfortunately, this is not always the case.
"Often a function may need to dynamically resolve data from an external API or a database, with no way of knowing about it beforehand. This typically results in an implementation where pure and impure concerns are interleaved with each other, creating a tightly coupled cohesive structure."
The article then proceeds to present the song recommendations example. It's a single C# method that queries a data store or third-party service to recommend songs. I'm imagining that it queries a third-party web service that contains usages data for a system like Spotify.
"The above algorithm works by retrieving the user's most listened songs, finding other people who have also listened to the same titles, and then extracting their top songs as well. Those songs are then aggregated into a list of recommendations and returned to the caller.
"It's quite clear that this function would benefit greatly from being pure, seeing how much business logic is encapsulated within it. Unfortunately, the technique we relied upon earlier won't work here.
"In order to fully isolate
GetRecommendationsAsync(...)from its impure dependencies, we would have to somehow supply the function with an entire list of songs, users, and their scrobbles upfront. If we assume that we're dealing with data on millions of users, it's obvious that this would be completely impractical and likely even impossible."
It does, indeed, sound impractical.
Data sizes #
Can you, however, trust your intuition? Research suggests that the human brain is ill-equipped to think about randomness and probabilities, and I've observed something similar when it comes to data sizes.

In the real world, a million of anything countable is an almost incomprehensible amount, so it's no wonder if our intuition fails us. A million records sounds like a lot, but if it's only a few integers, is it really that bad?
Many systems use 32-bit integers for various IDs. A million IDs, then, is 32 million bits, or approximately 4 MB. As I'm writing this, the smallest Azure instance (Free F1) has 1 GB of memory, and while the OS takes a big bite out of that, 4 MB is nothing.
The song recommendations problem implies larger memory pressure. It may not fit on every machine, but it's worth considering if, after all, it doesn't fit in RAM.
My real-life experience with developing streaming services #
It just so happens that I have professional experience developing REST APIs for a white-label audio streaming service. Back in the early 2010s I helped design and implement the company's online music catalogue, user system, and a few other services. The catalogue is particularly interesting in this regard, since it only changed nightly, and we were planning on relying on HTTP for caching.
I vividly recall a meeting we had with the IT operations specialist responsible for the new catalogue service. We explained that we'd set HTTP cache timeouts to 6 hours, and asked if he'd be able to set up a reverse proxy so that we didn't have to implement caching in our code base.
He asked how much cache space we needed.
We knew the size of a typical HTTP response, and the number of tracks, artists, and albums in the system, so after a back-of-the-envelope calculation, we told him: 18 GB.
He just shrugged and said "OK".
In 2012 I though that 18 GB was a fair amount of data (I actually still think that). Even so, the operations team had plenty of servers with that capacity.
Later, I did more work for that company, but most of it is less relevant to the song recommendations example. What does turn out to be relevant to the topic is something I learned the first few days of my engagement.
Early on, before I was involved, the company needed a recommendation system, but hadn't been able to find any off-the-shelf component. This was in the early 2000s and before Solr, but after Lucene. I'm not aware of all the forces that affected my then future client, but in the end, they decided to write their own search and recommendations engine.
Essentially, during the night a beefy server would read all relevant data from the database, crunch it, create data structures, and keep all data in memory. Like the reverse proxy, it required a server with more RAM than a normal pizza box, but not prohibitively so.
Costs #
Consider the cost of hardware, compared to developer time. A few specialised servers may set your organisation back a few thousand of dollars/pounds/euros. That's an amount you can easily burn through in salary if the code is too complicated, or has too many bugs.
You may argue that if you already have programmers on staff, they don't cost extra, but a too-complicated code base is still going to slow them down. Thus, the wrong software design could incur an opportunity cost greater than the cost of a server.
One of many reasons I'm interested in functional programming (FP) is its potential to make code bases simpler. The Impureim Sandwich is a wonderfully simple design, so it's worth pursuing; not only for some FP ideal, but because of its simplifying potential.
Intuition may tell us that the song recommendations scenario is prohibitively big, and therefore, an Impureim Sandwich is out of the question. As this overall article series explores, it's not the only alternative, but given its advantages, its worth giving it a second chance.
Analysis #
The GetRecommendationsAsync method from the example makes a lot of external calls, with its nested loops. The method uses the first call to GetTopScrobblesAsync to produce the scrobblesSnapshot variable, which is capped at 100 objects. If we assume that this method call returns at least 100 objects, the outer foreach loop will make 100 calls to GetTopListenersAsync.
If we again assume that each of these return enough data, the inner foreach loop will make 20 calls to GetTopScrobblesAsync, for each object in the outer loop. That's 2,000 external calls, plus the 100 calls in the outer loop, plus the initial call to GetTopScrobblesAsync, for a total of 2,101.
When I first saw the example, I didn't know much about the overall context. I didn't know if these impure actions were database queries or web service calls, so I asked Oleksii Holub.
It turns out that it's all web service calls, and as I interpret the response, GetRecommendationsAsync is being invoked from a background maintenance process.
"It takes around 10 min in total while maintaining it."
That's good to know, because if we're going to consider an Impureim Sandwich, it implies reading gigabytes of data in the first phase. That's going to take some time, but if this is a background process, we do have time.
Memory estimates #
One thing is to load an entire song catalogue into memory. That's what required 18 GB in 2012. Another thing is to load all scrobbles; i.e. statistics about plays. Fortunately, in order to produce song recommendations, we only need IDs. Consider again the data structures from the previous article:
public sealed record Song(int Id, bool IsVerifiedArtist, byte Rating); public sealed record Scrobble(Song Song, int ScrobbleCount); public sealed record User(string UserName, int TotalScrobbleCount);
Apart from the UserName all values are small predictable values: int, byte, and bool, and while a string may be arbitrarily long, we can make a guess at the average size of a user name. In the previous article, I assumed that the user name would be an alphanumeric string between one and twenty characters.
How many songs might a system contain? Some numbers thrown around for a system like Spotify suggest a number on the order of 100 million. With an int, a bool, and a byte, we can estimate that a song requires 6 bytes, plus some overhead. Let's guess 8 bytes. A 100 million songs would then require 800 million bytes, or around 800 MB. That eliminates the smallest cloud instances, but is in itself easily within reach for all modern computers. Your phone has more memory than that.
How about scrobbles? While I don't use Spotify, I do scrobble plays to Last.fm. At the moment I have around 114,000 scrobbles, and while I don't listen to music as much as I used to when I was younger, I have, on the other hand, been at it for a long time: Since 2007. If we assume that each user has 200,000 scrobbles, and a scrobble requires 8 bytes, that's 1,600,000 bytes, or 1.6 MB. Practically nothing.
The size of a User object depends on how long the user name is, but will probably, on average, be less than 32 bytes. Compared to the user's scrobbles, we can ignore the memory pressure of the user object itself.
As the number of users grow, it will dominate the memory requirements for the catalogue. How many users should we assume?
A million is probably too few, but for a frame of reference, that would require 1,6 TB. This is where it starts to sound unfeasible to keep all data in RAM. Even though servers with that much RAM exist, they're so expensive (still) that the above cost consideration no longer applies.
Still, there are some naive assumptions above. Instead of storing each scrobble in a separate Scrobble object, you could store repeated plays as a single object with the appropriate ScrobbleCount value. If you've listened to the same song 50 times, it doesn't require 400 bytes of storage, but only 8 bytes. That is, after all, orders of magnitude less.
In the end, back-of-the-envelope calculations are fine, but measurements are better. It might be worthwhile to develop a proof of concept and measure how much memory it requires.
In three articles, I'll explore how a song recommendations Impureim Sandwich looks in various constellations:
- Song recommendations as a C# Impureim Sandwich
- Song recommendations as an F# Impureim Sandwich
- Song recommendations as a Haskell Impureim Sandwich
In the end, it may turn out that for this particular system, an Impureim Sandwich truly is unfeasible. Keep in mind, though, that the purpose of this article series is to demonstrate alternative designs. The song recommendations problem is just a placeholder example. Perhaps you have another system where, intuitively, an Impureim Sandwich sounds impossible, but once you run the numbers, it might actually be not only possible, but desirable.
Conclusion #
Modern computers have so vast storage capacities that intuition often fails us. We may think that billions of data points sounds like something that can't possibly fit in RAM. When you run the numbers, however, it may turn out that the required data fits on a normal server.
If so, an Impureim Sandwich may still be an option. Load data into memory, pass it as argument to a pure function, and handle the return value.
The song recommendations scenario is interesting because an Impureim Sandwich seems to be pushing the envelope. It probably is impractical, but still worth a proof of concept. On the other hand, if it's impractical, it's worthwhile to also explore alternatives. Later articles will do that, but first, if you're interested, the next articles look at the proofs of concept in three languages.

Comments
Unfortunately I haven't read your book, so perhaps this question is already answered there: how would a transaction prevent a race condition? I would have expected to solve it using optimistic concurrency control.
My other point is regarding artificial delays. How is that deterministic? If you're injecting decorators to take advantage of seams in the code, and you know the number of operations, then you don't need delays at all. To highlight the race condition you need to ensure two requests have read the same data concurrently. After that you can allow the writes, expecting one to succeed and the other to fail. You could use a synchronization primitive, such as CountdownEvent. Initialize it with a count of 2 to represent your concurrent requests. Repository.ReadReservations() would call Signal() to decrement it after fetching from the database. Repository.Create() would call Wait() to ensure both reads had been made before writing to the database.
Nick, thank you for writing. Regarding the transaction, as the above
TryCreatesnippet shows, it wraps both the read and the write operation, and since the default isolation level isSerializable,As to the second point, I don't think I've claimed that inducing an artificial delay as a Decorator is deterministic. To the contrary, I explicitly discussed how this is only near-deterministic.
That said, you're correct that there's an even better way, and I have another article queued up that takes an approach similar to the one that you describe.