Monads by Mark Seemann

A monad is a common abstraction. While typically associated with Haskell, monads also exist in C# and other languages.

This article series is part of a larger series of articles about functors, applicatives, and other mappable containers.

If you understand what a functor is, it should be easy to grasp the idea of a monad. It's a functor you can flatten.

There's a little more to it than that, and you also need to learn what I mean by flatten, but that's the essence of it.

In this article-series-within-an-article series, I'll explain this disproportionally dreaded concept, giving you plenty of examples as well as a more formal definition. Examples will be in both C#, F#, and Haskell, although I plan to emphasise C#. I expect that there's little need of explaining monads to people already familiar with Haskell. I'll show examples as separate articles in this series. These articles are mostly aimed at object-oriented programmers curious about monads.

• Kleisli composition
• Monad laws
• The List monad
• The Maybe monad
• An Either monad
• The Identity monad
• The Lazy monad
• Asynchronous monads
• The State monad
• The Reader monad
• The IO monad
• Test Data Generator monad

This list is far from exhaustive; more monads exist.

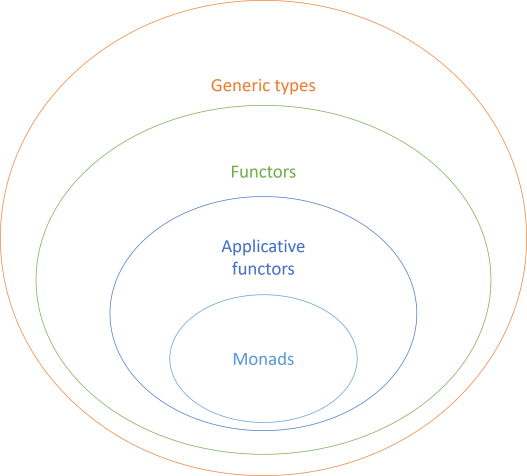
All monads are applicative functors, but not all applicative functors are monads. As the set diagram reiterates, applicative functors are functors, but again: not necessarily the other way around.

Flattening #

A monad is a functor you can flatten. What do I mean by flatten?

As in the article that introduces functors, imagine that you have some Functor<T> container. More concretely, this could be IEnumerable<T>, Maybe<T>, Task<T>, etcetera.

When working with functors, you sometimes run into situations where the containers nest inside each other. Instead of a Functor<decimal>, you may find yourself with a Functor<Functor<decimal>>, or maybe even an object that's thrice or quadruply nested.

If you can flatten such nested functor objects to just Functor<T>, then that functor also forms a monad.

In C#, you need a method with this kind of signature:

public static Functor<T> Flatten<T>(this Functor<Functor<T>> source)

Notice that this method takes a Functor<Functor<T>> as input and returns a Functor<T> as output. I'm not showing the actual implementation, since Functor<T> is really just a 'pretend' functor (and monad). In the example articles that follow, you'll see actual implementation code.

With Flatten you can write code like this:

Functor<decimal> dest = source.Flatten();

Here, source is a Functor<Functor<decimal>>.

This function also exists in Haskell, although there, it's called join:

join :: Monad m => m (m a) -> m a

For any Monad m you can flatten or join a nested monad m (m a) to a 'normal' monad m a.

This is the same function as Flatten, so in C# we could define an alias like this:

public static Functor<T> Join<T>(this Functor<Functor<T>> source)
{
    return source.Flatten();
}

Usually, however, you don't see monads introduced via join or Flatten. It's a shame, really, because it's the most straightforward description.

Bind #

Most languages that come with a notion of monads define them via a function colloquially referred to as monadic bind or just bind. In C# it's called SelectMany, F# computation expressions call it Bind, and Scala calls it flatMap (with a vestige of the concept of flattening). Haskell just defines it as an operator:

(>>=) :: Monad m => m a -> (a -> m b) -> m b

When talking about it, I tend to call the >>= operator bind.

Translated to C# it has this kind of signature:

public static Functor<TResult> SelectMany<T, TResult>(
    this Functor<T> source,
    Func<T, Functor<TResult>> selector)

It looks almost like a functor's Select method (AKA map or fmap function). The difference is that this selector returns a functor value (Functor<TResult>) rather than a 'naked' TResult value.

When a Flatten (or Join) method already exists, you can always implement SelectMany like this:

public static Functor<TResult> SelectMany<T, TResult>(
    this Functor<T> source,
    Func<T, Functor<TResult>> selector)
{
    Functor<Functor<TResult>> nest = source.Select(selector);
    return nest.Flatten();
}

I've split the implementation over two lines of code to make it clearer what's going on. That's also the reason I've used an explicit type declaration rather than var.

The Select method exists because the type is already a functor. When you call Select with selector you get a Functor<Functor<TResult>> because selector itself returns a Functor<TResult>. That's a nested functor, which you can Flatten.

You can use SelectMany like this:

Functor<TimeSpan> source = Functor.Return(TimeSpan.FromMinutes(32));
Functor<double> dest = source.SelectMany(x => Functor.Return(x.TotalSeconds + 192));

The lambda expression returns a Functor<double>. Had you called Select with this lambda expression, the result would have been a nested functor. SelectMany, however, flattens while it maps (it flatMaps). (This example is rather inane, since it would be simpler to use Select and omit wrapping the output of the lambda in the functor. The later articles in this series will show some more compelling examples.)

If you already have Flatten (or Join) you can always implement SelectMany like this. Usually, however, languages use monadic bind (e.g. SelectMany) as the foundation. Both C#, Haskell, and F# do that. In that case, it's also possible to go the other way and implement Flatten with SelectMany. You'll see examples of that in the subsequent articles.

Syntactic sugar #

Several languages understand monads well enough to provide some degree of syntactic sugar. While you can always use SelectMany in C# by simply calling the method, there are situations where that becomes awkward. The same is true with bind functions in F# and >>= in Haskell.

In C# you can use query syntax:

Functor<DateTime> fdt = Functor.Return(new DateTime(2001, 8, 3));
Functor<TimeSpan> fts = Functor.Return(TimeSpan.FromDays(4));
 
Functor<DateTime> dest = from dt in fdt
                         from ts in fts
                         select dt - ts;

In order to support more than a single from expression, however, you must supply a special SelectMany overload, or the code doesn't compile:

public static Functor<TResult> SelectMany<T, U, TResult>(
    this Functor<T> source,
    Func<T, Functor<U>> k,
    Func<T, U, TResult> s)
{
    return source.SelectMany(x => k(x).Select(y => s(x, y)));
}

This is an odd quirk of C# that I've yet to encounter in other languages, and I consider it ceremony that I have to perform to satiate the C# compiler. It's not part of the concept of what a monad is. As far as I can tell, you can always implement it like shown here.

Haskell's syntactic sugar is called do notation and works for all monads:

example :: (Monad m, Num a) => m a -> m a -> m a
example fdt fts = do
  dt <- fdt
  ts <- fts
  return $ dt - ts

In F#, computation expressions drive syntactic sugar, but still based (among other things) on the concept of a monad:

let example (fdt : Monad<DateTime>) (fts : Monad<TimeSpan>) = monad {
    let! dt = fdt
    let! ts = fts
    return dt - ts }

Here, we again have to pretend that a Monad<'a> type exists, with a companion monad computation expression.

Return #

The ability to flatten nested functors is the essence of what a monad is. There are, however, also some formal requirements. As is the case with functors, there are laws that a monad should obey. I'll dedicate a separate article for those, so we'll skip them for now.

Another requirement is that in addition to SelectMany/bind/flatMap/>>= a monad must also provide a method to 'elevate' a value to the monad. This function is usually called return. It should have a type like this:

public static Functor<T> Return<T>(T x)

You can see it in use in the above code snippet, and with the relevant parts repeated here:

Functor<DateTime> fdt = Functor.Return(new DateTime(2001, 8, 3));
Functor<TimeSpan> fts = Functor.Return(TimeSpan.FromDays(4));

This code example lifts the value DateTime(2001, 8, 3) to a Functor<DateTime> value, and the value TimeSpan.FromDays(4) to a Functor<TimeSpan> value.

Usually, in a language like C# a concrete monad type may either afford a constructor or factory method for this purpose. You'll see examples in the articles that give specific monad examples.

Conclusion #

A monad is a functor you can flatten. That's the simplest way I can put it.

In this article you learned what flattening means. You also learned that a monad must obey some laws and have a return function. The essence, however, is flattening. The laws just ensure that the flattening is well-behaved.

It may not yet be clear to you why some functors would need flattening in the first place, but subsequent articles will show examples.

The word monad has its own mystique in software development culture. If you've ever encountered some abstruse nomenclature about monads, then try to forget about it. The concept is really not hard to grasp, and it usually clicks once you've seen enough examples, and perhaps done some exercises.

Next: Kleisli composition.

Comments

• ← Previous
• Archive
• Next →