Unit isomorphisms by Mark Seemann
The C# and Java keyword 'void' is isomorphic to a data type called 'unit'.
This article is part of a series of articles about software design isomorphisms.
Many programming languages, such as C# and Java, distinguish between methods that return something, and methods that don't return anything. In C# and Java, a method must be declared with a return type, but if it doesn't return anything, you can use the special keyword void to indicate that this is the case:
public void Foo(int bar)
This is a C# example, but it would look similar (isomorphic?) in Java.
Two kinds of methods #
In C# and Java, void isn't a type, but a keyword. This means that there are two distinct types of methods:
- Methods that return something
- Methods that return nothing
public Foo Bar(Baz baz, Qux qux)
On the other hand, methods that return nothing must use the special void keyword:
public void Bar(Baz baz, Qux qux)
If you want to generalise, you can use generics like this:
public T Foo<T, T1, T2>(T1 x, T2 y)
Such a method could return anything, but, surprisingly, not nothing. In C# and Java, nothing is special. You can't generalise all methods to a common set. Even with generics, you must model methods that return nothing in a different way:
public void Foo<T1, T2>(T1 x, T2 y)
In C#, for example, this leads to the distinction between Func and Action. You can't reconcile these two fundamentally distinct types of methods into one.
Visual Basic .NET makes the same distinction, but uses the keywords Sub and Function instead of void.
Sometimes, particularly when writing code with generics, this dichotomy is really annoying. Wouldn't it be nice to be able to generalise all methods?
Unit #
While I don't recall the source, I've read somewhere the suggestion that the keyword void was chosen to go with null, because null and void is an English (legal) idiom. That choice is, however, unfortunate.
In category theory, the term void denotes a type or set with no inhabitants (e.g. an empty set). That sounds like the same concept. The problem, from a programming perspective, is that if you have a (static) type with no inhabitants, you can't create an instance of it. See Bartosz Milewski's article Types and Functions for a great explanation and more details.
Functional programming languages like F# and Haskell instead model nothing by a type called unit (often rendered as empty brackets: ()). This type is a type with exactly one inhabitant, a bit like a Singleton, but with the extra restriction that the inhabitant carries no information. It simply is.
It may sound strange and counter-intuitive that a singleton value represents nothing, but it turns out that this is, indeed, isomorphic to C# or Java's void.
This is admirably illustrated by F#, which consistently uses unit instead of void. F# is a multi-paradigmatic language, so you can write classes with methods as well as functions:
member this.Bar (x : int) = ()
This Bar method has the return type unit. When you compile F# code, it becomes Intermediate Language, which you can decompile into C#. If you do that, the above F# code becomes:
public void Bar(int x)
The inverse translation works as well. When you use F#'s interoperability features to interact with objects written in C# or Visual Basic, the F# compiler interprets void methods as if they return unit. For example, calling GC.Collect returns unit in F#, although C# sees it as 'returning' void:
> GC.Collect 0;; val it : unit = ()
F#'s unit is isomorphic to C#'s void keyword, but apart from that, there's nothing special about it. It's a value like any other, and can be used in generically typed functions, like the built-in id function:
> id 42;; val it : int = 42 > id "foo";; val it : string = "foo" > id ();; val it : unit = ()
The built-in function id simply returns its input argument. It has the type 'a -> 'a, and as the above F# Interactive session demonstrates, you can call it with unit as well as with int, string, and so on.
Monoid #
Unit, by the way, forms a monoid. This is most evident in Haskell, where this is encoded into the type. In general, a monoid is a binary operation, and not a type, but what could the combination of two () (unit) values be, other than ()?
λ> mempty :: () () λ> mappend () () ()
In fact, the above (rhetorical) question is imprecise, since there aren't two unit values. There's only one, but used twice.
Since only a single unit value exists, any binary operation is automatically associative, because, after all, it can only return unit. Likewise, unit is the identity (mempty) for the operation, because it doesn't change the output. Thus, the monoid laws hold, and unit forms a monoid.
This result is interesting when you start to think about composition, because a monoid can always be used to reduce (aggregate) multiple values to a single value. With this result, and unit isomorphism, we've already explained why Commands are composable.
Summary #
Since unit is a type only inhabited by a single value, people (including me) often use the word unit about both the type and its only value. Normally, the context surrounding such use is enough to dispel any ambiguity.
Unit is isomorphic to C# or Java void. This is an important result, because if we're to study software design and code structure, we don't have to deal with two distinct cases (methods that return nothing, and methods that return something). Instead, we can ignore methods that return nothing, because they can instead be modelled as methods that return unit.
The reason I've titled this article in the plural is that you could view the isomorphism between F# unit and C# void as a different isomorphism than the one between C# and Java void. Add Haskell's () (unit) type and Visual Basic's Sub keyword to the mix, and it should be clear that there are many translations to the category theory concept of Unit.
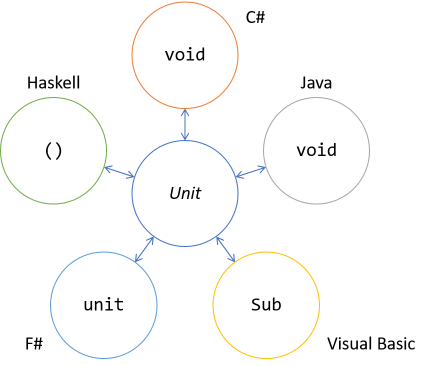
Unit isomorphism is an example of an interlingual isomorphism, in the sense that C# void maps to F# unit, and vice versa. In the next example, you'll see an isomorphism that mostly stays within a single language, although a translation between languages is also pertinent.
Next: Function isomorphisms.
