Angular addition monoid by Mark Seemann
Geometric angles can be added together. Angular addition forms a monoid.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
In geometry, an angle is a measure of how two crossing lines relate to each other. In mathematics, angles are usually represented in radians, but in daily use, they're mostly measured in degrees between 0 and 360.
Angular addition #
You can always draw an angle within a circle. Here's a 45° angle:

If you add another 90° angle to that, you get a 135° angle:

What do you get if you add 90° to 315°?

Well, you get 45°, of course!
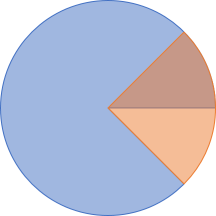
There's only 360° in a circle, so overflow is handled, in this case, by subtracting 360°. In general, however, angular addition is nothing but modulo 360 addition.
Angle struct #
You can model a geometric angle as a struct. Here's a simple example:
public struct Angle { private readonly decimal degrees; private Angle(decimal degrees) { this.degrees = degrees % 360m; if (this.degrees < 0) this.degrees += 360m; } public static Angle FromDegrees(decimal degrees) { return new Angle(degrees); } public static Angle FromRadians(double radians) { return new Angle((decimal)((180D / Math.PI) * radians)); } public Angle Add(Angle other) { return new Angle(this.degrees + other.degrees); } public readonly static Angle Identity = new Angle(0); public override bool Equals(object obj) { if (obj is Angle) return ((Angle)obj).degrees == this.degrees; return base.Equals(obj); } public override int GetHashCode() { return this.degrees.GetHashCode(); } public static bool operator ==(Angle x, Angle y) { return x.Equals(y); } public static bool operator !=(Angle x, Angle y) { return !x.Equals(y); } }
Notice the Add method, which is a binary operation; it's an instance method on Angle, takes another Angle as input, and returns an Angle value.
Associativity #
Not only is Add a binary operation; it's also associative. Here's an example:
var x = Angle.FromDegrees(135); var y = Angle.FromDegrees(180); var z = Angle.FromDegrees(300); var left = x.Add(y).Add(z); var right = x.Add(y.Add(z));
Notice that left first evaluates x.Add(y), which is 315°; then it adds 300°, which is 615°, but normalises to 255°. On the other hand, right first evaluates y.Add(z), which is 480°, but normalises to 120°. It then adds those 120° to x, for a final result of 255°. Since left and right are both 255°, this illustrates that Add is associative.
Obviously, this is only a single example, so it's no proof. While still not a proof, you can demonstrate the associativity property with more confidence by writing a property-based test. Here's one using FsCheck and xUnit.net:
[Property(QuietOnSuccess = true)] public void AddIsAssociative(Angle x, Angle y, Angle z) { Assert.Equal( x.Add(y).Add(z), x.Add(y.Add(z))); }
By default, FsCheck generates 100 test cases, but even when I experimentally change the configuration to run 100,000 test cases, they all pass. For full disclosure, however, I'll admit that I defined the data generators to only use NormalFloat for the radian values, and only decimal values with up to 10 decimal places. If you try to use entirely unconstrained floating points, you'll see test failures caused by rounding errors.
Changing the data generator is one way to address rounding errors. Another way is to add a bit of fuzzy tolerance to the assertion. In any case, though, the Add operation is associative. That rounding errors occur is an implementation detail of floating point arithmetic.
Identity #
The above code listing defines a value called Identity:
public readonly static Angle Identity = new Angle(0);
As an Angle, I want my Add and Identity members to obey the monoid laws so that I can be a monoid.
As an example, both left and right should be true in the following:
var x = Angle.FromDegrees(370); var left = x == Angle.Identity.Add(x); var right = x == x.Add(Angle.Identity);
That does, indeed, turn out to be the case.
Again, you can generalise using FsCheck:
[Property(QuietOnSuccess = true)] public void AddHasIdentity(Angle x) { Assert.Equal(x, Angle.Identity.Add(x)); Assert.Equal(x, x.Add(Angle.Identity)); }
Once more, a reservation identical to the one given above must be given when it comes to floating point arithmetic.
Conclusion #
The Add method is an associative, binary operation with identity; it's a monoid.
As far as I can tell, any modulo-based addition is a monoid, but while, say, modulo 37 addition probably doesn't have any practical application, modulo 360 addition does, because it's how you do angular addition.
