Devil's advocate by Mark Seemann

How do you know when you have enough test cases. The Devil's Advocate technique can help you decide.

When I review unit tests, I often utilise a technique I call Devil's Advocate. I do the same whenever I consider if I have a sufficient number of test cases. The first time I explicitly named the technique was, I think, in my Outside-in TDD Pluralsight course, in which I also discuss the so-called Gollum style variation. I don't think, however, that I've ever written an article explicitly about this topic. The current text attempts to rectify that omission.

Coverage #

Programmers new to unit testing often struggle with identifying useful test cases. I sometimes see people writing redundant unit tests, while, on the other hand, forgetting to add important test cases. How do you know which test cases to add, and how do you know when you've added enough?

I may return to the first question in another article, but in this, I wish to address the second question. How do you know that you have a sufficient set of test cases?

You may think that this is a question of turning on code coverage. Surely, if you have 100% code coverage, that's sufficient?

It's not. Consider this simple class:

public class MaîtreD
{
    public MaîtreD(int capacity)
    {
        Capacity = capacity;
    }
 
    public int Capacity { get; }
 
    public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
    {
        var reservedSeats = reservations.Sum(r => r.Quantity);
 
        if (Capacity < reservedSeats + reservation.Quantity)
            return false;
 
        return true;
    }
}

This class implements the (simplified) decision logic for an online restaurant reservation system. The CanAccept method has a cyclomatic complexity of 2, so it should be easy to cover with a pair of unit tests:

[Fact]
public void CanAcceptWithNoPriorReservations()
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 4
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(new Reservation[0], reservation);
 
    Assert.True(actual);
}
 
[Fact]
public void CanAcceptOnInsufficientCapacity()
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 4
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = 7 } },
        reservation);
 
    Assert.False(actual);
}

These two tests together completely cover the CanAccept method:

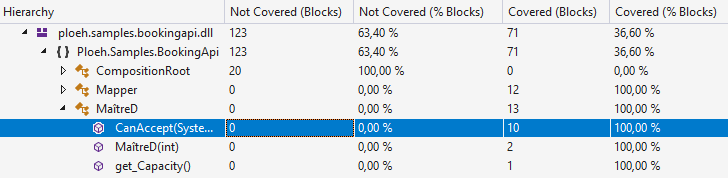
You'd think that this is a sufficient number of test cases of the method, then.

As the Devil reads the Bible #

In Scandinavia we have an idiom that Kent Beck (who's worked with Norwegian companies) has also encountered:

"TIL: "like the devil reads the Bible"--meaning someone who carefully reads a book to subvert its intent"

If you think of a unit test suite as an executable specification, you may consider if you can follow the specification to the letter while intentionally introduce a defect. You can easily do that with the above CanAccept method:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Sum(r => r.Quantity);
 
    if (Capacity <= reservedSeats + reservation.Quantity)
        return false;
 
    return true;
}

This still passes both tests, and still has a code coverage of 100%, yet it's 'obviously' wrong.

Can you spot the difference?

Instead of a less-than comparison, it now uses a less-than-or-equal comparison. You could easily, inadvertently, make such a mistake while programming. It belongs in the category of off-by-one errors, which is one of the most common type of bugs.

This is, in a nutshell, the Devil's Advocate technique. The intent isn't to break the software by sneaking in defects, but to explore how effectively the test suite detects bugs. In the current (simplified) example, the effectiveness of the test suite isn't impressive.

Add test cases #

The problem introduced by the Devil's Advocate is an edge case. If the reservation under consideration fits the restaurant's remaining capacity, but entirely consumes it, the MaîtreD class should still accept it. Currently, however, it doesn't.

It'd seem that the obvious solution is to 'fix' the unit test:

[Fact]
public void CanAcceptWithNoPriorReservations()
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 10
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(new Reservation[0], reservation);
 
    Assert.True(actual);
}

Changing the requested Quantity to 10 does, indeed, cause the test to fail.

Beyond mutation testing #

Until this point, you may think that the Devil's Advocate just looks like an ad-hoc, informally-specified, error-prone, manual version of half of mutation testing. So far, the change I made above could also have been made during mutation testing.

What I sometimes do with the Devil's Advocate technique is to experiment with other, less heuristically driven changes. For instance, based on my knowledge of the existing test cases, it's not too difficult to come up with this change:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Sum(r => r.Quantity);
 
    if (reservation.Quantity != 10)
        return false;
 
    return true;
}

That's an even simpler implementation than the original, but obviously wrong.

This should prompt you to add at least one other test case:

[Theory]
[InlineData( 4)]
[InlineData(10)]
public void CanAcceptWithNoPriorReservations(int quantity)
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(new Reservation[0], reservation);
 
    Assert.True(actual);
}

Notice that I converted the test to a parametrised test. This breaks the Devil's latest attempt, while the original implementation passes all tests.

The Devil, not to be outdone, now switches tactics and goes after the reservations instead:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    return !reservations.Any();
}

This still passes all tests, including the new test case. This indicates that you'll need to add at least one test case with existing reservations, but where there's still enough capacity to accept another reservation:

[Fact]
public void CanAcceptWithOnePriorReservation()
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 4
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = 4 } },
        reservation);
 
    Assert.True(actual);
}

This new test fails, prompting you to correct the implementation of CanAccept. The Devil, however, can do this:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Sum(r => r.Quantity);
    return reservedSeats != 7;
}

This is still not correct, but passes all tests. It does, however, look like you're getting closer to a proper implementation.

Reverse Transformation Priority Premise #

If you find this process oddly familiar, it's because it resembles the Transformation Priority Premise (TPP), just reversed.

“As the tests get more specific, the code gets more generic.”

When I test-drive code, I often try to follow the TPP, but when I review code with tests, the code and the tests are already in place, and it's my task to assess both.

Applying the Devil's Advocate review technique to CanAccept, it seems as though I'm getting closer to a proper implementation. It does, however, require more tests. As your next move you may, for instance, consider parametrising the test case that verifies what happens when capacity is insufficient:

[Theory]
[InlineData(7)]
[InlineData(8)]
public void CanAcceptOnInsufficientCapacity(int reservedSeats)
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 4
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = reservedSeats } },
        reservation);
 
    Assert.False(actual);
}

That doesn't help much, though, because this passes all tests:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Sum(r => r.Quantity);
    return reservedSeats < 7;
}

Compared to the initial, 'desired' implementation, there's at least two issues with this code:

• It doesn't consider reservation.Quantity
• It doesn't take into account the Capacity of the restaurant

[Theory]
[InlineData( 1, 10)]
[InlineData( 2,  9)]
[InlineData( 3,  8)]
[InlineData( 4,  7)]
[InlineData( 4,  8)]
[InlineData( 5,  6)]
[InlineData( 6,  5)]
[InlineData(10,  1)]
public void CanAcceptOnInsufficientCapacity(int quantity, int reservedSeats)
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = reservedSeats } },
        reservation);
 
    Assert.False(actual);
}

This makes it harder for the Devil to come up with a malevolent implementation. Harder, but not impossible.

It seems clear that since all test cases still use a hard-coded capacity, it ought to be possible to write an implementation that ignores the Capacity, but at this point I don't see a simple way to avoid looking at reservation.Quantity:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Sum(r => r.Quantity);
    return reservedSeats + reservation.Quantity < 11;
}

This implementation passes all the tests. The last batch of test cases forced the Devil to consider reservation.Quantity. This strongly implies that if you vary Capacity as well, the proper implementation out to emerge.

Diminishing returns #

What happens, then, if you add just one test case with a different Capacity?

[Theory]
[InlineData( 1, 10, 10)]
[InlineData( 2,  9, 10)]
[InlineData( 3,  8, 10)]
[InlineData( 4,  7, 10)]
[InlineData( 4,  8, 10)]
[InlineData( 5,  6, 10)]
[InlineData( 6,  5, 10)]
[InlineData(10,  1, 10)]
[InlineData( 1,  1,  1)]
public void CanAcceptOnInsufficientCapacity(
    int quantity,
    int reservedSeats,
    int capacity)
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = reservedSeats } },
        reservation);
 
    Assert.False(actual);
}

Notice that I just added one test case with a Capacity of 1.

You may think that this is about where the Devil ought to capitulate, but not so. This passes all tests:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = 0;
    foreach (var r in reservations)
    {
        reservedSeats = r.Quantity;
        break;
    }
    return reservedSeats + reservation.Quantity <= Capacity;
}

Here you may feel the urge to protest. So far, all the Devil's Advocate implementations have been objectively simpler than the 'desired' implementation because it has involved fewer elements and has had a lower or equivalent cyclomatic complexity. This new attempt to circumvent the specification seems more complex.

It's also seems clearly ill-intentioned. Recall that the intent of the Devil's Advocate technique isn't to 'cheat' the unit tests, but rather to explore how well the test describe the desired behaviour of the system. The motivation is that it's easy to make off-by-one errors like inadvertently use <= instead of <. It doesn't seem quite as reasonable that a well-intentioned programmer accidentally would leave behind an implementation like the above.

You can, however, make it look less complicated:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    var reservedSeats = reservations.Select(r => r.Quantity).FirstOrDefault();
    return reservedSeats + reservation.Quantity <= Capacity;
}

You could argue that this still looks intentionally wrong, but I've seen much code that looks like this. It seems to me that there's a kind of programmer who seems generally uncomfortable thinking in collections; they seem to subconsciously gravitate towards code that deals with singular objects. Code that attempts to get 'the' value out of a collection is, unfortunately, not that uncommon.

Still, you might think that at this point, you've added enough test cases. That's reasonable.

The Devil's Advocate technique isn't an algorithm; it has no deterministic exit criterion. It's just a heuristic that I use to explore the quality of tests. There comes a point where subjectively, I judge that the test cases sufficiently describe the desired behaviour.

You may find that we've reached that point now. You could, for example, argue that in order to calculate reservedSeats, reservations.Sum(r => r.Quantity) is simpler than reservations.Select(r => r.Quantity).FirstOrDefault(). I'd be inclined to agree.

There's diminishing returns to the Devil's Advocate technique. Once you find that the gains from insisting on intentionally pernicious implementations are smaller than the effort required to add more test cases, it's time to stop and commit to the test cases now in place.

Test case variability #

Tests specify desired behaviour. If the tests contain less variability than the code they cover, then how can you be certain that the implementation code is correct?

The discussion now moves into territory where I usually exercise a great deal of judgement. Read the following for inspiration, not as rigid instructions. My intent with the following is not to imply that you must always go to like extremes, but simply to demonstrate what you can do. Depending on circumstances (such as the cost of a defect in production), I may choose to do the following, and sometimes I may choose to skip it.

If you consider the original implementation of CanAccept at the top of the article, notice that it works with reservations of indefinite size. If you think of reservations as a finite collection, it can contain zero, one, two, ten, or hundreds of elements. Yet, no test case goes beyond a single existing reservation. This is, I think, a disconnect. The tests come not even close to the degree of variability that the method can handle. If this is a piece of mission-critical software, that could be a cause for concern.

You should add some test cases where there's two, three, or more existing reservations. People often don't do that because it seems that you'd now have to write a test method that exercises one or more test cases with two existing reservations:

[Fact]
public void CanAcceptWithTwoPriorReservations()
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = 4
    };
    var sut = new MaîtreD(capacity: 10);
 
    var actual = sut.CanAccept(
        new[] { new Reservation { Quantity = 4 }, new Reservation { Quantity = 1 } },
        reservation);
 
    Assert.True(actual);
}

While this method now covers the two-existing-reservations test case, you need one to cover the three-existing-reservations test case, and so on. This seems repetitive, and probably bothers you at more than one level:

• It's just plain tedious to have to add that kind of variability
• It seems to violate the DRY principle

What you can do instead is to parametrise the key values of the collection(s) in question. While you can't put collections of objects in [InlineData] attributes, you can put arrays of constants. For existing reservations, the key values are the quantities, so supply an array of integers as a test argument:

[Theory]
[InlineData( 4, new int[0])]
[InlineData(10, new int[0])]
[InlineData( 4, new[] { 4 })]
[InlineData( 4, new[] { 4, 1 })]
[InlineData( 2, new[] { 2, 1, 3, 2 })]
public void CanAcceptWhenCapacityIsSufficient(int quantity, int[] reservationQantities)
{
    var reservation = new Reservation
    {
        Date = new DateTime(2018, 8, 30),
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity: 10);
 
    var reservations = reservationQantities.Select(q => new Reservation { Quantity = q });
    var actual = sut.CanAccept(reservations, reservation);
 
    Assert.True(actual);
}

This single test method replaces the previous three 'happy path' test methods. The first four [InlineData] annotations reproduce the previous test cases, whereas the fifth [InlineData] annotation adds a new test case with four existing reservations.

I gave the method a new name to better reflect the more general nature of it.

Notice that the CanAcceptWhenCapacityIsSufficient method uses Select to turn the array of integers into a collection of Reservation objects.

You may think that I cheated, since I didn't supply any other values, such as the Date property, to the existing reservations. This is easily addressed:

[Theory]
[InlineData( 4, new int[0])]
[InlineData(10, new int[0])]
[InlineData( 4, new[] { 4 })]
[InlineData( 4, new[] { 4, 1 })]
[InlineData( 2, new[] { 2, 1, 3, 2 })]
public void CanAcceptWhenCapacityIsSufficient(int quantity, int[] reservationQantities)
{
    var date = new DateTime(2018, 8, 30);
    var reservation = new Reservation
    {
        Date = date,
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity: 10);
 
    var reservations =
        reservationQantities.Select(q => new Reservation { Quantity = q, Date = date });
    var actual = sut.CanAccept(reservations, reservation);
 
    Assert.True(actual);
}

The only change compared to before is that date is now a variable assigned not only to reservation, but also to all the Reservation objects in reservations.

Towards property-based testing #

Looking at a test method like CanAcceptWhenCapacityIsSufficient it should bother you that the capacity is still hard-coded. Why don't you make that a test argument as well?

[Theory]
[InlineData(10,  4, new int[0])]
[InlineData(10, 10, new int[0])]
[InlineData(10,  4, new[] { 4 })]
[InlineData(10,  4, new[] { 4, 1 })]
[InlineData(10,  2, new[] { 2, 1, 3, 2 })]
[InlineData(20, 10, new[] { 2, 2, 2, 2 })]
[InlineData(20,  4, new[] { 2, 2, 4, 1, 3, 3 })]
public void CanAcceptWhenCapacityIsSufficient(
    int capacity,
    int quantity,
    int[] reservationQantities)
{
    var date = new DateTime(2018, 8, 30);
    var reservation = new Reservation
    {
        Date = date,
        Quantity = quantity
    };
    var sut = new MaîtreD(capacity);
 
    var reservations =
        reservationQantities.Select(q => new Reservation { Quantity = q, Date = date });
    var actual = sut.CanAccept(reservations, reservation);
 
    Assert.True(actual);
}

The first five [InlineData] annotations just reproduce the test cases that were already present, whereas the bottom two annotations are new test cases with another capacity.

How do I come up with new test cases? It's easy: In the happy-path case, the sum of existing reservation quantities, plus the requested quantity, must be less than or equal to the capacity.

It sometimes helps to slightly reframe the test method. If you allow the collection of existing reservations to be the most variable element in the test method, you can express the other values relative to that input. For example, instead of supplying the capacity as an absolute number, you can express a test case's capacity in relation to the existing reservations:

[Theory]
[InlineData(6,  4, new int[0])]
[InlineData(0, 10, new int[0])]
[InlineData(2,  4, new[] { 4 })]
[InlineData(1,  4, new[] { 4, 1 })]
[InlineData(0,  2, new[] { 2, 1, 3, 2 })]
[InlineData(2, 10, new[] { 2, 2, 2, 2 })]
[InlineData(1,  4, new[] { 2, 2, 4, 1, 3, 3 })]
public void CanAcceptWhenCapacityIsSufficient(
    int capacitySurplus,
    int quantity,
    int[] reservationQantities)
{
    var date = new DateTime(2018, 8, 30);
    var reservation = new Reservation
    {
        Date = date,
        Quantity = quantity
    };
    var reservedSeats = reservationQantities.Sum();
    var capacity = reservedSeats + quantity + capacitySurplus;
    var sut = new MaîtreD(capacity);
 
    var reservations =
        reservationQantities.Select(q => new Reservation { Quantity = q, Date = date });
    var actual = sut.CanAccept(reservations, reservation);
 
    Assert.True(actual);
}

Notice that the value supplied as a test argument is now named capacitySurplus. This represents the surplus capacity for each test case. For example, in the first test case, the capacity was previously supplied as the absolute number 10. The requested quantity is 4, and since there's no prior reservations in that test case, the capacity surplus, after accepting the reservation, is 6.

Likewise, in the second test case, the requested quantity is 10, and since the absolute capacity is also 10, when you reframe the test case, the surplus capacity, after accepting the reservation, is 0.

This seems odd if you aren't used to it. You'd probably intuitively think of a restaurant's Capacity as 'the most absolute' number, in that it's often a number that originates from physical constraints.

When you're looking for test cases, however, you aren't looking for test cases for a particular restaurant. You're looking for test cases for an arbitrary restaurant. In other words, you're looking for test inputs that belong to the same equivalence class.

Property-based testing #

I haven't explicitly stated this yet, but both the capacity and each reservation Quantity should be a positive number. This should really have been captured as a proper domain object, but I chose to keep these values as primitive integers in order to not complicate the example too much.

If you look at the test parameters for the latest incarnation of CanAcceptWhenCapacityIsSufficient, you may now observe the following:

• capacitySurplus can be an arbitrary non-negative number
• quantity can be an arbitrary positive number
• reservationQantities can be an arbitrary array of positive numbers, including the empty array

[Property]
public void CanAcceptWhenCapacityIsSufficient(
    NonNegativeInt capacitySurplus,
    PositiveInt quantity,
    PositiveInt[] reservationQantities)
{
    var date = new DateTime(2018, 8, 30);
    var reservation = new Reservation
    {
        Date = date,
        Quantity = quantity.Item
    };
    var reservedSeats = reservationQantities.Sum(x => x.Item);
    var capacity = reservedSeats + quantity.Item + capacitySurplus.Item;
    var sut = new MaîtreD(capacity);
 
    var reservations =
        reservationQantities.Select(q => new Reservation { Quantity = q.Item, Date = date });
    var actual = sut.CanAccept(reservations, reservation);
 
    Assert.True(actual);
}

This refactoring takes advantage of FsCheck's built-in wrapper types NonNegativeInt and PositiveInt. If you'd like an introduction to FsCheck, you could watch my Introduction to Property-based Testing with F# Pluralsight course.

By default, FsCheck runs each property 100 times, so now, instead of seven test cases, you now have 100.

Limits to the Devil's Advocate technique #

There's a limit to the Devil's Advocate technique. Unless you're working with a problem where you can exhaust the entire domain of possible test cases, your testing strategy is always going to be a sampling strategy. You run your automated tests with either hard-coded values or randomly generated values, but regardless, a test run isn't going to cover all possible input combinations.

For example, a truly hostile Devil could make this change to the CanAccept method:

public bool CanAccept(IEnumerable<Reservation> reservations, Reservation reservation)
{
    if (reservation.Quantity == 3953911)
        return true;
 
    var reservedSeats = reservations.Sum(r => r.Quantity);
    return reservedSeats + reservation.Quantity <= Capacity;
}

Even if you increase the number of test cases that FsCheck generates to, say, 100,000, it's unlikely to find the poisonous branch. The chance of randomly generating a quantity of exactly 3953911 isn't that great.

The Devil's Advocate technique doesn't guarantee that you'll have enough test cases to protect yourself against all sorts of odd defects. It does, however, still work well as an analysis tool to figure out if there's 'enough' test cases.

Conclusion #

The Devil's Advocate technique is a heuristic you can use to evaluate whether more test cases would improve confidence in the test suite. You can use it to review existing (test) code, but you can also use it as inspiration for new test cases that you should consider adding.

The technique is to deliberately implement the system under test incorrectly. The more incorrect you can make it, the more test cases you'll be likely to have to add.

When there's only a few test cases, you can probably get away with a decidedly unsound implementation that still passes all tests. These are often simpler than the 'intended' implementation. In this phase of applying the heuristic, this clearly demonstrates the need for more test cases.

At a later stage, you'll have to go deliberately out of your way to produce a wrong implementation that still passes all tests. When that happens, it may be time to stop.

The intent of the technique is to uncover how many test cases you need to protect against common defects in the future. Thus, it's not a measure of current code coverage.

Comments

public static string Foo(int i)
{
    return "foo";
}

public static string Foo(int i)
{
    if (i < -1000)
        return "bar";
    return "foo";
}

• ← Previous
• Archive
• Next →