Referential transparency of IO by Mark Seemann
How the IO container guarantees referential integrity. An article for object-oriented programmers.
This article is part of an article series about the IO container in C#. In a previous article you got a basic introduction to the IO<T> container I use to explain how a type system like Haskell's distinguishes between pure functions and impure actions.
The whole point of the IO container is to effectuate the functional interaction law: a pure function mustn't be able to invoke an impure activity. This rule follows from referential transparency.
The practical way to think about it is to consider the two rules of pure functions:
- Pure functions must be deterministic
- Pure functions may have no side effects
IO<T> imposes those rules.
Determinism #
Like in the previous articles in this series, you must imagine that you're living in a parallel universe where all impure library functions return IO<T> objects. By elimination, then, methods that return naked values must be pure functions.
Consider the Greet function from the previous article. Since it returns a plain string, you can infer that it must be a pure function. What prevents it from doing something impure?
What if you thought that passing now as an argument is a silly design. Couldn't you just call Clock.GetLocalTime from the method?
Well, yes, in fact you can:
public static string Greet(DateTime now, string name) { IO<DateTime> now1 = Clock.GetLocalTime(); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
This compiles, but is only the first refactoring step you have in mind. Next, you want to extract the DateTime from now1 so that you can get rid of the now parameter. Alas, you now run into an insuperable barrier. How do you get the DateTime out of the IO?
You can't. By design.
While you can call the GetLocalTime method, you can't use the return value. The only way you can use it is by composing it with SelectMany, but that still accomplishes nothing unless you return the resulting IO object. If you do that, though, you've now turned the entire Greet method into an impure action.
You can't perform any non-deterministic behaviour inside a pure function.
Side effects #
How does IO<T> protect against side effects? In the Greet method, couldn't you just write to the console, like the following?
public static string Greet(DateTime now, string name) { Console.WriteLine("Side effect!"); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
This also compiles, despite our best efforts. That's unfortunate, but, as you'll see in a moment, it doesn't violate referential transparency.
In Haskell or F# equivalent code would make the compiler complain. Those compilers don't have special knowledge about IO, but they can see that an action returns a value. F# generates a compiler warning if you ignore a return value. In Haskell the story is a bit different, but the result is the same. Those compilers complain because you try to ignore the return value.
You can get around the issue using the language's wildcard pattern. This tells the compiler that you're actively ignoring the result of the action. You can do the same in C#:
public static string Greet(DateTime now, string name) { IO<Unit> _ = Console.WriteLine("Side effect!"); var greeting = "Hello"; if (IsMorning(now)) greeting = "Good morning"; if (IsAfternoon(now)) greeting = "Good afternoon"; if (IsEvening(now)) greeting = "Good evening"; if (string.IsNullOrWhiteSpace(name)) return $"{greeting}."; return $"{greeting}, {name.Trim()}."; }
The situation is now similar to the above treatment of non-determinism. While there's no value of interest in an IO<Unit>, the fact that there's an object at all is a hint. Like Lazy<T>, that value isn't a result. It's a placeholder for a computation.
If there's a way to make the C# compiler complain about ignored return values, I'm not aware of it, so I don't know if we can get closer to how Haskell works than this. Regardless, keep in mind that I'm not trying to encourage you to write C# like this; I'm only trying to explain how Haskell enforces referential transparency at the type level.
Referential transparency #
While the above examples compile without warnings in C#, both are still referentially transparent!
This may surprise you. Particularly the second example that includes Console.WriteLine looks like it has a side effect, and thus violates referential transparency.
Keep in mind, though, what referential transparency means. It means that you can replace a particular function call with its value. For example, you should be able to replace the function call Greeter.Greet(new DateTime(2020, 6, 4, 12, 10, 0), "Nearth") with its return value "Hello, Nearth.", or the function call Greeter.Greet(new DateTime(2020, 6, 4, 7, 30, 0), "Bru") with "Good morning, Bru.", without changing the behaviour of the software. This property still holds.
Even when the Greet method includes the Console.WriteLine call, that side effect never happens.
The reason is that an IO object represents a potential computation that may take place (also known as a thunk). Notice that the IO<T> constructor takes a Func as argument. It's basically just a lazily evaluated function wrapped in such a way that you can't force evaluation.
Instead, you should imagine that after Main returns its IO<Unit> object, the parallel-universe .NET framework executes it.
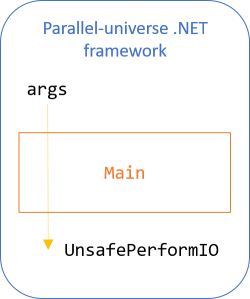
The framework supplies command-line arguments to the Main method. Once the method returns an IO<Unit> object, the framework executes it with a special method that only the framework can invoke. Any other IO values that may have been created (e.g. the above Console.WriteLine) never gets executed, because they're not included in the return value.
Conclusion #
The IO container makes sure that pure functions maintain referential transparency. The underlying assumption that makes all of this work is that all impure actions return IO objects. That's not how the .NET framework works, but that's how Haskell works. Since the IO container is opaque, pure functions can't see the contents of IO boxes.
Program entry points are all impure. The return value of the entry point must be IO<Unit>. The hypothetical parallel-universe framework executes the IO value returned by Main.
Haskell is a lazily evaluated language. That's an important piece of the puzzle, so I've modelled the IO<T> example so that it only wraps lazily evaluated Func values. That emulates Haskell's behaviour in C#. In the next article, you'll see how I wrote the C# code that supports these articles.

Comments
In a previous post, you said
In this post, you said
The first two items are not the same. Is this difference intentional?
Tyson, thank you for writing. Indeed, the words er verbatim not the same, but I do intend them to carry the same meaning.
If one wants to define purity in a way that leaves little ambiguity, one has to use more words. Just look at the linked Wikipedia article. I link to Wikipedia for the benefit of those readers who'd like to get a more rigorous definition of the term, while at the same time I enumerate the two rules as a summary for the benefit of those readers who just need a reminder.
Does that answer your question?
I don't think they don't mean the same thing. That is part of the discussion we are having on this previous post. I think the simplest example to see the difference is randomzied quicksort. For each input, the output is always the same. However, randomized quicksort is not deterministic because it uses randomness.
Do you still think they mean the same thing?
You made a standard variable declaration and I believe you meant to use a stand-alone discard rather than a wildcard pattern? Like below?
Tyson, I apologise in advance for my use of weasel words, but 'in the literature', a function that always returns the same output when given the same input is called 'deterministic'. I can't give you a comprehensive list of 'the literature' right now, but here's at least one example.
I'm well aware that this might be confusing. One could argue that querying a database is deterministic, because the output is completely determined by the state of the database. The same goes for reading the contents of a file. Such operations, however, may return different outputs for the same inputs, as the state of the resource changes. There's no stochastic process involved in such state changes, but we still consider such actions non-deterministic.
In the same vein, in this jargon, 'deterministic' doesn't imply the absence of internal randomness, as you have so convincingly argued. In the present context, 'deterministic' is defined as the property that a given input value always produces the same output value.
That's the reason I tend to use those phrases interchangeably. In this context, they literally mean the same. I can see how this might be confusing, though.
Atif, thank you for writing. I didn't know about that language construct. Thank you for pointing it out to me!
I am certainly still confused. I can't tell if you are purposefully providing your own definition for determinism, if you are accidentally misunderstanding the actual definition of determinism, if you think the definition of determinism is equivalent to the definition you gave due to being in some context or operating with an additional assumption (of which I am unsure), or maybe something else.
If I had to guess, then I think you do see the difference between the two definitions but are claiming that are equivalent due to being in some context or operating with an additional assumption. If this guess is correct, then what is the additional assumption you are making?
To ensure that you do understand determinism, I will interpret your statements as literally as possible and then respond to them. I apologize in advance if this is not the correct interpretation and for any harshness in the tone of my response.
You misquoted the Wikipedia article. Here is the exact text (after replacing "algorithm" with "function" since the difference between these is not important to us now).
Your quotation essentially excludes the phrase "with the underlying machine always passing through the same sequence of states". Let's put these two definitions next to each other.
Let
fbe a function. Consider the following two statements aboutfthat might or might not be true (depending on the exact value off).fwill always produce the same output.fwill always produce the same output, with the underlying machine always passing through the same sequence of states.Suppose some
fsatisfies statement 2. Thenfclearly satisfies statement 1 as well. These two sentences together are equivalent to saying that statement 2 implies statement 1. The contrapositive then says that not satisfying statement 1 implies not satisfying statement 2. Also, Wikipedia says that such anfis said to be deterministic.Now suppose some
fsatisfies statement 1. Thenfneed not also satisfy statement 2. An example that proves this is randomized quicksort (as I pointed out in this comment). This means that statement 1 does not imply statement 2."Wikipedia gave" a name to functions that satisfy statement 2. I do not recall ever seeing anyone give a name to functions that satisfy statement 1. In this comment, you asked me about what I meant by "weak determinism". I am trying to give a name to functions that satisfy statement 1. I am suggesting that we call them weakly deterministic. This name allows us to say that a deterministic function is also weakly deterministic, but a weakly deterministic function might not be deterministic. Furthermore, not being a weakly deterministic implies not being deterministic.
Indeed. I agree. If we distinguish determinism from weak determinism, then we can say that such a function is not weakly deterministic, which implies that it is not deterministic.
Tyson, I'm sorry, I picked a bad example. It's possible that my brain is playing a trick with me. I'm not purposefully providing my own definition of determinism.
I've learned all of this from diverse sources, and I don't recall all of them. Some of them are books, some were conference talks I attended, some may have been conversations, and some online resources. All of that becomes an amalgam of knowledge. Somewhere I've picked up the shorthand that 'deterministic' is the same as 'the same input produces the same output'; I can't tell you the exact source of that habit, and it may, indeed, be confusing.
It seems that I'm not the only person with that habit, though:
I'm not saying that John A De Goes is an authority you should unquestionably accept; I'm only pointing to that tweet to illustrate that I'm not the only person who occasionally use 'deterministic' in that way. And I don't think that John A De Goes picked up the habit from me.The key to all of this is referential transparency. In an ideal world, I wouldn't need to use the terms 'pure function' or 'deterministic'. I can't, however, write these articles and only refer to referential transparency. The articles are my attempt to share what I have learned with readers who would also like to learn. The problem with referential transparency is that it's an abstract concept: can I replace a function call with its output? This may be a tractable notion to pick up, but how do you evaluate that in practice?
I believe that it's easier for readers to learn that they have to look for two properties:
- Does the same input always produce the same output?
- Are there no side effects?
As far as I can tell, these two properties are enough to guarantee referential transparency. Again: this isn't a claim that I'm making; it's just my understanding based on what I've picked up so far.As all programmers know: language is imprecise. Even the above two bullets are vague. What's a side effect? Does the rule about input and output apply to all values in the function's domain?
I don't think that it's possible to write perfectly precise and unambiguous prose. Mathematical notation was developed as an attempt to be more precise and unambiguous. Source code has the same quality.
I'm not writing mathematical treatises, but I use C#, F#, and Haskell source code to demonstrate concepts as precisely as I can. The surrounding prose is my attempt at explaining what the code does, and why it's written the way it is. The prose will be ambiguous; I can't help it.
Sometimes, I need a shorthand to remind the reader about referential transparency in a way that (hopefully) assists him or her. Sometimes, this is best done by using a few adjectives, such as "a deterministic and side-effect-free function". It's not a definition, it's a reading aid.
Mark, I am also sorry. As I reread my comment, I think I was too critical. I admire your great compassion and humility, especially in your writing. I have been trying to write more like you, but my previous comment shows that I still have room for improvement. Your blog is still my favorite place to read and learn about software development and functional programming. It is almost scary how much I agree with you. I hope posting questions about my confusion or comments about our differences don't overshadow all the ways in which we agree and sour our relationship.
Tyson, don't worry about it. Questions teach me where there's room for improvement. You also sometimes point out genuine mistakes that I make. If you didn't do that, I might never realise my mistakes, and then I wouldn't be able to correct them.
I appreciate the feedback because it improves the content and teaches me things that I didn't know. On the other hand, as the cliché goes, all errors are my own.