Functional design is intrinsically testable by Mark Seemann
TDD with Functional Programming doesn't lead to test-induced damage. Here's why.
Over the years, there's been much criticism of Test-Driven Development (TDD). Perhaps David Heinemeier Hansson best condensed this criticism by claiming that TDD leads to test-induced design damage. This isn't a criticism you can just brush away; it hits a sore point.
Personally, I don't believe that TDD has to lead to test-induced damage (not even in Object-Oriented Programming), but I'm the first to admit that it's not a design methodology.
In this article, though, you're going to learn about the fundamental reason that TDD with Functional Programming doesn't lead to test-induced damage.
In Functional Programming, the ideal function is a Pure function. A Pure function is a function that always returns the same value given the same input, and has no side-effects.
Isolation #
The first characteristic of a Pure function means that an ideal function can't depend on any implicit knowledge about the external world. Only the input into the function can influence the evaluation of the function.
This is what Jessica Kerr calls Isolation. A function has the property of Isolation when the only information it has about the external word is passed into it via arguments.
You can think about Isolation as the dual of Encapsulation.
In Object-Oriented Programming, Encapsulation is a very important concept. It means that while an object contains state, the external world doesn't know about that state, unless the object explicitly makes it available.
In Functional Programming, a function is Isolated when it knows nothing about the state of the external world, unless it's explicitly made available to it.
A Pure function, the ideal of Functional Programming, is Isolated.
Unit testing #
Why is this interesting?
It's interesting if you start to think about what unit testing means. There are tons of conflicting definitions of what exactly constitutes a unit test, but most experts seem to be able to agree on this broad definition:
A unit test is an automated test that tests a unit in isolation from its dependencies.Notice the use of the word Isolation in that definition. In order to unit test, you'll have to be able to isolate the unit from its dependencies. This is the requirement that tends to lead to Test-Induced Damage in Object-Oriented Programming. While there's nothing about Encapsulation that explicitly states that it's forbidden to isolate an object from its dependencies, it offers no help on the matter either. Programmers are on their own, because this concern isn't ingrained into Object-Oriented Programming.
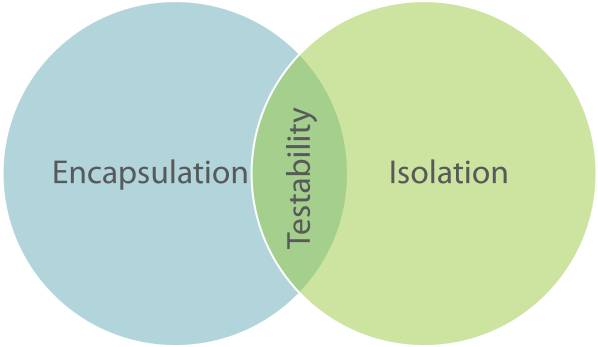
You can do TDD with Object-Oriented Programming, and as long as you stay within the intersection of Encapsulation and Isolation, you may be able to stay clear of test-induced damage. However, that zone of testability isn't particularly big, so it's easy to stray. You have to be very careful and know what you're doing. Not surprisingly, many books and articles have been written about TDD, including quite a few on this blog.
The best of both worlds #
In Functional Programming, on the other hand, Isolation is the ideal. An ideal function is already isolated from its dependencies, so no more design work is required to make it testable.
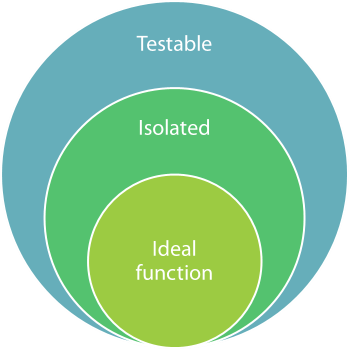
Ideal Functional design is not only ideal, but also perfectly testable, so there's no conflict. This is the underlying reason that TDD doesn't lead to test-induced damage with Functional Programming.
Summary #
Isolation is an important quality of Functional Programming. An ideal function is Isolated, and that means that it's intrinsically testable. You don't have to tweak any design principles in order to make a function testable - in fact, if a function isn't testable, it's a sign that it's poorly designed. Thus, TDD doesn't lead to Test-Induced Damage in Functional Programming.
If you want to learn more about this, as well as see lots of code examples, you can watch my Test-Driven Development with F# Pluralsight course.

Comments
What do you mean by "value"? Can an exception instance be a value? More specifically, would you say that the C# function
int Foo() => new Exception();is pure?Many of your posts mention pure funcitons and at least a few of them include your own definition. I decided to comment on this post since it was the oldest post I found that included your own definition of a pure function.
Tyson, thank you for writing. I don't think that
int Foo() => new Exception();compiles...Apart from that, how do you find that this is my own definition of a pure function? It seems to me to be a standard and non-controversial definition. I even link to the Wikipedia definition in the beginning of the article.
I am not trying claim that any particular definition of a pure function is non-standard or is controversial. I also don't mean that the text I quoted is "your definition" in the sense that it semantically differs from the one on Wikipedia. I just mean that it is "your definition" in the sense that you have syntactically included in your post the text that I quoted.
However, I am unsure about the precise meaning the defintion for a pure function that you have syntactically included in your post and that I quoted. To help me improve my understanding of that defintion, I tried to ask you if a particular C# function is pure.
Ah, yes. Thanks for alerting me to my mistake. I meant to include the
throwskeyword as well. For clarity, I now repeat that whole paragraph but with the prose "thrown" and the keywordthrowsadded.What do you mean by "value"? Can a thrown exception instance be a value? More specifically, would you say that the C# function
int Foo() => throws new Exception();is pure?Tyson, your code still doesn't compile, but I think I understand the question 😜
Yes,
int Foo() => throw new Exception();is still a pure function, but it isn't total. Rather, it's a partial function. This is an independent quality of functions.Purity relates to determinism and the lack of side effects. A total function, on the other hand, is a function that returns a proper value for every possible value in its domain. What do I mean by proper?
There's two ways in which a function can fail to return a value. One is if the function never returns. Due to the halting problem there's no general-purpose way to determine whether or not this is the case for a Turing-complete language.
Another way a function can fail to return a value is if it throws an exception. Most languages (even Haskell!) allows exception-throwing. This isn't considered a 'proper' value because, using the type system, you declared that
Fooreturns anint. It doesn't. It 'returns' an exception.Both non-termination and exceptions are typically considered a special value termed bottom, often written with the symbol
⊥.Functions can be pure, but partial. Your
Foofunction is an example of that. The holy grail in statically typed functional programming is pure and total functions. It's up to the programmer to provide the totality guarantee, though, since the type system can't enforce termination (due to the halting problem). You can, on the other hand, easily program without exceptions once you get the hang of it.Thanks for seeing pass my second compile error and understanding my question.
Ah, yes. I definitely know about partial and total functions from my experience with mathematics, and I am pretty sure I have previously called a function that throws an exception partial, but I completely forgot about this connection. (I think that is because I have so focused on purity.) Thank you for bringing this concept (back) to my attention.
I was asking about pure functions and exception throwing because I was thinking about the definition for a pure function given by Enrico Buonanno in Functional Programming in C#. He considers throwing an exception a side effect and includes this paragraph about this decision.
What do you think about Enrico's choice to define exception throwing as a side effect?
It might be worth considering
async void Foo() => throw new Exception();because it produces an unhandled exception, which crashes the executing process.I haven't seen anyone take that position before, so I can only evaluate it based on what you wrote. With that limited context, however, I don't find the argument convincing. First, that throwing exceptions will cause indeterminism to appear in code that handles exceptions says nothing about the function that throws the exception. It says something about the code that handles the exception.
Making decisions based on data is itself not non-deterministic. If it was,
if/elseblocks or pattern matching couldn't be pure. If the exception handler does something impure while handling an exception, then it's just an impure action. The functional interaction law explicitly allows this.Keep in mind that the definition of purity that we're discussing is really only a checklist to figure out whether a function is referentially transparent. That's the core definition: Can you replace a function call with its result?
Yes, if the function is pure. This includes a function that throws an exception. It basically just returns
⊥. If you have code that handles the exception, it'll do that based on the exception that was thrown. It doesn't really matter if the function 'actually executed' or not. We can replace the function call with the bottom value.If you don't handle the exception, then yes: the program crashes. It'll do so, however, regardless of whether you 'run' the function, or you just replace it with a thrown exception.
Yes, this helps. I agree with you. Thanks for your explanation.
The respective problems of deciding if a given function is total or pure are equally difficult; both are undecidable by Rice's theorem. A compiler for Haskell is not a general-purpose algorithm for deciding the purity of a function. It follows from the syntax of Haskell that all functions in Haskell with a return type different from the IO monad are pure (and technically all the others as well). Rice's theorem doesn't apply when the property being checked is syntactic.
In the same way, it is possible to design a programming language with two contexts: one in which partial functions can be defined and another in which only total functions can be defined. As before, the partial function context could be expressed by the syntactic requirement that the return type is some monad.
I'm not familiar with Rice's theorem, so I'll have to take your word on that. Haskell, however, seems to be doing a fairly good job of distinguishing between pure and impure, but this could be because the impure actions ultimately aren't implemented in Haskell (IIRC, they're written in C or C++). This might be analogous to the following escape hatch for partiality versus totality.
You can't define a Turing-complete language where you generally distinguish between total and partial functions. That's what Turing, Gödel, and Church proved in the 1930's. The escape hatch is that if you define a language that's not Turing-complete, you can distinguish between total and partial functions. If I remember correctly, that's the underlying design philosophy of Idris. I believe that Edwin Brady once called the concept Pac-Man-complete; while not Turing-complete, he was aiming for a language powerful enough that you could still implement Pac Man in it. I do believe that Idris also comes with an option where you can escape into the wider, Turing-complete part of the language by giving up on the compiler checking of totality versus partiality.
Ah, great. Your comment motivated me to read more about Idris, and I have learned some things.
First, Idris includes a totality checker for functions. By default, a function is not checked for totality. Putting the keyword
totalabove a function defintion enables the checker. Here are some examples of this. The code then compiles if and only if the checker (which is essentially a theorem prover) is able to prove that the function is total. So the two contexts are distinguished by the presence or absence of the keywordtotal. This is a completely different approach to creating the two contexts than what I was vaguely suggesting.Second, Idris is Turing-complete as confirmed by Edwin Brady himself. Furthermore, both Edwin and this page about coinductive that he cites say (paraphrased into my words) that one could also separate the partial and total contexts using a monad. Though the linked page goes onto say that "this is a heavyweight solution, and so we would like to avoid it whenever possible."
I am really glad to have learned those things. Thanks for the great conversation :)
Would you say that
int Foo() { if (new Random().Next() % 2 == 0) throw new Exception(); else throw new NotImplementedException(); }is pure?No, that variation of
Foois impure because of the non-deterministic behaviour. You can't replace a call toFoowith a corresponding bottom value.Idris is very interesting. Have you seen attempts to test totality in other languages?
Spencer, thank you for writing. Usually, the names Agda and Coq are thrown around when Idris is mentioned. As far as I understand things, however, both Agda and Coq are mostly intended to be additional tools that you use together with another language, whereas the vision for Idris is to be a complete programming language. I could be wrong, though. It's a rabbit hole that I've yet to explore.
Another language worth mentioning might be F*, but again, I know little about it, and have never written a line of code in it.
Thank you for the leads! These languages are very interesting. I'd never heard of "proof-oriented programming" or depdendant types before. It's going to a take a while to unpack these new approaches.
I notice all these languages take a proof-based approach to verifying totality. I'm curious about your take on a possible experimental approach.
I've been trying to meld ideas from Clojure.spec into a type-driven approach in F#, in line with Scott Wlaschin's Designing with Types and your Types + Properties = Software. Clojure Spec, in case you're unfamiliar, is the Specification pattern as an optional type system. Types are built up through combinations of constraints (e.g. InventoryCount must be an int of at least 0 and no more than 10000). Spec can then automatically test type-annotated functions to verify that any input that fits constraints produces output that fits constraints. It's basically property testing with generators automatically created from the in-code type specifications.
I think this kind of testing is effectively a measure of totality; a measure of how well a function's actual domain matches its advertized domain. Clojure does not make that claim, and I haven't found a similar approach from another language or framework yet.
While less thorough than proofs, such a technique could be applied to most any system with static typing through meta-programming and conventions to find type constraints (i.e. via factory functions). The proportion of inputs that error or timeout could be a consistent measure for migrating systems to more total, and less surprising, functions.
Thoughts?
Spencer, thank you for writing. While I know that Clojure.spec exists, I don't know more about it than what you've described. It's not quite the same, but it sounds not too dissimilar from QuickCheck
Arbitraryinstances. They don't describe predicates, but they do implement (pseudo-random) generators of values. Those generators then drive data generation for property-based tests.Parametrised tests (including properties) are essentially predicates. They take input and return a binary result. Granted, the result isn't true or false, but rather pass or fail, but I hope it's evident that these are isomorphic.
How does that relate to testing totality? It's better than nothing, but in practice we must suffer the reality of combinatorics. You can easily use brute force to prove total a function that takes a single Boolean value as input. A byte input requires 256 test cases, so that's also within the realm of the possible. Many input types, however, represent conceptually infinite sets. A string, for example, represents a conceptually infinite set.
Imagine an adversarial function that loops forever if the input string is a very particular value. This value might be a one-million-character string generated randomly at compile time. The odds that any random test case generator ever hits that particular value are effectively nil.
While I like property-based testing a lot, I don't consider it a measure of totality. If the domain of a function is infinite, it makes little difference if you exercise a hundred or a million test cases - you've still covered practically zero percent of the domain.
You make an excellent point. If I understand correctly, many domains are effectively infinite so coverage of random testing is effectively negligable.
My connection to totality came from trying to understand what Clojure spec's instrument function is really testing. It's a property, but the property only knows the shape of the domain and range. It knows nothing about relationships between specific input and output values. Therefore, it doesn't verify business domain correctness. Rather, it's checking that the range holds true for a sampling of valid input values.
In light of your insight, it may be more fair to say this is a coverage "surprise" check. It can run common edge cases and input scenarios to make sure they return values from the advertized range rather than exceptions (or fail to terminate). As you discerned, it cannot generally detect adversarial implementations that would violate totality.
Thank you for taking the time to consider this idea and share your expertise!
Spencer, thank you for writing. If I understand your description of Clojure.spec correctly, this makes sense in a dynamically typed language like Clojure. It's seems reminiscent of fuzz testing in the sense that you throw arbitrary input at a System Under Test and then monitor what happens. This makes sense in a system where input is mostly (or exclusively) checked at run time.
In a language like Haskell, on the other hand, that kind of testing is generally impossible. You can't just throw random, unconstrained input at a Haskell function, because if the input doesn't type-check, the code will not even compile. Languages like C# and Java seem to fall more on that side than on the Clojure side, even though their types systems involve more ceremony.
To be clear: You could imagine something akin to a 'totality check' even in Haskell. After all, we know from the papers of Church, Gödel, and Turing that no type system can prove arbitrary Turing-complete code total (i.e. the halting problem). Even with the best-designed Haskell API, one might conceivably want to write a QuickCheck property that throws random (typed) input at a function only to assert that it returns a value. In essence, this would be an assertion-free test. The implicit assertion is that if the function returns without exceptions or timing out, then it may be total.
While one could do that, once you've gone through the trouble of writing such a property, you can often think of some sort of explicit assertion to write. If so, why not do that? But if you do, you've now ventured into the territory of genuine property-based testing. There's nothing wrong with that - quite the contrary - but I think it explains why you tend to not see the above kind of totality checking in statically typed languages.
Another point to consider is this: With a decent static type system (and I count C# in that category), you can often design APIs so that the types take care of most concerns regarding totality. It helps to realise that in most languages, functions can be partial in two ways:
You can usually eliminate the first kind of partiality by carefully choosing input and output types. Thus, in a statically typed language, you're often left with the question: Will this function always terminate?
While the halting problem says that there's no general algorithm that will answer that question, it's often obvious for specific functions. For instance, if a function has no recursion or looping, it obviously will terminate. This, to be clear, involves 'white-box' analysis. You have to look at the code and convince yourself that the function will terminate.
I've possibly strayed off your original agenda, but I found your comments and responses inspiring. I hope you or someone else find these notes useful.
I'm glad you've found this line of thought interesting! I've definitely enjoyed and benefitted from our discourse.
I agree this kind of testing bears a strong resemblance to fuzzing and that static types eliminate the majority of invalid inputs up front.
I'm going to dig deeper into my journey to see if it can explain why I think these tests are valuable.
It may not be clear, but the best thing about Clojure Spec's fuzz-like tests is that they don't have to be written at all. All type information is present in the type annotation, including primitive constraints like bounded integers. An introspective function can generically infer generators and assertions from type annotations to create the tests. All annotated functions get these fuzz tests for free.
In static languages, we get the structural component of these tests for free from the compiler. However, we're still missing out on verifying constrained values.
Approaches to combat primitive obsession go a long way toward eliminating such errors and defensive programming from our domains by centralizing validation and coupling it to a type.
Scott Wlaschin demonstrates constrained types using unions
More traditionally, it'd be a constructor
These approaches implement constrained types as a pattern rather than a language construct. A programmer could undermine them by forgetting to keep constructors private, adding new constructors, assigning via reflection, etc.
I spent a while trying to figure out how to add constrained values to F#'s types system and understand what it could do for us. It ultimately failed, but you can check out my attempts and my reasoning in the github repo. This was prior to me learning about dependent type systems, which are the more mature realization of my line of thought.
I later realized that the constraints don't need to be part of the type to be useful. The constraints are represented in the code as factories or constructors. The code itself will enforce the expectations at runtime. At test time it's ok to rely on slow introspective approaches to identify constraints. In that way, we too have all the information we need to mechanically property test a system just like clojure spec does. In fact, we can test every function in the system, intentionally constrained or not, because static languages require typing.
What do these tests do? Like with spec, we can derive some confidence that our system handles the values it says it does. Though not total certainty, which requires a white-box approach as you mentioned.
If a system is migrating from heavy use of exceptions for defensive programming, or from general lack of defensive programming, then this kind of test can track progress away from exceptions.
It can also help consistency of our constrained types. For example, we can always select the most weakly constrained factory or constructor. This prevents accidental public constructors (which, admittedly, could also be accomplished with an annotation and a simple analyzer). We can also pressure towards conventions like naming the factory a certain way, or only using results over exceptions for communicating errors from factories.
As a side benefit, we can also leverage the introspected generators to write our own properties. This reduces duplicated knowledge of constraints between the system and tests, keeping them in line automatically.
Thanks for reading this far. This is all pretty conceptual at this point. I hope it's fun food for thought.
A bit more rumination and I realized my thoughts above can be summarized in a few key points
- Clojure Spec tests I refer to aren't written, they're programmatically inferred from code
- Static languages encode all the information needed to programmatically generate and assert constrained value types like Clojure Spec, it's just that part of information lives in functions rather than types.
- Constrained values are effectively a design pattern in most static languages.
The language can't guarantee a consistent approach or consistent application, so there's value in adding natural pressures to be consistent.
It's kind of like how you once explained the value of DI containers
-
These tests can smoke out defensive programming issues and misadvertized function signatures.
This is only generalizable if we can differentiate expectable failures from unintended issues, thus why these tests mostly measure movement away from exceptions.
Please let me know if you'd like anything clarified. These are far from fully formed ideas.Spencer, thank you for writing. I already got the sense that the Clojure.spec tests weren't written, but thank you for confirming that. I don't know the implementation details of how that works, but I may have an inkling.
Clojure is, as I'm sure that you're aware, homoiconic. Thus, I suppose that the specs are written in Clojure as well. A function or macro can extract the details of each spec and generate test data that are likely to fit.
Consider, as a though experiement, a type like this:
If this was, instead, Clojure, then from perusing the Clojure.spec documentation it looks as though you'd use a predefined specification called
int-in, but even if you'd be using normal less-than and greater-than operators, I suppose it wouldn't be beyond the abilities of a sophisticated function to tease apart such a predicate and compose a useful generator.In languages like C#, F#, Java, or Haskell, however, predicates and types are typically black boxes. For the
Narrowsclass, you have a static factory method. This factory method is total, but if you throw random 64-bit integers at it, the chance of ever getting a populated Maybe value is vanishingly small.If you now have a function that takes that type as input, you can't really exercise it because of the statistics involved. This is why most property-based testing frameworks that I've seen (QuickCheck, Hedgehog, FsCheck, CsCheck) are based on a generator API (usually called either
ArbitraryorGen).While you can compose a type-specific generator from other generators, you have to explicitly do that work. The testing framework can't infer the set of valid values to use.
I'm not disagreeing with what you wrote. I'm only trying to outline how I see such efforts interact with the capabilities of various languages.
If I interpret this correctly, you're saying languages like C# and similar would have to throw random values at the Narrows TryCreate function to find instances. However, Clojure could use its macro system to understand the functions symbolically and semantically.
I think that languages like C# and F# can also semantically analyze code, but it has to be done through the compiler platforms (i.e. Roslyn, FSharp Compiler Services) or similar meta-programming. These are performance heavy, not every language has one, and only work when we have access to code, but they do make semantic analysis possible for functions.
We could use the compiler platform to parse constraints from factories. For example, analyze Narrows.TryCreate to find comparison operators, and that those comparisons lead to a "None" value. The other conditional branch is "Some", thus Narrows requres a long greater than 2_993_329_992 and less than 3_001_322_003. Then we use the inferred constraints to create typical property test generators and arbitraries.
However, I think your musing from a few posts back are now clicking better. You mused that static languages can effectively eliminate exception-based partiality through careful choice of types. I see two main categories of exceptions
This is really interesting. Thank you for pushing my thinking.
Spencer, thank you for writing. I didn't meant to imply that we should make a general-purpose code analyser - this seems to me to move perilously close to the halting problem; that is, I don't think you this is generally possible. (I could be wrong, though, I haven't thought deeply about this.)
What I meant was more that since Clojure.spec is written in Clojure, and Clojure code is also data, it's fairly easy to search a spec for easy-to-detect predicates. Something like a specification is fair game for analysis exactly because of the role it plays. I wouldn't contemplate analysing the function body of a Clojure function like that.
In .NET a typical approach to these kinds of problems is to use attributes. There's been quite a few attempts at that over the years - I've previously engaged with that kind of design, but in summary, I'm not a fan. It does, however, provide some metadata that's fair game for analysis.
The distinction, then, seems more related to the nature of the languages. With a language like C#, if you need metadata, it seems as though you need to invent a language feature for that purpose: attributes. In Clojure, on the other hand, because it's homoiconic, you don't need a separate language feature for metadata. You just write the metadata in Clojure. This doesn't, however, change the role of the spec. Even though you're writing it in Clojure, it plays the role of metadata. One of the implications of that is that it's fair game for an analyser, whereas I think a Clojure function body is still off limits for the Spec engine.
Ah, I misunderstood. I hadn't thought about the relationship between metadata and analyzers. Clojure certainly has the edge for elegant and powerful metadata.
I suppose I feel hope for analyzing function bodies for constraints in this context because type factories tend to contain predicates similar to what we'd use in a spec. Unlike Clojure, this relies on some unenforced expectations on the code and wouldn't always come up with an answer.
Even with that hope, the value proposition seems shaky considering our previous comments.
Ruminating on our discussion, I decided it was worth creating an experimental constraints-as-data library, FsSpec, that leans into the advantages of a static type system.
It doesn't attempt to prove totality or be part of the type system, like is possible in Idris or F*. It normalizes the common activity of constraining primitive values and exposes those constraints as data that can be programmatically accessed.
It'll take use and feedback to determine if this approach really saves complexity, but it was very fun to write. The most fun part was realizing how boolean trees can be normalized to reliably interpret them for data generation.
I'd love to hear your thoughts if it interests you.
Spencer, thank you for writing. FsSpec looks interesting. It strikes me as one of those things where I'd need to try it out on a real code base before I could pass an informed verdict.
Very early in the discussion, Tyson Williams asked about Exceptions and purity. In one answer you talked about exceptions being a kind of bottom value. Does that mean that there are multiple values of type Bottom that can potentially be equatable? That doesn't feel right to me...
Daniel, thank you for writing. At this point, I'm basing my incomplete knowledge on all sorts of different sources, not all of which I can readily remember or identify. The Haskell wiki article on bottom, however, also discusses two kinds of bottom. That may have been where I've picked it up.
In general, bottom values originating from invalid input are avoidable in statically typed languages. Instead of throwing exceptions, it's possible to return a Maybe or Either value. In practice, we don't always do that. Division (which is not defined by zero) may be the most infamous example.
Infinite loops, on the other hand, can't be type-checked away, as already discussed here.