Visual Value Verification by Mark Seemann
Sometimes, the most efficient way to verify the outcome of executing a piece of code is to visualise it.
Recently, I've been working my way through Real World Haskell, and although some of the exercises in the book are exasperating, others are stimulating and engaging. One of the good exercises is to use the Graham Scan algorithm to find the convex hull for a set of points.
This proved to be unexpectedly difficult for me, but I also found the exercise captivating, so I kept at it. My main problems turned out to be related to the algorithm itself, so during the exercise, I temporarily switched to F# in order to work out the kinks of my implementation. This enabled me to focus on the problem itself without also having to fight with an unfamiliar programming language.
Surprisingly, it turned out that one of my biggest problems was that I didn't have a good way to verify my implementation.
Return values #
Since I was approaching the problem with Functional Programming, it ought to be easy to unit test. After all, Functional design is intrinsically testable. My overall function to find the convex hull looks like this:
let inline hull points = // ...
In simplified form, the type of this function is (^a * ^d) list -> (^a * ^d) list where the ^a and ^d generic type arguments have a whole lot of constraints that I don't want to bother you with. In practice, both ^a and ^d can be integers, so that the hull function gets the type (int * int) list -> (int * int) list. In other words: you supply a list of integer points, and you get a list of integer points back.
Here's a simple example:
> hull [(3, 1); (2, 3); (2, 4); (2, 5); (3, 7); (1, 2); (1, 6)];; val it : (int * int) list = [(3, 1); (3, 7); (2, 5); (1, 6); (1, 2)]
Quick! At a glance: is this result correct or incorrect?
How about this result?
> hull [(5, -2); (5, 6); (-4, 7); (-6, 0); (-8, 0); (-2, 5); (-3, -4); (-2, -2); (-9, -7); (2, -9); (4, -2); (2, -10); (4, -10); (4, -9); (2, -10); (3, -9); (8, 2); (-8, -5); (-9, -4); (5, -6); (6, 4); (8, -10); (-5, 0); (5, 9); (-5, -4); (-6, 8); (0, -9); (7, -4); (6, 4); (-8, -5); (-7, -7); (8, -9); (7, -3); (6, 4); (-6, -8); (-4, 4); (-2, -2); (-6, -10); (0, 1); (5, -7); (-5, 4); (5, -5); (6, 4); (0, 7); (5, 5); (-1, -4); (-6, 0); (-9, 3); (5, 6); (-7, 7); (4, -10); (5, -8); (9, -1); (0, -9); (6, 6); (6, -6); (9, 8); (-10, -2); (-3, 2); (-5, -7)];; val it : (int * int) list = [(-6, -10); (2, -10); (4, -10); (8, -10); (9, -1); (9, 8); (5, 9); (-6, 8); (-7, 7); (-9, 3); (-10, -2); (-9, -7)]
(In the first example, the output is incorrect, but in the second, it's correct.)
It's easy enough to write automated unit tests once you know what the expected outcome should be. In this case, my problem was that I didn't have an easy way to calculate if a given list of points was the correct answer or not. After all, I was trying to implement a function that could be used for this purpose, but I needed to know if the function returned the correct values.
In the beginning, I tried to plot the values into Excel, in order to draw them as diagrams, but that soon turned out to be tedious and inefficient.
Then I considered Property-Based Testing, but I couldn't come up with a good set of properties that didn't involve half of the algorithm I was trying to implement.
Visual Value Verification #
The concept of a convex hull is simple, and easy to verify if you can visualise it. That's what I tried to do with Excel, but here my problem was that the process was too cumbersome.
Instead, I decided to pull in FSharp.Charting, because it enabled me to easily visualise the result of calling the hull function. This is all it takes:
open System open FSharp.Charting let inline hullChart points = let hullPoints = hull points let hullChart = let closedHull = hullPoints @ [hullPoints.Head] Chart.Line(closedHull, Name = "Hull") |> Chart.WithStyling(Color = Drawing.Color.Blue) let pointsChart = Chart.Point(points, Name = "Points") |> Chart.WithStyling(Color = Drawing.Color.Black) [hullChart; pointsChart] |> Chart.Combine |> Chart.WithYAxis(MajorGrid = ChartTypes.Grid(Enabled = false)) |> Chart.WithXAxis(MajorGrid = ChartTypes.Grid(Enabled = false))
The signature of the hullChart function is (^a * ^d) list -> FSharp.Charting.ChartTypes.GenericChart (where, again, the ^a and ^d types are generic type arguments with various type constraints; think of them as numbers). It first calls the hull function with points. Then it creates a line chart to draw the hull, and a point chart to plot in all the input points. Finally, it combines both charts into a single chart.
With the hullChart function, it's easy to do ad-hoc testing in F# Interactive and visually inspect the results of calling the hull function with various input. At one point, I had a particular problem with my interpretation of the Graham Scan algorithm, and this was easy to see using the hullChart function, which would produce this chart:
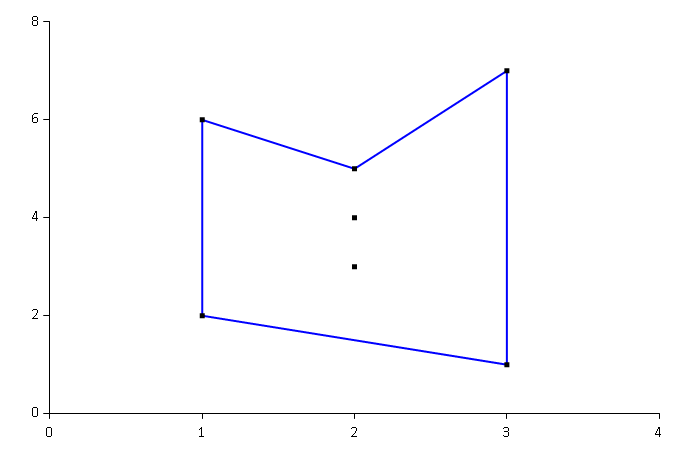
With this chart it's easy to see, at a glance, that the calculated hull is concave, and thus not a convex hull. There's an error in the implementation. (This is the first result set that I asked you to evaluate above.)
Struggling on with the exercise, I was able to solve my immediate problem and produce a convex hull from that particular input. Did that mean that I now had the correct implementation, or could there be other errors? I needed more test results before I felt that I had confidence in my implementation.
This, on the other hand, was now easy to get.
First, I could randomly generate points like this:
let randomPoints (r : Random) = [1..r.Next(1, 100)] |> List.map (fun _ -> (r.Next(-10, 10), r.Next(-10, 10)))
For ad-hoc testing, I could now create a random set of points and show the calculated hull:
> (randomPoints (Random()) |> hullChart).ShowChart();;
Immediately, a window would pop up, enabling me to visually verify the calculated hull value. Literally, verification at a glance.
From Visual Value Verification to automated tests #
You may object to this approach because such testing isn't sustainable. Ultimately, we'd like to have a suite of automated tests that can give us a succeed or failure result.
Still, the ability to visually verify the calculated hull values enabled me to produce a set of input points, as well as calculated hull points that I knew to be correct. I could, for example, use the randomPoints function to produce 100 input sets. For each of these 100 input sets, I could visually inspect the diagrams.
Here's an example of six diagrams, instead of 100, just to give you an idea about how quickly you can verify such a set:
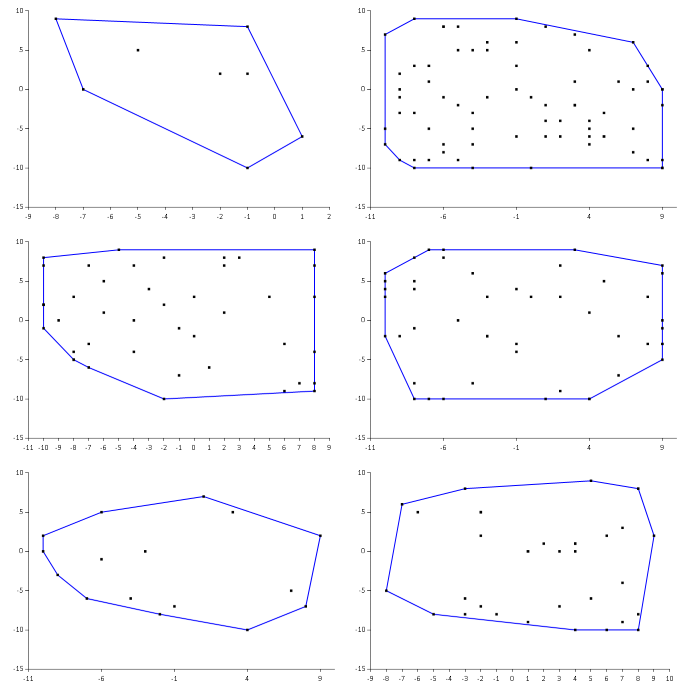
If all of the generated diagrams look okay, you know that for at least these 100 sets, the output of the hull function is correct. You can now capture those input values and the corresponding (correct) output values as a parametrised test. Here's an xUnit.net example with five test cases:
// No [<ClassData>] attribute in xUnit.net 2.0 :( type HullDataAttribute() = inherit Xunit.Sdk.DataAttribute () override this.GetData testMethod = // The following input data comes from randomly generated points. // The expected values come from a prototype of the hull function where // the output was subsequently visually inspected by drawing the input // points and the calculated hull on a coordinate system to verify that // the hull prototype function calculated the correct values. seq { yield [| // Points (input): [(3, 1); (3, 7); (2, 5); (2, 4); (1, 6); (2, 3); (1, 2)] // Expected: [(3, 1); (3, 7); (1, 6); (1, 2)] |] yield [| [(1, -4); (2, 5); (1, 3); (1, -3); (1, -2); (0, 4)] [(1, -4); (2, 5); (0, 4)] |] yield [| [(1, 1); (0, 3); (-2, 1); (-4, 3); (5, 2); (3, 2); (5, 5); (2, 5); (1, 3); (1, -3); (1, -2); (7, -4); (-1, 1); (-3, 0); (-5, -2); (1, -4); (0, 1); (0, 4); (3, -3); (6, 1)] [(1, -4); (7, -4); (6, 1); (5, 5); (2, 5); (-4, 3); (-5, -2)] |] yield [| [(-7, -7); (4, -7); (2, 3); (4, 4); (3, 1); (2, -1); (-3, -5); (4, -2); (-1, -7); (-6, 9); (4, 4); (-8, -2); (9, 4); (3, 0); (7, 0); (-7, 3); (0, 9); (4, -7); (-7, -6); (-1, 7); (6, 5); (7, -3); (-8, -8); (-6, -2); (3, 5); (-5, 7); (8, 1); (3, -2); (-9, -4); (-7, 8)] [(-8, -8); (4, -7); (7, -3); (9, 4); (0, 9); (-6, 9); (-7, 8); (-9, -4)] |] yield [| [(3, -3); (-9, -3); (0, 7); (3, 8); (3, -9); (1, 3); (-9, 5); (-4, 9); (-2, -10); (8, -2); (-4, 2); (-7, -9); (-5, -10); (0, 2); (9, -7); (6, -4); (4, 7); (-9, -7); (2, 1); (-3, -5); (-5, -1); (9, 6); (-3, 1); (6, -6); (-5, -4); (-6, 5); (0, 9); (-2, -9); (-6, -10); (-8, -1); (-4, -9); (8, -1); (-5, -5); (9, -6); (4, -8); (-3, 7); (2, 3); (-8, 6); (3, -4); (3, 4); (-6, -5); (-4, 3); (9, -10); (5, 4); (-1, 9); (9, 1); (-1, 7); (8, -7); (1, -1); (0, -9); (2, 1); (0, -8); (8, -3); (-8, 7); (7, 1); (-2, 8); (-4, -2); (-5, -10); (4, -6); (0, -5); (-1, -6); (5, 4); (-7, 6); (-3, 4); (4, 8); (-6, -7); (5, 2); (-9, 2); (5, -6); (4, 2); (7, 8); (7, 7)] [(-6, -10); (-5, -10); (-2, -10); (9, -10); (9, -7); (9, -6); (9, 1); (9, 6); (7, 8); (0, 9); (-1, 9); (-4, 9); (-8, 7); (-9, 5); (-9, 2); (-9, -3); (-9, -7)] |] } [<Theory; HullData>] let ``hull returns correct result`` (points : (int * int) list) (expected : (int * int) list) = let actual = hull points expected =! actual
(The =! operator is an assertion operator from Unquote; read it as should equal - i.e. expected should equal actual.)
This gives you a deterministic test suite you can run repeatedly to protect the hull function against regressions.
Summary #
Sometimes, the nature of the problem is such that the easiest way to verify that the System Under Test (SUT) produces the correct results, is to visually verify the resulting value of exercising the SUT. We can call this Visual Value Verification (VVV).
In this article, I used the problem of finding the convex hull for a set of points as an example, but I've encountered other problems where this technique has proven useful. The most prominent that comes to mind is when implementing Conway's Game of Life; that's another problem where, just by looking at lists of numbers, you can't easily verify that your implementation is correct.
Once you've visually verified that output looks correct, you can capture the known input and output into a test case that you can run repeatedly.
