Pure times in Haskell by Mark Seemann
A Polling Consumer implementation written in Haskell.
As you can read in the introductory article, I've come to realise that the Polling Consumer that I originally wrote in F# isn't particularly functional. Being the friendly and productive language that it is, F# doesn't protect you from mixing pure and impure code, but Haskell does. For that reason, you can develop a prototype in Haskell, and later port it to F#, if you want to learn how to solve the problem in a strictly functional way.
To recapitulate, the task is to implement a Polling Consumer that runs for a predefined duration, after which it exits (so that it can be restarted by a scheduler).
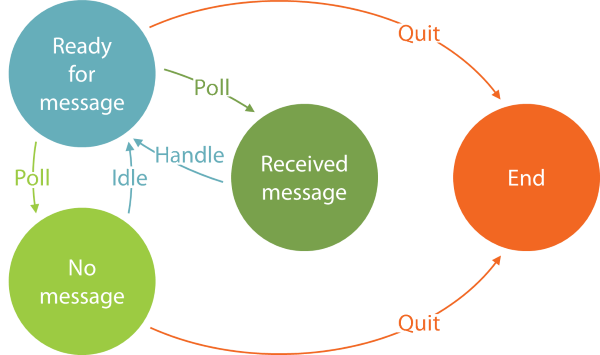
The program is a finite state machine that moves between four states. From the ready state, it'll need to decide whether to poll for a new message or exit. Polling and handling takes time (and at compile-time we don't know how long), and the program ought to stop at a pre-defined time. If it gets too close to that time, it should exit, but otherwise, it should attempt to handle a message (and keep track of how long this takes). You can read a more elaborate description of the problem in the original article.
State data types #
The premise in that initial article was that F#'s type system is so powerful that it can aid you in designing a good solution. Haskell's type system is even more powerful, so it can give you even better help.
The Polling Consumer program must measure and keep track of how long it takes to poll, handle a message, or idle. All of these are durations. In Haskell, we can represent them as NominalDiffTime values. I'm a bit concerned, though, that if I represent all of these durations as NominalDiffTime values, I may accidentally use a poll duration where I really need a handle duration, and so on. Perhaps I'm being overly cautious, but I like to get help from the type system. In the words of Igal Tabachnik, types prevent typos:
newtype PollDuration = PollDuration NominalDiffTime deriving (Eq, Show) newtype IdleDuration = IdleDuration NominalDiffTime deriving (Eq, Show) newtype HandleDuration = HandleDuration NominalDiffTime deriving (Eq, Show) data CycleDuration = CycleDuration { pollDuration :: PollDuration, handleDuration :: HandleDuration } deriving (Eq, Show)
This simply declares that PollDuration, IdleDuration, and HandleDuration are all NominalDiffTime values, but you can't mistakenly use a PollDuration where a HandleDuration is required, and so on.
In addition to those three types of duration, I also define a CycleDuration. This is the data that I actually need to keep track of: how long does it take to handle a single message? I'm assuming that polling for a message is an I/O-bound operation, so it may take significant time. Likewise, handling a message may take time. When deciding whether to exit or handle a new message, both durations count. Instead of defining CycleDuration as a newtype alias for NominalDiffTime, I decided to define it as a record type comprised of a PollDuration and a HandleDuration. It's not that I'm really interested in keeping track of these two values individually, but it protects me from making stupid mistakes. I can only create a CycleDuration value if I have both a PollDuration and a HandleDuration value.
In short, I'm trying to combat primitive obsession.
With these duration types in place, you can define the states of the finite state machine:
data PollingState msg = Ready [CycleDuration] | ReceivedMessage [CycleDuration] PollDuration msg | NoMessage [CycleDuration] PollDuration | Stopped [CycleDuration] deriving (Show)
Like the original F# code, state data can be represented as a sum type, with a case for each state. In all four cases, a CycleDuration list keeps track of the observed message-handling statistics. This is the way the program should attempt to calculate whether it's safe to handle another message, or exit. Two of the cases (ReceivedMessage and NoMessage) also contain a PollDuration, which informs the program about the duration of the poll operation that caused it to reach that state. Additionally, the ReceivedMessage case contains a message of the generic type msg. This makes the entire PollingState type generic. A message can be of any type: a string, a number, or a complex data structure. The Polling Consumer program doesn't care, because it doesn't handle messages; it only schedules the polling.
This is reminiscent of the previous F# attempt, with the most notable difference that it doesn't attempt to capture durations as Timed<'a> values. It does capture durations, but not when the operations started and stopped. So how will it know what time it is?
Interactions as pure values #
This is the heart of the matter. The Polling Consumer must constantly look at the clock. It's under a deadline, and it must also measure durations of poll, handle, and idle operations. All of this is non-deterministic, so not pure. The program has to interact with impure operations during its entire lifetime. In fact, its ultimate decision to exit will be based on impure data. How can you model this in a pure fashion?
You can model long-running (impure) interactions by defining a small instruction set for an Abstract Syntax Tree (AST). That sounds intimidating, but once you get the hang of it, it becomes routine. In later articles, I'll expand on this, but for now I'll refer you to an excellent article by Scott Wlaschin, who explains the approach in F#.
data PollingInstruction msg next = CurrentTime (UTCTime -> next) | Poll ((Maybe msg, PollDuration) -> next) | Handle msg (HandleDuration -> next) | Idle IdleDuration (IdleDuration -> next) deriving (Functor)
This PollingInstruction sum type defines four cases of interaction. Each case is
- named after the interaction
- defines the type of data used as input arguments for the interaction
- and also defines a continuation; that is: a function that will be executed with the return value of the interaction
Handle case contains all three elements: the interaction is named Handle, the input to the interaction is of the generic type msg, and the continuation is a function that takes a HandleDuration value as input, and returns a value of the generic type next. In other words, the interaction takes a msg value as input, and returns a HandleDuration value as output. That duration is the time it took to handle the input message. (The intent is that the operation that 'implements' this interaction also actually handles the message, whatever that means.)
Likewise, the Idle interaction takes an IdleDuration as input, and also returns an IdleDuration. The intent here is that the 'implementation' of the interaction suspends itself for the duration of the input value, and returns the time it actually spent in suspension (which is likely to be slightly longer than the requested duration).
Both CurrentTime and Poll, on the other hand, are degenerate, because they take no input. You don't need to supply any input argument to read the current time. You could model that interaction as taking () ('unit') as an input argument (CurrentTime () (UTCTime -> next)), but the () is redundant and can be omitted. The same is the case for the Poll case, which returns a Maybe msg and how long the poll took.
(The PollingInstruction sum type defines four cases, which is also the number of cases defined by PollingState. This is a coincidence; don't read anything into it.)
The PollingInstruction type is generic in a way that you can make it a Functor. Haskell can do this for you automatically, using the DeriveFunctor language extension; that's what deriving (Functor) does. If you'd like to see how to explicitly make such a data structure a functor, please refer to the F# example; F# can't automatically derive functors, so you'll have to do it manually.
Since PollingInstruction is a Functor, we can make a Monad out of it. You use a free monad, which allows you to build a monad from any functor:
type PollingProgram msg = Free (PollingInstruction msg)
In Haskell, it's literally a one-liner, but in F# you'll have to write the code yourself. Thus, if you're interested in learning how this magic happens, I'm going to dissect this step in the next article.
The motivation for defining a Monad is that we get automatic syntactic sugar for our PollingProgram ASTs, via Haskell's do notation. In F#, we're going to write a computation expression builder to achieve the same effect.
The final building blocks for the specialised PollingProgram API is a convenience function for each case:
currentTime :: PollingProgram msg UTCTime currentTime = liftF (CurrentTime id) poll :: PollingProgram msg (Maybe msg, PollDuration) poll = liftF (Poll id) handle :: msg -> PollingProgram msg HandleDuration handle msg = liftF (Handle msg id) idle :: IdleDuration -> PollingProgram msg IdleDuration idle d = liftF (Idle d id)
More one-liners, as you can tell. These all use liftF to turn PollingInstruction cases into PollingProgram values. The degenerate cases CurrentTime and Poll simply become values, whereas the complete cases become (pure) functions.
Support functions #
You may have noticed that until now, I haven't written much 'code' in the sense that most people think of it. It's mostly been type declarations and a few one-liners. A strong and sophisticated type system like Haskell's enable you to shift some of the programming burden from 'real programming' to type definitions, but you'll still have to write some code.
Before we get to the state transitions proper, we'll look at some support functions. These will, I hope, serve as a good introduction to how to use the PollingProgram API.
One decision the Polling Consumer program has to make is to decide whether it should suspend itself for a short time. That's easy to express using the API:
shouldIdle :: IdleDuration -> UTCTime -> PollingProgram msg Bool shouldIdle (IdleDuration d) stopBefore = do now <- currentTime return $ d `addUTCTime` now < stopBefore
The shouldIdle function returns a small program that, when evaluated, will decide whether or not to suspend itself. It first reads the current time using the above currentTime value. While currentTime has the type PollingProgram msg UTCTime, due to Haskell's do notation, the now value simply has the type UTCTime. This enables you to use the built-in addUTCTime function (here written using infix notation) to add now to d (a NominalDiffTime value, due to pattern matching into IdleDuration).
Adding the idle duration d to the current time now gives you the time the program would resume, were it to suspend itself. The shouldIdle function compares that time to the stopBefore argument (another UTCTime value). If the time the program would resume is before the time it ought to stop, the return value is True; otherwise, it's False.
Since the entire function is defined within a do block, the return type isn't just Bool, but rather PollingProgram msg Bool. It's a little PollingProgram AST, but it looks like imperative code.
You sometimes hear the bon mot that Haskell is the world's greatest imperative language. The combination of free monads and do notation certainly makes it easy to define small grammars (dare I say DSLs?) that look like imperative code, while still being strictly functional.
The crux is that shouldIdle is pure. It looks impure, but it's not. It's an Abstract Syntax Tree, and it only becomes non-deterministic if interpreted by an impure interpreter (more on that later).
The purpose of shouldIdle is to decide whether or not to idle or exit. If the program decides to idle, it should return to the ready state, as per the above state diagram. In this state, it needs to decide whether or not to poll for a message. If there's a message, it should be handled, and all of that takes time. In the ready state, then, the program must figure out how much time it thinks that handling a message will take.
One way to do that is to consider the observed durations so far. This helper function calculates the expected duration based on the average and standard deviation of the previous durations:
calculateExpectedDuration :: NominalDiffTime -> [CycleDuration] -> NominalDiffTime calculateExpectedDuration estimatedDuration [] = estimatedDuration calculateExpectedDuration _ statistics = toEnum $ fromEnum $ avg + stdDev * 3 where fromCycleDuration :: CycleDuration -> Float fromCycleDuration (CycleDuration (PollDuration pd) (HandleDuration hd)) = toEnum $ fromEnum $ pd + hd durations = fmap fromCycleDuration statistics l = toEnum $ length durations avg = sum durations / l stdDev = sqrt (sum (fmap (\x -> (x - avg) ** 2) durations) / l)
I'm not going to dwell much on this function, as it's a normal, pure, mathematical function. The only feature I'll emphasise is that in order to call it, you must pass an estimatedDuration that will be used when statistics is empty. This is because you can't calculate the average of an empty list. This estimated duration is simply your wild guess at how long you think it'll take to handle a message.
With this helper function, you can now write a small PollingProgram that decides whether or not to poll:
shouldPoll :: NominalDiffTime -> UTCTime -> [CycleDuration] -> PollingProgram msg Bool shouldPoll estimatedDuration stopBefore statistics = do let expectedHandleDuration = calculateExpectedDuration estimatedDuration statistics now <- currentTime return $ expectedHandleDuration `addUTCTime` now < stopBefore
Notice that the shouldPoll function looks similar to shouldIdle. As an extra initial step, it first calculates expectedHandleDuration using the above calculateExpectedDuration function. With that, it follows the same two steps as shouldIdle.
This function is also pure, because it returns an AST. While it looks impure, it's not, because it doesn't actually do anything.
Transitions #
Those are all the building blocks required to write the state transitions. In order to break down the problem in manageable chunks, you can write a transition function for each state. Such a function would return the next state, given a particular input state.
While it'd be intuitive to begin with the ready state, let's instead start with the simplest transition. In the end state, nothing should happen, so the transition is a one-liner:
transitionFromStopped :: Monad m => [CycleDuration] -> m (PollingState msg) transitionFromStopped statistics = return $ Stopped statistics
Once stopped, the program stays in the Stopped state. This function simply takes a list of CycleDuration values and elevates them to a monad type. Notice that the return value isn't specifically a PollingProgram, but any monad. Since PollingProgram is a monad, that'll work too, though.
Slightly more complicated than transitionFromStopped is the transition from the received state. There's no branching in that case; simply handle the message, measure how long it took, add the observed duration to the statistics, and transition back to ready:
transitionFromReceived :: [CycleDuration] -> PollDuration -> msg -> PollingProgram msg (PollingState msg) transitionFromReceived statistics pd msg = do hd <- handle msg return $ Ready (CycleDuration pd hd : statistics)
Again, this looks impure, but the return type is PollingProgram msg (PollingState msg), indicating that the return value is an AST. As is not uncommon in Haskell, the type declaration is larger than the implementation.
Things get slightly more interesting in the no message state. Here you get to use the above shouldIdle support function:
transitionFromNoMessage :: IdleDuration -> UTCTime -> [CycleDuration] -> PollingProgram msg (PollingState msg) transitionFromNoMessage d stopBefore statistics = do b <- shouldIdle d stopBefore if b then idle d >> return (Ready statistics) else return $ Stopped statistics
The first step in transitionFromNoMessage is calling shouldIdle. Thanks to Haskell's do notation, the b value is a simple Bool value that you can use to branch. If b is True, then first call idle and then return to the Ready state; otherwise, exit to the Stopped state.
Notice how PollingProgram values are composable. For instance, shouldIdle defines a small PollingProgram that can be (re)used in a bigger program, such as in transitionFromNoMessage.
Finally, from the ready state, the program can transition to three other states, so this is the most complex transition:
transitionFromReady :: NominalDiffTime -> UTCTime -> [CycleDuration] -> PollingProgram msg (PollingState msg) transitionFromReady estimatedDuration stopBefore statistics = do b <- shouldPoll estimatedDuration stopBefore statistics if b then do pollResult <- poll case pollResult of (Just msg, pd) -> return $ ReceivedMessage statistics pd msg (Nothing , pd) -> return $ NoMessage statistics pd else return $ Stopped statistics
Like transitionFromNoMessage, the transitionFromReady function first calls a supporting function (this time shouldPoll) in order to make a decision. If b is False, the next state is Stopped; otherwise, the program moves on to the next step.
The program polls for a message using the poll helper function defined above. While poll is a PollingProgram msg (Maybe msg, PollDuration) value, thanks to do notation, pollResult is a Maybe msg, PollDuration value. Matching on that value requires you to handle two separate cases: If a message was received (Just msg), then return a ReceivedMessage state with the message. Otherwise (Nothing), return a NoMessage state.
With those four functions you can now define a function that can transition from any input state:
transition :: NominalDiffTime -> IdleDuration -> UTCTime -> PollingState msg -> PollingProgram msg (PollingState msg) transition estimatedDuration idleDuration stopBefore state = case state of Ready stats -> transitionFromReady estimatedDuration stopBefore stats ReceivedMessage stats pd msg -> transitionFromReceived stats pd msg NoMessage stats _ -> transitionFromNoMessage idleDuration stopBefore stats Stopped stats -> transitionFromStopped stats
The transition function simply pattern-matches on the input state and delegates to each of the four above transition functions.
A short philosophical interlude #
All code so far has been pure, although it may not look that way. At this stage, it may be reasonable to pause and consider: what's the point, even?
After all, when interpreted, a PollingProgram can (and, in reality, almost certainly will) have impure behaviour. If we create an entire executable upon this abstraction, then we've essentially developed a big program with impure behaviour...
Indeed we have, but the alternative would have been to write it all in the context of IO. If you'd done that, then you'd allow any non-deterministic, side-effecty behaviour anywhere in your program. At least with a PollingProgram, any reader will quickly learn that only a maximum of four impure operations can happen. In other words, you've managed to control and restrict the impurity to exactly those interactions you want to model.
Not only that, but the type of impurity is immediately visible as part of a value's type. In a later article, you'll see how different impure interaction APIs can be composed.
Interpretation #
At this point, you have a program in the form of an AST. How do you execute it?
You write an interpreter:
interpret :: PollingProgram Message a -> IO a interpret program = case runFree program of Pure r -> return r Free (CurrentTime next) -> getCurrentTime >>= interpret . next Free (Poll next) -> pollImp >>= interpret . next Free (Handle msg next) -> handleImp msg >>= interpret . next Free (Idle d next) -> idleImp d >>= interpret . next
When you turn a functor into a monad using the Free constructor (see above), your functor is wrapped in a general-purpose sum type with two cases: Pure and Free. Your functor is always contained in the Free case, whereas Pure is the escape hatch. This is where you return the value of the entire computation.
An interpreter must match both Pure and Free. Pure is easy, because you simply return the result value.
In the Free case, you'll need to match each of the four cases of PollingInstruction. In all four cases, you invoke an impure implementation function, pass its return value to next, and finally recursively invoke interpret with the value returned by next.
Three of the implementations are details that aren't of importance here, but if you want to review them, the entire source code for this article is available as a gist. The fourth implementation is the built-in getCurrentTime function. They are all impure; all return IO values. This also implies that the return type of the entire interpret function is IO a.
This particular interpreter is impure, but nothing prevents you from writing a pure interpreter, for example for use in unit testing.
Execution #
You're almost done. You have a function that returns a new state for any given input state, as well as an interpreter. You need a function that can repeat this in a loop until it reaches the Stopped state:
run :: NominalDiffTime -> IdleDuration -> UTCTime -> PollingState Message -> IO (PollingState Message) run estimatedDuration idleDuration stopBefore state = do ns <- interpret $ transition estimatedDuration idleDuration stopBefore state case ns of Stopped _ -> return ns _ -> run estimatedDuration idleDuration stopBefore ns
This recursive function calls transition with the input state. You may recall that transition returns a PollingProgram msg (PollingState msg) value. Passing this value to interpret returns an IO (PollingState Message) value, and because of the do notation, the new state (ns) is a PollingState Message value.
You can now pattern match on ns. If it's a Stopped value, you return the value. Otherwise, you recursively call run once more.
The run function keeps doing this until it reaches the Stopped state.
Finally, then, you can write the entry point for the program:
main :: IO () main = do timeAtEntry <- getCurrentTime let estimatedDuration = 2 let idleDuration = IdleDuration 5 let stopBefore = addUTCTime 60 timeAtEntry s <- run estimatedDuration idleDuration stopBefore $ Ready [] timeAtExit <- getCurrentTime putStrLn $ "Elapsed time: " ++ show (diffUTCTime timeAtExit timeAtEntry) putStrLn $ printf "%d message(s) handled." $ report s
It defines the initial input parameters:
- My wild guess about the handle duration is 2 seconds
- I'd like the idle duration to be 5 seconds
- The program should run for 60 seconds
Ready []. These are all the arguments you need to call run.
Once run returns, you can print the number of messages handled using a (trivial) report function that I haven't shown (but which is available in the gist).
If you run the program, it'll produce output similar to this:
Polling Handling Polling Handling Polling Handling Polling Sleeping Polling Handling Polling Sleeping Polling Handling Polling Handling Polling Sleeping Polling Sleeping Polling Sleeping Polling Sleeping Polling Sleeping Polling Handling Polling Handling Polling Handling Polling Handling Polling Sleeping Polling Elapsed time: 56.6835022s 10 message(s) handled.
It does, indeed, exit before 60 seconds have elapsed.
Summary #
You can model long-running interactions with an Abstract Syntax Tree. Without do notation, writing programs as 'raw' ASTs would be cumbersome, but turning the AST into a (free) monad makes it all quite palatable.
Haskell's sophisticated type system makes this a fairly low-hanging fruit, once you understand how to do it. You can also port this type of design to F#, although, as you shall see next, more boilerplate is required.
Next: Pure times in F#.

Comments
Good introduction to the notion of programs-as-embedded-languages here, thanks for writing it!
In my experience a majority of
Freeinterpreters fit into thefoldFreepattern. Saves you the repetitous bits of yourinterpretfunction:Anyway, I just wanted to give an alternative viewpoint on the topic of
Freewhich will hopefully be some food for thought. I'm generally not an advocate of theFreeapproach to modelling effectful computation. I don't think it has much of an advantage over the old fashionedmtlstyle, especially since you have only one effect and only one interpreter. I'd have written your interface like this:It's a clearer, more direct expression of the monadic interface, in my opinion, and it admits simpler implementations (and it's faster because GHC can specialise and inline everything). Computations with access to only a
MonadPollcontext can only perform polling actions, so it's still pure, and you can swap out different implementations ofMonadPoll(eg, for testing) by writing types with different instances. You can do eg this if you need "decorator"-style interpreters. The main downside of themtlstyle is the "n^2 instances problem" (thoughGeneralizedNewtypeDerivingdoes somewhat ease the pain).Kiselyov has some good lecture notes about using the
mtlstyle to model abstract syntax trees and compositional interpreters. I probably wouldn't go that far if I were building a compiler! Type classes are good at effect systems and algebraic data types are good at syntax trees, and while each job can be done by either it pays to pick your tools carefully.Having said all that, the
Freeapproach is probably more attractive in F#, because it doesn't feature type classes or higher kinds. AndFreehas other uses outside of the world of effect systems.Hope all the above is interesting to you!
Benjamin
Benjamin, thank you for writing. It is, indeed, interesting to me, and I appreciate that you took the time to write such a helpful and concise comment.
I wasn't aware of
foldFree, but I can see that I'll have to look into it.One day (soon), I'll have to try writing a small Haskell program using the
mtlstyle instead. It looks as though the code would be quite similar, although the types are different. Are these approaches isomorphic?In any case, I hope that I'm not coming off as being too authoritative. In some sense, this blog often serves as my own elaborate journal documenting what I've been learning recently. I hope that what I write is mostly correct, but I don't presume that what I write is the one and only truth; it's bound by my knowledge at the time of writing. I still have much to learn, and I'm always happy when people help me expand my horizon.
I think that you hit the nail concerning F#. One of my motivations for exploring this space was to figure out what can be done in F#. As far as I can tell, the
mtlstyle doesn't translate well to F#. You can debate whether or not free monads translate well to F#, but at least the concept does carry over.Yep, they're isomorphic, in that you can round-trip in either direction between the two representations -
to . from = from . to = id:instance MonadPoll msg (Free (PollingInstruction msg)) where currentTime = liftF (CurrentTime id) poll = liftF (Poll id) handle msg = liftF (Handle msg id) idle d = liftF (Idle d id) to :: (forall m. MonadPoll msg m => m a) -> Free (PollingInstruction msg) a to x = x from :: MonadPoll msg m => Free (PollingInstruction msg) a -> m a from x = foldFree eta where eta (CurrentTime k) = k <$> currentTime eta (Poll k) = k <$> poll eta (Handle msg k) = k <$> handle msg eta (Idle d k) = k <$> idle dBut the representations being isomorphic doesn't mean they're equally convenient. (Another example of this would be lenses: van Laarhoven lenses (à la
lens) are isomorphic to "costate comonad coalgebra" (ieget/set) lenses, but they're much more composable.)Benjamin
Benjamin, thank you once again for writing. It's amazing that not only are they isomorphic, but you can actually prove it with code. I have to admit, though, that I haven't tried compiling or running your code yet. First, I need to digest this.
I was never under the impression that I knew most of what there was to know, but by Jove!, poking at Haskell unearths fathomless depths of knowledge of which I still only glance the surface. It's occasionally frustrating, but mostly exhilarating.