Magmas by Mark Seemann
A binary operation with no constraints on its behaviour is called a magma. An introduction for object-oriented programmers.
In the overall article series about group-like algebraic structures, you've so far seen examples of monoids, semigroups, and quasigroups. Common to all of these structures is that they are binary operations governed by at least one law. The laws are different for the different categories, but there are rules.
What if you have a binary operation that follows none of those rules?
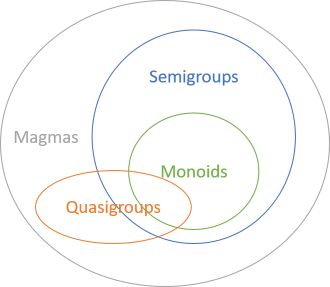
All binary operations are magmas. If they have additional properties, we may call them quasigroups, or monoids, or some such, depending on the specific properties, but they're still all magmas. This is the most inclusive category.
You've already seen examples of monoids and semigroups, but what about magma examples? In a sense, you've already seen those as well, because all the examples you've seen so far have also been magma examples. After all, since all monoids are magmas, all the monoid examples you've seen have also been magma examples.
Still, it's not that hard to come up with some programming examples of magmas that aren't semi- or quasigroups. In the next articles, you'll see some examples.
Particularly the second example is fairly realistic, which demonstrates that as programmers, we can benefit from having vocabulary that enables us to describe any binary operation that doesn't obey any particular laws. In fact, establishing a vocabulary has been my primary motivation for writing this article series.