Maybe catamorphism by Mark Seemann
The catamorphism for Maybe is just a simplification of its fold.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for Maybe, as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
Maybe is a data container that models the absence or presence of a value. Contrary to null, Maybe has a type, so offers a sane and reasonable way to model that situation.
C# catamorphism #
This article uses Church-encoded Maybe. Other, alternative implementations of Maybe are possible. The catamorphism for Maybe is the Match method:
TResult Match<TResult>(TResult nothing, Func<T, TResult> just);
Like the Peano catamorphism, the Maybe catamorphism is a pair of a value and a function. The nothing value corresponds to the absence of data, whereas the just function handles the presence of data.
Given, for example, a Maybe containing a number, you can use Match to get the value out of the Maybe:
> IMaybe<int> maybe = new Just<int>(42); > maybe.Match(0, x => x) 42 > IMaybe<int> maybe = new Nothing<int>(); > maybe.Match(0, x => x) 0
The functionality is, however, more useful than a simple get-value-or-default operation. Often, you don't have a good default value for the type potentially wrapped in a Maybe object. In the core of your application architecture, it may not be clear how to deal with, say, the absence of a Reservation object, whereas at the boundary of your system, it's evident how to convert both absence and presence of data into a unifying type, such as an HTTP response:
Maybe<Reservation> maybe = // ... return maybe .Select(r => Repository.Create(r)) .Match<IHttpActionResult>( nothing: Content( HttpStatusCode.InternalServerError, new HttpError("Couldn't accept.")), just: id => Ok(id));
This enables you to avoid special cases, such as null Reservation objects, or magic numbers like -1 to indicate the absence of id values. At the boundary of an HTTP-based application, you know that you must return an HTTP response. That's the unifying type, so you can return 200 OK with a reservation ID in the response body when data is present, and 500 Internal Server Error when data is absent.
Maybe F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
While F-Algebras and fixed points are mostly used for recursive data structures, you can also define an F-Algebra for a non-recursive data structure. You already saw an example of that in the article about Boolean catamorphism. The difference between Boolean values and Maybe is that the just case of Maybe carries a value. You can model this as a Functor with both a carrier type and a type argument for the data that Maybe may contain:
data MaybeF a c = NothingF | JustF a deriving (Show, Eq, Read) instance Functor (MaybeF a) where fmap _ NothingF = NothingF fmap _ (JustF x) = JustF x
I chose to call the 'data type' a and the carrier type c (for carrier). As was also the case with BoolF, the Functor instance ignores the map function because the carrier type is missing from both the NothingF case and the JustF case. Like the Functor instance for BoolF, it'd seem that nothing happens, but at the type level, this is still a translation from MaybeF a c to MaybeF a c1. Not much of a function, perhaps, but definitely an endofunctor.
In the previous articles, it was possible to work directly with the fixed points of both functors; i.e. Fix BoolF and Fix NatF. Haskell isn't happy about attempts to define various instances for Fix (MaybeF a), so in order to make this easier, you can define a newtype wrapper:
newtype MaybeFix a = MaybeFix { unMaybeFix :: Fix (MaybeF a) } deriving (Show, Eq, Read)
In order to make it easier to work with MaybeFix you can add helper functions to create values:
nothingF :: MaybeFix a nothingF = MaybeFix $ Fix NothingF justF :: a -> MaybeFix a justF = MaybeFix . Fix . JustF
You can now create MaybeFix values to your heart's content:
Prelude Fix Maybe> justF 42
MaybeFix {unMaybeFix = Fix (JustF 42)}
Prelude Fix Maybe> nothingF
MaybeFix {unMaybeFix = Fix NothingF}
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (MaybeF), and an object a, but you still need to find a morphism MaybeF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.
As in the previous article, start by writing a function that will become the catamorphism, based on cata:
maybeF = cata alg . unMaybeFix where alg NothingF = undefined alg (JustF x) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the NothingF case? You could pass an argument to the maybeF function:
maybeF n = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = undefined
The JustF case, contrary to NothingF, already contains a value, and it'd be incorrect to ignore it. On the other hand, x is a value of type a, and you need to return a value of type c. You'll need a function to perform the conversion, so pass such a function as an argument to maybeF as well:
maybeF :: c -> (a -> c) -> MaybeFix a -> c maybeF n f = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = f x
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of MaybeF, the compiler infers that the alg function has the type MaybeF a c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
Notice that maybeF, like the above C# Match method, takes as arguments a pair of a value and a function (together with the Maybe value itself). Those are two representations of the same idea. Furthermore, this is nearly identical to the maybe function in Haskell's Data.Maybe module. I found it fitting, therefore, to name the function maybeF.
Basis #
You can implement most other useful functionality with maybeF. Here's the Functor instance:
instance Functor MaybeFix where fmap f = maybeF nothingF (justF . f)
Since fmap should be a structure-preserving map, you'll have to map the nothing case to the nothing case, and just to just. When calling maybeF, you must supply a value for the nothing case and a function to deal with the just case. The nothing case is easy to handle: just use nothingF.
In the just case, first apply the function f to map from a to b, and then use justF to wrap the b value in a new MaybeFix container to get MaybeFix b.
Applicative is a little harder, but not much:
instance Applicative MaybeFix where pure = justF f <*> x = maybeF nothingF (<$> x) f
The pure function is just justF (pun intended). The apply operator <*> is more complex.
Both f and x surrounding <*> are MaybeFix values: f is MaybeFix (a -> b), and x is MaybeFix a. While it's becoming increasingly clear that you can use a catamorphism like maybeF to implement most other functionality, to which MaybeFix value should you apply it? To f or x?
Both are possible, but the code looks (in my opinion) more readable if you apply it to f. Again, when f is nothing, return nothingF. When f is just, use the functor instance to map x (using the infix fmap alias <$>).
The Monad instance, on the other hand, is almost trivial:
instance Monad MaybeFix where x >>= f = maybeF nothingF f x
As usual, map nothing to nothing by supplying nothingF. f is already a function that returns a MaybeFix b value, so just use that.
The Foldable instance is likewise trivial (although, as you'll see below, you can make it even more trivial):
instance Foldable MaybeFix where foldMap = maybeF mempty
The foldMap function must return a Monoid instance, so for the nothing case, simply return the identity, mempty. Furthermore, foldMap takes a function a -> m, but since the foldMap implementation is point-free, you can't 'see' that function as an argument.
Finally, for the sake of completeness, here's the Traversable instance:
instance Traversable MaybeFix where sequenceA = maybeF (pure nothingF) (justF <$>)
In the nothing case, you can put nothingF into the desired Applicative with pure. In the just case you can take advantage of the desired Applicative being also a Functor by simply mapping the inner value(s) with justF.
Since the Applicative instance for MaybeFix equals pure to justF, you could alternatively write the Traversable instance like this:
instance Traversable MaybeFix where sequenceA = maybeF (pure nothingF) (pure <$>)
I like this alternative less, since I find it confusing. The two appearances of pure relate to two different types. The pure in pure nothingF has the type MaybeFix a -> f (MaybeFix a), while the pure in pure <$> has the type a -> MaybeFix a!
Both implementations work the same, though:
Prelude Fix Maybe> sequenceA (justF ("foo", 42))
("foo",MaybeFix {unMaybeFix = Fix (JustF 42)})
Here, I'm using the Applicative instance of (,) String.
Finally, you can implement conversions to and from the standard Maybe type, using ana as the dual of cata:
toMaybe :: MaybeFix a -> Maybe a toMaybe = maybeF Nothing return fromMaybe :: Maybe a -> MaybeFix a fromMaybe = MaybeFix . ana coalg where coalg Nothing = NothingF coalg (Just x) = JustF x
This demonstrates that MaybeFix is isomorphic to Maybe, which again establishes that maybeF and maybe are equivalent.
Alternatives #
As usual, the above maybeF isn't the only possible catamorphism. A trivial variation is to flip its arguments, but other variations exist.
It's a recurring observation that a catamorphism is just a generalisation of a fold. In the above code, the Foldable instance already looked as simple as anyone could desire, but another variation of a catamorphism for Maybe is this gratuitously embellished definition:
maybeF :: (a -> c -> c) -> c -> MaybeFix a -> c maybeF f n = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = f x n
This variation redundantly passes n as an argument to f, thereby changing the type of f to a -> c -> c. There's no particular motivation for doing this, apart from establishing that this catamorphism is exactly the same as the fold:
instance Foldable MaybeFix where foldr = maybeF
You can still implement the other instances as well, but the rest of the code suffers in clarity. Here's a few examples:
instance Functor MaybeFix where fmap f = maybeF (const . justF . f) nothingF instance Applicative MaybeFix where pure = justF f <*> x = maybeF (const . (<$> x)) nothingF f instance Monad MaybeFix where x >>= f = maybeF (const . f) nothingF x
I find that the need to compose with const does nothing to improve the readability of the code, so this variation is mostly, I think, of academic interest. It does show, though, that the catamorphism of Maybe is isomorphic to its fold, as the diagram in the overview article indicated:
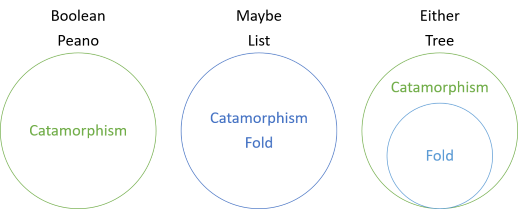
You can demonstrate that this variation, too, is isomorphic to Maybe with a set of conversion:
toMaybe :: MaybeFix a -> Maybe a toMaybe = maybeF (const . return) Nothing fromMaybe :: Maybe a -> MaybeFix a fromMaybe = MaybeFix . ana coalg where coalg Nothing = NothingF coalg (Just x) = JustF x
Only toMaybe has changed, compared to above; the fromMaybe function remains the same. The only change to toMaybe is that the arguments have been flipped, and return is now composed with const.
Since (according to Conceptual Mathematics) isomorphisms are transitive this means that the two variations of maybeF are isomorphic. The latter, more complex, variation of maybeF is identical foldr, so we can consider the simpler, more frequently encountered variation a simplification of fold.
Summary #
The catamorphism for Maybe is the same as its Church encoding: a pair made from a default value and a function. In Haskell's base library, this is simply called maybe. In the above C# code, it's called Match.
This function is total, and you can implement any other functionality you need with it. I therefore consider it the canonical representation of Maybe, which is also why it annoys me that most Maybe implementations come equipped with partial functions like fromJust, or F#'s Option.get. Those functions shouldn't be part of a sane and reasonable Maybe API. You shouldn't need them.
In this series of articles about catamorphisms, you've now seen the first example of catamorphism and fold coinciding. In the next article, you'll see another such example - probably the most well-known catamorphism example of them all.
Next: List catamorphism.
