Either catamorphism by Mark Seemann
The catamorphism for Either is a generalisation of its fold. The catamorphism enables operations not available via fold.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for Either (also known as Result), as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
Either is a data container that models two mutually exclusive results. It's often used to return values that may be either correct (right), or incorrect (left). In statically typed functional programming with a preference for total functions, Either offers a saner, more reasonable way to model success and error results than throwing exceptions.
C# catamorphism #
This article uses the Church encoding of Either. The catamorphism for Either is the Match method:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Until this article, all previous catamorphisms have been a pair made from an initial value and a function. The Either catamorphism is a generalisation, since it's a pair of functions. One function handles the case where there's a left value, and the other function handles the case where there's a right value. Both functions must return the same, unifying type, which is often a string or something similar that can be shown in a user interface:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3)); > e.Match(ts => ts.ToString(), i => i.ToString()) "00:03:00" > IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42); > e.Match(ts => ts.ToString(), i => i.ToString()) "42"
You'll often see examples like the above that turns both left and right cases into strings or something that can be represented as a unifying response type, but this is in no way required. If you can come up with a unifying type, you can convert both cases to that type:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid()); > e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length) 12 > IEither<Guid, string> e = new Right<Guid, string>("foo"); > e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length) 3
In the two above examples, you use two different functions that both reduce respectively Guid and string values to a number. The function that turns Guid values into a number counts how many of the hexadecimal digits that are greater than or equal to A (10). The other function simply returns the length of the string, if it's there. That example makes little sense, but the Match method doesn't care about that.
In practical use, Either is often used for error handling. The article on the Church encoding of Either contains an example.
Either F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
While F-Algebras and fixed points are mostly used for recursive data structures, you can also define an F-Algebra for a non-recursive data structure. You already saw an example of that in the articles about Boolean catamorphism and Maybe catamorphism. The difference between e.g. Maybe values and Either is that both cases of Either carry a value. You can model this as a Functor with both a carrier type and two type arguments for the data that Either may contain:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
I chose to call the 'data types' l (for left) and r (for right), and the carrier type c (for carrier). As was also the case with BoolF and MaybeF, the Functor instance ignores the map function because the carrier type is missing from both the LeftF case and the RightF case. Like the Functor instances for BoolF and MaybeF, it'd seem that nothing happens, but at the type level, this is still a translation from EitherF l r c to EitherF l r c1. Not much of a function, perhaps, but definitely an endofunctor.
As was also the case when deducing the Maybe and List catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (EitherF l r). To address that problem, you can introduce a newtype wrapper:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
You can define Functor, Applicative, Monad, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A pair of helper functions make it easier to define EitherFix values:
leftF :: l -> EitherFix l r leftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l r rightF = EitherFix . Fix . RightF
With those functions, you can create EitherFix values:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandom
EitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}
Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"
EitherFix {unEitherFix = Fix (RightF "foo")}
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (EitherF l r), and an object c, but you still need to find a morphism EitherF l r c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data types' l and r. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore l and r, as you'll see.
As in the previous articles, start by writing a function that will become the catamorphism, based on cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the LeftF case? You could pass an argument to the eitherF function:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
While you could, technically, pass an argument of the type c to eitherF and then return that value from the LeftF case, that would mean that you would ignore the l value. This would be incorrect, so instead, make the argument a function and call it with l. Likewise, you can deal with the RightF case in the same way:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> c eitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of EitherF, the compiler infers that the alg function has the type EitherF l r c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
This, then, is the catamorphism for Either. As has been consistent so far, it's a pair, but now made from two functions. As you've seen repeatedly, this isn't the only possible catamorphism, since you can, for example, trivially flip the arguments to eitherF.
I've chosen the representation shown here because it's isomorphic to the either function from Haskell's built-in Data.Either module, which calls the function the "Case analysis for the Either type". Both of these functions (eitherF and either) are equivalent to the above C# Match method.
Basis #
You can implement most other useful functionality with eitherF. Here's the Bifunctor instance:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
From that instance, the Functor instance trivially follows:
instance Functor (EitherFix l) where fmap = second
On top of Functor you can add Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Notice that the <*> implementation is similar to to the <*> implementation for MaybeFix. The same is the case for the Monad instance:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Not only is EitherFix Foldable, it's Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Notice, interestingly, that bifoldMap is identical to eitherF.
The Bifoldable instance enables you to trivially implement the Foldable instance:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
You may find the presence of mempty puzzling, since bifoldMap (or eitherF; they're identical) takes as arguments two functions. Is mempty a function?
Yes, mempty can be a function. Here, it is. There's a Monoid instance for any function a -> m, where m is a Monoid instance, and mempty is the identity for that monoid. That's the instance in use here.
Just as EitherFix is Bifoldable, it's also Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
You can comfortably implement the Traversable instance based on the Bitraversable instance:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Finally, you can implement conversions to and from the standard Either type, using ana as the dual of cata:
toEither :: EitherFix l r -> Either l r toEither = eitherF Left Right fromEither :: Either a b -> EitherFix a b fromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
This demonstrates that EitherFix is isomorphic to Either, which again establishes that eitherF and either are equivalent.
Relationships #
In this series, you've seen various examples of catamorphisms of structures that have no folds, catamorphisms that coincide with folds, and now a catamorphism that is more general than the fold. The introduction to the series included this diagram:
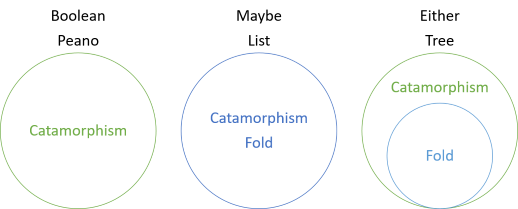
This shows that Boolean values and Peano numbers have catamorphisms, but no folds, whereas for Maybe and List, the fold and the catamorphism is the same. For Either, however, the fold is a special case of the catamorphism. The fold for Either 'pretends' that the left side doesn't exist. Instead, the left value is interpreted as a missing right value. Thus, in order to fold Either values, you must supply a 'fallback' value that will be used in case an Either value isn't a right value:
Prelude Fix Either> e = rightF LT :: EitherFix Integer Ordering Prelude Fix Either> foldr (const . show) "" e "LT" Prelude Fix Either> e = leftF 42 :: EitherFix Integer Ordering Prelude Fix Either> foldr (const . show) "" e ""
In a GHCi session like the above, you can create two Either values of the same type. The right case is an Ordering value, while the left case is an Integer value.
With foldr, there's no way to access the left case. While you can access and transform the right Ordering value, the number 42 is simply ignored during the fold. Instead, the default value "" is returned.
Contrast this with the catamorphism, which can access both cases:
Prelude Fix Either> e = rightF LT :: EitherFix Integer Ordering Prelude Fix Either> eitherF show show e "LT" Prelude Fix Either> e = leftF 42 :: EitherFix Integer Ordering Prelude Fix Either> eitherF show show e "42"
In a session like this, you recreate the same values, but using the catamorphism eitherF, you can now access and transform both the left and the right cases. In other words, the catamorphism enables you to perform operations not possible with the fold.
It's interesting, however, to note that while the fold is a specialisation of the catamorphism, the bifold is identical to the catamorphism.
Summary #
The catamorphism for Either is a pair of functions. One function transforms the left case, while the other function transforms the right case. For any Either value, only one of those functions will be used.
When I originally encountered the concept of a catamorphism, I found it difficult to distinguish between catamorphism and fold. My problem was, I think, that the tutorials I ran into mostly used linked lists to demonstrate how, in that case, the fold is the catamorphism. It turns out, however, that this isn't always the case. A catamorphism is a general abstraction. A fold, on the other hand, seems to me to be mostly related to collections.
In this article you saw the first example of a catamorphism that can do more than the fold. For Either, the fold is just a special case of the catamorphism. You also saw, however, how the catamorphism was identical to the bifold. Thus, it's still not entirely clear how these concepts relate. Therefore, in the next article, you'll get an example of a container where there's no bifold, and where the catamorphism is, indeed, a generalisation of the fold.
Next: Tree catamorphism.
