Tree catamorphism by Mark Seemann

The catamorphism for a tree is just a single function with a particular type.

This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.

This article presents the catamorphism for a tree, as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.

A tree is a general-purpose data structure where each node in a tree has an associated value. Each node can have an arbitrary number of branches, including none.

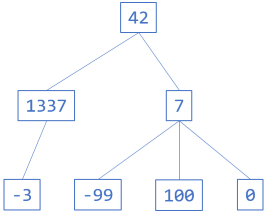
The diagram shows an example of a tree of integers. The left branch contains a sub-tree with only a single branch, whereas the right branch contains a sub-tree with three branches. Each of the leaf nodes are trees in their own right, but they all have zero branches.

In this example, each branch at the 'same level' has the same depth, but this isn't required.

C# catamorphism #

As a C# representation of a tree, I'll use the Tree<T> class from A Tree functor. The catamorphism is this instance method on Tree<T>:

public TResult Cata<TResult>(Func<T, IReadOnlyCollection<TResult>, TResult> func)
{
    return func(Item, children.Select(c => c.Cata(func)).ToArray());
}

Contrary to previous articles, I didn't call this method Match, but simply Cata (for catamorphism). The reason is that those other methods are called Match for a particular reason. The data structures for which they are catamorphisms are all Church-encoded sum types. For those types, the Match methods enable a syntax similar to pattern matching in F#. That's not the case for Tree<T>. It's not a sum type, and it isn't Church-encoded.

The method takes a single function as an input argument. This is the first catamorphism in this article series that isn't made up of a pair of some sort. The Boolean catamorphism is a pair of values, the Maybe catamorphism is a pair made up of a value and a function, and the Either catamorphism is a pair of functions. The tree catamorphism, in contrast, is just a single function.

The first argument to the function is a value of the type T. This will be an Item value. The second argument to the function is a finite collection of TResult values. This may take a little time getting used to, but it's a collection of already reduced sub-trees. When you supply such a function to Cata, that function must return a single value of the type TResult. Thus, the function must be able to digest a finite collection of TResult values, as well as a T value, to a single TResult value.

The Cata method accomplishes this by calling func with the current Item, as well as by recursively applying itself to each of the sub-trees. Eventually, Cata will recurse into leaf nodes, which means that children will be empty. When that happens, the lambda expression inside children.Select never runs, and recursion stops and unwinds.

Examples #

You can use Cata to implement most other behaviour you'd like Tree<T> to have. In the original article on the Tree functor you saw an ad-hoc implementation of Select, but instead, you can derive Select from Cata:

public Tree<TResult> Select<TResult>(Func<T, TResult> selector)
{
    return Cata<Tree<TResult>>((x, nodes) => new Tree<TResult>(selector(x), nodes));
}

The lambda expression receives x, an object of the type T, as well as nodes, which is a finite collection of already translated sub-trees. It simply translates x with selector and returns a new Tree<TResult> with the translated value and the already translated nodes.

This works just as well as the ad-hoc implementation; it passes all the same tests as shown in the previous article.

If you have a tree of numbers, you can add them all together:

public static int Sum(this Tree<int> tree)
{
    return tree.Cata<int>((x, xs) => x + xs.Sum());
}

This uses the built-in Sum method for IEnumerable<T> to add all the partly calculated sub-trees together, and then adds the value of the current node. In this and remaining examples, I'll use the tree shown in the above diagram:

Tree<int> tree =
    Tree.Create(42,
        Tree.Create(1337,
            Tree.Leaf(-3)),
        Tree.Create(7,
            Tree.Leaf(-99),
            Tree.Leaf(100),
            Tree.Leaf(0)));

You can now calculate the sum of all these nodes:

> tree.Sum()
1384

Another option is to find the maximum value anywhere in a tree:

public static int Max(this Tree<int> tree)
{
    return tree.Cata<int>((x, xs) => xs.Any() ? Math.Max(x, xs.Max()) : x);
}

This method again utilises one of the LINQ methods available via the .NET base class library: Max. It is, however, necessary to first check whether the partially reduced xs is empty or not, because the Max extension method on IEnumerable<int> doesn't know how to deal with an empty collection (it throws an exception). When xs is empty that implies a leaf node, in which case you can simply return x; otherwise, you'll first have to use the Max method on xs to find the maximum value there, and then use Math.Max to find the maximum of those two. (I'll here remind the attentive reader that finding the maximum number forms a semigroup and that semigroups accumulate when collections are non-empty. It all fits together. Isn't maths lovely?)

Using the same tree as before, you can see that this method, too, works as expected:

> tree.Max()
1337

So far, these two extension methods are just specialised folds. In Haskell, Foldable is a specific type class, and sum and max are available for all instances. As promised in the introduction to the series, though, there are some functions on trees that you can't implement using a fold. One of these is to count all the leaf nodes. You can still derive that functionality from the catamorphism, though:

public int CountLeaves()
{
    return Cata<int>((x, xs) => xs.Any() ? xs.Sum() : 1);
}

Like Max, the lambda expression used to implement CountLeaves uses Any to detect whether or not xs is empty, which is when Any is false. Empty xs indicates that you've found a leaf node, so return 1. When xs isn't empty, it contains a collection of 1 values - one for each leaf node recursively found; add them together with Sum.

This also works for the same tree as before:

> tree.CountLeaves()
4

You can also measure the maximum depth of a tree:

public int MeasureDepth()
{
    return Cata<int>((x, xs) => xs.Any() ? 1 + xs.Max() : 0);
}

This implementation considers a leaf node to have no depth:

> Tree.Leaf("foo").MeasureDepth()
0

This is a discretionary definition; you could also argue that, by definition, a leaf node ought to have a depth of one. If you think so, you'll need to change the 0 to 1 in the above MeasureDepth implementation.

Once more, you can use Any to detect leaf nodes. Whenever you find a leaf node, you return its depth, which, by definition, is 0. Otherwise, you find the maximum depth already found among xs, and add 1, because xs contains the maximum depths of all immediate sub-trees.

Using the same tree again:

> tree.MeasureDepth()
2

The above tree has the same depth for all sub-trees, so here's an example of a tilted tree:

> Tree.Create(3,
.   Tree.Create(1,
.     Tree.Leaf(0),
.     Tree.Leaf(0)),
.   Tree.Leaf(0),
.   Tree.Leaf(0),
.   Tree.Create(2,
.     Tree.Create(1,
.       Tree.Leaf(0))))
. .MeasureDepth()
3

To make it easier to understand, I've labelled all the leaf nodes with 0, because that's their depth. I've then labelled the other nodes with the maximum number 'under' them, plus one. That's the algorithm used.

Tree F-Algebra #

As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.

As always, start with the underlying endofunctor. I've taken some inspiration from Tree a from Data.Tree, but changed some names:

data TreeF a c = NodeF { nodeValue :: a, nodes :: ListFix c } deriving (Show, Eq, Read)
 
instance Functor (TreeF a) where
  fmap f (NodeF x ns) = NodeF x $ fmap f ns

Instead of using Haskell's standard list ([]) for the sub-forest, I've used ListFix from the article on list catamorphism. This should, hopefully, demonstrate how you can build on already established definitions derived from first principles.

As usual, I've called the 'data' type a and the carrier type c (for carrier). The Functor instance as usual translates the carrier type; the fmap function has the type (c -> c1) -> TreeF a c -> TreeF a c1.

As was the case when deducing the recent catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (TreeF a). To address that problem, you can introduce a newtype wrapper:

newtype TreeFix a = TreeFix { unTreeFix :: Fix (TreeF a) } deriving (Show, Eq, Read)

You can define Functor, Applicative, Monad, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.

A pair of helper functions make it easier to define TreeFix values:

leafF :: a -> TreeFix a
leafF x = TreeFix $ Fix $ NodeF x nilF
 
nodeF :: a -> ListFix (TreeFix a) -> TreeFix a
nodeF x = TreeFix . Fix . NodeF x . fmap unTreeFix

leafF creates a leaf node:

Prelude Fix List Tree> leafF "ploeh"
TreeFix {unTreeFix = Fix (NodeF "ploeh" (ListFix (Fix NilF)))}

nodeF is a helper function to create a non-leaf node:

Prelude Fix List Tree> nodeF 4 (consF (leafF 9) nilF)
TreeFix {unTreeFix =
  Fix (NodeF 4 (ListFix (Fix (ConsF (Fix (NodeF 9 (ListFix (Fix NilF)))) (Fix NilF)))))}

Even with helper functions, construction of TreeFix values is cumbersome, but keep in mind that the code shown here isn't meant to be used in practice. The goal is only to deduce catamorphisms from more basic universal abstractions, and you now have all you need to do that.

Haskell catamorphism #

At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (TreeF a), and an object c, but you still need to find a morphism TreeF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.

As in the previous articles, start by writing a function that will become the catamorphism, based on cata:

treeF = cata alg . unTreeFix
  where alg (NodeF x ns) = undefined

While this compiles, with its undefined implementation of alg, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from alg? You could pass a function argument to the treeF function and use it with x and ns:

treeF :: (a -> ListFix c -> c) -> TreeFix a -> c
treeF f = cata alg . unTreeFix
  where alg (NodeF x ns) = f x ns

This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of TreeF, the compiler infers that the alg function has the type TreeF a c -> c, which is just what you need!

You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.

This, then, is the catamorphism for a tree. So far in this article series, all previous catamorphisms have been pairs, but this one is just a single function. It's still not the only possible catamorphism, since you could trivially flip the arguments to f.

I've chosen the representation shown here because it's isomorphic to the foldTree function from Haskell's built-in Data.Tree module, which explicitly documents that the function "is also known as the catamorphism on trees." foldTree is defined using Haskell's standard list type ([]), so the type is simpler: (a -> [b] -> b) -> Tree a -> b. The two representations of trees, TreeFix and Tree are, however, isomorphic, so foldTree is equivalent to treeF. Notice how both of these functions are also equivalent to the above C# Cata method.

Basis #

You can implement most other useful functionality with treeF. Here's the Functor instance:

instance Functor TreeFix where
  fmap f = treeF (nodeF . f)

nodeF . f is just the point-free version of \x ns -> nodeF (f x) ns, which follows the exact same implementation logic as the above C# Select implementation.

The Applicative instance is, I'm afraid, the most complex code you've seen so far in this article series:

instance Applicative TreeFix where
  pure = leafF
  ft <*> xt = treeF (\f ts -> addNodes ts $ f <$> xt) ft
    where addNodes ns (TreeFix (Fix (NodeF x xs))) =
            TreeFix (Fix (NodeF x (xs <> (unTreeFix <$> ns))))

I'd be surprised if it's impossible to make this terser, but I thought that it was just complicated enough that I needed to make one of the steps explicit. The addNodes helper function has the type ListFix (TreeFix a) -> TreeFix a -> TreeFix a, and it adds a list of sub-trees to the top node of a tree. It looks worse than it is, but it really just peels off the wrappers (TreeFix, Fix, and NodeF) to access the data (x and xs) of the top node. It then concatenates xs with ns, and puts all the wrappers back on.

I have to admit, though, that the Applicative and Monad instance in general are mind-binding to me. The <*> operation, particularly, takes a tree of functions and has to combine it with a tree of values. What does that even mean? How does one do that?

Like the above, apparently. I took the Applicative behaviour from Data.Tree and made sure that my implementation is isomorphic. I even have a property to make 'sure' that's the case:

testProperty "Applicative behaves like Data.Tree" $ do
  xt :: TreeFix Integer <- fromTree <$> resize 10 arbitrary
  ft :: TreeFix (Integer -> String) <- fromTree <$> resize 5 arbitrary
 
  let actual = ft <*> xt
 
  let expected = toTree ft <*> toTree xt
  return $ expected === toTree actual

The Monad instance looks similar to the Applicative instance:

instance Monad TreeFix where
  t >>= f = treeF (\x ns -> addNodes ns $ f x) t
    where addNodes ns (TreeFix (Fix (NodeF x xs))) =
            TreeFix (Fix (NodeF x (xs <> (unTreeFix <$> ns))))

The addNodes helper function is the same as for <*>, so you may wonder why I didn't extract that as a separate, reusable function. I decided, however, to apply the rule of three, and since, ultimately, addNodes appear only twice, I left them as the implementation details they are.

Fortunately, the Foldable instance is easier on the eyes:

instance Foldable TreeFix where
  foldMap f = treeF (\x xs -> f x <> fold xs)

Since f is a function of the type a -> m, where m is a Monoid instance, you can use fold and <> to accumulate everything to a single m value.

The Traversable instance is similarly terse:

instance Traversable TreeFix where
  sequenceA = treeF (\x ns -> nodeF <$> x <*> sequenceA ns)

Finally, you can implement conversions to and from the Tree type from Data.Tree, using ana as the dual of cata:

toTree :: TreeFix a -> Tree a
toTree = treeF (\x ns -> Node x $ toList ns)
 
fromTree :: Tree a -> TreeFix a
fromTree = TreeFix . ana coalg
  where coalg (Node x ns) = NodeF x (fromList ns)

This demonstrates that TreeFix is isomorphic to Tree, which again establishes that treeF and foldTree are equivalent.

Relationships #

In this series, you've seen various examples of catamorphisms of structures that have no folds, catamorphisms that coincide with folds, and catamorphisms that are more general than the fold. The introduction to the series included this diagram:

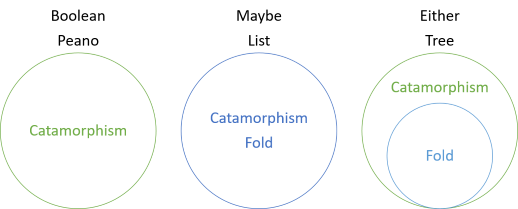
The Either catamorphism is another example of a catamorphism that is more general than the fold, but that one turned out to be identical to the bifold. That's not the case here, because TreeFix isn't a Bifoldable instance at all.

There are operations on trees that you can implement with a fold, but some that you can't. Consider the tree in shown in the diagram at the beginning of the article. This is also the tree that the above C# examples use. In Haskell, using TreeFix, you can define that tree like this:

tree =
  nodeF 42
    (consF (nodeF 1337
      (consF (leafF (-3)) nilF)) $
     consF (nodeF 7
      (consF (leafF (-99)) $
       consF (leafF 100) $
       consF (leafF 0) nilF))
     nilF)

Yes, that almost looks like some Lisp dialect...

Since TreeFix is Foldable, and that type class already comes with sum and maximum functions, no further work is required to repeat the first two of the above C# examples:

*Tree Fix List Tree> sum tree
1384
*Tree Fix List Tree> maximum tree
1337

Counting leaves, or measuring the depth of a tree, on the other hand, is impossible with the Foldable instance, but can be implemented using the catamorphism:

countLeaves :: Num n => TreeFix a -> n
countLeaves = treeF (\_ xs -> if null xs then 1 else sum xs)
 
treeDepth :: (Ord n, Num n) => TreeFix a -> n
treeDepth = treeF (\_ xs -> if null xs then 0 else 1 + maximum xs)

The reasoning is the same as already explained in the above C# examples. The functions also produce the same results:

*Tree Fix List Tree> countLeaves tree
4
*Tree Fix List Tree> treeDepth tree
2

This, hopefully, illustrates that the catamorphism is more capable, and that the fold is just a (list-biased) specialisation.

Summary #

The catamorphism for a tree is just a single function, which is recursively evaluated. It enables you to translate, traverse, and reduce trees in many interesting ways.

You can use the catamorphism to implement a (list-biased) fold, including enumerating all nodes as a flat list, but there are operations (such as counting leaves) that you can implement with the catamorphism, but not with the fold.

Next: Rose tree catamorphism.

---

Comments

• ← Previous
• Archive
• Next →