Contravariant functors by Mark Seemann
A more exotic kind of universal abstraction.
This article series is part of a larger series of articles about functors, applicatives, and other mappable containers.
So far in the article series, you've seen examples of mappable containers that map in the same direction of projections, so to speak. Let's unpack that.
Covariance recap #
Functors, applicative functors, and bifunctors all follow the direction of projections. Consider the illustration from the article about functors:
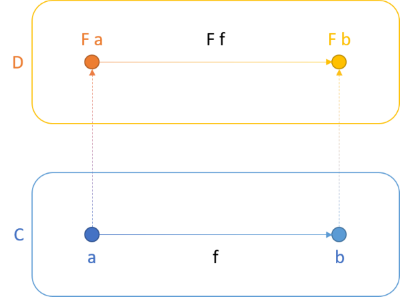
The function f maps from a to b. You can think of a and b as two types, or two sets. For example, if a is the set of all strings, it might correspond to the type String. Likewise, if b is the set of all integers, then it corresponds to a type called Int. The function f would, in that case, have the type String -> Int; that is: it maps strings to integers. The most natural such function seems to be one that counts the number of characters in a string:
> f = length > f "foo" 3 > f "ploeh" 5
This little interactive session uses Haskell, but even if you've never heard about Haskell before, you should still be able to understand what's going on.
A functor is a container of values, for example a collection, a Maybe, a lazy computation, or many other things. If f maps from a to b, then lifting it to the functor F retains the direction. That's what the above figure illustrates. Not only does the functor project a to F a and b to F b, it also maps f to F f, which is F a -> F b.
For lists it might look like this:
> fmap f ["bar", "fnaah", "Gauguin"] [3,5,7]
Here fmap lifts the function String -> Int to [String] -> [Int]. Notice that the types 'go in the same direction' when you lift a function to the functor. The types vary with the function - they co-vary; hence covariance.
While applicative functors and bifunctors are more complex, they are still covariant. Consult, for example, the diagrams in my bifunctor article to get an intuitive sense that this still holds.
Contravariance #
What happens if we change the direction of only one arrow? For example, we could change the direction of the f arrow, so that the function is now a function from b to a: b -> a. The figure would look like this:
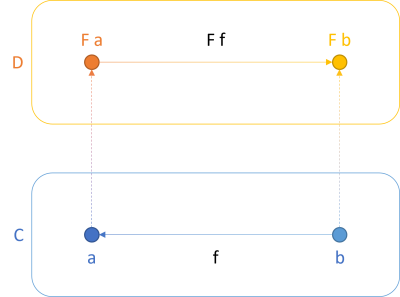
This looks almost like the first figure, with one crucial difference: The lower arrow now goes from right to left. Notice that the upper arrow still goes from left to right: F a -> F b. In other words, the functor varies in the contrary direction than the projected function. It's contravariant.
This seems really odd. Why would anyone do that?
As is so often the case with universal abstractions, it's not so much a question of coming up with an odd concept and see what comes of it. It's actually an abstract description of some common programming constructs. In this series of articles, you'll see examples of some contravariant functors:
- The Command Handler contravariant functor
- The Specification contravariant functor
- The Equivalence contravariant functor
- Reader as a contravariant functor
- Functor variance compared to C#'s notion of variance
- Contravariant Dependency Injection
These aren't the only examples, but they should be enough to get the point across. Other examples include equivalence and comparison.
Lifting #
How do you lift a function f to a contravariant functor? For covariant functors (normally just called functors), Haskell has the fmap function, while in C# you'd be writing a family of Select methods. Let's compare. In Haskell, fmap has this type:
fmap :: Functor f => (a -> b) -> f a -> f b
You can read it like this: For any Functor f, fmap lifts a function of the type a -> b to a function of the type f a -> f b. Another way to read this is that given a function a -> b and a container of type f a, you can produce a container of type f b. Due to currying, these two interpretations are both correct.
In C#, you'd be writing a method on Functor<T> that looks like this:
public Functor<TResult> Select<TResult>(Func<T, TResult> selector)
This fits the later interpretation of fmap: Given an instance of Functor<T>, you can call Select with a Func<T, TResult> to produce a Functor<TResult>.
What does the equivalent function look like for contravariant functors? Haskell defines it as:
contramap :: Contravariant f => (b -> a) -> f a -> f b
You can read it like this: For any Contravariant functor f, contramap lifts a function (b -> a) to a function from f a to f b. Or, in the alternative (but equally valid) interpretation that matches C# better, given a function (b -> a) and an f a, you can produce an f b.
In C#, you'd be writing a method on Contravariant<T> that looks like this:
public Contravariant<T1> ContraMap<T1>(Func<T1, T> selector)
The actual generic type (here exemplified by Contravariant<T>) will differ, but the shape of the method will be the same. In order to map from Contravariant<T> to Contravariant<T1>, you need a function that goes the other way: Func<T1, T> goes from T1 to T.
In C#, the function name doesn't have to be ContraMap, since C# doesn't have any built-in understanding of contravariant functors - as opposed to functors, where a method called Select will light up some language features. In this article series I'll stick with ContraMap since I couldn't think of a better name.
Laws #
Like functors, applicative functors, monoids, and other universal abstractions, contravariant functors are characterised by simple laws. The contravariant functor laws are equivalent to the (covariant) functor laws: identity and composition.
In pseudo-Haskell, we can express the identity law as:
contramap id = id
and the composition law as:
contramap (g . f) = contramap f . contramap g
The identity law is equivalent to the first functor law. It states that mapping a contravariant functor with the identity function is equivalent to a no-op. The identity function is a function that returns all input unchanged. (It's called the identity function because it's the identity for the endomorphism monoid.) In F# and Haskell, this is simply a built-in function called id.
In C#, you can write a demonstration of the law as a unit test. Here's the essential part of such a test:
Func<string, string> id = x => x; Contravariant<string> sut = createContravariant(); Assert.Equal(sut, sut.ContraMap(id), comparer);
The ContraMap method does return a new object, so a custom comparer is required to evaluate whether sut is equal to sut.ContraMap(id).
The composition law governs how composition works. Again, notice how lifting reverses the order of functions. In C#, the relevant unit test code might look like this:
Func<string, int> f = s => s.Length; Func<int, TimeSpan> g = i => TimeSpan.FromDays(i); Contravariant<TimeSpan> sut = createContravariant(); Assert.Equal( sut.ContraMap((string s) => g(f(s))), sut.ContraMap(g).ContraMap(f), comparer);
This may actually look less surprising in C# than it does in Haskell. Here the lifted composition doesn't look reversed, but that's because C# doesn't have a composition operator for raw functions, so I instead wrote it as a lambda expression: (string s) => g(f(s)). If you contrast this C# example with the equivalent assertion of the (covariant) second functor law, you can see that the function order is flipped: f(g(i)).
Assert.Equal(sut.Select(g).Select(f), sut.Select(i => f(g(i))));
It can be difficult to get your head around the order of contravariant composition without some examples. I'll provide examples in the following articles, but I wanted to leave the definition of the two contravariant functor laws here for reference.
Conclusion #
Contravariant functors are functors that map in the opposite direction of an underlying function. This seems counter-intuitive but describes the actual behaviour of quite normal functions.
This is hardly illuminating without some examples, so without further ado, let's proceed to the first one.
