Can one flatten a statically typed list? by Mark Seemann

What would be the type of a heterogeneously nested list?

Once again, I (inadvertently) managed to start a discussion on Twitter about static versus dynamic typing. I've touched on the topic before, but my agenda is not to fan any flames - quite the contrary. I'm trying (nay, struggling) to understand the other side of the debate.

This post isn't really about that, though, but in one of the threads spawned by my original tweet, Tom Johnson wrote:

"One of my favourite examples:

"What's the type of [[[3, 2], 7, [2, 4], 1], 0]?

"What's the type of flatten, which takes that value and yields [3, 2, 7, 2, 4, 1, 0]?"

The type, it turns out, is straightforward.

I'd like to be explicit about my agenda when writing this article. I'm not doing this to prove Tom Johnson wrong. In fact, I get the sense that he already knows the answer. Rather, I found it an interesting little exercise.

Syntax #

First, we need to get one thing out of the way. In many languages, [[[3, 2], 7, [2, 4], 1], 0] isn't valid syntax. Even as a 'normal' list, syntax like [3, 2, 7, 2, 4, 1, 0] wouldn't be valid syntax in some languages.

In Haskell [3, 2, 7, 2, 4, 1, 0] would be valid, but it wouldn't be valid syntax in C#. And while it'd be valid syntax in F#, it wouldn't mean what it means in Haskell. The F# equivalent would be [3; 2; 7; 2; 4; 1; 0].

The point is that that I don't consider myself bound by the specific syntax [[[3, 2], 7, [2, 4], 1], 0]. I'm going to answer the question using Haskell, and in Haskell, that code doesn't parse.

Instead, I'll use a data structure that represents the same data, but in a more verbose manner.

Tree #

In one of the Twitter threads, Alexis King already gave the answer:

"`flatten` is perfectly possible in Haskell, you just have to write a rose tree datatype, not use `[a]`."

The standard Tree a in Data.Tree, however, doesn't seem to quite fit. Instead, we can use a rose tree. As Meertens wrote:

"We consider trees whose internal nodes may fork into an arbitrary (natural) number of sub-trees. (If such a node has zero descendants, we still consider it internal.) Each external node carries a data item. No further information is stored in the tree; in particular, internal nodes are unlabelled."

With unlabelled nodes, we might draw Tom Johnson's 'list' like this:

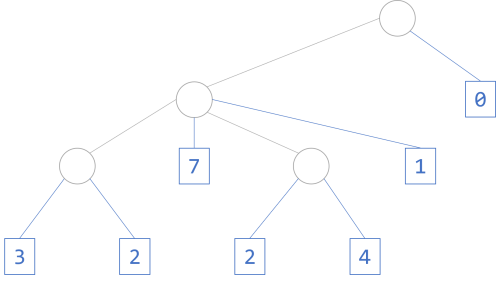
I'll use the Tree data type introduced in the article Picture archivist in Haskell:

data Tree a b = Node a [Tree a b] | Leaf b deriving (Eq, Show, Read)

If you would, you could define a type alias that has unlabelled internal nodes:

type MeertensTree = Tree ()

I'm not really going to bother doing that, though. I'm just going to create a Tree () b value.

Here we go:

> l = Node () [Node () [Node () [Leaf 3, Leaf 2], Leaf 7, Node () [Leaf 2, Leaf 4], Leaf 1], Leaf 0]
> :t l
l :: Num b => Tree () b

You could probably come up with a more succinct syntax to create trees like this in code, but I'm assuming that in 'reality', if you have the need to flatten nested lists, it'll be a values that arrive at the boundary of the application...

Flattening #

Can you flatten the 'list' l?

Yes, no problem. The Tree a b data type is an instance of various type classes, among these Foldable:

instance Foldable (Tree a) where
  foldMap = bifoldMap mempty

You can see the full definition of bifoldMap and its dependencies in the article that introduces the type.

One of the functions available via Foldable is toList, which is just what you need:

> toList l
[3,2,7,2,4,1,0]

This is the result required by Tom Johnson.

Summary #

In short, the answer to the question: "What's the type of [[[3, 2], 7, [2, 4], 1], 0]?" is: Num b => Tree () b, an example of which might be Tree () Integer. You could also call it MeertensTree Integer.

Likewise, the type of the requested flatten function is toList :: Foldable t => t a -> [a].

Comments

type Nested<T> = (Nested<T> | T)[];

const flatten = <T>(val: Nested<T>): T[] =>
  val.reduce(
    (r: T[], v) => [...r, ...(Array.isArray(v) ? flatten(v) : [v])],
    []
  );

const nested = [[[3, 2], 7, [2, 4], 1], 0];
const result = flatten(nested);
console.log(result); // [3, 2, 7, 2, 4, 1, 0] 

const silly: Nested<number | string | { name: string }> = [
  [[3, 2], 1],
  "cheese",
  { name: "Fred" },
];
const sillyResult = flatten(silly);
console.log(sillyResult); // [3, 2, 1, "cheese", {"name": "Fred"}]

• ← Previous
• Archive
• Next →