Picture archivist in Haskell by Mark Seemann

A comprehensive code example showing how to implement a functional architecture in Haskell.

This article shows how to implement the picture archivist architecture described in the previous article. In short, the task is to move some image files to directories based on their date-taken metadata. The architectural idea is to load a directory structure from disk into an in-memory tree, manipulate that tree, and use the resulting tree to perform the desired actions:

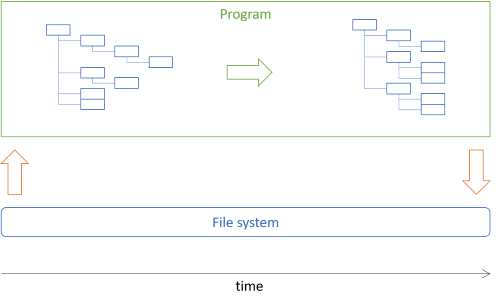
Much of the program will manipulate the tree data, which is immutable.

Tree #

You can start by defining a rose tree:

data Tree a b = Node a [Tree a b] | Leaf b deriving (Eq, Show, Read)

If you wanted to, you could put all the Tree code in a reusable library, because none of it is coupled to a particular application, such as moving pictures. You could also write a comprehensive test suite for the following functions, but in this article, I'll skip that.

Notice that this sort of tree explicitly distinguishes between internal and leaf nodes. This is necessary because you'll need to keep track of the directory names (the internal nodes), while at the same time you'll want to enrich the leaves with additional data - data that you can't meaningfully add to the internal nodes. You'll see this later in the article.

The rose tree catamorphism is this foldTree function:

foldTree :: (a -> [c] -> c) -> (b -> c) -> Tree a b -> c
foldTree  _ fl (Leaf x) = fl x
foldTree fn fl (Node x xs) = fn x $ foldTree fn fl <$> xs

Sometimes I name the catamorphism cata, sometimes something like tree, but using a library like Data.Tree as another source of inspiration, in this article I chose to name it foldTree.

In this article, tree functionality is (with one exception) directly or transitively implemented with foldTree.

Filtering trees #

It'll be useful to be able to filter the contents of a tree. For example, the picture archivist program will only move image files with valid metadata. This means that it'll need to filter out all files that aren't image files, as well as image files without valid metadata.

It turns out that it'll be useful to supply a function that throws away Nothing values from a tree of Maybe leaves. This is similar to the catMaybes function from Data.Maybe, so I call it catMaybeTree:

catMaybeTree :: Tree a (Maybe b) -> Maybe (Tree a b)
catMaybeTree = foldTree (\x -> Just . Node x . catMaybes) (fmap Leaf)

You may find the type of the function surprising. Why does it return a Maybe Tree, instead of simply a Tree? And if you accept the type as given, isn't this simply the sequence function?

While catMaybes simply returns a list, it can do this because lists can be empty. This Tree type, on the other hand, can't be empty. If the purpose of catMaybeTree is to throw away all Nothing values, then how do you return a tree from Leaf Nothing?

You can't return a Leaf because you have no value to put in the leaf. Similarly, you can't return a Node because, again, you have no value to put in the node.

In order to handle this edge case, then, you'll have to return Nothing:

Prelude Tree> catMaybeTree $ Leaf Nothing
Nothing

Isn't this the same as sequence, then? It's not, because sequence short-circuits all data, as this list example shows:

Prelude> sequence [Just 42, Nothing, Just 2112]
Nothing

Contrast this with the behaviour of catMaybes:

Prelude Data.Maybe> catMaybes [Just 42, Nothing, Just 2112]
[42,2112]

You've yet to see the Traversable instance for Tree, but it behaves in the same way:

Prelude Tree> sequence $ Node "Foo" [Leaf (Just 42), Leaf Nothing, Leaf (Just 2112)]
Nothing

The catMaybeTree function, on the other hand, returns a filtered tree:

Prelude Tree> catMaybeTree $ Node "Foo" [Leaf (Just 42), Leaf Nothing, Leaf (Just 2112)]
Just (Node "Foo" [Leaf 42,Leaf 2112])

While the resulting tree is wrapped in a Just case, the leaves contain unwrapped values.

Instances #

The article about the rose tree catamorphism already covered how to add instances of Bifunctor, Bifoldable, and Bitraversable, so I'll give this only cursory treatment. Refer to that article for a more detailed treatment. The code that accompanies that article also has QuickCheck properties that verify the various laws associated with those instances. Here, I'll just list the instances without further comment:

instance Bifunctor Tree where
  bimap f s = foldTree (Node . f) (Leaf . s)
 
instance Bifoldable Tree where
  bifoldMap f = foldTree (\x xs -> f x <> mconcat xs)
 
instance Bitraversable Tree where
  bitraverse f s =
    foldTree (\x xs -> Node <$> f x <*> sequenceA xs) (fmap Leaf . s)
 
instance Functor (Tree a) where
  fmap = second
 
instance Foldable (Tree a) where
  foldMap = bifoldMap mempty
 
instance Traversable (Tree a) where
  sequenceA = bisequenceA . first pure

The picture archivist program isn't going to explicitly need all of these, but transitively, it will.

Moving pictures #

So far, all the code shown here could be in a general-purpose reusable library, since it contains no functionality specifically related to image files. The rest of the code in this article, however, will be specific to the program. I'll put the domain model code in another module and import some functionality:

module Archive where
 
import Data.Time
import Text.Printf
import System.FilePath
import qualified Data.Map.Strict as Map
import Tree

Notice that Tree is one of the imported modules.

Later, we'll look at how to load a tree from the file system, but for now, we'll just pretend that we have such a tree.

The major logic of the program is to create a destination tree based on a source tree. The leaves of the tree will have to carry some extra information apart from a file path, so you can introduce a specific type to capture that information:

data PhotoFile =
  PhotoFile { photoFileName :: FilePath, takenOn :: LocalTime }
  deriving (Eq, Show, Read)

A PhotoFile not only contains the file path for an image file, but also the date the photo was taken. This date can be extracted from the file's metadata, but that's an impure operation, so we'll delegate that work to the start of the program. We'll return to that later.

Given a source tree of PhotoFile leaves, though, the program must produce a destination tree of files:

moveTo :: (Foldable t, Ord a, PrintfType a) => a -> t PhotoFile -> Tree a FilePath
moveTo destination =
  Node destination . Map.foldrWithKey addDir [] . foldr groupByDir Map.empty
  where
    dirNameOf (LocalTime d _) =
      let (y, m, _) = toGregorian d in printf "%d-%02d" y m
    groupByDir (PhotoFile fileName t) =
      Map.insertWith (++) (dirNameOf t) [fileName]
    addDir name files dirs = Node name (Leaf <$> files) : dirs

This moveTo function looks, perhaps, overwhelming, but it's composed of only three steps:

1. Create a map of destination folders (foldr groupByDir Map.empty).
2. Create a list of branches from the map (Map.foldrWithKey addDir []).
3. Create a tree from the list (Node destination).

Recall that when Haskell functions are composed with the . operator, you'll have to read the composition from right to left.

Notice that this function works with any Foldable data container, so it'd work with lists and other data structures besides trees.

The moveTo function starts by folding the input data into a map. The map is keyed by the directory name, which is formatted by the dirNameOf function. This function takes a LocalTime as input and formats it to a YYYY-MM format. For example, December 20, 2018 becomes "2018-12".

The entire mapping step groups the PhotoFile values into a map of the type Map a [FilePath]. All the image files taken in April 2014 are added to the list with the "2014-04" key, all the image files taken in July 2011 are added to the list with the "2011-07" key, and so on.

In the next step, the moveTo function converts the map to a list of trees. This will be the branches (or sub-directories) of the destination directory. Because of the desired structure of the destination tree, this is a list of shallow branches. Each node contains only leaves.

The only remaining step is to add that list of branches to a destination node.

Since this is a pure function, it's easy to unit test. Just create some input values and call the function:

"Move to destination" ~: do
  (source, destination, expected) <-
    [
      ( Leaf $ PhotoFile "1" $ lt 2018 11 9 11 47 17
      , "D"
      , Node "D" [Node "2018-11" [Leaf "1"]])
      ,
      ( Node "S" [
          Leaf $ PhotoFile "4" $ lt 1972 6 6 16 15 00]
      , "D"
      , Node "D" [Node "1972-06" [Leaf "4"]])
      ,
      ( Node "S" [
          Leaf $ PhotoFile "L" $ lt 2002 10 12 17 16 15,
          Leaf $ PhotoFile "J" $ lt 2007 4 21 17 18 19]
      , "D"
      , Node "D" [Node "2002-10" [Leaf "L"], Node "2007-04" [Leaf "J"]])
      ,
      ( Node "1" [
          Leaf $ PhotoFile "a" $ lt 2010 1 12 17 16 15,
          Leaf $ PhotoFile "b" $ lt 2010 3 12 17 16 15,
          Leaf $ PhotoFile "c" $ lt 2010 1 21 17 18 19]
      , "2"
      , Node "2" [
          Node "2010-01" [Leaf "a", Leaf "c"],
          Node "2010-03" [Leaf "b"]])
      ,
      ( Node "foo" [
          Node "bar" [
            Leaf $ PhotoFile "a" $ lt 2010 1 12 17 16 15,
            Leaf $ PhotoFile "b" $ lt 2010 3 12 17 16 15,
            Leaf $ PhotoFile "c" $ lt 2010 1 21 17 18 19],
          Node "baz" [
            Leaf $ PhotoFile "d" $ lt 2010 3 1 2 3 4,
            Leaf $ PhotoFile "e" $ lt 2011 3 4 3 2 1
          ]]
      , "qux"
      , Node "qux" [
          Node "2010-01" [Leaf "a", Leaf "c"],
          Node "2010-03" [Leaf "b", Leaf "d"],
          Node "2011-03" [Leaf "e"]])
    ]
  let actual = moveTo destination source
  return $ expected ~=? actual

This is an inlined parametrised HUnit test. While it looks like a big unit test, it still follows my test formatting heuristic. There's only three expressions, but the arrange expression is big because it creates a list of test cases.

Each test case is a triple of a source tree, a destination directory name, and an expected result. In order to make the test data code more compact, it utilises this test-specific helper function:

lt y mth d h m s = LocalTime (fromGregorian y mth d) (TimeOfDay h m s)

For each test case, the test calls the moveTo function with the destination directory name and the source tree. It then asserts that the expected value is equal to the actual value.

Calculating moves #

One pure step remains. The result of calling the moveTo function is a tree with the desired structure. In order to actually move the files, though, for each file you'll need to keep track of both the source path and the destination path. To make that explicit, you can define a type for that purpose:

data Move =
  Move { sourcePath :: FilePath, destinationPath :: FilePath }
  deriving (Eq, Show, Read)

A Move is simply a data structure. Contrast this with typical object-oriented design, where it would be a (possibly polymorphic) method on an object. In functional programming, you'll regularly model intent with a data structure. As long as intents remain data, you can easily manipulate them, and once you're done with that, you can run an interpreter over your data structure to perform the work you want accomplished.

The unit test cases for the moveTo function suggest that file names are local file names like "L", "J", "a", and so on. That was only to make the tests as compact as possible, since the function actually doesn't manipulate the specific FilePath values.

In reality, the file names will most likely be longer, and they could also contain the full path, instead of the local path: "C:\foo\bar\a.jpg".

If you call moveTo with a tree where each leaf has a fully qualified path, the output tree will have the desired structure of the destination tree, but the leaves will still contain the full path to each source file. That means that you can calculate a Move for each file:

calculateMoves :: Tree FilePath FilePath -> Tree FilePath Move
calculateMoves = imp ""
  where imp path    (Leaf x) = Leaf $ Move x $ replaceDirectory x path
        imp path (Node x xs) = Node (path </> x) $ imp (path </> x) <$> xs

This function takes as input a Tree FilePath FilePath, which is compatible with the output of moveTo. It returns a Tree FilePath Move, i.e. a tree where the leaves are Move values.

To be fair, returning a tree is overkill. A [Move] (list of moves) would have been just as useful, but in this article, I'm trying to describe how to write code with a functional architecture. In the overview article, I explained how you can model a file system using a rose tree, and in order to emphasise that point, I'll stick with that model a little while longer.

Earlier, I wrote that you can implement desired Tree functionality with the foldTree function, but that was a simplification. If you can implement the functionality of calculateMoves with foldTree, I don't know how. You can, however, implement it using explicit pattern matching and simple recursion.

The imp function builds up a file path (using the </> path combinator) as it recursively negotiates the tree. All Leaf nodes are converted to a Move value using the leaf node's current FilePath value as the sourcePath, and the path to figure out the desired destinationPath.

This code is still easy to unit test:

"Calculate moves" ~: do
  (tree, expected) <-
    [
      (Leaf "1", Leaf $ Move "1" "1"),
      (Node "a" [Leaf "1"], Node "a" [Leaf $ Move "1" $ "a" </> "1"]),
      (Node "a" [Leaf "1", Leaf "2"], Node "a" [
        Leaf $ Move "1" $ "a" </> "1",
        Leaf $ Move "2" $ "a" </> "2"]),
      (Node "a" [Node "b" [Leaf "1", Leaf "2"], Node "c" [Leaf "3"]],
       Node "a" [
         Node ("a" </> "b") [
           Leaf $ Move "1" $ "a" </> "b" </> "1",
           Leaf $ Move "2" $ "a" </> "b" </> "2"],
         Node ("a" </> "c") [
           Leaf $ Move "3" $ "a" </> "c" </> "3"]])
    ]
  let actual = calculateMoves tree
  return $ expected ~=? actual

The test cases in this parametrised test are tuples of an input tree and the expected tree. For each test case, the test calls the calculateMoves function with tree and asserts that the actual tree is equal to the expected tree.

That's all the pure code you need in order to implement the desired functionality. Now you only need to write some code that loads a tree from disk, and imprints a destination tree to disk, as well as the code that composes it all.

Loading a tree from disk #

The remaining code in this article is impure. You could put it in dedicated modules, but for this program, you're only going to need three functions and a bit of composition code, so you could also just put it all in the Main module. That's what I did.

To load a tree from disk, you'll need a root directory, under which you load the entire tree. Given a directory path, you read a tree using a recursive function like this:

readTree :: FilePath -> IO (Tree FilePath FilePath)
readTree path = do
  isFile <- doesFileExist path
  if isFile
    then return $ Leaf path
    else do
      dirsAndfiles <- listDirectory path
      let paths = fmap (path </>) dirsAndfiles
      branches <- traverse readTree paths
      return $ Node path branches

This recursive function starts by checking whether the path is a file or a directory. If it's a file, it creates a new Leaf with that FilePath.

If path isn't a file, it's a directory. In that case, use listDirectory to enumerate all the directories and files in that directory. These are only local names, so prefix them with path to create full paths, then traverse all those directory entries recursively. That produces all the branches for the current node. Finally, return a new Node with the path and the branches.

Loading metadata #

The readTree function only produces a tree with FilePath leaves, while the program requires a tree with PhotoFile leaves. You'll need to read the Exif metadata from each file and enrich the tree with the date-taken data.

In this code base, I've used the hsexif library for this. That enables you to write an impure operation like this:

readPhoto :: FilePath -> IO (Maybe PhotoFile)
readPhoto path = do
  exifData <- parseFileExif path
  let dateTaken = either (const Nothing) Just exifData >>= getDateTimeOriginal
  return $ PhotoFile path <$> dateTaken

This operation can fail for various reasons:

• The file may not exist.
• The file exists, but has no metadata.
• The file has metadata, but no date-taken metadata.
• The date-taken metadata string is malformed.

The program is just going to skip all files from which it can't extract date-taken metadata, so readPhoto converts the Either value returned by parseFileExif to Maybe and binds the result with getDateTimeOriginal.

When you traverse a Tree FilePath FilePath with readPhoto, you'll get a Tree FilePath (Maybe PhotoFile). That's when you'll need catMaybeTree. You'll see this soon.

Writing a tree to disk #

The above calculateMoves function creates a Tree FilePath Move. The final piece of impure code you'll need to write is an operation that traverses such a tree and executes each Move.

applyMoves :: Foldable t => t Move -> IO ()
applyMoves = traverse_ move
  where
    move m = copy m >> compareFiles m >>= deleteSource
    copy (Move s d) = do
      createDirectoryIfMissing True $ takeDirectory d
      copyFileWithMetadata s d
      putStrLn $ "Copied to " ++ show d
    compareFiles m@(Move s d) = do
      sourceBytes <- B.readFile s
      destinationBytes <- B.readFile d
      return $ if sourceBytes == destinationBytes then Just m else Nothing
    deleteSource           Nothing = return ()
    deleteSource (Just (Move s _)) = removeFile s

As I wrote above, a tree of Move values is, to be honest, overkill. Any Foldable container will do, as the applyMoves operation demonstrates. It traverses the data structure, and for each Move, it first copies the file, then it verifies that the copy was successful, and finally, if that's the case, it deletes the source file.

All of the operations invoked by these three steps are defined in various libraries part of the base GHC installation. You're welcome to peruse the source code repository if you're interested in the details.

Composition #

You can now compose an impure-pure-impure sandwich from all the Lego pieces:

movePhotos :: FilePath -> FilePath -> IO ()
movePhotos source destination = fmap fold $ runMaybeT $ do
  sourceTree <- lift $ readTree source
  photoTree <- MaybeT $ catMaybeTree <$> traverse readPhoto sourceTree
  let destinationTree = calculateMoves $ moveTo destination photoTree
  lift $ applyMoves destinationTree

First, you load the sourceTree using the readTree operation. This is a Tree FilePath FilePath value, because the code is written in do notation, and the context is MaybeT IO (). You then load the image metatadata by traversing sourceTree with readPhoto. This produces a Tree FilePath (Maybe PhotoFile) that you then filter with catMaybeTree. Again, because of do notation and monad transformer shenanigans, photoTree is a Tree FilePath PhotoFile value.

Those two lines of code is the initial impure step of the sandwich (yes: mixed metaphors, I know).

The pure part of the sandwich is the composition of the pure functions moveTo and calculateMoves. The result is a Tree FilePath Move value.

The final, impure step of the sandwich, then, is to applyMoves.

Execution #

The movePhotos operation takes source and destination arguments. You could hypothetically call it from a rich client or a background process, but here I'll just call if from a command-line program. The main operation will have to parse the input arguments and call movePhotos:

main :: IO ()
main = do
  args <- getArgs
  case args of
    [source, destination] -> movePhotos source destination
    _ -> putStrLn "Please provide source and destination directories as arguments."

You could write more sophisticated parsing of the program arguments, but that's not the topic of this article, so I only wrote the bare minimum required to get the program working.

You can now compile and run the program:

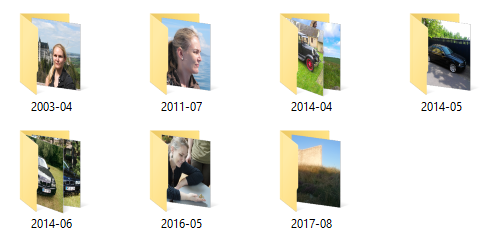
$ ./archpics "C:\Users\mark\Desktop\Test" "C:\Users\mark\Desktop\Test-Out"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2003-04\\2003-04-29 15.11.50.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2011-07\\2011-07-10 13.09.36.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2014-04\\2014-04-17 17.11.40.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2014-04\\2014-04-18 14.05.02.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2014-05\\2014-05-23 16.07.20.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2014-06\\2014-06-30 15.44.52.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2014-06\\2014-06-21 16.48.40.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2016-05\\2016-05-01 09.25.23.jpg"
Copied to "C:\\Users\\mark\\Desktop\\Test-Out\\2017-08\\2017-08-22 19.53.28.jpg"

This does indeed produce the expected destination directory structure.

It's always nice when something turns out to work in practice, as well as in theory.

Summary #

Functional software architecture involves separating pure from impure code so that no pure functions invoke impure operations. Often, you can achieve that with what I call the impure-pure-impure sandwich architecture. In this example, you saw how to model the file system as a tree. This enables you to separate the impure file interactions from the pure program logic.

The Haskell type system enforces the functional interaction law, which implies that the architecture is, indeed, properly functional. Other languages, like F#, don't enforce the law via the compiler, but that doesn't prevent you doing functional programming. Now that we've verified that the architecture is, indeed, functional, we can port it to F#.

Next: Picture archivist in F#.

---

Comments

• ← Previous
• Archive
• Next →