Picture archivist in F# by Mark Seemann

A comprehensive code example showing how to implement a functional architecture in F#.

This article shows how to implement the picture archivist architecture described in a previous article. In short, the task is to move some image files to directories based on their date-taken metadata. The architectural idea is to load a directory structure from disk into an in-memory tree, manipulate that tree, and use the resulting tree to perform the desired actions:

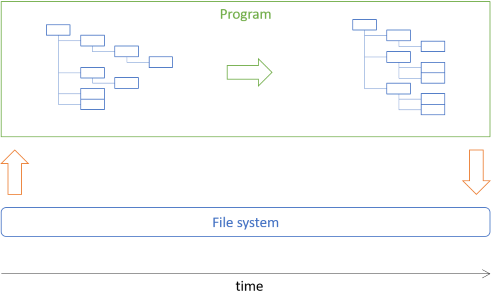
Much of the program will manipulate the tree data, which is immutable.

The previous article showed how to implement the picture archivist architecture in Haskell. In this article, you'll see how to do it in F#. This is essentially a port of the Haskell code.

Tree #

You can start by defining a rose tree:

type Tree<'a, 'b> = Node of 'a * Tree<'a, 'b> list | Leaf of 'b

If you wanted to, you could put all the Tree code in a reusable library, because none of it is coupled to a particular application, such as moving pictures. You could also write a comprehensive test suite for the following functions, but in this article, I'll skip that.

Notice that this sort of tree explicitly distinguishes between internal and leaf nodes. This is necessary because you'll need to keep track of the directory names (the internal nodes), while at the same time you'll want to enrich the leaves with additional data - data that you can't meaningfully add to the internal nodes. You'll see this later in the article.

While I typically tend to define F# types outside of modules (so that you don't have to, say, prefix the type name with the module name - Tree.Tree is so awkward), the rest of the tree code goes into a module, including two helper functions:

module Tree =
    // 'b -> Tree<'a,'b>
    let leaf = Leaf
    
    // 'a -> Tree<'a,'b> list -> Tree<'a,'b>
    let node x xs = Node (x, xs)

The leaf function doesn't add much value, but the node function offers a curried alternative to the Node case constructor. That's occasionally useful.

The rest of the code related to trees is also defined in the Tree module, but I'm going to present it formatted as free-standing functions. If you're confused about the layout of the code, the entire code base is available on GitHub.

The rose tree catamorphism is this cata function:

// ('a -> 'c list -> 'c) -> ('b -> 'c) -> Tree<'a,'b> -> 'c
let rec cata fd ff = function
    | Leaf x -> ff x
    | Node (x, xs) -> xs |> List.map (cata fd ff) |> fd x

In the corresponding Haskell implementation of this architecture, I called this function foldTree, so why not retain that name? The short answer is that the naming conventions differ between Haskell and F#, and while I favour learning from Haskell, I still want my F# code to be as idiomatic as possible.

While I don't enforce that client code must use the Tree module name to access the functions within, I prefer to name the functions so that they make sense when used with qualified access. Having to write Tree.foldTree seems redundant. A more idiomatic name would be fold, so that you could write Tree.fold. The problem with that name, though, is that fold usually implies a list-biased fold (corresponding to foldl in Haskell), and I'll actually need that name for that particular purpose later.

So, cata it is.

In this article, tree functionality is (with one exception) directly or transitively implemented with cata.

Filtering trees #

It'll be useful to be able to filter the contents of a tree. For example, the picture archivist program will only move image files with valid metadata. This means that it'll need to filter out all files that aren't image files, as well as image files without valid metadata.

It turns out that it'll be useful to supply a function that throws away None values from a tree of option leaves. This is similar to List.choose, so I call it Tree.choose:

// ('a -> 'b option) -> Tree<'c,'a> -> Tree<'c,'b> option
let choose f = cata (fun x -> List.choose id >> node x >> Some) (f >> Option.map Leaf)

You may find the type of the function surprising. Why does it return a Tree option, instead of simply a Tree?

While List.choose simply returns a list, it can do this because lists can be empty. This Tree type, on the other hand, can't be empty. If the purpose of Tree.choose is to throw away all None values, then how do you return a tree from Leaf None?

You can't return a Leaf because you have no value to put in the leaf. Similarly, you can't return a Node because, again, you have no value to put in the node.

In order to handle this edge case, then, you'll have to return None:

> let l : Tree<string, int option> = Leaf None;;
val l : Tree<string,int option> = Leaf None

> Tree.choose id l;;
val it : Tree<string,int> option = None

If you have anything other than a None leaf, though, you'll get a proper tree, but wrapped in an option:

> Tree.node "Foo" [Leaf (Some 42); Leaf None; Leaf (Some 2112)] |> Tree.choose id;;
val it : Tree<string,int> option = Some (Node ("Foo",[Leaf 42; Leaf 2112]))

While the resulting tree is wrapped in a Some case, the leaves contain unwrapped values.

Bifunctor, functor, and folds #

Through its type class language feature, Haskell has formal definitions of functors, bifunctors, and other types of folds (list-biased catamorphisms). F# doesn't have a similar degree of formalism, which means that while you can still implement the corresponding functionality, you'll have to rely on conventions to make the functions recognisable.

It's straighforward to start with the bifunctor functionality:

// ('a -> 'b) -> ('c -> 'd) -> Tree<'a,'c> -> Tree<'b,'d>
let bimap f g = cata (f >> node) (g >> leaf)

This is, apart from the syntax differences, the same implementation as in Haskell. Based on bimap, you can also trivially implement mapNode and mapLeaf functions if you'd like, but you're not going to need those for the code in this article. You do need, however, a function that we could consider an alias of a hypothetical mapLeaf function:

// ('b -> 'c) -> Tree<'a,'b> -> Tree<'a,'c>
let map f = bimap id f

This makes Tree a functor.

It'll also be useful to reduce a tree to a potentially more compact value, so you can add some specialised folds:

// ('c -> 'a -> 'c) -> ('c -> 'b -> 'c) -> 'c -> Tree<'a,'b> -> 'c
let bifold f g z t =
    let flip f x y = f y x
    cata (fun x xs -> flip f x >> List.fold (>>) id xs) (flip g) t z
 
// ('a -> 'c -> 'c) -> ('b -> 'c -> 'c) -> Tree<'a,'b> -> 'c -> 'c
let bifoldBack f g t z = cata (fun x xs -> List.foldBack (<<) xs id >> f x) g t z

In an attempt to emulate the F# naming conventions, I named the functions as I did. There are similar functions in the List and Option modules, for instance. If you're comparing the F# code with the Haskell code in the previous article, Tree.bifold corresponds to bifoldl, and Tree.bifoldBack corresponds to bifoldr.

These enable you to implement folds over leaves only:

// ('c -> 'b -> 'c) -> 'c -> Tree<'a,'b> -> 'c
let fold f = bifold (fun x _ -> x) f
 
// ('b -> 'c -> 'c) -> Tree<'a,'b> -> 'c -> 'c
let foldBack f = bifoldBack (fun _ x -> x) f

These, again, enable you to implement another function that'll turn out to be useful in this article:

// ('b -> unit) -> Tree<'a,'b> -> unit
let iter f = fold (fun () x -> f x) ()

The picture archivist program isn't going to explicitly need all of these, but transitively, it will.

Moving pictures #

So far, all the code shown here could be in a general-purpose reusable library, since it contains no functionality specifically related to image files. The rest of the code in this article, however, will be specific to the program. I'll put the domain model code in another module that I call Archive. Later in the article, we'll look at how to load a tree from the file system, but for now, we'll just pretend that we have such a tree.

The major logic of the program is to create a destination tree based on a source tree. The leaves of the tree will have to carry some extra information apart from a file path, so you can introduce a specific type to capture that information:

type PhotoFile = { File : FileInfo; TakenOn : DateTime }

A PhotoFile not only contains the file path for an image file, but also the date the photo was taken. This date can be extracted from the file's metadata, but that's an impure operation, so we'll delegate that work to the start of the program. We'll return to that later.

Given a source tree of PhotoFile leaves, though, the program must produce a destination tree of files:

// string -> Tree<'a,PhotoFile> -> Tree<string,FileInfo>
let moveTo destination t =
    let dirNameOf (dt : DateTime) = sprintf "%d-%02d" dt.Year dt.Month
    let groupByDir pf m =
        let key = dirNameOf pf.TakenOn
        let dir = Map.tryFind key m |> Option.defaultValue []
        Map.add key (pf.File :: dir) m
    let addDir name files dirs =
        Tree.node name (List.map Leaf files) :: dirs
 
    let m = Tree.foldBack groupByDir t Map.empty
    Map.foldBack addDir m [] |> Tree.node destination

This moveTo function looks, perhaps, overwhelming, but it's composed of three conceptual steps:

1. Create a map of destination folders (m).
2. Create a list of branches from the map (Map.foldBack addDir m []).
3. Create a tree from the list (Tree.node destination).

The moveTo function starts by folding the input data into a map m. The map is keyed by the directory name, which is formatted by the dirNameOf function. This function takes a DateTime as input and formats it to a YYYY-MM format. For example, December 20, 2018 becomes "2018-12".

The entire mapping step groups the PhotoFile values into a map of the type Map<string,FileInfo list>. All the image files taken in April 2014 are added to the list with the "2014-04" key, all the image files taken in July 2011 are added to the list with the "2011-07" key, and so on.

In the next step, the moveTo function converts the map to a list of trees. This will be the branches (or sub-directories) of the destination directory. Because of the desired structure of the destination tree, this is a list of shallow branches. Each node contains only leaves.

The only remaining step is to add that list of branches to a destination node. This is done by piping (|>) the list of sub-directories into Tree.node destination.

Since this is a pure function, it's easy to unit test. Just create some test cases and call the function. First, the test cases.

In this code base, I'm using xUnit.net 2.4.1, so I'll first create a set of test cases as a test-specific class:

type MoveToDestinationTestData () as this =
    inherit TheoryData<Tree<string, PhotoFile>, string, Tree<string, string>> ()
 
    let photoLeaf name (y, mth, d, h, m, s) =
        Leaf { File = FileInfo name; TakenOn = DateTime (y, mth, d, h, m, s) }
 
    do this.Add (
        photoLeaf "1" (2018, 11, 9, 11, 47, 17),
        "D",
        Node ( "D", [Node ("2018-11", [Leaf "1"])]))
    do this.Add (
        Node ("S", [photoLeaf "4" (1972, 6, 6, 16, 15, 0)]),
        "D",
        Node ("D", [Node ("1972-06", [Leaf "4"])]))
    do this.Add (
        Node ("S", [
            photoLeaf "L" (2002, 10, 12, 17, 16, 15);
            photoLeaf "J" (2007, 4, 21, 17, 18, 19)]),
        "D",
        Node ("D", [
            Node ("2002-10", [Leaf "L"]);
            Node ("2007-04", [Leaf "J"])]))
    do this.Add (
        Node ("1", [
            photoLeaf "a" (2010, 1, 12, 17, 16, 15);
            photoLeaf "b" (2010, 3, 12, 17, 16, 15);
            photoLeaf "c" (2010, 1, 21, 17, 18, 19)]),
        "2",
        Node ("2", [
            Node ("2010-01", [Leaf "a"; Leaf "c"]);
            Node ("2010-03", [Leaf "b"])]))
    do this.Add (
        Node ("foo", [
            Node ("bar", [
                photoLeaf "a" (2010, 1, 12, 17, 16, 15);
                photoLeaf "b" (2010, 3, 12, 17, 16, 15);
                photoLeaf "c" (2010, 1, 21, 17, 18, 19)]);
            Node ("baz", [
                photoLeaf "d" (2010, 3, 1, 2, 3, 4);
                photoLeaf "e" (2011, 3, 4, 3, 2, 1)])]),
        "qux",
        Node ("qux", [
            Node ("2010-01", [Leaf "a"; Leaf "c"]);
            Node ("2010-03", [Leaf "b"; Leaf "d"]);
            Node ("2011-03", [Leaf "e"])]))

That looks like a lot of code, but is really just a list of test cases. Each test case is a triple of a source tree, a destination directory name, and an expected result (another tree).

The test itself, on the other hand, is compact:

[<Theory; ClassData(typeof<MoveToDestinationTestData>)>]
let ``Move to destination`` source destination expected =
    let actual = Archive.moveTo destination source
    expected =! Tree.map string actual

The =! operator comes from Unquote and means something like must equal. It's an assertion that will throw an exception if expected isn't equal to Tree.map string actual.

The reason that the assertion maps actual to a tree of strings is that actual is a Tree<string,FileInfo>, but FileInfo doesn't have structural equality. So either I had to implement a test-specific equality comparer for FileInfo (and for Tree<string,FileInfo>), or map the tree to something with proper equality, such as a string. I chose the latter.

Calculating moves #

One pure step remains. The result of calling the moveTo function is a tree with the desired structure. In order to actually move the files, though, for each file you'll need to keep track of both the source path and the destination path. To make that explicit, you can define a type for that purpose:

type Move = { Source : FileInfo; Destination : FileInfo }

A Move is simply a data structure. Contrast this with typical object-oriented design, where it would be a (possibly polymorphic) method on an object. In functional programming, you'll regularly model intent with a data structure. As long as intents remain data, you can easily manipulate them, and once you're done with that, you can run an interpreter over your data structure to perform the work you want accomplished.

The unit test cases for the moveTo function suggest that file names are local file names like "L", "J", "a", and so on. That was only to make the tests as compact as possible, since the function actually doesn't manipulate the specific FileInfo objects.

In reality, the file names will most likely be longer, and they could also contain the full path, instead of the local path: "C:\foo\bar\a.jpg".

If you call moveTo with a tree where each leaf has a fully qualified path, the output tree will have the desired structure of the destination tree, but the leaves will still contain the full path to each source file. That means that you can calculate a Move for each file:

// Tree<string,FileInfo> -> Tree<string,Move>
let calculateMoves =
    let replaceDirectory (f : FileInfo) d =
        FileInfo (Path.Combine (d, f.Name))
    let rec imp path = function
        | Leaf x ->
            Leaf { Source = x; Destination = replaceDirectory x path }
        | Node (x, xs) ->
            let newNPath = Path.Combine (path, x)
            Tree.node newNPath (List.map (imp newNPath) xs)
    imp ""

This function takes as input a Tree<string,FileInfo>, which is compatible with the output of moveTo. It returns a Tree<string,Move>, i.e. a tree where the leaves are Move values.

Earlier, I wrote that you can implement desired Tree functionality with the cata function, but that was a simplification. If you can implement the functionality of calculateMoves with cata, I don't know how. You can, however, implement it using explicit pattern matching and simple recursion.

The imp function builds up a file path as it recursively negotiates the tree. All Leaf nodes are converted to a Move value using the leaf node's current FileInfo value as the Source, and the path to figure out the desired Destination.

This code is still easy to unit test. First, test cases:

type CalculateMovesTestData () as this =
    inherit TheoryData<Tree<string, FileInfo>, Tree<string, (string * string)>> ()
 
    do this.Add (Leaf (FileInfo "1"), Leaf ("1", "1"))
    do this.Add (
        Node ("a", [Leaf (FileInfo "1")]),
        Node ("a", [Leaf ("1", Path.Combine ("a", "1"))]))
    do this.Add (
        Node ("a", [Leaf (FileInfo "1"); Leaf (FileInfo "2")]),
        Node ("a", [
            Leaf ("1", Path.Combine ("a", "1"));
            Leaf ("2", Path.Combine ("a", "2"))]))
    do this.Add (
        Node ("a", [
            Node ("b", [
                Leaf (FileInfo "1");
                Leaf (FileInfo "2")]);
            Node ("c", [
                Leaf (FileInfo "3")])]),
        Node ("a", [
            Node (Path.Combine ("a", "b"), [
                Leaf ("1", Path.Combine ("a", "b", "1"));
                Leaf ("2", Path.Combine ("a", "b", "2"))]);
            Node (Path.Combine ("a", "c"), [
                Leaf ("3", Path.Combine ("a", "c", "3"))])]))

The test cases in this parametrised test are tuples of an input tree and the expected tree. For each test case, the test calls the Archive.calculateMoves function with tree and asserts that the actual tree is equal to the expected tree:

[<Theory; ClassData(typeof<CalculateMovesTestData>)>]
let ``Calculate moves`` tree expected =
    let actual = Archive.calculateMoves tree
    expected =! Tree.map (fun m -> (m.Source.ToString (), m.Destination.ToString ())) actual

Again, the test maps FileInfo objects to strings to support easy comparison.

That's all the pure code you need in order to implement the desired functionality. Now you only need to write some code that loads a tree from disk, and imprints a destination tree to disk, as well as the code that composes it all.

Loading a tree from disk #

The remaining code in this article is impure. You could put it in dedicated modules, but for this program, you're only going to need three functions and a bit of composition code, so you could also just put it all in the Program module. That's what I did.

To load a tree from disk, you'll need a root directory, under which you load the entire tree. Given a directory path, you read a tree using a recursive function like this:

// string -> Tree<string,string>
let rec readTree path =
    if File.Exists path
    then Leaf path
    else
        let dirsAndFiles = Directory.EnumerateFileSystemEntries path
        let branches = Seq.map readTree dirsAndFiles |> Seq.toList
        Node (path, branches)

This recursive function starts by checking whether the path is a file that exists. If it does, the path is a file, so it creates a new Leaf with that path.

If path isn't a file, it's a directory. In that case, use Directory.EnumerateFileSystemEntries to enumerate all the directories and files in that directory, and map all those directory entries recursively. That produces all the branches for the current node. Finally, return a new Node with the path and the branches.

Loading metadata #

The readTree function only produces a tree with string leaves, while the program requires a tree with PhotoFile leaves. You'll need to read the Exif metadata from each file and enrich the tree with the date-taken data.

In this code base, I've written a little Photo module to extract the desired metadata from an image file. I'm not going to list all the code here; if you're interested, the code is available on GitHub. The Photo module enables you to write an impure operation like this:

// FileInfo -> PhotoFile option
let readPhoto file =
    Photo.extractDateTaken file
    |> Option.map (fun dateTaken -> { File = file; TakenOn = dateTaken })

This operation can fail for various reasons:

• The file may not exist.
• The file exists, but has no metadata.
• The file has metadata, but no date-taken metadata.
• The date-taken metadata string is malformed.

When you traverse a Tree<string,string> with readPhoto, you'll get a Tree<string,PhotoFile option>. That's when you'll need Tree.choose. You'll see this soon.

Writing a tree to disk #

The above calculateMoves function creates a Tree<string,Move>. The final piece of impure code you'll need to write is an operation that traverses such a tree and executes each Move.

// Tree<'a,Move> -> unit
let writeTree t =
    let copy m =
        Directory.CreateDirectory m.Destination.DirectoryName |> ignore
        m.Source.CopyTo m.Destination.FullName |> ignore
        printfn "Copied to %s" m.Destination.FullName
    let compareFiles m =
        let sourceStream = File.ReadAllBytes m.Source.FullName
        let destinationStream = File.ReadAllBytes m.Destination.FullName
        sourceStream = destinationStream
    let move m =
        copy m
        if compareFiles m then m.Source.Delete ()
    Tree.iter move t

The writeTree function traverses the input tree, and for each Move, it first copies the file, then it verifies that the copy was successful, and finally, if that's the case, it deletes the source file.

Composition #

You can now compose an impure-pure-impure sandwich from all the Lego pieces:

// string -> string -> unit
let movePhotos source destination =
    let sourceTree = readTree source |> Tree.map FileInfo
    let photoTree = Tree.choose readPhoto sourceTree
    let destinationTree =
        Option.map (Archive.moveTo destination >> Archive.calculateMoves) photoTree
    Option.iter writeTree destinationTree

First, you load the sourceTree using the readTree operation. This returns a Tree<string,string>, so map the leaves to FileInfo objects. You then load the image metatadata by traversing sourceTree with Tree.choose readPhoto. Each call to readPhoto produces a PhotoFile option, so this is where you want to use Tree.choose to throw all the None values away.

Those two lines of code constitute the initial impure step of the sandwich (yes: mixed metaphors, I know).

The pure part of the sandwich is the composition of the pure functions moveTo and calculateMoves. Since photoTree is a Tree<string,PhotoFile> option, you'll need to perform that transformation inside of Option.map. The resulting destinationTree is a Tree<string,Move> option.

The final, impure step of the sandwich, then, is to apply all the moves with writeTree.

Execution #

The movePhotos operation takes source and destination arguments. You could hypothetically call it from a rich client or a background process, but here I'll just call if from a command-line program. The main operation will have to parse the input arguments and call movePhotos:

[<EntryPoint>]
let main argv =
    match argv with
    | [|source; destination|] -> movePhotos source destination
    | _ -> printfn "Please provide source and destination directories as arguments."
    0 // return an integer exit code

You could write more sophisticated parsing of the program arguments, but that's not the topic of this article, so I only wrote the bare minimum required to get the program working.

You can now compile and run the program:

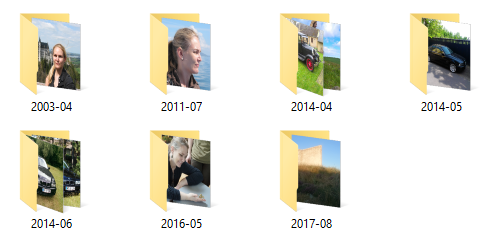
$ ./ArchivePictures "C:\Users\mark\Desktop\Test" "C:\Users\mark\Desktop\Test-Out"
Copied to C:\Users\mark\Desktop\Test-Out\2003-04\2003-04-29 15.11.50.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2011-07\2011-07-10 13.09.36.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-04\2014-04-18 14.05.02.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-04\2014-04-17 17.11.40.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-05\2014-05-23 16.07.20.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-06\2014-06-21 16.48.40.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-06\2014-06-30 15.44.52.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2016-05\2016-05-01 09.25.23.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2017-08\2017-08-22 19.53.28.jpg

This does indeed produce the expected destination directory structure.

It's always nice when something turns out to work in practice, as well as in theory.

Summary #

Functional software architecture involves separating pure from impure code so that no pure functions invoke impure operations. Often, you can achieve that with what I call the impure-pure-impure sandwich architecture. In this example, you saw how to model the file system as a tree. This enables you to separate the impure file interactions from the pure program logic.

---

Comments

• ← Previous
• Archive
• Next →