Range as a functor by Mark Seemann
With examples in C#, F#, and Haskell.
This article is an instalment in a short series of articles on the Range kata. In the previous three articles you've seen the Range kata implemented in Haskell, in F#, and in C#.
The reason I engaged with this kata was that I find that it provides a credible example of a how a pair of functors itself forms a functor. In this article, you'll see how that works out in three languages. If you don't care about one or two of those languages, just skip that section.
Haskell perspective #
If you've done any Haskell programming, you may be thinking that I have in mind the default Functor instances for tuples. As part of the base library, tuples (pairs, triples, quadruples, etc.) are already Functor instances. Specifically for pairs, we have this instance:
instance Functor ((,) a)
Those are not the functor instances I have in mind. To a degree, I find these default Functor instances unfortunate, or at least arbitrary. Let's briefly explore the above instance to see why that is.
Haskell is a notoriously terse language, but if we expand the above instance to (invalid) pseudocode, it says something like this:
instance Functor ((a,b) b)
What I'm trying to get across here is that the a type argument is fixed, and only the second type argument b can be mapped. Thus, you can map a (Bool, String) pair to a (Bool, Int) pair:
ghci> fmap length (True, "foo") (True,3)
but the first element (Bool, in this example) is fixed, and you can't map that. To be clear, the first element can be any type, but once you've fixed it, you can't change it (within the constraints of the Functor API, mind):
ghci> fmap (replicate 3) (42, 'f')
(42,"fff")
ghci> fmap ($ 3) ("bar", (* 2))
("bar",6)
The reason I find these default instances arbitrary is that this isn't the only possible Functor instance. Pairs, in particular, are also Bifunctor instances, so you can easily map over the first element, instead of the second:
ghci> first show (42, 'f')
("42",'f')
Similarly, one can easily imagine a Functor instance for triples (three-tuples) that map the middle element. The default instance, however, maps the third (i.e. last) element only.
There are some hand-wavy rationalizations out there that argue that in Haskell, application and reduction is usually done from the right, so therefore it's most appropriate to map over the rightmost element of tuples. I admit that it at least argues from a position of consistency, and it does make it easier to remember, but from a didactic perspective I still find it a bit unfortunate. It suggests that a tuple functor only maps the last element.
What I had in mind for ranges however, wasn't to map only the first or the last element. Neither did I wish to treat ranges as bifunctors. What I really wanted was the ability to project an entire range.
In my Haskell Range implementation, I'd simply treated ranges as tuples of Endpoint values, and although I didn't show that in the article, I ultimately declared Endpoint as a Functor instance:
data Endpoint a = Open a | Closed a deriving (Eq, Show, Functor)
This enables you to map a single Endpoint value:
ghci> fmap length $ Closed "foo" Closed 3
That's just a single value, but the Range kata API operates with pairs of Endpoint value. For example, the contains function has this type:
contains :: (Foldable t, Ord a) => (Endpoint a, Endpoint a) -> t a -> Bool
Notice the (Endpoint a, Endpoint a) input type.
Is it possible to treat such a pair as a functor? Yes, indeed, just import Data.Functor.Product, which enables you to package two functor values in a single wrapper:
ghci> import Data.Functor.Product ghci> Pair (Closed "foo") (Open "corge") Pair (Closed "foo") (Open "corge")
Now, granted, the Pair data constructor doesn't wrap a tuple, but that's easily fixed:
ghci> uncurry Pair (Closed "foo", Open "corge") Pair (Closed "foo") (Open "corge")
The resulting Pair value is a Functor instance, which means that you can project it:
ghci> fmap length $ uncurry Pair (Closed "foo", Open "corge") Pair (Closed 3) (Open 5)
Now, granted, I find the Data.Functor.Product API a bit lacking in convenience. For instance, there's no getPair function to retrieve the underlying values; you'd have to use pattern matching for that.
In any case, my motivation for covering this ground wasn't to argue that Data.Functor.Product is all we need. The point was rather to observe that when you have two functors, you can combine them, and the combination is also a functor.
This is one of the many reasons I get so much value out of Haskell. Its abstraction level is so high that it substantiates relationships that may also exist in other code bases, written in other programming languages. Even if a language like F# or C# can't formally express some of those abstraction, you can still make use of them as 'design patterns' (for lack of a better term).
F# functor #
What we've learned from Haskell is that if we have two functors we can combine them into one. Specifically, I made Endpoint a Functor instance, and from that followed automatically that a Pair of those was also a Functor instance.
I can do the same in F#, starting with Endpoint. In F# I've unsurprisingly defined the type like this:
type Endpoint<'a> = Open of 'a | Closed of 'a
That's just a standard discriminated union. In order to make it a functor, you'll have to add a map function:
module Endpoint = let map f = function | Open x -> Open (f x) | Closed x -> Closed (f x)
The function alone, however, isn't enough to give rise to a functor. We must also convince ourselves that the map function obeys the functor laws. One way to do that is to write tests. While tests aren't proofs, we may still be sufficiently reassured by the tests that that's good enough for us. While I could, I'm not going to prove that Endpoint.map satisfies the functor laws. I will, later, do just that with the pair, but I'll leave this one as an exercise for the interested reader.
Since I was already using Hedgehog for property-based testing in my F# code, it was obvious to write properties for the functor laws as well.
[<Fact>] let ``First functor law`` () = Property.check <| property { let genInt32 = Gen.int32 (Range.linearBounded ()) let! expected = Gen.choice [Gen.map Open genInt32; Gen.map Closed genInt32] let actual = Endpoint.map id expected expected =! actual }
This property exercises the first functor law for integer endpoints. Recall that this law states that if you map a value with the identity function, nothing really happens.
The second functor law is more interesting.
[<Fact>] let ``Second functor law`` () = Property.check <| property { let genInt32 = Gen.int32 (Range.linearBounded ()) let! endpoint = Gen.choice [Gen.map Open genInt32; Gen.map Closed genInt32] let! f = Gen.item [id; ((+) 1); ((*) 2)] let! g = Gen.item [id; ((+) 1); ((*) 2)] let actual = Endpoint.map (f << g) endpoint Endpoint.map f (Endpoint.map g endpoint) =! actual }
This property again exercises the property for integer endpoints. Not only does the property pick a random integer and varies whether the Endpoint is Open or Closed, it also picks two random functions from a small list of functions: The identity function (again), a function that increments by one, and a function that doubles the input. These two functions, f and g, might then be the same, but might also be different from each other. Thus, the composition f << g might be id << id or ((+) 1) << ((+) 1), but might just as well be ((+) 1) << ((*) 2), or one of the other possible combinations.
The law states that the result should be the same regardless of whether you first compose the functions and then map them, or map them one after the other.
Which is the case.
A Range is defined like this:
type Range<'a> = { LowerBound : Endpoint<'a>; UpperBound : Endpoint<'a> }
This record type also gives rise to a functor:
module Range = let map f { LowerBound = lowerBound; UpperBound = upperBound } = { LowerBound = Endpoint.map f lowerBound UpperBound = Endpoint.map f upperBound }
This map function uses the projection f on both the lowerBound and the upperBound. It, too, obeys the functor laws:
[<Fact>] let ``First functor law`` () = Property.check <| property { let genInt64 = Gen.int64 (Range.linearBounded ()) let genEndpoint = Gen.choice [Gen.map Open genInt64; Gen.map Closed genInt64] let! expected = Gen.tuple genEndpoint |> Gen.map Range.ofEndpoints let actual = expected |> Ploeh.Katas.Range.map id expected =! actual } [<Fact>] let ``Second functor law`` () = Property.check <| property { let genInt16 = Gen.int16 (Range.linearBounded ()) let genEndpoint = Gen.choice [Gen.map Open genInt16; Gen.map Closed genInt16] let! range = Gen.tuple genEndpoint |> Gen.map Range.ofEndpoints let! f = Gen.item [id; ((+) 1s); ((*) 2s)] let! g = Gen.item [id; ((+) 1s); ((*) 2s)] let actual = range |> Ploeh.Katas.Range.map (f << g) Ploeh.Katas.Range.map f (Ploeh.Katas.Range.map g range) =! actual }
These two Hedgehog properties are cast in the same mould as the Endpoint properties, only they create 64-bit and 16-bit ranges for variation's sake.
C# functor #
As I wrote about the Haskell result, it teaches us which abstractions are possible, even if we can't formalise them to the same degree in, say, C# as we can in Haskell. It should come as no surprise, then, that we can also make Range<T> a functor in C#.
In C# we idiomatically do that by giving a class a Select method. Again, we'll have to begin with Endpoint:
public Endpoint<TResult> Select<TResult>(Func<T, TResult> selector) { return Match( whenClosed: x => Endpoint.Closed(selector(x)), whenOpen: x => Endpoint.Open(selector(x))); }
Does that Select method obey the functor laws? Yes, as we can demonstrate (not prove) with a few properties:
[Fact] public void FirstFunctorLaw() { Gen.OneOf( Gen.Int.Select(Endpoint.Open), Gen.Int.Select(Endpoint.Closed)) .Sample(expected => { var actual = expected.Select(x => x); Assert.Equal(expected, actual); }); } [Fact] public void ScondFunctorLaw() { (from endpoint in Gen.OneOf( Gen.Int.Select(Endpoint.Open), Gen.Int.Select(Endpoint.Closed)) from f in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) from g in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) select (endpoint, f, g)) .Sample(t => { var actual = t.endpoint.Select(x => t.g(t.f(x))); Assert.Equal( t.endpoint.Select(t.f).Select(t.g), actual); }); }
These two tests follow the scheme laid out by the above F# properties, and they both pass.
The Range class gets the same treatment. First, a Select method:
public Range<TResult> Select<TResult>(Func<T, TResult> selector) where TResult : IComparable<TResult> { return new Range<TResult>(min.Select(selector), max.Select(selector)); }
which, again, can be demonstrated with two properties that exercise the functor laws:
[Fact] public void FirstFunctorLaw() { var genEndpoint = Gen.OneOf( Gen.Int.Select(Endpoint.Closed), Gen.Int.Select(Endpoint.Open)); genEndpoint.SelectMany(min => genEndpoint .Select(max => new Range<int>(min, max))) .Sample(sut => { var actual = sut.Select(x => x); Assert.Equal(sut, actual); }); } [Fact] public void SecondFunctorLaw() { var genEndpoint = Gen.OneOf( Gen.Int.Select(Endpoint.Closed), Gen.Int.Select(Endpoint.Open)); (from min in genEndpoint from max in genEndpoint from f in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) from g in Gen.OneOfConst<Func<int, int>>(x => x, x => x + 1, x => x * 2) select (sut : new Range<int>(min, max), f, g)) .Sample(t => { var actual = t.sut.Select(x => t.g(t.f(x))); Assert.Equal( t.sut.Select(t.f).Select(t.g), actual); }); }
These tests also pass.
Laws #
Exercising a pair of properties can give us a good warm feeling that the data structures and functions defined above are proper functors. Sometimes, tests are all we have, but in this case we can do better. We can prove that the functor laws always hold.
The various above incarnations of a Range type are all product types, and the canonical form of a product type is a tuple (see e.g. Thinking with Types for a clear explanation of why that is). That's the reason I stuck with a tuple in my Haskell code.
Consider the implementation of the fmap implementation of Pair:
fmap f (Pair x y) = Pair (fmap f x) (fmap f y)
We can use equational reasoning, and as always I'll use the the notation that Bartosz Milewski uses. It's only natural to begin with the first functor law, using F and G as placeholders for two arbitrary Functor data constructors.
fmap id (Pair (F x) (G y))
= { definition of fmap }
Pair (fmap id (F x)) (fmap id (G y))
= { first functor law }
Pair (F x) (G y)
= { definition of id }
id (Pair (F x) (G y))
Keep in mind that in this notation, the equal signs are true equalities, going both ways. Thus, you can read this proof from the top to the bottom, or from the bottom to the top. The equality holds both ways, as should be the case for a true equality.
We can proceed in the same vein to prove the second functor law, being careful to distinguish between Functor instances (F and G) and functions (f and g):
fmap (g . f) (Pair (F x) (G y))
= { definition of fmap }
Pair (fmap (g . f) (F x)) (fmap (g . f) (G y))
= { second functor law }
Pair ((fmap g . fmap f) (F x)) ((fmap g . fmap f) (G y))
= { definition of composition }
Pair (fmap g (fmap f (F x))) (fmap g (fmap f (G y)))
= { definition of fmap }
fmap g (Pair (fmap f (F x)) (fmap f (G y)))
= { definition of fmap }
fmap g (fmap f (Pair (F x) (G y)))
= { definition of composition }
(fmap g . fmap f) (Pair (F x) (G y))
Notice that both proofs make use of the functor laws. This may seem self-referential, but is rather recursive. When the proofs refer to the functor laws, they refer to the functors F and G, which are both assumed to be lawful.
This is how we know that the product of two lawful functors is itself a functor.
Negations #
During all of this, you may have thought: What happens if we project a range with a negation?
As a simple example, let's consider the range from -1 to 2:
ghci> uncurry Pair (Closed (-1), Closed 2) Pair (Closed (-1)) (Closed 2)
We may draw this range on the number line like this:

What happens if we map that range by multiplying with -1?
ghci> fmap negate $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 1) (Closed (-2))
We get a range from 1 to -2!
Aha! you say, clearly that's wrong! We've just found a counterexample. After all, range isn't a functor.
Not so. The functor laws say nothing about the interpretation of projections (but I'll get back to that in a moment). Rather, they say something about composition, so let's consider an example that reaches a similar, seemingly wrong result:
ghci> fmap ((+1) . negate) $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 2) (Closed (-1))
This is a range from 2 to -1, so just as problematic as before.
The second functor law states that the outcome should be the same if we map piecewise:
ghci> (fmap (+ 1) . fmap negate) $ uncurry Pair (Closed (-1), Closed 2) Pair (Closed 2) (Closed (-1))
Still a range from 2 to -1. The second functor law holds.
But, you protest, that's doesn't make any sense!
I disagree. It could make sense in at least three different ways.
What does a range from 2 to -1 mean? I can think of three interpretations:
- It's the empty set
- It's the range from -1 to 2
- It's the set of numbers that are either less than or equal to -1 or greater than or equal to 2
We may illustrate those three interpretations, together with the original range, like this:
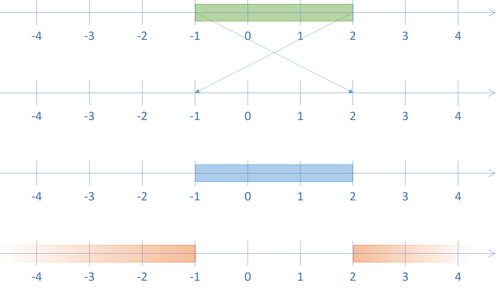
According to the first interpretation, we consider the range as the Boolean and of two predicates. In this interpretation the initial range is really the Boolean expression -1 ≤ x ∧ x ≤ 2. The projected range then becomes the expression 2 ≤ x ∧ x ≤ -1, which is not possible. This is how I've chosen to implement the contains function:
ghci> Pair x y = fmap ((+1) . negate) $ uncurry Pair (Closed (-1), Closed 2) ghci> contains (x, y) [0] False ghci> contains (x, y) [-3] False ghci> contains (x, y) [4] False
In this interpretation, the result is the empty set. The range isn't impossible; it's just empty. That's the second number line from the top in the above illustration.
This isn't, however, the only interpretation. Instead, we may choose to be liberal in what we accept and interpret the range from 2 to -1 as a 'programmer mistake': What you asked me to do is formally wrong, but I think that I understand that you meant the range from -1 to 2.
That's the third number line in the above illustration.
The fourth interpretation is that when the first element of the range is greater than the second, the range represents the complement of the range. That's the fourth number line in the above illustration.
The reason I spent some time on this is that it's easy to confuse the functor laws with other properties that you may associate with a data structure. This may lead you to falsely conclude that a functor isn't a functor, because you feel that it violates some other invariant.
If this happens, consider instead whether you could possibly expand the interpretation of the data structure in question.
Conclusion #
You can model a range as a functor, which enables you to project ranges, either moving them around on an imaginary number line, or changing the type of the range. This might for example enable you to map a date range to an integer range, or vice versa.
A functor enables mapping or projection, and some maps may produce results that you find odd or counter-intuitive. In this article you saw an example of that in the shape of a negated range where the first element (the 'minimum', in one interpretation) becomes greater than the second element (the 'maximum'). You may take that as an indication that the functor isn't, after all, a functor.
This isn't the case. A data structure and its map function is a functor if the the mapping obeys the functor laws, which is the case for the range structures you've seen here.
