Simpler encapsulation with immutability by Mark Seemann
A worked example.
I've noticed that many software organizations struggle with encapsulation with 'bigger' problems. It may be understandable and easily applicable to define a NaturalNumber type or ensure that a minimum value is less than a maximum value, and so on. How do you, however, guarantee invariants once the scope of the problem becomes bigger and more complex?
In this series of articles, I'll attempt to illustrate how and why this worthy design goal seems elusive, and what you can do to achieve it.
Contracts #
As usual, when I discuss encapsulation, I first need to establish what I mean by the term. It is, after all, one of the most misunderstood concepts in software development. As regular readers will know, I follow the lead of Object-Oriented Software Construction. In that perspective, encapsulation is the appropriate modelling and application of preconditions, invariants, and postconditions.
Particularly when it comes to invariants, things seem to fall apart as the problem being modelled grows in complexity. Teams eventually give up guaranteeing any invariants, leaving client developers with no recourse but defensive coding, which again leads to code duplication, bugs, and maintenance problems.
If you need a reminder, an invariant is an assertion about an object that is always true. The more invariants an object has, the better guarantees it gives, and the more you can trust it. The more you can trust it, the less defensive coding you have to write. You don't have to check if return values are null, strings empty, numbers negative, collections empty, or so on.
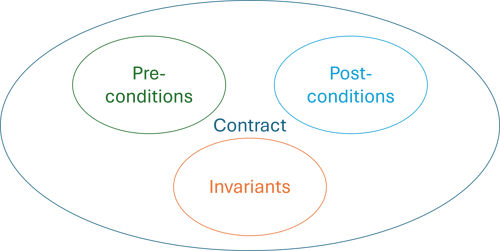
All together, I usually denote the collection of invariants, pre-, and postconditions as a type's contract.
For a simple example like modelling a natural number, or a range, or a user name, most people are able to produce sensible and coherent designs. Once, however, the problem becomes more complex, and the invariants involve multiple interacting values, maintaining the contract becomes harder.
Immutability to the rescue #
I'm not going to bury the lede any longer. It strikes me that mutation is a major source of complexity. It's not that hard to check a set of conditions when you create a value (or object or record). What makes it hard to maintain invariants is when objects are allowed to change. This implies that for every possible change to the object, it needs to examine its current state in order to decide whether or not it should allow the operation.
If the mutation happens on a leaf node in an object graph, the leaf may have to notify its parent, so that the parent can recheck the invariants. If the graph has cycles it becomes more complicated still, and if you want to make the problem truly formidable, try making the object thread-safe.
Making the object immutable makes most of these problems go away. You don't have to worry about thread-safety, because immutable values are automatically thread-safe; there's no state for any thread to change.
Even better, though, is that an immutable object's contract is smaller and simpler. It still has preconditions, because there are rules that govern what has to be true before you can create such an object. Furthermore, there may also be rules that stipulate what must be true before you can call a method on it.
Likewise, postconditions are still relevant. If you call a method on the object, it may give you guarantees about what it returns.
There are, however, no independent invariants.
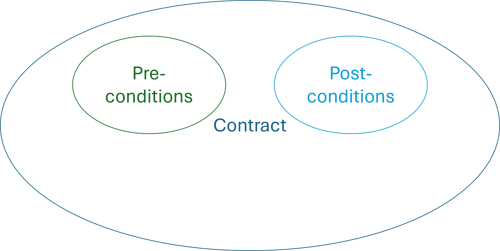
Or rather, the invariants for an immutable object entirely coincide with its preconditions. If it was valid at creation, it remains valid.
Priority collection #
As promised, I'll work through a problem to demonstrate what I mean. I'll first showcase how mutation makes the problem hard, and then how trivial it becomes with an immutable design.
The problem is this: Design and implement a class (or just a data structure if you don't want to do Object-Oriented programming) that models a priority list (not a Priority Queue) as you sometimes run into in surveys. You know, one of these survey questions that asks you to distribute 100 points on various different options:
- Option F: 30%
- Option A: 25%
- Option C: 25%
- Option E: 20%
- Option B: 0%
- Option D: 0%
If you have the time, I suggest that you treat this problem as a kata. Try to do the exercise before reading the next articles in this series. You can assume the following, which is what I did.
- The budget is 100. (You could make it configurable, but the problem is gnarly enough even with a hard-coded value.)
- You don't need to include items with priority value 0, but you should allow it.
- The sum of priorities must be exactly 100. This is the invariant.
The difficult part is that last invariant. Let me stress this requirement: At any time, the object should be in a consistent state; i.e. at any time should the sum of priorities be exactly 100. Not 101 or 99, but 100. Good luck with that.
The object should also be valid at initialization.
Of course, having read this far, you understand that all you have to do is to make the object immutable, but just for the sake of argument, try designing a mutable object with this invariant. Once you've tried your hand with that, read on.
Attempts #
There's educational value going through even failed attempts. When I thought of this example, I fairly quickly outlined in my head one approach that was unlikely to ever work, one that could work, and the nice immutable solution that trivially works.
I'll cover each in turn:
- A failed attempt at priority collection with inheritance
- A mutable priority collection
- An immutable priority collection
It's surprising how hard even a simple exercise like this one turns out to be, if you try to do it the object-oriented way.
In reality, business rules are much more involved than what's on display here. For only a taste of how bad it might get, read Hillel Wayne's suggestions regarding a similar kind of problem.
Conclusion #
If you've lived all your programming life with mutation as an ever-present possibility, you may not realize how much easier immutability makes everything. This includes invariants.
When you have immutable data, object graphs tend to be simpler. You can't easily define cyclic graphs (although Haskell, due to its laziness, surprisingly does enable this), and invariants essentially coincide with preconditions.
In the following articles, I'll show how mutability makes even simple invariants difficult to implement, and how immutability easily addresses the issue.
Next: A failed attempt at priority collection with inheritance.

Comments
I've been enjoying going through your articles in the past couple months, and I really like the very pedagogic treatment of functional programming and adjacent topics.
The kata here is an interesting one, but I don't think I'd link it with the concept of immutability/mutability. My immediate thought was a naïve struct that can represent illegal values and whose validity is managed through functions containing some tricky logic, but that didn't seem promising whether it was done immutably or not.
Instead, the phrase "distribute 100 points" triggered an association with the stars and bars method for similar problems. The idea is that we have N=100 points in a row, and inserting dividers to break it into (numOptions) groups. Concretely, our data structure is (dividers: int array), which is a sorted array of length (numOptions + 1) where the first element is 0 and the last element is N=100. The priorities are then exactly the differences between adjacent elements of the array. The example in the kata (A=25, B=0, C=25, D=0, E=20, F=30) is then represented by the array [| 0; 25; 25; 50; 50; 70; 100|].
This solution seems to respect the invariant, has a configurable budget, can work with other numerical types, and works well whether immutable or not (if mutable, just ensure the array remains sorted, has min 0, and max N). The invariant is encoded in the representation of the data, which seems to me to be the more relevant point than mutability.
And a somewhat disjoint thought, the kata reminded me of a WinForms TableLayoutPanel (or MS Word table) whose column widths all must fit within the container's width...
Thank you for writing. The danger of writing these article series is always that as soon as I've published the first one, someone comes by and puts a big hole through my premise. Well, I write this blog for a couple of independent reasons, and one of them is to learn.
And you just taught me something. Thank you. That is, at least, an elegant implementation.
How would you design the API encapsulating that implementation?
Clearly, arrays already have APIs, so you could obviously define an array-like API that performs the appropriate boundary checks. That, however, doesn't seem to model the given problem. Rather, it reveals the implementation, and forces a client developer to think in terms of the data structure, rather the problem (s)he has to solve.
Ideally, again channelling Bertrand Meyer, an object should present as an Abstract Data Structure (ADT) that doesn't require client developers to understand the implementation details. I'm curious what such an API would look like.
You've already surprised me once, and please do so once again. I'm always happy to learn something new, and that little stars-and-bars concept I've now added to my tool belt.
All that said, this article makes a more general claim, although its possible that the example it showcases is a tad too simple and naive to be a truly revealing one. The claim is that this kind of 'aggregate constraint' often causes so much trouble in the face of arbitrary state mutation that most programmers give up on encapsulation.
What happens if we instead expand the requirements a bit? Let's say that we will require the user to spend at least 90% of the budget, but no more than 100%. Also, there must be at least three prioritized items, and no individual item can receive more than a third of the budget.
Thank you for the response. Here's my thoughts - it's a bit of a wall of text, I might be wrong in any of the following, and the conclusion may be disappointing. When you ask how I'd design the API, I'd say it depends on how the priority list is going to be used. The implementation trick with stars and bars might just be a one-off trick that happens to work here, but it doesn't (shouldn't) affect the contract with the outside world.
If we're considering survey questions or budgets, the interest is in the priority values. So I think the problem then is about a list of priorities with an aggregate constraint. So I would define... an array-like API that performs the appropriate boundary checks (wow), but for the item priorities. My approach would be to go for "private data, public functions", and rely on a legal starting state and preserving the legality through the public API. In pseudocode:
type PriorityList = { budget: int; dividers: int list } create :: numItems: int -> budget: int -> PriorityList // Returns priorities. getAll :: plist: PriorityList -> int list get :: itemIdx: int -> plist: PriorityList -> int // *Sets the priority for an item (taking the priority from other items, starting from the back). set :: itemIdx: int -> priority: int -> plist: PriorityList -> PriorityList // *Adds a new item to (the end of) the PriorityList (with priority zero). addItem :: plist: PriorityList -> PriorityList // *Removes an item from the PriorityList (and assigns its priority to the last item). removeItem :: itemIdx: int -> plist PriorityList -> PriorityList // Utility functions: see text _toPriorities :: dividers: int list -> int list _toDividers :: priorities: int list -> int listCrucially: since
set,addItem, andremoveItemmust maintain the invariants, they must have "side effects" of altering other priorities. I think this is unavoidable here because we have aggregate/global constraints, rather than just elementwise/local constraints. (Is this why resizing rows and columns in WinForms tableLayoutPanels and MS Word tables is so tedious?) This will manifest in the API - the client needs to know what "side effects" there are (suggested behaviour in parentheses in the pseudocode comments above). See my crude attempt at implementation.You may already see where this is going. If I accept that boundary checks are needed, then my secondary goal in encapsulation is to express the constraints as clearly as possible, and hopefully not spread the checking logic all over the code.
Whence the utility functions: it turned out to be useful to convert from a list of dividers to priorities, and vice versa. This is because the elementwise operations/invariants like the individual priority values are easier to express in terms of raw priorities, while the aggregate ones like the total budget are easier in terms of "dividers" (the cumulative priorities). There is a runtime cost to the conversion, but the code becomes clearer. This smells similar to feature envy...
So why not just have the underlying implementation hold a list of priorities in the first place?! Almost everything in the implementation needs translation back to that anyway. D'oh! I refactored myself back to the naïve approach. The original representation seemed elegant, but I couldn't find a way to manipulate it that clients would find intuitive and useful in the given problem.
But... if I approach the design from the angle "what advantages does the cumulative priority model offer?", I might come up with the following candidate API functions, which could be implemented cleanly in the "divider" space:
// (same type, create, get, getAll, addItem as above) // Removes the item and merges its priority with the item before it. merge :: ItemIdx: int -> PriorityList // Sets the priority of an item to zero and gives it to the item after it. collapse :: itemIdx: int -> PriorityList // Swaps the priority of an item and the one after it (e.g. to "bubble" a priority value forwards or backwards, although this is easier in the "priority" space) swap :: itemIdx: int -> PriorityList // Sets (alternative: adds to) the priority of an item, taking the priority from the items after it in sequence ("consuming" them in the forward direction) consume :: itemIdx: int -> priority: int -> PriorityList // Splits the item into 2 smaller items each with half the priority (could be generalised to n items) split :: ItemIdx: int -> PriorityList // etc.And this seems like a more fitting API for that table column width example I keep bringing up. What's interesting to me is that despite the data structures of the budget/survey question and the table column widths being isomorphic, we can come up with rather different APIs depending on which view we consider. I think this is my main takeaway from this exploration, actually.
As for the additional requirements, individually each constraint is easy to handle, but their composition is tricky. If it's easy to transform an illegal PriorityList to make it respect the invariants, we can just apply the transformation after every create/set/add/remove. Something like:
type PriorityList = { budget: int dividers: int list budgetCondition: int -> bool maxPriority: int minChoices: int } let _enforceBudget (predicate: int -> bool) (defaultBudget: int) (dividers: int list) : int list = if (List.last dividers |> predicate) then dividers else List.take (dividers.Length - 1) dividers @ [ defaultBudget ] let _enforceMaxPriority (maxPriority: int) (dividers: int list) : int list = _toPriorities dividers |> List.map (fun p -> min p maxPriority) |> _toDividersThe problem is those transforms may not preserve each others' invariant. Life would be easy if we could write a single transform to preserve everything (I haven't found one - notice that the two above are operating on different int lists so it's tricky). Otherwise, we could write validations instead of transformations, then let create/set/add/remove fail by returning Option.None (explicitly fail) or the original list (silently fail). This comes at the cost of making the API less friendly.
Ultimately with this approach I can't see a way to make all illegal states unrepresentable without sprinkling ad-hoc checks everywhere in the code. The advantages of the "cumulative priorities" representation I can think of are (a) it makes the total budget invariant obvious, and (b) it maps nicely to a UI where you click and drag segments around. Since you might have gone down a different path in the series, I'm curious to see how that shapes up.
Hello and thank you for your blog. It is really informative and provides great food for thought.
What if it will be impossible to compile and run program which would lead to illegal (list) state?
I've tried to implement priority collection in Rust, and what I've ended up with is a heterogenous priority list with compile-time priority validation. Idea behind this implementation is simple: you declare recursive generic struct, which holds current element and tail (another list or unit type).
struct PriorityList<const B: usize, const P: usize, H, T> { head: H, tail: T, }If, for example, we need list of two Strings with budget 100, and 30/70 priority split, it will have the following type:
PriorityList<100, 30, String, PriorityList<100, 70, String, ()>>Note that information about list budget and current element priority is contained in generic arguments B and P respectively. These are compile-time "variables", and will be replaced be their values in compiled program.Since each element of such list is a list itself, and budget is the same for each element, all elements except the first are invalid priority lists. So, in order to make it possible to create lists other than containing one element, or only one element with >0 priority, validity check should be targeted and deferred. In order to target invariant validation on the first element of the list, I've included validation into list methods (except set_priority method). Every time list method is called, compiler does recursive computation of priority sum, and compares it with list budget, giving compile-time error if there is mismatch. Consider the following example, which will compile and run:
let list = ListBuilder::new::<10, 10>("Hello"); let list = list.set_priority::<5>();Seems like invariants have been violated and sum of priorities is less than the budget. But if we try to manipulate this list in any other way except to add element or change priority, program won't compile
// Won't compile let _ = list.pop(); // Won't compile let list = list.push::<4>("Hi"); // Will do let list = list.push::<5>("Hello there");This implementation may not be as practical as it could be due to verbose compilation error messages, but is a good showcase and exercise I've also uploaded full source code at GitLab: https://gitlab.com/studiedlist/priority-collection
Marken, thank you for writing. It's always interesting to learn new techniques, and, as I previously mentioned, the array-based implementation certainly seems to make illegal states unrepresentable. And then, as we'll see in the last (yet unpublished) article in this little series, if we also make the data structure immutable, we'll have a truly simple and easy-to-understand API to work with.
I've tried experimenting with the F# script you linked, but I must admit that I'm having trouble understanding how to use it. You did write that it was a crude attempt, so I'm not complaining, but on the other hand, it doesn't work well as an example of good encapsulation. The following may seem as though I'm moving the goalpost, so apologies for that in advance.
Usually, when I consult development organizations about software architecture, the failure to maintain invariants is so fundamental that I usually have to start with that problem. That's the reason that this article series is so narrow-mindedly focused on contract, and seemingly not much else. We must not, though, lose sight of what ultimately motivates us to consider encapsulation beneficial. This is what I've tried to outline in Code That Fits in Your Head: That the human brain is ill-suited to keep all implementation details in mind at the same time. One way we may attempt to address this problem is to hide implementation details behind an API which, additionally, comes with some guarantees. Thus (and this is where you may, reasonably, accuse me of moving the goal post), not only should an object fulfil its contract, it should also be possible to interact with its API without understanding implementation details.
The API you propose seem to have problems, some of which may be rectifiable:
I'll briefly expand on each.
As an example of the API being less that clear to me, I can't say that I understand what's going on here:
> create 1 100 |> set 1 50 |> addItem |> set 1 30;; val it: PriorityList = { budget = 100 dividers = [0; 50; 100] }As for what's being prioritized, you could probably mend that shortcoming by letting the array be an array of tuples.
The last part I'm not sure of, but you write:
As the most recent article in this series demonstrates, this isn't an overall limitation imposed by the invariant, but rather by your chosen API design. Specifically, assuming that you initially have a 23, 31, 46 distribution, how do you transition to a 19, 29, 43, 7, 2 distribution?
Aliaksei, thank you for writing. I've never programmed in Rust, so I didn't know it had that capability. At first I though it was dependent typing, but after reading up on it, it seems as though it's not quite that.
An exercise like the one in this article series is useful because it can help shed light on options and their various combinations of benefits and drawbacks. Thus, there are no entirely right or wrong solutions to such an exercise.
Since I don't know Rust, I can't easily distinguish what might be possible drawbacks here. I usually regard making illegal states unrepresentable as a benefit, but we must always be careful not to go too far in that direction. One thing is to reject invalid states, but can we still represent all valid states? What if priority distributions are run-time values?