Full binary tree catamorphism by Mark Seemann
The catamorphism for a full binary tree is a pair of functions.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for a full binary tree, as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
A full binary tree (also known as a proper or plane binary tree) is a tree in which each node has either two or no branches.
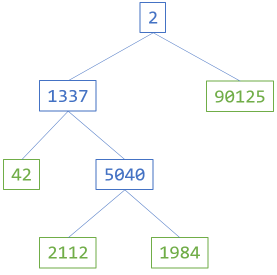
The diagram shows an example of a tree of integers. The left branch contains two children, of which the right branch again contains two sub-branches. The rest of the nodes are leaf-nodes with no sub-branches.
C# catamorphism #
As a C# representation of a full binary tree, I'll start with the IBinaryTree<T> API from A Visitor functor. The catamorphism is the Accept method:
TResult Accept<TResult>(IBinaryTreeVisitor<T, TResult> visitor);
So far in this article series, you've mostly seen Church-encoded catamorphisms, so a catamorphism represented as a Visitor may be too big of a cognitive leap. We know, however, from Visitor as a sum type that a Visitor representation is isomorphic to a Church encoding. Since these are isomorphic, it's possible to refactor IBinaryTree<T> to a Church encoding. The GitHub repository contains a series of commits that demonstrates how that refactoring works. Once you're done, you arrive at this Match method, which is the refactored Accept method:
TResult Match<TResult>(Func<TResult, T, TResult, TResult> node, Func<T, TResult> leaf);
This method takes a pair of functions as arguments. The node function deals with an internal node in the tree (the blue nodes in the above diagram), whereas the leaf function deals with the leaf nodes (the green nodes in the diagram).
The leaf function may be the easiest one to understand. A leaf node only contains a value of the type T, so the only operation the function has to support is translating the T value to a TResult value. This is also the premise of the Leaf class' implementation of the method:
private readonly T item; public TResult Match<TResult>(Func<TResult, T, TResult, TResult> node, Func<T, TResult> leaf) { return leaf(item); }
The node function is more tricky. It takes three input arguments, of the types TResult, T, and TResult. The roles of these are respectively left, item, and right. This is a typical representation of a binary node. Since there's always a left and a right branch, you put the node's value in the middle. As was the case with the tree catamorphism, the catamorphism function receives the branches as already-translated values; that is, both the left and right branch have already been translated to TResult when node is called. While it looks like magic, as always it's just the result of recursion:
private readonly IBinaryTree<T> left; private readonly T item; private readonly IBinaryTree<T> right; public TResult Match<TResult>(Func<TResult, T, TResult, TResult> node, Func<T, TResult> leaf) { return node(left.Match(node, leaf), item, right.Match(node, leaf)); }
This is the Node<T> class implementation of the Match method. It calls node and returns whatever it returns, but notice that as the left and right arguments, if first, recursively, calls left.Match and right.Match. This is how it can call node with the translated branches, as well as with the basic item.
The recursion stops and unwinds on left and right whenever one of those are Leaf instances.
Examples #
You can use Match to implement most other behaviour you'd like IBinaryTree<T> to have. In the original article on the full binary tree functor you saw how to implement Select with a Visitor, but now that the API is Church-encoded, you can derive Select from Match:
public static IBinaryTree<TResult> Select<TResult, T>( this IBinaryTree<T> tree, Func<T, TResult> selector) { if (tree == null) throw new ArgumentNullException(nameof(tree)); if (selector == null) throw new ArgumentNullException(nameof(selector)); return tree.Match( node: (l, x, r) => Create(l, selector(x), r), leaf: x => Leaf(selector(x))); }
In the leaf case, the Select method simply calls selector with the x value it receives, and puts the resulting TResult object into a new Leaf object.
In the node case, the lambda expression receives three arguments: l and r are the already-translated left and right branches, so you only need to call selector on x and call the Create helper method to produce a new Node object.
You can also implement more specialised functionality, like calculating the sum of nodes, measuring the depth of the tree, and similar functions. You saw equivalent examples in the previous article.
For the examples in this article, I'll use the tree shown in the above diagram. Using static helper methods, you can write it like this:
var tree = BinaryTree.Create( BinaryTree.Create( BinaryTree.Leaf(42), 1337, BinaryTree.Create( BinaryTree.Leaf(2112), 5040, BinaryTree.Leaf(1984))), 2, BinaryTree.Leaf(90125));
To calculate the sum of all nodes, you can write a function like this:
public static int Sum(this IBinaryTree<int> tree) { return tree.Match((l, x, r) => l + x + r, x => x); }
The leaf function just returns the value of the node, while the node function adds the numbers together. It works for the above tree:
> tree.Sum() 100642
To find the maximum value, you can write another extension method:
public static int Max(this IBinaryTree<int> tree) { return tree.Match((l, x, r) => Math.Max(Math.Max(l, r), x), x => x); }
Again, the leaf function just returns the value of the node. The node function receives the value of the current node x, as well as the already-found maximum value of the left branch and the right branch; it then returns the maximum of these three values:
> tree.Max() 90125
As was also the case for trees, both of these operations are part of the standard repertoire available via a data structure's fold. That's not the case for the next two functions, which can't be implemented using a fold, but which can be defined with the catamorphism. The first is a function to count the leaves of a tree:
public static int CountLeaves<T>(this IBinaryTree<T> tree) { return tree.Match((l, _, r) => l + r, _ => 1); }
Since the leaf function handles a leaf node, the number of leaf nodes in a leaf node is, by definition, one. Thus, that function can ignore the value of the node and always return 1. The node function, on the other hand, receives the number of leaf nodes on the left-hand side (l), the value of the current node, and the number of leaf nodes on the right-hand side (r). Notice that since an internal node is never a leaf node, it doesn't count; instead, just add l and r together. Notice that, again, the value of the node itself is irrelevant.
How many leaf nodes does the above tree have?
> tree.CountLeaves() 4
You can also measure the maximum depth of a tree:
public static int MeasureDepth<T>(this IBinaryTree<T> tree) { return tree.Match((l, _, r) => 1 + Math.Max(l, r), _ => 0); }
Like in the previous article, I've arbitrarily decided that the depth of a leaf node is zero; therefore, the leaf function always returns 0. The node function receives the depth of the left and right branches, and returns the maximum of those two values, plus one, since the current node adds one level of depth.
> tree.MeasureDepth() 3
You may not have much need for working with full binary trees in your normal, day-to-day C# work, but I found it worthwhile to include this example for a couple of reasons. First, because the original of the API shows that a catamorphism may be hiding in a Visitor. Second, because binary trees are interesting, in that they're foldable functors, but not monads.
Where does the catamorphism come from, though? How can you trust that the Match method is the catamorphism?
Binary tree F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
As always, start with the underlying endofunctor. You can think of this one as a specialisation of the rose tree from the previous article:
data FullBinaryTreeF a c = LeafF a | NodeF c a c deriving (Show, Eq, Read) instance Functor (FullBinaryTreeF a) where fmap _ (LeafF x) = LeafF x fmap f (NodeF l x r) = NodeF (f l) x (f r)
As usual, I've called the 'data' type a and the carrier type c (for carrier). The Functor instance as usual translates the carrier type; the fmap function has the type (c -> c1) -> FullBinaryTreeF a c -> FullBinaryTreeF a c1.
As was the case when deducing the recent catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (FullBinaryTreeF a). To address that problem, you can introduce a newtype wrapper:
newtype FullBinaryTreeFix a = FullBinaryTreeFix { unFullBinaryTreeFix :: Fix (FullBinaryTreeF a) } deriving (Show, Eq, Read)
You can define Functor, Foldable, and Traversable instances (but not Monad) for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A pair of helper functions make it easier to define FullBinaryTreeFix values:
fbtLeafF :: a -> FullBinaryTreeFix a fbtLeafF = FullBinaryTreeFix . Fix . LeafF fbtNodeF :: FullBinaryTreeFix a -> a -> FullBinaryTreeFix a -> FullBinaryTreeFix a fbtNodeF (FullBinaryTreeFix l) x (FullBinaryTreeFix r) = FullBinaryTreeFix $ Fix $ NodeF l x r
In order to distinguish these helper functions from the ones that create TreeFix a values, I prefixed them with fbt (for Full Binary Tree). fbtLeafF creates a leaf node:
Prelude Fix FullBinaryTree> fbtLeafF "fnaah"
FullBinaryTreeFix {unFullBinaryTreeFix = Fix (LeafF "fnaah")}
fbtNodeF is a helper function to create an internal node:
Prelude Fix FullBinaryTree> fbtNodeF (fbtLeafF 1337) 42 (fbtLeafF 2112)
FullBinaryTreeFix {unFullBinaryTreeFix = Fix (NodeF (Fix (LeafF 1337)) 42 (Fix (LeafF 2112)))}
The FullBinaryTreeFix type, or rather the underlying FullBinaryTreeF a functor, is all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (FullBinaryTreeF a), and an object c, but you still need to find a morphism FullBinaryTreeF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.
As in the previous articles, start by writing a function that will become the catamorphism, based on cata:
fullBinaryTreeF = cata alg . unFullBinaryTreeFix where alg (LeafF x) = undefined alg (NodeF l x r) = undefined
While this compiles, with its undefined implementation of alg, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from alg? You could pass a function argument to the fullBinaryTreeF function and use it with x:
fullBinaryTreeF fl = cata alg . unFullBinaryTreeFix where alg (LeafF x) = fl x alg (NodeF l x r) = undefined
I called the function fl for function, leaf, because we're also going to need a function for the NodeF case:
fullBinaryTreeF :: (c -> a -> c -> c) -> (a -> c) -> FullBinaryTreeFix a -> c fullBinaryTreeF fn fl = cata alg . unFullBinaryTreeFix where alg (LeafF x) = fl x alg (NodeF l x r) = fn l x r
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of FullBinaryTreeF, the compiler infers that the alg function has the type FullBinaryTreeF a c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
This, then, is the catamorphism for a full binary tree. As always, it's not the only possible catamorphism, since you can easily reorder the arguments to both fullBinaryTreeF, fn, and fl. These would all be isomorphic, though.
Basis #
You can implement most other useful functionality with treeF. Here's the Functor instance:
instance Functor FullBinaryTreeFix where fmap f = fullBinaryTreeF (\l x r -> fbtNodeF l (f x) r) (fbtLeafF . f)
The fl function first invokes f, followed by fbtLeafF. The fn function uses the fbtNodeF helper function to create a new internal node. l and r are already-translated branches, so you just need to call f with the node value x.
There's no Monad instance for binary trees, because you can't flatten a binary tree of binary trees. You can, on the other hand, define a Foldable instance:
instance Foldable FullBinaryTreeFix where foldMap f = fullBinaryTreeF (\l x r -> l <> f x <> r) f
The f function passed to foldMap has the type Monoid m => (a -> m), so the fl function that handles leaf nodes simply calls f with the contents of the node. The fn function receives two branches already translated to m, so it just has to call f with x and combine all the m values using the <> operator.
The Traversable instance follows right on the heels of Foldable:
instance Traversable FullBinaryTreeFix where sequenceA = fullBinaryTreeF (liftA3 fbtNodeF) (fmap fbtLeafF)
There are operations on binary trees that you can implement with a fold, but some that you can't. Consider the tree shown in the diagram at the beginning of the article. This is also the tree that the above C# examples use. In Haskell, using FullBinaryTreeFix, you can define that tree like this:
tree = fbtNodeF (fbtNodeF (fbtLeafF 42) 1337 (fbtNodeF (fbtLeafF 2112) 5040 (fbtLeafF 1984))) 2 (fbtLeafF 90125)
Since FullBinaryTreeFix is Foldable, and that type class already comes with sum and maximum functions, no further work is required to repeat the first two of the above C# examples:
Prelude Fix FullBinaryTree> sum tree 100642 Prelude Fix FullBinaryTree> maximum tree 90125
Counting leaves, or measuring the depth of a tree, on the other hand, is impossible with the Foldable instance, but can be implemented using the catamorphism:
countLeaves :: Num n => FullBinaryTreeFix a -> n countLeaves = fullBinaryTreeF (\l _ r -> l + r) (const 1) treeDepth :: (Ord n, Num n) => FullBinaryTreeFix a -> n treeDepth = fullBinaryTreeF (\l _ r -> 1 + max l r) (const 0)
The reasoning is the same as already explained in the above C# examples. The functions also produce the same results:
Prelude Fix FullBinaryTree> countLeaves tree 4 Prelude Fix FullBinaryTree> treeDepth tree 3
This, hopefully, illustrates that the catamorphism is more capable, and that the fold is just a (list-biased) specialisation.
Summary #
The catamorphism for a full binary tree is a pair of functions. One function handles internal nodes, while the other function handles leaf nodes.
I thought it was interesting to show this example for two reasons: First, the original example was a Visitor implementation, and I think it's worth realising that a Visitor's Accept method can also be viewed as a catamorphism. Second, a binary tree is an example of a data structure that has a fold, but isn't a monad.
All articles in the article series have, so far, covered data structures well-known from computer science. The next example will, on the other hand, demonstrate that even completely ad-hoc domain-specific data structures have catamorphisms.
Next: Payment types catamorphism.
