Refactoring registration flow to functional architecture by Mark Seemann

An example showing a refactoring from F# partial application 'dependency injection' to an impure/pure/impure sandwich.

In a comment to Dependency rejection, I wrote:

"I'd welcome a simplified, but still concrete example where the impure/pure/impure sandwich described here isn't going to be possible."

The code in question relates to validationverification of user accounts. You can read the complete description in the linked comment, but I'll try to summarise it here. I'll then show a refactoring to a functional architecture - specifically, to an impure/pure/impure sandwich.

The code is available on GitHub.

Registration flow #

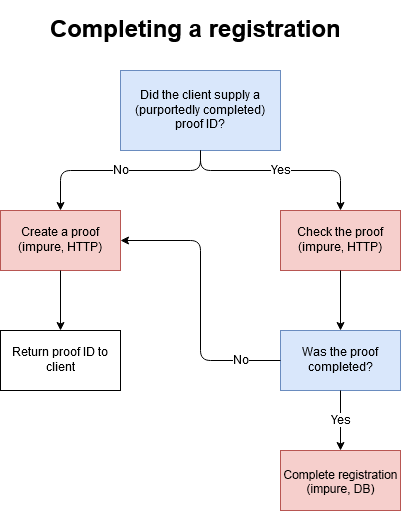
The system in question uses two-factor authentication with mobile phones. When you sign up for the service, you give your phone number. You then receive an SMS, and must use whatever is in that SMS to prove ownership of the phone number. Christer van der Meeren illustrates the flow like this:

He also supplies sample code:

let completeRegistrationWorkflow
    (createProof: Mobile -> Async<ProofId>)
    (verifyProof: Mobile -> ProofId -> Async<bool>)
    (completeRegistration: Registration -> Async<unit>)
    (proofId: ProofId option)
    (registration: Registration)
    : Async<CompleteRegistrationResult> =
    async {
        match proofId with
        | None ->
            let! proofId = createProof registration.Mobile
            return ProofRequired proofId
        | Some proofId ->
            let! isValid = verifyProof registration.Mobile proofId
            if isValid then
                do! completeRegistration registration
                return RegistrationCompleted
            else
                let! proofId = createProof registration.Mobile
                return ProofRequired proofId
    }

While this is F#, it's not functional, since it uses partial application for dependency injection. From the description, I find it safe to assume that we can consider Async as a surrogate for IO.

The code implies the existence of other types. I decided to define them like this:

type Mobile = Mobile of int
type ProofId = ProofId of Guid
type Registration = { Mobile : Mobile }
type CompleteRegistrationResult = ProofRequired of ProofId | RegistrationCompleted

In reality, they're probably more complicated, but this is enough to make the code compile.

Is it possible to refactor completeRegistrationWorkflow to an impure/pure/impure sandwich?

Applicability #

It is possible to refactor completeRegistrationWorkflow to an impure/pure/impure sandwich. You'll see how to do that soon. Before we start that work, however, I'd like to warn against jumping to conclusions. It's possible that the problem statement doesn't capture some subtleties that one would have to deal with in the real world. It's also possible that I've misunderstood the essence of Christer van der Meeren's problem description.

It's (relatively) easy to teach the basics of programming. You teach a beginner about keywords, programming constructs, how to compile or interpret a program, and so on.

On the other hand, it's hard to write about dealing with complicated code. There are ways to make legacy code better, but the moves you have to make depend on myriad details. Complicated code is, by definition, something that's hard to learn. This means that truly complicated legacy code is rarely suitable for instructive examples. One has to strike a delicate balance and produce an example that looks complicated enough to warrant improvement, but on the other hand still be simple enough to be understood.

I think that Christer van der Meeren has struck that balance. With three dependencies, the sample code looks just complicated enough to warrant refactoring. On the other hand, you can understand what it's supposed to do in a few minutes. There's a risk, however, that the example is too simplified. That could weaken the result of the refactoring that follows. Could you still apply that refactoring if the problem was more complicated?

It's my experience that it's conspicuously often possible to implement an impure/pure/impure sandwich.

Fakes #

In the rest of this article, I want to show how to refactor completeRegistrationWorkflow to an impure/pure/impure sandwich. As Refactoring admonishes:

"to refactor, the essential precondition is [...] solid tests"

The tests will need some Test Doubles to stand in for the three dependency functions. If possible, I prefer state-based testing over interaction-based testing. First, then, we need some Fakes.

While completeRegistrationWorkflow takes three dependency functions, it looks as though there's only two architectural dependencies:

• A two-factor authentication service
• A registration database (or service)

type Fake2FA () =
    let mutable proofs = Map.empty
 
    member _.CreateProof mobile =
        match Map.tryFind mobile proofs with
        | Some (proofId, _) -> proofId
        | None ->
            let proofId = ProofId (Guid.NewGuid ())
            proofs <- Map.add mobile (proofId, false) proofs
            proofId
        |> fun proofId -> async { return proofId }
 
    member _.VerifyProof mobile proofId =
        match Map.tryFind mobile proofs with
        | Some (_, true) -> true
        | _ -> false
        |> fun b -> async { return b }
 
    member _.VerifyMobile mobile =
        match Map.tryFind mobile proofs with
        | Some (proofId, _) ->
            proofs <- Map.add mobile (proofId, true) proofs
        | _ -> ()

In F#, I find that the easiest way to model a mutable resource is to use an object. This one just keeps track of a collection of proofs. The CreateProof method fits the function signature of completeRegistrationWorkflow's createProof function argument. It looks for an existing proof for the mobile number so that it can reuse the same proof multiple times. If there's no proof for mobile, it creates a new Guid and returns it after having first added it to the collection.

Likewise, the VerifyProof method fits the type of the verifyProof function argument. Proofs are actually tuples of IDs and a flag that keeps track of whether or not they've been verified. The method returns the flag if it's there, and false otherwise.

The third VerifyMobile method is a test-specific functionality that enables a test to mark a proof as having been verified via two-factor authentication.

Compared to Fake2FA, the Fake registration database is simple:

type FakeRegistrationDB () =
    inherit Collection<Registration> ()
 
    member this.CompleteRegistration r = async { this.Add r }

Again, the CompleteRegistration method fits the completeRegistration function argument to completeRegistrationWorkflow. It just makes the inherited Add method Async.

Fixture creation #

My plan is to add Characterisation Tests so that I can refactor. I do, however, plan to change the API of the System Under Test (SUT). This could break the tests, which would defy their purpose. To protect against this, I'll test against a Facade. Initially, this Facade will be equivalent to the completeRegistrationWorkflow function, but this will change as I refactor.

In addition to the SUT Facade, the tests will also need access to the 'injected' dependencies. You can address this by creating a Fixture Object:

let createFixture () =
    let twoFA = Fake2FA ()
    let db = FakeRegistrationDB ()
    let sut =
        completeRegistrationWorkflow
            twoFA.CreateProof
            twoFA.VerifyProof
            db.CompleteRegistration
    sut, twoFA, db

This function return a triple of values: the SUT Facade and the two Fakes.

The SUT Facade is a partially applied function of the type ProofId option -> Registration -> Async<CompleteRegistrationResult>. In other words, it abstracts away the specifics about how impure actions are executed. It seems reasonable to imagine that the two remaining input arguments, ProofId option and Registration, are run-time values. Regardless of refactoring, the resulting function should be able to receive those arguments and produce the desired outcome.

Characterising the missing proof ID case #

It looks like the cyclomatic complexity of completeRegistrationWorkflow is 3, so you're going to need three Characterisation Tests. You can add them in any order you like, but in this case I found it natural to follow the order in which the branches are laid out in the SUT.

This test case verifies what happens if the proof ID is missing:

[<Theory>]
[<InlineData 123>]
[<InlineData 432>]
let ``Missing proof ID`` mobile = async {
    let sut, twoFA, db = createFixture ()
    let r = { Mobile = Mobile mobile }
 
    let! actual = sut None r
 
    let! expectedProofId = twoFA.CreateProof r.Mobile
    let expected = ProofRequired expectedProofId
    expected =! actual
    test <@ Seq.isEmpty db @> }

All the tests in this article use xUnit.net 2.4.0 with Unquote 5.0.0.

This test calls the sut Facade with a None proof ID and an arbitrary Registration r. Had I used a property-based testing framework such as FsCheck or Hedgehog, I could have made the Registration value itself an arbitrary test argument, but I thought that this was overkill for this situation.

In order to figure out the expectedProofId, the test relies on the behaviour of the Fake2FA class. The CreateProof method is idempotent, so calling it several times with the same number should return the same proof. In this test case, we expect the sut to have done so already, so calling the method once more from the test should return the same value that the SUT received. The test then wraps the proof ID in the ProofRequired case and uses Unquote's =! (must equal) operator to verify that expected is equal to actual.

Finally, the test also verifies that the reservations database remains empty.

Since this is a Characterisation Test it already passes, which makes it untrustworthy. How do I know that I didn't write a Tautological Assertion?

When I write Characterisation Tests, I always try to change the SUT to verify that the test fails for the appropriate reason. In order to fail the first assertion, I can make this change to the None branch of the SUT:

match proofId with
| None ->
    //let! proofId = createProof registration.Mobile
    let proofId = ProofId (Guid.NewGuid ())
    return ProofRequired proofId

This fails the expected =! actual assertion, as expected.

Likewise, you can fail the second assertion with this change:

match proofId with
| None ->
    do! completeRegistration registration
    let! proofId = createProof registration.Mobile
    return ProofRequired proofId

The addition of the completeRegistration statement causes the test <@ Seq.isEmpty db @> assertion to fail, again as expected.

Now I trust that test.

Characterising the valid proof ID case #

Next, you have the case where all is good. The proof ID is present and valid. You can characterise the behaviour with this test:

[<Theory>]
[<InlineData 987>]
[<InlineData 247>]
let ``Valid proof ID`` mobile = async {
    let sut, twoFA, db = createFixture ()
    let r = { Mobile = Mobile mobile }
    let! p = twoFA.CreateProof r.Mobile
    twoFA.VerifyMobile r.Mobile
 
    let! actual = sut (Some p) r
 
    RegistrationCompleted =! actual
    test <@ Seq.contains r db @> }

This test uses CreateProof to create a proof before the sut is exercised. It also uses the test-specific VerifyMobile method to mark the mobile number (and thereby the proof) as valid.

Again, there's two assertions: one against the return value actual, and one that verifies that the registration database db now contains the registration r.

As before, you can't trust a Characterisation Test before you've seen it fail, so first edit the isValid branch of the SUT like this:

if isValid then
    do! completeRegistration registration
    //return RegistrationCompleted
    return ProofRequired proofId

This fails the RegistrationCompleted =! actual assertion, as expected.

Now make this change:

if isValid then
    //do! completeRegistration registration
    return RegistrationCompleted

Now the test <@ Seq.contains r db @> assertion fails, as expected.

This test also seems trustworthy.

Characterising the invalid proof ID case #

The final test case is when a proof ID exists, but it's invalid:

[<Theory>]
[<InlineData 327>]
[<InlineData 666>]
let ``Invalid proof ID`` mobile = async {
    let sut, twoFA, db = createFixture ()
    let r = { Mobile = Mobile mobile }
    let! p = twoFA.CreateProof r.Mobile
 
    let! actual = sut (Some p) r
 
    let! expectedProofId = twoFA.CreateProof r.Mobile
    let expected = ProofRequired expectedProofId
    expected =! actual
    test <@ Seq.isEmpty db @> }

The arrange phase of the test is comparable to the previous test case. The only difference is that the new test doesn't invoke twoFA.VerifyMobile r.Mobile. This leaves the generated proof ID p invalid.

The assertions, on the other hand, are identical to those of the Missing proof ID test case, which means that you can make the same edits to the else branch as you can to the None branch, as described above. If you do that, the assertions fail as they're supposed to. You can also trust this Characterisation Test.

Eta expansion #

While I want to keep the SUT Facade's type unchanged, I do want change the way I compose it. The goal is an impure/pure/impure sandwich: Do something impure first, then call a pure function with the data obtained, and finally do something impure with the output of the pure function.

This means that the composition is going to manipulate the input values to the SUT Facade. To make that easier, I perform an eta conversion on the sut:

let createFixture () =
    let twoFA = Fake2FA ()
    let db = FakeRegistrationDB ()
    let sut pid r =
        completeRegistrationWorkflow
            twoFA.CreateProof
            twoFA.VerifyProof
            db.CompleteRegistration
            pid
            r
    sut, twoFA, db

This doesn't change the behaviour or how the SUT is composed. It only makes the pid and r arguments explicitly visible.

Move proof verification #

When you consider the current implementation of completeRegistrationWorkflow, it seems that the impure actions are interleaved with the decision-making code. How to separate them?

The first opportunity that I identified was that it always calls verifyProof in the Some case. Whenever you want to call a method only in the Some case, but not in the None case, it suggest Option.map.

It should be possible to run Option.map (twoFA.VerifyProof r.Mobile) pid as the initial impure action of the impure/pure/impure sandwich. If that's possible, we could pass the output of that pure function as an argument to completeRegistrationWorkflow. That would already make it simpler:

let completeRegistrationWorkflow
    (createProof: Mobile -> Async<ProofId>)
    (completeRegistration: Registration -> Async<unit>)
    (proof: bool option)
    (registration: Registration)
    : Async<CompleteRegistrationResult> =
    async {
        match proof with
        | None ->
            let! proofId = createProof registration.Mobile
            return ProofRequired proofId
        | Some isValid ->
            if isValid then
                do! completeRegistration registration
                return RegistrationCompleted
            else
                let! proofId = createProof registration.Mobile
                return ProofRequired proofId
    }

Notice that by changing the proof argument to a bool option, you no longer need to call verifyProof, so you can remove it.

There's just one problem. The result of Option.map (twoFA.VerifyProof r.Mobile) pid is an Option<Async<bool>>, but you need an Option<bool>.

You can compose the SUT Facade in an asynchronous workflow, and use a let! binding, but that's not going to solve the problem. A let! binding only works when the outer container is Async. Here, the outermost container is Option. You're going to need to flip the containers around so that you get an Async<Option<bool>> that you can let!-bind:

let sut pid r = async {
    let! p =
        match Option.map (twoFA.VerifyProof r.Mobile) pid with
        | Some b -> async {
            let! b' = b
            return Some b' }
        | None -> async { return None }
    return! completeRegistrationWorkflow
        twoFA.CreateProof
        db.CompleteRegistration
        p
        r
    }

By pattern-matching on Option.map (twoFA.VerifyProof r.Mobile) pid, you can return one of two alternative asynchronous workflows.

Due to the let! binding, p is a bool option that you can pass to completeRegistrationWorkflow.

Traversal #

I know what you're going to say. You'll protest that I just moved complex behaviour out of completeRegistrationWorkflow. The implied assumption here is that completeRegistrationWorkflow is the top-level behaviour that you'd compose in a Composition Root. The createFixture function plays that role in this refactoring exercise.

You'd normally view the Composition Root as a Humble Object - an object that we accept isn't covered by tests because it has a cyclomatic complexity of one. This is no longer the case.

The conversion of Option<Async<bool>> to Async<Option<bool>> is, however, a well-known operation. In Haskell this is known as a traversal, and it's a completely generic operation:

// ('a -> Async<'b>) -> 'a option -> Async<'b option>
let traverse f = function
    | Some x -> async {
        let! x' = f x
        return Some x' }
    | None -> async { return None }

You can put this function in a general-purpose module called AsyncOption and cover it by unit tests if you will. You can even put this module in a separate library; it's perfectly decoupled from the the specifics of the registration flow domain.

If you do that, completeRegistrationWorkflow doesn't change, but the composition does:

let sut pid r = async {
    let! p = AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    return! completeRegistrationWorkflow
        twoFA.CreateProof
        db.CompleteRegistration
        p
        r
    }

You're now back where you'd like to be: One impure action produces a value that you can pass to another function. There's no explicit branching in the code. The cyclomatic complexity remains one.

Change return type #

That first refactoring takes care of one out of three impure dependencies. Next, you can get rid of createProof. This one seems to be more difficult to get rid of. It doesn't seem to be required only in the Some case, so a map or traverse can't work. In both cases, however, the result of calling createProof is handled in exactly the same way.

Here's another common trick in functional programming: Decouple decisions from effects. Return a value that indicates the decision that the function reaches, and then let the second impure action of the impure/pure/impure sandwich act on the decision.

In this case, you can model your decision as a Mobile option. You might want to consider a more explicit type, in order to better communicate intent, but it's best to keep each refactoring step small:

let completeRegistrationWorkflow
    (completeRegistration: Registration -> Async<unit>)
    (proof: bool option)
    (registration: Registration)
    : Async<Mobile option> =
    async {
        match proof with
        | None -> return Some registration.Mobile
        | Some isValid ->
            if isValid then
                do! completeRegistration registration
                return None
            else
                return Some registration.Mobile
    }

Notice that the createProof dependency is no longer required. I've removed it from the argument list of completeRegistrationWorkflow.

The composition now looks like this:

let createFixture () =
    let twoFA = Fake2FA ()
    let db = FakeRegistrationDB ()
    let sut pid r = async {
        let! p = AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
        let! res = completeRegistrationWorkflow db.CompleteRegistration p r
        let! pidr = AsyncOption.traverse twoFA.CreateProof res
        return pidr
            |> Option.map ProofRequired
            |> Option.defaultValue RegistrationCompleted }

Thanks to the let! binding, the result res is a Mobile option. You can now let the twoFA.CreateProof method traverse over res. This produces an Async<Option<ProofId>> that you can let!-bind to pidr - a ProofId option.

You can use Option.map to wrap the ProofId value in a ProofRequired case, if it's there. This step of the final pipeline produces a CompleteRegistrationResult option.

Finally, you can use Option.defaultValue to fold the option into a CompleteRegistrationResult. The default value is RegistrationCompleted. This is the case value that'll be used if the option is None.

Again, the composition has a cyclomatic complexity of one, and the type of the sut remains ProofId option -> Registration -> Async<CompleteRegistrationResult>. This is a true refactoring. The type of the SUT remains the same, and no behaviour changes. The tests still pass, even though I haven't had to edit them.

Change return type to Result #

Consider the intent of completeRegistrationWorkflow. The purpose of the operation is to complete a registration workflow. The name is quite explicit. Thus, the happy path is when the proof ID is valid and the function can call completeRegistration.

Usually, when you call a function that returns an option, the implied contract is that the Some case represents the happy path. That's not the case here. The Some case carries information about the error paths. This isn't idiomatic.

It'd be more appropriate to use a Result return value:

let completeRegistrationWorkflow
    (completeRegistration: Registration -> Async<unit>)
    (proof: bool option)
    (registration: Registration)
    : Async<Result<unit, Mobile>> =
    async {
        match proof with
        | None -> return Error registration.Mobile
        | Some isValid ->
            if isValid then
                do! completeRegistration registration
                return Ok ()
            else
                return Error registration.Mobile
    }

This change is in itself small, but it does require some changes to the composition. Just as you had to add an Option.traverse function when the return type was an option, you'll now have to add similar functionality to Result. Result is also known as Either. Not only is it a bifunctor, you can also traverse both axes. Haskell calls this a bitraversable functor.

// ('a -> Async<'b>) -> ('c -> Async<'d>) -> Result<'a,'c> -> Async<Result<'b,'d>>
let traverseBoth f g = function
    | Ok x -> async {
        let! x' = f x
        return Ok x' }
    | Error e -> async {
        let! e' = g e
        return Error e' }

Here I just decided to call the function traverseBoth and the module AsyncResult.

You're also going to need the equivalent of Option.defaultValue for Result. Something that translates both dimensions of Result into the same type. That's the Either catamorphism, so you could, for example, introduce another general-purpose function called cata:

// ('a -> 'b) -> ('c -> 'b) -> Result<'a,'c> -> 'b
let cata f g = function
    | Ok x -> f x
    | Error e -> g e

This is another entirely general-purpose function that you can put in a general-purpose module called Result, in a general-purpose library. You can also cover it by unit tests, if you like.

These two general-purpose functions enable you to compose the workflow:

let createFixture () =
    let twoFA = Fake2FA ()
    let db = FakeRegistrationDB ()
    let sut pid r = async {
        let! p = AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
        let! res = completeRegistrationWorkflow db.CompleteRegistration p r
        let! pidr =
            AsyncResult.traverseBoth
                (fun () -> async { return () })
                twoFA.CreateProof
                res
        return pidr
            |> Result.cata (fun () -> RegistrationCompleted) ProofRequired }
    sut, twoFA, db

This looks more confused than previous iterations. From here, though, it'll get better again. The first two lines of code are the same as before, but now res is a Result<unit, Mobile>. You still need to let twoFA.CreateProof traverse the 'error path', but now you also need to take care of the happy path.

In the Ok case you have a unit value (()), but traverseBoth expects its f and g functions to return Async values. I could have fixed that with a more specialised traverseError function, but we'll soon move on from here, so it's hardly worthwhile.

In Haskell, you can 'elevate' a value simply with the pure function, but in F#, you need the more cumbersome (fun () -> async { return () }) to achieve the same effect.

The traversal produces pidr (for Proof ID Result) - a Result<unit, ProofId> value.

Finally, it uses Result.cata to turn both the Ok and Error dimensions into a single CompleteRegistrationResult that can be returned.

Removing the last dependency #

There's still one dependency left: the completeRegistration function, but it's now trivial to remove. Instead of calling the dependency function from within completeRegistrationWorkflow you can use the same trick as before. Decouple the decision from the effect.

Return information about the decision the function made. In the above incarnation of the code, the Ok dimension is currently empty, since it only returns unit. You can use that 'channel' to communicate that you decided to complete a registration:

let completeRegistrationWorkflow
    (proof: bool option)
    (registration: Registration)
    : Async<Result<Registration, Mobile>> =
    async {
        match proof with
        | None -> return Error registration.Mobile
        | Some isValid ->
            if isValid then
                return Ok registration
            else
                return Error registration.Mobile
    }

This is another small change. When isValid is true, the function no longer calls completeRegistration. Instead, it returns Ok registration. This means that the return type is now Async<Result<Registration, Mobile>>. It also means that you can remove the completeRegistration function argument.

In order to compose this variation, you need one new general-purpose function. Perhaps you find this barrage of general-purpose functions exhausting, but it's an artefact of a design philosophy of the F# language. The F# base library contains only few general-purpose functions. Contrast this with GHC's base library, which comes with all of these functions built in.

The new function is like Result.cata, but over Async<Result<_>>.

// ('a -> 'b) -> ('c -> 'b) -> Async<Result<'a,'c>> -> Async<'b>
let cata f g r = async {
    let! r' = r
    return Result.cata f g r' }

Since this function does conceptually the same as Result.cata I decided to retain the name cata and just put it in the AsyncResult module. (This may not be strictly correct, as I haven't really given a lot of thought to what a catamorphism for Async would look like, if one exists. I'm open to suggestions about better naming. After all, cata is hardly an idiomatic F# name.)

With AsyncResult.cata you can now compose the system:

let sut pid r = async {
    let! p = AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    let! res = completeRegistrationWorkflow p r
    return!
        res
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

Not only did the call to completeRegistrationWorkflow get even simpler, but you also now avoid the awkwardly named pidr value. Thanks to the let! binding, res has the type Result<Registration, Mobile>.

Note that you can now let both impure actions (db.CompleteRegistration and twoFA.CreateProof) traverse the result. This step produces an Async<Result<unit, ProofId>> that's immediately piped to AsyncResult.cata. This reduces the two alternative dimensions of the Result to a single Async<CompleteRegistrationResult> value.

The completeRegistrationWorkflow function now begs to be further simplified.

Pure registration workflow #

Once you remove all dependencies, your domain logic doesn't have to be asynchronous. Nothing asynchronous happens in completeRegistrationWorkflow, so simplify it:

let completeRegistrationWorkflow
    (proof: bool option)
    (registration: Registration)
    : Result<Registration, Mobile> =
    match proof with
    | None -> Error registration.Mobile
    | Some isValid ->
        if isValid then Ok registration
        else Error registration.Mobile

Gone is the async computation expression, including the return keyword. This is now a pure function.

You'll have to adjust the composition once more, but it's only a minor change:

let sut pid r = async {
    let! p = AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    return!
        completeRegistrationWorkflow p r
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

The result of invoking completeRegistrationWorkflow is no longer an Async value, so there's no reason to let!-bind it. Instead, you can call it and immediately pipe its output to AsyncResult.traverseBoth.

DRY #

Consider completeRegistrationWorkflow. Can you make it simpler?

At this point it should be evident that two of the branches contain duplicate code. Applying the DRY principle you can simplify it:

let completeRegistrationWorkflow
    (proof: bool option)
    (registration: Registration)
    : Result<Registration, Mobile> =
    match proof with
    | Some true -> Ok registration
    | _ -> Error registration.Mobile

I'm not too fond of this style of type annotation for simple functions like this, so I'd like to remove it:

let completeRegistrationWorkflow proof registration =
    match proof with
    | Some true -> Ok registration
    | _ -> Error registration.Mobile

These two steps are pure refactorings: they only reorganise the code that implements completeRegistrationWorkflow, so the composition doesn't change.

Essential complexity #

While reading this article, you may have felt frustration gather. This is cheating! You took out all of the complexity. Now there's nothing left! You're likely to feel that I've moved a lot of behaviour into untestable code. I've done nothing of the sort.

I'll remind you that while functions like AsyncOption.traverse and AsyncResult.cata do contain branching behaviour, they can be tested. In fact, since they're pure functions, they're intrinsically testable.

It's true that a composition of a pure function with its impure dependencies may not be (unit) testable, but that's also true for a Dependency Injection-based object graph composed in a Composition Root.

Compositions of functions may look non-trivial, but to a degree, the type system will assist you. If your composition compiles, it's likely that you've composed the impure/pure/impure sandwich correctly.

Did I take out all the complexity? I didn't. There's a bit left; the function now has a cyclomatic complexity of two. If you look at the original function, you'll see that the duplication was there all along. Once you remove all the accidental complexity, you uncover the essential complexity. This happens to me so often when I apply functional programming principles that I fancy that functional programming is a silver bullet.

Pipeline composition #

We're mostly done now. The problem now appears in all its simplicity, and you have an impure/pure/impure sandwich.

You can still improve the code, though.

If you consider the current composition, you may find that p isn't the best variable name. I admit that I struggled with naming that variable. Sometimes, variable names are in the way and the code might be clearer if you could elide them by composing a pipeline of functions.

That's always worth an attempt. This time, ultimately I find that it doesn't improve things, but even an attempt can be illustrative.

If you want to eliminate a named value, you can often do so by piping the output of the function that produced the variable directly to the next function. This does, however, require that the function argument is the right-most. Currently, that's not the case. registration is right-most, and proof is to the left.

There's no compelling reason that the arguments should come in that order, so flip them:

let completeRegistrationWorkflow registration proof =
    match proof with
    | Some true -> Ok registration
    | _ -> Error registration.Mobile

This enables you to write the entire composition as a single pipeline:

let sut pid r = async {
    return!
        AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
        |> Async.map (completeRegistrationWorkflow r)
        |> Async.bind (
            AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
            >> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired)
    }

This does, however, call for two new general-purpose functions: Async.map and Async.bind:

// ('a -> 'b) -> Async<'a> -> Async<'b>
let map f x = async {
    let! x' = x
    return f x' }
 
// ('a -> Async<'b>) -> Async<'a> -> Async<'b>
let bind f x = async {
    let! x' = x
    return! f x' }

In my opinion, these functions ought to belong to F#'s Async module, but for for reasons that aren't clear to me, they don't. As you can see, though, they're easy to add.

While the this change gets rid of the p variable, I don't think it makes the overall composition easier to understand. The action of swapping the function arguments does, however, enable another simplification.

Eta reduction #

Now that proof is completeRegistrationWorkflow's last function argument, you can perform an eta reduction:

let completeRegistrationWorkflow registration = function
    | Some true -> Ok registration
    | _ -> Error registration.Mobile

Not everyone is a fan of the point-free style, but I like it. YMMV.

Sandwich #

Regardless of whether you prefer completeRegistrationWorkflow in point-free or pointed style, I think that the composition needs improvement. It should explicitly communicate that it's an impure/pure/impure sandwich. This makes it necessary to reintroduce some variables, so I'm also going to bite the bullet and devise some better names.

let sut pid r = async {
    let! validityOfProof = 
        AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    let decision = completeRegistrationWorkflow r validityOfProof
    return!
        decision
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

Instead of p, I decided to call the first value validityOfProof. This is the result of the first impure action in the sandwich (the upper slice of bread).

While validityOfProof is the result of an impure action, the value itself is pure and can be used as input to completeRegistrationWorkflow. This is the pure part of the sandwich. I called the output decision because the workflow makes a decision based on its input, and it's up to the caller to act on that decision.

Notice that decision is bound with a let binding (instead of a let! binding), despite taking place inside an async workflow. This is because completeRegistrationWorkflow is pure. It doesn't return an Async value.

The second impure action acts on decision through a pipeline of AsyncResult.traverseBoth and AsyncResult.cata, as previously explained.

I think that the impure/pure/impure sandwich is more visible like this, so that was my final edit. I'm happy with how it looks now.

Conclusion #

I don't claim that you can always refactor code to an impure/pure/impure sandwich. In fact, I can easily envision categories of software where such an architecture seems impossible.

Still, I find it intriguing that when I find myself in the realm of web services or message-based applications, I can't recall a case where a sandwich has been impossible. Surely, there must cases where it is so. That's the reason that I solicit examples. This article was a response to such an example. I found it fruitful, because it enabled me to discuss several useful techniques for composing behaviour in a functional architecture. On the other hand, it failed to be a counter-example.

I'm sure that some readers are left with a nagging doubt. That's all very impressive, but would you actually write code like that in a piece of production software?

If it was up to me, then: yes. I find that when I can keep code pure, it's trivial to unit test and there's no test-induced damage. Functions also compose in a way objects don't easily do, so there's many advantages to functional programming. I'll take them when they're available.

As always, context matters. I've been in team settings where other team members would embrace this style of programming, and in other environments where team members wouldn't understand what was going on. In the latter case, I'd adjust my approach to challenge, not alienate, other team members.

My intention with this article was to show what's possible, not to dictate what you should do. That's up to you.

This article is the December 2 entry in the F# Advent Calendar in English 2019.

Comments

let completeRegistrationWorkflow
    (createProof: Mobile -> Async<ProofId>)
    (verifyProof: Mobile -> ProofId -> Async<bool>)
    (completeRegistration: Registration -> Async<Result<unit, CompleteRegistrationError>>)
    (proofId: ProofId option)
    (registration: Registration)
    : Async<Result<CompleteRegistrationResult, CompleteRegistrationError>> =
  asyncResult {
    match proofId with
    | None ->
        let! proofId = createProof registration.Mobile
        return ProofRequired proofId
    | Some proofId ->
        let! isValid = verifyProof registration.Mobile proofId
        if isValid then
          do! completeRegistration registration
          return RegistrationCompleted
        else
          let! proofId = createProof registration.Mobile
          return ProofRequired proofId
  }

let complete proofId validReg =
  Workflows.Registration.complete
    Http.createMobileClaimProof
    Http.verifyMobileClaimProof
    Db.completeRegistration
    proofId
    validReg

let completePure reg proofValidity =
  match proofValidity with
  | Some true -> Ok reg
  | Some false | None -> Error reg.Mobile

let complete proofId reg : Async<Result<CompleteRegistrationResult, CompleteRegistrationError>> =
  asyncResult {
    let! proofValidity =
      proofId |> Option.traverseAsync (Http.verifyMobileClaimProof reg.Mobile)

    match completePure reg proofValidity with
    | Ok reg ->
        do! Db.completeRegistration reg
        return RegistrationCompleted
    | Error mobile ->
        let! proofId = Http.createMobileClaimProof mobile
        return ProofRequired proofId
  }

let sut pid r = async {
    let! validityOfProof = 
        AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    let decision = completeRegistrationWorkflow r validityOfProof
    return!
        decision
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

let privateKey = ...
let sut' ciphertext = async {
    let (pid, r) = decrypt privateKey ciphertext
    let! validityOfProof = 
        AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    let decision = completeRegistrationWorkflow r validityOfProof
    return!
        decision
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

let malroyInTheMiddle aliceToMalory = async {
    let maloryToBob = convertIncoming aliceToMalory
    let! bobToMalory = service maloryToBob
    let maloryToAlice = convertOutgoing bobToMalory
    return maloryToAlice
}

let malroyInTheMiddle  =
    Async.fromResult
    >> Async.map convertIncoming
    >> Async.bind service
    >> Async.map convertOutgoing

let completeRegistrationWorkflow
    (createProof: Mobile -> Async<ProofId>)
    (verifyProof: Mobile -> ProofId -> Async<bool>)
    (completeRegistration: Registration -> Async<unit>)
    (proofId: ProofId option)
    (registration: Registration)
    : Async<CompleteRegistrationResult> =
    async {
        match proofId with
        | None ->
            let! proofId = createProof registration.Mobile
            return ProofRequired proofId
        | Some proofId ->
            let! isValid = verifyProof registration.Mobile proofId
            if isValid then
                do! completeRegistration registration
                return RegistrationCompleted
            else
                let! proofId = createProof registration.Mobile
                return ProofRequired proofId
    }

let sut =
    completeRegistrationWorkflow
        twoFA.CreateProof
        twoFA.VerifyProof
        db.CompleteRegistration

let completeRegistrationWorkflow registration = function
    | Some true -> Ok registration
    | _ -> Error registration.Mobile

let sut pid r = async {
    let! validityOfProof = 
        AsyncOption.traverse (twoFA.VerifyProof r.Mobile) pid
    let decision = completeRegistrationWorkflow r validityOfProof
    return!
        decision
        |> AsyncResult.traverseBoth db.CompleteRegistration twoFA.CreateProof
        |> AsyncResult.cata (fun () -> RegistrationCompleted) ProofRequired
    }

• ← Previous
• Archive
• Next →