Endomorphism as an invariant functor by Mark Seemann
An article (also) for object-oriented programmers.
This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details.
An endomorphism is a function where the return type is the same as the input type.
In Haskell we denote an endomorphism as a -> a, in F# we have to add an apostrophe: 'a -> 'a, while in C# such a function corresponds to the delegate Func<T, T> or, alternatively, to a method that has the same return type as input type.
In Haskell you can treat an endomorphism like a monoid by wrapping it in a container called Endo: Endo a. In C#, we might model it as an interface called IEndomorphism<T>.
That looks enough like a functor that you might wonder if it is one, but it turns out that it's neither co- nor contravariant. You can deduce this with positional variance analysis (which I've learned from Thinking with Types). In short, this is because T appears as both input and output - it's neither co- nor contravariant, but rather invariant.
Explicit endomorphism interface in C# #
Consider an IEndomorphism<T> interface in C#:
public interface IEndomorphism<T> { T Run(T x); }
I've borrowed this interface from the article From State tennis to endomorphism. In that article I explain that I only introduce this interface for educational reasons. I don't expect you to use something like this in production code bases. On the other hand, everything that applies to IEndomorphism<T> also applies to 'naked' functions, as you'll see later in the article.
As outlined in the introduction, you can make a container an invariant functor by implementing a non-standard version of Select:
public static IEndomorphism<B> Select<A, B>( this IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { return new SelectEndomorphism<A, B>(endomorphism, aToB, bToA); } private class SelectEndomorphism<A, B> : IEndomorphism<B> { private readonly IEndomorphism<A> endomorphism; private readonly Func<A, B> aToB; private readonly Func<B, A> bToA; public SelectEndomorphism( IEndomorphism<A> endomorphism, Func<A, B> aToB, Func<B, A> bToA) { this.endomorphism = endomorphism; this.aToB = aToB; this.bToA = bToA; } public B Run(B x) { return aToB(endomorphism.Run(bToA(x))); } }
Since the Select method has to return an IEndomorphism<B> implementation, one option is to use a private, nested class. Most of this is ceremony required because it's working with interfaces. The interesting part is the nested class' Run implementation.
In order to translate an IEndomorphism<A> to an IEndomorphism<B>, the Run method first uses bToA to translate x to an A value. Once it has the A value, it can Run the endomorphism, which returns another A value. Finally, the method can use aToB to convert the returned A value to a B value that it can return.
Here's a simple example. Imagine that you have an endomorphism like this one:
public sealed class Incrementer : IEndomorphism<BigInteger> { public BigInteger Run(BigInteger x) { return x + 1; } }
This one simply increments a BigInteger value. Since BigInteger is isomorphic to a byte array, it's possible to transform this BigInteger endomorphism to a byte array endomorphism:
[Theory] [InlineData(new byte[0], new byte[] { 1 })] [InlineData(new byte[] { 1 }, new byte[] { 2 })] [InlineData(new byte[] { 255, 0 }, new byte[] { 0, 1 })] public void InvariantSelection(byte[] bs, byte[] expected) { IEndomorphism<BigInteger> source = new Incrementer(); IEndomorphism<byte[]> destination = source.Select(bi => bi.ToByteArray(), arr => new BigInteger(arr)); Assert.Equal(expected, destination.Run(bs)); }
You can convert a BigInteger to a byte array with the ToByteArray method, and convert such a byte array back to a BigInteger using one of its constructor overloads. Since this is possible, the example test can convert this IEndomorphism<BigInteger> to an IEndomorphism<byte[]> and later Run it.
Mapping functions in F# #
You don't need an interface in order to turn an endomorphism into an invariant functor. An endomorphism is just a function that has the same input and output type. In C# such a function has the type Func<T, T>, while in F# it's written 'a -> 'a.
You could write an F# module that defines an invmap function, which would be equivalent to the above Select method:
module Endo = // ('a -> 'b) -> ('b -> 'a) -> ('a -> 'a) -> ('b -> 'b) let invmap (f : 'a -> 'b) (g : 'b -> 'a) (h : 'a -> 'a) = g >> h >> f
Since this function doesn't have to deal with the ceremony of interfaces, the implementation is simple function composition: For any input, first apply it to the g function, then apply the output to the h function, and again apply the output of that function to the f function.
Here's the same example as above:
let increment (bi : BigInteger) = bi + BigInteger.One // byte [] -> byte [] let bArrInc = Endo.invmap (fun (bi : BigInteger) -> bi.ToByteArray ()) BigInteger increment
Here's a simple sanity check of the bArrInc function executed in F# Interactive:
> let bArr = bArrInc [| 255uy; 255uy; 0uy |];; val bArr : byte [] = [|0uy; 0uy; 1uy|]
If you are wondering about that particular output value, I'll refer you to the BigInteger documentation.
Function composition #
The F# implementation of invmap (g >> h >> f) makes it apparent that an endomorphism is an invariant functor via function composition. In F#, though, that fact almost disappears in all the type declaration ceremony. In the Haskell instance from the invariant package it's even clearer:
instance Invariant Endo where invmap f g (Endo h) = Endo (f . h . g)
Perhaps a diagram is helpful:
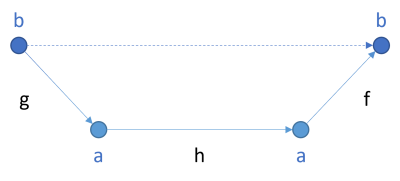
If you have a function h from the type a to a and you need a function b -> b, you can produce it by putting g in front of h, and f after. That's also what the above C# implementation does. In F#, you can express such a composition as g >> h >> f, which seems natural to most westerners, since it goes from left to right. In Haskell, most expressions are instead expressed from right to left, so it becomes: f . h . g. In any case, the result is the desired function that takes a b value as input and returns a b value as output. That composed function is indicated by a dashed arrow in the above diagram.
Identity law #
Contrary to my usual habit, I'm going to prove that both invariant functor laws hold for this implementation. I'll use equational reasoning with the notation that Bartosz Milewski uses. Here's the proof that the invmap instance obeys the identity law:
invmap id id (Endo h)
= { definition of invmap }
Endo (id . h . id)
= { eta expansion }
Endo (\x -> (id . h . id) x)
= { defintion of composition (.) }
Endo (\x -> id (h (id x)))
= { defintion of id }
Endo (\x -> h x)
= { eta reduction }
Endo h
= { definition of id }
id (Endo h)
While I'm not going to comment further on that, I can show you what the identity law looks like in C#:
[Theory] [InlineData(0)] [InlineData(1)] [InlineData(9)] public void IdentityLaw(long l) { IEndomorphism<BigInteger> e = new Incrementer(); IEndomorphism<BigInteger> actual = e.Select(x => x, x => x); Assert.Equal(e.Run(l), actual.Run(l)); }
In C#, you typically write the identity function (id in F# and Haskell) as the lambda expression x => x, since the identity function isn't 'built in' for C# like it is for F# and Haskell. (You can define it yourself, but it's not as idiomatic.)
Composition law #
As with the identity law, I'll start by suggesting a proof for the composition law for the Haskell instance:
invmap f2 f2' $ invmap f1 f1' (Endo h)
= { definition of invmap }
invmap f2 f2' $ Endo (f1 . h . f1')
= { defintion of ($) }
invmap f2 f2' (Endo (f1 . h . f1'))
= { definition of invmap }
Endo (f2 . (f1 . h . f1') . f2')
= { associativity of composition (.) }
Endo ((f2 . f1) . h . (f1' . f2'))
= { definition of invmap }
invmap (f2 . f1) (f1' . f2') (Endo h)
As above, a C# example may also help. First, assume that you have some endomorphism like this:
public sealed class SecondIncrementer : IEndomorphism<TimeSpan> { public TimeSpan Run(TimeSpan x) { return x + TimeSpan.FromSeconds(1); } }
A test then demonstrates the composition law in action:
[Theory] [InlineData(-3)] [InlineData(0)] [InlineData(11)] public void CompositionLaw(long x) { IEndomorphism<TimeSpan> i = new SecondIncrementer(); Func<TimeSpan, long> f1 = ts => ts.Ticks; Func<long, TimeSpan> f1p = l => new TimeSpan(l); Func<long, IntPtr> f2 = l => new IntPtr(l); Func<IntPtr, long> f2p = ip => ip.ToInt64(); IEndomorphism<IntPtr> left = i.Select(f1, f1p).Select(f2, f2p); IEndomorphism<IntPtr> right = i.Select(ts => f2(f1(ts)), ip => f1p(f2p(ip))); Assert.Equal(left.Run(new IntPtr(x)), right.Run(new IntPtr(x))); }
Don't try to make any sense of this. As outlined in the introductory article, in order to use an invariant functor, you're going to need an isomorphism. In order to demonstrate the composition law, you need three types that are isomorphic. Since you can convert back and forth between TimeSpan and IntPtr via long, this requirement is formally fulfilled. It doesn't make any sense to add a second to a value and then turn it into a function that changes a pointer. It sounds more like a security problem waiting to happen... Don't try this at home, kids.
Conclusion #
Since an endomorphism can be modelled as a 'generic type', it may look like a candidate for a functor or contravariant functor, but alas, neither is possible. The best we can get (apart from a monoid instance) is an invariant functor.
The invariant functor instance for an endomorphism turns out to be simple function composition. That's not how all invariant functors, work, though.
