The State pattern and the State monad by Mark Seemann
The names are the same. Is there a connection? An article for object-oriented programmers.
This article is part of a series of articles about specific design patterns and their category theory counterparts. In this article I compare the State design pattern to the State monad.
Since the design pattern and the monad share the name State you'd think that they might be isomorphic, but it's not quite that easy. I find it more likely that the name is an example of parallel evolution. Monads were discovered by Eugenio Moggi in the early nineties, and Design Patterns is from 1994. That's close enough in time that I find it more likely that whoever came up with the names found them independently. State, after all, is hardly an exotic word.
Thus, it's possible that the choice of the same name is coincidental. If this is true (which is only my conjecture), does the State pattern have anything in common with the State monad? I find that the answer is a tentative yes. The State design pattern describes an open polymorphic stateful computation. That kind of computation can also be described with the State monad.
This article contains a significant amount of code, and it's all quite abstract. It examines the abstract shape of the pattern, so there's little prior intuition on which to build an understanding. While later articles will show more concrete examples, if you want to follow along, you can use the GitHub repository.
Shape #
Design Patterns is a little vague when it comes to representing the essential form of the pattern. What one can deduce from the diagram in the Structure section describing the pattern, you have an abstract State class with a Handle method like this:
public virtual void Handle(Context context) { }
This, however, doesn't capture all scenarios. What if you need to pass more arguments to the method? What if the method returns a result? What if there's more than one method?
Taking into account all those concerns, you might arrive at a more generalised description of the State pattern where an abstract State class might define methods like these:
public abstract Out1 Handle1(Context context, In1 in1); public abstract Out2 Handle2(Context context, In2 in2);
There might be an arbitrary number of Handle methods, from Handle1 to HandleN, each with their own input and return types.
The idea behind the State pattern is that clients don't interact directly with State objects. Instead, they interact with a Context object that delegates operations to a State object, passing itself as an argument:
public Out1 Request1(In1 in1) { return State.Handle1(this, in1); } public Out2 Request2(In2 in2) { return State.Handle2(this, in2); }
Classes that derive from the abstract State may then mutate context.State.
public override Out2 Handle2(Context context, In2 in2) { if (in2 == In2.Epsilon) context.State = new ConcreteStateB(); return Out2.Eta; }
Clients interact with the Context object and aren't aware of this internal machinery:
var actual = ctx.Request2(in2);
With such state mutation going on, is it possible to refactor to a design that uses immutable data and pure functions?
State pair #
When you have a void method that mutates state, you can refactor it to a pure function by leaving the existing state unchanged and instead returning the new state. What do you do, however, when the method in question already returns a value?
This is the case with the generalised HandleN methods, above.
One way to resolve this problem is to introduce a more complex type to return. To avoid too much duplication or boilerplate code, you could make it a generic type:
public sealed class StatePair<T> { public StatePair(T value, State state) { Value = value; State = state; } public T Value { get; } public State State { get; } public override bool Equals(object obj) { return obj is StatePair<T> result && EqualityComparer<T>.Default.Equals(Value, result.Value) && EqualityComparer<State>.Default.Equals(State, result.State); } public override int GetHashCode() { return HashCode.Combine(Value, State); } }
This enables you to change the signatures of the Handle methods:
public abstract StatePair<Out1> Handle1(Context context, In1 in1); public abstract StatePair<Out2> Handle2(Context context, In2 in2);
This refactoring is always possible. Even if the original return type of a method was void, you can use a unit type as a replacement for void. While redundant but consistent, a method could return StatePair<Unit>.
Generic pair #
The above StatePair type is so coupled to a particular State class that it's not reusable. If you had more than one implementation of the State pattern in your code base, you'd have to duplicate that effort. That seems wasteful, so why not make the type generic in the state dimension as well?
public sealed class StatePair<TState, T> { public StatePair(T value, TState state) { Value = value; State = state; } public T Value { get; } public TState State { get; } public override bool Equals(object obj) { return obj is StatePair<TState, T> pair && EqualityComparer<T>.Default.Equals(Value, pair.Value) && EqualityComparer<TState>.Default.Equals(State, pair.State); } public override int GetHashCode() { return HashCode.Combine(Value, State); } }
When you do that then clearly you'd also need to modify the Handle methods accordingly:
public abstract StatePair<State, Out1> Handle1(Context context, In1 in1); public abstract StatePair<State, Out2> Handle2(Context context, In2 in2);
Notice that, as is the case with the State functor, the type declares the type with TState before T, while the constructor takes T before TState. While odd and potentially confusing, I've done this to stay consistent with my previous articles, which again do this to stay consistent with prior art (mainly Haskell).
With StatePair you can make the methods pure.
Pure functions #
Since Handle methods can now return a new state instead of mutating objects, they can be pure functions. Here's an example:
public override StatePair<State, Out2> Handle2(Context context, In2 in2) { if (in2 == In2.Epsilon) return new StatePair<State, Out2>(Out2.Eta, new ConcreteStateB()); return new StatePair<State, Out2>(Out2.Eta, this); }
The same is true for Context:
public StatePair<Context, Out1> Request1(In1 in1) { var pair = State.Handle1(this, in1); return new StatePair<Context, Out1>(pair.Value, new Context(pair.State)); } public StatePair<Context, Out2> Request2(In2 in2) { var pair = State.Handle2(this, in2); return new StatePair<Context, Out2>(pair.Value, new Context(pair.State)); }
Does this begin to look familiar?
Monad #
The StatePair class is nothing but a glorified tuple. Armed with that knowledge, you can introduce a variation of the IState interface I used to introduce the State functor:
public interface IState<TState, T> { StatePair<TState, T> Run(TState state); }
This variation uses the explicit StatePair class as the return type of Run, rather than a more anonymous tuple. These representations are isomorphic. (That might be a good exercise: Write functions that convert from one to the other, and vice versa.)
You can write the usual Select and SelectMany implementations to make IState a functor and monad. Since I have already shown these in previous articles, I'm also going to skip those. (Again, it might be a good exercise to implement them if you're in doubt of how they work.)
You can now, for example, use C# query syntax to run the same computation multiple times:
IState<Context, (Out1 a, Out1 b)> s = from a in in1.Request1() from b in in1.Request1() select (a, b); StatePair<Context, (Out1 a, Out1 b)> t = s.Run(ctx);
This example calls Request1 twice, and collects both return values in a tuple. Running the computation with a Context will produce both a result (the two outputs a and b) as well as the 'current' Context (state).
Request1 is a State-valued extension method on In1:
public static IState<Context, Out1> Request1(this In1 in1) { return from ctx in Get<Context>() let p = ctx.Request1(in1) from _ in Put(p.State) select p.Value; }
Notice the abstraction level in play. This extension method doesn't return a StatePair, but rather an IState computation, defined by using the State monad's Get and Put functions. Since the computation is running with a Context state, the computation can Get a ctx object and call its Request1 method. This method returns a pair p. The computation can then Put the pair's State (here, a Context object) and return the pair's Value.
This stateful computation is composed from the building blocks of the State monad, including query syntax supported by SelectMany, Get, and Put.
This does, however, still feel unsatisfactory. After all, you have to know enough of the details of the State monad to know that ctx.Request1 returns a pair of which you must remember to Put the State. Would it be possible to also express the underlying Handle methods as stateful computations?
StatePair bifunctor #
The StatePair class is isomorphic to a pair (a two-tuple), and we know that a pair gives rise to a bifunctor:
public StatePair<TState1, T1> SelectBoth<TState1, T1>( Func<T, T1> selectValue, Func<TState, TState1> selectState) { return new StatePair<TState1, T1>( selectValue(Value), selectState(State)); }
You can use SelectBoth to implement both Select and SelectState. In the following we're only going to need SelectState:
public StatePair<TState1, T> SelectState<TState1>(Func<TState, TState1> selectState) { return SelectBoth(x => x, selectState); }
This enables us to slightly simplify the Context methods:
public StatePair<Context, Out1> Request1(In1 in1) { return State.Handle1(this, in1).SelectState(s => new Context(s)); } public StatePair<Context, Out2> Request2(In2 in2) { return State.Handle2(this, in2).SelectState(s => new Context(s)); }
Keep in mind that Handle1 returns a StatePair<State, Out1>, Handle2 returns StatePair<State, Out2>, and so on. While Request1 calls Handle1, it must return a StatePair<Context, Out1> rather than a StatePair<State, Out1>. Since StatePair is a bifunctor, the Request1 method can use SelectState to map the State to a Context.
Unfortunately, this doesn't seem to move us much closer to being able to express the underlying functions as stateful computations. It does, however, set up the code so that the next change is a little easier to follow.
State computations #
Is it possible to express the Handle methods on State as IState computations? One option is to write another extension method:
public static IState<State, Out1> Request1S(this In1 in1) { return from s in Get<State>() let ctx = new Context(s) let p = s.Handle1(ctx, in1) from _ in Put(p.State) select p.Value; }
I had to add an S suffix to the name, since it only differs from the above Request1 extension method on its return type, and C# doesn't allow method overloading on return types.
You can add a similar Request2S extension method. It feels like boilerplate code, but enables us to express the Context methods in terms of running stateful computations:
public StatePair<Context, Out1> Request1(In1 in1) { return in1.Request1S().Run(State).SelectState(s => new Context(s)); } public StatePair<Context, Out2> Request2(In2 in2) { return in2.Request2S().Run(State).SelectState(s => new Context(s)); }
This still isn't entirely satisfactory, since the return types of these Request methods are state pairs, and not IState values. The above Request1S function, however, contains a clue about how to proceed. Notice how it can create a Context object from the underlying State, and convert that Context object back to a State object. That's a generalizable idea.
Invariant functor #
While it's possible to map the TState dimension of the state pair, it seems harder to do it on IState<TState, T>. A tuple, after all, is covariant in both dimensions. The State monad, on the other hand, is neither co- nor contravariant in the state dimension. You can deduce this with positional variance analysis (which I've learned from Thinking with Types). In short, this is because TState appears as both input and output in StatePair<TState, T> Run(TState state) - it's neither co- nor contravariant, but rather invariant.
What little option is left us, then, is to make IState an invariant functor in the state dimension:
public static IState<TState1, T> SelectState<TState, TState1, T>( this IState<TState, T> state, Func<TState, TState1> forward, Func<TState1, TState> back) { return from s1 in Get<TState1>() let s = back(s1) let p = state.Run(s) from _ in Put(forward(p.State)) select p.Value; }
Given an IState<TState, T> the SelectState function enables us to turn it into a IState<TState1, T>. This is, however, only possible if you can translate both forward and back between two representations. When we have two such translations, we can produce a new computation that runs in TState1 by first using Get to retrieve a TState1 value from the new environment, translate it back to TState, which enables the expression to Run the state. Then translate the resulting p.State forward and Put it. Finally, return the Value.
As Sandy Maguire explains:
"... an invariant type
Tallows you to map fromatobif and only ifaandbare isomorphic. [...] an isomorphism betweenaandbmeans they're already the same thing to begin with."
This may seem limiting, but is enough in this case. The Context class is only a wrapper of a State object:
public Context(State state) { State = state; } public State State { get; }
If you have a State object, you can create a Context object via the Context constructor. On the other hand, if you have a Context object, you can get the wrapped State object by reading the State property.
The first improvement this offers is simplification of the Request1 extension method:
public static IState<Context, Out1> Request1(this In1 in1) { return in1.Request1S().SelectState(s => new Context(s), ctx => ctx.State); }
Recall that Request1S returns a IState<State, Out1>. Since a two-way translation between State and Context exists, SelectState can translate IState<State, Out1> to IState<Context, Out1>.
The same applies to the equivalent Request2 extension method.
This, again, enables us to rewrite the Context methods:
public StatePair<Context, Out1> Request1(In1 in1) { return in1.Request1().Run(this); } public StatePair<Context, Out2> Request2(In2 in2) { return in2.Request2().Run(this); }
While this may seem like an insignificant change, one result has been gained: This last refactoring pushed the Run call to the right. It's now clear that each expression is a stateful computation, and that the only role that the Request methods play is to Run the computations.
This illustrates that the Request methods can be decomposed into two decoupled steps:
- A stateful computation expression
- Running the expression
Context wrapper class now?
Eliminating the Context #
A reasonable next refactoring might be to remove the context parameter from each of the Handle methods. After all, this parameter is a remnant of the State design pattern. Its original purpose was to enable State implementers to mutate the context by changing its State.
After refactoring to immutable functions, the context parameter no longer needs to be there - for that reason. Do we need it for other reasons? Does it carry other information that a State implementer might need?
In the form that the code now has, it doesn't. Even if it did, we could consider moving that data to the other input parameter: In1, In2, etcetera.
Therefore, it seems sensible to remove the context parameter from the State methods:
public abstract StatePair<State, Out1> Handle1(In1 in1); public abstract StatePair<State, Out2> Handle2(In2 in2);
This also means that a function like Request1S becomes simpler:
public static IState<State, Out1> Request1S(this In1 in1) { return from s in Get<State>() let p = s.Handle1(in1) from _ in Put(p.State) select p.Value; }
Since Context and State are isomorphic, you can rewrite all callers of Context to instead use State, like the above example:
IState<State, (Out1 a, Out1 b)> s = from a in in1.Request1() from b in in1.Request1() select (a, b); var t = s.Run(csa);
Do this consistently, and you can eventually delete the Context class.
Further possible refactorings #
With the Context class gone, you're left with the abstract State class and its implementers:
public abstract class State { public abstract StatePair<State, Out1> Handle1(In1 in1); public abstract StatePair<State, Out2> Handle2(In2 in2); }
One further change worth considering might be to change the abstract base class to an interface.
In this article, I've considered the general case where the State class supports an arbitrary number of independent state transitions, symbolised by the methods Handle1 and Handle2. With an arbitrary number of such state transitions, you would have additional methods up to HandleN for N independent state transitions.
At the other extreme, you may have just a single polymorphic state transition function. My intuition tells me that that's more likely to be the case than one would think at first.
Relationship between pattern and monad #
You can view the State design pattern as a combination of two common practices in object-oriented programming: Mutation and polymorphism.
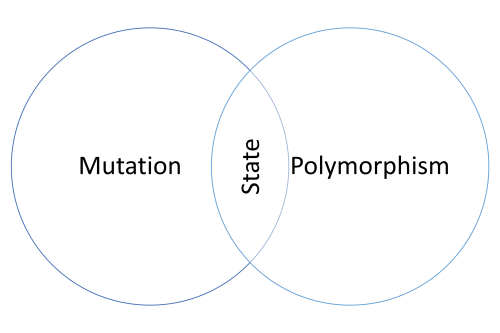
The patterns in Design Patterns rely heavily on mutation of object state. Most other 'good' object-oriented code tends to do likewise.
Proper object-oriented code also makes good use of polymorphism. Again, refer to Design Patterns or a book like Refactoring for copious examples.
I view the State pattern as the intersection of these two common practices. The problem to solve is this:
"Allow an object to alter its behavior when its internal state changes."
The State pattern achieves that goal by having an inner polymorphic object (State) wrapped by an container object (Context). The State objects can mutate the Context, which enables them to replace themselves with other states.
While functional programming also has notions of polymorphism, a pure function can't mutate state. Instead, a pure function must return a new state, leaving the old state unmodified. If there's nothing else to return, you can model such state-changing behaviour as an endomorphism. The article From State tennis to endomorphism gives a quite literal example of that.
Sometimes, however, an object-oriented method does more than one thing: It both mutates state and returns a value. (This, by the way, violates the Command Query Separation principle.) The State monad is the functional way of doing that: Return both the result and the new state.
Essentially, you replace mutation with the State monad.
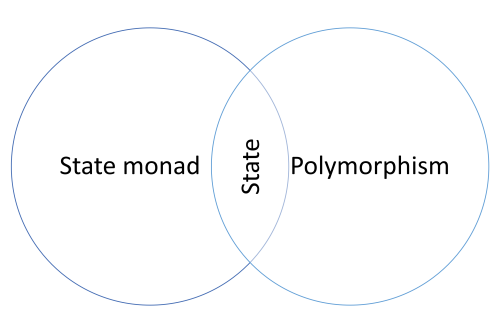
From a functional perspective, then, we can view the State pattern as the intersection of polymorphism and the State monad.
Examples #
This article is both long and abstract. Some examples might be helpful, so I'll give a few in separate articles:
- Refactoring the TCP State pattern example to pure functions
- Refactoring a saga from the State pattern to the State monad
Conclusion #
You can view the State design pattern as the intersection of polymorphism and mutation. Both are object-oriented staples. The pattern uses polymorphism to model state, and mutation to change from one polymorphic state to another.
In functional programming pure functions can't mutate state. You can often design around that problem, but if all else fails, the State monad offers a general-purpose alternative to both return a value and change object state. Thus, you can view the functional equivalent of the State pattern as the intersection of polymorphism and the State monad.
Next: Refactoring the TCP State pattern example to pure functions.
