Natural transformations as invariant functors by Mark Seemann

An article (also) for object-oriented programmers.

This article is part of a series of articles about invariant functors. An invariant functor is a functor that is neither covariant nor contravariant. See the series introduction for more details. The previous article described how you can view an endomorphism as an invariant functor. This article generalises that result.

Endomorphism as a natural transformation #

An endomorphism is a function whose domain and codomain is the same. In C# you'd denote the type as Func<T, T>, in F# as 'a -> 'a, and in Haskell as a -> a. T, 'a, and a all symbolise generic types - the notation is just different, depending on the language.

A 'naked' value is isomorphic to the Identity functor. You can wrap a value of the type a in Identity a, and if you have an Identity a, you can extract the a value.

An endomorphism is thus isomorphic to a function from Identity to Identity. In C#, you might denote that as Func<Identity<T>, Identity<T>>, and in Haskell as Identity a -> Identity a.

In fact, you can lift any function to an Identity-valued function:

Prelude Data.Functor.Identity> :t \f -> Identity . f . runIdentity
\f -> Identity . f . runIdentity
  :: (b -> a) -> Identity b -> Identity a

While this is a general result that allows a and b to differ, when a ~ b this describes an endomorphism.

Since Identity is a functor, a function Identity a -> Identity a is a natural transformation.

The identity function (id in F# and Haskell; x => x in C#) is the only one possible entirely general endomorphism. You can use the natural-transformation package to make it explicit that this is a natural transformation:

idNT :: Identity :~> Identity
idNT = NT $ Identity . id . runIdentity

The point, so far, is that you can view an endomorphism as a natural transformation.

Since an endomorphism forms an invariant functor, this suggests a promising line of inquiry.

Natural transformations as invariant functors #

Are all natural transformations invariant functors?

Yes, they are. In Haskell, you can implement it like this:

instance (Functor f, Functor g) => Invariant (NT f g) where
  invmap f g (NT h) = NT $ fmap f . h . fmap g

Here, I chose to define NT from scratch, rather than relying on the natural-transformation package.

newtype NT f g a = NT { unNT :: f a -> g a }

Notice how the implementation (fmap f . h . fmap g) looks like a generalisation of the endomorphism implementation of invmap (f . h . g). Instead of pre-composing with g, the generalisation pre-composes with fmap g, and instead of post-composing with f, it post-composes with fmap f.

Using the same kind of diagram as in the previous article, this composition now looks like this:

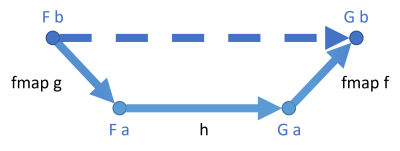
I've used thicker arrows to indicate that each one potentially involves 'more work'. Each is a mapping from a functor to a functor. For the List functor, for example, the arrow implies zero to many values being mapped. Thus, 'more data' moves 'through' each arrow, and for that reason I thought it made sense to depict them as being thicker. This 'more data' view is not always correct. For example, for the Maybe functor, the amount of data transported though each arrow is zero or one, which rather suggests a thinner arrow. For something like the State functor or the Reader functor, there's really no data in the strictest sense moving through the arrows, but rather functions (which are also, however, a kind of data). Thus, don't take this metaphor of the thicker arrows literally. I did, however, wish to highlight that there's something 'more' going on.

The diagram shows a natural transformation h from some functor F to another functor G. It transports objects of the type a. If a and b are isomorphic, you can map that natural transformation to one that transports objects of the type b.

Compared to endomorphisms, where you need to, say, map b to a, you now need to map F b to F a. If g maps b to a, then fmap g maps F b to F a. The same line of argument applies to fmap f.

In C# you can implement the same behaviour as follows. Assume that you have a natural transformation H from the functor F to the functor G:

public Func<F<A>, G<A>> H { get; }

You can now implement a non-standard Select overload (as described in the introductory article) that maps a natural transformation FToG<A> to a natural transformation FToG<B>:

public FToG<B> Select<B>(Func<A, B> aToB, Func<B, A> bToA)
{
    return new FToG<B>(fb => H(fb.Select(bToA)).Select(aToB));
}

The implementation looks more imperative than in Haskell, but the idea is the same. First it uses Select on F in order to translate fb (of the type F<B>) to an F<A>. It then uses H to transform the F<A> to an G<A>. Finally, now that it has a G<A>, it can use Select on that functor to map to a G<B>.

Note that there's two different functors (F and G) in play, so the two Select methods are different. This is also true in the Haskell code. fmap g need not be the same as fmap f.

Identity law #

As in the previous article, I'll set out to prove the two laws for invariant functors, starting with the identity law. Again, I'll use equational reasoning with the notation that Bartosz Milewski uses. Here's the proof that the invmap instance obeys the identity law:

  invmap id id (NT h)
= { definition of invmap }
  NT $ fmap id . h . fmap id
= { first functor law }
  NT $ id . h . id
= { eta expansion }
  NT $ (\x -> (id . h . id) x)
= { definition of (.) }
  NT $ (\x -> id(h(id(x))))
= { defintion of id }
  NT $ (\x -> h(x))
= { eta reduction }
  NT h
= { definition of id }
  id (NT h)

I'll leave it here without further comment. The Haskell type system is so expressive and abstract that it makes little sense to try to translate these findings to C# or F# in the abstract. Instead, you'll see some more concrete examples later.

Composition law #

As with the identity law, I'll offer a proof for the composition law for the Haskell instance:

  invmap f2 f2' $ invmap f1 f1' (NT h)
= { definition of invmap }
  invmap f2 f2' $ NT $ fmap f1 . h . fmap f1'
= { defintion of ($) }
  invmap f2 f2' (NT (fmap f1 . h . fmap f1'))
= { definition of invmap }
  NT $ fmap f2 . (fmap f1 . h . fmap f1') . fmap f2'
= { associativity of composition (.) }
  NT $ (fmap f2 . fmap f1) . h . (fmap f1' . fmap f2')
= { second functor law }
  NT $ fmap (f2 . f1) . h . fmap (f1' . f2')
= { definition of invmap }
  invmap (f2 . f1) (f1' . f2') (NT h)

Unless I've made a mistake, these two proofs should demonstrate that all natural transformations can be turned into an invariant functor - in Haskell, at least, but I'll conjecture that that result carries over to other languages like F# and C# as long as one stays within the confines of pure functions.

The State functor as a natural transformation #

I'll be honest and admit that my motivation for embarking on this exegesis was because I'd come to the realisation that you can think about the State functor as a natural transformation. Recall that State is usually defined like this:

newtype State s a = State { runState :: s -> (a, s) }

You can easily establish that this definition of State is isomorphic with a natural transformation from the Identity functor to the tuple functor:

stateToNT :: State s a -> NT Identity ((,) a) s
stateToNT (State h) = NT $ h . runIdentity
 
ntToState :: NT Identity ((,) a) s -> State s a
ntToState (NT h) = State $ h . Identity

Notice that this is a natural transformation in s - not in a.

Since I've already established that natural transformations form invariant functors, this also applies to the State monad.

State mapping #

My point with all of this isn't really to insist that anyone makes actual use of all this machinery, but rather that this line of reasoning helps to identify a capability. We now know that it's possible to translate a State s a value to a State t a value if s is isomorphic to t.

As an example, imagine that you have some State-valued function that attempts to find the maximum value based on various criteria. Such a pickMax function may have the type State (Max Integer) String where the state type (Max Integer) is used to keep track of the maximum value found while examining candidates.

You could conceivably turn such a function around to instead look for the minimum by mapping the state to a Min value instead:

pickMin :: State (Min Integer) String
pickMin = ntToState $ invmap (Min . getMax) (Max . getMin) $ stateToNT pickMax

You can use getMax to extract the underlying Integer from the Max Integer and then Min to turn it into a Min Integer value, and vice versa. Max Integer and Min Integer are isomorphic.

In C#, you can implement a similar method. The code shown here extends the code shown in The State functor. I chose to call the method SelectState so as to not make things too confusing. The State functor already comes with a Select method that maps T to T1 - that's the 'normal', covariant functor implementation. The new method is the invariant functor implementation that maps the state S to S1:

public static IState<S1, T> SelectState<T, S, S1>(
    this IState<S, T> state,
    Func<S, S1> sToS1,
    Func<S1, S> s1ToS)
{
    return new InvariantStateMapper<T, S, S1>(state, sToS1, s1ToS);
}
 
private class InvariantStateMapper<T, S, S1> : IState<S1, T>
{
    private readonly IState<S, T> state;
    private readonly Func<S, S1> sToS1;
    private readonly Func<S1, S> s1ToS;
 
    public InvariantStateMapper(
        IState<S, T> state,
        Func<S, S1> sToS1,
        Func<S1, S> s1ToS)
    {
        this.state = state;
        this.sToS1 = sToS1;
        this.s1ToS = s1ToS;
    }
 
    public Tuple<T, S1> Run(S1 s1)
    {
        return state.Run(s1ToS(s1)).Select(sToS1);
    }
}

As usual when working in C# with interfaces instead of higher-order functions, there's some ceremony to be expected. The only interesting line of code is the Run implementation.

It starts by calling s1ToS in order to translate the s1 parameter into an S value. This enables it to call Run on state. The result is a tuple with the type Tuple<T, S>. It's necessary to translate the S to S1 with sToS1. You could do that by extracting the value from the tuple, mapping it, and returning a new tuple. Since a tuple gives rise to a functor (two, actually) I instead used the Select method I'd already defined on it.

Notice how similar the implementation is to the implementation of the endomorphism invariant functor. The only difference is that when translating back from S to S1, this happens inside a Select mapping. This is as predicted by the general implementation of invariant functors for natural transformations.

In a future article, you'll see an example of SelectState in action.

Other natural transformations #

As the natural transformations article outlines, there are infinitely many natural transformations. Each one gives rise to an invariant functor.

It might be a good exercise to try to implement a few of them as invariant functors. If you want to do it in C#, you could, for example, start with the safe head natural transformation.

If you want to stick to interfaces, you could define one like this:

public interface ISafeHead<T>
{
    Maybe<T> TryFirst(IEnumerable<T> ts);
}

The exercise is now to define and implement a method like this:

public static ISafeHead<T1> Select<T, T1>(
    this ISafeHead<T> source,
    Func<T, T1> tToT1,
    Func<T1, T> t1ToT)
{
    // Implementation goes here...
}

The implementation, once you get the handle of it, is entirely automatable. After all, in Haskell it's possible to do it once and for all, as shown above.

Conclusion #

A natural transformation forms an invariant functor. This may not be the most exciting result ever, because invariant functors are limited in use. They only work when translating between types that are already isomorphic. Still, I did find a use for this result when I was working with the relationship between the State design pattern and the State monad.

Next: Functors as invariant functors.

Comments

type (~>) f g = forall a. f a -> g a
 
-- Use the natural transformation twice, for different types
convertLists :: ([] ~> g) -> (g Int, g Bool)
convertLists nt = (nt [1,2], nt [True])
 
newtype NT f g a = NT (f a -> g a)
 
-- Does not type check, does not work; not a natural transformation
convertLists2 :: NT [] g a -> (g Int, g Bool)
convertLists2 (NT f) = (f [1,2], f [True])

* Couldn't match type `a' with `Int'
  `a' is a rigid type variable bound by
    the type signature for:
      convertLists2 :: forall (g :: * -> *) a.
                       NT [] g a -> (g Int, g Bool)
  Expected type: g Int
    Actual type: g a
* In the expression: f [1, 2]
  In the expression: (f [1, 2], f [True])
  In an equation for `convertLists2':
      convertLists2 (NT f) = (f [1, 2], f [True])

• ← Previous
• Archive
• Next →