NonEmpty catamorphism by Mark Seemann
The universal API for generic non-empty collections, with examples in C# and Haskell.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
I was recently doing some work that required a data structure like a collection, but with the additional constraint that it should be guaranteed to have at least one element. I've known about Haskell's NonEmpty type, and how to port it to C# for years. This time I needed to implement it in a third language, and since I had a little extra time available, I thought it'd be interesting to pursue a conjecture of mine: It seems as though you can implement most (all?) of a generic data structure's API based on its catamorphism.
While I could make a guess as to how a catamorphism might look for a non-empty collection, I wasn't sure. A quick web search revealed nothing conclusive, so I decided to deduce it from first principles. As this article series demonstrates, you can derive the catamorphism from a type's isomorphic F-algebra.
The beginning of this article presents the catamorphism in C#, with an example. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
C# catamorphism #
This article will use a custom C# class called NonEmptyCollection<T>, which is near-identical to the NotEmptyCollection<T> originally introduced in the article Semigroups accumulate.
I don't know why I originally chose to name the class NotEmptyCollection instead of NonEmptyCollection, but it's annoyed me ever since. I've finally decided to rectify that mistake, so from now on, the name is NonEmptyCollection.
The catamorphism for NonEmptyCollection is this instance method:
public TResult Aggregate<TResult>(Func<T, IReadOnlyCollection<T>, TResult> algebra) { return algebra(Head, Tail); }
Because the NonEmptyCollection class is really just a glorified tuple, the algebra is any function which produces a single value from the two constituent values.
It's easy to fall into the trap of thinking of the catamorphism as 'reducing' the data structure to a more compact form. While this is a common kind of operation, loss of data is not inevitable. You can, for example, return a new collection, essentially doing nothing:
var nec = new NonEmptyCollection<int>(42, 1337, 2112, 666); var same = nec.Aggregate((x, xs) => new NonEmptyCollection<int>(x, xs.ToArray()));
This Aggregate method enables you to safely find a maximum value:
var nec = new NonEmptyCollection<int>(42, 1337, 2112, 666); var max = nec.Aggregate((x, xs) => xs.Aggregate(x, Math.Max));
or to safely calculate an average:
var nec = new NonEmptyCollection<int>(42, 1337, 2112, 666); var average = nec.Aggregate((x, xs) => xs.Aggregate(x, (a, b) => a + b) / (xs.Count + 1.0));
Both of these two last examples use the built-in Aggregate function to accumulate the xs. It uses the overload that takes a seed, for which it supplies x. This means that there's guaranteed to be at least that one value.
The catamorphism given here is not unique. You can create a trivial variation by swapping the two function arguments, so that x comes after xs.
NonEmpty F-algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-algebras.
As always, start with the underlying endofunctor:
data NonEmptyF a c = NonEmptyF { head :: a, tail :: ListFix a } deriving (Eq, Show, Read) instance Functor (NonEmptyF a) where fmap _ (NonEmptyF x xs) = NonEmptyF x xs
Instead of using Haskell's standard list ([]) for the tail, I've used ListFix from the article on list catamorphism. This should, hopefully, demonstrate how you can build on already established definitions derived from first principles.
Since a non-empty collection is really just a glorified tuple of head and tail, there's no recursion, and thus, the carrier type c is not used. You could argue that going through all of these motions is overkill, but it still provides some insights. This is similar to the Boolean catamorphism and Maybe catamorphism.
The fmap function ignores the mapping argument (often called f), since the Functor instance maps NonEmptyF a c to NonEmptyF a c1, but the c or c1 type is not used.
As was the case when deducing the recent catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (NonEmptyF a). To address that problem, you can introduce a newtype wrapper:
newtype NonEmptyFix a = NonEmptyFix { unNonEmptyFix :: Fix (NonEmptyF a) } deriving (Eq, Show, Read)
You can define Functor, Applicative, Monad, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that, ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A helper function makes it easier to define NonEmptyFix values:
createNonEmptyF :: a -> ListFix a -> NonEmptyFix a createNonEmptyF x xs = NonEmptyFix $ Fix $ NonEmptyF x xs
Here's how to use it:
ghci> createNonEmptyF 42 $ consF 1337 $ consF 2112 nilF
NonEmptyFix {
unNonEmptyFix = Fix (NonEmptyF 42 (ListFix (Fix (ConsF 1337 (Fix (ConsF 2112 (Fix NilF)))))))}
While this is quite verbose, keep in mind that the code shown here isn't meant to be used in practice. The goal is only to deduce catamorphisms from more basic universal abstractions, and you now have all you need to do that.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (NonEmptyF a), and an object c, but you still need to find a morphism NonEmptyF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.
As in the previous articles, start by writing a function that will become the catamorphism, based on cata:
nonEmptyF = cata alg . unNonEmptyFix where alg (NonEmptyF x xs) = undefined
While this compiles, with its undefined implementation of alg, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from alg? You could pass a function argument to the nonEmptyF function and use it with x and xs:
nonEmptyF :: (a -> ListFix a -> c) -> NonEmptyFix a -> c nonEmptyF f = cata alg . unNonEmptyFix where alg (NonEmptyF x xs) = f x xs
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of NonEmptyF, the compiler infers that the alg function has the type NonEmptyF a c -> c1, which fits the bill, since c may be the same type as c1.
This, then, is the catamorphism for a non-empty collection. This one is just a single function. It's still not the only possible catamorphism, since you could trivially flip the arguments to f.
I've chosen this representation because the arguments x and xs are defined in the same order as the order of head before tail. Notice how this is the same order as the above C# Aggregate method.
Basis #
You can implement most other useful functionality with nonEmptyF. Here's the Semigroup instance and a useful helper function:
toListFix :: NonEmptyFix a -> ListFix a toListFix = nonEmptyF consF instance Semigroup (NonEmptyFix a) where xs <> ys = nonEmptyF (\x xs' -> createNonEmptyF x $ xs' <> toListFix ys) xs
The implementation uses nonEmptyF to operate on xs. Inside the lambda expression, it converts ys to a list, and uses the ListFix Semigroup instance to concatenate xs with it.
Here's the Functor instance:
instance Functor NonEmptyFix where fmap f = nonEmptyF (\x xs -> createNonEmptyF (f x) $ fmap f xs)
Like the Semigroup instance, this fmap implementation uses fmap on xs, which is the ListFix Functor instance.
The Applicative instance is much harder to write from scratch (or, at least, I couldn't come up with a simpler way):
instance Applicative NonEmptyFix where pure x = createNonEmptyF x nilF liftA2 f xs ys = nonEmptyF (\x xs' -> nonEmptyF (\y ys' -> createNonEmptyF (f x y) (liftA2 f (consF x nilF) ys' <> liftA2 f xs' (consF y ys'))) ys) xs
While that looks complicated, it's not that bad. It uses nonEmptyF to 'loop' over the xs, and then a nested call to nonEmptyF to 'loop' over the ys. The inner lambda expression uses f x y to calculate the head, but it also needs to calculate all other combinations of values in xs and ys.
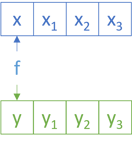
First, it keeps x fixed and 'loops' through all the remaining ys'; that's the liftA2 f (consF x nilF) ys' part:
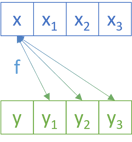
Then it 'loops' over all the remaining xs' and all the ys; that is, liftA2 f xs' (consF y ys').
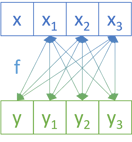
The two liftA2 functions apply to the ListFix Applicative instance.
You'll be happy to see, I think, that the Monad instance is simpler:
instance Monad NonEmptyFix where xs >>= f = nonEmptyF (\x xs' -> nonEmptyF (\y ys -> createNonEmptyF y $ ys <> (xs' >>= toListFix . f)) (f x)) xs
And fortunately, Foldable and Traversable are even simpler:
instance Foldable NonEmptyFix where foldr f seed = nonEmptyF (\x xs -> f x $ foldr f seed xs) instance Traversable NonEmptyFix where traverse f = nonEmptyF (\x xs -> liftA2 createNonEmptyF (f x) (traverse f xs))
Finally, you can implement conversions to and from the NonEmpty type from Data.List.NonEmpty:
toNonEmpty :: NonEmptyFix a -> NonEmpty a toNonEmpty = nonEmptyF (\x xs -> x :| toList xs) fromNonEmpty :: NonEmpty a -> NonEmptyFix a fromNonEmpty (x :| xs) = createNonEmptyF x $ fromList xs
This demonstrates that NonEmptyFix is isomorphic to NonEmpty.
Conclusion #
The catamorphism for a non-empty collection is a single function that produces a single value from the head and the tail of the collection. While it's possible to implement a 'standard fold' (foldr in Haskell), the non-empty catamorphism doesn't require a seed to get started. The data structure guarantees that there's always at least one value available, and this value can then be use to 'kick off' a fold.
In C# one can define the catamorphism as the above Aggregate method. You could then define all other instance functions based on Aggregate.
Next: Either catamorphism.
