Functors, applicatives, and friends by Mark Seemann

Functors and related data structures are containers of values. It's a family of abstractions. An overview for object-oriented programmers.

This article series is part of an even larger series of articles about the relationship between design patterns and category theory.

If you've worked with C# or Java recently, you've most likely encountered types such as Foo<T> or Bar<T> (specifically, on .NET, e.g. List<T>). Perhaps you've also noticed that often, you can translate the type inside of the container. For example, if you have a Foo<string>, perhaps you can call some method on it that returns a Foo<int>. If so, it may be a functor.

Not all generic types are functors. In order to be a functor, a generic type must obey a couple of intuitive laws. You'll learn about those in future articles.

Some functors have extra capabilities, and you'll learn about some of those as well. Some are called applicative functors, and some are called bifunctors. There are others, as well.

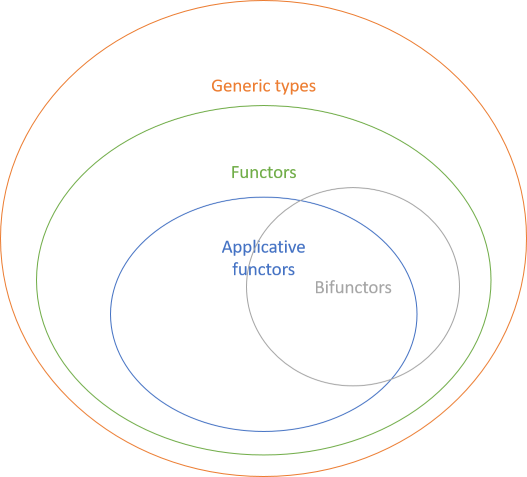
All applicative functors are functors, and this is true for bifunctors as well.

In this article series, you'll learn about the following categories:

• Functors
  • The Maybe functor
  • An Either functor
  • A Tree functor
  • A rose tree functor
  • A Visitor functor
  • Reactive functor
  • The Identity functor
  • The Lazy functor
  • Asynchronous functors
  • The State functor
  • The Reader functor
  • The IO functor
  • Monomorphic functors
  • Set is not a functor
• Applicative functors
  • Full deck
  • An applicative password list
  • Applicative combinations of functions
  • The Maybe applicative functor
  • Applicative validation
  • The Test Data Generator applicative functor
  • Danish CPR numbers in F#
  • The Lazy applicative functor
  • Applicative monoids
• Bifunctors
  • Tuple bifunctor
  • Either bifunctor
  • Rose tree bifunctor
• Contravariant functors
  • The Command Handler contravariant functor
  • The Specification contravariant functor
  • The Equivalence contravariant functor
  • Reader as a contravariant functor
  • Functor variance compared to C#'s notion of variance
  • Contravariant Dependency Injection
• Profunctors
  • Reader as a profunctor
• Invariant functors
  • Endomorphism as an invariant functor
  • Natural transformations as invariant functors
  • Functors as invariant functors
  • Contravariant functors as invariant functors
• Monads
  • Kleisli composition
  • Monad laws
  • The List monad
  • The Maybe monad
  • An Either monad
  • The Identity monad
  • The Lazy monad
  • Asynchronous monads
  • The State monad
  • The Reader monad
  • The IO monad
  • Test Data Generator monad
• Functor relationships
  • Natural transformations
  • Traversals
  • Functor compositions
  • Functor products
  • Functor sums

You'll see plenty of examples along the way. Most examples will be in C#, but some articles will have code examples in F# or Haskell. You can read or skip those articles as you prefer.

Next: Functors.

• ← Previous
• Archive
• Next →