Catamorphisms by Mark Seemann

A catamorphism is a general abstraction that enables you to handle multiple values, for example in order to reduce them to a single value.

This article series is part of an even larger series of articles about the relationship between design patterns and category theory. In another article series in this big series of articles, you learned about functors, applicatives, and other types of data containers.

You may have heard about map-reduce architectures. Much software can be designed around two general types of operations: those that map data, and those that reduce data. A functor is a container of data that supports structure-preserving maps. Thus, you can think of functors as the general abstraction for map operations (also sometimes called projections). Does a similar universal abstraction exist for operations that reduce data?

Yes, that abstraction is called a catamorphism.

Aggregation #

Catamorphism is an intimidating word, so let's start with an example. You often have a collection of values that you'd like to reduce to a single value. Such a collection can contain arbitrarily complex objects, but I'll keep it simple and start with a collection of numbers:

new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 };

This particular list of numbers is an array, but that's not important. What comes next works for any IEnumerable<T>, including arrays. I only chose an array because the C# syntax for array creation is more compact than for other collection types.

How do you reduce those seven numbers to a single number? That depends on what you want that number to tell you. One option is to add the numbers together. There's a specific, built-in function for that:

> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 }.Sum();
100647

The Sum extension method is a one of many built-in functions that enable you to reduce a list of numbers to a single number: Average, Max, Count, and so on.

What do you do, though, if you need to reduce many values to one, and there's no existing function for that? What if, for example, you need to add all the numbers using modulo 360 addition?

In that case, you use Aggregate:

> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 }.Aggregate((x, y) => (x + y) % 360)
207

The way to interpret this result is that the initial array represents a sequence of rotations (measured in degrees), and the result is the final angle after all the rotations have completed.

In other (functional) languages, such a 'reduce' operation is called a fold. The metaphor, I suppose, is that you fold multiple values together, two by two.

A fold is a catamorphism, but a catamorphism is a more general abstraction. For some data structures, the catamorphism is more powerful than the fold, but for collections, there's no difference.

There's one edge case we need to be aware of, though. What if the collection is empty?

Aggregation of empty containers #

What happens if you attempt to aggregate an empty collection?

> new int[0].Aggregate((x, y) => (x + y) % 360)
Sequence contains no elements
  + System.Linq.Enumerable.Aggregate<TSource>(IEnumerable<TSource>, Func<TSource, TSource, TSource>)

The Aggregate method throws an exception because it doesn't know how to deal with empty collections. The lambda expression you supply tells the Aggregate method how to combine two values into one. This is, for instance, how semigroups accumulate.

The lambda expression handles all cases where you have two or more values. If you have only a single value, then that's no problem either:

> new[] { 1337 }.Aggregate((x, y) => (x + y) % 360)
1337

In that case, the lambda expression isn't involved at all, because the single value is simply returned without modification. In this example, this could even be interpreted as being incorrect, since you'd expect the result to be 257 (1337 % 360).

It's safer to use the Aggregate overload that takes a seed value:

> new int[0].Aggregate(0, (x, y) => (x + y) % 360)
0

Not only does that gracefully handle empty collections, it also gives you a 'better' result for a single value:

> new[] { 1337 }.Aggregate(0, (x, y) => (x + y) % 360)
257

This works better because the method always starts with the seed value, which means that even if there's only a single value (1337), the lambda expression still runs ((0 + 1337) % 360).

This overload of Aggregate has a different type, though:

public static TAccumulate Aggregate<TSource, TAccumulate>(
    this IEnumerable<TSource> source,
    TAccumulate seed,
    Func<TAccumulate, TSource, TAccumulate> func);

Notice that the func doesn't require the accumulator to have the same type as elements from the source collection. This enables you to translate on the fly, so to speak. You can still use binary operations like the above modulo 360 addition, because that just implies that both TSource and TAccumulate are int.

With this overload, you could, for example, use the Angle class to perform the work:

> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 }
. .Aggregate(Angle.Identity, (a, i) => a.Add(Angle.FromDegrees(i)))
[{ Angle = 207° }]

Now the seed argument is Angle.Identity, which implies that TAccumulate is Angle. The source is still a collection of numbers, so TSource is int. Hence, I called the angle a and the integer i in the lambda expression. The output is an Angle object that represents 207°.

That Aggregate overload is the catamorphism for collections. It reduces a collection to an object.

Catamorphisms and folds #

Is catamorphism just an intimidating word for aggregate, accumulate, fold, or reduce?

It took me a long time to be able to tell the difference, because in many cases, it seems that there's no difference. The purpose of this article series is to make the distinction clearer. In short, a catamorphism is a more general concept.

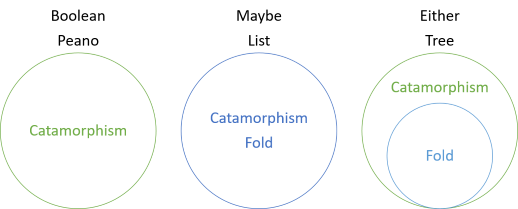
For some data structures, such as Boolean values, or Peano numbers, the catamorphism is all there is; no fold exists. For other data structures, such as Maybe or collections, the catamorphism and the fold coincide. Still other data structures, such as Either and trees, support folding, but the fold is based on the catamorphism. For those types, there are operations you can do with the catamorphism that are impossible to implement with the fold function. One example is that a tree's catamorphism enables you to count its leaves; you can't do that with its fold function.

You'll see plenty of examples in this article series:

• Boolean catamorphism
• Peano catamorphism
• Maybe catamorphism
• List catamorphism
• NonEmpty catamorphism
• Either catamorphism
• Tree catamorphism
• Rose tree catamorphism
• Full binary tree catamorphism
• Payment types catamorphism

Each of these articles will contain a fair amount of Haskell code, but even if you're an object-oriented programmer who doesn't read Haskell, you should still scan them, as I'll start each with some C# examples. The Haskell code, by the way, is available on GitHub.

Greek #

When encountering a word like catamorphism, your reaction might be:

"Catamorphism?! What does that even mean? It's all Greek to me."

The morph suffix generally means 'shape'. While the cata prefix appears in common words like catastrophe, the morph suffix mostly appears in more academic contexts. Programmers will probably have encountered polymorphism and skeuomorphism, not to mention isomorphism. While morphism is heavily used in mathematics, other sciences use the suffix too, like dimorphism in biology.

In category theory, a morphism is basically just an arrow that points from one object to another. Think of it as a function.

If a morphism is just a function, why don't we just call it that, then? Is it really necessary with this intimidating terminology? Yes and no.

If someone had originally figured all of this out in the context of mainstream programming, he or she would probably have used friendlier names, like condense, reduce, fold, and so on. This would have been more encouraging, although I'm not sure it would have been better.

In software architecture we use many overloaded terms. For example, what's a service, or a client? What does tier mean? Is it the same as a layer, or is it something different? What's the difference between a library and a framework?

At least a word like catamorphism is concise. It's not in common use, so isn't overloaded and vague.

Another, more pragmatic, concern is that whether you like it or not, the terminology is already established. Mathematicians decided to name the concept catamorphism. While the name may seem intimidating, I prefer to teach concepts like these using established terminology. This means that if my articles are unclear, you can do further research with other resources. That's the benefit of established terminology, whether you like the specific words or not.

Summary #

You can compose entire applications based on the abstractions of map and reduce. You can see one example of such a system in my A Functional Architecture with F# Pluralsight course.

The terms map and reduce may, however, not be helpful, because it may not be clear exactly what types of data you can map, and what types you can reduce. One of the most important goals of this overall article series about universal abstractions is to help you identify when such software architectures apply. This is more often that you think.

What sort of data can you map? You can map functors. While hardly finite, there's a catalogue of well-known functors, of which I've covered some, but not all. That catalogue contains data containers like Maybe, Tree, lazy computations, tasks, and perhaps a score more. The catalogue of (actually useful) functors has, in my experience, a manageable size.

Likewise you could ask: What sort of data can you reduce? How do you implement that reduction? Again, there's a compact set of well-known catamorphisms. How do you reduce a collection? You use its catamorphism (which is equal to a fold). How do you reduce a tree? You use its catamorphism. How do you reduce an Either object? You use its catamorphism.

When we learn new programming languages, new libraries, new frameworks, we gladly invest time in learning hundreds, if not thousands, of keywords, APIs, extensibility points, and so on. May I offer, for your consideration, that your mental resources are better spent learning only a handful of universal abstractions?

Next: Boolean catamorphism.

Comments

let foo = reduce xs bar

• ← Previous
• Archive
• Next →