Backwards compatibility as a profunctor by Mark Seemann
In order to keep backwards compatibility, you can weaken preconditions or strengthen postconditions.
Like the previous articles on Postel's law as a profunctor and the Liskov Substitution Principle as a profunctor, this article is part of a series titled Some design patterns as universal abstractions. And like the previous articles, it's a bit of a stretch including the present article in that series, since backwards compatibility isn't a design pattern, but rather a software design principle or heuristic. I still think, however, that the article fits the spirit of the article series, if not the letter.
Backwards compatibility is often (but not always) a desirable property of a system. Even in Zoo software, it pays to explicitly consider versioning. In order to support Continuous Delivery, you must be able to evolve a system in such a way that it's always in a working state.
When other systems depend on a system, it's important to maintain backwards compatibility. Evolve the system, but support legacy dependents as well.
Adding new test code #
In Code That Fits in Your Head, chapter 11 contains a subsection on adding new test code. Despite admonitions to the contrary, I often experience that programmers treat test code as a second-class citizen. They casually change test code in a more undisciplined way than they'd edit production code. Sometimes, that may be in order, but I wanted to show that you can approach the task of editing test code in a more disciplined way. After all, the more you edit tests, the less you can trust them.
After a preliminary discussion about adding entirely new test code, the book goes on to say:
You can also append test cases to a parametrised test. If, for example, you have the test cases shown in listing 11.1, you can add another line of code, as shown in listing 11.2. That’s hardly dangerous.
Listing 11.1 A parametrised test method with three test cases. Listing 11.2 shows the updated code after I added a new test case. (Restaurant/b789ef1/Restaurant.RestApi.Tests/ReservationsTests.cs)
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] public async Task PostInvalidReservation(Listing 11.2 A test method with a new test case appended, compared to listing 11.1. The line added is highlighted. (Restaurant/745dbf5/Restaurant.RestApi.Tests/ReservationsTests.cs)
[Theory] [InlineData(null, "j@example.net", "Jay Xerxes", 1)] [InlineData("not a date", "w@example.edu", "Wk Hd", 8)] [InlineData("2023-11-30 20:01", null, "Thora", 19)] [InlineData("2022-01-02 12:10", "3@example.org", "3 Beard", 0)] public async Task PostInvalidReservation(You can also add assertions to existing tests. Listing 11.3 shows a single assertion in a unit test, while listing 11.4 shows the same test after I added two more assertions.
Listing 11.3 A single assertion in a test method. Listing 11.4 shows the updated code after I added more assertions. (Restaurant/36f8e0f/Restaurant.RestApi.Tests/ReservationsTests.cs)
Assert.Equal( HttpStatusCode.InternalServerError, response.StatusCode);Listing 11.4 Verification phase after I added two more assertions, compared to listing 11.3. The lines added are highlighted. (Restaurant/0ab2792/Restaurant.RestApi.Tests/ReservationsTests.cs)
Assert.Equal( HttpStatusCode.InternalServerError, response.StatusCode); Assert.NotNull(response.Content); var content = await response.Content.ReadAsStringAsync(); Assert.Contains( "tables", content, StringComparison.OrdinalIgnoreCase);These two examples are taken from a test case that verifies what happens if you try to overbook the restaurant. In listing 11.3, the test only verifies that the HTTP response is
500 Internal Server Error. The two new assertions verify that the HTTP response includes a clue to what might be wrong, such as the messageNo tables available.I often run into programmers who’ve learned that a test method may only contain a single assertion; that having multiple assertions is called Assertion Roulette. I find that too simplistic. You can view appending new assertions as a strengthening of postconditions. With the assertion in listing 11.3 any
500 Internal Server Errorresponse would pass the test. That would include a 'real' error, such as a missing connection string. This could lead to false negatives, since a general error could go unnoticed.Adding more assertions strengthens the postconditions. Any old
500 Internal Server Errorwill no longer do. The HTTP response must also come with content, and that content must, at least, contain the string"tables".This strikes me as reminiscent of the Liskov Substitution Principle. There are many ways to express it, but in one variation, we say that subtypes may weaken preconditions and strengthen postconditions, but not the other way around. You can think of of subtyping as an ordering, and you can think of time in the same way, as illustrated by figure 11.1. Just like a subtype depends on its supertype, a point in time 'depends' on previous points in time. Going forward in time, you’re allowed to strengthen the postconditions of a system, just like a subtype is allowed to strengthen the postcondition of a supertype.
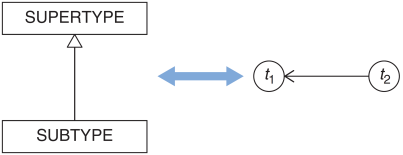
Figure 11.1 A type hierarchy forms a directed graph, as indicated by the arrow from subtype to supertype. Time, too, forms a directed graph, as indicated by the arrow from t2 to t1. Both present a way to order elements.
Think of it another way, adding new tests or assertions is fine; deleting tests or assertions would weaken the guarantees of the system. You probably don’t want that; herein lie regression bugs and breaking changes.
The book leaves it there, but I find it worthwhile to expand on that thought.
Function evolution over time #
As in the previous articles about x as a profunctor, let's first view 'a system' as a function. As I've repeatedly suggested, with sufficient imagination, every operation looks like a function. Even an HTTP POST request, as suggested in the above test snippets, can be considered a function, albeit one with the IO effect.
You can envision a function as a pipe. In previous articles, I've drawn horizontal pipes, with data flowing from left to right, but we can also rotate them 90° and place them on a timeline:
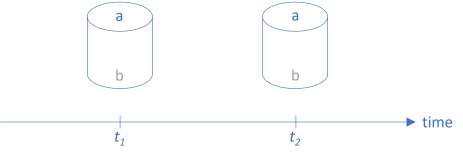
As usually depicted in Western culture, time moves from left to right. In a stable system, functions don't change: The function at t1 is equal to the function at t2.
The function in the illustration takes values belonging to the set a as input and returns values belonging to the set b as output. A bit more formally, we can denote the function as having the type a -> b.
We can view the passing of time as a translation of the function a -> b at t1 to a -> b at t2. If we just leave the function alone (as implied by the above figure), it corresponds to mapping the function with the identity function.
Clients that rely on the function are calling it by supplying input values from the set a. In return, they receive values from the set b. As already discussed in the article about Postel's law as a profunctor, we can illustrate such a fit between client and function as snugly fitting pipes:
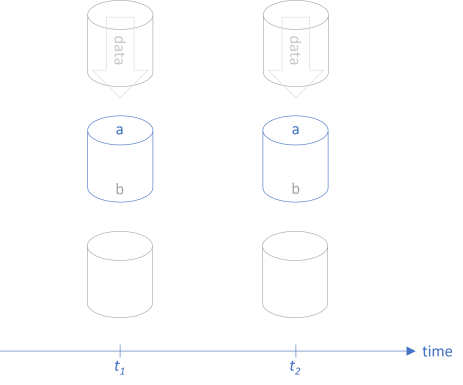
As long as the clients keep supplying elements from a and expecting elements from b in return, the function remains compatible.
If we have to change the function, which kind of change will preserve compatibility?
We can make the function accept a wider set of input, and let it return narrower set of output:
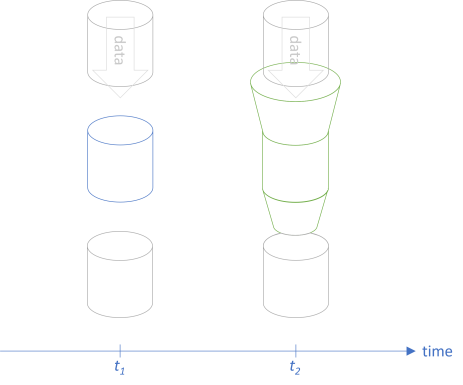
This will not break any existing clients, because they'll keep calling the function with a input and expecting b output values. The drawing is similar to the drawings from the articles on Postel's law as a profunctor and The Liskov Substitution Principle as a profunctor. It seems reasonable to consider backwards compatibility in the same light.
Profunctor #
Consider backwards compatible function evolution as a mapping of a function a -> b at t1 to a' -> b' at t2.
What rules should we institute for this mapping?
In order for this translation to be backwards compatible, we must be able to translate the larger input set a' to a; that is: a' -> a. That's the top flange in the above figure.
Likewise, we must be able to translate the original output set b to the smaller b': b -> b'. That's the bottom nozzle in the above figure.
Thus, armed with the two functions a' -> a and b -> b', we can translate a -> b at t1 to a' -> b' at t2 in a way that preserves backwards compatibility. More formally:
(a' -> a) -> (b -> b') -> (a -> b) -> (a' -> b')
This is exactly the definition of dimap for the Reader profunctor!
Arrow directions #
That's why I wrote as I did in Code That Fits in Your Head. The direction of the arrows in the book's figure 11.1 may seem counter-intuitive, but I had them point in that direction because that's how most readers are used to see supertypes and subtypes depicted.
When thinking of concepts such as Postel's law, it may be more intuitive to think of the profunctor as a mapping from a formal specification a -> b to the more robust implementation a' -> b'. That is, the arrow would point in the other direction.
Likewise, when we think of the Liskov Substitution Principle as rule about how to lawfully derive subtypes from supertypes, again we have a mapping from the supertype a -> b to the subtype a' -> b'. Again, the arrow direction goes from supertype to subtype - that is, in the opposite direction from the book's figure 11.1.
This now also better matches how we intuitively think about time, as flowing from left to right. The arrow, again, goes from t1 to t2.
Most of the time, the function doesn't change as time goes by. This corresponds to the mapping dimap id id - that is, applying the identity function to the mapping.
Implications for tests #
Consider the test snippets shown at the start of the article. When you add test cases to an existing test, you increase the size of the input set. Granted, unit test inputs are only samples of the entire input set, but it's still clear that adding a test case increases the input set. Thus, we can view such an edit as a mapping a -> a', where a ⊂ a'.
Likewise, when you add more assertions to an existing set of assertions, you add extra constraints. Adding an assertion implies that the test must pass all of the previous assertions, as well as the new one. That's a Boolean and, which implies a narrowing of the allowed result set (unless the new assertion is a tautological assertion). Thus, we can view adding an assertion as a mapping b -> b', where b' ⊂ b.
This is why it's okay to add more test cases, and more assertions, to an existing test, whereas you should be weary of the opposite: It may imply (or at least allow) a breaking change.
Conclusion #
As Michael Feathers observed, Postel's law seems universal. That's one way to put it.
Another way to view it is that Postel's law is a formulation of a kind of profunctor. And it certainly seems as though profunctors pop up here, there, and everywhere, once you start looking for that idea.
We can think of the Liskov Substitution Principle as a profunctor, and backwards compatibility as well. It seems reasonable enough: In order to stay backwards compatible, a function can become more tolerant of input, or more conservative in what it returns. Put another way: Contravariant in input, and covariant in output.
