Extracting data from a small CSV file with Haskell by Mark Seemann
Statically typed languages are also good for ad-hoc scripting.
This article is part of a short series of articles that compares ad-hoc scripting in Haskell with solving the same problem in Python. The introductory article describes the problem to be solved, so here I'll jump straight into the Haskell code. In the next article I'll give a similar walkthrough of my Python script.
Getting started #
When working with Haskell for more than a few true one-off expressions that I can type into GHCi (the Haskell REPL), I usually create a module file. Since I'd been asked to crunch some data, and I wasn't feeling very imaginative that day, I just named the module (and the file) Crunch. After some iterative exploration of the problem, I also arrived at a set of imports:
module Crunch where import Data.List (sort) import qualified Data.List.NonEmpty as NE import Data.List.Split import Control.Applicative import Control.Monad import Data.Foldable
As we go along, you'll see where some of these fit in.
Reading the actual data file, however, can be done with just the Haskell Prelude:
inputLines = words <$> readFile "survey_data.csv"
Already now, it's possible to load the module in GHCi and start examining the data:
ghci> :l Crunch.hs [1 of 1] Compiling Crunch ( Crunch.hs, interpreted ) Ok, one module loaded. ghci> length <$> inputLines 38
Looks good, but reading a text file is hardly the difficult part. The first obstacle, surprisingly, is to split comma-separated values into individual parts. For some reason that I've never understood, the Haskell base library doesn't even include something as basic as String.Split from .NET. I could probably hack together a function that does that, but on the other hand, it's available in the split package; that explains the Data.List.Split import. It's just a bit of a bother that one has to pull in another package only to do that.
Grades #
Extracting all the grades are now relatively easy. This function extracts and parses a grade from a single line:
grade :: Read a => String -> a grade line = read $ splitOn "," line !! 2
It splits the line on commas, picks the third element (zero-indexed, of course, so element 2), and finally parses it.
One may experiment with it in GHCi to get an impression that it works:
ghci> fmap grade <$> inputLines :: IO [Int] [2,2,12,10,4,12,2,7,2,2,2,7,2,7,2,4,2,7,4,7,0,4,0,7,2,2,2,2,2,2,4,4,2,7,4,0,7,2]
This lists all 38 expected grades found in the data file.
In the introduction article I spent some time explaining how languages with strong type inference don't need type declarations. This makes iterative development easier, because you can fiddle with an expression until it does what you'd like it to do. When you change an expression, often the inferred type changes as well, but there's no programmer overhead involved with that. The compiler figures that out for you.
Even so, the above grade function does have a type annotation. How does that gel with what I just wrote?
It doesn't, on the surface, but when I was fiddling with the code, there was no type annotation. The Haskell compiler is perfectly happy to infer the type of an expression like
grade line = read $ splitOn "," line !! 2
The human reader, however, is not so clever (I'm not, at least), so once a particular expression settles, and I'm fairly sure that it's not going to change further, I sometimes add the type annotation to aid myself.
When writing this, I was debating the didactics of showing the function with the type annotation, against showing it without it. Eventually I decided to include it, because it's more understandable that way. That decision, however, prompted this explanation.
Binomial choice #
The next thing I needed to do was to list all pairs from the data file. Usually, when I run into a problem related to combinations, I reach for applicative composition. For example, to list all possible combinations of the first three primes, I might do this:
ghci> liftA2 (,) [2,3,5] [2,3,5] [(2,2),(2,3),(2,5),(3,2),(3,3),(3,5),(5,2),(5,3),(5,5)]
You may now protest that this is sampling with replacement, whereas the task is to pick two different rows from the data file. Usually, when I run into that requirement, I just remove the ones that pick the same value twice:
ghci> filter (uncurry (/=)) $ liftA2 (,) [2,3,5] [2,3,5] [(2,3),(2,5),(3,2),(3,5),(5,2),(5,3)]
That works great as long as the values are unique, but what if that's not the case?
ghci> liftA2 (,) "foo" "foo"
[('f','f'),('f','o'),('f','o'),('o','f'),('o','o'),('o','o'),('o','f'),('o','o'),('o','o')]
ghci> filter (uncurry (/=)) $ liftA2 (,) "foo" "foo"
[('f','o'),('f','o'),('o','f'),('o','f')]
This removes too many values! We don't want the combinations where the first o is paired with itself, or when the second o is paired with itself, but we do want the combination where the first o is paired with the second, and vice versa.
This is relevant because the data set turns out to contain identical rows. Thus, I needed something that would deal with that issue.
Now, bear with me, because it's quite possible that what i did do isn't the simplest solution to the problem. On the other hand, I'm reporting what I did, and how I used Haskell to solve a one-off problem. If you have a simpler solution, please leave a comment.
You often reach for the tool that you already know, so I used a variation of the above. Instead of combining values, I decided to combine row indices instead. This meant that I needed a function that would produce the indices for a particular list:
indices :: Foldable t => t a -> [Int] indices f = [0 .. length f - 1]
Again, the type annotation came later. This just produces sequential numbers, starting from zero:
ghci> indices <$> inputLines [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20, 21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]
Such a function hovers just around the Fairbairn threshold; some experienced Haskellers would probably just inline it.
Since row numbers (indices) are unique, the above approach to binomial choice works, so I also added a function for that:
choices :: Eq a => [a] -> [(a, a)] choices = filter (uncurry (/=)) . join (liftA2 (,))
Combined with indices I can now enumerate all combinations of two rows in the data set:
ghci> choices . indices <$> inputLines [(0,1),(0,2),(0,3),(0,4),(0,5),(0,6),(0,7),(0,8),(0,9),...
I'm only showing the first ten results here, because in reality, there are 1406 such pairs.
Perhaps you think that all of this seems quite elaborate, but so far it's only four lines of code. The reason it looks like more is because I've gone to some lengths to explain what the code does.
Sum of grades #
The above combinations are pairs of indices, not values. What I need is to use each index to look up the row, from the row get the grade, and then sum the two grades. The first parts of that I can accomplish with the grade function, but I need to do if for every row, and for both elements of each pair.
While tuples are Functor instances, they only map over the second element, and that's not what I need:
ghci> rows = ["foo", "bar", "baz"] ghci> fmap (rows!!) <$> [(0,1),(0,2)] [(0,"bar"),(0,"baz")]
While this is just a simple example that maps over the two pairs (0,1) and (0,2), it illustrates the problem: It only finds the row for each tuple's second element, but I need it for both.
On the other hand, a type like (a, a) gives rise to a functor, and while a wrapper type like that is not readily available in the base library, defining one is a one-liner:
newtype Pair a = Pair { unPair :: (a, a) } deriving (Eq, Show, Functor)
This enables me to map over pairs in one go:
ghci> unPair <$> fmap (rows!!) <$> Pair <$> [(0,1),(0,2)]
[("foo","bar"),("foo","baz")]
This makes things a little easier. What remains is to use the grade function to look up the grade value for each row, then add the two numbers together, and finally count how many occurrences there are of each:
sumGrades ls = liftA2 (,) NE.head length <$> NE.group (sort (uncurry (+) . unPair . fmap (grade . (ls !!)) . Pair <$> choices (indices ls)))
You'll notice that this function doesn't have a type annotation, but we can ask GHCi if we're curious:
ghci> :t sumGrades sumGrades :: (Ord a, Num a, Read a) => [String] -> [(a, Int)]
This enabled me to get a count of each sum of grades:
ghci> sumGrades <$> inputLines [(0,6),(2,102),(4,314),(6,238),(7,48),(8,42),(9,272),(10,6), (11,112),(12,46),(14,138),(16,28),(17,16),(19,32),(22,4),(24,2)]
The way to read this is that the sum 0 occurs six times, 2 appears 102 times, etc.
There's one remaining task to accomplish before we can produce a PMF of the sum of grades: We need to enumerate the range, because, as it turns out, there are sums that are possible, but that don't appear in the data set. Can you spot which ones?
Using tools already covered, it's easy to enumerate all possible sums:
ghci> import Data.List ghci> sort $ nub $ (uncurry (+)) <$> join (liftA2 (,)) [-3,0,2,4,7,10,12] [-6,-3,-1,0,1,2,4,6,7,8,9,10,11,12,14,16,17,19,20,22,24]
The sums -6, -3, -1, and more, are possible, but don't appear in the data set. Thus, in the PMF for two randomly picked grades, the probability that the sum is -6 is 0. On the other hand, the probability that the sum is 0 is 6/1406 ~ 0.004267, and so on.
Difference of experience levels #
The other question posed in the assignment was to produce the PMF for the absolute difference between two randomly selected students' experience levels.
Answering that question follows the same mould as above. First, extract experience level from each data row, instead of the grade:
experience :: Read a => String -> a experience line = read $ splitOn "," line !! 3
Since I was doing an ad-hoc script, I just copied the grade function and changed the index from 2 to 3. Enumerating the experience differences were also a close copy of sumGrades:
diffExp ls = liftA2 (,) NE.head length <$> NE.group (sort (abs . uncurry (-) . unPair . fmap (experience . (ls !!)) . Pair <$> choices (indices ls)))
Running it in the REPL produces some other numbers, to be interpreted the same way as above:
ghci> diffExp <$> inputLines [(0,246),(1,472),(2,352),(3,224),(4,82),(5,24),(6,6)]
This means that the difference 0 occurs 246 times, 1 appears 472 times, and so on. From those numbers, it's fairly simple to set up the PMF.
Figures #
Another part of the assignment was to produce plots of both PMFs. I don't know how to produce figures with Haskell, and since the final results are just a handful of numbers each, I just copied them into a text editor to align them, and then pasted them into Excel to produce the figures there.
Here's the PMF for the differences:
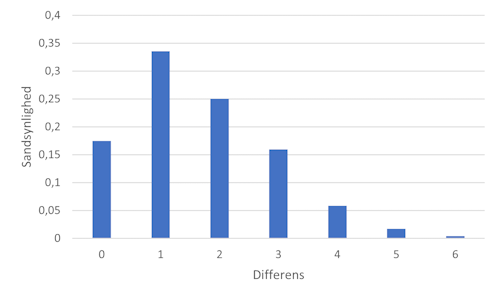
I originally created the figure with Danish labels. I'm sure that you can guess what differens means, and sandsynlighed means probability.
Conclusion #
In this article you've seen the artefacts of an ad-hoc script to extract and analyze a small data set. While I've spent quite a few words to explain what's going on, the entire Crunch module is only 34 lines of code. Add to that a few ephemeral queries done directly in GHCi, but never saved to a file. It's been some months since I wrote the code, but as far as I recall, it took me a few hours all in all.
If you do stuff like this every day, you probably find that appalling, but data crunching isn't really my main thing.
Is it quicker to do it in Python? Not for me, it turns out. It also took me a couple of hours to repeat the exercise in Python.
