ploeh blog danish software design
EnsureSuccessStatusCode as an assertion
It finally dawned on me that EnsureSuccessStatusCode is a fine test assertion.
Okay, I admit that sometimes I can be too literal and rigid in my thinking. At least as far back as 2012 I've been doing outside-in TDD against self-hosted HTTP APIs. When you do that, you'll regularly need to verify that an HTTP response is successful.
Assert equality #
You can, of course, write an assertion like this:
Assert.Equal(HttpStatusCode.OK, response.StatusCode);
If the assertion fails, it'll produce a comprehensible message like this:
Assert.Equal() Failure Expected: OK Actual: BadRequest
What's not to like?
Assert success #
The problem with testing strict equality in this context is that it's often too narrow a definition of success.
You may start by returning 200 OK as response to a POST request, but then later evolve the API to return 201 Created or 202 Accepted. Those status codes still indicate success, and are typically accompanied by more information (e.g. a Location header). Thus, evolving a REST API from returning 200 OK to 201 Created or 202 Accepted isn't a breaking change.
It does, however, break the above assertion, which may now fail like this:
Assert.Equal() Failure Expected: OK Actual: Created
You could attempt to fix this issue by instead verifying IsSuccessStatusCode:
Assert.True(response.IsSuccessStatusCode);
That permits the API to evolve, but introduces another problem.
Legibility #
What happens when an assertion against IsSuccessStatusCode fails?
Assert.True() Failure Expected: True Actual: False
That's not helpful. At least, you'd like to know which other status code was returned instead. You can address that concern by using an overload to Assert.True (most unit testing frameworks come with such an overload):
Assert.True( response.IsSuccessStatusCode, $"Actual status code: {response.StatusCode}.");
This produces more helpful error messages:
Actual status code: BadRequest. Expected: True Actual: False
Granted, the Expected: True, Actual: False lines are redundant, but at least the information you care about is there; in this example, the status code was 400 Bad Request.
Conciseness #
That's not bad. You can use that Assert.True overload everywhere you want to assert success. You can even copy and paste the code, because it's an idiom that doesn't change. Still, since I like to stay within 80 characters line width, this little phrase takes up three lines of code.
Surely, a helper method can address that problem:
internal static void AssertSuccess(this HttpResponseMessage response) { Assert.True( response.IsSuccessStatusCode, $"Actual status code: {response.StatusCode}."); }
I can now write a one-liner as an assertion:
response.AssertSuccess();
What's not to like?
Carrying coals to Newcastle #
If you're already familiar with the HttpResponseMessage class, you may have been reading this far with some frustration. It already comes with a method called EnsureSuccessStatusCode. Why not just use that instead?
response.EnsureSuccessStatusCode();
As long as the response status code is in the 200 range, this method call succeeds, but if not, it throws an exception:
Response status code does not indicate success: 400 (Bad Request).
That's exactly the information you need.
I admit that I can sometimes be too rigid in my thinking. I've known about this method for years, but I never thought of it as a unit testing assertion. It's as if there's a category in my programming brain that's labelled unit testing assertions, and it only contains methods that originate from unit testing.
I even knew about Debug.Assert, so I knew that assertions also exist outside of unit testing. That assertion isn't suitable for unit testing, however, so I never included it in my category of unit testing assertions.
The EnsureSuccessStatusCode method doesn't have assert in its name, but it behaves just like a unit testing assertion: it throws an exception with a useful error message if a criterion is not fulfilled. I just never thought of it as useful for unit testing purposes because it's part of 'production code'.
Conclusion #
The built-in EnsureSuccessStatusCode method is fine for unit testing purposes. Who knows, perhaps other class libraries contain similar assertion methods, although they may be hiding behind names that don't include assert. Perhaps your own production code contains such methods. If so, they can double as unit testing assertions.
I've been doing test-driven development for close to two decades now, and one of many consistent experiences is this:
- In the beginning of a project, the unit tests I write are verbose. This is natural, because I'm still getting to know the domain.
- After some time, I begin to notice patterns in my tests, so I refactor them. I introduce helper APIs in the test code.
- Finally, I realise that some of those unit testing APIs might actually be useful in the production code too, so I move them over there.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
An XPath query for long methods
A filter for Visual Studio code metrics.
I consider it a good idea to limit the size of code blocks. Small methods are easier to troubleshoot and in general fit better in your head. When it comes to vertical size, however, the editors I use don't come with visual indicators like they do for horizontal size.
When you're in the midst of developing a feature, you don't want to be prevented from doing so by a tool that refuses to compile your code if methods get too long. On the other hand, it might be a good idea to regularly run a tool over your code base to identify which methods are getting too long.
With Visual Studio you can calculate code metrics, which include a measure of the number of lines of code for each method. One option produces an XML file, but if you have a large code base, those XML files are big.
The XML files typically look like this:
<?xml version="1.0" encoding="utf-8"?> <CodeMetricsReport Version="1.0"> <Targets> <Target Name="Restaurant.RestApi.csproj"> <Assembly Name="Ploeh.Samples.Restaurants.RestApi, ..."> <Metrics> <Metric Name="MaintainabilityIndex" Value="87" /> <Metric Name="CyclomaticComplexity" Value="537" /> <Metric Name="ClassCoupling" Value="208" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="3188" /> <Metric Name="ExecutableLines" Value="711" /> </Metrics> <Namespaces> <Namespace Name="Ploeh.Samples.Restaurants.RestApi"> <Metrics> <Metric Name="MaintainabilityIndex" Value="87" /> <Metric Name="CyclomaticComplexity" Value="499" /> <Metric Name="ClassCoupling" Value="204" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="3100" /> <Metric Name="ExecutableLines" Value="701" /> </Metrics> <Types> <NamedType Name="CalendarController"> <Metrics> <Metric Name="MaintainabilityIndex" Value="73" /> <Metric Name="CyclomaticComplexity" Value="14" /> <Metric Name="ClassCoupling" Value="34" /> <Metric Name="DepthOfInheritance" Value="1" /> <Metric Name="SourceLines" Value="190" /> <Metric Name="ExecutableLines" Value="42" /> </Metrics> <Members> <Method Name="Task<ActionResult> CalendarController.Get(..."> <Metrics> <Metric Name="MaintainabilityIndex" Value="64" /> <Metric Name="CyclomaticComplexity" Value="2" /> <Metric Name="ClassCoupling" Value="12" /> <Metric Name="SourceLines" Value="28" /> <Metric Name="ExecutableLines" Value="7" /> </Metrics> </Method> <!--Much more data goes here--> </Members> </NamedType> </Types> </Namespace> </Namespaces> </Assembly> </Target> </Targets> </CodeMetricsReport>
How can you filter such a file to find only those methods that are too long?
That sounds like a job for XPath. I admit, though, that I use XPath only rarely. While the general idea of the syntax is easy to grasp, it has enough subtle pitfalls that it's not that easy to use, either.
Partly for my own benefit, and partly for anyone else who might need it, here's an XPath query that looks for long methods:
//Members/child::*[Metrics/Metric[@Value > 24 and @Name = "SourceLines"]]
This query looks for methods longer that 24 lines of code. If you don't agree with that threshold you can always change it to another value. You can also change @Name to look for CyclomaticComplexity or one of the other metrics.
Given the above XML metrics report, the XPath filter would select (among other members) the CalendarController.Get method, because it has 28 lines of source code. It turns out, though, that the filter produces some false positives. The method in question is actually fine:
/* This method loads a year's worth of reservations in order to segment * them all. In a realistic system, this could be quite stressful for * both the database and the web server. Some of that concern can be * addressed with an appropriate HTTP cache header and a reverse proxy, * but a better solution would be a CQRS-style architecture where the * calendars get re-rendered as materialised views in a background * process. That's beyond the scope of this example code base, though. */ [ResponseCache(Duration = 60)] [HttpGet("restaurants/{restaurantId}/calendar/{year}")] public async Task<ActionResult> Get(int restaurantId, int year) { var restaurant = await RestaurantDatabase .GetRestaurant(restaurantId).ConfigureAwait(false); if (restaurant is null) return new NotFoundResult(); var period = Period.Year(year); var days = await MakeDays(restaurant, period) .ConfigureAwait(false); return new OkObjectResult( new CalendarDto { Name = restaurant.Name, Year = year, Days = days }); }
That method only has 18 lines of actual source code, from the beginning of the method declaration to the closing bracket. Visual Studio's metrics calculator, however, also counts the attributes and the comments.
In general, I only add comments when I want to communicate something that I can't express as a type or a method name, so in this particular code base, it's not much of an issue. If you consistently adorn every method with doc comments, on the other hand, you may need to perform some pre-processing on the source code before you calculate the metrics.
We need young programmers; we need old programmers
The software industry loves young people, but old-timers serve an important purpose, too.
Our culture idolises youth. There's several reasons for this, I believe. Youth seems synonymous with vigour, strength, beauty, and many other desirable qualities. The cynical perspective is that young people, while rebellious, also tend to be easy to manipulate, if you know which buttons to push. A middle-aged man like me isn't susceptible to the argument that I should buy a particular pair of Nike shoes because they're named after Michael Jordan, but for a while, one pair wasn't enough for my teenage daughter.
In intellectual pursuits (like software development), youth is often extolled as the source of innovation. You're often confronted with examples like that of Évariste Galois, who made all his discoveries before turning 21. Ada Lovelace was around 28 years when she produced what is considered the 'first computer program'. Alan Turing was 24 when he wrote On Computable Numbers, with an Application to the Entscheidungsproblem.
Clearly, young age is no detriment to making ground-breaking contributions. It has even become folklore that everyone past the age of 35 is a has-been whose only chance at academic influence is to write a textbook.
The story of the five monkeys #
You may have seen a story called the five monkeys experiment. It's most likely a fabrication, but it goes like this:
A group of scientists placed five monkeys in a cage, and in the middle, a ladder with bananas on the top. Every time a monkey went up the ladder, the scientists soaked the rest of the monkeys with cold water. After a while, every time a monkey went up the ladder, the others would beat it up.
After some time, none of the monkeys dared go up the ladder regardless of the temptation. The scientists then substituted one of the monkeys with a new one, who'd immediately go for the bananas, only to be beaten up by the others. After several beatings, the new member learned not to climb the ladder even though it never knew why.
A second monkey was substituted and the same occurred. The first monkey participated in beating the second. A third monkey was exchanged and the story repeated. The fourth was substituted and the beating was repeated. Finally the fifth monkey was replaced.
Left was a group of five monkeys who, even though they never received a cold shower, continued to beat up any monkey who attempted to climb the ladder. If it was possible to ask the monkeys why they would beat up all who attempted to go up the ladder, the answer would probably be:
"That's how we do things here."
While the story is probably just that: a story, it tells us something about the drag induced by age and experience. If you've been in the business for decades, you've seen numerous failed attempts at something you yourself tried when you were young. You know that it can't be done.
Young people don't know that a thing can't be done. If they can avoid the monkey-beating, they'll attempt the impossible.
Changing circumstances #
Is attempting the impossible a good idea?
In general, no, because it's... impossible. There's a reason older people tell young people that a thing can't be done. It's not just because they're stodgy conservatives who abhor change. It's because they see the effort as wasteful. Perhaps they're even trying to be kind, guiding young people off a path where only toil and disappointment is to be found.
What old people don't realise is that sometimes, circumstances change.
What was impossible twenty years ago may not be impossible today. We see this happening in many fields. Producing a commercially viable electric car was impossible for decades, until, with the advances made in battery technology, it became possible.
Technology changes rapidly in software development. People trying something previously impossible may find that it's possible today. Once, if you had lots of data, you had to store it in fully normalised form, because storage was expensive. For a decade, relational databases were the only game in town. Then circumstances changed. Storage became cheaper, and a new movement of NoSQL storage emerged. What was before impossible became possible.
Older people often don't see the new opportunities, because they 'know' that some things are impossible. Young people push the envelope driven by a combination of zest and ignorance. Most fail, but a few succeed.
Lottery of the impossible #
I think of this process as a lottery. Imagine that every impossible thing is a red ball in an urn. Every young person who tries the impossible draws a random ball from the urn.
The urn contains millions of red balls, but every now and then, one of them turns green. You don't know which one, but if you draw it, it represents something that was previously impossible which has now become possible.
This process produces growth, because once discovered, the new and better way of doing things can improve society in general. Occasionally, the young discoverer may even gain some fame and fortune.
It seems wasteful, though. Most people who attempt the impossible will reach the predictable conclusion. What was deemed impossible was, indeed, impossible.
When I'm in a cynical mood, I don't think that it's youth in itself that is the source of progress. It's just the law of large numbers applied. If there's a one in million chance that something will succeed, but ten million people attempt it, it's only a matter of time before one succeeds.
Society at large can benefit from the success of the few, but ten million people still wasted their efforts.
We need the old, too #
If you accept the argument that young people are more likely to try the impossible, we need the young people. Do we need the old people?
I'm turning fifty in 2020. You may consider that old, but I expect to work for many more years. I don't know if the software industry needs fifty-year-olds, but that's not the kind of old I have in mind. I'm thinking of people who have retired, or are close to retirement.
In our youth-glorifying culture, we tend to dismiss the opinion and experiences of old people. Oh, well, it's just a codgy old man (or woman), we'll say.
We ignore the experience of the old, because we believe that they haven't been keeping up with times. Their experiences don't apply to us, because we live under new circumstance. Well, see above.
I'm not advocating that we turn into a gerontocracy that venerates our elders solely because of their age. Again, according to the law of large numbers, some people live to old age. There need not be any correlation between survivors and wisdom.
We need the old to tell us the truth, because they have little to lose.
Nothing to lose #
In the last couple of years, I've noticed a trend. A book comes out, exposing the sad state of affairs in some organisation. This has happened regularly in Denmark, where I live. One book may expose the deplorable conditions of the Danish tax authorities, one may describe the situation in the ministry of defence, one criticises the groupthink associated with the climate crisis, and so on.
Invariably, it turns out that the book is written by a professor emeritus or a retired department head.
I don't think that these people, all of a sudden, had an epiphany after they retired. They knew all about the rot in the system they were part of, while they were part of it, but they've had too much to lose. You could argue that they should have said something before they retired, but that requires a moral backbone we can't expect most people to have.
When people retire, the threat of getting fired disappears. Old people can speak freely to a degree most other people can't.
Granted, many may simply use that freedom to spew bile or shout Get off my lawn!, but many are in the unique position to reveal truths no-one else dare speak. Many are, perhaps, just bitter, but some may possess knowledge that they are in a unique position to reveal.
When that grumpy old guy on Twitter writes something that makes you uncomfortable, consider this: he may still be right.
Being unreasonable #
In a way, you could say that we need young and old people for the same fundamental reason. Not all of them, but enough of them, are in a position to be unreasonable.
Young people and old people are unreasonable in each their own way, and we need both."The reasonable man adapts himself to the world: the unreasonable one persists in trying to adapt the world to himself. Therefore all progress depends on the unreasonable man."
Conclusion #
We need young people in the software development industry. Because of their vigour and inexperience, they'll push the envelope. Most will fail to do the impossible, but a few succeed.
This may seem like a cynical view, but we've all been young, and most of us have been through such a phase. It's like a rite of passage, and even if you fail to make your mark on the world, you're still likely to have learned a lot.
We need old people because they're in a position to speak truth to the world. Notice that I didn't make my argument about the experience of old-timers. Actually, I find that valuable as well, but that's the ordinary argument: Listen to old people, because they have experience and wisdom.
Some of them do, at least.
I didn't make much out of that argument, because you already know it. There'd be no reason to write this essay if that was all I had to say. Old people have less on the line, so they can speak more freely. If someone you used to admire retires and all of a sudden starts saying or writing unpleasant and surprising things, there might be a good explanation, and it might be a good idea to pay attention.
Or maybe he or she is just bitter or going senile...
Add null check without brackets in Visual Studio
A Visual Studio tweak.
The most recent versions of Visual Studio have included many new Quick Actions, accessible with Ctrl + . or Alt + Enter. The overall feature has been around for some years, but the product group has been adding features at a good pace recently, it seems to me.
One feature has been around for at least a year: Add null check. In a default installation of Visual Studio, it looks like this:
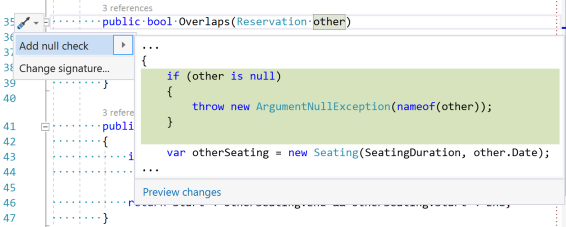
As the screen shot shows, it'll auto-generate a Guard Clause like this:
public bool Overlaps(Reservation other) { if (other is null) { throw new ArgumentNullException(nameof(other)); } var otherSeating = new Seating(SeatingDuration, other.Date); return Overlaps(otherSeating); }
Part of my personal coding style is that I don't use brackets for one-liners. This is partially motivated by the desire to save vertical space, since I try to keep methods as small as possible. Some people worry that not using brackets for one-liners makes the code more vulnerable to defects, but I typically have automated regressions tests to keep an eye on correctness.
The above default behaviour of the Add null check Quick Action annoyed me because I had to manually remove the brackets. It's one of those things that annoy you a little, but not enough that you throw aside what you're doing to figure out if you can change the situation.
Until it annoyed me enough to investigate whether there was something I could do about it. It turns out to be easy to tweak the behaviour.
In Visual Studio 2019, go to Tools, Options, Text Editor, C#, Code Style, General and change the Prefer braces option to No:
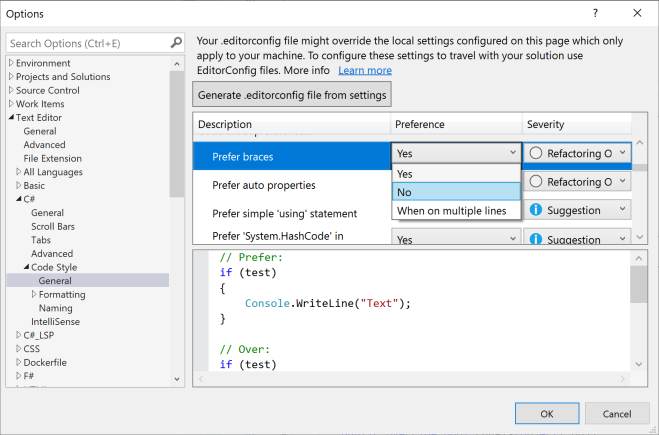
This changes the behaviour of the Add null check Quick Action:
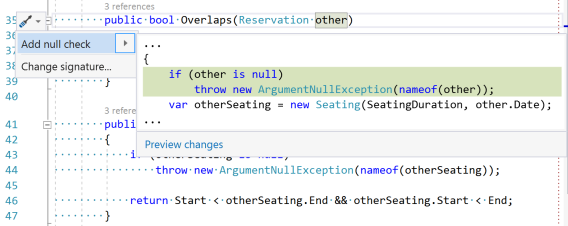
After applying the Quick Action, my code now looks like this:
public bool Overlaps(Reservation other) { if (other is null) throw new ArgumentNullException(nameof(other)); var otherSeating = new Seating(SeatingDuration, other.Date); return Overlaps(otherSeating); }
This better fits my preference.
Comments
The same should go for if's, switch's, try/catch and perhaps a few other things. While we are at it, spacing is also a good source for changing layout in code, e.g: decimal.Round( amount * 1.0000m, provider.Getdecimals( currency ) ) ).
When assigning parameters to fields, I like this one-line option for a null check:
_thing = thing ?? throw new ArgumentNullException(nameof(thing));.
How do you feel about it? You could even use a disard in your example:
_ = thing ?? throw new ArgumentNullException(nameof(thing));
James, thank you for writing. I'm aware of that option, but rarely use it in my examples. I try to write my example code in a way that they may also be helpful to Java developers, or programmers that use other C-based languages. Obviously, that concern doesn't apply if I discuss something specific to C#, but when I try to explain design patterns or low-level architecture, I try to stay away from language features exclusive to C#.
In other contexts, I might or might not use that language feature, but I admit that it jars me. I find that it's a 'clever' solution to something that's not much of a problem. The ?? operator is intended as a short-circuiting operator one can use to simplify variable assignment. Throwing on the right-hand side never assigns a value.
It's as though you would use the coalescing monoid to pick the left-hand side, but let the program fail on the right-hand side. In Haskell it would look like this:
x = thing <> undefined
The compiler infers that x has the same type as thing, e.g. Semigroup a => Maybe a. If thing, however, is Nothing, the expression crashes when evaluated.
While this compiles in Haskell, I consider it unidiomatic. It too blatantly advertises the existence of the so-called bottom value (⊥). We know it's there, but we prefer to pretend that it's not.
That line of reasoning is subjective, and if I find myself in a code base that uses ?? like you've shown, I'd try to fit in with that style. It doesn't annoy me that much, after all.
It's also shorter, I must admit that.
The above default behaviour of the Add null check Quick Action annoyed me because I had to manually remove the brackets. It's one of those things that annoy you a little, but not enough that you throw aside what you're doing to figure out if you can change the situation.
Until it annoyed me enough to investigate whether there was something I could do about it. It turns out to be easy to tweak the behaviour.
In Visual Studio 2019, go to Tools, Options, Text Editor, C#, Code Style, General and change the Prefer braces option to No:
You can do more than that. As suggested by Visual Studio in your second screenshot, you can (after making the change to not prefer braces) generate an .editorconfig file containing your coding style settings. Visual Studio will prompt you to save the file alongside your solution. If you do so, then any developer that opens these files with Visual Studio with also have your setting to not prefer braces. I wrote a short post about EditorConfig that contains more information.
Properties for all
Writing test cases for all possible input values.
I've noticed that programmers new to automated testing struggle with a fundamental task: how to come up with good test input?
There's plenty of design patterns that address that issue, including Test Data Builders. Still, test-driven development, when done right, gives you good feedback on the design of your API. I don't consider having to resort to Test Data Builder as much of a compromise, but still, it's even better if you can model the API in question so that it requires no redundant data.
Most business processes can be modelled as finite state machines. Once you've understood the problem well enough to enumerate the possible states, you can reverse-engineer an algebraic data type from that enumeration.
While the data carried around in the state machine may be unconstrained, the number of state and state transitions is usually limited. Model the states as enumerable values, and you can cover all input values with simple combinatorics.
Tennis states #
The Tennis kata is one of my favourite exercises. Just like a business process, it turns out that you can model the rules as a finite state machine. There's a state where both players have love, 15, 30, or 40 points (although both can't have 40 points; that state is called deuce); there's a state where a player has the advantage; and so on.
I've previously written about how to design the states of the Tennis kata with types, so here, I'll just limit myself to the few types that turn out to matter as test input: players and points.
Here are both types defined as Haskell sum types:
data Player = PlayerOne | PlayerTwo deriving (Eq, Show, Read, Enum, Bounded) data Point = Love | Fifteen | Thirty deriving (Eq, Show, Read, Enum, Bounded)
Notice that both are instances of the Enum and Bounded type classes. This means that it's possible to enumerate all values that inhabit each type. You can use that to your advantage when writing unit tests.
Properties for every value #
Most people think of property-based testing as something that involves a special framework such as QuickCheck, Hedgehog, or FsCheck. I often use such frameworks, but as I've written about before, sometimes enumerating all possible input values is simpler and faster than relying on randomly generated values. There's no reason to generate 100 random values of a type inhabited by only three values.
Instead, write properties for the entire domain of the function in question.
In Haskell, you can define a generic enumeration like this:
every :: (Enum a, Bounded a) => [a] every = [minBound .. maxBound]
I don't know why this function doesn't already exist in the standard library, but I suppose that most people just rely on the list comprehension syntax [minBound .. maxBound]...
With it you can write simple properties of the Tennis game. For example:
"Given deuce, when player wins, then that player has advantage" ~: do player <- every let actual = score Deuce player return $ Advantage player ~=? actual
Here I'm using inlined HUnit test lists. With the Tennis kata, it's easiest to start with the deuce case, because regardless of player, the new state is that the winning player has advantage. That's what that property asserts. Because of the do notation, the property produces a list of test cases, one for every player. There's only two Player values, so it's only two test cases.
The beauty of do notation (or the list monad in general) is that you can combine enumerations, for example like this:
"Given forty, when player wins ball, then that player wins the game" ~: do player <- every opp <- every let actual = score (Forty $ FortyData player opp) player return $ Game player ~=? actual
While player is a Player value, opp (Other Player's Point) is a Point value. Since there's two possible Player values and three possible Point values, the combination yields six test cases.
I've been doing the Tennis kata a couple of times using this approach. I've also done it in C# with xUnit.net, where the first test of the deuce state looks like this:
[Theory, MemberData(nameof(Player))] public void TransitionFromDeuce(IPlayer player) { var sut = new Deuce(); var actual = sut.BallTo(player); var expected = new Advantage(player); Assert.Equal(expected, actual); }
C# takes more ceremony than Haskell, but the idea is the same. The Player data source for the [Theory] is defined as an enumeration of the possible values:
public static IEnumerable<object[]> Player { get { yield return new object[] { new PlayerOne() }; yield return new object[] { new PlayerTwo() }; } }
All the times I've done the Tennis kata by fully exhausting the domain of the transition functions in question, I've arrived at 40 test cases. I wonder if that's the number of possible state transitions of the game, or if it's just an artefact of the way I've modelled it. I suspect the latter...
Conclusion #
You can sometimes enumerate all possible inputs to an API. Even if a function takes a Boolean value and a byte as input, the enumeration of all possible combinations is only 2 * 256 = 512 values. You computer will tear through all of those combinations faster than you can say random selection. Consider writing APIs that take algebraic data types as input, and writing properties that exhaust the domain of the functions in question.
Adding REST links as a cross-cutting concern
Use a piece of middleware to enrich a Data Transfer Object. An ASP.NET Core example.
When developing true REST APIs, you should use hypermedia controls (i.e. links) to guide clients to the resources they need. I've always felt that the code that generates these links tends to make otherwise readable Controller methods unreadable.
I'm currently experimenting with generating links as a cross-cutting concern. So far, I like it very much.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
Links from home #
Consider an online restaurant reservation system. When you make a GET request against the home resource (which is the only published URL for the API), you should receive a representation like this:
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/reservations"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/8"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/8/13"
}
]
}
As you can tell, my example just runs on my local development machine, but I'm sure that you can see past that. There's three calendar links that clients can use to GET the restaurant's calendar for the current day, month, or year. Clients can use these resources to present a user with a date picker or a similar user interface so that it's possible to pick a date for a reservation.
When a client wants to make a reservation, it can use the URL identified by the rel (relationship type) "urn:reservations" to make a POST request.
Link generation as a Controller responsibility #
I first wrote the code that generates these links directly in the Controller class that serves the home resource. It looked like this:
public IActionResult Get() { var links = new List<LinkDto>(); links.Add(Url.LinkToReservations()); if (enableCalendar) { var now = DateTime.Now; links.Add(Url.LinkToYear(now.Year)); links.Add(Url.LinkToMonth(now.Year, now.Month)); links.Add(Url.LinkToDay(now.Year, now.Month, now.Day)); } return Ok(new HomeDto { Links = links.ToArray() }); }
That doesn't look too bad, but 90% of the code is exclusively concerned with generating links. (enableCalendar, by the way, is a feature flag.) That seems acceptable in this special case, because there's really nothing else the home resource has to do. For other resources, the Controller code might contain some composition code as well, and then all the link code starts to look like noise that makes it harder to understand the actual purpose of the Controller method. You'll see an example of a non-trivial Controller method later in this article.
It seemed to me that enriching a Data Transfer Object (DTO) with links ought to be a cross-cutting concern.
LinksFilter #
In ASP.NET Core, you can implement cross-cutting concerns with a type of middleware called IAsyncActionFilter. I added one called LinksFilter:
internal class LinksFilter : IAsyncActionFilter { private readonly bool enableCalendar; public IUrlHelperFactory UrlHelperFactory { get; } public LinksFilter( IUrlHelperFactory urlHelperFactory, CalendarFlag calendarFlag) { UrlHelperFactory = urlHelperFactory; enableCalendar = calendarFlag.Enabled; } public async Task OnActionExecutionAsync( ActionExecutingContext context, ActionExecutionDelegate next) { var ctxAfter = await next().ConfigureAwait(false); if (!(ctxAfter.Result is OkObjectResult ok)) return; var url = UrlHelperFactory.GetUrlHelper(ctxAfter); switch (ok.Value) { case HomeDto homeDto: AddLinks(homeDto, url); break; case CalendarDto calendarDto: AddLinks(calendarDto, url); break; default: break; } } // ...
There's only one method to implement. If you want to run some code after the Controllers have had their chance, you invoke the next delegate to get the resulting context. It should contain the response to be returned. If Result isn't an OkObjectResult there's no content to enrich with links, so the method just returns.
Otherwise, it switches on the type of the ok.Value and passes the DTO to an appropriate helper method. Here's the AddLinks overload for HomeDto:
private void AddLinks(HomeDto dto, IUrlHelper url) { if (enableCalendar) { var now = DateTime.Now; dto.Links = new[] { url.LinkToReservations(), url.LinkToYear(now.Year), url.LinkToMonth(now.Year, now.Month), url.LinkToDay(now.Year, now.Month, now.Day) }; } else { dto.Links = new[] { url.LinkToReservations() }; } }
You can probably recognise the implemented behaviour from before, where it was implemented in the Get method. That method now looks like this:
public ActionResult Get() { return new OkObjectResult(new HomeDto()); }
That's clearly much simpler, but you probably think that little has been achieved. After all, doesn't this just move some code from one place to another?
Yes, that's the case in this particular example, but I wanted to start with an example that was so simple that it highlights how to move the code to a filter. Consider, then, the following example.
A calendar resource #
The online reservation system enables clients to navigate its calendar to look up dates and time slots. A representation might look like this:
{
"links": [
{
"rel": "previous",
"href": "http://localhost:53568/calendar/2020/8/12"
},
{
"rel": "next",
"href": "http://localhost:53568/calendar/2020/8/14"
}
],
"year": 2020,
"month": 8,
"day": 13,
"days": [
{
"links": [
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/8"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/8/13"
}
],
"date": "2020-08-13",
"entries": [
{
"time": "18:00:00",
"maximumPartySize": 10
},
{
"time": "18:15:00",
"maximumPartySize": 10
},
{
"time": "18:30:00",
"maximumPartySize": 10
},
{
"time": "18:45:00",
"maximumPartySize": 10
},
{
"time": "19:00:00",
"maximumPartySize": 10
},
{
"time": "19:15:00",
"maximumPartySize": 10
},
{
"time": "19:30:00",
"maximumPartySize": 10
},
{
"time": "19:45:00",
"maximumPartySize": 10
},
{
"time": "20:00:00",
"maximumPartySize": 10
},
{
"time": "20:15:00",
"maximumPartySize": 10
},
{
"time": "20:30:00",
"maximumPartySize": 10
},
{
"time": "20:45:00",
"maximumPartySize": 10
},
{
"time": "21:00:00",
"maximumPartySize": 10
}
]
}
]
}
This is a JSON representation of the calendar for August 13, 2020. The data it contains is the identification of the date, as well as a series of entries that lists the largest reservation the restaurant can accept for each time slot.
Apart from the data, the representation also contains links. There's a general collection of links that currently holds only next and previous. In addition to that, each day has its own array of links. In the above example, only a single day is represented, so the days array contains only a single object. For a month calendar (navigatable via the urn:month link), there'd be between 28 and 31 days, each with its own links array.
Generating all these links is a complex undertaking all by itself, so separation of concerns is a boon.
Calendar links #
As you can see in the above LinksFilter, it branches on the type of value wrapped in an OkObjectResult. If the type is CalendarDto, it calls the appropriate AddLinks overload:
private static void AddLinks(CalendarDto dto, IUrlHelper url) { var period = dto.ToPeriod(); var previous = period.Accept(new PreviousPeriodVisitor()); var next = period.Accept(new NextPeriodVisitor()); dto.Links = new[] { url.LinkToPeriod(previous, "previous"), url.LinkToPeriod(next, "next") }; if (dto.Days is { }) foreach (var day in dto.Days) AddLinks(day, url); }
It both generates the previous and next links on the dto, as well as the links for each day. While I'm not going to bore you with more of that code, you can tell, I hope, that the AddLinks method calls other helper methods and classes. The point is that link generation involves more than just a few lines of code.
You already saw that in the first example (related to HomeDto). The question is whether there's still some significant code left in the Controller class?
Calendar resource #
The CalendarController class defines three overloads of Get - one for a single day, one for a month, and one for an entire year. Each of them looks like this:
public async Task<ActionResult> Get(int year, int month) { var period = Period.Month(year, month); var days = await MakeDays(period).ConfigureAwait(false); return new OkObjectResult( new CalendarDto { Year = year, Month = month, Days = days }); }
It doesn't look as though much is going on, but at least you can see that it returns a CalendarDto object.
While the method looks simple, it's not. Significant work happens in the MakeDays helper method:
private async Task<DayDto[]> MakeDays(IPeriod period) { var firstTick = period.Accept(new FirstTickVisitor()); var lastTick = period.Accept(new LastTickVisitor()); var reservations = await Repository .ReadReservations(firstTick, lastTick).ConfigureAwait(false); var days = period.Accept(new DaysVisitor()) .Select(d => MakeDay(d, reservations)) .ToArray(); return days; }
After having read relevant reservations from the database, it applies complex business logic to allocate them and thereby being able to report on remaining capacity for each time slot.
Not having to worry about link generation while doing all that work seems like a benefit.
Filter registration #
You must tell the ASP.NET Core framework about any filters that you add. You can do that in the Startup class' ConfigureServices method:
public void ConfigureServices(IServiceCollection services) { services.AddControllers(opts => opts.Filters.Add<LinksFilter>()); // ...
When registered, the filter executes for each HTTP request. When the object represents a 200 OK result, the filter populates the DTOs with links.
Conclusion #
By treating RESTful link generation as a cross-cutting concern, you can separate if from the logic of generating the data structure that represents the resource. That's not the only way to do it. You could also write a simple function that populates DTOs, and call it directly from each Controller action.
What I like about using a filter is that I don't have to remember to do that. Once the filter is registered, it'll populate all the DTOs it knows about, regardless of which Controller generated them.
Comments
Thanks for your good and insightful posts.
Separation of REST concerns from MVC controller's concerns is a great idea, But in my opinion this solution has two problems:
Distance between related REST implementations #
When implementing REST by MVC pattern often REST archetypes are the reasons for a MVC Controller class to be created. As long as the MVC Controller class describes the archetype, And links of a resource is a part of the response when implementing hypermedia controls, having the archetype and its related links in the place where the resource described is a big advantage in easiness and readability of the design. pulling out link implementations and putting them in separate classes causes higher readability and uniformity of the code abstranction levels in the action method at the expense of making a distance between related REST implementation.
Implementation scalability #
There is a switch statement on the ActionExecutingContext's result in the LinksFilter to decide what links must be represented to the client in the response.The DTOs thre are the results of the clients's requests for URIs. If this solution generalised for every resources the API must represent there will be several cases for the switch statement to handle. Beside that every resources may have different implemetations for generating their links. Putting all this in one place leads the LinksFilter to be coupled with too many helper classes and this coupling process never stops.
Solution #
LinkDescriptor and LinkSubscriber for resources links definition
public class LinkDescriptor { public string Rel { get; set; } public string Href { get; set; } public string Resource { get; set; } }
Letting the MVC controller classes have their resource's links definitions but not in action methods.
public ActionResult Get() { return new OkObjectResult(new HomeDto()); } public static void RegisterLinks(LinkSubscriber subscriber) { subscriber .Add( resource: "/Home", rel: "urn:reservations", href: "/reservations") .Add( resource: "/Home", rel: "urn:year", href: "/calendar/2020") .Add( resource: "/Home", rel: "urn:month", href: "/calendar/2020/8") .Add( resource: "/Home", rel: "urn:day", href: "/calendar/2020/8/13"); }
Registering resources links by convention
public static class MvcBuilderExtensions { public static IMvcBuilder AddRestLinks(this IMvcBuilder mvcBuilder) { var subscriber = new LinkSubscriber(); var linkRegistrationMethods = GetLinkRegistrationMethods(mvcBuilder.Services); PopulateLinks(subscriber, linkRegistrationMethods); mvcBuilder.Services.AddSingleton<IEnumerable<LinkDescriptor>>(subscriber.LinkDescriptors); return mvcBuilder; } private static List<MethodInfo> GetLinkRegistrationMethods(IServiceCollection services) { return typeof(MvcBuilderExtensions).Assembly.ExportedTypes .Where(tp => typeof(ControllerBase).IsAssignableFrom(tp)) .Select(tp => tp.GetMethod("RegisterLinks", new[] { typeof(LinkSubscriber) })) .Where(mi => mi != null) .ToList(); } private static void PopulateLinks(LinkSubscriber subscriber, List<MethodInfo> linkRegistrationMethods) { foreach (var method in linkRegistrationMethods) { method.Invoke(null, new[] { subscriber }); } } }
Add dependencies and execute procedures for adding links to responses
public void ConfigureServices(IServiceCollection services) { services.AddControllers(conf => conf.Filters.Add<LinksFilter>()) .AddRestLinks(); }
And Last letting the LinksFilter to dynamicaly add resources links by utilizing ExpandoObject
public class LinksFilter : IAsyncActionFilter { private readonly IEnumerable<LinkDescriptor> links; public LinksFilter(IEnumerable<LinkDescriptor> links) { this.links = links; } public async Task OnActionExecutionAsync(ActionExecutingContext context, ActionExecutionDelegate next) { var relatedLinks = links .Where(lk => context.HttpContext.Request.Path.Value.ToLower() == lk.Resource); if (relatedLinks.Any()) await ManipulateResponseAsync(context, next, relatedLinks); } private async Task ManipulateResponseAsync(ActionExecutingContext context, ActionExecutionDelegate next, IEnumerable<LinkDescriptor> relatedLinks) { var ctxAfter = await next().ConfigureAwait(false); if (!(ctxAfter.Result is ObjectResult objRes)) return; var expandoResult = new ExpandoObject(); FillExpandoWithResultProperties(expandoResult, objRes.Value); FillExpandoWithLinks(expandoResult, relatedLinks); objRes.Value = expandoResult; } private void FillExpandoWithResultProperties(ExpandoObject resultExpando, object value) { var properties = value.GetType().GetProperties(); foreach (var property in properties) { resultExpando.TryAdd(property.Name, property.GetValue(value)); } } private void FillExpandoWithLinks(ExpandoObject resultExpando, IEnumerable<LinkDescriptor> relatedLinks) { var linksToAdd = relatedLinks.Select(lk => new { Rel = lk.Rel, Href = lk.Href }); resultExpando.TryAdd("Links", linksToAdd); } }
If absoulute URI in href field is prefered, IUriHelper can be injected in LinksFilter to create URI paths.
Mark, thanks for figuring out the tricky parts so we don't have to. :-)
I did not see a link to a repo with the completed code from this article, and a cursory look around your Github profile didn't give away any obvious clues. Is the example code in the article part of a repo we can clone? If so, could you please provide a link?
Jes, it's part of a larger project that I'm currently working on. Eventually, I hope to publish it, but it's not yet in a state where I wish to do that.
Did I leave out essential details that makes it hard to reproduce the idea?
No, your presentation was fine. Looking forward to see the completed project!
Mehdi, thank you for writing. It's true that the LinksFilter implementation code contains a switch statement, and that this is one of multiple possible designs. I do believe that this is a trade-off rather than a problem per se.
That switch statement is an implementation detail of the filter, and something I might decide to change in the future. I did choose that implementation, though, because I it was the simplest design that came to my mind. As presented, the switch statement just calls some private helper methods (all called AddLinks), but if one wanted that code close to the rest of the Controller code, one could just move those helper methods to the relevant Controller classes.
While you wouldn't need to resort to Reflection to do that, it's true that this would leave that switch statement as a central place where developers would have to go if they add a new resource. It's true that your proposed solution addresses that problem, but doesn't it just shift the burden somewhere else? Now, developers will have to know that they ought to add a RegisterLinks method with a specific signature to their Controller classes. This replaces a design with compile-time checking with something that may fail at run time. How is that an improvement?
I think that I understand your other point about the distance of code, but it assumes a particular notion of REST that I find parochial. Most (.NET) developers I've met design REST APIs in a code-centric (if not a database-centric) way. They tend to conflate representations with resources and translate both to Controller classes.
The idea behind Representational State Transfer, however, is to decouple state from representation. Resources have state, but can have multiple representations. Vice versa, many resources may share the same representation. In the code base I used for this article, not only do I have three overloaded Get methods on CalendarController that produce CalendarDto representations, I also have a ScheduleController class that does the same.
Granted, not all REST API code bases are designed like this. I admit that what actually motivated me to do things like this was to avoid having to inherit from ControllerBase. Moving all the code that relies heavily on the ASP.NET infrastructure keeps the Controller classes lighter, and thus easier to test. I should probably write an article about that...
Unit testing is fine
Unit testing considered harmful? I think not.
Once in a while, some article, video, or podcast makes the rounds on social media, arguing that unit testing is bad, overrated, harmful, or the like. I'm not going to link to any specific resources, because this post isn't an attack on any particular piece of work. Many of these are sophisticated, thoughtful, and make good points, but still arrive at the wrong conclusion.
The line of reasoning tends to be to show examples of bad unit tests and conclude that, based on the examples, unit tests are bad.
The power of examples is great, but clearly, this is a logical fallacy.
Symbolisation #
In case it isn't clear that the argument is invalid, I'll demonstrate it using the techniques I've learned from Howard Pospesel's introduction to predicate logic.
We can begin by symbolising the natural-language arguments into well-formed formulas. I'll keep this as simple as possible:
∃xBx ⊢ ∀xBx (Domain: unit tests; Bx = x is bad)
Basically, Bx states that x is bad, where x is a unit test. ∃xBx is a statement that there exists a unit test x for which x is bad; i.e. bad unit tests exist. The statement ∀xBx claims that for all unit tests x, x is bad; i.e. all unit tests are bad. The turnstile symbol ⊢ in the middle indicates that the antecedent on the left proves the consequent to the right.
Translated back to natural language, the claim is this: Because bad unit tests exist, all unit tests are bad.
You can trivially prove this sequent invalid.
Logical fallacy #
One way to prove the sequent invalid is to use a truth tree:
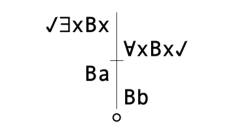
Briefly, the way this works is that the statements on the left-hand side represent truth, while the ones to the right are false. By placing the antecedent on the left, but the consequent on the right, you're basically assuming the sequent to be wrong. This is is also the way you prove correct sequents true; if the conclusion is assumed false, a logical truth should lead to a contradiction. If it doesn't, the sequent is invalid. That's what happens here.
The tree remains open, which means that the original sequent is invalid. It's a logical fallacy.
Counter examples #
You probably already knew that. All it takes to counter a universal assertion such as all unit tests are bad is to produce a counter example. One is sufficient, because if just a single good unit test exists, it can't be true that all are bad.
Most of the think pieces that argue that unit testing is bad do so by showing examples of bad unit tests. These tests typically involve lots of mocks and stubs; they tend to test the interaction between internal components instead of the components themselves, or the system as a whole. I agree that this often leads to fragile tests.
While I still spend my testing energy according to the Test Pyramid, I don't write unit tests like that. I rarely use dynamic mock libraries. Instead, I push impure actions to the boundary of the system and write most of the application code as pure functions, which are intrinsically testable. No test-induced damage there.
I follow up with boundary tests that demonstrate that the functions are integrated into a working system. That's just another layer in the Test Pyramid, but smaller. You don't need that many integration tests when you have a foundation of good unit tests.
While I'm currently working on a larger body of work that showcases this approach, this blog already has examples of this.
Conclusion #
You often hear or see the claim that unit tests are bad. The supporting argument is that a particular (popular, I admit) style of unit testing is bad.
If the person making this claim only knows of that single style of unit testing, it's natural to jump to the conclusion that all unit testing must be bad.
That's not the case. I write most of my unit tests in a style dissimilar from the interaction-heavy, mocks-and-stubs-based style that most people use. These test have a low maintenance burden and don't cause test-induced damage.
Unit testing is fine.
An ASP.NET Core URL Builder
A use case for the Immutable Fluent Builder design pattern variant.
The Fluent Builder design pattern is popular in object-oriented programming. Most programmers use the mutable variant, while I favour the immutable alternative. The advantages of Immutable Fluent Builders, however, may not be immediately clear.
It inspires me when I encounter a differing perspective. Could I be wrong? Or did I fail to produce a compelling example?"I never thought of someone reusing a configured builder (soulds like too big class/SRP violation)."
It's possible that I'm wrong, but in my my recent article on Builder isomorphisms I focused on the pattern variations themselves, to the point where a convincing example wasn't my top priority.
I recently encountered a good use case for an Immutable Fluent Builder.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
Build links #
I was developing a REST API and wanted to generate some links like these:
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/reservations"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/7"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/7/7"
}
]
}
As I recently described, the ASP.NET Core Action API is tricky, and since there was some repetition, I was looking for a way to reduce the code duplication. At first I just thought I'd make a few private helper methods, but then it occurred to me that an Immutable Fluent Builder as an Adapter to the Action API might offer a fertile alternative.
UrlBuilder class #
The various Action overloads all accept null arguments, so there's effectively no clear invariants to enforce on that dimension. While I wanted an Immutable Fluent Builder, I made all the fields nullable.
public sealed class UrlBuilder { private readonly string? action; private readonly string? controller; private readonly object? values; public UrlBuilder() { } private UrlBuilder(string? action, string? controller, object? values) { this.action = action; this.controller = controller; this.values = values; } // ...
I also gave the UrlBuilder class a public constructor and a private copy constructor. That's the standard way I implement that pattern.
Most of the modification methods are straightforward:
public UrlBuilder WithAction(string newAction) { return new UrlBuilder(newAction, controller, values); } public UrlBuilder WithValues(object newValues) { return new UrlBuilder(action, controller, newValues); }
I wanted to encapsulate the suffix-handling behaviour I recently described in the appropriate method:
public UrlBuilder WithController(string newController) { if (newController is null) throw new ArgumentNullException(nameof(newController)); const string controllerSuffix = "controller"; var index = newController.LastIndexOf( controllerSuffix, StringComparison.OrdinalIgnoreCase); if (0 <= index) newController = newController.Remove(index); return new UrlBuilder(action, newController, values); }
The WithController method handles both the case where newController is suffixed by "Controller" and the case where it isn't. I also wrote unit tests to verify that the implementation works as intended.
Finally, a Builder should have a method to build the desired object:
public Uri BuildAbsolute(IUrlHelper url) { if (url is null) throw new ArgumentNullException(nameof(url)); var actionUrl = url.Action( action, controller, values, url.ActionContext.HttpContext.Request.Scheme, url.ActionContext.HttpContext.Request.Host.ToUriComponent()); return new Uri(actionUrl); }
One could imagine also defining a BuildRelative method, but I didn't need it.
Generating links #
Each of the objects shown above are represented by a simple Data Transfer Object:
public class LinkDto { public string? Rel { get; set; } public string? Href { get; set; } }
My next step was to define an extension method on Uri, so that I could turn a URL into a link:
internal static LinkDto Link(this Uri uri, string rel) { return new LinkDto { Rel = rel, Href = uri.ToString() }; }
With that function I could now write code like this:
private LinkDto CreateYearLink() { return new UrlBuilder() .WithAction(nameof(CalendarController.Get)) .WithController(nameof(CalendarController)) .WithValues(new { year = DateTime.Now.Year }) .BuildAbsolute(Url) .Link("urn:year"); }
It's acceptable, but verbose. This only creates the urn:year link; to create the urn:month and urn:day links, I needed similar code. Only the WithValues method calls differed. The calls to WithAction and WithController were identical.
Shared Immutable Builder #
Since UrlBuilder is immutable, I can trivially define a shared instance:
private readonly static UrlBuilder calendar = new UrlBuilder() .WithAction(nameof(CalendarController.Get)) .WithController(nameof(CalendarController));
This enabled me to write more succinct methods for each of the relationship types:
internal static LinkDto LinkToYear(this IUrlHelper url, int year) { return calendar.WithValues(new { year }).BuildAbsolute(url).Link("urn:year"); } internal static LinkDto LinkToMonth(this IUrlHelper url, int year, int month) { return calendar.WithValues(new { year, month }).BuildAbsolute(url).Link("urn:month"); } internal static LinkDto LinkToDay(this IUrlHelper url, int year, int month, int day) { return calendar.WithValues(new { year, month, day }).BuildAbsolute(url).Link("urn:day"); }
This is possible exactly because UrlBuilder is immutable. Had the Builder been mutable, such sharing would have created an aliasing bug, as I previously described. Immutability enables reuse.
Conclusion #
I got my first taste of functional programming around 2010. Since then, when I'm not programming in F# or Haskell, I've steadily worked on identifying good ways to enjoy the benefits of functional programming in C#.
Immutability is a fairly low-hanging fruit. It requires more boilerplate code, but apart from that, it's easy to make classes immutable in C#, and Visual Studio has plenty of refactorings that make it easier.
Immutability is one of those features you're unlikely to realise that you're missing. When it's not there, you work around it, but when it's there, it simplifies many tasks.
The example you've seen in this article relates to the Fluent Builder pattern. At first glance, it seems as though a mutable Fluent Builder has the same capabilities as a corresponding Immutable Fluent Builder. You can, however, build upon shared Immutable Fluent Builders, which you can't with mutable Fluent Builders.
Using the nameof C# keyword with ASP.NET 3 IUrlHelper
How to generate links to other resources in a refactoring-friendly way.
I recently spent a couple of hours yak-shaving, and despite much Googling couldn't find any help on the internet. I'm surprised that the following problem turned out to be so difficult to figure out, so it may just be that I'm ignorant or that my web search skills failed me that day. On the other hand, if this really is as difficult as I found it, perhaps this article can save some other poor soul an hour or two.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
I was developing a REST API and wanted to generate some links like these:
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/reservations"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/7"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/7/7"
}
]
}
Like previous incarnations of the framework, ASP.NET Core 3 has an API for generating links to a method on a Controller. I just couldn't get it to work.
Using nameof #
I wanted to generate a URL like http://localhost:53568/calendar/2020 in a refactoring-friendly way. While ASP.NET wants you to define HTTP resources as methods (actions) on Controllers, the various Action overloads want you to identify these actions and Controllers as strings. What happens if someone renames one of those methods or Controller classes?
That's what the C# nameof keyword is for.
I naively called the Action method like this:
var href = Url.Action( nameof(CalendarController.Get), nameof(CalendarController), new { year = DateTime.Now.Year }, Url.ActionContext.HttpContext.Request.Scheme, Url.ActionContext.HttpContext.Request.Host.ToUriComponent());
Looks good, doesn't it?
I thought so, but it didn't work. In the time-honoured tradition of mainstream programming languages, the method just silently fails to return a value and instead returns null. That's not helpful. What might be the problem? No clue is provided. It just doesn't work.
Strip off the suffix #
It turns out that the Action method expects the controller argument to not contain the Controller suffix. Not surprisingly, nameof(CalendarController) becomes the string "CalendarController", which doesn't work.
It took me some time to figure out that I was supposed to pass a string like "Calendar". That works!
As a first pass at the problem, then, I changed my code to this:
var controllerName = nameof(CalendarController); var controller = controllerName.Remove( controllerName.LastIndexOf( "Controller", StringComparison.Ordinal)); var href = Url.Action( nameof(CalendarController.Get), controller, new { year = DateTime.Now.Year }, Url.ActionContext.HttpContext.Request.Scheme, Url.ActionContext.HttpContext.Request.Host.ToUriComponent());
That also works, and is more refactoring-friendly. You can rename both the Controller class and the method, and the link should still work.
Conclusion #
The UrlHelperExtensions.Action methods expect the controller to be the 'semantic' name of the Controller, if you will - not the actual class name. If you're calling it with values produced with the nameof keyword, you'll have to strip the Controller suffix away.
Task asynchronous programming as an IO surrogate
Is task asynchronous programming a substitute for the IO container? An article for C# programmers.
This article is part of an article series about the IO container in C#. In the previous articles, you've seen how a type like IO<T> can be used to distinguish between pure functions and impure actions. While it's an effective and elegant solution to the problem, it depends on a convention: that all impure actions return IO objects, which are opaque to pure functions.
In reality, .NET base class library methods don't do that, and it's unrealistic that this is ever going to happen. It'd require a breaking reset of the entire .NET ecosystem to introduce this design.
A comparable reset did, however, happen a few years ago.
TAP reset #
Microsoft introduced the task asynchronous programming (TAP) model some years ago. Operations that involve I/O got a new return type. Not IO<T>, but Task<T>.
The .NET framework team began a long process of adding asynchronous alternatives to existing APIs that involve I/O. Not as breaking changes, but by adding new, asynchronous methods side-by-side with older methods. ExecuteReaderAsync as an alternative to ExecuteReader, ReadAllLinesAsync side by side with ReadAllLines, and so on.
Modern APIs exclusively with asynchronous methods appeared. For example, the HttpClient class only affords asynchronous I/O-based operations.
The TAP reset was further strengthened by the move from .NET to .NET Core. Some frameworks, most notably ASP.NET, were redesigned on a fundamentally asynchronous core.
In 2020, most I/O operations in .NET are easily recognisable, because they return Task<T>.
Task as a surrogate IO #
I/O operations are impure. Either you're receiving input from outside the running process, which is consistently non-deterministic, or you're writing to an external resource, which implies a side effect. It might seem natural to think of Task<T> as a replacement for IO<T>. Szymon Pobiega had a similar idea in 2016, and I investigated his idea in an article. This was based on F#'s Async<'a> container, which is equivalent to Task<T> - except when it comes to referential transparency.
Unfortunately, Task<T> is far from a perfect replacement of IO<T>, because the .NET base class library (BCL) still contains plenty of impure actions that 'look' pure. Examples include Console.WriteLine, the parameterless Random constructor, Guid.NewGuid, and DateTime.Now (arguably a candidate for the worst-designed API in the BCL). None of those methods return tasks, which they ought to if tasks should serve as easily recognisable signifiers of impurity.
Still, you could write asynchronous Adapters over such APIs. Your Console Adapter might present this API:
public static class Console { public static Task<string> ReadLine(); public static Task WriteLine(string value); }
Moreover, the Clock API might look like this:
public static class Clock { public static Task<DateTime> GetLocalTime(); }
Modern versions of C# enable you to write asynchronous entry points, so the hello world example shown in this article series becomes:
static async Task Main(string[] args) { await Console.WriteLine("What's your name?"); var name = await Console.ReadLine(); var now = await Clock.GetLocalTime(); var greeting = Greeter.Greet(now, name); await Console.WriteLine(greeting); }
That's nice idiomatic C# code, so what's not to like?
No referential transparency #
The above Main example is probably as good as it's going to get in C#. I've nothing against that style of C# programming, but you shouldn't believe that this gives you compile-time checking of referential transparency. It doesn't.
Consider a simple function like this, written using the IO container shown in previous articles:
public static string AmIEvil() { Console.WriteLine("Side effect!"); return "No, I'm not."; }
Is this method referentially transparent? Surprisingly, despite the apparent side effect, it is. The reason becomes clearer if you write the code so that it explicitly ignores the return value:
public static string AmIEvil() { IO<Unit> _ = Console.WriteLine("Side effect!"); return "No, I'm not."; }
The Console.WriteLine method returns an object that represents a computation that might take place. This IO<Unit> object, however, never escapes the method, and thus never runs. The side effect never takes place, which means that the method is referentially transparent. You can replace AmIEvil() with its return value "No, I'm not.", and your program would behave exactly the same.
Consider what happens when you replace IO with Task:
public static string AmIEvil() { Task _ = Console.WriteLine("Side effect!"); return "Yes, I am."; }
Is this method a pure function? No, it's not. The problem is that the most common way that .NET libraries return tasks is that the task is already running when it's returned. This is also the case here. As soon as you call this version of Console.WriteLine, the task starts running on a background thread. Even though you ignore the task and return a plain string, the side effect sooner or later takes place. You can't replace a call to AmIEvil() with its return value. If you did, the side effect wouldn't happen, and that would change the behaviour of your program.
Contrary to IO, tasks don't guarantee referential transparency.
Conclusion #
While it'd be technically possible to make C# distinguish between pure and impure code at compile time, it'd require such a breaking reset to the entire .NET ecosystem that it's unrealistic to hope for. It seems, though, that there's enough overlap with the design of IO<T> and task asynchronous programming that the latter might fill that role.
Unfortunately it doesn't, because it fails to guarantee referential transparency. It's better than nothing, though. Most C# programmers have now learned that while Task objects come with a Result property, you shouldn't use it. Instead, you should write your entire program using async and await. That, at least, takes you halfway towards where you want to be.
The compiler, on the other hand, doesn't help you when it comes to those impure actions that look pure. Neither does it protect you against asynchronous side effects. Diligence, code reviews, and programming discipline are still required if you want to separate pure functions from impure actions.
Comments
This is a great idea. It seems like the only Problem with Tasks is that they are usually already started, either on the current or a Worker Thread. If we return Tasks that are not started yet, then Side-Effects don't happen until we await them. And we have to await them to get their Result or use them in other Tasks. I experimented with a modified GetTime() Method returning a new Task that is not run yet:
public static Task<DateTime> GetTime() => new Task<DateTime>(() => DateTime.Now);
Using a SelectMany Method that ensures that Tasks have been run, the Time is not evaluated until the resulting Task is awaited or another SelectMany is built using the Task from the first SelectMany. The Time of one such Task is also evaluated only once. On repeating Calls the same Result is returned:
public static async Task<TResult> SelectMany<T, TResult>(this Task<T> source
, Func<T, Task<TResult>> project) {
T t = await source.GetResultAsync();
Task<TResult>? ret = project(t);
return await ret.GetResultAsync();
}
/// <summary> Asynchronously runs the <paramref name="task"/> to Completion </summary>
/// <returns><see cref="Task{T}.Result"/></returns>
public static async Task<T> GetResultAsync<T>(this Task<T> task) {
switch (task.Status) {
case TaskStatus.Created: await Task.Run(task.RunSynchronously); return task.Result;
case TaskStatus.WaitingForActivation:
case TaskStatus.WaitingToRun:
case TaskStatus.Running:
case TaskStatus.WaitingForChildrenToComplete: return await task;
case TaskStatus.Canceled:
case TaskStatus.Faulted:
case TaskStatus.RanToCompletion: return task.Result; //let the Exceptions fly...
default: throw new ArgumentOutOfRangeException();
}
}
Since I/O Operations with side-effects are usually asynchronous anyway,
Tasks and I/O are a good match.
Consistenly not starting Tasks and using this SelectMany Method
either ensures Method purity or enforces to return the Task.
To avoid ambiguity with started Tasks a Wrapper-IO-Class could be constructed,
that always takes and creates unstarted Tasks.
Am I missing something or do you think this would not be worth the effort?
Are there more idiomatic ways to start enforcing purity in C#,
except e.g. using the [Pure] Attribute and StyleCop-Warnings for unused Return Values?
Matt, thank you for writing. That's essentially how F# asynchronous workflows work.

Comments
Unfortunately, I can't agree that it's fine to use
EnsureSuccessStatusCodeor other similar methods for assertions. An exception of a kind different from assertion (XunitExceptionfor XUnit,AssertionExceptionfor NUnit) is handled in a bit different way by the testing framework.EnsureSuccessStatusCodemethod throwsHttpRequestException. Basically, a test that fails with such exception is considered as "Failed by error".For example, the test result message in case of 404 status produced by the
EnsureSuccessStatusCodemethod is:Where "System.Net.Http.HttpRequestException :" text looks redundant, as we do assertion. This also may make other people think that the reason for this failure is not an assertion, but an unexpected exception. In case of regular assertion exception type, that text is missing.
Other points are related to NUnit:
- Failure: a test assertion failed. (Status=Failed, Label=empty)
- Error: an unexpected exception occurred. (Status=Failed, Label=Error)
See NUnit Common Outcomes. Thus `EnsureSuccessStatusCode` produces "Error" status instead of desirable "Failure".EnsureSuccessStatusCodeas assertion inside multiple asserts."assertions"property gets into the test results XML file and might be useful. This property increments on assertion methods,EnsureSuccessStatusCode- obviously doesn't increment it.Yevgeniy, thank you for writing. This shows, I think, that all advice is contextual. It's been more than a decade since I regularly used NUnit, but I vaguely recall that it gives special treatment to its own assertion exceptions.
I also grant that the "System.Net.Http.HttpRequestException" part of the message is redundant. To make matters worse, even without that 'prologue' the information that we care about (the actual status code) is all the way to the right. It'll often require horizontal scrolling to see it.
That doesn't much bother me, though. I think that one should optimise for the most frequent scenario. For example, I favour taking a bit of extra time to write readable code, because the bottleneck in programming isn't typing. In the same vein, I find it a good trade-off being able to avoid adding more code against an occasional need to scroll horizontally. The cost of code isn't the time it takes to write it, but the maintenance burden it imposes, as well as the cognitive load it adds.
The point here is that while horizontal scrolling is inconvenient, the most frequent scenario is that tests don't fail. The inconvenience only manifests in the rare circumstance that a test fails.
I want to thank you, however, for pointing out the issues with NUnit. It reinforces the impression I already had of it, as a framework to stay away from. That design seems to me to impose a lock-in that prevents you from mixing NUnit with improved APIs.
In contrast, the xunit.core library doesn't include xunit.assert. I often take advantage of that when I write unit tests in F#. While the xUnit.net assertion library is adequate, Unquote is much better for F#. I appreciate that xUnit.net enables me to combine the tools that work best in a given situation.
I see your point, Mark. Thanks for your reply.
I would like to add a few words in defense of the NUnit.
First of all, there is no problem to use an extra library for NUnit assertions too. For example, I like FluentAssertions that works great for both XUnit and NUnit.
NUnit 3 also has a set of useful features that are missing in XUnit like:
I can recommend to reconsider the view of NUnit, as the library progressed well during its 3rd version. XUnit and NUnit seem interchangeable for unit testing. But NUnit, from my point of view, provides the features that are helpful in integration and UI testing.
Yevgeniy, I haven't done UI testing since sometime in 2005, I think, so I wasn't aware of that. It's good to know that NUnit may excel at that, and the other scenarios you point out.
To be clear, while I still think I may prefer xUnit.net, I don't consider it perfect.
I would like to mention FluentAssertions.Web, a library I wrote with the purpose to solve exact this problem I had while maintaining API tests. It's frustrating not to tell in two seconds why a test failed. Yeah, it is a Bad Request, but why. Maybe the response is in the respons content?
Wouldn't be an idea to see the response content? This FluentAssertions extension outputs everything starting from the request to the response, when the test fails.Adrian, thank you for writing. Your comment inspired me to write an article on when tests fail. This article is now in the publication queue. I'll try to remember to come back here and add a link once it's published.
(Placeholder)