ploeh blog danish software design
Filtering as domain logic
Performance and correctness are two independent concerns with overlapping solutions.
How do you design, implement, maintain, and test complex filter logic as part of out-of-process (e.g. database) queries?
One option is to implement parts of the filtering logic twice: Once as an easily-testable in-memory implementation to ensure correctness, and another, possibly simpler, query using the query language (usually, SQL) of the data source.
Does this not imply duplication of effort? Yes, to a degree it does. Should you always do this? No, only when warranted. As usual, I present this idea as an option you may consider; a tool for your software design tool belt. You decide if it's useful in your particular context.
Motivation #
When extracting data from a data source, an application usually needs some of the data, but not all of it. If the software system in question has a certain size, the subset required for an operation is only a miniscule fraction of the entire database. For example, a user may want to see his or her latest order in a web shop, but the entire system contains millions of orders. Another example could be a system for managing help desk requests: Each supporter may need a dashboard of open cases assigned to him or her, but the system holds millions of tickets, and most of them are closed.
If a data store supports server-side querying, for example with SQL or Cypher, it's reasonable to let the data store itself do the filtering.
As anyone who has worked professionally with SQL can attest, SQL queries can become complicated. When this happens, you may become concerned with the correctness of a query. Does it include all the data it should? Does it exclude irrelevant data? If you later change a query, how can you verify that it still works as intended? How do you even version it?
Automated testing can address several of these concerns, but testing against a real database, while possible, tends to be cumbersome and slow. Do alternatives, or augmentations, exist?
How it works #
If a server-side query threatens to become too complicated, consider shifting some of the work to clients. You may retain some filtering logic in the server-side query, but only enough to keep performance good, and simple enough that you are no longer concerned about its correctness.
Implement the difficult filtering logic in a client-side library. Since you implement this part in a programming language of your choice, you can use any tool or technique available in that context to ensure correctness: Test-driven development, static code analysis, type checking, property-based testing, code coverage, mutation testing, etc.
Using a funnel as a symbol of filtering, this diagram depicts the idea:
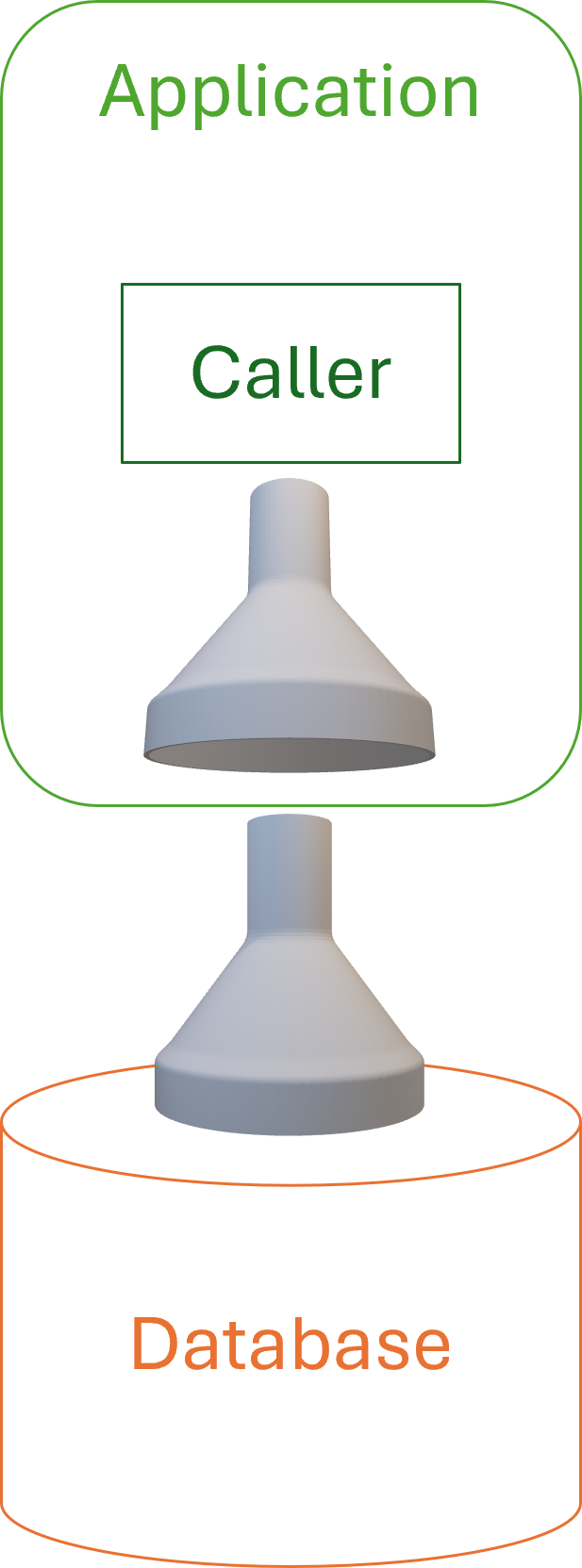
Normally a funnel is only useful when the widest part faces up, but on the other hand, we usually depict application architectures with the database under the the application. You have to imagine data being 'sucked up' through the funnels.
In reality, the two filters will differ, but have overlapping functionality.
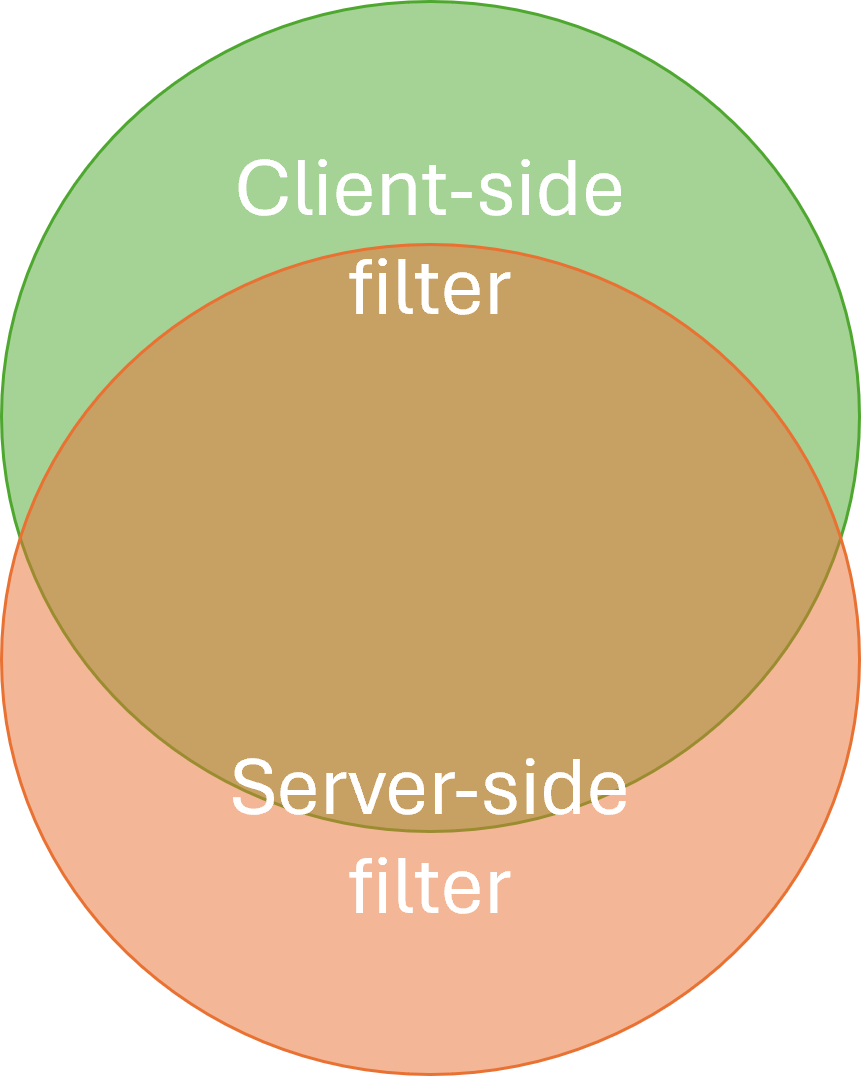
If based on a relational database, the server-side query will still hold table joins and column projections that are effectively irrelevant to the client-side Domain Model. On the other hand, while the server-side query may apply a rough filter, the more detailed selection of what is, and is not, included happens in the client.
The server-side query is defined using the query language of the data store, such as SQL or Cypher. The client-side query is part of the application code base, and written in the same programming language.
When to use it #
Use this pattern if a server-side query becomes so complicated that you are concerned about its correctness, or if correctness is an essential part of a Domain Model's contract.
While it is conceptually possible to load the entire data store's data into memory, this is often prohibitively expensive in terms of time and memory. It is often necessary to retain some filtering logic (e.g. one or more SQL WHERE clauses) on the server to pare down data to acceptable sizes. This implies a degree of duplicated logic, since the client-side filter shouldn't assume that any filtering has been applied.
Duplication comes with its own set of problems, even if this looks like the benign kind. Alternatives include keeping all logic on the database server, which is viable if the logic is simple, or can be sufficiently simplified. Another alternative is to perform all filtering in the client, which may be an attractive solution if the entire data set is small.
Encapsulation #
If a Domain Model is composed of pure functions, data must be supplied as normal input arguments. In a more object-oriented style, data may arrive as indirect input. In both object-oriented and functional architecture, encapsulation is important. This entails being explicit about invariants and pre- and postconditions; i.e. contracts.
To enforce preconditions, a Domain Model must ensure that input is correct. While it could choose to reject input if it contains 'too much' data, a Tolerant Reader should instead pare the data down to size. This implies that filtering should be part of a Domain Model's contract.
This further implies that a Domain Model becomes less vulnerable to changes in data access code.
Implementation details #
Server-side filtering (with e.g. SQL) is often difficult to test with sufficient rigour. The point of moving the complex filtering logic to the Domain Model is that this makes it easier to test, and thereby to maintain.
If no filtering takes place on the server, however, the entire data set of the system would have to be transmitted to, and filtered on, the client. This is usually too expensive, so some filtering must still take place at the data source. The whole point of this exercise is that the 'correct' filtering is too complicated to maintain as a server-side query, so whatever filtering still takes place on the server only happens for performance reasons, and can be simpler, as long as it's wider.
Specifically, the simplified server-side query can (and probably should) be wider, in the sense that it returns more data than is required for the correctness of the overall system. The client, receiving more data than strictly required, can perform more sophisticated (and testable) filtering.
The simplified filtering on the server must not, on the other hand, narrow the result set. If relevant data is left out at the source, the client has no chance to restore it, or even know that it exists.
Motivating example #
The code base that accompanies Code That Fits in Your Head contains an example. When a user attempts to make a restaurant reservation, the system must look at existing reservations on the same date to check whether it has a free table. Many restaurants operate with seating windows, and the logic involved in figuring out if a time slot is free is easy to get wrong. On top of that, the decision logic needs to take opening hours and last seating into account. The book, as well as the article The Maître d' kata, has more details.
Based on information about seating duration, opening hours, and so on, it seems as though it should be possible to form an exact SQL query that only returns existing reservations that overlap the new reservation. Even so, this struck me as error-prone. Instead, I decided to make input filtering part of the Domain Model.
The Domain Model in question, an immutable class named MaitreD, uses the WillAccept method to decide whether to accept a reservation request. Apart from the candidate reservation, it also takes as parameters existingReservations as well as the current time.
public bool WillAccept( DateTime now, IEnumerable<Reservation> existingReservations, Reservation candidate)
The function uses the existingReservations to filter so that only the relevant reservations are considered:
var seating = new Seating(SeatingDuration, candidate.At); var relevantReservations = existingReservations.Where(seating.Overlaps);
As implied by this code snippet, a specialized Domain Model named Seating contains the actual filtering logic:
public bool Overlaps(Reservation otherReservation) { if (otherReservation is null) throw new ArgumentNullException(nameof(otherReservation)); var other = new Seating(SeatingDuration, otherReservation.At); return Overlaps(other); } public bool Overlaps(Seating other) { if (other is null) throw new ArgumentNullException(nameof(other)); return Start < other.End && other.Start < End; }
Notice how the core implementation, the overload that takes another Seating object, implements a binary relation. To extrapolate from Domain-Driven Design, whenever you arrive at 'proper' mathematics to describe the application domain, it's usually a sign that you've arrived at something fundamental.
The Overlaps functions are public and easy to unit test in their own right. Even so, in the code base that accompanies Code That Fits in Your Head, there are no tests that directly exercise these functions, since they only grew out of refactoring the implementation of MaitreD.WillAccept, which is covered by many tests. Since the Overlaps functions only emerged as a result of test-driven development, they might as well have been private helper methods, but I later needed them for verifying some unrelated test outcomes.
The filtering performed in WillAccept will throw away any reservations that don't overlap. Even if existingReservations contained the entire data set from the database, it would still be correct. Given, however, that there could be hundreds of thousands of reservations, it seems prudent to perform some coarse-grained filtering in the database.
The ReservationsController that calls WillAccept first queries the database, getting all the reservation on the relevant date.
var reservations = await Repository .ReadReservations(restaurant.Id, reservation.At) .ConfigureAwait(false);
Now that I write this description, I realize this query, while wide in one sense, could actually be too narrow. None of my test restaurants have a last seating after midnight, but I wouldn't rule that out in certain cultures. If so, it's easy to widen the coarse-grained query to include reservations for the day before (for breakfast restaurants, perhaps) and the day after, assuming that no seating lasts more than 24 hours.
All that said, the point is that ReadReservations(restaurant.Id, reservation.At) (which is an extension method) performs a simple, coarse-grained query for reservations that may be relevant to consider, given the candidate reservation. This query should return a 'gross' data set that contains all relevant, but also some irrelevant, reservations, thereby keeping the query simple. An indeed, the actual database interaction is this parametrised query:
SELECT [PublicId], [At], [Name], [Email], [Quantity] FROM [dbo].[Reservations] WHERE [RestaurantId] = @RestaurantId AND @Min <= [At] AND [At] <= @Max
This range query should be simple enough that a few integration tests should be sufficient to give you confidence that it works correctly.
Consequences #
The main benefit from a design like this is that it shifts some of the burden of correctness to the Domain Model, which is easier to test, maintain, and version than is typically the case for query languages. An added advantage is improved separation of concerns.
In practice, server-side filtering tends to mix two independent concerns: Performance and correctness. Filtering is important for performance, because the alternative is to transmit all rows to the client. Filtering is also important for correctness, because the code making use of the data should only consider data relevant for its purpose. Exclusive server-side filtering performs both of these tasks, thereby mixing concerns. Moving filtering for correctness to a Domain Model can make explicit that these are two separate concerns.
While a Domain Model can implement in-memory filtering, it can only deal with data that is too wide; that is, it can identify and remove superfluous data. If, on the other hand, the dataset passed to the Domain Model lacks relevant records, the Domain Model can't detect that. The above discussion about the reservation system contains a concrete discussion of such a problem. Thus, Domain-based filtering does not alleviate developers from the burden of ensuring that any server-side filtering is sufficiently permissible.
Another consequence of this design is that as server-side queries become more coarse-grained, this could increase potential cache hit ratios. If you somehow cache queries, when queries become more general, there will be less variation, and thus caches will need fewer entries that will statistically be hit more often. This applies to CQRS-style architectures, too.
Consider the restaurant reservation example, above. Since queries are only distinguished by date, you can easily cache query results by date, and all reservation requests for a given date may go through that cache. If, as a counter-example, all filtering took place in the database, a query for a reservation at 18:00 would be different from a query for 18:30, and so on. This would make a hypothetical cache bigger, and decrease the frequency of cache hits.
Test evidence #
When I originally decided that WillAccept should perform in-memory filtering, my motivation was one of correctness. I was concerned whether I could get the seating overlap detection correct without comprehensive testing, and I thought that it would be easier to test a function doing in-memory filtering than to drive all of this via integration tests involving a real SQL Server instance. (Not that I don't know how to do this. The code base accompanying the book has examples of tests that exercise the database. These tests are, however, more work to write and maintain, and they execute slower.)
As discussed in Coupling from a big-O perspective, I much later realized that I actually had no test coverage of edge cases related to querying the database. It was only after attempting to write such a test that I realized that the design had the consequence that a marginal error in the database query had no impact on the correctness of the overall system. Here's that test:
[Fact] public async Task AttemptEdgeCaseBooking() { var twentyFour7 = new Restaurant( 247, "24/7", new MaitreD( opensAt: TimeSpan.FromHours(0), lastSeating: TimeSpan.FromHours(0), seatingDuration: TimeSpan.FromDays(1), tables: Table.Standard(1))); var db = new FakeDatabase(); var now = DateTime.Now; var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(twentyFour7), db); var r1 = Some.Reservation.WithDate(now.AddDays(3).Date); await sut.Post(twentyFour7.Id, r1.ToDto()); var r2 = Some.Reservation.WithDate(now.AddDays(2).Date); var ar = await sut.Post(twentyFour7.Id, r2.ToDto()); Assert.IsAssignableFrom<CreatedAtActionResult>(ar); // More assertions could go here. }
This test is an attempt to cover the edge case related to how the system queries the database, just like the Moq-based test shown in Greyscale-box test-driven development. The idea is to create a reservation that just barely touches a reservation the following day, and thereby trigger a test failure when a change is made to the query, similar to how the Moq-based test fails. Even with a custom restaurant, I can't, however, get this test to fail, because of the Domain-based filtering, which keeps the system working correctly.
It was then that I realized that what I had inadvertently done was to strengthen the contract of WillAccept, compared to a more stereotypical design. Who knew test-driven development could lead to better encapsulation?
Conclusion #
Some queries may become so complicated that they are difficult to maintain. Bugs creep in, you address them, only to reanimate regressions. When this happens, consider moving the complicated parts of data filtering to the client, preferably to a Domain Model. This enables you to test the filtering logic with as much rigour as is required.
For small databases, you may read the entire dataset into memory, but usually you will need to retain some coarse-grained filtering on the database server.
This design, while more complicated than letting a query language like SQL handle all filtering, can lead to better encapsulation and separation of concerns.
Two regimes of Git
Using Git for CI is not the same as Tactical Git.
Git is such a versatile tool that when discussing it, interlocutors may often talk past each other. One person's use is so different from the way the next person uses it that every discussion is fraught with risk of misunderstandings. This happens to me a lot, because I use Git in two radically different ways, depending on context.
Should you rebase? Merge? Squash? Cherry-pick?
Often, being more explicit about a context can help address confusion.
I know of at least two ways of using Git that differ so much from each other that I think we may term them two different regimes. The rules I follow in one regime don't all apply in the other, and vice versa.
In this article I'll describe both regimes.
Collaboration #
Most people use Git because it facilitates collaboration. Like other source-control systems, it's a way to share a code base with coworkers, or open-source contributors. Continuous Integration is a subset in this category, and to my knowledge still the best way to collaborate.
When I work in this regime, I follow one dominant rule: Once history is shared with others, it should be considered immutable. When you push to a shared instance of the repository, other people may pull your changes. Changing the history after having shared it is going to confuse most Git clients. It's much easier to abstain from editing shared history.
What if you shared something that contains an error? Then fix the error and push that update, too. Sometimes, you can use git revert for this.
A special case is reserved for mistakes that involve leaking security-sensitive data. If you accidentally share a password, a revert doesn't rectify the problem. The data is still in the history, so this is a singular case where I know of no better remedy than rewriting history. That is, however, quite bothersome, because you now need to communicate to every other collaborator that this is going to happen, and that they may be best off making a new clone of the repository. If there's a better way to address such situations, I don't know of it, but would be happy to learn.
Another consequence of the Collaboration regime follows from the way pull requests are typically implemented. In GitHub, sending a pull request is a two-step process: First you push a branch, and then you click a button to send the pull request. I usually use the GitHub web user interface to review my own pull-request branch before pushing the button. Occasionally I spot an error. At this point I consider the branch 'unshared', so I may decide to rewrite the history of that branch and force-push it. Once, however, I've clicked the button and sent the pull request, I consider the branch shared, and the same rules apply: Rewriting history is not allowed.
One implication of this is that the set of Git actions you need to know is small: You can effectively get by with git add, commit, pull, push, and possibly a few more.
Many of the 'advanced' Git features, such as rebase and squash, allow you to rewrite history, so aren't allowed in this regime.
Tactical Git #
As far as I can tell, Git wasn't originally created for this second use case, but it turns out that it's incredibly useful for local management of code files. This is what I've previously described as Tactical Git.
Once you realize that you have a version-control system at your fingertips, the opportunities are manifold. You can perform experiments in a branch that only exists on your machine. You may, for example, test alternative API design ideas, implementations, etc. There's no reason to litter the code base with commented-out code because you're afraid that you'll need something later. Just commit it on a local branch. If it later turns out that the experiment didn't turn out to your liking, commit it anyway, but then check out master. You'll leave the experiment on your local machine, and it's there if you need it later.
You can even used failed experiments as evidence that a particular idea has undesirable consequences. Have you ever been in a situation where a coworker suggests a new way of doing things. You may have previously responded that you've already tried that, and it didn't work. How well did that answer go over with your coworker?
He or she probably wasn't convinced.
What if, however, you've kept that experiment on your own machine? Now you can say: "Not only have I already tried this, but I'm happy to share the relevant branch with you."
You can see an example of that in listing 8.10 in Code That Fits in Your Head. This code listing is based on a side-branch never merged into master. If you have the book, you also have access to the entire Git repository, and you can check for yourself that commit 0bb8068 is a dead-end branch named explode-maitre-d-arguments.
Under the Tactical Git regime, you can also go back and edit mistakes when working on code that you haven't yet shared. I use micro-commits, so I tend to check in small commits often. Sometimes, as I'm working with the code, I notice that I made a mistake a few commits ago. Since I'm a neat freak, I often use interactive rebase to go back and correct my mistakes before sharing the history with anyone else. I don't do that to look perfect, but rather to leave behind a legible trail of changes. If I already know that I made a mistake before I've shared my code with anyone else, there's no reason to burden others with both the mistake and its rectification.
In general, I aim to leave as nice a Git history as possible. This is not only for my collaborators' sake, but for my own, too. Legible Git histories and micro-commits make it easier to troubleshoot later, as this story demonstrates.
The toolset useful for Tactical Git is different than for collaboration. You still use add and commit, of course, but I also use (interactive) rebase often, as well as stash and branch. Only rarely do I need cherry-pick, but it's useful when I do need it.
Conclusion #
When discussing good Git practices, it's easy to misunderstand each other because there's more than one way to use Git. I know of at least two radically different modes: Collaboration and Tactical Git. The rules that apply under the Collaboration regime should not all be followed slavishly when in the Tactical Git regime. Specifically, the rule about rewriting history is almost turned on its head. Under the Collaboration regime, do not rewrite Git history; under the Tactical Git regime, rewriting history is encouraged.
Coupling from a big-O perspective
Don't repeat yourself (DRY) implies O(1) edits.
Here's a half-baked idea: We may view coupling in software through the lens of big-O notation. Since this isn't yet a fully-formed idea of mine, this is one of those articles I write in order to learn from the process of having to formulate the idea to other people.
Widening the scope of big-O analysis #
Big-O analysis is usually described in terms of functions on ℝ (the real numbers), such as O(n), O(lg n), O(n3), O(2n) and so on. This is somewhat ironic because when analysing algorithm efficiency, n is usually an integer (i.e. n ∈ ℕ). That, however, suits me fine, because it establishes precedence for what I have in mind.
Usually, big-O analysis is applied to algorithms, and usually by measuring an abstract notion of an 'instruction step'. You can, however, also apply such analysis to other aspects of resource utilization. Even within the confines of algorithm analysis, you may instead of instruction count be concerned with memory consumption. In other words, you may analyze an algorithm in order to determine that it uses O(n2) memory.
With that in mind, nothing prevents you from widening the scope further. While I tend to be disinterested in the small-scale performance optimizations involved with algorithms, I have a keen eye on how it applies to software architecture. In modern computers, CPU cycles are fast, but network hops are still noticeable to human perception. For example, the well-known n+1 problem really just implies O(n) network calls. Given that a single network hop may already (depending on topology and distance) be observable, even moderate numbers of n (e.g. 100) may be a problem.
What I have in mind for this article is to once more transplant the thinking behind big-O notation to a new area. Instead of instructions or network calls, let O(...) indicate the number of edits you have to make in a code base in order to make a change. If we want to be more practical about it, we may measure this number in how many methods or functions we need to edit, or, even more coarsely, the number of files we need to change.
Don't Repeat Yourself #
In this view, the old DRY principle implies O(1) edits. You create a single point in your code base responsible for a given behaviour. If you need to make changes, you edit a single part of the code base. This seems obvious.
What the big-O perspective implies, however, is that a small constant number of edits may be fine, too. For instance, 'dual' coupling, where two code blocks change together, is not that uncommon. This could for example be where you model messages on an internal queue. Every time you add a new message type, you'll need to define both how to send it (i.e. what data it contains and how it serializes) and how to handle it. If you are using a statically typed language, you can use a sum type or Visitor to keep track of all message types, which means that the type checker will remind you if you forget one or the other.
In big-O notation, we simplify all constants to 1, so even if you have systematic, but constant, coupling like this, we would still consider it O(1). In other words, if your architecture contains some coupling that remains constant, we may deem it O(1) and perhaps benign.
This also suggests why we have a heuristic like the rule of three. Dual duplication is still O(1), and as long as the coupling stays constant, there's no evidence that it's growing. Once you make the third copy does evidence begin to suggest that the coupling is O(n) rather than O(1).
Small values of 1 #
Big-O notation is concerned with comparing orders of magnitude, which is why specific constants are simplified to 1. The number 1 is a stand-in for any constant value, 1, 2, 10, og even six billion. When editing source code, however, the actual number of edits does matter. In the following sections, I'll give concrete examples where '1' is small.
Test-specific equality #
The first example we may consider is test-specific equality. My first treatment related to this topic was in 2010, and again in 2012. Since then, I've come to view the need for test-specific equality as a test smell. If you are doing test-driven development (which you chiefly should), giving your objects or values sane equality semantics makes testing much easier. And a well-known benefit of test-driven development (TDD) is that code that is easy to test is easy to use.
Still, if you must work with mutable objects (as in naive object-oriented design), you can't give objects structural equality. And as I recently rediscovered, functional programming doesn't entirely shield you from this kind of problem either. Functions, for example, don't have clear equality semantics in practice, so when bundling data and behaviour (does that sound familiar?), data structures can't have structural equality.
Still, TDD suggests that you should reconsider your API design when that happens. Sometimes, however, part of an API is locked. I recently described such a situation, which prompted me to write test-specific Eq instances. In short, the Haskell data type Finch was not an Eq instance, so I added this test-specific data type to improve testability:
data FinchEq = FinchEq { feqID :: Int , feqHP :: Galapagos.HP , feqRoundsLeft :: Galapagos.Rounds , feqColour :: Galapagos.Colour , feqStrategyExp :: Exp } deriving (Eq, Show)
Later, I also introduced a second test-specific data structure, CellStateEq to address the equivalent problem that CellState isn't an Eq instance. This means that I have two representations of essentially the same kind of data. If I, much later, learn that I need to add, remove, or modify a field of, say, Finch, I would also need to edit FinchEq.
There's a clear edit-time coupling with constant value 2. When I edit one, I also need to edit the other. In big-O perspective, we could say that the specific value of 1 is 2, or 1~2, and so the edits required to maintain this part of the code base is of the order O(1).
Maintaining Fake objects #
Another interesting example is the one that originally elicited this chain of thought. In Greyscale-box test-driven development I showed an example of how using interactive white-box testing with Dynamically Generated Test Doubles (AKA Dynamic Mocks) leads to Fragile Tests. More on this later, but I also described how using Fake Objects and state-based testing doesn't have the same problem.
In a response on Bluesky Laszlo (@ladeak.net) pointed out that this seemed to imply a three-way coupling that I had, frankly, overlooked.
You can review the full description of the example in the article Greyscale-box test-driven development, but in summary it proceeds like this: We wish to modify an implementation detail related to how the system queries its database. Specifically, we wish to change an inclusive integer-based upper bound to an exclusive bound. Thus, we change the relevant part of the SQL WHERE clause from
@Min <= [At] AND [At] <= @Max"
to
@Min <= [At] AND [At] < @Max"
Specifically, the single-character edit removes = from the rightmost <=.
Since this modification changes the implied contract, we also need to edit the calling code. That's another single-line edit that changes
var max = min.AddDays(1).AddTicks(-1);
to
var max = min.AddDays(1);
What I had overlooked was that I should also have changed the single test-specific Fake object used for state-based testing. Since I changed the contract of the IReservationsRepository interface, and since Fakes are Test Doubles with contracts, it follows that the FakeDatabase class must also change.
This I had overlooked because no tests based on FakeDatabase failed. More on that in a future post, but the required edit is easy enough. Change
.Where(r => min <= r.At && r.At <= max).ToList());
to
.Where(r => min <= r.At && r.At < max).ToList());
Again, the edit involves deleting a single = character.
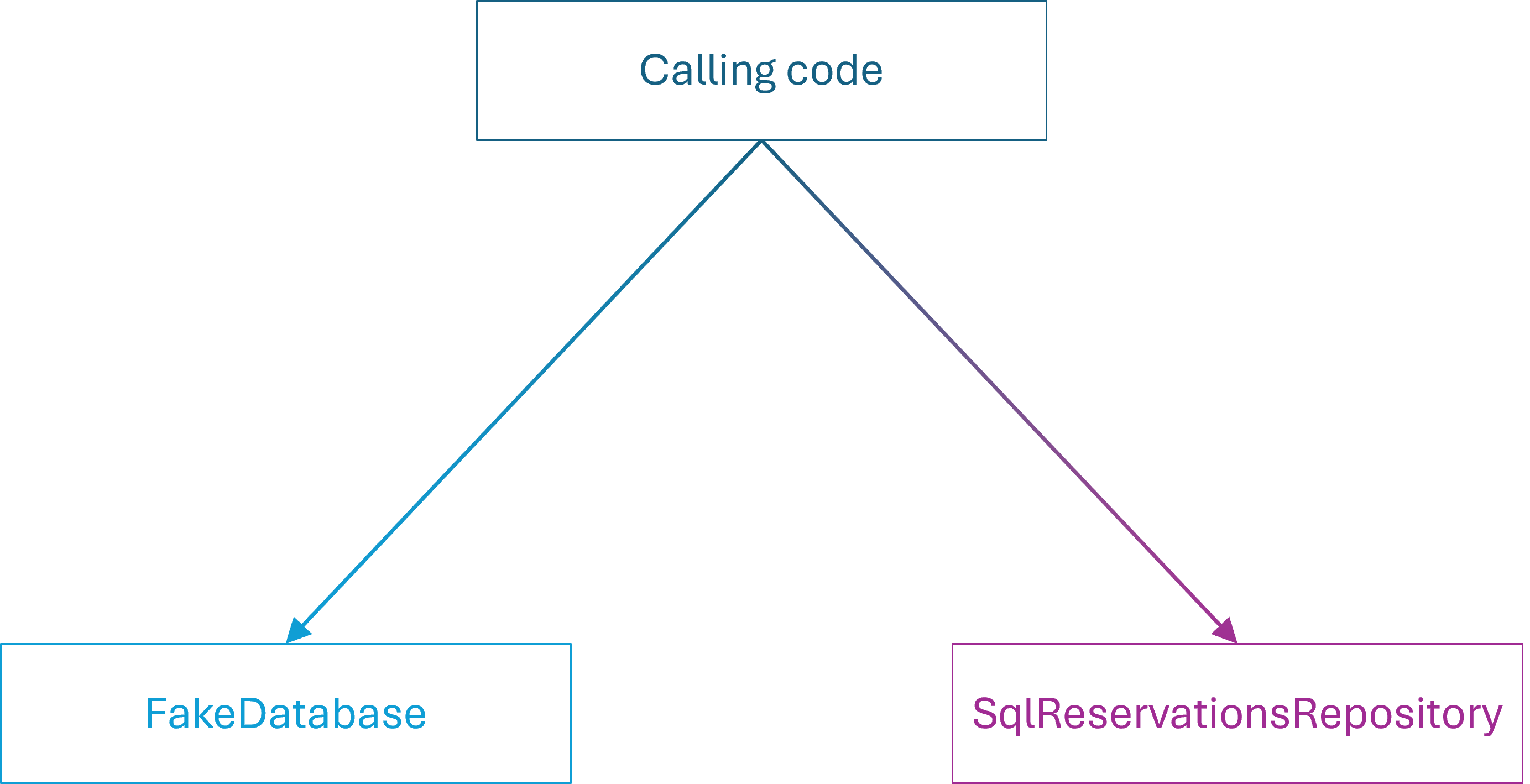
Still, in this example, not only two, but three files are coupled. With the perspective of big-O notation, however, we may say that 1~3, and the order of edits required to maintain this part of the code base remains O(1). Later in this article, I will discuss the maintenance burden of dynamic mocks, which I consider to be O(n). Thus, even if I have a three-way coupling, I don't expect the coupling to grow over time. That's the point: I prefer O(1) over O(n).
Large values of 1 #
As I'm sure practical programmers know, big-O notation has limitations. First, as Rob Pike observed, "n is usually small". More germane to this discussion
"algorithms have big constants."
In this context, this implies that the constant we're deliberately ignoring when we label something O(1) could, in theory, be significant. We don't write O(2,000,000), but if we did, it would look like more, wouldn't it? Even if it doesn't depend on n.
It looks to me that when we discuss source code edits, 5 or 6 could already be considered large.
Layers #
Although software design thought leaders have denounced layered software architecture more than a decade ago, I don't entirely agree with that position. That, however, is a topic for a different article. In any case, I still regularly see examples of design that involves a UI DTO, a Domain Model, and a Data Access layer.
As I enumerated in 2012, a simple operation, such as adding a label field, involves at least six steps.
- "A Label column must be added to the database schema and the DbTrack class.
- "A Label property must be added to the Track class.
- "The mapping from DbTrack to Track must be updated.
- "A Label property must be added to the TopTrackViewModel class.
- "The mapping from Track to TopTrackViewModel must be updated.
- "The UI must be updated."
People often complain about all the seemingly redundant work involved with such layering, and I don't blame them. At least, if there's no clear motivation for a design like that, and no evident benefit, it looks like redundant work. While you can make good use of separating concerns across layers, that's outside the scope of this article. In the naive way most often employed, it seems like mindless ceremony.
Even so, how would we denote the above enumeration in terms of big-O notation? Adding a label field is an O(1) edit.
How so? Adding, changing, or deleting a field in a particular database table always entails the same number of steps (six) as outlined above. If, in addition to the Track table you want to add, say, an Album table, you create it according to the three-layer model. This again means that every edit of that table involves six steps. It's still O(1), with 1~6, but already it hurts.
Apparently, six may be a 'large constant'.
Linear edits #
So far, we've exclusively examined multiple examples of O(1) edits. Some of them, particularly the layered-architecture example, may seem counterintuitive at first. If it requires editing six different 'blocks' of code to make a single change (not counting tests!) is still O(1), then does anything constitute O(n), or any other kind of relationship?
To be realistic, I don't think we're in an analytical regime that allows us fine distinctions like identifying any kind of code organization to be, say O(lg n) or O(n lg n). On the other hand, examples of O(n) abound.
Every time you run into the Shotgun Surgery anti-pattern, you are looking at O(n) edits. As a simple example, consider poorly-factored logging, as for example shown initially in Repeatable execution. In such situations, you have n classes that log. If you need to change how logging is done, you must change n classes.
More generally, the main (unstated) goal of the DRY principle is to turn O(n) edits into O(1) edits.
Every junior developer already knows this. Notwithstanding, there's a category of code where even senior programmers routinely forget this.
Linear test coupling #
When it comes to automated testing, many developers treat test code stepmotherly. The most common mistake is the misguided notion that copy-and-paste code is fine in test code. It's not. Duplicated test code means that when you make a change in the System Under Test, n tests break, and you will have to fix each one individually, a clear O(n) edit (where n is the number of tests).
A more subtle example of an O(n) test maintenance burden can be found in test code that uses dynamic mocks. When you use a configurable mock object, each test contains isolated configuration code related to that specific test.
Let's look at an example. Consider the Moq-based tests from An example of interaction-based testing in C#. One test contains this Assert phase:
readerTD .Setup(r => r.Lookup(user.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(user)); readerTD .Setup(r => r.Lookup(otherUser.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(otherUser));
Another test arranges the same two Test Doubles, but configures the second differently.
readerTD .Setup(r => r.Lookup(user.Id.ToString())) .Returns(Result.Success<User, IUserLookupError>(user)); readerTD .Setup(r => r.Lookup(otherUserId)) .Returns(Result.Error<User, IUserLookupError>( UserLookupError.InvalidId));
Yet more tests arrange the System Under Test (SUT) in other combinations. Refer to the article for the full example.
Such tests don't contain duplication per se, but each test is coupled to the SUT's dependencies. When you change one of the interfaces, you break O(n) tests, and you have to fix each one individually.
As suggested earlier in the article, this is the reason to favour Fake Objects. While an interface change may still break the tests, the effort to correct them is O(1) edits.
Two kinds of coupling #
The big-O perspective on coupling suggests that there are two kinds of coupling: O(1) coupling and O(n) coupling. We can find duplication in both categories.
In the O(1) case, duplication is somehow limited. It may be that you are following the rule of three. This allows two copies of a piece of code to exist. It may be that you've made a particular architectural decision, such as using Fake Objects for testing (triplication), or using layered architecture (sextuplication). In these cases, there's a fixed number of edits that you have to make, and in principle, you should know where to make them.
I tend to be less concerned about this kind of coupling because it's manageable. In many cases, you may be able to lean on the compiler to guide you through the task of making a change. In other cases, you could have a checklist. Consider the above example of layered architecture. A checklist would enumerate the six separate steps you need to perform. Once you've checked off all six, you're done.
It may be slow, tedious work, but it's generally safe, because you are unlikely to forget a spot.
The O(n) case is where real trouble lies. This is the case when you copy and paste a snippet of code every time you need it somewhere new. When, later, you discover that there's a bug in the original 'source', you need to find all the places it occurs. Typical copy-paste code is often slightly modified after paste, so a naive search-and-replace strategy is likely to miss some instances.
Of course, if you've copied a whole method, function, class, or module, you may still be able to find it by name, but if you've only copied an unnamed block of code, that will not work either.
Not all edits are equally difficult #
To be fair, we should acknowledge that not all edit are equally difficult. There are kinds of changes you can automate. Most modern code editors come with refactoring support. In the case of testing with dynamic mocks, for example, you can rename methods, rearrange parameter lists, or remove a parameter.
Even so, some edits are harder. Changing the return type of a method tends to break calling code in most high-ceremony languages. Likewise, changing a primitive parameter (an integer, a Boolean, a string) to a complex object is non-trivial, as is adding a parameter with no obvious good default value. This is when O(n) coupling hurts.
Limitations #
So far, we've considered O(1) and O(n) edits. Are there O(lg n) edits, O(n2), or even O(2n) edits?
I can't rule it out, and if the reader can furnish some convincing examples, I'd be keen to learn about them. To be honest, though, I'm not sure it's that helpful. One could perhaps construe an example where inheritance creates a quadratic growth of subclasses, because someone is trying to model two independent features in a single inheritance tree. This, however, is just bad design, and we don't need the big-O lens to tell us that.
Conclusion #
As a thought experiment, one may adopt big-O notation as a viewpoint on code organisation. This seems particularly valuable when distinguishing between benign and malignant duplication. Duplication usually entails coupling. For a 'code architect', one of the most important tasks is to reduce, or at least control, coupling.
Some coupling is of the order O(1). Hidden in this notation is a constant, which may indicate that a change can be made with a single edit, two edits, six edits, and so on. Even if the actual number is 'large', you can put tools in place to minimize risk: A simple checklist may be enough, or perhaps you can leverage a static type system.
Other coupling is of the order O(n). Here, a single change must be made in O(n) different places, where n tends to grow over time, and there's no clear way to systematically find and identify them all. This kind of coupling strikes me as more dangerous than O(1) coupling.
When I sometimes seem to have a cavalier attitude to duplication, it's likely because I've already subconsciously identified a particular duplication as of the order O(1).
Git integration is ten years away
We'll get commercial nuclear fusion earlier.
Although, as I've described earlier, I tend to be conservative about updating my laptop, I tend to make exceptions for Visual Studio and Visual Studio Code. I was recently perusing the "what's new" notes after updating one or the other, and among all the new AI capabilities that I'm not interested in, I noticed something else: 'improved Git integration.'
As I reflected on that, a thought occurred to me. It seems to me that I've seen these update notes for at least a decade. Improved Git integration.
I'm not even exaggerating. Git support for Visual Studio was announced in 2013. It has, indeed, been around for a long time, and I've been blissfully ignoring it throughout. Even so, it struck me when reading release notes in 2025, that the product in question had improved Git integration.
Is it not done yet?
Apparently not.
It wasn't done ten years ago? Is there any reason to believe that it's done now? Or are we witnessing some reverse Lindy effect? The longer something has been in development, the longer you may expect it to be in development yet?
Sarcasm aside, you don't need Git integration in your development environment. Do yourself a favour and learn the fundamentals of Git. It takes a few hours to learn the basics, a few days to become more comfortable with it, but from then, no 'integration' need hold you back. You don't have to wait for the next update. Use Git tactically today.
Test-specific Eq
Adding Eq instances for better assertions.
Most well-written unit tests follow some variation of the Arrange Act Assert pattern. In the Assert phase, you may write a sequence of assertions that verify different aspects of what 'success' means. Even so, it boils down to this: You check that the expected outcome is equal to the actual outcome. Some testing frameworks like to turn the order around, but the idea remains the same. After all, equality is symmetric.
The ideal assertion is one that simply checks that actual is equal to expected. Some languages allow custom infix operators, in which case it's natural to define this fundamental assertion as an operator, such as @?=.
Since this is Haskell, however, the @?= operator comes with type constraints. Specifically, what we compare must be an Eq instance. In other words, the type in question must support the == operator. What do you do when a type is no Eq instance?
No Eq #
In a recent article you saw how a complicated test induced a tautological assertion. The main reason that the test was complicated was that the values involved were not Eq instances.
This got me thinking: Might test-specific equality help?
The easiest way to find out is to try. In this article, you'll see how that experiment turns out. First, however, you need a quick introduction to the problem space. The task at hand was to implement a cellular automaton, ostensibly modelling Galápagos finches meeting. When two finches encounter each other, they play out a game of Prisoner's Dilemma according to a strategy implemented in a domain-specific language.
Specifically, a finch is modelled like this:
data Finch = Finch { finchID :: Int, finchHP :: HP, finchRoundsLeft :: Rounds, -- The colour is used for visualisation, but has no semantic significance. finchColour :: Colour, -- The current strategy. finchStrategy :: Strategy, -- The expression that is evaluated to produce the strategy. finchStrategyExp :: Exp }
The Finch data type is not an Eq instance. The reason is that Strategy is effectively a free monad over this functor:
data EvalOp a
= ErrorOp Error
| MeetOp (FinchID -> a)
| GroomOp (Bool -> a)
| IgnoreOp (Bool -> a)
Since EvalOp is a sum of functions, it can't be an Eq instance, and this then applies transitively to Finch, as well as the CellState container that keeps track of each cell in the cellular grid:
data CellState = CellState { cellFinch :: Maybe Finch, cellRNG :: StdGen }
An important part of working with this particular code base is that the API is given, and must not be changed.
Given these constraints and data types, is there a way to improve test assertions?
Smelly tests #
The lack of Eq instances makes it difficult to write simple assertions. The worst test I wrote is probably this, making use of a predefined example Finch value named flipflop:
testCase "Cell 1 reproduces" $ let cell1 = Galapagos.CellState (Just flipflop) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 6) -- seeded to reprod actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) in do -- Sanity check on first finch. Unfortunately, CellState is no Eq -- instance, so we can't just compare the entire record. Instead, -- using HP as a sample: (Galapagos.finchHP <$> Galapagos.cellFinch (fst actual)) @?= Just 20 -- New finch should have HP from params: (Galapagos.finchHP <$> Galapagos.cellFinch (snd actual)) @?= Just 14 -- New finch should have lifespan from params: (Galapagos.finchRoundsLeft <$> Galapagos.cellFinch (snd actual)) @?= Just 23 -- New finch should have same colour as parent: ( Galapagos.finchColour <$> Galapagos.cellFinch (snd actual)) @?= Galapagos.finchColour <$> Galapagos.cellFinch cell1 -- More assertions, described by their error messages: ( (Galapagos.finchID <$> Galapagos.cellFinch (fst actual)) /= (Galapagos.finchID <$> Galapagos.cellFinch (snd actual))) @? "Finches have same ID, but they should be different." ((/=) `on` Galapagos.cellRNG) cell2 (snd actual) @? "New cell 2 should have an updated RNG."
As you can tell from the apologies all these assertions leave something to be desired. The first assertion uses finchHP as a proxy for the entire finch in cell1, which is not supposed to change. Instead of an assertion for each of the first finch's attributes, the test 'hopes' that if finchHP didn't change, then so didn't the other values.
The test then proceeds to verify various fields of the new finch in cell2, checking them one by one, since the lack of Eq makes it impossible to simply check that the actual value is equal to the expected value.
In comparison, the test you saw in the previous article is almost pretty. It uses another example Finch value named cheater.
testCase "Cell 1 does not reproduce" $ let cell1 = Galapagos.CellState (Just cheater) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 1) -- seeded: no repr. actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) in do -- Sanity check that cell 1 remains, sampling on strategy: ( Galapagos.finchStrategyExp <$> Galapagos.cellFinch (fst actual)) @?= Galapagos.finchStrategyExp <$> Galapagos.cellFinch cell1 ( Galapagos.finchHP <$> Galapagos.cellFinch (snd actual)) @?= Nothing
The apparent simplicity is mostly because at that time, I'd almost given up on more thorough testing. In this test, I chose finchStrategyExp as a proxy for each value, and 'hoped' that if these properties behaved as expected, other attributes would, too.
Given that I was following test-driven development and thus engaging in grey-box testing, I had reason to believe that the implementation was correct if the test passes.
Still, those tests exhibit more than one code smell. Could test-specific equality be the answer?
Test utilities for finches #
The fundamental problem is that the finchStrategy field prevents Finch from being an Eq instance. Finding a way to compare Strategy values seems impractical. A more realistic course of action might be to compare all other fields. One option is to introduce a test-specific type with proper Eq and Show instances.
data FinchEq = FinchEq { feqID :: Int , feqHP :: Galapagos.HP , feqRoundsLeft :: Galapagos.Rounds , feqColour :: Galapagos.Colour , feqStrategyExp :: Exp } deriving (Eq, Show)
This data type only exists in the test code base. It has all the fields of Finch, except finchStrategy.
While I could use it as-is, it quickly turns out that a helper function to turn a CellState value into a FinchEq value would also be useful.
finchEq :: Galapagos.Finch -> FinchEq finchEq f = FinchEq { feqID = Galapagos.finchID f , feqHP = Galapagos.finchHP f , feqRoundsLeft = Galapagos.finchRoundsLeft f , feqColour = Galapagos.finchColour f , feqStrategyExp = Galapagos.finchStrategyExp f } cellFinchEq :: Galapagos.CellState -> Maybe FinchEq cellFinchEq = fmap finchEq . Galapagos.cellFinch
Finally, the System Under Test (the reproduce function) takes a tuple as input, and returns a tuple of the same type as output. To avoid some code duplication, it's practical to introduce a data type that can map over both components.
newtype Pair a = Pair (a, a) deriving (Eq, Show, Functor)
This newtype wrapper makes it possible to map both the first and the second component of a pair (a two-tuple) using a single projection, since Pair is a Functor instance.
That's all the machinery required to rewrite the two tests shown above.
Improving the first test #
The first test may be rewritten as this:
testCase "Cell 1 reproduces" $ let cell1 = Galapagos.CellState (Just flipflop) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 6) -- seeded to reprod actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) expected = Just $ finchEq $ flipflop { Galapagos.finchID = -1142203427417426925 -- From Character. Test , Galapagos.finchHP = 14 , Galapagos.finchRoundsLeft = 23 } in do (cellFinchEq <$> Pair actual) @?= Pair (cellFinchEq cell1, expected) ((/=) `on` Galapagos.cellRNG) cell2 (snd actual) @? "New cell 2 should have an updated RNG."
That's still a bit of code. If you're used to C# or Java code, you may not bat an eyelid over a fifteen-line code block (that even has a few blank lines), but fifteen lines of Haskell code is still significant.
There are compound reasons for this. One is that the Galapagos module is a qualified import, which makes the code more verbose than it otherwise could have been. It doesn't help that I follow a strict rule of staying within an 80-character line width.
That said, this version of the test has stronger assertions than before. Notice that the first assertion compares two Pairs of FinchEq values. This means that all five comparable fields of each finch is compared against the expected value. Since the assertion compares two Pairs, that's ten comparisons in all. The previous test only made five comparisons on the finches.
The second assertion remains as before. It's there to ensure that the System Under Test (SUT) remembers to update its pseudo-random number generator.
Perhaps you wonder about the expected values. For the finchID, hopefully the comment gives a hint. I originally set this value to 0, ran the test, observed the actual value, and used what I had observed. I could do that because I was refactoring an existing test that exercised an existing SUT, following the rules of empirical Characterization Testing.
The finchID values are in practice randomly generated numbers. These are notoriously awkward in test contexts, so I could also have excluded that field from FinchEq. Even so, I kept the field, because it's important to be able to verify that the new finch has a different finchID than the parent that begat it.
Derived values #
Where do the magic constants 14 and 23 come from? Although we could use comments to explain their source, another option is to use Derived Values to explicitly document their origin:
testCase "Cell 1 reproduces" $ let cell1 = Galapagos.CellState (Just flipflop) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 6) -- seeded to reprod actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) expected = Just $ finchEq $ flipflop { Galapagos.finchID = -1142203427417426925 -- From Character. Test , Galapagos.finchHP = Galapagos.startHP Galapagos.defaultParams , Galapagos.finchRoundsLeft = Galapagos.lifespan Galapagos.defaultParams } in do (cellFinchEq <$> Pair actual) @?= Pair (cellFinchEq cell1, expected) ((/=) `on` Galapagos.cellRNG) cell2 (snd actual) @? "New cell 2 should have an updated RNG."
We now learn that the finchHP value originates from the startHP value of the defaultParams, and similarly for finchRoundsLeft.
To be honest, I'm not sure that this is an improvement. It makes the test more abstract, and if we wish that tests may serve as executable documentation, concrete example values may be easier to understand. Besides, this gets uncomfortably close to duplicating the actual implementation code contained in the SUT.
This variation only serves as an exploration of alternatives. I would strongly consider rolling this change back, and instead add some comments to the magic numbers.
Improving the second test #
The second test improves better.
testCase "Cell 1 does not reproduce" $ let cell1 = Galapagos.CellState (Just cheater) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 1) -- seeded: no repr. actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) in (cellFinchEq <$> Pair actual) @?= Pair (cellFinchEq cell1, Nothing)
Not only is it shorter, the assertion is much stronger. It achieves the ideal of verifying that the actual value is equal to the expected value, comparing five data fields on each of the two finches.
Comparing cells #
The reproduce function uses the pseudo-random number generators embedded in the CellState data type to decide whether a finch reproduces in a given round. Thus, the number generators change in deterministic, but by human cognition unpredictable, ways. It makes sense to exclude the generators from the assertions, apart from the above assertion that verifies the change itself.
Other functions in the Galapagos module also work on CellState values, but are entirely deterministic; that is, they don't make use of the pseudo-random number generators. One such function is groom, which models what happens when two finches meet and play out their game of Prisoner's Dilemma by deciding to groom the other for parasites, or not. The function has this type:
groom :: Params -> (CellState, CellState) -> (CellState, CellState)
By specification, this function has no random behaviour, which means that we expect the number generators to stay the same. Even so, due to the lack of an Eq instance, comparing cells is difficult.
testCase "Groom when right cell is empty" $ let cell1 = Galapagos.CellState (Just flipflop) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 1) actual = Galapagos.groom Galapagos.defaultParams (cell1, cell2) in do ( Galapagos.finchHP <$> Galapagos.cellFinch (fst actual)) @?= Galapagos.finchHP <$> Galapagos.cellFinch cell1 ( Galapagos.finchHP <$> Galapagos.cellFinch (snd actual)) @?= Nothing
Instead of comparing cells, this test only considers the contents of each cell, and it only compares a single field, finchHP, as a proxy for comparing the more complete data structure.
With FinchEq we have a better way of comparing two finches, but we don't have to stop there. We may introduce another test-utility type that can compare cells.
data CellStateEq = CellStateEq { cseqFinch :: Maybe FinchEq , cseqRNG :: StdGen } deriving (Eq, Show)
A helper function also turns out to be useful.
cellStateEq :: Galapagos.CellState -> CellStateEq cellStateEq cs = CellStateEq { cseqFinch = cellFinchEq cs , cseqRNG = Galapagos.cellRNG cs }
We can now rewrite the test to compare both cells in their entirety (minus the finchStrategy).
testCase "Groom when right cell is empty" $ let cell1 = Galapagos.CellState (Just flipflop) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 1) actual = Galapagos.groom Galapagos.defaultParams (cell1, cell2) in (cellStateEq <$> Pair actual) @?= cellStateEq <$> Pair (cell1, cell2)
Again, the test is both simpler and stronger.
A fly in the ointment #
Introducing FinchEq and CellStateEq allowed me to improve most of the tests, but a few annoying issues remain. The most illustrative example is this test of the core groom behaviour, which lets two example Finch values named samaritan and cheater interact.
testCase "Groom two finches" $ let cell1 = Galapagos.CellState (Just samaritan) (mkStdGen 0) cell2 = Galapagos.CellState (Just cheater) (mkStdGen 1) actual = Galapagos.groom Galapagos.defaultParams (cell1, cell2) expected = Just <$> Pair ( finchEq $ samaritan { Galapagos.finchHP = 16 } , finchEq $ cheater { Galapagos.finchHP = 13 } ) in (cellFinchEq <$> Pair actual) @?= expected
This test ought to compare cells with CellStateEq, but only compares finches. The practical reason is that defining the expected value as a pair of cells entails embedding the expected finches in their respective cells. This is possible, but awkward, due to the nested nature of the data types.
It's possible to do something about that, too, but that's the topic for another article.
Conclusion #
If a test is difficult to write, it may be a symptom that the System Under Test (SUT) has an API which is difficult to use. When doing test-driven development you may want to reconsider the API. Is there a way to model the desired data and behaviour in such a way that the tests become simpler? If so, the API may improve in general.
Sometimes, however, you can't change the SUT API. Perhaps it's already given. Perhaps improving it would be a breaking change. Or perhaps you simply can't think of a better way.
An alternative to changing the SUT API is to introduce test utilities, such as types with test-specific equality. This is hardly better than improving the SUT API, but may be useful in those situations where the best option is unavailable.
Tautological assertions are not always caused by aliasing
You can also make mistakes that compile in Haskell.
Seeing a (unit) test fail before making it pass is an important part of empirical software engineering. This is nothing new. We've known about the red-green-refactor cycle for at least twenty years, so we know that ensuring that a test can fail is of the essence.
A fundamental problem of automated testing is that we're writing code to test code. How do we know that our test code works? After all, it's easy enough to make mistakes, even with simple code.
The importance of discipline #
When I test-drive a programming task, it regularly happens that I write a test that I expect to fail, only for it to pass. Even so, it doesn't happen that often. During a week of intensive coding, it may happen once or twice.
After all, a unit test is supposed to be a simple, short block of code, ideally with a cyclomatic complexity of 1. If you're an experienced programmer, working in a language that you know, you wouldn't expect to make simple mistakes too often.
It's easy to get lulled into a false sense of security. When new tests fail (as they should) more than 95% of the time, you may be tempted to cut corners: Just write the test, implement the desired code, and move on.
My experience is, however, that I inadvertently write a passing test now and then. I've been doing test-driven development (TDD) for more than twenty years, and this still happens. It is therefore important to keep up discipline and run that damned test, even if you don't feel like it. It's exactly when your attention is flagging that you need this safety mechanism the most.
Until you've tried a couple of times writing a test that unexpectedly pass, it can be hard to grasp why the red phase is essential. Therefore I've always felt that it was important to publish examples.
Tautologies #
A new test that passes on the first run is almost always a tautology. Theoretically, it may be that you think that the System Under Test does not yet have a certain capability, but after writing the test, it turns out that, after all, it does. This almost never happens to me. I can't rule out that this may have been the case once or twice in the last few decades, but it's as scarce as hen's teeth.
Usually, the problem is that the test is a tautology. While you believe that the test correctly self-checks something relevant, in reality, it's written in such a way that it can't possibly fail.
The first time I had the opportunity to document such a tautological assertion the underlying problem turned out to be aliasing. The next examples I ran into also had their roots in aliasing.
I began to wonder: Is the problem of tautological assertions mostly related to aliasing? If so, does it mean that the phenomenon of writing a passing test by mistake is mostly isolated to procedural and object-oriented programming? Could it be that this doesn't happen in functional programming?
If it compiles, it works #
Many so-called functional programming languages are in reality mixed-paradigm languages. The one that I know best is F#, which Don Syme calls functional-first. Even so, it's explicitly designed to interact with .NET libraries written in other languages (almost always C#), so it can still suffer from aliasing problems. The same situation applies to Clojure and Scala, which both run on the JVM.
A few languages are, however, unapologetically functional. Haskell is probably the most famous. If you rule out actions that run in IO, shared mutable state is not a concern.
Haskell's type system is so advanced and powerful that there are programmers who still seem to approach the language with an implied attitude that if it compiles, it works. Clearly, as we shall see, that is not the case.
Example #
Last week, I was writing tests against an API that was already given. As the 53rd test, I wrote this:
testCase "Cell 1 does not reproduce" $ let cell1 = Galapagos.CellState (Just cheater) (mkStdGen 0) cell2 = Galapagos.CellState Nothing (mkStdGen 1) -- seeded: no repr. actual = Galapagos.reproduce Galapagos.defaultParams (cell1, cell2) in do -- Sanity check that cell 1 remains, sampling on strategy: ( Galapagos.finchStrategyExp <$> Galapagos.cellFinch (fst actual)) @?= Galapagos.finchStrategyExp <$> Galapagos.cellFinch cell1 ( Galapagos.finchHP <$> Galapagos.cellFinch cell2) @?= Nothing
To my surprise, it immediately passed. What's wrong with it? Before reading on, see if you can spot the problem.
I know that you don't know the problem domain or the particular API. Even so, the problem is in the test itself, not in the implementation code. After all, according to the red-green-refactor cycle, I hadn't yet added the code that would make this test pass.
The error is that I meant to verify that the actual value's second component remained Nothing, but either due to a brain fart, or because I copied an earlier test, the last assertion checks that cell2 is Nothing.
Since cell2 is originally initialized with Nothing, and Haskell values are immutable, there's no way it could be anything else. This is a tautological assertion. The correct assertion is
(Galapagos.finchHP <$> Galapagos.cellFinch (snd actual)) @?= Nothing
Notice that it examines snd actual rather than cell2.
Causes #
How could I be so stupid? First, to err is human, and this is exactly why it's important to start with a failing test. The error was mine, but even so, it sometimes pays to analyse if there might be an underlying driving force behind the error. In this case, I can identify at least two, although they are related.
First, I don't recall exactly how I wrote this test, but looking at previous commits, I find it likely that I copied and pasted an earlier test case. Evidently, I failed to correctly alter the assertion to specify the new test case.
Why was I even copying and pasting the test? Because the test is too complicated. As a rule of thumb, pay attention to copy-and-paste, also of test cases. Test code should be well-factored, without too much duplication, for the same reasons that apply to other code. If a test is too difficult to write, it indicates that the API is too difficult to use. This is feedback about the API design, and you should consider if simplification is possible.
And the test is, indeed, too complicated. What I wanted to verify is that Galapagos.cellFinch (snd actual) is Nothing. If so, why didn't I just write Galapagos.cellFinch (snd actual) @?= Nothing? Because that doesn't compile.
The issue is that the data type in question (Finch) doesn't have an Eq instance, which @?= requires. Thus, I had to project the value I wanted to examine to a value that does have an Eq instance, such finchHP, which is an Int.
Why didn't I assert on isNothing instead? Eventually, I did, but the problem with asserting on raw Boolean values is that when the assertion fails, you get no good feedback. The test runner will only tell you that the expected value was True, but the actual value False.
The assertBool action offers a solution, but then you have to write your own error message, and I wasn't yet ready to do that. Eventually, I did, though.
The bottom line is that the risk of making mistakes increases, the more complicated things become. This also applies to functional programming, but in reality, simple is rarely easy.
Conclusion #
Tautological assertions are not only caused by aliasing, but also plain human error. In this article, you've seen an example of such an error in Haskell. This is a language with a type system that can identify many errors at compile time. Even so, some errors are run-time errors, and when it comes to TDD, in the red phase, the absence of failure indicates an error.
I find it important to share such errors when they occur, because they are at the same time regular and uncommon. While rare, they still happen with some periodicity. Since, after all, they don't happen that often, it may take time if you only have your own mistakes to learn from. So learn from mine, too.
Pattern guards for a protocol
A Haskell example.
Recently, I was doing a Haskell project implementing a cellular automaton according to predefined rules. Specifically, the story was one of Galápagos finches meeting and deciding whether or not to groom each other for parasites, effectively playing out a round of prisoner's dilemma.
Each finch is equipped with a particular strategy for repeated play. This strategy is implemented in a custom domain-specific language that enables each finch to remember past actions of other finches, and make decisions based on this memory.
Meeting protocol #
An evaluator runs over the code that implements each strategy, returning a free monad that embeds the possible actions a finch may take when meeting another finch.
The possible actions are defined by this sum type:
data EvalOp a
= ErrorOp Error
| MeetOp (FinchID -> a)
| GroomOp (Bool -> a)
| IgnoreOp (Bool -> a)
When two finches a and b meet, they must interact according to a protocol.
- Evaluate the strategy of the finch a up to the next effect, which must be a
MeetOp. - Invoke the continuation of the
MeetOpwith thefinchIDof finch b. - Evaluate the strategy up to next effect, which must be
GroomOporIgnoreOp. This decides the behaviour of finch a during this meeting. - Similarly, determine the behaviour of finch b, using the
finchIDof finch a. - For each finch, invoke the continuation of the
GroomOporIgnoreOpwith the behaviour of the other finch (Truefor grooming,Falsefor ignoring), yielding two newStrategys (sic). - The resulting
Strategys (sic) are then stored in theFinchobjects for the next meeting of the finches.
If at any step a strategy does not produce one of the expected effects (or no effect at all), then the finch has behaved illegally. For example, if in step 1 the first effect is a GroomOp, then this is illegal.
This sounds rather complicated, and I was concerned that even though I could pattern-match against the EvalOp cases, I'd end up with duplicated and deeply indented code.
Normal pattern matching #
Worrying about duplication, I tried to see if I could isolate each finch's 'handshake' as a separate function. I was still concerned that using normal pattern matching would cause too much indentation, but subsequent experimentation shows that in this case, it's not really that bad.
Ultimately, I went with pattern guards, but I think that it may be more helpful to lead with an example of what the code would look like using plain vanilla pattern matching.
tryRun :: EvalM a -> FinchID -> Maybe (Bool -> EvalM a, Bool) tryRun (Free (MeetOp nextAfterMeet)) other = case nextAfterMeet other of (Free (GroomOp nextAfterGroom)) -> Just (nextAfterGroom, True) (Free (IgnoreOp nextAfterIgnore)) -> Just (nextAfterIgnore, False) _ -> Nothing tryRun _ _ = Nothing
Now that I write this article, I realize that I should have named the function handshake, but hindsight is twenty-twenty. In the moment, I went with tryRun, using the try prefix to indicate that this operation may fail, as also indicated by the Maybe return type. That naming convention is probably more idiomatic in F#, but I digress.
As announced, that's not half as bad as I had originally feared. There's the beginning of arrow code, but I suppose you could also say that of any use of if/then/else. Imagine, however, that the protocol involved a few more steps, and you'd have something quite ugly at hand.
Another slight imperfection is the repetition of returning Nothing. Again, this code would not keep me up at night, but it just so happened that I originally thought that it would be worse, so I immediately cast about for alternatives.
Using pattern guards #
Originally, I thought that perhaps view patterns would be suitable, but while looking around, I came across pattern guards and thought: What's that?
This language feature has been around since 2010, but it's new to me. It's a good fit for the problem at hand, and that's how I actually wrote the tryRun function:
tryRun :: EvalM a -> FinchID -> Maybe (Bool -> EvalM a, Bool) tryRun strategy other | (Free (MeetOp nextAfterMeet)) <- strategy , (Free (GroomOp nextAfterGroom)) <- nextAfterMeet other = Just (nextAfterGroom, True) tryRun strategy other | (Free (MeetOp nextAfterMeet)) <- strategy , (Free (IgnoreOp nextAfterIgnore)) <- nextAfterMeet other = Just (nextAfterIgnore, False) tryRun _ _ = Nothing
Now that I have the opportunity to compare the two alternatives, it's not clear that one is better than the other. You may even prefer the first, normal version.
The version using pattern guards has more lines of code, and code duplication in the repetition of the | (Free (MeetOp nextAfterMeet)) <- strategy pattern. On the other hand, we get rid of the duplicated Nothing return value. What is perhaps more interesting is that had the handshake protocol involved more steps, the pattern-guards version would remain flat, whereas the other version would require indentation.
To be honest, now that I write this article, the example has lost some of its initial lustre. Still, I learned about a Haskell language feature that I didn't know about, and thought I'd share the example.
Conclusion #
Most mature programming languages have so many features that a programmer may use a language for years, and still be unaware of useful alternatives. Haskell is the oldest language I use, and although I've programmed in it for a decade, I still learn new things.
In this article, you saw a simple example of using pattern guards. Perhaps you will find this language feature useful in your own code. Perhaps you already use it.
Treat test code like production code
You have to read and maintain test code, too.
I don't think I've previously published an article with the following simple message, which is clearly an omission on my part. Better late than never, though.
Treat test code like production code.
You should apply the same coding standards to test code as you do to production code. You should make sure the code is readable, well-factored, goes through review, etc., just like your production code.
Test mess #
It's not uncommon to encounter test code that has received a stepmotherly treatment. Such test code may still pay lip service to an organization's overall coding standards by having correct indents, placement of brackets, and other superficial signs of care. You don't have to dig deep, however, before you discover that the quality of the test code leaves much to be desired.
The most common problem is a disregard for the DRY principle. Duplication abound. It's almost as though people feel unburdened by the shackles of good software engineering practices, and as result relish in the freedom to copy and paste.
That freedom is, however, purely illusory. We'll return to that shortly.
Perhaps the second-most common category of poor coding practices applied to test code is the high frequency of Zombie Code. Commented-out code is common.
Other, less frequent examples of bad practices include use of arbitrary waits instead of proper thread synchronization, unwrapping of monadic values, including calling Task.Result instead of properly awaiting a value, and so on.
I'm sure that you can think of other examples.
Why good code is important #
I think that I can understand why people treat test code as a second-class citizen. It seems intuitive, although the intuition is wrong. Nevertheless, I think it goes like this: Since the test code doesn't go into production, it's seen as less important. And as we shall see below, there are, indeed, a few areas where you can safely cut corners when it comes to test code.
As a general rule, however, it's a bad idea to slack on quality in test code.
The reason lies in why we even have coding standards and design principles in the first place. Here's a hint: It's not to placate the computer.
"Any fool can write code that a computer can understand. Good programmers write code that humans can understand."
The reason we do our best to write code of good quality is that if we don't, it's going to make our work more difficult in the future. Either our own, or someone else's. But frequently, our own.
Forty (or fifty?) years of literature on good software development practices grapple with this fundamental problem. This is why my most recent book is called Code That Fits in Your Head. We apply software engineering heuristics and care about architecture because we know that if we fail to structure the code well, our mission is in jeopardy: We will not deliver on time, on budget, or with working features.
Once we understand this, we see how this applies to test code, too. If you have good test coverage, you will likely have a substantial amount of test code. You need to maintain this part of the code base too. The best way to do so is to treat it like your production code. Apply the same standards and design principles to test code as you do to your production code. This especially means keeping test code DRY.
Test-specific practices #
Since test code has a specialized purpose, you'll run into problems unique to that space. How should you structure a unit test? How should you organize them? How should you name them? How do you make them deterministic?
Fortunately, thoughtful people have collected and systematized their experience. The absolute most comprehensive such collection is xUnit Test Patterns, which has been around since 2007. Nothing in that book invalidates normal coding practices. Rather, it suggests specializations of good practices that apply to test code.
You may run into the notion that tests should be DAMP rather than DRY. If you expand the acronym, however, it stands for Descriptive And Meaningful Phrases, and you may realize that it's a desired quality of code independent of whether or not you repeat yourself. (Even the linked article fails, in my opinion, to erect a convincing dichotomy. Its notion of DRY is clearly not the one normally implied.) I think of the DAMP notion as related to Domain-Driven Design, which is another thematic take on making code fit in your head.
For a few years, however, I did, too, believe that copy-and-paste was okay in test code, but have long since learned that duplication slows you down in test code for exactly the same reason that it hurts in 'real' code. One simple change leads to Shotgun Surgery; many tests break, and you have to fix each one individually.
Dispensations #
All the same, there are exceptions to the general rule. In certain, well-understood ways, you can treat your test code with less care than production code.
Specifically, assuming that test code remains undeployed, you can skip certain security practices. You may, for example, hard-code test-only passwords directly in the tests. The code base that accompanies Code That Fits in Your Head contains an example of that.
You may also skip input validation steps, since you control the input for each test.
In my experience, security is the dominating exemption from the rule, but there may be other language- or platform-specific details where deviating from normal practices is warranted for test code.
One example may be in .NET, where a static code analysis rule may insist that you call ConfigureAwait. This rule is intended for library code that may run in arbitrary environments. When code runs in a unit-testing environment, on the other hand, the context is already known, and this rule can be dispensed with.
Another example is that in Haskell GHC may complain about orphan instances. In test code, it may occasionally be useful to give an existing type a new instance, most commonly an Arbitrary instance. While you can also get around this problem with well-named newtypes, you may also decide that orphan instances are no problem in a test code base, since you don't have to export the test modules as reusable libraries.
Conclusion #
You should treat test code like production code. The coding standards that apply to production code should also apply to test code. If you follow the DRY principle for production code, you should also follow the DRY principle in the test code base.
The reason is that most coding standards and design principles exist to make code maintainability easier. Since test code is also code, this still applies.
There are a few exception, most notably in the area of security, assuming that the test code is never deployed to production.
Comments
What are your thoughts on abstractions in test code? I have never found it necessary, but have at times been tempted to create abstractions in my test projects that themselves would require testing. This is usually only a consideration in projects with a complex test setup or very large test suites.
I am also curious about your thoughts on adding additional logic to the implementation code with the sole purpose of making it easier to test. As an example: Adding a method to a class that makes it a more complete abstraction, but that method is never called in production code.
My own opinion is split between keeping tests readable and potentially easier to maintain by using reusable abstractions, and keeping them simple and robust.
Thank you for writing. Regarding abstractions in test code, the answer depends on how you define the term abstraction. I find Robert C. Martin's definition useful.
"Abstraction is the elimination of the irrelevant and the amplification of the essential."
Using this definition, I have no objection to adding abstractions to test code if necessary, but as you imply, if the test code is simple enough, it may not be necessary. You could consider Test Data Builders, custom assertions, setup methods, etc. as test-specific abstractions. But again, if you simplify the System Under Test (SUT) by making data immutable, you don't need Test Data Builders either, so I agree that the need for substantial test abstractions may be a smell indicating that the SUT is too complicated.
Regarding your other question, I try to avoid APIs that exist exclusively to support testing, but even so, I think you can subcategorize doing that into a few buckets. Adding new methods or constructors that exist only to be called from unit tests? I don't do that, although you could argue that Constructor Injection is just that: Dependency Injection is often introduced to support testing, but it's also applicable in production code. The constructor that receives dependencies is also used to compose the production application.
Additionally, people often ask whether it's okay to make internal or private methods public so that it's possible to test them. In a code base created with test-driven development, this shouldn't be necessary, but again, if you have a legacy code base, other rules apply.
Another category of code that may at first spring into existence to support testing is what we may term inspection APIs. This could be a read-only property or field accessor that you can query in order to make an assertion. You may also decide to give an composite value structural equality to improve testing. Or, in property-based testing, you may use the There and back again technique, where one of the directions isn't entirely required. For example, if I were to repeat the Roman Numerals kata with property-based testing today, I'd add a 'formatter' or 'serializer', so that I could take any normal integer, format it as a Roman numeral, and then parse it again. This is quite common when testing parsers and the like. You could argue that the formatter isn't strictly required for the job, but it makes testing easier, and usually turns out to be handy in its own right.
This tends to be a generalizable observation. A test is the first client of the SUT, so if a test needs a capability, it's likely that other client code might find that capability useful, too. It happens that I write a bit of test-helper code that I eventually decide to move to the production code base for that reason.
Result is the most boring sum type
If you don't see the point, you may be looking in the wrong place.
I regularly encounter programmers who are curious about statically typed functional programming, but are struggling to understand the point of sum types (also known as Discriminated Unions, Union Types, or similar). Particularly, I get the impression that recently various thought leaders have begun talking about Result types.
There are deep mathematical reasons to start with Results, but on the other hand, I can understand if many learners are left nonplussed. After all, Result types are roughly equivalent to exceptions, and since most languages already come with exceptions, it can be difficult to see the point.
The short response is that there's a natural explanation. A Result type is, so to speak, the fundamental sum type. From it, you can construct all other sum types. Thus, you can say that Results are the most abstract of all sum types. In that light, it's understandable if you struggle to see how they are useful.
Coproduct #
My goal with this article is to point out why and how Result types are the most abstract, and perhaps least interesting, sum types. The point is not to make Result types compelling, or sell sum types in general. Rather, my point is that if you're struggling to understand what all the fuss is about algebraic data types, perhaps Result types are the wrong place to start.
In the following, I will tend to call Result by another name: Either, which is also the name used in Haskell, where it encodes a universal construction called a coproduct. Where Result indicates a choice between success and failure, Either models a choice between 'left' and 'right'.
Although the English language allows the pun 'right = correct', and thereby the mnemonic that the right value is the opposite of failure, 'left' and 'right' are otherwise meant to be as neutral as possible. Ideally, Either carries no semantic value. This is what we would expect from a 'most abstract' representation.
Canonical representation #
As Thinking with Types does an admirable job of explaining, Either is part of a canonical representation of types, in which we can rewrite any type as a sum of products. In this context, a product is a pair, as also outlined by Bartosz Milewski.
The point is that we may rewrite any type to a combination of pairs and Either values, with the Either values on the outside. Such rewrites work both ways. You can rewrite any type to a combination of pairs and Eithers, or you can turn a combination of pairs and Eithers into more descriptive types. Since two-way translation is possible, we observe that the representations are isomorphic.
Isomorphism with Maybe #
Perhaps the simplest example is the natural transformation between Either () a and Maybe a, or, in F# syntax, Result<'a,unit> and 'a option. The Natural transformations article shows an F# example.
For illustration, we may translate this isomorphism to C# in order to help readers who are more comfortable with object-oriented C-like syntax. We may reuse the IgnoreLeft implementation, also from Natural transformations, to implement a translation from IEither<Unit, R> to IMaybe<R>.
public static IMaybe<R> ToMaybe<R>(this IEither<Unit, R> source) { return source.IgnoreLeft(); }
In order to go the other way, we may define ToMaybe's counterpart like this:
public static IEither<Unit, T> ToEither<T>(this IMaybe<T> source) { return source.Accept(new ToEitherVisitor<T>()); } private class ToEitherVisitor<T> : IMaybeVisitor<T, IEither<Unit, T>> { public IEither<Unit, T> VisitNothing => new Left<Unit, T>(Unit.Instance); public IEither<Unit, T> VisitJust(T just) { return new Right<Unit, T>(just); } }
The following two parametrized tests demonstrate the isomorphisms.
[Theory, ClassData(typeof(UnitIntEithers))] public void IsomorphismViaMaybe(IEither<Unit, int> expected) { var actual = expected.ToMaybe().ToEither(); Assert.Equal(expected, actual); } [Theory, ClassData(typeof(StringMaybes))] public void IsomorphismViaEither(IMaybe<string> expected) { var actual = expected.ToEither().ToMaybe(); Assert.Equal(expected, actual); }
The first test starts with an Either value, converts it to Maybe, and then converts the Maybe value back to an Either value. The second test starts with a Maybe value, converts it to Either, and converts it back to Maybe. In both cases, the actual value is equal to the expected value, which was also the original input.
Being able to map between Either and Maybe (or Result and Option, if you prefer) is hardly illuminating, since Maybe, too, is a general-purpose data structure. If this all seems a bit abstract, I can see why. Some more specific examples may help.
Calendar periods in F# #
Occasionally I run into the need to treat different calendar periods, such as days, months, and years, in a consistent way. To my recollection, the first time I described a model for that was in 2013. In short, in F# you can define a discriminated union for that purpose:
type Period = Year of int | Month of int * int | Day of int * int * int
A year is just a single integer, whereas a day is a triple, obviously with the components arranged in a sane order, with Day (2025, 11, 14) representing November 14, 2025.
Since this is a three-way discriminated union, whereas Either (or, in F#: Result) only has two mutually exclusive options, we need to nest one inside of another to represent this type in canonical form: Result<int, Result<(int * int), (int * (int * int))>>. Note that the 'outer' Result is a choice between a single integer (the year) and another Result value. The inner Result value then presents a choice between a month and a day.
Converting back and forth is straightforward:
let periodToCanonical = function | Year y -> Ok y | Month (y, m) -> Error (Ok (y, m)) | Day (y, m, d) -> Error (Error (y, (m, d))) let canonicalToPeriod = function | Ok y -> Year y | Error (Ok (y, m)) -> Month (y, m) | Error (Error (y, (m, d))) -> Day (y, m, d)
In F# this translations may strike you as odd, since the choice between Ok and Error hardly comes across as neutral. Even so, there's no loss of information when translating back and forth between the two representations.
> Month (2025, 12) |> periodToCanonical;; val it: Result<int,Result<(int * int),(int * (int * int))>> = Error (Ok (2025, 12)) > Error (Ok (2025, 12)) |> canonicalToPeriod;; val it: Period = Month (2025, 12)
The implied semantic difference between Ok and Error is one reason I favour Either over Result, when I have the choice. When translating to C#, I do have a choice, since there's no built-in coproduct data type.
Calendar periods in C# #
If you have been perusing the code base that accompanies Code That Fits in Your Head, you may have noticed an IPeriod interface. Since this is internal by default, I haven't discussed it much, but it's equivalent to the above F# discriminated union. It's used to enumerate restaurant reservations for a day, a month, or even a whole year.
Since this is a Visitor-encoded sum type, most of the information about data representation can be discerned from the Visitor interface:
internal interface IPeriodVisitor<T> { T VisitYear(int year); T VisitMonth(int year, int month); T VisitDay(int year, int month, int day); }
Given an appropriate Either definition, we can translate any IPeriod value into a nested Either, just like the above F# example.
private class ToCanonicalPeriodVisitor : IPeriodVisitor<IEither<int, IEither<(int, int), (int, (int, int))>>> { public IEither<int, IEither<(int, int), (int, (int, int))>> VisitDay( int year, int month, int day) { return new Right<int, IEither<(int, int), (int, (int, int))>>( new Right<(int, int), (int, (int, int))>((year, (month, day)))); } public IEither<int, IEither<(int, int), (int, (int, int))>> VisitMonth( int year, int month) { return new Right<int, IEither<(int, int), (int, (int, int))>>( new Left<(int, int), (int, (int, int))>((year, month))); } public IEither<int, IEither<(int, int), (int, (int, int))>> VisitYear(int year) { return new Left<int, IEither<(int, int), (int, (int, int))>>(year); } }
Look out! I've encoded year, month, and day from left to right as I did before. This means that the leftmost alternative indicates a year, and the rightmost alternative in the nested Either value indicates a day. This is structurally equivalent to the above F# encoding. If, however, you are used to thinking about left values indicating error, and right values indicating success, then the two mappings are not similar. In the F# encoding, an 'outer' Ok value indicates a year, whereas here, a left value indicates a year. This may be confusing if your are expecting a right value, corresponding to Ok.
The structure is the same, but this may be something to be aware of going forward.
You can translate the other way without loss of information.
private class ToPeriodVisitor : IEitherVisitor<int, IEither<(int, int), (int, (int, int))>, IPeriod> { public IPeriod VisitLeft(int left) { return new Year(left); } public IPeriod VisitRight(IEither<(int, int), (int, (int, int))> right) { return right.Accept(new ToMonthOrDayVisitor()); } private class ToMonthOrDayVisitor : IEitherVisitor<(int, int), (int, (int, int)), IPeriod> { public IPeriod VisitLeft((int, int) left) { var (y, m) = left; return new Month(y, m); } public IPeriod VisitRight((int, (int, int)) right) { var (y, (m, d)) = right; return new Day(y, m, d); } } }
It's all fairly elementary, although perhaps a bit cumbersome. The point of it all, should you have forgotten, is only to demonstrate that we can encode any sum type as a combination of Either values (and pairs).
A test like this demonstrates that these two translations comprise a true isomorphism:
[Theory, ClassData(typeof(PeriodData))] public void IsomorphismViaEither(IPeriod expected) { var actual = expected .Accept(new ToCanonicalPeriodVisitor()) .Accept(new ToPeriodVisitor()); Assert.Equal(expected, actual); }
This test converts arbitrary IPeriod values to nested Either values, and then translates them back to the same IPeriod value.
Payment types in F# #
Perhaps you are not convinced by a single example, so let's look at one more. In 2016 I was writing some code to integrate with a payment gateway. To model the various options that the gateway made available, I defined a discriminated union, repeated here:
type PaymentService = { Name : string; Action : string } type PaymentType = | Individual of PaymentService | Parent of PaymentService | Child of originalTransactionKey : string * paymentService : PaymentService
This looks a little more complicated, since it also makes use of the custom PaymentService type. Even so, converting to the canonical sum of products representation, and back again, is straightforward:
let paymentToCanonical = function | Individual { Name = n; Action = a } -> Ok (n, a) | Parent { Name = n; Action = a } -> Error (Ok (n, a)) | Child (k, { Name = n; Action = a }) -> Error (Error (k, (n, a))) let canonicalToPayment = function | Ok (n, a) -> Individual { Name = n; Action = a } | Error (Ok (n, a)) -> Parent { Name = n; Action = a } | Error (Error (k, (n, a))) -> Child (k, { Name = n; Action = a })
Again, there's no loss of information going back and forth between these two representations, even if the use of the Error case seems confusing.
> Child ("1234ABCD", { Name = "MasterCard"; Action = "Pay" }) |> paymentToCanonical;;
val it:
Result<(string * string),
Result<(string * string),(string * (string * string))>> =
Error (Error ("1234ABCD", ("MasterCard", "Pay")))
> Error (Error ("1234ABCD", ("MasterCard", "Pay"))) |> canonicalToPayment;;
val it: PaymentType = Child ("1234ABCD", { Name = "MasterCard"
Action = "Pay" })
Again, you might wonder why anyone would ever do that, and you'd be right. As a general rule, there's no reason to do this, and if you think that the canonical representation is more abstract, and harder to understand, I'm not going to argue. The point is, rather, that products (pairs) and coproducts (Either values) are universal building blocks of algebraic data types.
Payment types in C# #
As in the calendar-period example, it's possible to demonstrate the concept in alternative programming languages. For the benefit of programmers with a background in C-like languages, I once more present the example in C#. The starting point is where Visitor as a sum type ends. The code is also available on GitHub.
Translation to canonical form may be done with a Visitor like this:
private class ToCanonicalPaymentTypeVisitor : IPaymentTypeVisitor< IEither<(string, string), IEither<(string, string), (string, (string, string))>>> { public IEither<(string, string), IEither<(string, string), (string, (string, string))>> VisitChild(ChildPaymentService child) { return new Right<(string, string), IEither<(string, string), (string, (string, string))>>( new Right<(string, string), (string, (string, string))>( ( child.OriginalTransactionKey, ( child.PaymentService.Name, child.PaymentService.Action ) ))); } public IEither<(string, string), IEither<(string, string), (string, (string, string))>> VisitIndividual(PaymentService individual) { return new Left<(string, string), IEither<(string, string), (string, (string, string))>>( (individual.Name, individual.Action)); } public IEither<(string, string), IEither<(string, string), (string, (string, string))>> VisitParent(PaymentService parent) { return new Right<(string, string), IEither<(string, string), (string, (string, string))>>( new Left<(string, string), (string, (string, string))>( (parent.Name, parent.Action))); } }
If you find the method signatures horrible and near-unreadable, I don't blame you. This is an excellent example that C# (together with similar languages) inhabit the zone of ceremony; compare this ToCanonicalPaymentTypeVisitor to the above F# paymentToCanonical function, which performs exactly the same work while being as strongly statically typed.
Another Visitor translates the other way.
private class FromCanonicalPaymentTypeVisitor : IEitherVisitor< (string, string), IEither<(string, string), (string, (string, string))>, IPaymentType> { public IPaymentType VisitLeft((string, string) left) { var (name, action) = left; return new Individual(new PaymentService(name, action)); } public IPaymentType VisitRight(IEither<(string, string), (string, (string, string))> right) { return right.Accept(new CanonicalParentChildPaymentTypeVisitor()); } private class CanonicalParentChildPaymentTypeVisitor : IEitherVisitor<(string, string), (string, (string, string)), IPaymentType> { public IPaymentType VisitLeft((string, string) left) { var (name, action) = left; return new Parent(new PaymentService(name, action)); } public IPaymentType VisitRight((string, (string, string)) right) { var (k, (n, a)) = right; return new Child(new ChildPaymentService(k, new PaymentService(n, a))); } } }
Here I even had to split one generic type signature over multiple lines, in order to prevent horizontal scrolling. At least you have to grant the C# language that it's flexible enough to allow that.
Now that it's possible to translate both ways, a simple tests demonstrates the isomorphism.
[Theory, ClassData(typeof(PaymentTypes))] public void IsomorphismViaEither(IPaymentType expected) { var actual = expected .Accept(new ToCanonicalPaymentTypeVisitor()) .Accept(new FromCanonicalPaymentTypeVisitor()); Assert.Equal(expected, actual); }
This test translates an arbitrary IPaymentType into canonical form, then translates that representation back to an IPaymentType value, and checks that the two values are identical. There's no loss of information either way.
This and the previous example may seem like a detour around the central point that I'm trying to make: That Result (or Either) is the most boring sum type. I could have made the point, including examples, in a few lines of Haskell, but that language is so efficient at that kind of work that I fear that the syntax would look like pseudocode to programmers used to C-like languages. Additionally, Haskell programmers don't need my help writing small mappings like the ones shown here.
Conclusion #
Result (or Either) is as a fundamental building block in the context of algebraic data types. As such, this type may be considered the most boring sum type, since it effectively represents any other sum type, up to isomorphism.
Object-oriented programmers trying to learn functional programming sometimes struggle to see the light. One barrier to understanding the power of algebraic data types may be related to starting a learning path with a Result type. Since Results are equivalent to exceptions, people understandably have a hard time seeing how Result values are better. Since Result types are so abstract, it can be difficult to see the wider perspective. This doubly applies if a teacher leads with Result, with it's success/failure semantics, rather than with Either and its more neutral left/right labels.
Since Either is the fundamental sum type, it follows that any other sum type, being more specialized, carries more meaning, and therefore may be more interesting, and more illuminating as examples. In this article, I've used a few simple, but specialized sum types with the intention to help the reader see the difference.
Empirical software prototyping
How do you add tests to a proof-of-concept? Should you?
This is the second article in a small series on empirical test-after development. I'll try to answer an occasionally-asked question: Should one use test-driven development (TDD) for prototyping?
There are variations on this question, but it tends to come up when discussing TDD. Some software thought leaders proclaim that you should always take advantage of TDD when writing code. The short response is that there are exceptions to that rule. Those thought leaders know that, too, but they choose to communicate the way that they do in order to make a point. I don't blame them, and I use a similar style of communication from time to time. If you hedge every sentence you utter with qualifications, the message often disappears in unclear language. Thus, when someone admonishes that you should always follow TDD, what they really mean (I suppose; I'm not a telepath) is that you should predominantly use TDD. More than 80% of the time.
This is a common teaching tool. A competent teacher takes into account the skill level of a student. A new learner has to start with the basics before advanced topics. Early in the learning process, there's no room for sophistication. Even when a teacher understands that there are exceptions, he or she starts with a general rule, like 'you should always do TDD'.
While this may seem like a digression, this detour answers most of the questions related to software prototyping. People find it difficult to apply TDD when developing a prototype. I do, too. So don't.
Prototyping or proof-of-concept? #
I've already committed the sin of using prototype and proof-of-concept interchangeably. This only reflects how I use these terms in conversation. While I'm aware that the internet offers articles to help me distinguish, I find the differences too subtle to be of use when communicating with other people. Even if I learn the fine details that separate one from the other, I can't be sure that the person I'm talking to shares that understanding.
Since prototype is easier to say, I tend to use that term more than proof-of-concept. In any case, a prototype in this context is an exploration of an idea. You surmise that it's possible to do something in a certain way, but you're not sure. Before committing to the uncertain idea, you develop an isolated code base to vet the concept.
This could be an idea for an algorithm, use of a new technology such as a framework or reusable library, a different cloud platform, or even a new programming language.
Such exploration is already challenging in itself. How is the API of the library structured? Should you call IsFooble or HasFooble here? How do you write a for loop in APL? How does one even compile a Java program? How do you programmatically provision new resources in Microsoft Fabric? How do you convert a JPG file to PDF on the server?
There are plenty of questions like these where you don't even know the shape of things. The point of the exercise is often to figure those things out. When you don't know how APIs are organized, or which technologies are available to you, writing tests first is difficult. No wonder people sometimes ask me about this.
Code to throw away #
The very nature of a prototype is that it's an experiment designed to explore an idea. The safest way to engage with a prototype is to create an isolated code base for that particular purpose. A prototype is not an MVP or an early version of the product. It is a deliberately unstructured exploration of what's possible. The entire purpose of a prototype is to learn. Often the exploration process is time-boxed.
If the prototype turns out to be successful, you may proceed to implement the idea in your production code base. Even if you didn't use TDD for the prototype, you should now have learned enough that you can apply TDD for the production implementation.
The most common obstacle to this chain of events, I understand, is that 'bosses' demand that a successful prototype be put into production. Try to resist such demands. It often helps planning for this from the outset. If you can, do the prototype in a way that effectively prevents such predictable demands. If you're exploring the viability of a new algorithm, write it in an alternative programming language. For example, I've written prototypes in Haskell, which very effectively prevents demands that the code be put into production.
If your organization is a little behind the cutting edge, you can also write the prototype in a newer version of your language or run-time. Use functional programming if you normally use object-oriented design. Or you may pick an auxiliary technology incompatible with how you normally do things: Use the 'wrong' JSON serializer library, an in-memory database, write a command-line program if you need a GUI, or vice versa.
You're the technical expert. Make technical decisions. Surely, you can come up with something that sounds convincing enough to a non-technical stakeholder to prevent putting the prototype into production.
To be sure we're on firm moral ground here: I'm not advocating that you should be dishonest, or work against the interests of your organization. Rather, I suggest that you act politically. Understand what motivates other people. Non-technical stakeholders usually don't have the insight to understand why a successful prototype shouldn't be promoted to production code. Unfortunately, they often view programmers as typists, and with that view, it seems wasteful to repeat the work of typing in the prototype code. Typing, however, is not a bottleneck, but it can be hard to convince other people of this.
If all else fails, and you're forced to promote the prototype to production code, you now have a piece of legacy code on hand, in which case the techniques outlined in the previous article should prove useful.
Prototyping in existing code bases #
A special case occurs when you need to do a prototype in an existing code base. You already have a big, complicated system, and you would like to explore whether a particular idea is applicable in that context. Perhaps data access is currently too slow, and you have an idea of how to speed things up, for example by speculative prefetching. When the problem is one of performance, you'll need to measure in a realistic environment. This may prevent you from creating an isolated prototype code base.
In such cases, use Git to your advantage. Make a new prototype branch and work there. You may deliberately choose to make it a long-lived feature branch. Once the prototype is done, the code may now be so out of sync with master that 'merge conflicts' sounds like a plausible excuse to a non-technical stakeholder. As above, be political.
In any case, don't merge the prototype branch, even if you could. Instead, use the knowledge gained during the prototype work to re-implement the new idea, this time using empirical software engineering techniques like TDD.
Conclusion #
Prototyping is usually antithetical to TDD. On the other hand, TDD is an effective empirical method for software development. Without it, you have to seek other answers to the question: How do we know that this works?
Due to the explorative nature of prototyping, testing of the prototype tends to be explorative as well. Start up the prototype, poke at it, see if it behaves as expected. While you do gain a limited amount of empirical knowledge from such a process, it's unsystematic and non-repeatable, so little corroboration of hypothesis takes place. Therefore, once the prototype work is done, it's important to proceed on firmer footing if the prototype was successful.
The safest way is to put the prototype to the side, but use the knowledge to test-drive the production version of the idea. This may require a bit of political manoeuvring. If that fails, and you're forced to promote the prototype to production use, you may use the techniques for adding empirical Characterization Tests.

Comments
Hi, Mark. Thanks for the article. Regarding the issue of secrets being added to the soure code, wouldn't it be better to rotate the secrets (i.e, change the password, revoke the API key, etc), instead of changing shared history? Unless that can't be done for some reason, of course.
Thank you for writing. Honestly, that option hadn't crossed my mind, but whenever possible, that sounds like the best alternative.