Rose tree catamorphism by Mark Seemann
The catamorphism for a tree with different types of nodes and leaves is made up from two functions.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for a rose tree, as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
A rose tree is a general-purpose data structure where each node in a tree has an associated value. Each node can have an arbitrary number of branches, including none. The distinguishing feature from a rose tree and just any tree is that internal nodes can hold values of a different type than leaf values.
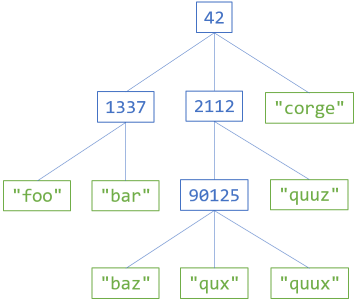
The diagram shows an example of a tree of internal integers and leaf strings. All internal nodes contain integer values, and all leaves contain strings. Each node can have an arbitrary number of branches.
C# catamorphism #
As a C# representation of a rose tree, I'll use the Church-encoded rose tree I've previously described. The catamorphism is this extension method:
public static TResult Cata<N, L, TResult>( this IRoseTree<N, L> tree, Func<N, IEnumerable<TResult>, TResult> node, Func<L, TResult> leaf) { return tree.Match( node: (n, branches) => node(n, branches.Select(t => t.Cata(node, leaf))), leaf: leaf); }
Like most of the other catamorphisms shown in this article series, this one consists of two functions. One that handles the leaf case, and one that handles the partially reduced node case. Compare it with the tree catamorphism: notice that the rose tree catamorphism's node function is identical to the the tree catamorphism. The leaf function, however, is new.
In previous articles, you've seen other examples of catamorphisms for Church-encoded types. The most common pattern has been that the Church encoding (the Match method) was also the catamorphism, with the Peano catamorphism being the only exception so far. When it comes to the Peano catamorphism, however, I'm not entirely confident that the difference between Church encoding and catamorphism is real, or whether it's just an artefact of the way I originally designed the Church encoding.
When it comes to the present rose tree, however, notice that the catamorphisms is distinctly different from the Church encoding. That's the reason I called the method Cata instead of Match.
The method simply delegates the leaf handler to Match, while it adds behaviour to the node case. It works the same way as for the 'normal' tree catamorphism.
Examples #
You can use Cata to implement most other behaviour you'd like IRoseTree<N, L> to have. In a future article, you'll see how to turn the rose tree into a bifunctor and functor, so here, we'll look at some other, more ad hoc, examples. As is also the case for the 'normal' tree, you can calculate the sum of all nodes, if you can associate a number with each node.
Consider the example tree in the above diagram. You can create it as an IRoseTree<int, string> object like this:
IRoseTree<int, string> exampleTree = RoseTree.Node(42, RoseTree.Node(1337, new RoseLeaf<int, string>("foo"), new RoseLeaf<int, string>("bar")), RoseTree.Node(2112, RoseTree.Node(90125, new RoseLeaf<int, string>("baz"), new RoseLeaf<int, string>("qux"), new RoseLeaf<int, string>("quux")), new RoseLeaf<int, string>("quuz")), new RoseLeaf<int, string>("corge"));
If you want to calculate a sum for a tree like that, you can use the integers for the internal nodes, and perhaps the length of the strings of the leaves. That hardly makes much sense, but is technically possible:
> exampleTree.Cata((x, xs) => x + xs.Sum(), x => x.Length) 93641
Perhaps slightly more useful is to count the number of leaves:
> exampleTree.Cata((_, xs) => xs.Sum(), _ => 1) 7
A leaf node has, by definition, exactly one leaf node, so the leaf lambda expression always returns 1. In the node case, xs contains the partially summed leaf node count, so just Sum those together while ignoring the value of the internal node.
You can also measure the maximum depth of the tree:
> exampleTree.Cata((_, xs) => 1 + xs.Max(), _ => 0) 3
Consistent with the example for 'normal' trees, you can arbitrarily decide that the depth of a leaf node is 0, so again, the leaf lambda expression just returns a constant value. The node lambda expression takes the Max of the partially reduced xs and adds 1, since an internal node represents another level of depth in a tree.
Rose tree F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
As always, start with the underlying endofunctor:
data RoseTreeF a b c = NodeF { nodeValue :: a, nodes :: ListFix c } | LeafF { leafValue :: b } deriving (Show, Eq, Read) instance Functor (RoseTreeF a b) where fmap f (NodeF x ns) = NodeF x $ fmap f ns fmap _ (LeafF x) = LeafF x
Instead of using Haskell's standard list ([]) for the nodes, I've used ListFix from the article on list catamorphism. This should, hopefully, demonstrate how you can build on already established definitions derived from first principles.
As usual, I've called the 'data' types a and b, and the carrier type c (for carrier). The Functor instance as usual translates the carrier type; the fmap function has the type (c -> c1) -> RoseTreeF a b c -> RoseTreeF a b c1.
As was the case when deducing the recent catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (RoseTreeF a b). To address that problem, you can introduce a newtype wrapper:
newtype RoseTreeFix a b = RoseTreeFix { unRoseTreeFix :: Fix (RoseTreeF a b) } deriving (Show, Eq, Read)
You can define Bifunctor, Bifoldable, Bitraversable, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A pair of helper functions make it easier to define RoseTreeFix values:
roseLeafF :: b -> RoseTreeFix a b roseLeafF = RoseTreeFix . Fix . LeafF roseNodeF :: a -> ListFix (RoseTreeFix a b) -> RoseTreeFix a b roseNodeF x = RoseTreeFix . Fix . NodeF x . fmap unRoseTreeFix
roseLeafF creates a leaf node:
Prelude Fix List RoseTree> roseLeafF "ploeh"
RoseTreeFix {unRoseTreeFix = Fix (LeafF "ploeh")}
roseNodeF is a helper function to create internal nodes:
Prelude Fix List RoseTree> roseNodeF 6 (consF (roseLeafF 0) nilF)
RoseTreeFix {unRoseTreeFix = Fix (NodeF 6 (ListFix (Fix (ConsF (Fix (LeafF 0)) (Fix NilF)))))}
Even with helper functions, construction of RoseTreeFix values is cumbersome, but keep in mind that the code shown here isn't meant to be used in practice. The goal is only to deduce catamorphisms from more basic universal abstractions, and you now have all you need to do that.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (RoseTreeF a b), and an object c, but you still need to find a morphism RoseTreeF a b c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not any of the 'data types' a or b. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a or b, as you'll see.
As in the previous articles, start by writing a function that will become the catamorphism, based on cata:
roseTreeF = cata alg . unRoseTreeFix where alg (NodeF x ns) = undefined alg (LeafF x) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the LeafF case? You could pass a function argument to the roseTreeF function and use it with x:
roseTreeF fl = cata alg . unRoseTreeFix where alg (NodeF x ns) = undefined alg (LeafF x) = fl x
While you could, technically, pass an argument of the type c to roseTreeF and then return that value from the LeafF case, that would mean that you would ignore the x value. This would be incorrect, so instead, make the argument a function and call it with x. Likewise, you can deal with the NodeF case in the same way:
roseTreeF :: (a -> ListFix c -> c) -> (b -> c) -> RoseTreeFix a b -> c roseTreeF fn fl = cata alg . unRoseTreeFix where alg (NodeF x ns) = fn x ns alg (LeafF x) = fl x
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of RoseTreeF, the compiler infers that the alg function has the type RoseTreeF a b c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
This, then, is the catamorphism for a rose tree. As has been the most common pattern so far, it's a pair, made from two functions. It's still not the only possible catamorphism, since you could trivially flip the arguments to roseTreeF, or the arguments to fn.
I've chosen the representation shown here because it's similar to the catamorphism I've shown for a 'normal' tree, just with the added function for leaves.
Basis #
You can implement most other useful functionality with roseTreeF. Here's the Bifunctor instance:
instance Bifunctor RoseTreeFix where bimap f s = roseTreeF (roseNodeF . f) (roseLeafF . s)
Notice how naturally the catamorphism implements bimap.
From that instance, the Functor instance trivially follows:
instance Functor (RoseTreeFix a) where fmap = second
You could probably also add Applicative and Monad instances, but I find those hard to grasp, so I'm going to skip them in favour of Bifoldable:
instance Bifoldable RoseTreeFix where bifoldMap f = roseTreeF (\x xs -> f x <> fold xs)
The Bifoldable instance enables you to trivially implement the Foldable instance:
instance Foldable (RoseTreeFix a) where foldMap = bifoldMap mempty
You may find the presence of mempty puzzling, since bifoldMap takes two functions as arguments. Is mempty a function?
Yes, mempty can be a function. Here, it is. There's a Monoid instance for any function a -> m, where m is a Monoid instance, and mempty is the identity for that monoid. That's the instance in use here.
Just as RoseTreeFix is Bifoldable, it's also Bitraversable:
instance Bitraversable RoseTreeFix where bitraverse f s = roseTreeF (\x xs -> roseNodeF <$> f x <*> sequenceA xs) (fmap roseLeafF . s)
You can comfortably implement the Traversable instance based on the Bitraversable instance:
instance Traversable (RoseTreeFix a) where sequenceA = bisequenceA . first pure
That rose trees are Traversable turns out to be useful, as a future article will show.
Relationships #
As was the case for 'normal' trees, the catamorphism for rose trees is more powerful than the fold. There are operations that you can express with the Foldable instance, but other operations that you can't. Consider the tree shown in the diagram at the beginning of the article. This is also the tree that the above C# examples use. In Haskell, using RoseTreeFix, you can define that tree like this:
exampleTree = roseNodeF 42 ( consF ( roseNodeF 1337 ( consF (roseLeafF "foo") $ consF (roseLeafF "bar") nilF)) $ consF ( roseNodeF 2112 ( consF ( roseNodeF 90125 ( consF (roseLeafF "baz") $ consF (roseLeafF "qux") $ consF (roseLeafF "quux") nilF)) $ consF (roseLeafF "quuz") nilF)) $ consF ( roseLeafF "corge") nilF)
You can trivially calculate the sum of string lengths of all leaves, using only the Foldable instance:
Prelude RoseTree> sum $ length <$> exampleTree 25
You can also fairly easily calculate a sum of all nodes, using the length of the strings as in the above C# example, but that requires the Bifoldable instance:
Prelude Data.Bifoldable Data.Semigroup RoseTree> bifoldMap Sum (Sum . length) exampleTree
Sum {getSum = 93641}
Fortunately, we get the same result as above.
Counting leaves, or measuring the depth of a tree, on the other hand, is impossible with the Foldable instance, but interestingly, it turns out that counting leaves is possible with the Bifoldable instance:
countLeaves :: (Bifoldable p, Num n) => p a b -> n countLeaves = getSum . bifoldMap (const $ Sum 0) (const $ Sum 1)
This works well with the example tree:
Prelude RoseTree> countLeaves exampleTree 7
Notice, however, that countLeaves works for any Bifoldable instance. Does that mean that you can 'count the leaves' of a tuple? Yes, it does:
Prelude RoseTree> countLeaves ("foo", "bar")
1
Prelude RoseTree> countLeaves (1, 42)
1
Or what about EitherFix:
Prelude RoseTree Either> countLeaves $ leftF "foo" 0 Prelude RoseTree Either> countLeaves $ rightF "bar" 1
Notice that 'counting the leaves' of tuples always returns 1, while 'counting the leaves' of Either always returns 0 for Left values, and 1 for Right values. This is because countLeaves considers the left, or first, data type to represent internal nodes, and the right, or second, data type to indicate leaves.
You can further follow that train of thought to realise that you can convert both tuples and EitherFix values to small rose trees:
fromTuple :: (a, b) -> RoseTreeFix a b fromTuple (x, y) = roseNodeF x (consF (roseLeafF y) nilF) fromEitherFix :: EitherFix a b -> RoseTreeFix a b fromEitherFix = eitherF (`roseNodeF` nilF) roseLeafF
The fromTuple function creates a small rose tree with one internal node and one leaf. The label of the internal node is the first value of the tuple, and the label of the leaf is the second value. Here's an example:
Prelude RoseTree> fromTuple ("foo", 42)
RoseTreeFix {unRoseTreeFix = Fix (NodeF "foo" (ListFix (Fix (ConsF (Fix (LeafF 42)) (Fix NilF)))))}
The fromEitherFix function turns a left value into an internal node with no leaves, and a right value into a leaf. Here are some examples:
Prelude RoseTree Either> fromEitherFix $ leftF "foo"
RoseTreeFix {unRoseTreeFix = Fix (NodeF "foo" (ListFix (Fix NilF)))}
Prelude RoseTree Either> fromEitherFix $ rightF 42
RoseTreeFix {unRoseTreeFix = Fix (LeafF 42)}
While counting leaves can be implemented using Bifoldable, that's not the case for measuring the depths of trees (I think; leave a comment if you know of a way to do this with one of the instances shown here). You can, however, measure tree depth with the catamorphism:
treeDepth :: RoseTreeFix a b -> Integer treeDepth = roseTreeF (\_ xs -> 1 + maximum xs) (const 0)
The implementation is similar to the implementation for 'normal' trees. I've arbitrarily decided that leaves have a depth of zero, so the function that handles leaves always returns 0. The function that handles internal nodes receives xs as a partially reduced list of depths below the node in question. Take the maximum of those and add 1, since each internal node has a depth of one.
Prelude RoseTree> treeDepth exampleTree 3
This, hopefully, illustrates that the catamorphism is more capable, and that the fold is just a (list-biased) specialisation.
Summary #
The catamorphism for rose trees is a pair of functions. One function transforms internal nodes with their partially reduced branches, while the other function transforms leaves.
For a realistic example of using a rose tree in a real program, see Picture archivist in Haskell.
This article series has so far covered progressively more complex data structures. The first examples (Boolean catamorphism and Peano catamorphism) were neither functors, applicatives, nor monads. All subsequent examples, on the other hand, are all of these, and more. The next example presents a functor that's neither applicative nor monad, yet still foldable. Obviously, what functionality it offers is still based on a catamorphism.

Comments
Because of this sentence, in the picture of an example after the containing paragraph, I expected to see a(n) (internal) node with no branches.
Maxwill throw an exception when given an internal node with no children. What value do you want to return in that case?Tyson, thank you for writing. You're right that my implementation doesn't properly handle the empty edge case. That's also the case for Haskell's
maximumfunction. I find it annoying that it's a partial function.One can handle that edge case by assigning an arbitrary depth to an empty node, just as is the case for leaf nodes. If leaf nodes get assigned a depth of 0, wouldn't it be natural to also give empty internal nodes a depth of 0?
Yes, very natural. In particular, such a definition would be consistent with the corresponding definition for
Tree<>. More specifically, we want the behaviors to be the same when the two type parameters inIRoseTree<,>are the same (and the function passed in forleafis the same as the one passed in fornodeafter fixing the second argument toEnumberable.Empty<TResult>()>).I think the smallest change to get the depth to be
0for an internal node with no children is to replaceMaxwith a slight variant that returns-1when there are no children. I don't think this is readable though. It is quite the magic number. But it is just the codification of the thought process that lead to it.It is because of such edge cases that Jeremy Gibbons in his PhD thesis Algebras for Tree Algorithms says (on page 44) that the internal nodes of his rose tree must include at least one child.
I think Jeremy has me convinced. One could say that this heterogenous rose tree was obtained from the homogeneous variant by adding a type for the leaves. The homogeneous variant denoted leaves via an empty list of children. It makes sense then to remove the empty list approach for making a leaf when adding the typed approach. So, I think the best fix then would be to modify your definition of
RoseNode<,>in your first rose tree article to be the same as Jeremy's (by requiring thatIEnumerable<>of children is non-empty). This change would also better match your example pictures of a rose tree, which do not include an internal node without children.Yes, it'd definitely be an option to change the definition of an internal node to a NonEmptyCollection.
My underlying motivation for defining the type like I've done in these articles, however, was to provide the underlying abstraction for a functional file system. In order to model a file system, empty nodes should be possible, because they correspond to empty directories.