Conservative codomain conjecture by Mark Seemann
An API design heuristic.
For a while now, I've been wondering whether, in the language of Postel's law, one should favour being liberal in what one accepts over being conservative in what one sends. Yes, according to the design principle, a protocol or API should do both, but sometimes, you can't do that. Instead, you'll have to choose. I've recently reached the tentative conclusion that it may be a good idea favouring being conservative in what one sends.
Good API design explicitly considers contracts. What are the preconditions for invoking an operation? What are the postconditions? Are there any invariants? These questions are relevant far beyond object-oriented design. They are equally important in Functional Programming, as well as in service-oriented design.
If you have a type system at your disposal, you can often model pre- and postconditions as types. In practice, however, it frequently turns out that there's more than one way of doing that. You can model an additional precondition with an input type, but you can also model potential errors as a return type. Which option is best?
That's what this article is about, and my conjecture is that constraining the input type may be preferable, thus being conservative about what is returned.
An average example #
That's all quite abstract, so for the rest of this article, I'll discuss this kind of problem in the context of an example. We'll revisit the good old example of calculating an average value. This example, however, is only a placeholder for any kind of API design problem. This article is only superficially about designing an API for calculating an average. More generally, this is about API design. I like the average example because it's easy to follow, and it does exhibit some characteristics that you can hopefully extrapolate from.
In short, what is the contract of the following method?
public static TimeSpan Average(this IEnumerable<TimeSpan> timeSpans) { var sum = TimeSpan.Zero; var count = 0; foreach (var ts in timeSpans) { sum += ts; count++; } return sum / count; }
What are the preconditions? What are the postconditions? Are there any invariants?
Before I answer these questions, I'll offer equivalent code in two other languages. Here it is in F#:
let average (timeSpans : TimeSpan seq) = timeSpans |> Seq.averageBy (_.Ticks >> double) |> int64 |> TimeSpan.FromTicks
And in Haskell:
average :: (Fractional a, Foldable t) => t a -> a average xs = sum xs / fromIntegral (length xs)
These three examples have somewhat different implementations, but the same externally observable behaviour. What is the contract?
It seems straightforward: If you input a sequence of values, you get the average of all of those values. Are there any preconditions? Yes, the sequence can't be empty. Given an empty sequence, all three implementations throw an exception. (The Haskell version is a little more nuanced than that, but given an empty list of NominalDiffTime, it does throw an exception.)
Any other preconditions? At least one more: The sequence must be finite. All three functions allow infinite streams as input, but if given one, they will fail to return an average.
Are there any postconditions? I can only think of a statement that relates to the preconditions: If the preconditions are fulfilled, the functions will return the correct average value (within the precision allowed by floating-point calculations).
All of this, however, is just warming up. We've been over this ground before.
Modelling contracts #
Keep in mind that this average function is just an example. Think of it as a stand-in for a procedure that's much more complicated. Think of the most complicated operation in your code base.
Not only do real code bases have many complicated operations. Each comes with its own contract, different from the other operations, and if the team isn't explicitly thinking in terms of contracts, these contracts may change over time, as the team adds new features and fixes bugs.
It's difficult work to keep track of all those contracts. As I argue in Code That Fits in Your Head, it helps if you can automate away some of that work. One way is having good test coverage. Another is to leverage a static type system, if you're fortunate enough to work in a language that has one. As I've also already covered, you can't replace all rules with types, but it doesn't mean that using the type system is ineffectual. Quite the contrary. Every part of a contract that you can offload to the type system frees up your brain to think about something else - something more important, hopefully.
Sometimes there's no good way to to model a precondition with a type, or perhaps it's just too awkward. At other times, there's really only a single way to address a concern. When it comes to the precondition that you can't pass an infinite sequence to the average function, change the type so that it takes some finite collection instead. That's not what this article is about, though.
Assuming that you've already dealt with the infinite-sequence issue, how do you address the other precondition?
Error-handling #
A typical object-oriented move is to introduce a Guard Clause:
public static TimeSpan Average(this IReadOnlyCollection<TimeSpan> timeSpans) { if (!timeSpans.Any()) throw new ArgumentOutOfRangeException( nameof(timeSpans), "Can't calculate the average of an empty collection."); var sum = TimeSpan.Zero; foreach (var ts in timeSpans) sum += ts; return sum / timeSpans.Count; }
You could do the same in F#:
let average (timeSpans : TimeSpan seq) = if Seq.isEmpty timeSpans then raise ( ArgumentOutOfRangeException( nameof timeSpans, "Can't calculate the average of an empty collection.")) timeSpans |> Seq.averageBy (_.Ticks >> double) |> int64 |> TimeSpan.FromTicks
You could also replicate such behaviour in Haskell, but it'd be highly unidiomatic. Instead, I'd rather discuss one idiomatic solution in Haskell, and then back-port it.
While you can throw exceptions in Haskell, you typically handle predictable errors with a sum type. Here's a version of the Haskell function equivalent to the above C# code:
average :: (Foldable t, Fractional a) => t a -> Either String a average xs = if null xs then Left "Can't calculate the average of an empty collection." else Right $ sum xs / fromIntegral (length xs)
For the readers that don't know the Haskell base library by heart, null is a predicate that checks whether or not a collection is empty. It has nothing to do with null pointers.
This variation returns an Either value. In practice you shouldn't just return a String as the error value, but rather a strongly-typed value that other code can deal with in a robust manner.
On the other hand, in this particular example, there's really only one error condition that the function is able to detect, so you often see a variation where instead of a single error message, such a function just doesn't return anything:
average :: (Foldable t, Fractional a) => t a -> Maybe a average xs = if null xs then Nothing else Just $ sum xs / fromIntegral (length xs)
This iteration of the function returns a Maybe value, indicating that a return value may or may not be present.
Liberal domain #
We can back-port this design to F#, where I'd also consider it idiomatic:
let average (timeSpans : IReadOnlyCollection<TimeSpan>) = if timeSpans.Count = 0 then None else timeSpans |> Seq.averageBy (_.Ticks >> double) |> int64 |> TimeSpan.FromTicks |> Some
This version returns a TimeSpan option rather than just a TimeSpan. While this may seem to put the burden of error-handling on the caller, nothing has really changed. The fundamental situation is the same. Now the function is just being more explicit (more honest, you could say) about the pre- and postconditions. The type system also now insists that you deal with the possibility of error, rather than just hoping that the problem doesn't occur.
In C# you can expand the codomain by returning a nullable TimeSpan value, but such an option may not always be available at the language level. Keep in mind that the Average method is just an example standing in for something that may be more complicated. If the original return type is a reference type rather than a value type, only recent versions of C# allows statically-checked nullable reference types. What if you're working in an older version of C#, or another language that doesn't have that feature?
In that case, you may need to introduce an explicit Maybe class and return that:
public static Maybe<TimeSpan> Average(this IReadOnlyCollection<TimeSpan> timeSpans)
{
if (timeSpans.Count == 0)
return new Maybe<TimeSpan>();
var sum = TimeSpan.Zero;
foreach (var ts in timeSpans)
sum += ts;
return new Maybe<TimeSpan>(sum / timeSpans.Count);
}
Two things are going on here; one is obvious while the other is more subtle. Clearly, all of these alternatives change the static type of the function in order to make the pre- and postconditions more explicit. So far, they've all been loosening the codomain (the return type). This suggests a connection with Postel's law: be conservative in what you send, be liberal in what you accept. These variations are all liberal in what they accept, but it seems that the API design pays the price by also having to widen the set of possible return values. In other words, such designs aren't conservative in what they send.
Do we have other options?
Conservative codomain #
Is it possible to instead design the API in such a way that it's conservative in what it returns? Ideally, we'd like it to guarantee that it returns a number. This is possible by making the preconditions even more explicit. I've also covered that alternative already, so I'm just going to repeat the C# code here without further comments:
public static TimeSpan Average(this NotEmptyCollection<TimeSpan> timeSpans) { var sum = timeSpans.Head; foreach (var ts in timeSpans.Tail) sum += ts; return sum / timeSpans.Count; }
This variation promotes another precondition to a type. The precondition that the input collection mustn't be empty can be explicitly modelled with a type. This enables us to be conservative about the codomain. The method now guarantees that it will return a value.
This idea is also easily ported to F#:
type NonEmpty<'a> = { Head : 'a; Tail : IReadOnlyCollection<'a> }
let average (timeSpans : NonEmpty<TimeSpan>) =
[ timeSpans.Head ] @ List.ofSeq timeSpans.Tail
|> List.averageBy (_.Ticks >> double)
|> int64
|> TimeSpan.FromTicks
The average function now takes a NonEmpty collection as input, and always returns a proper TimeSpan value.
Haskell already comes with a built-in NonEmpty collection type, and while it oddly doesn't come with an average function, it's easy enough to write:
import qualified Data.List.NonEmpty as NE average :: Fractional a => NE.NonEmpty a -> a average xs = sum xs / fromIntegral (NE.length xs)
You can find a recent example of using a variation of that function here.
Choosing between the two alternatives #
While Postel's law recommends having liberal domains and conservative codomains, in the case of the average API, we can't have both. If we design the API with a liberal input type, the output type has to be liberal as well. If we design with a restrictive input type, the output can be guaranteed. In my experience, you'll often find yourself in such a conundrum. The average API examined in this article is just an example, while the problem occurs often.
Given such a choice, what should you choose? Is it even possible to give general guidance on this sort of problem?
For decades, I considered such a choice a toss-up. After all, these solutions seem to be equivalent. Perhaps even isomorphic?
When I recently began to explore this isomorphism more closely, it dawned on me that there's a small asymmetry in the isomorphism that favours the conservative codomain option.
Isomorphism #
An isomorphism is a two-way translation between two representations. You can go back and forth between the two alternatives without loss of information.
Is this possible with the two alternatives outlined above? For example, if you have the conservative version, can create the liberal alternative? Yes, you can:
average' :: Fractional a => [a] -> Maybe a average' = fmap average . NE.nonEmpty
Not surprisingly, this is trivial in Haskell. If you have the conservative version, you can just map it over a more liberal input.
In F# it looks like this:
module NonEmpty =
let tryOfSeq xs =
if Seq.isEmpty xs then None
else Some { Head = Seq.head xs; Tail = Seq.tail xs |> List.ofSeq }
let average' (timeSpans : IReadOnlyCollection<TimeSpan>) =
NonEmpty.tryOfSeq timeSpans |> Option.map average
In C# we can create a liberal overload that calls the conservative method:
public static TimeSpan? Average(this IReadOnlyCollection<TimeSpan> timeSpans)
{
if (timeSpans.Count == 0)
return null;
var arr = timeSpans.ToArray();
return new NotEmptyCollection<TimeSpan>(arr[0], arr[1..]).Average();
}
Here I just used a Guard Clause and explicit construction of the NotEmptyCollection. I could also have added a NotEmptyCollection.TryCreate method, like in the F# and Haskell examples, but I chose the above slightly more imperative style in order to demonstrate that my point isn't tightly coupled to the concept of functors, mapping, and other Functional Programming trappings.
These examples highlight how you can trivially make a conservative API look like a liberal API. Is it possible to go the other way? Can you make a liberal API look like a conservative API?
Yes and no.
Consider the liberal Haskell version of average, shown above; that's the one that returns Maybe a. Can you make a conservative function based on that?
average' :: Fractional a => NE.NonEmpty a -> a average' xs = fromJust $ average xs
Yes, this is possible, but only by resorting to the partial function fromJust. I'll explain why that is a problem once we've covered examples in the two other languages, such as F#:
let average' (timeSpans : NonEmpty<TimeSpan>) = [ timeSpans.Head ] @ List.ofSeq timeSpans.Tail |> average |> Option.get
In this variation, average is the liberal version shown above; the one that returns a TimeSpan option. In order to make a conservative version, the average' function can call the liberal average function, but has to resort to the partial function Option.get.
The same issue repeats a third time in C#:
public static TimeSpan Average(this NotEmptyCollection<TimeSpan> timeSpans)
{
return timeSpans.ToList().Average().Value;
}
This time, the partial function is the unsafe Value property, which throws an InvalidOperationException if there's no value.
This even violates Microsoft's own design guidelines:
"AVOID throwing exceptions from property getters."
I've cited Cwalina and Abrams as the authors, since this rule can be found in my 2006 edition of Framework Design Guidelines. This isn't a new insight.
While the two alternatives are 'isomorphic enough' that we can translate both ways, the translations are asymmetric in the sense that one is safe, while the other has to resort to an inherently unsafe operation to make it work.
Encapsulation #
I've called the operations fromJust, Option.get, and Value partial, and only just now used the word unsafe. You may protest that neither of the three examples are unsafe in practice, since we know that the input is never empty. Thus, we know that the liberal function will always return a value, and therefore it's safe to call a partial function, even though these operations are unsafe in the general case.
While that's true, consider how the burden shifts. When you want to promote a conservative variant to a liberal variant, you can rely on all the operations being total. On the other hand, if you want to make a liberal variant look conservative, the onus is on you. None of the three type systems on display here can perform that analysis for you.
This may not be so bad when the example is as simple as taking the average of a collection of numbers, but does it scale? What if the operation you're invoking is much more complicated? Can you still be sure that you safely invoke a partial function on the return value?
As Code That Fits in Your Head argues, procedures quickly become so complicated that they no longer fit in your head. If you don't have well-described and patrolled contracts, you don't know what the postconditions are. You can't trust the return values from method calls, or even the state of the objects you passed as arguments. This tend to lead to defensive coding, where you write code that checks the state of everything all too often.
The remedy is, as always, good old encapsulation. In this case, check the preconditions at the beginning, and capture the result of that check in an object or type that is guaranteed to be always valid. This goes beyond making illegal states unrepresentable because it also works with predicative types. Once you're past the Guard Clauses, you don't have to check the preconditions again.
This kind of thinking illustrates why you need a multidimensional view on API design. As useful as Postel's law sometimes is, it doesn't address all problems. In fact, it turned out to be unhelpful in this context, while another perspective proves more fruitful. Encapsulation is the art and craft of designing APIs in such a way that they suggest or even compels correct interactions. The more I think of this, the more it strikes me that a ranking is implied: Preconditions are more important than postconditions, because if the preconditions are unfulfilled, you can't trust the postconditions, either.
Mapping #
What's going on here? One perspective is to view types as sets. In the average example, the function maps from one set to another:
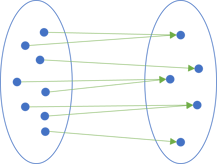
Which sets are they? We can think of the average function as a mapping from the set of non-empty collections of numbers to the set of real numbers. In programming, we can't represent real numbers, so instead, the left set is going to be the set of all the non-empty collections the computer or the language can represent and hold in (virtual) memory, and the right-hand set is the set of all the possible numbers of whichever type you'd like (32-bit signed integers, 64-bit floating-point numbers, 8-bit unsigned integers, etc.).
In reality, the left-hand set is much larger than the set to the right.
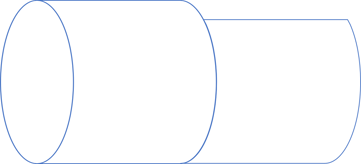
Drawing all those arrows quickly becomes awkward , so instead, we may draw each mapping as a pipe. Such a pipe also corresponds to a function. Here's an intermediate step in such a representation:
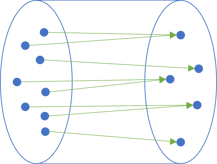
One common element is, however, missing from the left set. Which one?
Pipes #
The above mapping corresponds to the conservative variation of the function. It's a total function that maps all values in the domain to a value in the codomain. It accomplishes this trick by explicitly constraining the domain to only those elements on which it's defined. Due to the preconditions, that excludes the empty collection, which is therefore absent from the left set.
What if we also want to allow the empty collection to be a valid input?
Unless we find ourselves in some special context where it makes sense to define a 'default average value', we can't map an empty collection to any meaningful number. Rather, we'll have to map it to some special value, such as Nothing, None, or null:
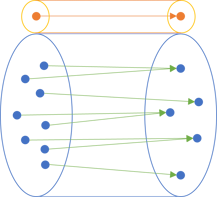
This extra pipe is free, because it's supplied by the Maybe functor's mapping (Select, map, fmap).
What happens if we need to go the other way? If the function is the liberal variant that also maps the empty collection to a special element that indicates a missing value?
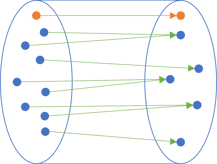
In this case, it's much harder to disentangle the mappings. If you imagine that a liquid flows through the pipes, we can try to be careful and avoid 'filling up' the pipe.
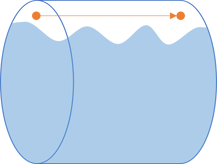
The liquid represents the data that we do want to transmit through the pipe. As this illustration suggests, we now have to be careful that nothing goes wrong. In order to catch just the right outputs on the right side, you need to know how high the liquid may go, and attach a an 'flat-top' pipe to it:
As this illustration tries to get across, this kind of composition is awkward and error-prone. What's worse is that you need to know how high the liquid is going to get on the right side. This depends on what actually goes on inside the pipe, and what kind of input goes into the left-hand side.
This is a metaphor. The longer the pipe is, the more difficult it gets to keep track of that knowledge. The stubby little pipe in these illustrations may correspond to the average function, which is an operation that easily fits in our heads. It's not too hard to keep track of the preconditions, and how they map to postconditions.
Thus, turning such a small liberal function into a conservative function is possible, but already awkward. If the operation is complicated, you can no longer keep track of all the details of how the inputs relate to the outputs.
Additive extensibility #
This really shouldn't surprise us. Most programming languages come with all sorts of facilities that enable extensibility: The ability to add more functionality, more behaviour, more capabilities, to existing building blocks. Conversely, few languages come with removability facilities. You can't, commonly, declare that an object is an instance of a class, except one method, or that a function is just like another function, except that it doesn't accept a particular subset of input.
This explains why we can safely make a conservative function liberal, but why it's difficult to make a liberal function conservative. This is because making a conservative function liberal adds functionality, while making a liberal function conservative attempts to remove functionality.
Conjecture #
All this leads me to the following conjecture: When faced with a choice between two versions of an API, where one has a liberal domain, and the other a conservative codomain, choose the design with the conservative codomain.
If you need the liberal version, you can create it from the conservative operation. The converse need not be true.
Conclusion #
Postel's law encourages us to be liberal with what we accept, but conservative with what we return. This is a good design heuristic, but sometimes you're faced with mutually exclusive alternatives. If you're liberal with what you accept, you'll also need to be too loose with what you return, because there are input values that you can't handle. On the other hand, sometimes the only way to be conservative with the output is to also be restrictive when it comes to input.
Given two such alternatives, which one should you choose?
This article conjectures that you should choose the conservative alternative. This isn't a political statement, but simply a result of the conservative design being the smaller building block. From a small building block, you can compose something bigger, whereas from a bigger unit, you can't easily extract something smaller that's still robust and useful.
