Traversals by Mark Seemann

How to convert a list of tasks into an asynchronous list, and similar problems.

This article is part of a series of articles about functor relationships. In a previous article you learned about natural transformations, and then how functors compose. You can skip several of them if you like, but you might find the one about functor compositions relevant. Still, this article can be read independently of the rest of the series.

You can go a long way with just a single functor or monad. Consider how useful C#'s LINQ API is, or similar kinds of APIs in other languages - typically map and flatMap methods. These APIs work exclusively with the List monad (which is also a functor). Working with lists, sequences, or collections is so useful that many languages have other kinds of special syntax specifically aimed at working with multiple values: List comprehension.

Asynchronous monads like Task<T> or F#'s Async<'T> are another kind of functor so useful in their own right that languages have special async and await keywords to compose them.

Sooner or later, though, you run into situations where you'd like to combine two different functors.

Lists and tasks #

It's not unusual to combine collections and asynchrony. If you make an asynchronous database query, you could easily receive something like Task<IEnumerable<Reservation>>. This, in isolation, hardly causes problems, but things get more interesting when you need to compose multiple reads.

Consider a query like this:

public static Task<Foo> Read(int id)

What happens if you have a collection of IDs that you'd like to read? This happens:

var ids = new[] { 42, 1337, 2112 };
IEnumerable<Task<Foo>> fooTasks = ids.Select(id => Foo.Read(id));

You get a collection of Tasks, which may be awkward because you can't await it. Perhaps you'd rather prefer a single Task that contains a collection: Task<IEnumerable<Foo>>. In other words, you'd like to flip the functors:

IEnumerable<Task<Foo>>
Task<IEnumerable<Foo>>

The top type is what you have. The bottom type is what you'd like to have.

The combination of asynchrony and collections is so common that .NET has special methods to do that. I'll briefly mention one of these later, but what's the general solution to this problem?

Whenever you need to flip two functors, you need a traversal.

Sequence #

As is almost always the case, we can look to Haskell for a canonical definition of traversals - or, as the type class is called: Traversable.

A traversable functor is a functor that enables you to flip that functor and another functor, like the above C# example. In more succinct syntax:

t (f a) -> f (t a)

Here, t symbolises any traversable functor (like IEnumerable<T> in the above C# example), and f is another functor (like Task<T>, above). By flipping the functors I mean making t and f change places; just like IEnumerable and Task, above.

Thinking of functors as containers we might depict the function like this:

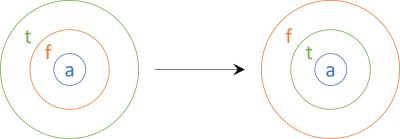
To the left, we have an outer functor t (e.g. IEnumerable) that contains another functor f (e.g. Task) that again 'contains' values of type a (in C# typically called T). We'd like to flip how the containers are nested so that f contains t.

Contrary to what you might expect, the function that does that isn't called traverse; it's called sequence. (For those readers who are interested in Haskell specifics, the function I'm going to be talking about is actually called sequenceA. There's also a function called sequence, but it's not as general. The reason for the odd names are related to the evolution of various Haskell type classes.)

The sequence function doesn't work for any old functor. First, t has to be a traversable functor. We'll get back to that later. Second, f has to be an applicative functor. (To be honest, I'm not sure if this is always required, or if it's possible to produce an example of a specific functor that isn't applicative, but where it's still possible to implement a sequence function. The Haskell sequenceA function has Applicative f as a constraint, but as far as I can tell, this only means that this is a sufficient requirement - not that it's necessary.)

Since tasks (e.g. Task<T>) are applicative functors (they are, because they are monads, and all monads are applicative functors), that second requirement is fulfilled for the above example. I'll show you how to implement a Sequence function in C# and how to use it, and then we'll return to the general discussion of what a traversable functor is:

public static Task<IEnumerable<T>> Sequence<T>(
    this IEnumerable<Task<T>> source)
{
    return source.Aggregate(
        Task.FromResult(Enumerable.Empty<T>()),
        async (acc, t) =>
        {
            var xs = await acc;
            var x = await t;
            return xs.Concat(new[] { x });
        });
}

This Sequence function enables you to flip any IEnumerable<Task<T>> to a Task<IEnumerable<T>>, including the above fooTasks:

Task<IEnumerable<Foo>> foosTask = fooTasks.Sequence();

You can also implement sequence in F#:

// Async<'a> list -> Async<'a list>
let sequence asyncs =
    let go acc t = async {
        let! xs = acc
        let! x  = t
        return List.append xs [x] }
    List.fold go (fromValue []) asyncs

and use it like this:

let fooTasks = ids |> List.map Foo.Read
let foosTask = fooTasks |> Async.sequence

For this example, I put the sequence function in a local Async module; it's not part of any published Async module.

These C# and F# examples are specific translations: From lists of tasks to a task of list. If you need another translation, you'll have to write a new function for that particular combination of functors. Haskell has more general capabilities, so that you don't have to write functions for all combinations. I'm not assuming that you know Haskell, however, so I'll proceed with the description.

Traversable functor #

The sequence function requires that the 'other' functor (the one that's not the traversable functor) is an applicative functor, but what about the traversable functor itself? What does it take to be a traversable functor?

I have to admit that I have to rely on Haskell specifics to a greater extent than normal. For most other concepts and abstractions in the overall article series, I've been able to draw on various sources, chief of which are Category Theory for Programmers. In various articles, I've cited my sources whenever possible. While I've relied on Haskell libraries for 'canonical' ways to represent concepts in a programming language, I've tried to present ideas as having a more universal origin than just Haskell.

When it comes to traversable functors, I haven't come across universal reasoning like that which gives rise to concepts like monoids, functors, Church encodings, or catamorphisms. This is most likely a failing on my part.

Traversals of the Haskell kind are, however, so useful that I find it appropriate to describe them. When consulting, it's a common solution to a lot of problems that people are having with functional programming.

Thus, based on Haskell's Data.Traversable, a traversable functor must:

• be a functor
• be a 'foldable' functor
• define a sequence or traverse function

You've already seen examples of sequence functions, and I'm also assuming that (since you've made it so far in the article already) you know what a functor is. But what's a foldable functor?

Haskell comes with a Foldable type class. It defines a class of data that has a particular type of catamorphism. As I've outlined in my article on catamorphisms, Haskell's notion of a fold sometimes coincides with a (or 'the') catamorphism for a type, and sometimes not. For Maybe and List they do coincide, while they don't for Either or Tree. It's not that you can't define Foldable for Either or Tree, it's just that it's not 'the' general catamorphism for that type.

I can't tell whether Foldable is a universal abstraction, or if it's just an ad-hoc API that turns out to be useful in practice. It looks like the latter to me, but my knowledge is only limited. Perhaps I'll be wiser in a year or two.

I will, however, take it as licence to treat this topic a little less formally than I've done with other articles. While there are laws associated with Traversable, they are rather complex, so I'm going to skip them.

The above requirements will enable you to define traversable functors if you run into some more exotic ones, but in practice, the common functors List, Maybe, Either, Tree, and Identity are all traversable. That it useful to know. If any of those functors is the outer functor in a composition of functors, then you can flip them to the inner position as long as the other functor is an applicative functor.

Since IEnumerable<T> is traversable, and Task<T> (or Async<'T>) is an applicative functor, it's possible to use Sequence to convert IEnumerable<Task<Foo>> to Task<IEnumerable<Foo>>.

Traverse #

The C# and F# examples you've seen so far arrive at the desired type in a two-step process. First they produce the 'wrong' type with ids.Select(Foo.Read) or ids |> List.map Foo.Read, and then they use Sequence to arrive at the desired type.

When you use two expressions, you need two lines of code, and you also need to come up with a name for the intermediary value. It might be easier to chain the two function calls into a single expression:

Task<IEnumerable<Foo>> foosTask = ids.Select(Foo.Read).Sequence();

Or, in F#:

let foosTask = ids |> List.map Foo.Read |> Async.sequence

Chaining Select/map with Sequence/sequence is so common that it's a named function: traverse. In C#:

public static Task<IEnumerable<TResult>> Traverse<T, TResult>(
    this IEnumerable<T> source,
    Func<T, Task<TResult>> selector)
{
    return source.Select(selector).Sequence();
}

This makes usage a little easier:

Task<IEnumerable<Foo>> foosTask = ids.Traverse(Foo.Read);

In F# the implementation might be similar:

// ('a -> Async<'b>) -> 'a list -> Async<'b list>
let traverse f xs = xs |> List.map f |> sequence

Usage then looks like this:

let foosTask = ids |> Async.traverse Foo.Read

As you can tell, if you've already implemented sequence you can always implement traverse. The converse is also true: If you've already implemented traverse, you can always implement sequence. You'll see an example of that later.

A reusable idea #

If you know the .NET Task Parallel Library (TPL), you may demur that my implementation of Sequence seems like an inefficient version of Task.WhenAll, and that Traverse could be written like this:

public static async Task<IEnumerable<TResult>> Traverse<T, TResult>(
    this IEnumerable<T> source,
    Func<T, Task<TResult>> selector)
{
    return await Task.WhenAll(source.Select(selector));
}

This alternative is certainly possible. Whether it's more efficient I don't know; I haven't measured. As foreshadowed in the beginning of the article, the combination of collections and asynchrony is so common that .NET has special APIs to handle that. You may ask, then: What's the point?

The point of is that a traversable functor is a reusable idea.

You may be able to find existing APIs like Task.WhenAll to deal with combinations of collections and asynchrony, but what if you need to deal with asynchronous Maybe or Either? Or a List of Maybes?

There may be no existing API to flip things around - before you add it. Now you know that there's a (dare I say it?) design pattern you can implement.

Asynchronous Maybe #

Once people go beyond collections they often run into problems. You may, for example, decide to use the Maybe monad in order to model the presence or absence of a value. Then, once you combine Maybe-based decision values with asynchronous processesing, you may run into problems.

For example, in my article Asynchronous Injection I modelled the core domaim logic as returning Maybe<Reservation>. When handling an HTTP request, the application should use that value to determine what to do next. If the return value is empty it should do nothing, but when the Maybe value is populated, it should save the reservation in a data store using this method:

Task<int> Create(Reservation reservation)

Finally, if accepting the reservation, the HTTP handler (ReservationsController) should return the resevation ID, which is the int returned by Create. Please refer to the article for details. It also links to the sample code on GitHub.

The entire expression is, however, Task-based:

public async Task<IActionResult> Post(Reservation reservation)
{
    return await Repository.ReadReservations(reservation.Date)
        .Select(rs => maîtreD.TryAccept(rs, reservation))
        .SelectMany(m => m.Traverse(Repository.Create))
        .Match(InternalServerError("Table unavailable"), Ok);
}

The Select and SelectMany methods are defined on the Task monad. The m in the SelectMany lambda expression is the Maybe<Reservation> returned by TryAccept. What would happen if you didn't have a Traverse method?

Task<Maybe<Task<int>>> whatIsThis = Repository.ReadReservations(reservation.Date)
    .Select(rs => maîtreD.TryAccept(rs, reservation))
    .Select(m => m.Select(Repository.Create));

Notice that whatIsThis (so named because it's a temporary variable used to investigate the type of the expression so far) has an awkward type: Task<Maybe<Task<int>>>. That's a Task within a Maybe within a Task.

This makes it difficult to continue the composition and return an HTTP result.

Instead, use Traverse:

Task<Task<Maybe<int>>> whatIsThis = Repository.ReadReservations(reservation.Date)
    .Select(rs => maîtreD.TryAccept(rs, reservation))
    .Select(m => m.Traverse(Repository.Create));

This flips the inner Maybe<Task<int>> to Task<Maybe<int>>. Now you have a Maybe within a Task within a Task. The outer two Tasks are now nicely nested, and it's a job for a monad to remove one level of nesting. That's the reason that the final composition uses SelectMany instead of Select.

The Traverse function is implemented like this:

public static Task<Maybe<TResult>> Traverse<T, TResult>(
    this Maybe<T> source,
    Func<T, Task<TResult>> selector)
{
    return source.Match(
        nothing: Task.FromResult(new Maybe<TResult>()),
        just: async x => new Maybe<TResult>(await selector(x)));
}

The idea is reusable. You can also implement a similar traversal in F#:

// ('a -> Async<'b>) -> 'a option -> Async<'b option>
let traverse f = function
    | Some x -> async {
        let! x' = f x
        return Some x' }
    | None -> async { return None }

You can see the F# function as well as a usage example in the article Refactoring registration flow to functional architecture.

Sequence from traverse #

You've already seen that if you have a sequence function, you can implement traverse. I also claimed that the reverse is true: If you have traverse you can implement sequence.

When you've encountered these kinds of dual definitions a couple of times, you start to expect the ubiquitous identity function to make an appearance, and indeed it does:

let sequence x = traverse id x

That's the F# version where the identity function is built in as id. In C# you'd use a lambda expression:

public static Task<Maybe<T>> Sequence<T>(this Maybe<Task<T>> source)
{
    return source.Traverse(x => x);
}

Since C# doesn't come with a predefined identity function, it's idiomatic to use x => x instead.

Conclusion #

Traversals are useful when you need to 'flip' the order of two different, nested functors. The outer one must be a traversable functor, and the inner an applicative functor.

Common traversable functors are List, Maybe, Either, Tree, and Identity, but there are more than those. In .NET you often need them when combining them with Tasks. In Haskell, they are useful when combined with IO.

Next: Nested monads.

---

Comments

• ← Previous
• Archive
• Next →