ploeh blog danish software design
AFK
Software development productivity tip: regularly step away from the computer.
In these days of covid-19, people are learning that productivity is imperfectly correlated to the amount of time one is physically present in an office. Indeed, the time you spend in front of you computer is hardly correlated to your productivity. After all, programming productivity isn't measured by typing speed. Additionally, you can waste much time at the computer, checking Twitter, watching cat videos on YouTube, etc.
Pomodorobut #
I've worked from home for years, so I thought I'd share some productivity tips. I only report what works for me. If you can use some of the tips, then great. If they're not for you, that's okay too. I don't pretend that I've found any secret sauce or universal truth.
A major problem with productivity is finding the discipline to work. I use Pomodorobut. It's like Scrumbut, but for the Pomodoro technique. For years I thought I was using the Pomodoro technique, but Arialdo Martini makes a compelling case that I'm not. He suggests just calling it timeboxing.
I think it's a little more than that, though, because the way I use Pomodorobut has two equally important components:
- The 25-minute work period
- The 5-minute break
When you program, you often run into problems:
- There's a bug that you don't understand.
- You can't figure out the correct algorithm to implement a particular behaviour.
- Your code doesn't compile, and you don't understand why.
- A framework behaves inexplicably.
The solution: take a break.
Breaks give a fresh perspective #
I take my Pomodorobut breaks seriously. My rule is that I must leave my office during the break. I usually go get a glass of water or the like. The point is to get out of the chair and afk (away from keyboard).
While I'm out the room, it often happens that I get an insight. If I'm stuck on something, I may think of a potential solution, or I may realise that the problem is irrelevant, because of a wider context I forgot about when I sat in front of the computer.
You may have heard about rubber ducking. Ostensibly
I've tried it enough times: you ask a colleague if he or she has a minute, launch into an explanation of your problem, only to break halfway through and say: "Never mind! I suddenly realised what the problem is. Thank you for your help.""By having to verbalize [...], you may suddenly gain new insight into the problem."
Working from home, I haven't had a colleague I could disturb like that for years, and I don't actually use a rubber duck. In my experience, getting out of my chair works equally well.
The Pomodorobut technique makes me productive because the breaks, and the insights they spark, reduce the time I waste on knotty problems. When I'm in danger of becoming stuck, I often find a way forward in less than 30 minutes: at most 25 minutes being stuck, and a 5-minute break to get unstuck.
Hammock-driven development #
Working from home gives you extra flexibility. I have a regular routine where I go for a run around 10 in the morning. I also routinely go grocery shopping around 14 in the afternoon. Years ago, when I still worked in an office, I'd ride my bicycle to and from work every day. I've had my good ideas during those activities.
In fact, I can't recall ever having had a profound insight in front of the computer. They always come to me when I'm away from it. For instance, I distinctly remember walking around in my apartment doing other things when I realised that the Visitor design pattern is just another encoding of a sum type.
Insights don't come for free. As Rich Hickey points out in his talk about hammock-driven development, you must feed your 'background mind'. That involves deliberate focus on the problem.
Good ideas don't come if you're permanently away from the computer, but neither do they arrive if all you do is stare at the screen. It's the variety that makes you productive.
Conclusion #
Software development productivity is weakly correlated with the time you spend in front of the computer. I find that I'm most productive when I can vary my activities during the day. Do a few 25-minute sessions, rigidly interrupted by breaks. Go for a run. Work a bit more on the computer. Have lunch. Do one or two more time-boxed sessions. Go grocery shopping. Conclude with a final pair of work sessions.
Significant whitespace is DRY
Languages with explicit scoping encourage you to repeat yourself.
When the talk falls on significant whitespace, the most common reaction I hear seems to be one of nervous apotropaic deflection.
I've always wondered why people react like that. What's the problem with significant whitespace?"Indentation matters? Oh, no! I'm horrified."
If given a choice, I'd prefer indentation to matter. In that way, I don't have to declare scope more than once.
Explicit scope #
If you had to choose between the following three C# implementations of the FizzBuzz kata, which one would you choose?
a:
class Program { static void Main() { for (int i = 1; i < 100; i++) { if (i % 15 == 0) { Console.WriteLine("FizzBuzz"); } else if (i % 3 == 0) { Console.WriteLine("Fizz"); } else if (i % 5 == 0) { Console.WriteLine("Buzz"); } else { Console.WriteLine(i); } } } }
b:
class Program { static void Main() { for (int i = 1; i < 100; i++) { if (i % 15 == 0) { Console.WriteLine("FizzBuzz"); } else if (i % 3 == 0) { Console.WriteLine("Fizz"); } else if (i % 5 == 0) { Console.WriteLine("Buzz"); } else { Console.WriteLine(i); } } } }
c:
class Program { static void Main() { for (int i = 1; i < 100; i++) { if (i % 15 == 0) { Console.WriteLine("FizzBuzz"); } else if (i % 3 == 0) { Console.WriteLine("Fizz"); } else if (i % 5 == 0) { Console.WriteLine("Buzz"); } else { Console.WriteLine(i); } } } }
Which of these do you prefer? a, b, or c?
You prefer b. Everyone does.
Yet, those three examples are equivalent. Not only do they behave the same - except for whitespace, they're identical. They produce the same effective abstract syntax tree.
Even though a language like C# has explicit scoping and statement termination with its curly brackets and semicolons, indentation still matters. It doesn't matter to the compiler, but it matters to humans.
When you format code like option b, you express scope twice. Once for the compiler, and once for human readers. You're repeating yourself.
Significant whitespace #
Some languages dispense with the ceremony and let indentation indicate scope. The most prominent is Python, but I've more experience with F# and Haskell. In F#, you could write FizzBuzz like this:
[<EntryPoint>] let main argv = for i in [1..100] do if i % 15 = 0 then printfn "FizzBuzz" else if i % 3 = 0 then printfn "Fizz" else if i % 5 = 0 then printfn "Buzz" else printfn "%i" i 0
You don't have to explicitly scope variables or expressions. The scope is automatically indicated by the indentation. You don't repeat yourself. Scope is expressed once, and both compiler and human understand it.
I've programmed in F# for a decade now, and I don't find its use of significant whitespace to be a problem. I'd recommend, however, to turn on the feature in your IDE of choice that shows whitespace characters.
Summary #
Significant whitespace is a good language feature. You're going to indent your code anyway, so why not let the indentation carry meaning? In that way, you don't repeat yourself.
An F# implementation of the Maître d' kata
This article walks you through the Maître d' kata done in F#.
In a previous article, I presented the Maître d' kata and promised to publish a walkthrough. Here it is.
Preparation #
I used test-driven development and F# for both unit tests and implementation. As usual, my test framework was xUnit.net (2.4.0) with Unquote (5.0.0) as the assertion library.
I could have done the exercise with a property-based testing framework like FsCheck or Hedgehog, but I chose instead to take my own medicine. In the kata description, I suggested some test cases, so I wanted to try and see if they made sense.
The entire code base is available on GitHub.
Boutique restaurant #
I wrote the first suggested test case this way:
[<Fact>]
let ``Boutique restaurant`` () =
test <@ canAccept 12 [] { Quantity = 1 } @>
This uses Unquote's test function to verify that a Boolean expression is true. The expression is a function call to canAccept with the capacity 12, no existing reservations, and a reservation with Quantity = 1.
The simplest thing that could possibly work was this:
type Reservation = { Quantity : int } let canAccept _ _ _ = true
The Reservation type was required to make the test compile, but the canAccept function didn't have to consider its arguments. It could simply return true.
Parametrisation #
The next test case made me turn the test function into a parametrised test:
[<Theory>] [<InlineData( 1, true)>] [<InlineData(13, false)>] let ``Boutique restaurant`` quantity expected = expected =! canAccept 12 [] { Quantity = quantity }
So far, the only test parameters were quantity and the expected result. I could no longer use test to verify the result of calling canAccept, since I added variation to the expected result. I changed test into Unquote's =! (must equal) operator.
The simplest passing implementation I could think of was:
let canAccept _ _ { Quantity = q } = q = 1
It ignored the capacity and instead checked whether q is 1. That passed both tests.
Test data API #
Before adding another test case, I decided to refactor my test code a bit. When working with a real domain model, you often have to furnish test data in order to make code compile - even if that data isn't relevant to the test. I wanted to demonstrate how to deal with this issue. My first step was to introduce an 'arbitrary' Reservation value in the spirit of Test data without Builders.
let aReservation = { Quantity = 1 }
This enabled me to rewrite the test:
[<Theory>] [<InlineData( 1, true)>] [<InlineData(13, false)>] let ``Boutique restaurant`` quantity expected = expected =! canAccept 12 [] { aReservation with Quantity = quantity }
This doesn't look like an immediate improvement, but it made it possible to make the Reservation record type more realistic without damage to the test:
type Reservation = {
Date : DateTime
Name : string
Email : string
Quantity : int }
I added some fields that a real-world reservation would have. The Quantity field will be useful later on, but the Name and Email fields are irrelevant in the context of the kata.
This is the type of API change that often gives people grief. To create a Reservation value, you must supply all four fields. This often adds noise to tests.
Not here, though, because the only concession I had to make was to change aReservation:
let aReservation = { Date = DateTime (2019, 11, 29, 12, 0, 0) Name = "" Email = "" Quantity = 1 }
The test code remained unaltered.
With that in place, I could add the third test case:
[<Theory>] [<InlineData( 1, true)>] [<InlineData(13, false)>] [<InlineData(12, true)>] let ``Boutique restaurant`` quantity expected = expected =! canAccept 12 [] { aReservation with Quantity = quantity }
The simplest passing implementation I could think of was:
let canAccept _ _ { Quantity = q } = q <> 13
This implementation still ignored the restaurant's capacity and simply checked that q was different from 13. That was enough to pass all three tests.
Refactor test case code #
Adding the next suggested test case proved to be a problem. I wanted to write a single [<Theory>]-driven test function fed by all the Boutique restaurant test data. To do that, I'd have to supply arrays of test input, but unfortunately, that wasn't possible in F#.
Instead I decided to refactor the test case code to use ClassData-driven test cases.
type BoutiqueTestCases () as this = inherit TheoryData<int, bool> () do this.Add ( 1, true) this.Add (13, false) this.Add (12, true) [<Theory; ClassData(typeof<BoutiqueTestCases>)>] let ``Boutique restaurant`` quantity expected = expected =! canAccept 12 [] { aReservation with Quantity = quantity }
These are the same test cases as before, but now expressed by a class inheriting from TheoryData<int, bool>. The implementing code remains the same.
Existing reservation #
The next suggested test case includes an existing reservation. To support that, I changed the test case base class to TheoryData<int, int list, int, bool>, and passed empty lists for the first three test cases. For the new, fourth test case, I supplied a number of seats.
type BoutiqueTestCases () as this = inherit TheoryData<int, int list, int, bool> () do this.Add (12, [], 1, true) this.Add (12, [], 13, false) this.Add (12, [], 12, true) this.Add ( 4, [2], 3, false) [<Theory; ClassData(typeof<BoutiqueTestCases>)>] let ``Boutique restaurant`` capacity reservatedSeats quantity expected = let rs = List.map (fun s -> { aReservation with Quantity = s }) reservatedSeats let actual = canAccept capacity rs { aReservation with Quantity = quantity } expected =! actual
This also forced me to to change the body of the test function. At this stage, it could be prettier, but it got the job done. I soon after improved it.
My implementation, as usual, was the simplest thing that could possibly work.
let canAccept _ reservations { Quantity = q } =
q <> 13 && Seq.isEmpty reservations
Notice that although the fourth test case varied the capacity, I still managed to pass all tests without looking at it.
Accept despite existing reservation #
The next test case introduced another existing reservation, but this time with enough capacity to accept a new reservation.
type BoutiqueTestCases () as this = inherit TheoryData<int, int list, int, bool> () do this.Add (12, [], 1, true) this.Add (12, [], 13, false) this.Add (12, [], 12, true) this.Add ( 4, [2], 3, false) this.Add (10, [2], 3, true)
The test function remained unchanged.
In the spirit of the Devil's advocate technique, I actively sought to avoid a correct implementation. I came up with this:
let canAccept capacity reservations { Quantity = q } = let reservedSeats = match Seq.tryHead reservations with | Some r -> r.Quantity | None -> 0 reservedSeats + q <= capacity
Since all test cases supplied at most one existing reservation, it was enough to consider the first reservation, if present.
To many people, it may seem strange to actively seek out incorrect implementations like this. An incorrect implementation that passes all tests does, however, demonstrate the need for more tests.
The sum of all reservations #
I then added another test case, this time with three existing reservations:
type BoutiqueTestCases () as this = inherit TheoryData<int, int list, int, bool> () do this.Add (12, [], 1, true) this.Add (12, [], 13, false) this.Add (12, [], 12, true) this.Add ( 4, [2], 3, false) this.Add (10, [2], 3, true) this.Add (10, [3;2;3], 3, false)
Again, I left the test function untouched.
On the side of the implementation, I couldn't think of more hoops to jump through, so I finally gave in and provided a 'proper' implementation:
let canAccept capacity reservations { Quantity = q } = let reservedSeats = Seq.sumBy (fun r -> r.Quantity) reservations reservedSeats + q <= capacity
Not only does it look simpler that before, but I also felt that the implementation was warranted.
Although I'd only tested“As the tests get more specific, the code gets more generic.”
canAccept with lists, I decided to implement it with Seq. This was a decision I later regretted.
Another date #
The last Boutique restaurant test case was to supply an existing reservation on another date. The canAccept function should only consider existing reservations on the date in question.
First, I decided to model the two separate dates as two values:
let d1 = DateTime (2023, 9, 14) let d2 = DateTime (2023, 9, 15)
I hoped that it would make my test cases more readable, because the dates would have a denser representation.
type BoutiqueTestCases () as this = inherit TheoryData<int, (int * DateTime) list, (int * DateTime), bool> () do this.Add (12, [], ( 1, d1), true) this.Add (12, [], (13, d1), false) this.Add (12, [], (12, d1), true) this.Add ( 4, [(2, d1)], ( 3, d1), false) this.Add (10, [(2, d1)], ( 3, d1), true) this.Add (10, [(3, d1);(2, d1);(3, d1)], ( 3, d1), false) this.Add ( 4, [(2, d2)], ( 3, d1), true)
I changed the representation of a reservation from just an int to a tuple of a number and a date. I also got tired of looking at that noisy unit test, so I introduced a test-specific helper function:
let reserve (q, d) = { aReservation with Quantity = q; Date = d }
Since it takes a tuple of a number and a date, I could use it to simplify the test function:
[<Theory; ClassData(typeof<BoutiqueTestCases>)>] let ``Boutique restaurant`` (capacity, rs, r, expected) = let reservations = List.map reserve rs let actual = canAccept capacity reservations (reserve r) expected =! actual
The canAccept function now had to filter the reservations on Date:
let canAccept capacity reservations { Quantity = q; Date = d } = let relevantReservations = Seq.filter (fun r -> r.Date = d) reservations let reservedSeats = Seq.sumBy (fun r -> r.Quantity) relevantReservations reservedSeats + q <= capacity
This implementation specifically compared dates, though, so while it passed all tests, it'd behave incorrectly if the dates were as much as nanosecond off. That implied that another test case was required.
Same date, different time #
The final test case for the Boutique restaurant, then, was to use two DateTime values on the same date, but with different times.
type BoutiqueTestCases () as this = inherit TheoryData<int, (int * DateTime) list, (int * DateTime), bool> () do this.Add (12, [], ( 1, d1 ), true) this.Add (12, [], (13, d1 ), false) this.Add (12, [], (12, d1 ), true) this.Add ( 4, [(2, d1)], ( 3, d1 ), false) this.Add (10, [(2, d1)], ( 3, d1 ), true) this.Add (10, [(3, d1);(2, d1);(3, d1)], ( 3, d1 ), false) this.Add ( 4, [(2, d2)], ( 3, d1 ), true) this.Add ( 4, [(2, d1)], ( 3, d1.AddHours 1.), false)
I just added a new test case as a new line and lined up the data. The test function, again, didn't change.
To address the new test case, I generalised the first filter.
let canAccept capacity reservations { Quantity = q; Date = d } = let relevantReservations = Seq.filter (fun r -> r.Date.Date = d.Date) reservations let reservedSeats = Seq.sumBy (fun r -> r.Quantity) relevantReservations reservedSeats + q <= capacity
An expression like r.Date.Date looks a little odd. DateTime values have a Date property that represents its date part. The first Date is the Reservation field, and the second is the date part.
I was now content with the Boutique restaurant implementation.
Haute cuisine #
In the next phase of the kata, I now had to deal with a configuration of more than one table, so I introduced a type:
type Table = { Seats : int }
It's really only a glorified wrapper around an int, but with a real domain model in place, I could make its constructor private and instead afford a smart constructor that only accepts positive integers.
I changed the canAccept function to take a list of tables, instead of capacity. This also required me to change the existing test function to take a singleton list of tables:
let actual = canAccept [table capacity] reservations (reserve r)
where table is a test-specific helper function:
let table s = { Seats = s }
I also added a new test function and a single test case:
let d3 = DateTime (2024, 6, 7) type HauteCuisineTestCases () as this = inherit TheoryData<int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add ([2;2;4;4], [], (4, d3), true) [<Theory; ClassData(typeof<HauteCuisineTestCases>)>] let ``Haute cuisine`` (tableSeats, rs, r, expected) = let tables = List.map table tableSeats let reservations = List.map reserve rs let actual = canAccept tables reservations (reserve r) expected =! actual
The change to canAccept is modest:
let canAccept tables reservations { Quantity = q; Date = d } = let capacity = Seq.sumBy (fun t -> t.Seats) tables let relevantReservations = Seq.filter (fun r -> r.Date.Date = d.Date) reservations let reservedSeats = Seq.sumBy (fun r -> r.Quantity) relevantReservations reservedSeats + q <= capacity
It still works by looking at a total capacity as if there was just a single communal table. Now it just calculates capacity from the sequence of tables.
Reject reservation that doesn't fit largest table #
Then I added the next test case to the new test function:
type HauteCuisineTestCases () as this = inherit TheoryData<int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add ([2;2;4;4], [], (4, d3), true) this.Add ([2;2;4;4], [], (5, d3), false)
This one attempts to make a reservation for five people. The largest table only fits four people, so this reservation should be rejected. The current implementation just considered the total capacity of all tables, to it accepted the reservation, and thereby failed the test.
This change to canAccept passes all tests:
let canAccept tables reservations { Quantity = q; Date = d } = let capacity = tables |> Seq.map (fun t -> t.Seats) |> Seq.max let relevantReservations = Seq.filter (fun r -> r.Date.Date = d.Date) reservations let reservedSeats = Seq.sumBy (fun r -> r.Quantity) relevantReservations reservedSeats + q <= capacity
The function now only considered the largest table in the restaurant. While it's incorrect to ignore all other tables, all tests passed.
Accept when there's still a remaining table #
Only considering the largest table is obviously wrong, so I added another test case where there's an existing reservation.
type HauteCuisineTestCases () as this = inherit TheoryData<int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add ([2;2;4;4], [], (4, d3), true) this.Add ([2;2;4;4], [], (5, d3), false) this.Add ( [2;2;4], [(2, d3)], (4, d3), true)
While canAccept should accept the reservation, it didn't when I added the test case. In a variation of the Devil's Advocate technique, I came up with this implementation to pass all tests:
let canAccept tables reservations { Quantity = q; Date = d } = let largestTable = tables |> Seq.map (fun t -> t.Seats) |> Seq.max let capacity = tables |> Seq.sumBy (fun t -> t.Seats) let relevantReservations = Seq.filter (fun r -> r.Date.Date = d.Date) reservations let reservedSeats = Seq.sumBy (fun r -> r.Quantity) relevantReservations q <= largestTable && reservedSeats + q <= capacity
This still wasn't the correct implementation. It represented a return to looking at the total capacity of all tables, with the extra rule that you couldn't make a reservation larger than the largest table. At least one more test case was needed.
Accept when remaining table is available #
I added another test case to the haute cuisine test cases. This one came with one existing reservation for three people, effectively reserving the four-person table. While the remaining tables have an aggregate capacity of four, it's two separate tables. Therefore, a reservation for four people should be rejected.
type HauteCuisineTestCases () as this = inherit TheoryData<int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add ([2;2;4;4], [], (4, d3), true) this.Add ([2;2;4;4], [], (5, d3), false) this.Add ( [2;2;4], [(2, d3)], (4, d3), true) this.Add ( [2;2;4], [(3, d3)], (4, d3), false)
It then dawned on me that I had to explicitly distinguish between a communal table configuration, and individual tables that aren't communal, regardless of size. This triggered quite a refactoring.
I defined a new type to distinguish between these two types of table layout:
type TableConfiguration = Communal of int | Tables of Table list
I also had to change the existing test functions, including the boutique restaurant test
[<Theory; ClassData(typeof<BoutiqueTestCases>)>] let ``Boutique restaurant`` (capacity, rs, r, expected) = let reservations = List.map reserve rs let actual = canAccept (Communal capacity) reservations (reserve r) expected =! actual
and the haute cuisine test
[<Theory; ClassData(typeof<HauteCuisineTestCases>)>] let ``Haute cuisine`` (tableSeats, rs, r, expected) = let tables = List.map table tableSeats let reservations = List.map reserve rs let actual = canAccept (Tables tables) reservations (reserve r) expected =! actual
In both cases I had to change the call to canAccept to pass either a Communal or a Tables value.
Delete first #
I'd previously done the kata in Haskell and was able to solve this phase of the kata using the built-in deleteFirstsBy function. This function doesn't exist in the F# core library, so I decided to add it. I created a new module named Seq and first defined a function that deletes the first element that satisfies a predicate:
// ('a -> bool) -> seq<'a> -> seq<'a> let deleteFirstBy pred (xs : _ seq) = seq { let mutable found = false use e = xs.GetEnumerator () while e.MoveNext () do if found then yield e.Current else if pred e.Current then found <- true else yield e.Current }
It moves over a sequence of elements and looks for an element that satisfies pred. If such an element is found, it's omitted from the output sequence. The function only deletes the first occurrence from the sequence, so any other elements that satisfy the predicate are still included.
This function corresponds to Haskell's deleteBy function and can be used to implement deleteFirstsBy:
// ('a -> 'b -> bool) -> seq<'b> -> seq<'a> -> seq<'b> let deleteFirstsBy pred = Seq.fold (fun xs x -> deleteFirstBy (pred x) xs)
As the Haskell documentation explains, the "deleteFirstsBy function takes a predicate and two lists and returns the first list with the first occurrence of each element of the second list removed." My F# function does the same, but works on sequences instead of linked lists.
I could use it to find and remove tables that were already reserved.
Find remaining tables #
I first defined a little helper function to determine whether a table can accommodate a reservation:
// Reservation -> Table -> bool let private fits r t = r.Quantity <= t.Seats
The rule is simply that the table's number of Seats must be greater than or equal to the reservation's Quantity. I could use this function for the predicate for Seq.deleteFirstsBy:
let canAccept config reservations ({ Quantity = q; Date = d } as r) = let contemporaneousReservations = Seq.filter (fun r -> r.Date.Date = d.Date) reservations match config with | Communal capacity -> let reservedSeats = Seq.sumBy (fun r -> r.Quantity) contemporaneousReservations reservedSeats + q <= capacity | Tables tables -> let rs = Seq.sort contemporaneousReservations let remainingTables = Seq.deleteFirstsBy fits (Seq.sort tables) rs Seq.exists (fits r) remainingTables
The canAccept function now branched on Communal versus Tables configurations. In the Communal configuration, it simply compared the reservedSeats and reservation quantity to the communal table's capacity.
In the Tables case, the function used Seq.deleteFirstsBy fits to remove all the tables that are already reserved. The result is the remainingTables. If there exists a remaining table that fits the reservation, then the function accepts the reservation.
This seemed to me an appropriate implementation of the haute cuisine phase of the kata.
Second seatings #
Now it was time to take seating duration into account. While I could have written my test cases directly against the TimeSpan API, I didn't want to write TimeSpan.FromHours 2.5, TimeSpan.FromDays 1., and so on. I found that it made my test cases harder to read, so I added some literal extensions:
type Int32 with member x.hours = TimeSpan.FromHours (float x) member x.days = TimeSpan.FromDays (float x)
This enabled me to write expressions like 1 .days and 2 .hours, as shown in the first test case:
let d4 = DateTime (2023, 10, 22, 18, 0, 0) type SecondSeatingsTestCases () as this = inherit TheoryData<TimeSpan, int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add (2 .hours, [2;2;4], [(4, d4)], (3, d4.Add (2 .hours)), true)
I used this initial parametrised test case for a new test function:
[<Theory; ClassData(typeof<SecondSeatingsTestCases>)>] let ``Second seatings`` (dur, tableSeats, rs, r, expected) = let tables = List.map table tableSeats let reservations = List.map reserve rs let actual = canAccept dur (Tables tables) reservations (reserve r) expected =! actual
My motivation for this test case was mostly to introduce an API change to canAccept. I didn't want to rock the boat too much, so I picked a test case that wouldn't trigger a big change to the implementation. I prefer incremental changes. The only change is the introduction of the seatingDur argument:
let canAccept (seatingDur : TimeSpan) config reservations ({ Date = d } as r) = let contemporaneousReservations = Seq.filter (fun x -> x.Date.Subtract seatingDur < d.Date) reservations match config with | Communal capacity -> let reservedSeats = Seq.sumBy (fun r -> r.Quantity) contemporaneousReservations reservedSeats + r.Quantity <= capacity | Tables tables -> let rs = Seq.sort contemporaneousReservations let remainingTables = Seq.deleteFirstsBy fits (Seq.sort tables) rs Seq.exists (fits r) remainingTables
While the function already considered seatingDur, the way it filtered reservation wasn't entirely correct. It passed all tests, though.
Filter reservations based on seating duration #
The next test case I added made me write what I consider the right implementation, but I subsequently decided to add two more test cases just for confidence. Here's all of them:
type SecondSeatingsTestCases () as this = inherit TheoryData<TimeSpan, int list, (int * DateTime) list, (int * DateTime), bool> () do this.Add ( 2 .hours, [2;2;4], [(4, d4)], (3, d4.Add (2 .hours)), true) this.Add ( 2.5 .hours, [2;4;4], [(2, d4);(1, d4.AddMinutes 15.);(2, d4.Subtract (15 .minutes))], (3, d4.AddHours 2.), false) this.Add ( 2.5 .hours, [2;4;4], [(2, d4);(2, d4.Subtract (15 .minutes))], (3, d4.AddHours 2.), true) this.Add ( 2.5 .hours, [2;4;4], [(2, d4);(1, d4.AddMinutes 15.);(2, d4.Subtract (15 .minutes))], (3, d4.AddHours 2.25), true)
The new test cases use some more literal extensions:
type Int32 with member x.minutes = TimeSpan.FromMinutes (float x) member x.hours = TimeSpan.FromHours (float x) member x.days = TimeSpan.FromDays (float x) type Double with member x.hours = TimeSpan.FromHours x
I added a private isContemporaneous function to the code base and used it to filter the reservation to pass the tests:
let private isContemporaneous (seatingDur : TimeSpan) (candidate : Reservation) (existing : Reservation) = let aSeatingBefore = candidate.Date.Subtract seatingDur let aSeatingAfter = candidate.Date.Add seatingDur aSeatingBefore < existing.Date && existing.Date < aSeatingAfter let canAccept (seatingDur : TimeSpan) config reservations r = let contemporaneousReservations = Seq.filter (isContemporaneous seatingDur r) reservations match config with | Communal capacity -> let reservedSeats = Seq.sumBy (fun r -> r.Quantity) contemporaneousReservations reservedSeats + r.Quantity <= capacity | Tables tables -> let rs = Seq.sort contemporaneousReservations let remainingTables = Seq.deleteFirstsBy fits (Seq.sort tables) rs Seq.exists (fits r) remainingTables
I could have left the functionality of isContemporaneous inside of canAccept, but I found it just hard enough to get my head around that I preferred to put it in a named helper function. Checking that a value is in a range is in itself trivial, but for some reason, figuring out the limits of the range didn't come naturally to me.
This version of canAccept only considered existing reservations if they in any way overlapped with the reservation in question. It passed all tests. It also seemed to me to be a satisfactory implementation of the second seatings scenario.
Alternative table configurations #
This state of the kata introduces groups of tables that can be reserved individually, or combined. To support that, I changed the definition of Table:
type Table = Discrete of int | Group of int list
A Table is now either a Discrete table that can't be combined, or a Group of tables that can either be reserved individually, or combined.
I had to change the test-specific table function to behave like before.
let table s = Discrete s
Before this change to the Table type, all tables were implicitly Discrete tables.
This enabled me to add the first test case:
type AlternativeTableConfigurationTestCases () as this = inherit TheoryData<Table list, int list, int, bool> () do this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 2, true) [<Theory; ClassData(typeof<AlternativeTableConfigurationTestCases>)>] let ``Alternative table configurations`` (tables, rs, r, expected) = let res i = reserve (i, d4) let reservations = List.map res rs let actual = canAccept (1 .days) (Tables tables) reservations (res r) expected =! actual
Like I did when I introduced the seatingDur argument, I deliberately chose a test case that didn't otherwise rock the boat too much. The same was the case now, so the only other change I had to make to pass all tests was to adjust the fits function:
// Reservation -> Table -> bool let private fits r = function | Discrete seats -> r.Quantity <= seats | Group _ -> true
It's clearly not correct to return true for any Group, but it passed all tests.
Accept based on sum of table group #
I wanted to edge a little closer to correctly handling the Group case, so I added a test case:
type AlternativeTableConfigurationTestCases () as this = inherit TheoryData<Table list, int list, int, bool> () do this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 2, true) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 7, false)
A restaurant with this table configuration can't accept a reservation for seven people, but because fits returned true for any Group, canAccept would return true. Since the test expected the result to be false, this caused the test to fail.
Edging closer to correct behaviour, I adjusted fits again:
// Reservation -> Table -> bool let private fits r = function | Discrete seats -> r.Quantity <= seats | Group tables -> r.Quantity <= List.sum tables
This was still not correct, because it removed an entire group of tables when fits returned true, but it passed all tests so far.
Accept reservation by combining two tables #
I added another failing test:
type AlternativeTableConfigurationTestCases () as this = inherit TheoryData<Table list, int list, int, bool> () do this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 2, true) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 7, false) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2;1], 4, true)
The last test case failed because the existing reservations should only have reserved one of the tables in the group, but because of the way fits worked, the entire group was deleted by Seq.deleteFirstsBy fits. This made canAccept reject the four-person reservation.
To be honest, this step was difficult for me. I should probably have found out how to make a smaller step.
I wanted a function that would compare a Reservation to a Table, but unlike Fits return None if it decided to 'use' the table, or a Some value if it decided that it didn't need to use the entire table. This would enable me to pick only some of the tables from a Group, but still return a Some value with the rest of tables.
I couldn't figure out an elegant way to do this with the existing Seq functionality, so I started to play around with something more specific. The implementation came accidentally as I was struggling to come up with something more general. As I was experimenting, all of a sudden, all tests passed!
// Reservation -> Table -> Table option let private allot r = function | Discrete seats -> if r.Quantity <= seats then None else Some (Discrete seats) | Group tables -> Some (Group tables) // seq<Table> -> Reservation -> seq<Table> let private allocate (tables : Table seq) r = seq { let mutable found = false use e = tables.GetEnumerator () while e.MoveNext () do if found then yield e.Current else match allot r e.Current with | None -> found <- true | Some t -> yield t } let canAccept (seatingDur : TimeSpan) config reservations r = let contemporaneousReservations = Seq.filter (isContemporaneous seatingDur r) reservations match config with | Communal capacity -> let reservedSeats = Seq.sumBy (fun r -> r.Quantity) contemporaneousReservations reservedSeats + r.Quantity <= capacity | Tables tables -> let rs = Seq.sort contemporaneousReservations let remainingTables = Seq.fold allocate (Seq.sort tables) rs Seq.exists (fits r) remainingTables
I wasn't too happy with the implementation, which I found (and still find) too complicated. This was, however, the first time I've done this part of the kata (in any language), so I wasn't sure where this was going.
The allocate function finds and allocates one of its input tables to a reservation. It does that by not yielding the first table it finds that can accommodate the reservation. Don't hurt your head too much with the code in this version, because there's plenty of cases that it incorrectly handles. It's full of bugs. Still, it passed all tests.
Reject when group has been reduced #
The implementation was wrong because the allot function would just keep returning a Group without consuming it. This would imply that canAccept would use it more than once, which was wrong, so I added a test case:
type AlternativeTableConfigurationTestCases () as this = inherit TheoryData<Table list, int list, int, bool> () do this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 2, true) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2], 7, false) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2;1], 4, true) this.Add ( [Discrete 4; Discrete 1; Discrete 2; Group [2;2;2]], [3;1;2;1;4], 3, false)
Given the existing reservations, this restaurant is effectively sold out that day. All the Discrete tables are reserved, and the last two reservations for one and four effectively consumes the Group. The latest test case expected canAccept to return false, but it returned true. Since I was following test-driven development, I expected that.
Consume #
I needed a function that would consume from a Group of tables and return the remaining tables from that group; that is, the tables not consumed. I've already discussed this function in a different context.
// int -> seq<int> -> seq<int> let consume quantity = let go (acc, xs) x = if quantity <= acc then (acc, Seq.append xs (Seq.singleton x)) else (acc + x, xs) Seq.fold go (0, Seq.empty) >> snd
I put this function in my own Seq module. It consumes values from the left until the sum is greater than or equal to the desired quantity. It then returns the rest of the sequence:
> consume 1 [1;2;3];; val it : seq<int> = seq [2; 3] > consume 2 [1;2;3];; val it : seq<int> = seq [3] > consume 3 [1;2;3];; val it : seq<int> = seq [3] > consume 4 [1;2;3];; val it : seq<int> = seq []
The first example consumes only the leading 1, while both the second and the third example consumes both 1 and 2 because the sum of those values is 3, and the requested quantity is 2 and 3, respectively. The fourth example consumes all elements because the requested quantity is 4, and you need both 1, 2, and 3 before the sum is large enough. You have to pick strictly from the left, so you can't decide to just take the elements 1 and 3.
Consuming tables from a group #
I could now use my Seq.consume function to improve allot:
// Reservation -> Table -> Table option let private allot r = function | Discrete seats -> if r.Quantity <= seats then None else Some (Discrete seats) | Group tables -> tables |> Seq.consume r.Quantity |> Seq.toList |> Group |> Some
It handles the Group case by consuming the reservation Quantity and then returning a Some Group with the remaining tables.
It also turned out that sorting the reservations wasn't appropriate, mainly because it's not entirely clear how to sort a list with elements of a discriminated union. My final implementation of canAccept was this:
// TimeSpan -> TableConfiguration -> seq<Reservation> -> Reservation -> bool let canAccept seatingDur config reservations r = let contemporaneousReservations = Seq.filter (isContemporaneous seatingDur r) reservations match config with | Communal capacity -> let reservedSeats = Seq.sumBy (fun r -> r.Quantity) contemporaneousReservations reservedSeats + r.Quantity <= capacity | Tables tables -> let remainingTables = Seq.fold allocate (Seq.ofList tables) contemporaneousReservations Seq.exists (fits r) remainingTables
Nothing much has changed - only that neither reservations nor tables are now sorted. It passes all tests.
Retrospective #
I must admit that I ran out of steam towards the end. It's possible that there's some edge cases I didn't think of. I'd probably feel more confident of the final implementation if I'd used property-based testing instead of Example-Guided Development.
I also took some unfortunate turns along the way. Early in the kata, I could easily implement canAccept with functionality from the Seq module. This meant that the function could take a seq<Reservation> as an input argument. I'm always inclined to follow Postel's law and be liberal with what I accept. I thought that being able to accept any seq<Reservation> was a good design decision. It might have been if I'd been publishing a reusable library, but it made things more awkward.
I'm also not sure that I chose to model the table layouts in the best way. For example, I currently can't handle a scenario with both bar seating and individual tables. I think I should have made Communal a case of Table. This would have enabled me to model layouts with several communal tables combined with discrete tables, and even groups of tables.
In general, my solution seems too complicated, but I don't see an easy fix. Often, if I work some more with the problem, insight arrives. It usually arrives when you least need it, so I thought it better to let the problem rest for a while. I can always return to it when I feel that I have a fresh approach.
Summary #
This article walks you through my first F# attempt at the Maître d' kata. The repository is available on GitHub.
I'm not entirely happy with how it turned out, but I don't consider it an utter failure either.
Unit bias against collections
How do you get the value out of a collection? Mu. Which value?
The other day I was looking for documentation on how to write automated tests with a self-hosted ASP.NET Core 3 web application. I've done this numerous times with previous versions of the framework, but ASP.NET Core 3 is new, so I wanted to learn how I'm supposed to do it this year. I found official documentation that helped me figure it out.
One of the code examples in that article displays a motif that I keep encountering. It displays behaviour close enough to unit bias that I consider it reasonable to use that label. Unit bias is the cognitive tendency to consider a unit of something the preferred amount. Our brains don't like fractions, and they don't like multiples either.
Unit bias in action #
The sample code in the ASP.NET Core documentation differs in the type of dependency it looks for, but is otherwise identical to this:
var descriptor = services.SingleOrDefault( d => d.ServiceType == typeof(IReservationsRepository)); if (descriptor != null) { services.Remove(descriptor); }
The goal is to enable an automated integration test to run against a Fake database instead of an actual relational database. My production Composition Root registers an implementation of IReservationsRepository that communicates with an actual database. In an automated integration test, I'd like to unregister the existing dependency and replace it with a Fake. Here's the code in context:
public class RestaurantApiFactory : WebApplicationFactory<Startup> { protected override void ConfigureWebHost(IWebHostBuilder builder) { if (builder is null) throw new ArgumentNullException(nameof(builder)); builder.ConfigureServices(services => { var descriptor = services.SingleOrDefault( d => d.ServiceType == typeof(IReservationsRepository)); if (descriptor != null) { services.Remove(descriptor); } services.AddSingleton<IReservationsRepository>( new FakeDatabase()); }); } }
It works as intended, so what's the problem?
How do I get the value out of my collection? #
The problem is that it's fragile. What happens if there's more than one registration of IReservationsRepository?
This happens:
System.InvalidOperationException : Sequence contains more than one matching element
This is a completely avoidable error, stemming from unit bias.
A large proportion of programmers I meet seem to be fundamentally uncomfortable with thinking in multitudes. They subconsciously prefer thinking in procedures and algorithms that work on a single object. The programmer who wrote the above call to SingleOrDefault exhibits behaviour putting him or her in that category.
This is nothing but a specific instantiation of a more general programmer bias: How do I get the value out of the monad?
As usual, the answer is mu. You don't. The question borders on the nonsensical. How do I get the value out of my collection? Which value? The first? The last? Some arbitrary value at an unknown position? Which value do you want if the collection is empty? Which value do you want if there's more than one that fits a predicate?
If you can answer such questions, you can get 'the' value out of a collection, but often, you can't. In the current example, the code doesn't handle multiple IReservationsRepository registrations.
It easily could, though.
Inject the behaviour into the collection #
The best answer to the question of how to get the value out of the monad (in this case, the collection) is that you don't. Instead, you inject the desired behaviour into it.
In this case, the desired behaviour is to remove a descriptor. The monad in question is the collection of services. What does that mean in practice?
A first attempt might be something like this:
var descriptors = services .Where(d => d.ServiceType == typeof(IReservationsRepository)); foreach (var descriptor in descriptors) services.Remove(descriptor);
Unfortunately, this doesn't quite work:
System.InvalidOperationException : Collection was modified; enumeration operation may not execute.
This happens because descriptors is a lazily evaluated Iterator over services, and you're not allowed to remove elements from a collection while you enumerate it. It could lead to bugs if you could.
That problem is easily solved. Just copy the selected descriptors to an array or list:
var descriptors = services .Where(d => d.ServiceType == typeof(IReservationsRepository)) .ToList(); foreach (var descriptor in descriptors) services.Remove(descriptor);
This achieves the desired outcome regardless of the number of matches to the predicate. This is a more robust solution, and it requires the same amount of code.
You can stop there, since the code now works, but if you truly want to inject the behaviour into the collection, you're not quite done yet.
But you're close. All you have to do is this:
services .Where(d => d.ServiceType == typeof(IReservationsRepository)) .ToList() .ForEach(d => services.Remove(d));
Notice how this statement never produces an output. Instead, you 'inject' the call to services.Remove into the list, using the ForEach method, which then mutates the services collection.
Whether you prefer the version that uses the foreach keyword or the version that uses List<T>.ForEach doesn't matter. What matters is that you don't use the partial SingleOrDefault function.
Conclusion #
It's a common code smell when programmers try to extract a single value from a collection. Sometimes it's appropriate, but there are several edge cases you should be prepared to address. What should happen if the collection is empty? What should happen if the collection contains many elements? What should happen if the collection is infinite? (I didn't address that in this article.)
You can often both simplify your code and make it more robust by staying 'in' the collection, so to speak. Let the desired behaviour apply to all appropriate elements of the collection.
Don't be biased against collections.
Comments
I concur that often the first element of a collection is picked without thinking. Anecdotally, I experienced a system that would not work if set up freshly because in some places there was no consideration for empty collections. (The testing environment always contained some data)
Yet I would reverse the last change (towards .ForEach). For one, because (to my biased eye) it
looks side effect free but isn't. And then it does add value compared to a forech loop, also both solutions
are needlessy inefficient.
If you want to avoid the foreach, go for the RemoveAll() method (also present on List<T>):
services.RemoveAll<IReservationsRepository>();
Julius, thank you for writing. Yes, I agree that in C# it's more idiomatic to use foreach.
How would using RemoveAll work? Isn't that going to remove the entries from the List instead of from services?
Hi Mark,
As you"re calling IServiceCollection.RemoveAll(),
it will remove it from the collection. I tried it, and to me it seems to be working. (As long as you are not copying the services into a list beforehand)
But to your main point, I remember when I wrote .Single() once, and years later I got a bug report because of it. I see two approaches there:
Fail as fast and hard as possible or check just as much as needed for the moment.
Considering TDD in the former approach, one would need to write a lot of test code for scenarios, that should never happen to verify the exceptions happen.
Still, in the latter approach, a subtle bug could stay in the system for quite some time... What do you prefer?
Julius, thank you for writing. It turns out that RemoveAll are a couple of extension methods on IServiceCollection. One has to import Microsoft.Extensions.DependencyInjection.Extensions with a using directive before one can use them. I didn't know about these methods, but I agree that they seem to do their job. Thank you for the tip.
As for your question, my preference is for robustness. In my experience, there's rarely such a thing as a scenario that never happens. If the code allows something to happen, it'll likely happen sooner or later. Code changes, so even if you've analysed that some combination of input isn't possible today, a colleague may change the situation tomorrow. It pays to write that extra unit test or two to make sure that encapsulation isn't broken.
This is also one of the reasons I'm fond of property-based testing. You automatically get coverage of all sorts of boundary conditions you'd normally not think about testing.
Curb code rot with thresholds
Code bases deteriorate unless you actively prevent it. Institute some limits that encourage developers to clean up.
From time to time I manage to draw the ire of people, with articles such as The 80/24 rule or Put cyclomatic complexity to good use. I can understand why. These articles suggest specific constraints to which people should consider consenting. Don't write code wider than 80 characters. Don't write code with a cyclomatic complexity higher than 7.
It makes people uncomfortable.
Sophistication #
I hope that regular readers understand that I'm a more sophisticated thinker than some of my texts may suggest. I deliberately simplify my points.
I do this to make the text more readable. I also aspire to present sufficient arguments, and enough context, that a charitable reader will understand that everything I write should be taken as food for thought rather than gospel.
Consider a sentence like the above: I deliberately simplify my points. That sentence, in itself, is an example of deliberate simplification. In reality, I don't always simplify my points. Perhaps sometimes I simplify, but it's not deliberate. I could have written: I often deliberately simplify some of my points. Notice the extra hedge words. Imagine an entire text written like that. It would be less readable.
I could hedge my words when I write articles, but I don't. I believe that a text that states its points as clearly as possible is easier to understand for any careful reader. I also believe that hedging my language will not prevent casual readers from misunderstanding what I had in mind.
Archetypes #
Why do I suggest hard limits on line width, cyclomatic complexity, and so on?
In light of the above, realise that the limits I offer are suggestions. A number like 80 characters isn't a hard limit. It's a representation of an idea; a token. The same is true for the magic number seven, plus or minus two. That too, represents an idea - the idea that human short-term memory is limited, and that this impacts our ability to read and understand code.
The number seven serves as an archetype. It's a proxy for a more complex idea. It's a simplification that, hopefully, makes it easier to follow the plot.
Each method should have a maximum cyclomatic complexity of seven. That's easier to understand than each method should have a maximum cyclomatic complexity small enough that it fits within the cognitive limits of the human brain's short-term memory.
I've noticed that a subset of the developer population is quite literal-minded. If I declare: don't write code wider than 80 characters they're happy if they agree, and infuriated if they don't.
If you've been paying attention, you now understand that this isn't about the number 80, or 24, or 7. It's about instituting useful quantitative guidance. The actual number is less important.
I have reasons to prefer those specific values. I've already motivated them in previous articles. I'm not, though, obdurately attached to those particular numbers. I'd rather work with a team that has agreed to a 120-character maximum width than with a team that follows no policy.
How code rots #
No-one deliberately decides to write legacy code. Code bases gradually deteriorate.
Here's another deliberate simplification: code gradually becomes more complicated because each change seems small, and no-one pays attention to the overall quality. It doesn't happen overnight, but one day you realise that you've developed a legacy code base. When that happens, it's too late to do anything about it.
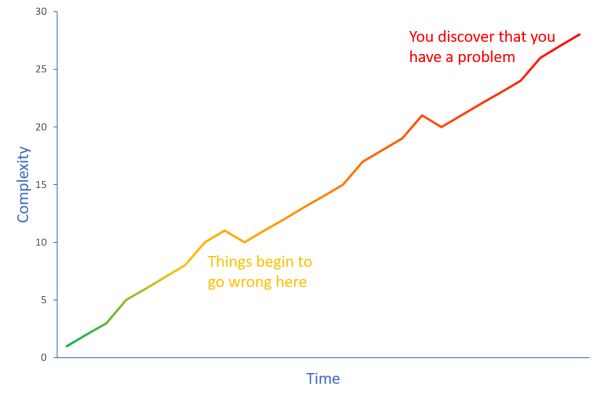
At the beginning, a method has low complexity, but as you fix defects and add features, the complexity increases. If you don't pay attention to cyclomatic complexity, you pass 7 without noticing it. You pass 10 without noticing it. You pass 15 and 20 without noticing it.
One day you discover that you have a problem - not because you finally look at a metric, but because the code has now become so complicated that everyone notices. Alas, now it's too late to do anything about it.
Code rot sets in a little at a time; it works like boiling the proverbial frog.
Thresholds #
Agreeing on a threshold can help curb code rot. Institute a rule and monitor a metric. For example, you could agree to keep an eye on cyclomatic complexity. If it exceeds 7, you reject the change.
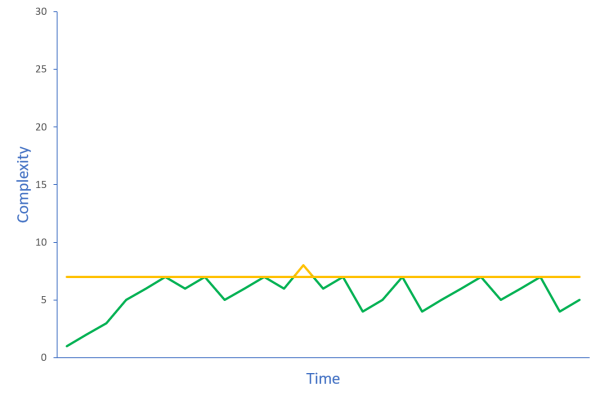
Such rules work because they can be used to counteract gradual decay. It's not the specific value 7 that contributes to better code quality; it's the automatic activation of a rule based on a threshold. If you decide that the threshold should be 10 instead, that'll also make a difference.
Notice that the above diagram suggests that exceeding the threshold is still possible. Rules are in the way if you must rigidly obey them. Situations arise where breaking a rule is the best response. Once you've responded to the situation, however, find a way to bring the offending code back in line. Once a threshold is exceeded, you don't get any further warnings, and there's a risk that that particular code will gradually decay.
What you measure is what you get #
You could automate the process. Imagine running cyclomatic complexity analysis as part of a Continuous Integration build and rejecting changes that exceed a threshold. This is, in a way, a deliberate attempt to hack the management effect where you get what you measure. With emphasis on a metric like cyclomatic complexity, developers will pay attention to it.
Be aware, however, of Goodhart's law and the law of unintended consequences. Just as code coverage is a useless target measure, you have to be careful when you institute hard rules.
I've had success with introducing threshold rules because they increase awareness. It can help a technical leader shift emphasis to the qualities that he or she wishes to improve. Once the team's mindset has changed, the rule itself becomes redundant.
I'm reminded of the Dreyfus model of skill acquisition. Rules make great training wheels. Once you become proficient, the rules are no longer required. They may even be in your way. When that happens, get rid of them.
Conclusion #
Code deteriorates gradually, when you aren't looking. Instituting rules that make you pay attention can combat code rot. Using thresholds to activate your attention can be an effective countermeasure. The specific value of the threshold is less important.
In this article, I've mostly used cyclomatic complexity as an example of a metric where a threshold could be useful. Another example is line width; don't exceed 80 characters. Or line height: methods shouldn't exceed 24 lines of code. Those are examples. If you agree that keeping an eye on a metric would be useful, but you disagree with the threshold I suggest, pick a value that suits you better.
It's not the specific threshold value that improves your code; paying attention does.
Comments
In F#, it's not uncommon to have inner functions (local functions defined inside other functions). How would you calculate the cyclomatic complexity of a function that contains inner functions?
To be specific, I'm actually wondering about how to count the number of activated objects in a function, which you talk about in your book, Code That Fits in Your Head. I have been wanting to ask you this for some time, but haven't been able to find a good article to comment on. I think this is the closest I can get.
In terms of activated objects: Would you count all activated objects in all sub-functions as counting towards the top-level function? Or would you count the inner functions separately, and have calls to the inner function contribute only "one point" to the top-level functions? I think the latter makes most sense, but I'm not sure. I base my reasoning on the fact that an inner function, being a closure, is similar to a class with fields and a single method (closures are a poor man's objects and vice versa). Another way to view it is that you could refactor by extracting the function and adding any necessary parameters.
PS, this is not just theoretical. I am toying with a linter for F# and want "number of activated objects" as one of the rules.
Christer, thank you for writing. For the purposes of calculating cyclomatic complexity of inner functions, aren't they equivalent to (private) helper methods?
If so, they don't count towards the cyclomatic complexity of the containing function.
As for the other question, I don't count functions as activated objects, but I do count the values they return. When the function is referentially transparent, however, they're equal. I do talk more about this in my talk Fractal Architecture, of which you can find several recordings on the internet; here's one.
The book also discusses this, and that part is also freely available here on the blog.
The short answer is that it's essential that you can prevent 'inner' objects from leaking out from method calls. Per definition, functions that are referentially transparent do have that property. For methods that aren't referentially transparent, encapsulation may still achieve the same effect, if done right. Usually, however, it isn't.
Mark, thank you for the response. What you say about cyclomatic complexity makes sense, especially given your previous writings on the subject. I am still a bit fuzzy on how to count activated objects, though.
If a function returns a tuple of which one item is ignored, would that ignored object count as an activated object? (Does the fact that a tuple could technically be considered as a single object with .Item1 and .Item2 properties change the answer?) And what about piping? Eta reduction?
An example would be handy right about now, so what would you say are the activated object counts of the following functionally identical functions, and why?
let f (a, b) = let c, _ = getCD (a, b) in clet f (a, b) = (a, b) |> getCD |> fstlet f = getCD >> fstlet f = getCDFst
Note the "trick" of number 3: By removing the explicit parameter, it is now impossible to tell just from looking at the code how many tupled items f accepts, if any. And in number 4, even the knowledge that an intermediate function in the composition returns a tuple of 2 values is removed.
Additionally: I assume that returning a value counts as "activating" an object? So let f x = x has 1 activated object? What about the functionally identical let f = id? Would that be 1 or 0?
I guess what I'm after is a more fully developed concept of "the number of activated objects" of a function/method, to the point where a useful linter rule could be implemented based on it; something similar to your previous writings on how method calls do not increase the cyclomatic complexity, which was a very useful clarification that I have seen you repeat several times. I have given the matter some thought myself, but as you can see, I haven't been able to come up with good answer.
It seems that I should have been more explicit about the terminology related to the adjective activated. I was inspired by the notion of object activation described in Thinking Fast and Slow. The idea is that certain pieces of information move to the forefront in the mind, and that these 'objects' impact decision-making. Kahneman labels such information as activated when it impacts the decision process.
The heuristic I had in mind was to port that idea to an (informal) readability analysis. Given that the human short-time memory is quite limited, I find it useful to count the mental load of a given piece of code.
The point, then, is not to count all objects or values in scope, but rather those that are required to understand what a piece of code does. For example, if you look at an instance method on a class, the class could have four class fields, but if only one of those fields are used in the method, only that one is activated - even though the other three are also in scope.
With that in mind, let's try to look at your four examples.
- This example activates
a,b, andc: 3 objects. - This example activates
aandb: 2 objects. - No objects, unless you now want to count
getCDas an object. - Again, probably no objects.
Note that I've employed qualifying words. The point of the analysis is to highlight objects that might stress our short-term memory. It's not an exact science, and I never intended it to be. Rather, I see it as a possible springboard for having a discussion about relative readability of code. A team can use the heuristic to compare alternatives.
With your examples in mind, you'd be likely to run into programmers who find the first two examples more readable than the third. It's certainly more 'detailed', so, in a sense, it's easier to understand what's going on. That works as long as you only have a few values in play, but cognitively, it doesn't scale.
I do tend to prefer eta reductions and point-free notation exactly because they tend to reduce the number of activated objects, but these techniques certainly also raise the abstraction level. On the other hand, once someone understands something like function composition (>>) or point-free notation, they can now leverage long-term memory for that, instead of having to rely on limited short-term memory in order to understand a piece of code. By moving more information to long-term memory, we can reduce the load on short-term memory, thereby freeing it up for other information.
Perhaps that's a bit of a digression, but I always intended the notion of object activation to be a heuristic rather than an algorithm.
Mark, thank you for the excellent clarification. It gave me one of those "a-ha" moments that accompanies a sudden jump in understanding. In hindsight, of course this is about the cognitive load of a piece of code, and of course that will be different for different people, based for example on which abstractions they are used to.
In terms of the code examples, I think we both agree that let f = a >> b requires less mental load than let f = a >> b >> c >> d >> e. In other words, I would argue that functions in a composition do contribute to cognitive load. This may however also depend on the actual functions that are composed.
In any case, I am now less certain than before that a simple linter rule (i.e., an algorithm) can capture cognitive load in a way that is generally useful. I will have to think about this some more.
Repeatable execution in C#
A C# example of Goldilogs.
This article is part of a series of articles about repeatable execution. The introductory article argued that if you've logged the impure actions that a system made, you have enough information to reproduce what happened. The previous article verified that for the example scenario, the impure actions were limited to reading the current time and interacting with the application database.
This article shows how to implement equivalent functionality in C#. You should be able to extrapolate from this to other object-oriented programming languages.
The code is available on GitHub.
Impure actions #
In the previous article I modelled impure actions as free monads. In C#, it'd be more idiomatic to use Dependency Injection. Model each impure interaction as an interface.
public interface IClock { DateTime GetCurrentDateTime(); }
The demo code demonstrates a single feature of a REST API and it only requires a single method on this interface to work. Following the Dependency Inversion Principle
This interface only defines a single method, because that's all the client code requires."clients [...] own the abstract interfaces"
Likewise, the client code only needs two methods to interact with the database:
public interface IReservationsRepository { IEnumerable<Reservation> ReadReservations(DateTime date); void Create(Reservation reservation); }
In the Haskell example code base, I also implemented GET for /reservations, but I forgot to do that here. There's only two methods on the interface: one to query the database, and one to create a new row.
Receive a reservation #
The central feature of the service is to receive and handle an HTTP POST request, as described in the introductory article. When a document arrives it triggers a series of non-trivial work:
- The service validates the input data. Among other things, it checks that the reservation is in the future. It uses
GetCurrentDateTimefor this. - It queries the database for existing reservations. It uses
ReadReservationsfor this. - It uses complex business logic to determine whether to accept the reservation. This essentially implements the Maître d' kata.
- If it accepts the reservation, it stores it. It uses
Createfor this.
public ActionResult Post(ReservationDto dto) { if (!DateTime.TryParse(dto.Date, out var _)) return BadRequest($"Invalid date: {dto.Date}."); Reservation reservation = Mapper.Map(dto); if (reservation.Date < Clock.GetCurrentDateTime()) return BadRequest($"Invalid date: {reservation.Date}."); var reservations = Repository.ReadReservations(reservation.Date); bool accepted = maîtreD.CanAccept(reservations, reservation); if (!accepted) return StatusCode(StatusCodes.Status500InternalServerError, "Couldn't accept."); Repository.Create(reservation); return Ok(); }
Clock and Repository are injected dependencies, and maîtreD is an object that implements the decision logic as the pure CanAccept function.
Composition #
The Post method is defined on a class called ReservationsController with these dependencies:
public ReservationsController( TimeSpan seatingDuration, IReadOnlyCollection<Table> tables, IReservationsRepository repository, IClock clock)
The seatingDuration and tables arguments are primitive dependencies used to configure the maîtreD object. I could also have injected maîtreD as a concrete dependency, but I decided against that for no particular reason.
There's no logging dependency, but the system still logs. Like in the previous example, logging is a cross-cutting concern and exclusively addressed through composition:
if (controllerType == typeof(ReservationsController)) { var l = new ScopedLog(new FileLog(LogFile)); var controller = new ReservationsController( SeatingDuration, Tables, new LogReservationsRepository( new SqlReservationsRepository(ConnectionString), l), new LogClock( new SystemClock(), l)); Logs.AddOrUpdate(controller, l, (_, x) => x); return controller; }
Each dependency is wrapped by a logger. We'll return to that in a minute, but consider first the actual implementations.
Using the system clock #
Using the system clock is easy:
public class SystemClock : IClock { public DateTime GetCurrentDateTime() { return DateTime.Now; } }
This implementation of IClock simply delegates to DateTime.Now. Again, no logging service is injected.
Using the database #
Using the database isn't much harder. I don't find that ORMs offer any benefits, so I prefer to implement database functionality using basic database APIs:
public void Create(Reservation reservation) { using (var conn = new SqlConnection(ConnectionString)) using (var cmd = new SqlCommand(createReservationSql, conn)) { cmd.Parameters.Add( new SqlParameter("@Guid", reservation.Id)); cmd.Parameters.Add( new SqlParameter("@Date", reservation.Date)); cmd.Parameters.Add( new SqlParameter("@Name", reservation.Name)); cmd.Parameters.Add( new SqlParameter("@Email", reservation.Email)); cmd.Parameters.Add( new SqlParameter("@Quantity", reservation.Quantity)); conn.Open(); cmd.ExecuteNonQuery(); } } private const string createReservationSql = @" INSERT INTO [dbo].[Reservations] ([Guid], [Date], [Name], [Email], [Quantity]) OUTPUT INSERTED.Id VALUES (@Guid, @Date, @Name, @Email, @Quantity)";
The above code snippet implements the Create method of the IReservationsRepository interface. Please refer to the Git repository for the full code if you need more details.
If you prefer to implement your database functionality with an ORM, or in another way, you can do that. It doesn't change the architecture of the system. No logging service is required to interact with the database.
Compose with logging #
As the above composition code snippet suggests, logging is implemented with Decorators. The ultimate implementation of IClock is SystemClock, but the Composition Root decorates it with LogClock:
public class LogClock : IClock { public LogClock(IClock inner, ScopedLog log) { Inner = inner; Log = log; } public IClock Inner { get; } public ScopedLog Log { get; } public DateTime GetCurrentDateTime() { var currentDateTime = Inner.GetCurrentDateTime(); Log.Observe( new Interaction { Operation = nameof(GetCurrentDateTime), Output = currentDateTime }); return currentDateTime; } }
ScopedLog is a Concrete Dependency that, among other members, affords the Observe method. Notice that LogClock implements IClock by decorating another polymorphic IClock instance. It delegates functionality to inner, logs the currentDateTime and returns it.
The LogReservationsRepository class implements the same pattern:
public class LogReservationsRepository : IReservationsRepository { public LogReservationsRepository(IReservationsRepository inner, ScopedLog log) { Inner = inner; Log = log; } public IReservationsRepository Inner { get; } public ScopedLog Log { get; } public void Create(Reservation reservation) { Log.Observe( new Interaction { Operation = nameof(Create), Input = new { reservation } }); Inner.Create(reservation); } public IEnumerable<Reservation> ReadReservations(DateTime date) { var reservations = Inner.ReadReservations(date); Log.Observe( new Interaction { Operation = nameof(ReadReservations), Input = new { date }, Output = reservations }); return reservations; } }
This architecture not only implements the desired functionality, but also Goldilogs: not too little, not too much, but just what you need. Notice that I didn't have to change any of my Domain Model or HTTP-specific code to enable logging. This cross-cutting concern is enabled entirely via composition.
Repeatability #
An HTTP request like this:
POST /reservations/ HTTP/1.1
Content-Type: application/json
{
"id": "7bc3fc93-a777-4138-8630-a805e7246335",
"date": "2020-03-20 18:45:00",
"name": "Kozue Kaburagi",
"email": "ninjette@example.net",
"quantity": 4
}
produces a log entry like this:
{
"entry": {
"time": "2020-01-02T09:50:34.2678703+01:00",
"operation": "Post",
"input": {
"dto": {
"id": "7bc3fc93-a777-4138-8630-a805e7246335",
"date": "2020-03-20 18:45:00",
"email": "ninjette@example.net",
"name": "Kozue Kaburagi",
"quantity": 4
}
},
"output": null
},
"interactions": [
{
"time": "2020-01-02T09:50:34.2726143+01:00",
"operation": "GetCurrentDateTime",
"input": null,
"output": "2020-01-02T09:50:34.2724012+01:00"
},
{
"time": "2020-01-02T09:50:34.3571224+01:00",
"operation": "ReadReservations",
"input": { "date": "2020-03-20T18:45:00" },
"output": [
{
"id": "c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c",
"date": "2020-03-20T19:00:00",
"email": "emp@example.com",
"name": "Elissa Megan Powers",
"quantity": 3
}
]
},
{
"time": "2020-01-02T09:50:34.3587586+01:00",
"operation": "Create",
"input": {
"reservation": {
"id": "7bc3fc93-a777-4138-8630-a805e7246335",
"date": "2020-03-20T18:45:00",
"email": "ninjette@example.net",
"name": "Kozue Kaburagi",
"quantity": 4
}
},
"output": null
}
],
"exit": {
"time": "2020-01-02T09:50:34.3645105+01:00",
"operation": null,
"input": null,
"output": { "statusCode": 200 }
}
}
I chose to gather all information regarding a single HTTP request into a single log entry and format it as JSON. I once worked with an organisation that used the ELK stack in that way, and it made it easy to identify and troubleshoot issues in production.
You can use such a log file to reproduce the observed behaviour, for example in a unit test:
[Fact] public void NinjetteRepro() { string log = Log.LoadFile("Ninjette.json"); (ReservationsController sut, ReservationDto dto) = Log.LoadReservationsControllerPostScenario(log); var actual = sut.Post(dto); Assert.IsAssignableFrom<OkResult>(actual); }
This test reproduces the behaviour that was recorded in the above JSON log. While there was already one existing reservation (returned from ReadReservations), the system had enough remaining capacity to accept the new reservation. Therefore, the expected result is an OkResult.
Replay #
You probably noticed the helper methods Log.LoadFile and Log.LoadReservationsControllerPostScenario. This API is just a prototype to get the point across. There's little to say about LoadFile, since it just reads the file. The LoadReservationsControllerPostScenario method performs the bulk of the work. It parses the JSON string into a collection of observations. It then feeds these observations to test-specific implementations of the dependencies required by ReservationsController.
For example, here's the test-specific implementation of IClock:
public class ReplayClock : IClock { private readonly Queue<DateTime> times; public ReplayClock(IEnumerable<DateTime> times) { this.times = new Queue<DateTime>(times); } public DateTime GetCurrentDateTime() { return times.Dequeue(); } }
The above JSON log example only contains a single observation of GetCurrentDateTime, but an arbitrary log may contain zero, one, or several observations. The idea is to replay them, starting with the earliest. ReplayClock just creates a Queue of them and Dequeue every time GetCurrentDateTime executes.
The test-specific ReplayReservationsRepository class works the same way:
public class ReplayReservationsRepository : IReservationsRepository { private readonly IDictionary<DateTime, Queue<IEnumerable<Reservation>>> reads; public ReplayReservationsRepository( IDictionary<DateTime, Queue<IEnumerable<Reservation>>> reads) { this.reads = reads; } public void Create(Reservation reservation) { } public IEnumerable<Reservation> ReadReservations(DateTime date) { return reads[date].Dequeue(); } }
You'll notice that in order to implement ReadReservations, the ReplayReservationsRepository class needs a dictionary of queues. The ReplayClock class didn't need a dictionary, because GetCurrentDateTime takes no input. The ReadReservations method, on the other hand, takes a date as a method argument. You might have observations of ReadReservations for different dates, and multiple observations for each date. That's the reason that ReplayReservationsRepository needs a dictionary of queues.
The Create method doesn't return anything, so I decided that this methods should do nothing.
The LoadReservationsControllerPostScenario function parses the JSON log and creates instances of these Test Doubles.
var repository = new ReplayReservationsRepository(reads); var clock = new ReplayClock(times); var controller = new ReservationsController(seatingDuration, tables, repository, clock);
And that, together with the parsed HTTP input, is what LoadReservationsControllerPostScenario returns:
return (controller, dto);
This is only a prototype to illustrate the point that you can reproduce an interaction if you have all the impure inputs and outputs. The details are available in the source code repository.
Summary #
This article demonstrated how making the distinction between pure and impure code is useful in many situations. For logging purposes, you only need to log the impure inputs and outputs. That's neither too little logging, nor too much, but just right: Goldilogs.
Model any (potentially) impure interaction as a dependency and use Dependency Injection. This enables you to reproduce observed behaviour from logs. Don't inject logging services into your Controllers or Domain Models.
Repeatable execution in Haskell
A way to figure out what to log, and what not to log, using Haskell.
This article is part of a series of articles about repeatable execution. The previous article argued that if you've logged the impure actions that a system made, you have enough information to reproduce what happened.
In most languages, it's difficult to discriminate between pure functions and impure actions, but Haskell explicitly makes that distinction. I often use it for proof of concepts for that reason. I'll do that here as well.
This proof of concept is mostly to verify what a decade of functional programming has already taught me. For the functionality that the previous article introduced, the impure actions involve a database and the system clock.
The code shown in this article is available on GitHub.
Pure interactions #
I'll use free monads to model impure interactions as pure functions. For this particular example code base, an impureim sandwich would have been sufficient. I do, however, get the impression that many readers find it hard to extrapolate from impureim sandwiches to a general architecture. For the benefit of those readers, the example uses free monads.
The system clock interaction is the simplest:
newtype ClockInstruction next = CurrentTime (LocalTime -> next) deriving Functor
There's only one instruction. It takes no input, but returns the current time and date.
For database interactions, I went through a few iterations and arrived at this set of instructions:
data ReservationsInstruction next = ReadReservation UUID (Maybe Reservation -> next) | ReadReservations LocalTime ([Reservation] -> next) | CreateReservation Reservation next deriving Functor
There's two queries and a command. The intent with the CreateReservation command is to create a new reservation row in the database. The two queries fetch a single reservation based on ID, or a set of reservations based on a date. A central type for this instruction set is Reservation:
data Reservation = Reservation { reservationId :: UUID , reservationDate :: LocalTime , reservationName :: String , reservationEmail :: String , reservationQuantity :: Int } deriving (Eq, Show, Read, Generic)
The program has to interact both with the system clock and the database, so ultimately it turned out to be useful to combine these two instruction sets into one:
type ReservationsProgram = Free (Sum ReservationsInstruction ClockInstruction)
I used the Sum functor to combine the two instruction sets, and then turned them into a Free monad.
With free monads, I find that my code becomes more readable if I define helper functions for each instruction:
readReservation :: UUID -> ReservationsProgram (Maybe Reservation) readReservation rid = liftF $ InL $ ReadReservation rid id readReservations :: LocalTime -> ReservationsProgram [Reservation] readReservations t = liftF $ InL $ ReadReservations t id createReservation :: Reservation -> ReservationsProgram () createReservation r = liftF $ InL $ CreateReservation r () currentTime :: ReservationsProgram LocalTime currentTime = liftF $ InR $ CurrentTime id
There's much else going on in the code base, but that's how I model feature-specific impure actions.
Receive a reservation #
The central feature of the service is to receive and handle an HTTP POST request, as described in the introductory article. When a document arrives it triggers a series of non-trivial work:
- The service validates the input data. Among other things, it checks that the reservation is in the future. It uses
currentTimefor this. - It queries the database for existing reservations. It uses
readReservationsfor this. - It uses complex business logic to determine whether to accept the reservation. This essentially implements the Maître d' kata.
- If it accepts the reservation, it stores it. It uses
createReservationfor this.
tryAccept :: NominalDiffTime -> [Table] -> Reservation -> ExceptT (APIError ByteString) ReservationsProgram () tryAccept seatingDuration tables r = do now <- lift currentTime _ <- liftEither $ validateReservation now r reservations <- fmap (removeNonOverlappingReservations seatingDuration r) <$> lift $ readReservations $ reservationDate r _ <- liftEither $ canAccommodateReservation tables reservations r lift $ createReservation r
If you're interested in details, the code is available on GitHub. I may later write other articles about interesting details.
In the context of repeatable execution and logging, the key is that this is a pure function. It does, however, return a ReservationsProgram (free monad), so it's not going to do anything until interpreted. The interpreters are impure, so this is where logging has to take place.
HTTP API #
The above tryAccept function is decoupled from boundary concerns. It has little HTTP-specific functionality.
I've written the actual HTTP API using Servant. The following function translates the above Domain Model to an HTTP API:
type ReservationsProgramT = FreeT (Sum ReservationsInstruction ClockInstruction) reservationServer :: NominalDiffTime -> [Table] -> ServerT ReservationAPI (ReservationsProgramT Handler) reservationServer seatingDuration tables = getReservation :<|> postReservation where getReservation rid = do mr <- toFreeT $ readReservation rid case mr of Just r -> return r Nothing -> throwError err404 postReservation r = do e <- toFreeT $ runExceptT $ tryAccept seatingDuration tables r case e of Right () -> return () Left (ValidationError err) -> throwError $ err400 { errBody = err } Left (ExecutionError err) -> throwError $ err500 { errBody = err }
This API also exposes a reservation as a resource you can query with a GET request, but I'm not going to comment much on that. It uses the above readReservation helper function, but there's little logic involved in the implementation.
The above reservationServer function implements, by the way, only a partial API. It defines the /reservations resource, as explained in the overview article. Its type is defined as:
type ReservationAPI = Capture "reservationId" UUID :> Get '[JSON] Reservation :<|> ReqBody '[JSON] Reservation :> Post '[JSON] ()
That's just one resource. Servant enables you define many resources and combine them into a larger API. For this example, the /reservations resource is all there is, so I define the entire API like this:
type API = "reservations" :> ReservationAPI
You can also define your complete server from several partial services, but in this example, I only have one:
server = reservationServer
Had I had more resources, I could have combined several values with a combinator, but now that I have only reservationServer it seems redundant, I admit.
Hosting the API #
The reservationServer function, and thereby also server, returns a ServerT value. Servant ultimately demands a Server value to serve it. We need to transform the ServerT value into a Server value, which we can do with hoistServer:
runApp :: String -> Int -> IO () runApp connStr port = do putStrLn $ "Starting server on port " ++ show port ++ "." putStrLn "Press Ctrl + C to stop the server." ls <- loggerSet let logLn s = pushLogStrLn ls $ toLogStr s let hoistSQL = hoistServer api $ runInSQLServerAndOnSystemClock logLn $ pack connStr (seatingDuration, tables) <- readConfig logHttp <- logHttpMiddleware ls run port $ logHttp $ serve api $ hoistSQL $ server seatingDuration tables
The hoistServer function enables you to translate a ServerT api m into a ServerT api n value. Since Server is a type alias for ServerT api Handler, we need to translate the complicated monad returned from server into a Handler. The runInSQLServerAndOnSystemClock function does most of the heavy lifting.
You'll also notice that the runApp function configures some logging. Apart from some HTTP-level middleware, the logLn function logs a line to a text file. The runApp function passes it as an argument to the runInSQLServerAndOnSystemClock function. We'll return to logging later in this article, but first I find it instructive to outline what happens in runInSQLServerAndOnSystemClock.
As the name implies, two major actions take place. The function interprets database interactions by executing impure actions against SQL Server. It also interprets clock interactions by querying the system clock.
Using the system clock #
The system-clock-based interpreter is the simplest of the two interpreters. It interprets ClockInstruction values by querying the system clock for the current time:
runOnSystemClock :: MonadIO m => ClockInstruction (m a) -> m a runOnSystemClock (CurrentTime next) = liftIO (zonedTimeToLocalTime <$> getZonedTime) >>= next
This function translates a ClockInstruction (m a) to an m a value by executing the impure getZonedTime function. From the returned ZonedTime value, it then extracts the local time, which it passes to next.
You may have two questions:
- Why map
ClockInstruction (m a)instead ofClockInstruction a? - Why
MonadIO?
My ultimate goal with each of these interpreters is to compose them into runInSQLServerAndOnSystemClock. As described above, this function transforms ServerT API (ReservationsProgramT Handler) into a ServerT API Handler (also known as Server API). Another way to put this is that we need to collapse ReservationsProgramT Handler to Handler by, so to speak, removing ReservationsProgramT.
Recall that a type like ReservationsProgramT Handler is really in 'curried' form. This is actually the parametrically polymorphic type ReservationsProgramT Handler a. Likewise, Handler is also parametrically polymorphic: Handler a. What we need, then, is a function with the type ReservationsProgramT Handler a -> Handler a or, more generally, FreeT f m a -> m a. This follows because ReservationsProgramT is an alias for FreeT ..., and Handler is a container of a values.
There's a function for that in Control.Monad.Trans.Free called iterT:
iterT :: (Functor f, Monad m) => (f (m a) -> m a) -> FreeT f m a -> m a
This fits our need. For each of the functors in ReservationsProgramT, then, we need a function f (m a) -> m a. Specifically, for ClockInstruction, we need to define a function with the type ClockInstruction (Handler a) -> Handler a. Consider, however, the definition of Handler. It's a newtype over a newtype, so much wrapping is required. If I specifically wanted to return that explicit type, I'd have to take the IO vale produced by getZonedTime and wrap it in Handler, which would require me to first wrap it in ExceptT, which again would require me to wrap it in Either. That's a lot of bother, but Handler is also a MonadIO instance, and that elegantly sidesteps the issue. By implementing runOnSystemClock with liftIO, it works for all MonadIO instances, including Handler.
Hopefully, that explains why runOnSystemClock has the type that it has.
Using the database #
The database interpreter is more complex than runOnSystemClock, but it follows the same principles. The reasoning outlined above also apply here.
runInSQLServer :: MonadIO m => Text -> ReservationsInstruction (m a) -> m a runInSQLServer connStr (ReadReservation rid next) = liftIO (readReservation connStr rid) >>= next runInSQLServer connStr (ReadReservations t next) = liftIO (readReservations connStr t) >>= next runInSQLServer connStr (CreateReservation r next) = liftIO (insertReservation connStr r) >> next
Since ReservationsInstruction is a sum type with three cases, the runInSQLServer action has to handle all three. Each case calls a dedicated helper function. I'll only show one of these to give you a sense for how they look.
readReservations :: Text -> LocalTime -> IO [Reservation] readReservations connStr (LocalTime d _) = let sql = "SELECT [Guid], [Date], [Name], [Email], [Quantity]\ \FROM [dbo].[Reservations]\ \WHERE CONVERT(DATE, [Date]) = " <> toSql d in withConnection connStr $ \conn -> fmap unDbReservation <$> query conn sql
You can see all the details about withConnection, unDbReservation, etcetera in the Git repository. The principal point is that these are just normal IO actions.
Basic composition #
The two interpreters are all we need to compose a working system:
runInSQLServerAndOnSystemClock :: MonadIO m => Text -> ReservationsProgramT m a -> m a runInSQLServerAndOnSystemClock connStr = iterT go where go (InL rins) = DB.runInSQLServer connStr rins go (InR cins) = runOnSystemClock cins
The iterT function enables you to interpret a FreeT value, of which ReservationsProgramT is an alias. The go function just pattern-matches on the two cases of the Sum functor, and delegates to the corresponding interpreter.
This composition enables the system to run and do the intended work. You can start the server and make GET and POST requests against the /reservations resource, as outlined in the first article in this small series.
This verifies what I already hypothesized. This feature set requires two distinct sets of impure interactions:
- Getting the current time
- Querying and writing to a database
It does make it clear what ought to be logged. All the pure functionality can be reproduced if you have the inputs. You only need to log the impure interactions, and now you know what they are.
Compose with logging #
You need to log the impure operations, and you know that they're interacting with the system clock and the database. As usual, starting with the system clock is most accessible. You can write what's essentially a Decorator of any ClockInstruction interpreter:
logClock :: MonadIO m => (String -> IO ()) -> (forall x. ClockInstruction (m x) -> m x) -> ClockInstruction (m a) -> m a logClock logLn inner (CurrentTime next) = do output <- inner $ CurrentTime return liftIO $ writeLogEntry logLn "CurrentTime" () output next output
The logClock action decorates any inner interpreter with the logging action logLn. It returns an action of the same type as it decorates.
It relies on a helper function called writeLogEntry, which handles some of the formalities of formatting and time-stamping each log entry.
You can decorate any database interpreter in the same way:
logReservations :: MonadIO m => (String -> IO ()) -> (forall x. ReservationsInstruction (m x) -> m x) -> ReservationsInstruction (m a) -> m a logReservations logLn inner (ReadReservation rid next) = do output <- inner $ ReadReservation rid return liftIO $ writeLogEntry logLn "ReadReservation" rid output next output logReservations logLn inner (ReadReservations t next) = do output <- inner $ ReadReservations t return liftIO $ writeLogEntry logLn "ReadReservations" t output next output logReservations logLn inner (CreateReservation r next) = do output <- inner $ CreateReservation r (return ()) liftIO $ writeLogEntry logLn "CreateReservation" r output next
The logReservations action follows the same template as logClock; only it has more lines of code because ReservationsInstruction is a discriminated union with three cases.
With these Decorator actions you can change the application composition so that it logs all impure inputs and outputs:
runInSQLServerAndOnSystemClock :: MonadIO m => (String -> IO ()) -> Text -> ReservationsProgramT m a -> m a runInSQLServerAndOnSystemClock logLn connStr = iterT go where go (InL rins) = logReservations logLn (DB.runInSQLServer connStr) rins go (InR cins) = logClock logLn runOnSystemClock cins
This not only implements the desired functionality, but also Goldilogs: not too little, not too much, but just what you need. Notice that I didn't have to change any of my Domain Model or HTTP-specific code to enable logging. This cross-cutting concern is enabled entirely via composition.
Repeatability #
An HTTP request like this:
POST /reservations/ HTTP/1.1
Content-Type: application/json
{
"id": "c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c",
"date": "2020-03-20 19:00:00",
"name": "Elissa Megan Powers",
"email": "emp@example.com",
"quantity": 3
}
produces a series of log entries like these:
LogEntry {logTime = 2019-12-29 20:21:53.0029235 UTC, logOperation = "CurrentTime", logInput = "()", logOutput = "2019-12-29 21:21:53.0029235"}
LogEntry {logTime = 2019-12-29 20:21:54.0532677 UTC, logOperation = "ReadReservations", logInput = "2020-03-20 19:00:00", logOutput = "[]"}
LogEntry {logTime = 2019-12-29 20:21:54.0809254 UTC, logOperation = "CreateReservation", logInput = "Reservation {reservationId = c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c, reservationDate = 2020-03-20 19:00:00, reservationName = \"Elissa Megan Powers\", reservationEmail = \"emp@example.com\", reservationQuantity = 3}", logOutput = "()"}
LogEntry {logTime = 2019-12-29 20:21:54 UTC, logOperation = "PostReservation", logInput = "\"{ \\\"id\\\": \\\"c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c\\\", \\\"date\\\": \\\"2020-03-20 19:00:00\\\", \\\"name\\\": \\\"Elissa Megan Powers\\\", \\\"email\\\": \\\"emp@example.com\\\", \\\"quantity\\\": 3 }\"", logOutput = "()"}
This is only a prototype to demonstrate what's possible. In an attempt to make things simple for myself, I decided to just log data by using the Show instance of each value being logged. In order to reproduce behaviour, I'll rely on the corresponding Read instance for the type. This was probably naive, and not a decision I would employ in a production system, but it's good enough for a prototype.
For example, the above log entry states that the CurrentTime instruction was evaluated and that the output was 2019-12-29 21:21:53.0029235. Second, the ReadReservations instruction was evaluated with the input 2020-03-20 19:00:00 and the output was the empty list ([]). The third line records that the CreateReservation instruction was evaluated with a particular input, and that the output was ().
The fourth and final record is the the actual values observed at the HTTP boundary.
You can load and parse the logged data into a unit test or an interactive session:
λ> l <- lines <$> readFile "the/path/to/the/log.txt"
λ> replayData = readReplayData l
λ> replayData
ReplayData {
observationsOfPostReservation =
[Reservation {
reservationId = c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c,
reservationDate = 2020-03-20 19:00:00,
reservationName = "Elissa Megan Powers",
reservationEmail = "emp@example.com",
reservationQuantity = 3}],
observationsOfRead = fromList [],
observationsOfReads = fromList [(2020-03-20 19:00:00,[[]])],
observationsOfCurrentTime = [2019-12-29 21:21:53.0029235]}
λ> r = head $ observationsOfPostReservation replayData
λ> r
Reservation {
reservationId = c3cbfbc7-6d64-4ead-84ef-7f89de5b7e1c,
reservationDate = 2020-03-20 19:00:00,
reservationName = "Elissa Megan Powers",
reservationEmail = "emp@example.com",
reservationQuantity = 3}
(I've added line breaks and indentation to some of the output to make it more readable, compared to what GHCi produces.)
The most important thing to notice is the readReplayData function that parses the log file into Haskell data. I've also written a prototype of a function that can replay the actions as they happened:
λ> (seatingDuration, tables) <- readConfig λ> replay replayData $ tryAccept seatingDuration tables r Right ()
The original HTTP request returned 200 OK and that's exactly how reservationServer translates a Right () result. So the above interaction is a faithful reproduction of what actually happened.
Replay #
You may have noticed that I used a replay function above. This is only a prototype to get the point across. It's just another interpreter of ReservationsProgram (or, rather an ExceptT wrapper of ReservationsProgram):
replay :: ReplayData -> ExceptT e ReservationsProgram a -> Either e a replay d = replayImp d . runExceptT where replayImp :: ReplayData -> ReservationsProgram a -> a replayImp rd p = State.evalState (iterM go p) rd go (InL (ReadReservation rid next)) = replayReadReservation rid >>= next go (InL (ReadReservations t next)) = replayReadReservations t >>= next go (InL (CreateReservation _ next)) = next go (InR (CurrentTime next)) = replayCurrentTime >>= next
While this is compact Haskell code that I wrote, I still found it so abstruse that I decided to add a type annotation to a local function. It's not required, but I find that it helps me understand what replayImp does. It uses iterM (a cousin to iterT) to interpret the ReservationsProgram. The entire interpretation is stateful, so runs in the State monad. Here's an example:
replayCurrentTime :: State ReplayData LocalTime replayCurrentTime = do xs <- State.gets observationsOfCurrentTime let (observation:rest) = xs State.modify (\s -> s { observationsOfCurrentTime = rest }) return observation
The replayCurrentTime function replays log observations of CurrentTime instructions. The observationsOfCurrentTime field is a list of observed values, parsed from a log. A ReservationsProgram might query the CurrentTime multiple times, so there could conceivably be several such observations. The idea is to replay them, starting with the earliest.
Each time the function replays an observation, it should remove it from the log. It does that by first retrieving all observations from the state. It then pattern-matches the observation from the rest of the observations. I execute my code with the -Wall option, so I'm puzzled that I don't get a warning from the compiler about that line. After all, the xs list could be empty. This is, however, prototype code, so I decided to ignore that issue.
Before the function returns the observation it updates the replay data by effectively removing the observation, but without touching anything else.
The replayReadReservation and replayReadReservations functions follow the same template. You can consult the source code repository if you're curious about the details. You may also notice that the go function doesn't do anything when it encounters a CreateReservation instruction. This is because that instruction has no return value, so there's no reason to consult a log to figure out what to return.
Summary #
The point of this article was to flesh out a fully functional feature (a vertical slice, if you're so inclined) in Haskell, in order to verify that the only impure actions involved are:
- Getting the current time
- Interacting with the application database
Furthermore, prototype code demonstrates that based on a log of impure interactions, you can repeat the logged execution.
Now that we know what is impure and what can be pure, we can reproduce the same architecture in C# (or another mainstream programming language).
Next: Repeatable execution in C#.
Comments
The Free Monad, as any monad, enforces sequential operations.
How would you deal with having to sent multiple transactions (let's say to the db and via http), while also retrying n times if it fails?
Jiehong, thank you for writing. I'm not sure that I can give you a complete answer, as this is something that I haven't experimented with in Haskell.
In C#, on the other hand, you can implement stability patterns like Circuit Breaker and retries with Decorators. I don't see why you can't do that in Haskell as well.
Repeatable execution
What to log, and how to log it.
When I visit software organisations to help them make their code more maintainable, I often see code like this:
public ILog Log { get; } public ActionResult Post(ReservationDto dto) { Log.Debug($"Entering {nameof(Post)} method..."); if (!DateTime.TryParse(dto.Date, out var _)) { Log.Warning("Invalid reservation date."); return BadRequest($"Invalid date: {dto.Date}."); } Log.Debug("Mapping DTO to Domain Model."); Reservation reservation = Mapper.Map(dto); if (reservation.Date < DateTime.Now) { Log.Warning("Invalid reservation date."); return BadRequest($"Invalid date: {reservation.Date}."); } Log.Debug("Reading existing reservations from database."); var reservations = Repository.ReadReservations(reservation.Date); bool accepted = maîtreD.CanAccept(reservations, reservation); if (!accepted) { Log.Warning("Not enough capacity"); return StatusCode( StatusCodes.Status500InternalServerError, "Couldn't accept."); } Log.Info("Adding reservation to database."); Repository.Create(reservation); Log.Debug($"Leaving {nameof(Post)} method..."); return Ok(); }
Logging like this annoys me. It adds avoidable noise to the code, making it harder to read, and thus, more difficult to maintain.
Ideal #
The above code ought to look like this:
public ActionResult Post(ReservationDto dto) { if (!DateTime.TryParse(dto.Date, out var _)) return BadRequest($"Invalid date: {dto.Date}."); Reservation reservation = Mapper.Map(dto); if (reservation.Date < Clock.GetCurrentDateTime()) return BadRequest($"Invalid date: {reservation.Date}."); var reservations = Repository.ReadReservations(reservation.Date); bool accepted = maîtreD.CanAccept(reservations, reservation); if (!accepted) { return StatusCode( StatusCodes.Status500InternalServerError, "Couldn't accept."); } Repository.Create(reservation); return Ok(); }
This is more readable. The logging statements are gone from the code, thereby amplifying the essential behaviour of the Post method. The noise is gone.
Wait a minute! you might say, You can't just remove logging! Logging is important.
Yes, I agree, and I didn't. This code still logs. It logs just what you need to log. No more, no less.
Types of logging #
Before we talk about the technical details, I think it's important to establish some vocabulary and context. In this article, I use the term logging broadly to describe any sort of action of recording what happened while software executed. There's more than one reason an application might have to do that:
- Instrumentation. You may log to support your own work. The first code listing in this article is a typical example of this style of logging. If you've ever had the responsibility of having to support an application that runs in production, you know that you need insight into what happens. When people report strange behaviours, you need those logs to support troubleshooting.
- Telemetry. You may log to support other people's work. You can write status updates, warnings, and errors to support operations. You can record Key Performance Indicators (KPIs) to support 'the business'.
- Auditing. You may log because you're legally obliged to do so.
- Metering. You may log who does what so that you can bill users based on consumption.
Particularly when it comes to instrumentation, I often see examples of 'overlogging'. When logging is done to support future troubleshooting, you can't predict what you're going to need, so it's better to log too much data than too little.
It'd be even better to log only what you need. Not too little, not too much, but just the right amount of logging. Obviously, we should call this Goldilogs.
Repeatability #
How do you know what to log? How do you know that you've logged everything that you'll need, when you don't know your future needs?
The key is repeatability. Just like you should be able to reproduce builds and repeat deployments, you should also be able to reproduce execution.
If you can replay what happened when a problem manifested itself, you can troubleshoot it. You need to log just enough data to enable you to repeat execution. How do you identify that data?
Consider a line of code like this:
int z = x + y;
Would you log that?
It might make sense to log what x and y are, particularly if these values are run-time values (e.g. entered by a user, the result of a web service call, etc.):
Log.Debug($"Adding {x} and {y}."); int z = x + y;
Would you ever log the result, though?
Log.Debug($"Adding {x} and {y}."); int z = x + y; Log.Debug($"Result of addition: {z}");
There's no reason to log the result of the calculation. Addition is a pure function; it's deterministic. If you know the inputs, you can always repeat the calculation to get the output. Two plus two is always four.
The more your code is composed from pure functions, the less you need to log.
Log only impure actions #
In principle, all code bases interleave pure functions with impure actions. In most procedural or object-oriented code, no attempt is made of separating the two:

I've here illustrated impure actions with red and pure functions with green. Imagine that this is a conceptual block of code, with execution flowing from top to bottom. When you write normal procedural or object-oriented code, most of the code will have some sort of local side effect in the form of a state change, a more system-wide side effect, or be non-deterministic. Occasionally, arithmetic calculation or similar will form small pure islands.
While you don't need to log the output of those pure functions, it hardly makes a difference, since most of the code is impure. It would be a busy log, in any case.
Once you shift towards functional-first programming, your code may begin to look like this instead:

You may still have some code that occasionally executes impure actions, but largely, most of the code is pure. If you know the inputs to all the pure code, you can reproduce that part of the code. This means that you only need to log the non-deterministic parts: the impure actions. Particularly, you need to log the outputs from the impure actions, because these impure output values become the inputs to the next pure block of code.
This style of architecture is what you'll often get with a well-designed F# code base, but you can also replicate it in C# or another object-oriented programming language. I'd also draw a diagram like this to illustrate how Haskell code works if you model interactions with free monads.
This is the most generally applicable example, so articles in this short series show a Haskell code base with free monads, as well as a C# code base.
In reality, you can often get away with an impureim sandwich:

This architecture makes things simpler, including logging. You only need to log the inital and the concluding impure actions. The rest, you can always recompute.
I could have implemented the comprehensive example code shown in the next articles as impureim sandwiches, but I chose to use free monads in the Haskell example, and Dependency Injection in the C# example. I did this in order to offer examples from which you can extrapolate a more complex architecture for your production code.
Examples #
I've produced two equivalent example code bases to show how to log just enough data. The first is in Haskell because it's the best way to be sure that pure and impure code is properly separated.
Both example applications have the same externally visible behaviour. They showcase a focused vertical slice of a restaurant reservation system. The only feature they support is the creation of a reservation.
Clients make reservations by making an HTTP POST request to the reservation system:
POST /reservations HTTP/1.1
Content-Type: application/json
{
"id": "84cef648-1e5f-467a-9d13-1b81db7f6df3",
"date": "2021-12-21 19:00:00",
"email": "mark@example.com",
"name": "Mark Seemann",
"quantity": 4
}
This is an attempt to make a reservation for four people at December 21, 2021 at seven in the evening. Both code bases support this HTTP API.
If the web service accepts the reservation, it'll write the reservation as a record in a SQL Server database. The table is defined as:
CREATE TABLE [dbo].[Reservations] ( [Id] INT NOT NULL IDENTITY, [Guid] UNIQUEIDENTIFIER NOT NULL UNIQUE, [Date] DATETIME2 NOT NULL, [Name] NVARCHAR (50) NOT NULL, [Email] NVARCHAR (50) NOT NULL, [Quantity] INT NOT NULL PRIMARY KEY CLUSTERED ([Id] ASC)
Both implementations of the service can run on the same database.
The examples follow in separate articles:
Readers not comfortable with Haskell are welcome to skip directly to the C# article.Log metadata #
In this article series, I focus on run-time data. The point is that there's a formal method to identify what to log: Log the inputs to and outputs from impure actions.
I don't focus on metadata, but apart from run-time data, each log entry should be accompanied by metadata. As a minimum, each entry should come with information about the time it was observed, but here's a list of metadata to consider:
- Date and time of the log entry. Make sure to include the time zone, or alternatively, log exclusively in UTC.
- The version of the software that produced the entry. This is particularly important if you deploy new versions of the software several times a day.
- The user account or security context in which the application runs.
- The machine ID, if you consolidate server farm logs in one place.
- Correlation IDs, if present.
Conclusion #
You only need to log what happens in impure actions. In a normal imperative or object-oriented code base, this is almost a useless selection criterion, because most of what happens is impure. Thus, you need to log almost everything.
There's many benefits to be had from moving towards a functional architecture. One of them is that it simplifies logging. Even a functional-first approach, as is often seen in idiomatic F# code bases, can simplify your logging efforts. The good news is that you can adopt a similar architecture in object-oriented code. You don't even have to compromise the design.
I've worked on big C# code bases where we logged all the impure actions. It was typically less than a dozen impure actions per HTTP request. When there was a problem in production, I could usually reproduce what caused it based on the logs.
You don't have to overlog to be able to troubleshoot your production code. Log the data that matters, and only that. Log the impure inputs and outputs.
Comments
I like the simplicity of "log the impure inputs and outputs", and logging to ensure repeatability. But consider a common workflow: Load a (DDD) aggregate from DB, call pure domain logic it, and store the result.
The aggregate may be very complex, e.g. an order with not just many properties itself, but also many sub-entities (line items, etc.) and value objects. In order to get repeatability, you need to log the entire aggregate that was loaded. This is hard/verbose (don't get too tempted by F#'s nice stringification of records and unions – you'll want to avoid logging sensitive information), and you'll still end up with huge multi-line dumps in your log (say, 10 lines for the order and 10 lines per line item = 100 lines for an order with 9 line items, for a single operation / log statement).
Intuitively to me, that seems like a silly amount of logging, but I can't see any alternative if you want to get full repeatability in order to debug problems. Thoughts?
...you'll want to avoid logging sensitive information...
If your application caches sensitive information, then it would be reasonble to only cache an encrypted version. That way, logging the information is not a security issue and neither is holding that infomration in memory (where malware could read it via memory-scraping).
...you'll still end up with huge multi-line dumps in your log...
Not all logging is meant to be directly consumed by humans. Structued logging is makes it easy for computers to consume logging events. For an event sourcing architecture (such as the Elm architecture), one can record all events and then create tooling to allow playback. I hope Elmish.WPF gets something like this if/when some of the Fable debugging tools are ported to F#.
Christer, thank you for writing. There's two different concerns, as far as I can see. I'd like to start with the size issue.
The size of software data is unintuitive to the human brain. A data structure that looks overwhelmingly vast to us is nothing but a few hundred kilobytes in raw data. I often have that discussion regarding API design, but the same arguments could apply to logging. How much would 100 lines of structured JSON entail?
Let's assume some that JSON properties are numbers (prices, quantities, IDs, etcetera.) while others could be unbounded strings. Let's assume that the numbers all take up four bytes, while Unicode strings are each 100 bytes on average. The average byte size of a 'line' could be around 50 bytes, depending on the proportion of numbers to strings. 100 lines, then, would be 5,000 bytes, or around 5 kB.
Even if data structures were a few orders of magnitude larger, that in itself wouldn't keep me up at night.
Of course, that's not the whole story. The volume of data is also important. If you log hundred such entries every second, it obviously adds up. It could be prohibitive.
That scenario doesn't fit my experience, but for the sake of argument, let's assume that that's the case. What's the alternative to logging the impure operations?
You can decide to log less, but that has to be an explicit architectural decision, because if you do that, there's going to be behaviour that you can't reproduce. Logging all impure operations is the minimum amount of logging that'll guarantee that you can fully reproduce all behaviour. You may decide that there's behaviour that you don't need to be able to reconstruct, but I think that this ought to be an explicit decision.
There may be a better alternative. It also addresses the issue regarding sensitive data.
Write pure functions that take as little input as possible, and produce as little output as possible. In the realm of security design there's the concept of datensparsamkeit (data frugality). Only deal with the data you really need.
Does that pure function really need to take as input an entire aggregate, or would a smaller projection do? If the latter, implement the impure operation so that it returns the projection. That's a smaller data set, so less to log.
The same goes for sensitive input. Perhaps instead of a CPR number the function only needs an age value. If so, then you only need to log the age.
These are deliberate design decision you must take. You don't get such solutions for free, but you can if you will.
Thank you for the reply. It makes sense that this should be a deliberate design decision.
I'm working full-time with F# myself, and would be very interested in seeing how you think this could be solved in F#. In this series, you are demonstrating solutions for Haskell (free monads) and C# (dependency injection), but as you have alluded to previously on your blog, neither of those are idiomatic solutions in F# (free monads are cumbersome without higher-kinded types, and DI primarily fits an object-oriented architecture).
I realize you may not choose to write another blog post in this series tackling F# (though it would nicely "fill the gap" between Haskell and C#, and you're definitely the one to write it!), but even a few keywords/pointers would be helpful.
Christer, thank you for writing. I am, indeed, not planning to add another article to this small series. Not that writing the article itself would be too much trouble, but in order to stay on par with the two other articles, I'd have to develop the corresponding F# code base. That currently doesn't look like it'd be the best use of my time.
In F# you can use partial application for dependency injection. I hope that nothing I wrote gave the impression that this isn't idiomatic F#. What I've demonstrated is that it isn't functional, but since F# is a multiparadigmatic language, that's still fine.
The C# example in this article series shows what's essentially an impureim sandwich, so it shouldn't be too hard to translate that architecture to F#. It's already quite functional.
Conway's Law: latency versus throughput
Organising work in one way optimises for low latency; in another for throughput.
It's a cliché that the software industry is desperate for talent. I also believe that it's a myth. As I've previously observed, the industry seems desperate for talent within commute range. The implication is that although we perform some of the most intangible and digitised work imaginable, we're expected to be physically present in an office.
Since 2014 I've increasingly been working from home, and I love it. I also believe that it's an efficient way to develop software, but not only for the reasons usually given.
I believe that distributed, asynchronous software development optimises throughput, but may sacrifice reaction time (i.e. increase latency).
The advantages of working in an office #
It's easy to criticise office work, but if it's so unpopular, why is it still the mainstream?
I think that there's a multitude of answers to that question. One is that this may be the only way that management can imagine. Since programming is so intangible, it's impossible to measure productivity. What a manager can do, though, is to watch who arrives early, who's the last to leave, and who seems to be always in front of his or her computer, or in a meeting, and so on.
Another answer to the question is that people actually like working together. I currently advice IDQ on software development principles and architecture. They have a tight-knit development team. The first day I visited them, I could feel a warm and friendly vibe. I've been visiting them regularly for about a year, now, and the first impression has proven correct. As we Danes say, that work place is positively hyggelig.
Some people also prefer to go to the office to have a formal boundary between their professional and private lives.
Finally, if you're into agile software development, you've probably heard about the benefits of team co-location.
When the team is located in the same room, working towards the same goals, communication is efficient - or is it?
You can certainly get answers to your questions quickly. All you have to do is to interrupt the person who can answer. If you don't know who that is, you just interrupt everybody until you've figured it out. While offices are interruption factories (as DHH puts it), this style of work can reduce latency.
If you explicitly follow e.g. lean software development and implement something like one-piece flow, you can reduce your cycle time. The less delay between activities, the faster you can deliver value. Once you've delivered one piece (e.g. a feature), you move on to the next.

If this is truly the goal, then putting all team members in the same office makes sense. You don't get higher communications bandwidth than when you're physically together. All the subtle intonations of the way your colleagues speak, the non-verbal cues, etcetera are there if you know how to interpret them.
Consequences of team co-location #
I've seen team co-location work for small teams. People can pair program or even mob program. You can easily draw on the expertise of your co-workers. It does require, however, that everyone respects boundaries.
It's a balancing act. You may get your answer sooner, but your interruption could break your colleague's concentration. The net result could be negative productivity.
While I've seen team co-location work, I've seen it fail more frequently. There are many reasons for this.
First, there's all the interruptions. Most programmers don't like being interrupted.
Second, the opportunity for ad-hoc communication easily leads to poor software architecture. This follows from Conway's law, which argues that
"Any organization that designs a system [...] will inevitably produce a design whose structure is a copy of the organization's communication structure."
I know that it's not a law in any rigid sense of the word, but it can often be fruitful to keep an eye out for this sort of interaction. Based on my experience, it seems to happen often.
Ad-hoc office communication leads to ad-hoc communication structures in the code. There's typically little explicit architecture. Knowledge is in the heads of people.
Such an organisation tends to have an oral culture. There's no permanence of knowledge, no emphasis on readability of code (because you can always ask someone if there's code you don't understand), and meetings all the time.
I once worked as a consultant for a company where there was only one old-timer around. He spent most of his time in meetings, because he knew all the intricate details of how everything worked and talked together, and other people needed to know.
After I'd been involved with that (otherwise wonderful) company on and off for a few years, I accumulated some knowledge as well, and people wanted to have meetings with me.
In the beginning, I obliged. Then it turned out that a week after I'd had a meeting, I'd be called to what would essentially be the same meeting again. Why? Because some other stakeholder heard about the first meeting and decided that he or she also required that information. The solution? Call another meeting.
My counter-move was to begin to write things down. When people would call a meeting, I'd ask for an agenda. That alone filtered away more than half of the meetings. When I did receive an agenda, I could often reply:
"Based on the agenda, I believe you'll find everything you need to know here. If not, please let me know what's missing so that I can update the document"
I'd attach said document. By doing that, I eliminated ninety percent of my meetings.
Notice what I did. I changed the communication structure - at least locally around me. Soon after, I went remote with that client, and had a few successful years doing that.
I hope that the previous section outlined that working in an office can be effective, but as I've now outlined, it can also be dysfunctional.
If you truly must deliver as soon as possible, because if you don't, the organisation isn't going to be around in five years, office work, with its low communications latency may be the best option.
Remote office work #
I often see companies advertise for programmers. When remote work is an option, it often comes with the qualification that it must be within a particular country, or a particular time zone.
There can be legal or bureaucratic reasons why a company only wants to hire within a country. I get that, but I consider a time zone requirement a danger sign. The same goes for "we use Slack" or whatever other 'team room' instant messaging technology is cool these days.
That tells me that while the company allows people to be physically not in the office, they must still obey office hours. This indicates to me that communication remains ad-hoc and transient. Again, code quality suffers.
These days, because of the Corona virus, many organisations deeply entrenched in the oral culture of co-location find that they must now work as a distributed team. They try to address the situation by setting up day-long video conference calls.
It may work in an office, but it's not the best fit for a distributed team.
Distributed asynchronous software development #
Decades of open-source development has shown another way. Successful open-source software (OSS) projects are distributed and use asynchronous communication channels (mailing lists, issue trackers). It's worth considering the causation. I don't think anyone sat down and decided to do it this way in order to be successful. I think that the OSS projects that became successful became successful exactly because they organised work that way.
When contributions are voluntary, you have to cast a wide net. A successful OSS project should accept contributions from around the world. If an excellent contribution from Japan falters because the project team is based in the US, and immediate, real-time communication is required, then that project has odds against it.
An OSS project that works asynchronously can receive contributions from any time zone. The disadvantage can be significant communication lag.
If you get a contribution from Australia, but you're in Europe, you may send a reply asking for clarifications or improvements. At the time you do that, the contributor may have already gone to bed. He or she isn't going to reply later, at which time you've gone to bed.
It can take days to get anything done. That doesn't sound efficient, and if you're in a one-piece flow mindset it isn't. You need to enable parallel development. If you do that, you can work on something else while you wait for your asynchronous collaborator to respond.
In this diagram, the wait-times in the production of one piece (e.g. one feature) can be used to move forward with another feature. The result is that you may actually be able to finish both tasks sooner than if you stick strictly to one-piece flow.
Before you protest: in reality, delay times are much longer than implied by the diagram. An activity could be something as brief as responding to a request for more information. You may be able to finish this activity in 30 minutes, whereafter the delay time is another twenty hours. Thus, in order to keep throughput comparable, you need to juggle not two, but dozens of parallel processes.
You may also feel the urge to protest that the diagram postulates a false dichotomy. That's not my intention. Even with co-location, you could do parallel development.
There's also the argument that parallel development requires context switching. That's true, and it comes with overhead.
My argument is only this: if you decide to shift to an asynchronous process, then I consider parallel development essential. Even with parallel development, you can't get the same (low) latency as is possible in the office, but you may be able to get better throughput.
This again has implications for software architecture. Parallel development works when features can be developed independently of each other - when there's only minimal dependencies between various areas of the code.
Conway's law is relevant here as well. If you decouple the communication between various parts of the system, you can also decouple the development of said parts. Ultimately, the best fit for a distributed, asynchronous software development process may be a distributed, asynchronous system.
Quadrants #
This is the point where, if this was a Gartner report, it'd include a 2x2 table with four quadrants. It's not, but I'll supply it anyway:
| Synchronous | Asynchronous | |
| Distributed | Virtual office | OSS-like parallel development |
| Co-located | Scrum, XP, etc. | Emailing the person next to you |
I've yet to discuss the fourth quadrant. This is where people sit next to each other, yet still email each other. That's just weird. Like the virtual office, I don't think it's a long-term sustainable process. The advantages of just talking to each other is just too great. If you're co-located, ad-hoc communication is possible, so that's where the software architecture will gravitate as well. Again, Conway's law applies.
If you want to move towards a sustainable distributed process, you should consider adjusting everything accordingly. A major endeavour in that shift involves migrating from an oral to a written culture. Basecamp has a good guide to get you started.
Your writer reveals himself #
I intend this to be an opinion piece. It's based on a combination of observations made by others, mixed with my personal experiences, but I also admit that it's coloured by my personal preferences. I strongly prefer distributed, asynchronous processes with an emphasis on written communication. Since this blog contains more than 500 articles, it should hardly come as a surprise to anyone that I'm a prolific writer.
I've had great experiences with distributed, asynchronous software development. One such experience was the decade I led the AutoFixture open-source project. Other experiences include a handful of commercial, closed-source projects where I did the bulk of the work remotely.
This style of work benefits my employer. By working asynchronously, I have to document what I do, and why I do it. I leave behind a trail of text artefacts other people can consult when I'm not available.
I like asynchronous processes because they liberate me to work when I want to, where I want to. I take advantage of this to go for a run during daylight hours (otherwise an issue during Scandinavian winters), to go grocery shopping outside of rush hour, to be with my son when he comes home from school, etcetera. I compensate by working at other hours (evenings, weekends). This isn't a lifestyle that suits everyone, but it suits me.
This preference produces a bias in the way that I see the world. I don't think I can avoid that. Like DHH I view offices as interruption factories. I self-identify as an introvert. I like being alone.
Still, I've tried to describe some forces that affect how work is done. I've tried to be fair to co-location, even though I don't like it.
Conclusion #
Software development with a co-located team can be efficient. It offers the benefits of high-bandwidth communication, pair programming, and low-latency decision making. It also implies an oral tradition. Knowledge has little permanence and the team is vulnerable to key team members going missing.
While such a team organisation can work well when team members are physically close to each other, I believe that this model comes under pressure when team members work remotely. I haven't seen the oral, ad-hoc team process work well in a distributed setting.
Successful distributed software development is asynchronous and based on a literate culture. It only works if the software architecture allows it. Code has to be decoupled and independently deployable. If it is, though, you can perform work in parallel. Conway's law still applies.
Polymorphic Builder
Keeping illegal states unrepresentable with the Builder pattern.
As a reaction to my article on Builder isomorphisms Tyson Williams asked:
I'm happy to receive that question, because I struggled to find a compelling example of a Builder where polymorphism seems warranted. Here, it does."If a
GETorDELETErequest had a body or if aPOSTrequest did not have a body, then I would suspect that such behavior was a bug."For the sake of a question that I would like to ask, let's suppose that a body must be added if and only if the method is
POST. Under this assumption,HttpRequestMessageBuildercan create invalid messages. For example, it can create aGETrequest with a body, and it can create aPOSTrequest without a body. Under this assumption, how would you modify your design so that only valid messages can be created?"
Valid combinations #
Before showing code, I think a few comments are in order. As far as I'm aware, the HTTP specification doesn't prohibit weird combinations like a GET request with a body. Still, such a combination is so odd that it seems fair to design an API to prevent this.
On the other hand I think that a POST request without a body should still be allowed. It's not too common, but there are edge cases where this combination is valid. If you want to cause a side effect to happen, a GET is inappropriate, but sometimes all you want do to is to produce an effect. In the Restful Web Services Cookbook Subbu Allamaraju gives this example of a fire-and-forget bulk task:
POST /address-correction?before=2010-01-01 HTTP/1.1
As he puts it, "in essence, the client is "flipping a switch" to start the work."
I'll design the following API to allow this combination, also because it showcases how that sort of flexibility can still be included. On the other hand, I'll prohibit the combination of a request body in a GET request, as Tyson Williams suggested.
Expanded API #
I'll expand on the HttpRequestMessageBuilder example shown in the previous article. As outlined in another article, apart from the Build method the Builder really only has two capabilities:
- Change the HTTP method
- Add (or update) a JSON body
- Add or change the
Acceptheader - Add or change a
Bearertoken
HttpRequestMessageBuilder class now looks like this:
public class HttpRequestMessageBuilder { private readonly Uri url; private readonly object? jsonBody; private readonly string? acceptHeader; private readonly string? bearerToken; public HttpRequestMessageBuilder(string url) : this(new Uri(url)) { } public HttpRequestMessageBuilder(Uri url) : this(url, HttpMethod.Get, null, null, null) { } private HttpRequestMessageBuilder( Uri url, HttpMethod method, object? jsonBody, string? acceptHeader, string? bearerToken) { this.url = url; Method = method; this.jsonBody = jsonBody; this.acceptHeader = acceptHeader; this.bearerToken = bearerToken; } public HttpMethod Method { get; } public HttpRequestMessageBuilder WithMethod(HttpMethod newMethod) { return new HttpRequestMessageBuilder( url, newMethod, jsonBody, acceptHeader, bearerToken); } public HttpRequestMessageBuilder AddJsonBody(object jsonBody) { return new HttpRequestMessageBuilder( url, Method, jsonBody, acceptHeader, bearerToken); } public HttpRequestMessageBuilder WithAcceptHeader(string newAcceptHeader) { return new HttpRequestMessageBuilder( url, Method, jsonBody, newAcceptHeader, bearerToken); } public HttpRequestMessageBuilder WithBearerToken(string newBearerToken) { return new HttpRequestMessageBuilder( url, Method, jsonBody, acceptHeader, newBearerToken); } public HttpRequestMessage Build() { var message = new HttpRequestMessage(Method, url); BuildBody(message); AddAcceptHeader(message); AddBearerToken(message); return message; } private void BuildBody(HttpRequestMessage message) { if (jsonBody is null) return; string json = JsonConvert.SerializeObject(jsonBody); message.Content = new StringContent(json); message.Content.Headers.ContentType.MediaType = "application/json"; } private void AddAcceptHeader(HttpRequestMessage message) { if (acceptHeader is null) return; message.Headers.Accept.ParseAdd(acceptHeader); } private void AddBearerToken(HttpRequestMessage message) { if (bearerToken is null) return; message.Headers.Authorization = new AuthenticationHeaderValue("Bearer", bearerToken); } }
Notice that I've added the methods WithAcceptHeader and WithBearerToken, with supporting implementation. So far, those are the only changes.
It enables you to build HTTP request messages like this:
HttpRequestMessage msg = new HttpRequestMessageBuilder(url) .WithBearerToken("cGxvZWg=") .Build();
Or this:
HttpRequestMessage msg = new HttpRequestMessageBuilder(url) .WithMethod(HttpMethod.Post) .AddJsonBody(new { id = Guid.NewGuid(), date = "2021-02-09 19:15:00", name = "Hervor", email = "hervor@example.com", quantity = 2 }) .WithAcceptHeader("application/vnd.foo.bar+json") .WithBearerToken("cGxvZWg=") .Build();
It still doesn't address Tyson Williams' requirement, because you can build an HTTP request like this:
HttpRequestMessage msg = new HttpRequestMessageBuilder(url) .AddJsonBody(new { id = Guid.NewGuid(), date = "2020-03-22 19:30:00", name = "Ælfgifu", email = "ælfgifu@example.net", quantity = 1 }) .Build();
Recall that the default HTTP method is GET. Since the above code doesn't specify a method, it creates a GET request with a message body. That's what shouldn't be possible. Let's make illegal states unrepresentable.
Builder interface #
Making illegal states unrepresentable is a catch phrase coined by Yaron Minsky to describe advantages of statically typed functional programming. Unintentionally, it also describes a fundamental tenet of object-oriented programming. In Object-Oriented Software Construction Bertrand Meyer describes object-oriented programming as the discipline of guaranteeing that an object can never be in an invalid state.
In the present example, we can't allow an arbitrary HTTP Builder object to afford an operation to add a body, because that Builder object might produce a GET request. On the other hand, there are operations that are always legal: adding an Accept header or a Bearer token. Because these operations are always legal, they constitute a shared API. Extract those to an interface:
public interface IHttpRequestMessageBuilder { IHttpRequestMessageBuilder WithAcceptHeader(string newAcceptHeader); IHttpRequestMessageBuilder WithBearerToken(string newBearerToken); HttpRequestMessage Build(); }
Notice that both the With[...] methods return the new interface. Any IHttpRequestMessageBuilder must implement the interface, but is free to support other operations not part of the interface.
HTTP GET Builder #
You can now implement the interface to build HTTP GET requests:
public class HttpGetMessageBuilder : IHttpRequestMessageBuilder { private readonly Uri url; private readonly string? acceptHeader; private readonly string? bearerToken; public HttpGetMessageBuilder(string url) : this(new Uri(url)) { } public HttpGetMessageBuilder(Uri url) : this(url, null, null) { } private HttpGetMessageBuilder( Uri url, string? acceptHeader, string? bearerToken) { this.url = url; this.acceptHeader = acceptHeader; this.bearerToken = bearerToken; } public IHttpRequestMessageBuilder WithAcceptHeader(string newAcceptHeader) { return new HttpGetMessageBuilder(url, newAcceptHeader, bearerToken); } public IHttpRequestMessageBuilder WithBearerToken(string newBearerToken) { return new HttpGetMessageBuilder(url, acceptHeader, newBearerToken); } public HttpRequestMessage Build() { var message = new HttpRequestMessage(HttpMethod.Get, url); AddAcceptHeader(message); AddBearerToken(message); return message; } private void AddAcceptHeader(HttpRequestMessage message) { if (acceptHeader is null) return; message.Headers.Accept.ParseAdd(acceptHeader); } private void AddBearerToken(HttpRequestMessage message) { if (bearerToken is null) return; message.Headers.Authorization = new AuthenticationHeaderValue("Bearer", bearerToken); } }
Notice that the Build method hard-codes HttpMethod.Get. When you're using an HttpGetMessageBuilder object, you can't modify the HTTP method. You also can't add a request body, because there's no API that affords that operation.
What you can do, for example, is to create an HTTP request with an Accept header:
HttpRequestMessage msg = new HttpGetMessageBuilder(url) .WithAcceptHeader("application/vnd.foo.bar+json") .Build();
This creates a request with an Accept header, but no Bearer token.
HTTP POST Builder #
As a peer to HttpGetMessageBuilder you can implement the IHttpRequestMessageBuilder interface to support POST requests:
public class HttpPostMessageBuilder : IHttpRequestMessageBuilder { private readonly Uri url; private readonly object? jsonBody; private readonly string? acceptHeader; private readonly string? bearerToken; public HttpPostMessageBuilder(string url) : this(new Uri(url)) { } public HttpPostMessageBuilder(Uri url) : this(url, null, null, null) { } public HttpPostMessageBuilder(string url, object jsonBody) : this(new Uri(url), jsonBody) { } public HttpPostMessageBuilder(Uri url, object jsonBody) : this(url, jsonBody, null, null) { } private HttpPostMessageBuilder( Uri url, object? jsonBody, string? acceptHeader, string? bearerToken) { this.url = url; this.jsonBody = jsonBody; this.acceptHeader = acceptHeader; this.bearerToken = bearerToken; } public IHttpRequestMessageBuilder WithAcceptHeader(string newAcceptHeader) { return new HttpPostMessageBuilder( url, jsonBody, newAcceptHeader, bearerToken); } public IHttpRequestMessageBuilder WithBearerToken(string newBearerToken) { return new HttpPostMessageBuilder( url, jsonBody, acceptHeader, newBearerToken); } public HttpRequestMessage Build() { var message = new HttpRequestMessage(HttpMethod.Post, url); BuildBody(message); AddAcceptHeader(message); AddBearerToken(message); return message; } private void BuildBody(HttpRequestMessage message) { if (jsonBody is null) return; string json = JsonConvert.SerializeObject(jsonBody); message.Content = new StringContent(json); message.Content.Headers.ContentType.MediaType = "application/json"; } private void AddAcceptHeader(HttpRequestMessage message) { if (acceptHeader is null) return; message.Headers.Accept.ParseAdd(acceptHeader); } private void AddBearerToken(HttpRequestMessage message) { if (bearerToken is null) return; message.Headers.Authorization = new AuthenticationHeaderValue("Bearer", bearerToken); } }
This class affords various constructor overloads. Two of them don't take a JSON body, and two of them do. This supports both the case where you do want to supply a request body, and the edge case where you don't.
I didn't add an explicit WithJsonBody method to the class, so you can't change your mind once you've created an instance of HttpPostMessageBuilder. The only reason I didn't, though, was to save some space. You can add such a method if you'd like to. As long as it's not part of the interface, but only part of the concrete HttpPostMessageBuilder class, illegal states are still unrepresentable. You can represent a POST request with or without a body, but you can't represent a GET request with a body.
You can now build requests like this:
HttpRequestMessage msg = new HttpPostMessageBuilder( url, new { id = Guid.NewGuid(), date = "2021-02-09 19:15:00", name = "Hervor", email = "hervor@example.com", quantity = 2 }) .WithAcceptHeader("application/vnd.foo.bar+json") .WithBearerToken("cGxvZWg=") .Build();
This builds a POST request with both a JSON body, an Accept header, and a Bearer token.
Is polymorphism required? #
In my previous Builder article, I struggled to produce a compelling example of a polymorphic Builder. It seems that I've now mended the situation. Or have I?
Is the IHttpRequestMessageBuilder interface really required?
Perhaps. It depends on your usage scenarios. I can actually delete the interface, and none of the usage examples I've shown here need change.
On the other hand, had I written helper methods against the interface, obviously I couldn't just delete it.
The bottom line is that polymorphism can be helpful, but it still strikes me as being non-essential to the Builder pattern.
Conclusion #
In this article, I've shown how to guarantee that Builders never get into invalid states (according to the rules we've arbitrarily established). I used the common trick of using constructors for object initialisation. If a constructor completes without throwing an exception, we should expect the object to be in a valid state. The price I've paid for this design is some code duplication.
You may have noticed that there's duplicated code between HttpGetMessageBuilder and HttpPostMessageBuilder. There are ways to address that concern, but I'll leave that as an exercise.
For the sake of brevity, I've only shown examples written as Immutable Fluent Builders. You can refactor all the examples to mutable Fluent Builders or to the original Gang-of-Four Builder pattern. This, too, will remain an exercise for the interested reader.
Comments
I'm happy to receive that question, because I struggled to find a compelling example of a Builder where polymorphism seems warranted. Here, it does.
I know of essentially one occurrence in .NET. Starting with IEnumerable<T>, calling either of the extension methods OrderBy or OrderByDescending returns IOrderedEnumerable<T>, which has the additional extension methods ThenBy and ThenByDescending.
Quoting your recent Builder isomorphisms post.
The Builder pattern isn't useful only because it enables you to "separate the construction of a complex object from its representation." It's useful because it enables you to present an API that comes with good default behaviour, but which can be tweaked into multiple configurations.
I also find the builder pattern useful because its methods typically accept one argument one at a time. The builders in your recent posts are like this. The OrderBy and ThenBy methods and their Descending alternatives in .NET are also examples of this.
However, some of the builders in your recent posts have some constructors that take multiple arguments. That is the situation that I was trying to address when I asked
Have you ever written a builder that accepted multiple arguments one at a time none of which have reasonable defaults?
This could be a kata variation: all public functions accept at most one argument. So Foo(a, b) would not be allowed but Foo.WithA(a).WithB(b) would. In an issue on this blog's GitHub, jaco0646 nicely summerized the reasoning that could lead to applying this design philosophy to production code by saying
Popular advice for a builder with required parameters is to put those in a constructor; but with more than a handful of required parameters, we return to the original problem: too much complexity in a constructor.
That comment by jaco0646 also supplied names by which this type of design is known. Those names (with the same links from the comment) are Builder with a twist or Step Builder. This is great, because I didn't have any good names. (I vaguely recall once thinking that another name was "progressive API" or "progressive fluent API", but now when I search for anything with "progressive", all I get are false positives for progressive web app.
When replacing a multi-argument constructor with a sequence of function calls that each accept one argument, care must be taken to ensure that illegal state remains unrepresentable. My general impression is that many libraries have designed such APIs well. The two that I have enough experience with to recommend as good examples of this design are the fluent configuration API in Entity Framework and Fluent Assertions. As I said before, the most formal treatment I have seen about this type of API design was in this blog post.
Tyson, apart from as a kata constraint, is there any reason to prefer such a design?
I'll be happy to give it a more formal treatment if there's reasonable scenario. Can you think of one?
I don't find the motivation given by jaco0646 convincing. If you have more than a handful of required parameters, I agree that that's an issue with complexity, but I don't agree that the solution is to add more complexity on top of it. Builders add complexity.
At a glance, though, with something like Foo.WithA(a).WithB(b) it seems to me that you're essentially reinventing currying the hard way around.
Related to the overall Builder discussion (but not to currying) you may also find this article and this Stack Overflow answer interesting.
...is there any reason to prefer such a design?
Yes. Just like you, I want to write small functions. In that post, you suggest an arbitrary maximum of 24 lines. One thing I find fascinating about functional programming is how useful the common functions are (such as map) and how they are implemented in only a few lines (often just one line). There is a correlation between the number of function arguments and the length of the function. So to help control the length of a function, it helps to control the number of arguments to the functions. I think Robert Martin has a similar argument. When talking about functions in chapter 3 of Clean Code, his first section is about writing small functions and a later section about function arguments open by saying
The ideal number of arguments for a function is zero (niladic). Next comes one (monadic), followed closely by two (dyadic). Three arguments (triadic) should be avoided where possible. More than three (polyadic) requires very special justification--and then shouldn't be used anyway.
In the C# code a.Foo(b), Foo is an instance method that "feels" like it only has one argument. In reality, its two inputs are a and b, and that code uses infix notation. The situation is similar in the F# code a |> List.map f. The function List.map (as well as the operator |>) has two arguments and is applied using infix notation. I try to avoid creating functions that have more than two arguments.
I don't find the motivation given by jaco0646 convincing. If you have more than a handful of required parameters, I agree that that's an issue with complexity, but I don't agree that the solution is to add more complexity on top of it. Builders add complexity.
I am not sure how you are measuring complexity. I like to think that there are two types of complexity: local and global. For the sake of argument, let's suppose
- that local complexity is only defined for a function and is the number of arguments of that function and
- that global complexity is only defined for a entire program and is the number of lines in the program.
...you may also find this article [titled The Builder pattern is a finite state machine]...interesting.
Indeed, that is a nice article. Finite state machines/automata (both deterministic and nondeterministic) have the same expressiveness as regular expressions.
At a glance, though, with something like Foo.WithA(a).WithB(b) it seems to me that you're essentially reinventing currying the hard way around.
It is. As a regular expression, it would be something like AB. I was just trying to give a simple example. The point of the article you shared is that the builder pattern is much more expressive. I have previously shared a similar article, but I like yours better. Thanks :)
...you may also find...this Stack Overflow answer interesting.
Wow. That is extremely cleaver! I would never thought of that. Thank you very much for sharing.
I'll be happy to give it a more formal treatment if there's reasonable scenario. Can you think of one?
As I said above, I often try to find ways to minimize the maximum complexity of the code that I write. In this case, the reason that I originally asked you about the builder pattern is that I was trying to improve the API for creating a binding in Elmish.WPF. The tutorial has a great section about bindings. There are many binding types, and each has multiple ways to create it. Most arguments are required and some are optional.
Here is a closed issue that was created during the transition to the current binding API, which uses method overloading. In an attempt to come up with a better API, I suggested that we could use your suggestion to replace overloading with discriminated unions, but my co-maintainer wasn't convinced that it would be better.
Three days later, I increased the expressiveness of our bindings in this pull request. Conceptually it was a small change; I added a single optional argument. For a regular expression, such a change is trivial. However, in my case it was a delta of +300 lines of mind-numbingly boring code.
I agree with my co-maintainer that the current binding API is pretty good for the user. On the implementation side though, I am not satisfied. I want to find something better without sacrificing (and maybe even improving) the user's experience.

Comments
You could leverage library functions and avoid mutability like so:
Ghillie, thank you for writing. It looks like you're on the right track, but I think you have to write the function like this: