ploeh blog danish software design
Bifunctors
Bifunctors are like functors, only they vary in two dimensions instead of one. An article for object-oriented programmers.
This article is a continuation of the article series about functors and about applicative functors. In this article, you'll learn about a generalisation called a bifunctor. The prefix bi typically indicates that there's two of something, and that's also the case here.
As you've already seen in the functor articles, a functor is a mappable container of generic values, like Foo<T>, where the type of the contained value(s) can be any generic type T. A bifunctor is just a container with two independent generic types, like Bar<T, U>. If you can map each of the types independently of the other, you may have a bifunctor.
The two most common bifunctors are tuples and Either.
Maps #
A normal functor is based on a structure-preserving map of the contents within a container. You can, for example, translate an IEnumerable<int> to an IEnumerable<string>, or a Maybe<DateTime> to a Maybe<bool>. The axis of variability is the generic type argument T. You can translate T1 to T2 inside a container, but the type of the container remains the same: you can translate Tree<T1> to Tree<T2>, but it remains a Tree<>.

A bifunctor involves a pair of maps, one for each generic type. You can map a Bar<string, int> to a Bar<bool, int>, or to a Bar<string, DateTime>, or even to a Bar<bool, DateTime>. Notice that the last example, mapping from Bar<string, int> to Bar<bool, DateTime> could be viewed as translating both axes simultaneously.
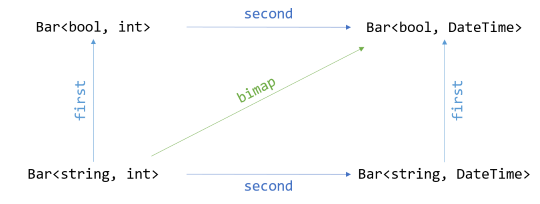
In Haskell, the two maps are called first and second, while the 'simultaneous' map is called bimap.
The first translation translates the first, or left-most, value in the container. You can use it to map Bar<string, int> to a Bar<bool, int>. In C#, we could decide to call the method SelectFirst, or SelectLeft, in order to align with the C# naming convention of calling the functor morphism Select.
Likewise, the second map translates the second, or right-most, value in the container. This is where you map Bar<string, int> to Bar<string, DateTime>. In C#, we could call the method SelectSecond, or SelectRight.
The bimap function maps both values in the container in one go. This corresponds to a translation from Bar<string, int> to Bar<bool, DateTime>. In C#, we could call the method SelectBoth. There's no established naming conventions for bifunctors in C# that I know of, so these names are just some that I made up.
You'll see examples of how to implement and use such functions in the next articles:
Other bifunctors exist, but the first two are the most common.Identity laws #
As is the case with functors, laws govern bifunctors. Some of the functor laws carry over, but are simply repeated over both axes, while other laws are generalisations of the functor laws. For example, the first functor law states that if you translate a container with the identity function, the result is the original input. This generalises to bifunctors as well:
bimap id id ≡ id
This just states that if you translate both axes using the endomorphic Identity, it's equivalent to applying the Identity.

Using C# syntax, you could express the law like this:
bf.SelectBoth(id, id) == bf;
Here, bf is some bifunctor, and id is the identity function. The point is that if you translate over both axes, but actually don't perform a real translation, nothing happens.
Likewise, if you consider a bifunctor a functor over two dimensions, the first functor law should hold for both:
first id ≡ id second id ≡ id
Both of those equalities only restate the first functor law for each dimension. If you map an axis with the identity function, nothing happens:
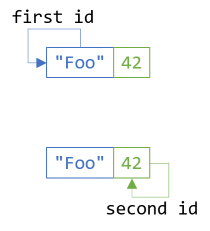
In C#, you can express both laws like this:
bf.SelectFirst(id) == bf; bf.SelectSecond(id) == bf;
When calling SelectFirst, you translate only the first axis while you keep the second axis constant. When calling SelectSecond it's the other way around: you translate only the second axis while keeping the first axis constant. In both cases, though, if you use the identity function for the translation, you effectively keep the mapped dimension constant as well. Therefore, one would expect the result to be the same as the input.
Consistency law #
As you'll see in the articles on tuple and Either bifunctors, you can derive bimap or SelectBoth from first/SelectFirst and second/SelectSecond, or the other way around. If, however, you decide to implement all three functions, they must act in a consistent manner. The name Consistency law, however, is entirely my own invention. If it has a more well-known name, I'm not aware of it.
In pseudo-Haskell syntax, you can express the law like this:
bimap f g ≡ first f . second g
This states that mapping (using the functions f and g) simultaneously should produce the same result as mapping using an intermediary step:
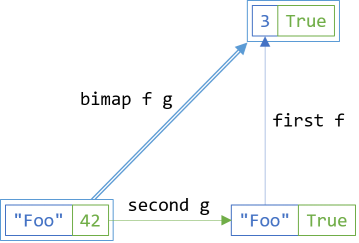
In C#, you could express it like this:
bf.SelectBoth(f, g) == bf.SelectSecond(g).SelectFirst(f);
You can project the input bifunctor bf using both f and g in a single step, or you can first translate the second dimension with g and then subsequently map that intermediary result along the first axis with f.
The above diagram ought to commute:
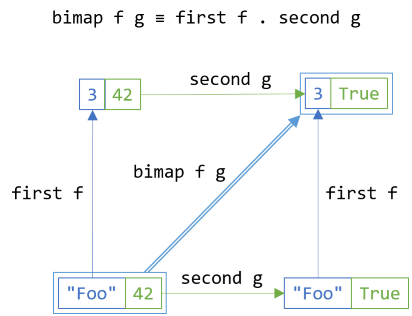
It shouldn't matter whether the intermediary step is applying f along the first axis or g along the second axis. In C#, we can write it like this:
bf.SelectFirst(f).SelectSecond(g) == bf.SelectSecond(g).SelectFirst(f);
On the left-hand side, you first translate the bifunctor bf along the first axis, using f, and then translate that intermediary result along the second axis, using g. On the right-hand side, you first project bf along the second axis, using g, and then map that intermediary result over the first dimension, using f.
Regardless of order of translation, the result should be the same.
Composition laws #
Similar to how the first functor law generalises to bifunctors, the second functor law generalises as well. For (mono)functors, the second functor law states that if you have two functions over the same dimension, it shouldn't matter whether you perform a projection in one, composed step, or in two steps with an intermediary result.
For bifunctors, you can generalise that law and state that you can project over both dimensions in one or two steps:
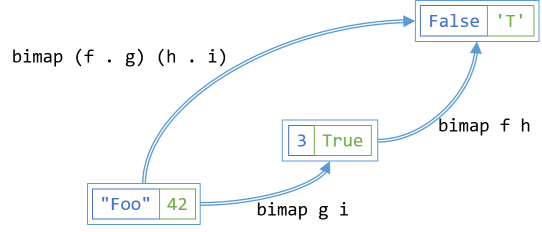
bimap (f . g) (h . i) ≡ bimap f h . bimap g i
If you have two functions, f and g, that compose, and two other functions, h and i, that also compose, you can translate in either one or two steps; the result should be the same.
In C#, you can express the law like this:
bf.SelectBoth(x => f(g(x)), y => h(i(y))) == bf.SelectBoth(g, i).SelectBoth(f, h);
On the left-hand side, the first dimension is translated in one step. For each x contained in bf, the translation first invokes g(x), and then immediately calls f with the output of g(x). The second dimension also gets translated in one step. For each y contained in bf, the translation first invokes i(y), and then immediately calls h with the output of i(y).
On the right-hand side, you first translate bf along both axes using g and i. This produces an intermediary result that you can use as input for a second translation with f and h.
The translation on the left-hand side should produce the same output as the right-hand side.
Finally, if you keep one of the dimensions fixed, you essentially have a normal functor, and the second functor law should still hold. For example, if you hold the second dimension fixed, translating over the first dimension is equivalent to a normal functor projection, so the second functor law should hold:
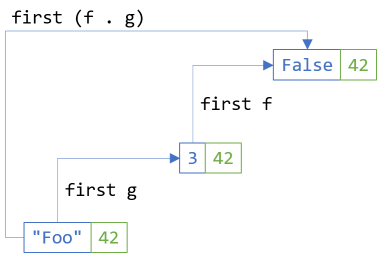
first (f . g) ≡ first f . first g
If you replace first with fmap, you have the second functor law.
In C#, you can write it like this:
bf.SelectFirst(x => f(g(x))) == bf.SelectFirst(g).SelectFirst(f);
Likewise, you can keep the first dimension constant and apply the second functor law to projections along the second axis:
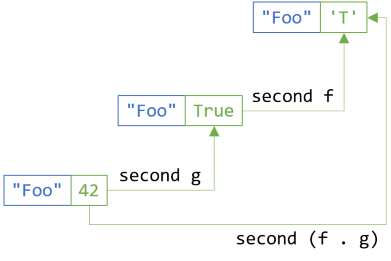
second (f . g) ≡ second f . second g
Again, if you replace second with fmap, you have the second functor law.
In C#, you express it like this:
bf.SelectSecond(x => f(g(x))) == bf.SelectSecond(g).SelectSecond(f);
The last two of these composition laws are specialisations of the general composition law, but where you fix either one or the other dimension.
Summary #
A bifunctor is a container that can be translated over two dimensions, instead of a (mono)functor, which is a container that can be translated over a single dimension. In reality, there isn't a multitude of different bifunctors. While others exist, tuples and Either are the two most common bifunctors. They share an abstraction, but are still fundamentally different. A tuple always contains values of both dimensions at the same time, whereas Either only contains one of the values.
Do trifunctors, quadfunctors, and so on, exist? Nothing prevents that, but they aren't particularly useful; in practice, you never run into them.
Next: Tuple bifunctor.
The Lazy applicative functor
Lazy computations form an applicative functor.
This article is an instalment in an article series about applicative functors. A previous article has described how lazy computations form a functor. In this article, you'll see that lazy computations also form an applicative functor.
Apply #
As you have previously seen, C# isn't the best fit for the concept of applicative functors. Nevertheless, you can write an Apply extension method following the applicative 'code template':
public static Lazy<TResult> Apply<TResult, T>( this Lazy<Func<T, TResult>> selector, Lazy<T> source) { return new Lazy<TResult>(() => selector.Value(source.Value)); }
The Apply method takes both a lazy selector and a lazy value called source. It applies the function to the value and returns the result, still as a lazy value. If you have a lazy function f and a lazy value x, you can use the method like this:
Lazy<Func<int, string>> f = // ... Lazy<int> x = // ... Lazy<string> y = f.Apply(x);
The utility of Apply, however, mostly tends to emerge when you need to chain multiple containers together; in this case, multiple lazy values. You can do that by adding as many overloads to Apply as you need:
public static Lazy<Func<T2, TResult>> Apply<T1, T2, TResult>( this Lazy<Func<T1, T2, TResult>> selector, Lazy<T1> source) { return new Lazy<Func<T2, TResult>>(() => y => selector.Value(source.Value, y)); }
This overload partially applies the input function. When selector is a function that takes two arguments, you can apply a single of those two arguments, and the result is a new function that closes over the value, but still waits for its second input argument. You can use it like this:
Lazy<Func<char, int, string>> f = // ... Lazy<char> c = // ... Lazy<int> i = // ... Lazy<string> s = f.Apply(c).Apply(i);
Notice that you can chain the various overloads of Apply. In the above example, you have a lazy function that takes a char and an int as input, and returns a string. It could, for instance, be a function that invokes the equivalent string constructor overload.
Calling f.Apply(c) uses the overload that takes a Lazy<Func<T1, T2, TResult>> as input. The return value is a Lazy<Func<int, string>>, which the first Apply overload then picks up, to return a Lazy<string>.
Usually, you may have one, two, or several lazy values, whereas your function itself isn't contained in a Lazy container. While you can use a helper method such as Lazy.FromValue to 'elevate' a 'normal' function to a lazy function value, it's often more convenient if you have another Apply overload like this:
public static Lazy<Func<T2, TResult>> Apply<T1, T2, TResult>( this Func<T1, T2, TResult> selector, Lazy<T1> source) { return new Lazy<Func<T2, TResult>>(() => y => selector(source.Value, y)); }
The only difference to the equivalent overload is that in this overload, selector isn't a Lazy value, while source still is. This simplifies usage:
Func<char, int, string> f = // ... Lazy<char> c = // ... Lazy<int> i = // ... Lazy<string> s = f.Apply(c).Apply(i);
Notice that in this variation of the example, f is no longer a Lazy<Func<...>>, but just a normal Func.
F# #
F#'s type inference is more powerful than C#'s, so you don't have to resort to various overloads to make things work. You could, for example, create a minimal Lazy module:
module Lazy = // ('a -> 'b) -> Lazy<'a> -> Lazy<'b> let map f (x : Lazy<'a>) = lazy f x.Value // Lazy<('a -> 'b)> -> Lazy<'a> -> Lazy<'b> let apply (x : Lazy<_>) (f : Lazy<_>) = lazy f.Value x.Value
In this code listing, I've repeated the map function shown in a previous article. It's not required for the implementation of apply, but you'll see it in use shortly, so I thought it was convenient to include it in the listing.
If you belong to the camp of F# programmers who think that F# should emulate Haskell, you can also introduce an operator:
let (<*>) f x = Lazy.apply x f
Notice that this <*> operator simply flips the arguments of Lazy.apply. If you introduce such an operator, be aware that the admonition from the overview article still applies. In Haskell, the <*> operator applies to any Applicative, which makes it truly general. In F#, once you define an operator like this, it applies specifically to a particular container type, which, in this case, is Lazy<'a>.
You can replicate the first of the above C# examples like this:
let f : Lazy<int -> string> = // ... let x : Lazy<int> = // ... let y : Lazy<string> = Lazy.apply x f
Alternatively, if you want to use the <*> operator, you can compute y like this:
let y : Lazy<string> = f <*> x
Chaining multiple lazy computations together also works:
let f : Lazy<char -> int -> string> = // ... let c : Lazy<char> = // ... let i : Lazy<int> = // ... let s = Lazy.apply c f |> Lazy.apply i
Again, you can compute s with the operator, if that's more to your liking:
let s : Lazy<string> = f <*> c <*> i
Finally, if your function isn't contained in a Lazy value, you can start out with Lazy.map:
let f : char -> int -> string = // ... let c : Lazy<char> = // ... let i : Lazy<int> = // ... let s : Lazy<string> = Lazy.map f c |> Lazy.apply i
This works without requiring additional overloads. Since F# natively supports partial function application, the first step in the pipeline, Lazy.map f c has the type Lazy<int -> string> because f is a function of the type char -> int -> string, but in the first step, Lazy.map f c only supplies c, which contains a char value.
Once more, if you prefer the infix operator, you can also compute s as:
let s : Lazy<string> = lazy f <*> c <*> i
While I find operator-based syntax attractive in Haskell code, I'm more hesitant about such syntax in F#.
Haskell #
As outlined in the previous article, Haskell is already lazily evaluated, so it makes little sense to introduce an explicit Lazy data container. While Haskell's built-in Identity isn't quite equivalent to .NET's Lazy<T> object, some similarities remain; most notably, the Identity functor is also applicative:
Prelude Data.Functor.Identity> :t f f :: a -> Int -> [a] Prelude Data.Functor.Identity> :t c c :: Identity Char Prelude Data.Functor.Identity> :t i i :: Num a => Identity a Prelude Data.Functor.Identity> :t f <$> c <*> i f <$> c <*> i :: Identity String
This little GHCi session simply illustrates that if you have a 'normal' function f and two Identity values c and i, you can compose them using the infix map operator <$>, followed by the infix apply operator <*>. This is equivalent to the F# expression Lazy.map f c |> Lazy.apply i.
Still, this makes little sense, since all Haskell expressions are already lazily evaluated.
Summary #
The Lazy functor is also an applicative functor. This can be used to combine multiple lazily computed values into a single lazily computed value.
Next: Applicative monoids.
Danish CPR numbers in F#
An example of domain-modelling in F#, including a fine example of using the option type as an applicative functor.
This article is an instalment in an article series about applicative functors, although the applicative functor example doesn't appear until towards the end. This article also serves the purpose of showing an example of Domain-Driven Design in F#.
Danish personal identification numbers #
As outlined in the previous article, in Denmark, everyone has a personal identification number, in Danish called CPR-nummer (CPR number).
CPR numbers have a simple format: DDMMYY-SSSS, where the first six digits indicate a person's birth date, and the last four digits are a sequence number. Some information, however, is also embedded in the sequence number. An example could be 010203-1234, which indicates a woman born February 1, 1903.
One way to model this in F# is with a single-case discriminated union:
type CprNumber = private CprNumber of (int * int * int * int) with override x.ToString () = let (CprNumber (day, month, year, sequenceNumber)) = x sprintf "%02d%02d%02d-%04d" day month year sequenceNumber
This is a common idiom in F#. In object-oriented design with e.g. C# or Java, you'd typically create a class and put guard clauses in its constructor. This would prevent a user from initialising an object with invalid data (such as 401500-1234). While you can create classes in F# as well, a single-case union with a private case constructor can achieve the same degree of encapsulation.
In this case, I decided to use a quadruple (4-tuple) as the internal representation, but this isn't visible to users. This gives me the option to refactor the internal representation, if I need to, without breaking existing clients.
Creating CPR number values #
Since the CprNumber case constructor is private, you can't just create new values like this:
let cpr = CprNumber (1, 1, 1, 1118)
If you're outside the Cpr module that defines the type, this doesn't compile. This is by design, but obviously you need a way to create values. For convenience, input values for day, month, and so on, are represented as ints, which can be zero, negative, or way too large for CPR numbers. There's no way to statically guarantee that you can create a value, so you'll have to settle for a tryCreate function; i.e. a function that returns Some CprNumber if the input is valid, or None if it isn't. In Haskell, this pattern is called a smart constructor.
There's a couple of rules to check. All integer values must fall in certain ranges. Days must be between 1 and 31, months must be between 1 and 12, and so on. One way to enable succinct checks like that is with an active pattern:
let private (|Between|_|) min max candidate = if min <= candidate && candidate <= max then Some candidate else None
Straightforward: return Some candidate if candidate is between min and max; otherwise, None. This enables you to pattern-match input integer values to particular ranges.
Perhaps you've already noticed that years are represented with only two digits. CPR is an old system (from 1968), and back then, bits were expensive. No reason to waste bits on recording the millennium or century in which people were born. It turns out, after all, that there's a way to at least partially figure out the century in which people were born. The first digit of the sequence number contains that information:
// int -> int -> int let private calculateFourDigitYear year sequenceNumber = let centuryDigit = sequenceNumber / 1000 // Integer division // Table from https://da.wikipedia.org/wiki/CPR-nummer match centuryDigit, year with | Between 0 3 _, _ -> 1900 | 4 , Between 0 36 _ -> 2000 | 4 , _ -> 1900 | Between 5 8 _, Between 0 57 _ -> 2000 | Between 5 8 _, _ -> 1800 | _ , Between 0 36 _ -> 2000 | _ -> 1900 + year
As the code comment informs the reader, there's a table that defines the century, based on the two-digit year and the first digit of the sequence number. Note that birth dates in the nineteenth century are possible. No Danes born before 1900 are alive any longer, but at the time the CPR system was introduced, one person in the system was born in 1863!
The calculateFourDigitYear function starts by pulling the first digit out of the sequence number. This is a four-digit number, so dividing by 1,000 produces the digit. I left a comment about integer division, because I often miss that detail when I read code.
The big pattern-match expression uses the Between active pattern, but it ignores the return value from the pattern. This explains the wild cards (_), I hope.
Although a pattern-match expression is often formatted over several lines of code, it's a single expression that produces a single value. Often, you see code where a let-binding binds a named value to a pattern-match expression. Another occasional idiom is to pipe a pattern-match expression to a function. In the calculateFourDigitYear function I use a language construct I've never seen anywhere else: the eight-lines pattern-match expression returns an int, which I simply add to year using the + operator.
Both calculateFourDigitYear and the Between active pattern are private functions. They're only there as support functions for the public API. You can now implement a tryCreate function:
// int -> int -> int -> int -> CprNumber option let tryCreate day month year sequenceNumber = match month, year, sequenceNumber with | Between 1 12 m, Between 0 99 y, Between 0 9999 s -> let fourDigitYear = calculateFourDigitYear y s if 1 <= day && day <= DateTime.DaysInMonth (fourDigitYear, m) then Some (CprNumber (day, m, y, s)) else None | _ -> None
The tryCreate function begins by pattern-matching a triple (3-tuple) using the Between active pattern. The month must always be between 1 and 12 (both included), the year must be between 0 and 99, and the sequenceNumber must always be between 0 and 9999 (in fact, I'm not completely sure if 0000 is valid).
Finding the appropriate range for the day is more intricate. Is 31 always valid? Clearly not, because there's no November 31, for example. Is 30 always valid? No, because there's never a February 30. Is 29 valid? This depends on whether or not the year is a leap year.
This reveals why you need calculateFourDigitYear. While you can use DateTime.DaysInMonth to figure out how many days a given month has, you need the year. Specifically, February 1900 had 28 days, while February 2000 had 29.
Ergo, if day, month, year, and sequenceNumber all fall within their appropriate ranges, tryCreate returns a Some CprNumber value; otherwise, it returns None.
Notice how this is different from an object-oriented constructor with guard clauses. If you try to create an object with invalid input, it'll throw an exception. If you try to create a CprNumber value, you'll receive a CprNumber option, and you, as the client developer, must handle both the Some and the None case. The compiler will enforce this.
> let gjern = Cpr.tryCreate 11 11 11 1118;; val gjern : Cpr.CprNumber option = Some 111111-1118 > gjern |> Option.map Cpr.born;; val it : DateTime option = Some 11.11.1911 00:00:00
As most F# developers know, F# gives you enough syntactic sugar to make this a joy rather than a chore... and the warm and fuzzy feeling of safety is priceless.
CPR data #
The above FSI session uses Cpr.born, which you haven't seen yet. With the tools available so far, it's trivial to implement; all the work is already done:
// CprNumber -> DateTime let born (CprNumber (day, month, year, sequenceNumber)) = DateTime (calculateFourDigitYear year sequenceNumber, month, day)
While the CprNumber case constructor is private, it's still available from inside of the module. The born function pattern-matches day, month, year, and sequenceNumber out of its input argument, and trivially delegates the hard work to calculateFourDigitYear.
Another piece of data you can deduce from a CPR number is the gender of the person:
// CprNumber -> bool let isFemale (CprNumber (_, _, _, sequenceNumber)) = sequenceNumber % 2 = 0 let isMale (CprNumber (_, _, _, sequenceNumber)) = sequenceNumber % 2 <> 0
The rule is that if the sequence number is even, then the person is female; otherwise, the person is male (and if you change sex, you get a new CPR number).
> gjern |> Option.map Cpr.isFemale;; val it : bool option = Some true
Since 1118 is even, this is a woman.
Parsing CPR strings #
CPR numbers are often passed around as text, so you'll need to be able to parse a string representation. As described in the previous article, you should follow Postel's law. Input could include extra white space, and the middle dash could be missing.
The .NET Base Class Library contains enough utility methods working on string values that this isn't going to be particularly difficult. It can, however, be awkward to interoperate with object-oriented APIs, so you'll often benefit from adding a few utility functions that give you curried functions instead of objects with methods. Here's one that adapts Int32.TryParse:
module private Int = // string -> int option let tryParse candidate = match candidate |> Int32.TryParse with | true, i -> Some i | _ -> None
Nothing much goes on here. While F# has pleasant syntax for handling out parameters, it can be inconvenient to have to pattern-match every time you'd like to try to parse an integer.
Here's another helper function:
module private String = // int -> int -> string -> string option let trySubstring startIndex length (s : string) = if s.Length < startIndex + length then None else Some (s.Substring (startIndex, length))
This one comes with two benefits: The first benefit is that it's curried, which enables partial application and piping. You'll see an example of this further down. The second benefit is that it handles at least one error condition in a type-safe manner. When trying to extract a sub-string from a string, the Substring method can throw an exception if the index or length arguments are out of range. This function checks whether it can extract the requested sub-string, and returns None if it can't.
I wouldn't be surprised if there are edge cases (for example involving negative integers) that trySubstring doesn't handle gracefully, but as you may have noticed, this is a function in a private module. I only need it to handle a particular use case, and it does that.
You can now add the tryParse function:
// string -> CprNumber option let tryParse (candidate : string ) = let (<*>) fo xo = fo |> Option.bind (fun f -> xo |> Option.map f) let canonicalized = candidate.Trim().Replace("-", "") let dayCandidate = canonicalized |> String.trySubstring 0 2 let monthCandidate = canonicalized |> String.trySubstring 2 2 let yearCandidate = canonicalized |> String.trySubstring 4 2 let sequenceNumberCandidate = canonicalized |> String.trySubstring 6 4 Some tryCreate <*> Option.bind Int.tryParse dayCandidate <*> Option.bind Int.tryParse monthCandidate <*> Option.bind Int.tryParse yearCandidate <*> Option.bind Int.tryParse sequenceNumberCandidate |> Option.bind id
The function starts by defining a private <*> operator. Readers of the applicative functor article series will recognise this as the 'apply' operator. The reason I added it as a private operator is that I don't need it anywhere else in the code base, and in F#, I'm always worried that if I add <*> at a more visible level, it could collide with other definitions of <*> - for example one for lists. This one particularly makes option an applicative functor.
The first step in parsing candidate is to remove surrounding white space and the interior dash.
The next step is to use String.trySubstring to pull out candidates for day, month, and so on. Each of these four are string option values.
All four of these must be Some values before we can even start to attempt to turn them into a CprNumber value. If only a single value is None, tryParse should return None as well.
You may want to re-read the article on the List applicative functor for a detailed explanation of how the <*> operator works. In tryParse, you have four option values, so you apply them all using four <*> operators. Since four values are being applied, you'll need a function that takes four curried input arguments of the appropriate types. In this case, all four are int option values, so for the first expression in the <*> chain, you'll need an option of a function that takes four int arguments.
Lo and behold! tryCreate takes four int arguments, so the only action you need to take is to make it an option by putting it in a Some case.
The only remaining hurdle is that tryCreate returns CprNumber option, and since you're already 'in' the option applicative functor, you now have a CprNumber option option. Fortunately, bind id is always the 'flattening' combo, so that's easily dealt with.
> let andreas = Cpr.tryParse " 0109636221";; val andreas : Cpr.CprNumber option = Some 010963-6221
Since you now have both a way to parse a string, and turn a CprNumber into a string, you can write the usual round-trip property:
[<Fact>] let ``CprNumber correctly round-trips`` () = Property.check <| property { let! expected = Gen.cprNumber let actual = expected |> string |> Cpr.tryParse Some expected =! actual }
This test uses Hedgehog, Unquote, and xUnit.net. The previous article demonstrates a way to test that Cpr.tryParse can handle mangled input.
Summary #
This article mostly exhibited various F# design techniques you can use to achieve an even better degree of encapsulation than you can easily get with object-oriented languages. Towards the end, you saw how using option as an applicative functor enables you to compose more complex optional values from smaller values. If just a single value is None, the entire expression becomes None, but if all values are Some values, the computation succeeds.
This article is an entry in the F# Advent Calendar in English 2018.
Next: The Lazy applicative functor.
Set is not a functor
Sets aren't functors. An example for object-oriented programmers.
This article is an instalment in an article series about functors. The way functors are frequently presented to programmers is as a generic container (Foo<T>) equipped with a translation method, normally called map, but in C# idiomatically called Select.
It'd be tempting to believe that any generic type with a Select method is a functor, but it takes more than that. The Select method must also obey the functor laws. This article shows an example of a translation that violates the second functor law.
Mapping sets #
The .NET Base Class Library comes with a class called HashSet<T>. This generic class implements IEnumerable<T>, so, via extension methods, it has a Select method.
Unfortunately, that Select method isn't a structure-preserving translation of sets. The problem is that it treats sets as enumerable sequences, which implies an order to elements that isn't part of a set's structure.
In order to understand what the problem is, consider this xUnit.net test:
[Fact] public void SetAsEnumerableSelectLeadsToWrongConclusions() { var set1 = new HashSet<int> { 1, 2, 3 }; var set2 = new HashSet<int> { 3, 2, 1 }; Assert.True(set1.SetEquals(set2)); Func<int, int> id = x => x; var seq1 = set1.AsEnumerable().Select(id); var seq2 = set2.AsEnumerable().Select(id); Assert.False(seq1.SequenceEqual(seq2)); }
This test creates two sets, and by using a Guard Assertion demonstrates that they're equal to each other. It then proceeds to Select over both sets, using the identity function id. The return values aren't HashSet<T> objects, but rather IEnumerable<T> sequences. Due to an implementation detail in HashSet<T>, these two sequences are different, because they were populated in reverse order of each other.
The problem is that the Select extension method has the signature IEnumerable<TResult> Select<T, TResult>(IEnumerable<T>, Func<T, TResult>). It doesn't operate on HashSet<T>, but instead treats it as an ordered sequence of elements. A set isn't intrinsically ordered, so that's not the translation you need.
To be clear, IEnumerable<T> is a functor (as long as the sequence is referentially transparent). It's just not the functor you're looking for. What you need is a method with the signature HashSet<TResult> Select<T, TResult>(HashSet<T>, Func<T, TResult>). Fortunately, such a method is trivial to implement:
public static HashSet<TResult> Select<T, TResult>( this HashSet<T> source, Func<T, TResult> selector) { return new HashSet<TResult>(source.AsEnumerable().Select(selector)); }
This extension method offers a proper Select method that translates one HashSet<T> into another. It does so by enumerating the elements of the set, then using the Select method for IEnumerable<T>, and finally wrapping the resulting sequence in a new HashSet<TResult> object.
This is a better candidate for a translation of sets. Is it a functor, then?
Second functor law #
Even though HashSet<T> and the new Select method have the correct types, it's still only a functor if it obeys the functor laws. It's easy, however, to come up with a counter-example that demonstrates that Select violates the second functor law.
Consider a pair of conversion methods between string and DateTimeOffset:
public static DateTimeOffset ParseDateTime(string s) { DateTimeOffset dt; if (DateTimeOffset.TryParse(s, out dt)) return dt; return DateTimeOffset.MinValue; } public static string FormatDateTime(DateTimeOffset dt) { return dt.ToString("yyyy'-'MM'-'dd'T'HH':'mm':'sszzz"); }
The first method, ParseDateTime, converts a string into a DateTimeOffset value. It tries to parse the input, and returns the corresponding DateTimeOffset value if this is possible; for all other input values, it simply returns DateTimeOffset.MinValue. You may dislike how the method deals with input values it can't parse, but that's not important. In order to prove that sets aren't functors, I just need one counter-example, and the one I'll pick will not involve unparseable strings.
The FormatDateTime method converts any DateTimeOffset value to an ISO 8601 string.
The DateTimeOffset type is the interesting piece of the puzzle. In case you're not intimately familiar with it, a DateTimeOffset value contains a date, a time, and a time-zone offset. You can, for example create one like this:
> new DateTimeOffset(2018, 4, 17, 15, 9, 55, TimeSpan.FromHours(2)) [17.04.2018 15:09:55 +02:00]
This represents April 17, 2018, at 15:09:55 at UTC+2. You can convert that value to UTC:
> new DateTimeOffset(2018, 4, 17, 15, 9, 55, TimeSpan.FromHours(2)).ToUniversalTime() [17.04.2018 13:09:55 +00:00]
This value clearly contains different constituent elements, but it does represent the same instant in time. This is how DateTimeOffset implements Equals. These two object are considered equal, as the following test will demonstrate.
In a sense, you could argue that there's some sense in implementing equality for DateTimeOffset in that way, but this unusual behaviour provides just the counter-example that demonstrates that sets aren't functors:
[Fact] public void SetViolatesSecondFunctorLaw() { var x = "2018-04-17T13:05:28+02:00"; var y = "2018-04-17T11:05:28+00:00"; Assert.Equal(ParseDateTime(x), ParseDateTime(y)); var set = new HashSet<string> { x, y }; var l = set.Select(ParseDateTime).Select(FormatDateTime); var r = set.Select(s => FormatDateTime(ParseDateTime(s))); Assert.False(l.SetEquals(r)); }
This passing test provides the required counter-example. It first creates two ISO 8601 representations of the same instant. As the Guard Assertion demonstrates, the corresponding DateTimeOffset values are considered equal.
In the act phase, the test creates a set of these two strings. It then performs two round-trips over DateTimeOffset and back to string. The second functor law states that it shouldn't matter whether you do it in one or two steps, but it does. Assert.False passes because l is not equal to r. Q.E.D.
An illustration #
The problem is that sets only contain one element of each value, and due to the way that DateTimeOffset interprets equality, two values that both represent the same instant are collapsed into a single element when taking an intermediary step. You can illustrate it like this:
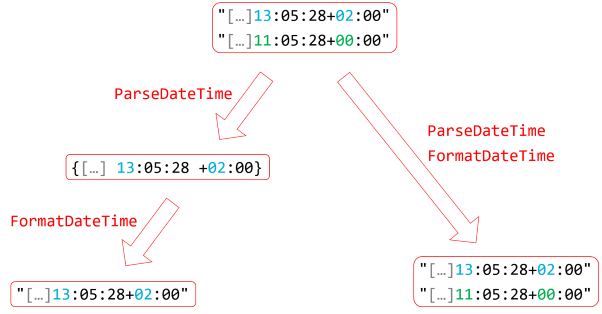
In this illustration, I've hidden the date behind an ellipsis in order to improve clarity. The date segments are irrelevant in this example, since they're all identical.
You start with a set of two string values. These are obviously different, so the set contains two elements. When you map the set using the ParseDateTime function, you get two DateTimeOffset values that .NET considers equal. For that reason, HashSet<DateTimeOffset> considers the second value redundant, and ignores it. Therefore, the intermediary set contains only a single element. When you map that set with FormatDateTime, there's only a single element to translate, so the final set contains only a single string value.
On the other hand, when you map the input set without an intermediary set, each string value is first converted into a DateTimeOffset value, and then immediately thereafter converted back to a string value. Since the two resulting strings are different, the resulting set contains two values.
Which of these paths is correct, then? Both of them. That's the problem. When considering the semantics of sets, both translations produce correct results. Since the results diverge, however, the translation isn't a functor.
Summary #
A functor must not only preserve the structure of the data container, but also of functions. The functor laws express that a translation of functions preserves the structure of how the functions compose, in addition to preserving the structure of the containers. Mapping a set doesn't preserve those structures, and that's the reason that sets aren't functors.
P.S. #
2019-01-09. There's been some controversy around this post, and more than one person has pointed out to me that the underlying reason that the functor laws are violated in the above example is because DateTimeOffset behaves oddly. Specifically, its Equals implementation breaks the substitution property of equality. See e.g. Giacomo Citi's response for details.
The term functor originates from category theory, and I don't claim to be an expert on that topic. It's unclear to me if the underlying concept of equality is explicitly defined in category theory, but it wouldn't surprise me if it is. If that definition involves the substitution property, then the counter-example presented here says nothing about Set as a functor, but rather that DateTimeOffset has unlawful equality behaviour.
Next: Applicative functors.
Comments
The Problem here is not the HashSet, but the DateTimeOffset Class. It defines Equality loosely, so Time-Comparison is possible between different Time-Zones. The Functor Property can be restored by applying a stricter Equality Comparer like this one:
var l = set.Select(ParseDateTime, StrictDateTimeOffsetComparer._).Select(FormatDateTime);
/// <summary> Compares both <see cref="DateTimeOffset.Offset"/> and <see cref="DateTimeOffset.UtcTicks"/> </summary>
public class StrictDateTimeOffsetComparer : IEqualityComparer<DateTimeOffset> {
public bool Equals(DateTimeOffset x, DateTimeOffset y)
=> x.Offset.Equals(y.Offset) && x.UtcTicks == y.UtcTicks;
public int GetHashCode(DateTimeOffset obj) => HashCode.Combine(obj.Offset, obj.UtcTicks);
/// <summary> Singleton Instance </summary>
public static readonly StrictDateTimeOffsetComparer _ = new();
StrictDateTimeOffsetComparer(){}
}
As for preserving Referential Transparency, the Distinction between Equality and Identity is important.
By Default, Classes implement 'Equals' and '==' using ReferenceEquals which guarantees Substitution.
Structs don't have a Reference unless they are boxed, instead they are copied and usually have Value Semantics.
To be truly 'referentially transparent' though, Equality must be based on ALL Fields.
When someone overrides Equals with a weaker Equivalence Relation than ReferenceEquals,
it is their Responsibility to preserve Substitution.
No Library Author can cover all possible application cases for HashSet.
Matt, thank you for writing. DateTimeOffset already defines the EqualsExact method. Wouldn't it be easier to use that?
In order to prove that sets aren't functors, I just need one counter-example, and the one I'll pick will not involve unparseable strings.
In context, you are correct; you can pick whatever example you want to create a counter-example. However, your counter-example does not prove that HashSet<> is not a functor.
We often say that a type is or isn't a functor. That is not quite right. It is more correct to say that a type T<> and a function with inputs T<A> and A and output T<B> are or are not a functor. Then I think it is reasonable to say some type is a functor if (and only if) there exists a function such that the type and that functor are a functor. In that case, to conclude that HashSet<> is not a functor requires one to prove that, for all functions f, the pair HashSet<> and f are not a functor. Because of the universal quantification, this cannot be achieved via a single counter-example.
Your counter-example shows that the type HashSet<> and your function that you called Select is not a functor. Your Select function uses this constructor overload of HashSet<>, which eventually uses EqualityComparer<T>.Default in places like here and here. The instance of EqualityComparer<DateTimeOffset>.Default implements its Equals method via DateTimeOffset.Equals. The comments by Giacomo Citi and others explained "why" your Select function (and the type HashSet<>) doesn't satisfy the second functor law: you picked a constructor overload of HashSet<> that uses an implementation of IEqualityComparer<DateTimeOffset> that depends on DateTimeOffset.Equals, which doesn't satisfy the substitution property.
The term functor originates from category theory, and I don't claim to be an expert on that topic. It's unclear to me if the underlying concept of equality is explicitly defined in category theory, but it wouldn't surprise me if it is. If that definition involves the substitution property, then the counter-example presented here says nothing about Set as a functor, but rather that DateTimeOffset has unlawful equality behaviour.
I think this is a red herring. Microsoft can implement HashSet<> however it wants and you can implement your Select function however you want. Then the pair are either a functor or not. Independent of this is that Microsoft gets to define the contract for IEqualityComparer<>.Equals. The documentation states that a valid implementation must be reflexive, symmetric, and transitive but does not require that the substitution property is satisifed.
I think the correct question is this: Is HashSet<> a functor?...which is equivalent to: Does there exist a function such that HashSet<> and that function are a functor? I think the answer is "yes".
Implement Select by calling the constructor overload of HashSet<> that takes an instance of IEnumerable<> as well as an instance of IEqualityComparer<>. For the second argument, provide an instance that implements Equals by always returning false (and it suffices to implement GetHashCode by returning a constant). I claim that HashSet<> and that function are a functor. In fact, I further claim that this functor is isomorphic to the functor IEnumerable<> (with the function Enumerable.Select). That doesn't make it a very interesting functor, but it is a functor nonetheless. (Also, notice that this implementation of Equals is not reflexive, but I still used it to create a functor.)
Tyson, thank you for writing. Yes, I agree with most of what you write. As I added in the P.S., I'm aware that this post draws the wrong conclusions. I also understand why.
It's true that one way to think of a functor is a type and an associated function. When I (and others) sometimes fall into the trap of directly equating types with functors, it's because this is the most common implementation of functors (and monads) in statically typed programming. This is probably most explicit in Haskell, where a particular functor is explicitly associated with a type. This has the implication that in order to distinguish between multiple functors, Haskell comes with all sort of wrapper types. You mostly see this in the context of semigroups and monoids, where the Sum and Product wrappers exist only to distinguish between two monoids over the same type (numbers).
You could imagine something similar happening with Either and tuple bifunctors. By conventions (and because of a bit pseudo-principled hand-waving), we conventionally pick one of the their dimensions for the 'functor instance'. For example, we pick the right dimension of Either for the functor instance. In both Haskell, F#, and C#, this enables certain syntax, such as Haskell do notation, F# computation expressions, or C# query syntax.
If we wanted to instead make mapping over, say, left, the 'functor instance', we can't do that without throwing away the language support for the right side. The solution is to introduce a new type that comes with the desired function associated. This enables the compiler to distinguish between two (or more) functors over what would otherwise be the same type.
That aside, can we resolve the issue in the way that you suggest? Possibly. I haven't thought deep and long about it, but what you write sounds plausible.
For anyone who wants to use such a set functor for real code, I'd suggest wrapping it in another type, since relying on client developers to use the 'correct' constructor overload seems too brittle.
Well, yes, but since you have to implement a proper matching HashCode Function anyway, I thought it would be more obvious to write a matching Equals Function too.
Ah, so you're proposing to subclass HashSet<DateTimeOffset> and pass the proper EqualityComparer to the base class. Alright, that would be a proper Functor then.
The Test Data Generator applicative functor
Test Data Generator modelled as an applicative functor, with examples in C# and F#.
This article is an instalment in an article series about applicative functors. It shows yet another example of an applicative functor. I tend to think of applicative functors as an abstraction of 'combinations' of values and functions, but this is most evident for lists and other collections. Even so, I think that the intuition also holds for Maybe as an applicative functor as well as validation as an applicative functor. This is also the case for the Test Data Generator functor.
Applicative generator in C# #
In a previous article, you saw how to implement a Test Data Generator as a functor in C#. The core class is this Generator<T> class:
public class Generator<T> { private readonly Func<Random, T> generate; public Generator(Func<Random, T> generate) { if (generate == null) throw new ArgumentNullException(nameof(generate)); this.generate = generate; } public Generator<T1> Select<T1>(Func<T, T1> f) { if (f == null) throw new ArgumentNullException(nameof(f)); Func<Random, T1> newGenerator = r => f(this.generate(r)); return new Generator<T1>(newGenerator); } public T Generate(Random random) { if (random == null) throw new ArgumentNullException(nameof(random)); return this.generate(random); } }
This is merely repetition from the earlier article.
Generator<T> is already a functor, but you can make it an applicative functor by adding an extension method like this:
public static Generator<TResult> Apply<T, TResult>( this Generator<Func<T, TResult>> selectors, Generator<T> generator) { if (selectors == null) throw new ArgumentNullException(nameof(selectors)); if (generator == null) throw new ArgumentNullException(nameof(generator)); Func<Random, TResult> newGenerator = r => { var f = selectors.Generate(r); var x = generator.Generate(r); return f(x); }; return new Generator<TResult>(newGenerator); }
The Apply function combines a generator of functions with a generator of values. Given these two generators, it defines a closure over both, and packages that function in a new generator object.
CPR example #
When is it interesting to combine a randomly selected function with a randomly generated value? Here's an example.
In Denmark, everyone has a personal identification number, in Danish called CPR-nummer (CPR number). It's somewhat comparable to the U.S. Social Security number, but surely more Orwellian.
CPR numbers have a simple format: DDMMYY-SSSS, where the first six digits indicate a person's birth date, and the last four digits are a sequence number. An example could be 010203-1234, which indicates a woman born February 1, 1903. Assume that you're writing a system that has to accept CPR numbers as input. You've represented CPR number as a class called CprNumber, and you've already written a parser, but now it turns out that sometimes users enter slightly malformed data.
Sometimes users copy and paste CPR numbers from other sources, and occasionally, they inadvertently include a leading or trailing space. Other users forget the dash between the birth date and the sequence number. In other words, sometimes you receive input like "050301-4231 " or "1211993321".
Using your fancy Test Data Generator, you'd like to write a test that verifies that your parser follows Postel's law: Be conservative in what you send, be liberal in what you accept.
Assume that you already have a generator that can produce valid CprNumber objects. One test strategy, then, could be to generate a valid CprNumber object, convert it to a string, slightly taint or mangle that string, and then attempt to parse the tainted string.
There's more than one way to taint a valid CPR number string. You could, for example, define three functions like these:
Func<string, string> addLeadingSpace = s => " " + s; Func<string, string> addTrailingSpace = s => s + " "; Func<string, string> removeDash = s => s.Replace("-", "");
The first function adds a leading space to a string, the second adds a trailing space, and the third removes all dashes it finds. Can you make a generator out of those functions?
Yes, you can, with this common general-purpose method:
public static Generator<T> Elements<T>(params T[] alternatives) { if (alternatives == null) throw new ArgumentNullException(nameof(alternatives)); return new Generator<T>(r => { var index = r.Next(alternatives.Length); return alternatives[index]; }); }
This generator randomly selects a value from an array of values, with equal probability. It's a common method, because you'll find equivalent functions in QuickCheck, FsCheck, and Hedgehog (where it's called item).
You can write the entire test like this:
[Fact] public void ParseCorrectlyHandlesTaintedInput() { Func<string, string> addLeadingSpace = s => " " + s; Func<string, string> addTrailingSpace = s => s + " "; Func<string, string> removeDash = s => s.Replace("-", ""); Generator<Func<string, string>> tainters = Gen.Elements( addLeadingSpace, addTrailingSpace, removeDash, s => addLeadingSpace(removeDash(s)), s => addTrailingSpace(addLeadingSpace(s))); var g = tainters.Apply(Gen.CprNumber.Select(n => n.ToString())); var rnd = new Random(); var candidate = g.Generate(rnd); CprNumber dummy; var actual = CprNumber.TryParse(candidate, out dummy); Assert.True(actual); }
You first define the three 'tainting' functions, and then create the tainters generator. Notice that this generator not only contains the three functions, but also combinations of these functions. I didn't include all possible combinations of functions, but in an earlier article, you saw how to do just that.
Gen.CprNumber is a Generator<CprNumber>, while you actually need a Generator<string>. Since Generator<T> is a functor, you can easily map Gen.CprNumber with its Select method.
You now have a Generator<Func<string, string>> (tainters) and a Generator<string>, so you can combine them using Apply. The result g is another Generator<string> that generates 'tainted', but still valid, CPR string representations.
In order to keep the example as simple as possible, the Arrange and Assert phases of the test only checks if CprNumber.TryParse returns true. A better test would also verify that the resulting CprNumber value was correct, but in order to do that, you need to keep the originally generated CprNumber object around so that you can compare this expected value to the actual value. This is possible, but complicates the code, so I left it out of the example.
F# Hedgehog #
You can translate the above unit test to F#, using Hedgehog as a property-based testing library. Another option would be FsCheck. Without further ado, I present to you the test:
[<Fact>] let ``Correctly parses tainted text`` () = Property.check <| property { let removeDash (s : string) = s.Replace ("-", "") let! candidate = Gen.item [ sprintf " %s" sprintf "%s " removeDash removeDash >> sprintf " %s" sprintf " %s "] <*> Gen.map string Gen.cprNumber let actual = Cpr.tryParse candidate test <@ actual |> Option.isSome @> }
As I already mentioned in passing, Hedgehog's equivalent to the above Elements method is called Gen.item. Here, you see the same five functions as above passed in a list. Thanks to partial application and type inference, an expression like sprintf " %s" is already a function of the type string -> string, as is removeDash. For the last of the five functions, I found it easier to write (and read) sprintf " %s " instead of sprintf " %s" >> sprintf "%s ".
Equivalent to the C# example, Gen.cprNumber is a Gen<CprNumber>, so mapping it with the built-in string function translates it to a Gen<string>.
Hedgehog already includes an <*> operator; Gen is an applicative functor.
Summary #
Applicative functors are fairly common. I find it intuitive to think of them as an abstraction of how to make combinations of things. Modelling a Test Data Generator as an applicative functor enables you to create random combinations of functions and values.
While working on the Hedgehog example, I discovered another great use of option as an applicative functor. You can see this in the next article.
Next: Danish CPR numbers in F#.
Functional architecture: a definition
How do you know whether your software architecture follows good functional programming practices? Here's a way to tell.
Over the years, I've written articles on functional architecture, including Functional architecture is Ports and Adapters, given conference talks, and even produced a Pluralsight course on the topic. How should we define functional architecture, though?
People sometimes ask me about their F# code: How do I know that my F# code is functional?
Please permit me a little detour before I answer that question.
What's the definition of object-oriented design? #
Object-oriented design (OOD) has been around for decades; at least since the nineteen-sixties. Sometimes people get into discussions about whether or not a particular design is good object-oriented design. I know, since I've found myself in such discussions more than once.
These discussions usually die out without resolution, because it seems that no-one can provide a sufficiently rigorous definition of OOD that enables people to determine an outcome. One thing's certain, though, so I'd like to posit this corollary to Godwin's law:
As a discussion about OOD grows longer, the probability of a comparison involving Alan Kay approaches 1.Not that I, in any way, wish to suggest any logical relationship between Alan Kay and Hitler, but in a discussion about OOD, sooner or later someone states:
"That's not what Alan Kay had in mind!"That may be true, even.
My problem with that assertion is that I've never been able to figure out exactly what Alan Kay had in mind. It's something that involves message-passing and Smalltalk, and conceivably, the best modern example of this style of programming might be Erlang (often, ironically, touted as a functional programming language).
This doesn't seem to be a good basis for determining whether or not something is object-oriented.
In any case, despite what Alan Kay had in mind, that wasn't the object-oriented programming we got. While Eiffel is in many ways a strange programming language, the philosophy of OOD presented in Object-Oriented Software Construction feels, to me, like something from which Java could develop.
I'm not aware of the detailed history of Java, but the spirit of the language seems more compatible with Bertrand Meyer's vision than with Alan Kay's.
Subsequently, C# would hardly look the way it does had it not been for Java.
The OOD we got wasn't the OOD originally envisioned. To make matters worse, the OOD we did get seems to be driven by unclear principles. Yes, there's the idea about encapsulation, but while Meyer had some very specific ideas about design-by-contract, that was the distinguishing trait of his vision that didn't make the transition to Java or C#.
It's not clear what OOD is, but I think we can do better when it comes to functional programming (FP).
Referential transparency #
It's possible to pinpoint what FP is to a degree not possible with OOD. Some people may be uncomfortable with the following definition; I don't claim that this is a generally accepted definition. It does have, however, the advantage that it's precise and supports falsification.
The foundation of FP is referential transparency. It's the idea that, for an expression, the left- and right-hand sides of the equal sign are truly equal:
two = 1 + 1
In Haskell, this is enforced by the compiler. The = operator truly implies equality. To be clear, this isn't the case in C#:
var two = 1 + 1;
In C#, Java, and other imperative languages, the = implies assignment, not equality. Here, two can change, despite the absurdity of the claim.
When code is referentially transparent, then you can substitute the expression on the right-hand side with the symbol on the left-hand side. This seems obvious when we consider addition of two numbers, but becomes less clear when we consider function invocation:
i = findBestNumber [42, 1337, 2112, 90125]
In Haskell, functions are referentially transparent. You don't know exactly what findBestNumber does, but you do know that you can substitute i with findBestNumber [42, 1337, 2112, 90125], or vice versa.
In order for a function to be referentially transparent (also known as a pure function), it must have two properties:
- It must always return the same output for the same input. We call this quality determinism.
- It must have no side effects.
The reason I prefer this definition is that it supports falsification. You can assert that a function or value is pure; all it takes is a single counter-example to prove that it's not. A counter-example can be either an input value that doesn't always produce the same return value, or a function call that produces a side effect.
I'm not aware of any other definition that offers similar decision power.
IO #
All software produces side effects: Changing a pixel on a monitor is a side effect. Writing a byte to disk is a side effect. Transmitting a bit over a network is a side effect. It seems that it'd be impossible to interact with pure functions, and indeed, it is, without some sort of affordance for impurity.
Haskell resolves this problem with the IO monad, but the purpose of this article isn't to serve as an introduction to Haskell, monads, or IO. The point is only that in FP, you need some sort of 'wormhole' that will enable you to interact with the real world. There's no way around that, but logically, the rules still apply. Pure functions must stay deterministic and free of side effects.
It follows that you have two groups of operations: impure activities and pure functions.
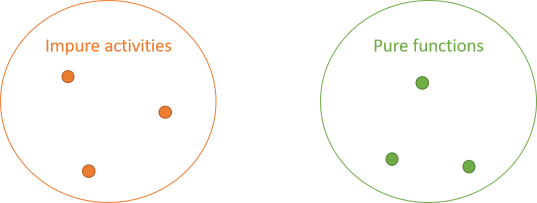
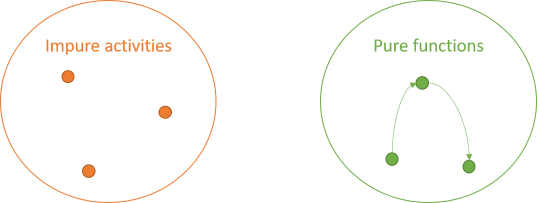
While there are rules for pure functions, those rules still allow for interaction. One pure function can call another pure function. Such an interaction doesn't change the properties of any of those functions. Both caller and callee remain side-effect-free and deterministic.
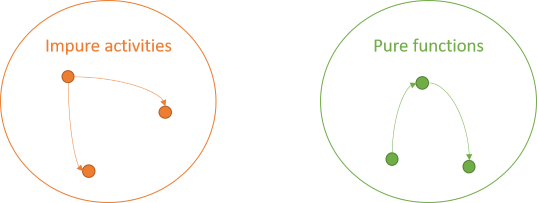
The impure activities can also interact. No rules apply to them:
Finally, since no rules apply to impure activities, they can invoke pure functions:
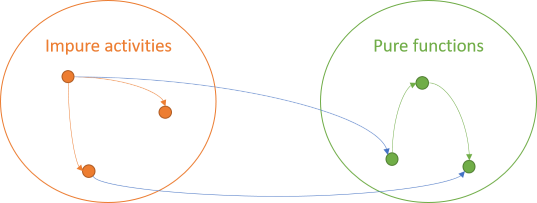
Impure activities are unbound by rules, so they can do anything they need to do, including painting pixels, writing to files, or calling pure functions. A pure function is deterministic and has no side effects. Those properties don't change just because the result is subsequently displayed on a screen.
The fourth combination of arrows is, however, illegal.
A pure function can't invoke an impure activity.If it did, it would either transitively produce a side effect or non-deterministic behaviour.
This is the rule of functional architecture. You can also explain it with a table:
| Callee | |||
|---|---|---|---|
| Impure | Pure | ||
| Caller | Impure | Valid | Valid |
| Pure | Invalid | Valid | |
Clearly, you can trivially obey the functional interaction law by writing exclusively impure code. In a sense, this is what you do by default in imperative programming languages. If you're familiar with Haskell, imagine writing an entire program in IO. That would be possible, but pointless.
Thus, we need to add the qualifier that a significant part of the code base should consist of pure code. How much? The more, the better. Subjectively, I'd say significantly more than half the code base should be pure. I'm concerned, though, that stating a hard limit is as useful here as it is for code coverage.
Tooling #
How do you verify that you obey the functional interaction law? Unfortunately, in most languages the answer is that this requires painstaking analysis. This can be surprisingly tricky to get right. Consider this realistic F# example:
let createEmailNotification templates msg (user : UserEmailData) = let { SubjectLine = subjectTemplate; Content = contentTemplate } = templates |> Map.tryFind user.Localization |> Option.defaultValue (Map.find Localizations.english templates) let r = Templating.append (Templating.replacementOfEnvelope msg) (Templating.replacementOfFlatRecord user) let subject = Templating.run subjectTemplate r let content = Templating.run contentTemplate r { RecipientUserId = user.UserId EmailAddress = user.EmailAddress NotificationSubjectLine = subject NotificationText = content CreatedDate = DateTime.UtcNow }
Is this a pure function?
You may protest that this isn't a fair question, because you don't know what, say, Templating.replacementOfFlatRecord does, but that turns out to be irrelevant. The presence of DateTime.UtcNow makes the entire function impure, because getting the current date and time is non-deterministic. This trait is transitive, which means that any code that calls createEmailNotification is also going to be impure.
That means that the purity of an expression like the following easily becomes obscure.
let emailMessages = specificUsers |> Seq.map (createEmailNotification templates msg)
Is this a pure expression? In this case, we've just established that createEmailNotification is impure, so that wasn't hard to answer. The problem, however, is that the burden is on you, the code reader, to remember which functions are pure, and which ones aren't. In a large code base, this soon becomes a formidable endeavour.
It'd be nice if there was a tool that could automatically check the functional interaction law.
This is where many people in the functional programming community become uncomfortable about this definition of functional architecture. The only tools that I'm aware of that enforce the functional interaction law are a few programming languages, most notably Haskell (others exist, too).
Haskell enforces the functional interaction law via its IO type. You can't use an IO value from within a pure function (a function that doesn't return IO). If you try, your code doesn't compile.
I've personally used Haskell repeatedly to understand the limits of functional architecture, for example to establish that Dependency Injection isn't functional because it makes everything impure.
The overall lack of tooling, however, may make people uncomfortable, because it means that most so-called functional languages (e.g. F#, Erlang, Elixir, and Clojure) offer no support for validating or enforcing functional architecture.
My own experience with writing entire applications in F# is that I frequently, inadvertently violate the functional interaction law somewhere deep in the bowels of my code.
Conclusion #
What's functional architecture? I propose that it's code that obeys the functional architecture law, and that is made up of a significant portion of pure functions.
This is a narrow definition. It excludes a lot of code bases that could easily be considered 'functional enough'. By the definition, I don't intend to denigrate fine programming languages like F#, Clojure, Erlang, etcetera. I personally find it a joy to write in F#, which is my default language choice for .NET programming.
My motivation for offering this definition, albeit restrictive, is to avoid the OOD situation where it seems entirely subjective whether or not something is object-oriented. With the functional interaction law, we may conclude that most (non-Haskell) programs are probably not 'really' functional, but at least we establish a falsifiable ideal to strive for.
This would enable us to look at, say, an F# code base and start discussing how close to the ideal is it?
Ultimately, functional architecture isn't a goal in itself. It's a means to achieve an objective, such as a sustainable code base. I find that FP helps me keep a code base sustainable, but often, 'functional enough' is sufficient to accomplish that.
Comments
Good idea of basing the definition on falsifiability!
The createEmailNotification example makes me wonder though. If it is not a functional design, then what design it actually is? I mean it has to be some design and it does not looks like object-oriented or procedural one.
Max, thank you for writing. I'm not sure whether the assertion that it has to be some design or other is axiomatically obvious, but I suppose that we humans have an innate need to categorise things.
Don Syme calls F# a functional-first language, and that epithet could easily apply to that style of programming as well. Other options could be near-functional, or perhaps, if we're in a slightly more academic mood, quasi-functional.
In daily use, we'd probably still call code like that functional, and I don't think it'll cause much confusion.
If I remember the history of programming correctly, the first attempts at functional programming didn't focus on referential transparency, but simply on the concept of functions as first-class language features, including lambda expressions and higher-order functions. The little I know of Lisp corroborates that view on the history of functional programming.
Only later (I think) did languages appear that make compile-time distinction between pure and impure code.
My purpose with this article wasn't to exclude a large number of languages or code bases from being functional, but just to offer a falsifiable test that we can use for evaluation purposes, if we're ever in doubt. This is something that I feel is sorely missing from the object-oriented debate, and while I can't think of a way to remedy the OOD situation, I hope that the present definition of functional architecture presents firmer ground upon which to have a debate.
Thank you for your definition that forms good grounds for reasoning about functional property of code. I remember some people say that even C# is functional as it allows for delegates. Several thoughts:
1. Remember [Pure] attribute and CodeContracts? It aided the purpose of defensive programming to hold pre/postconditions and invariants. I have this impression that both functional purity and defensive programming help us find ad-hoc quasi-mathematical proofs of code correctness after we load a codebase to our heads. It's way easier then to presume how it works and make changes. Of course it's not mathematical in the strict sense, but still - we tend to trust the code more (e.g. threading). I'm pretty sure unit tests belong to this family too.
2. Isn't the purity concept anywhere close to gateways (code that crosses the boundaries of program determinism control zone, e.g. IO, time, volatile memory)? It's especially evident while refactoring legacy code to make it unit testable. We often extract out infrastructure dependent parts (impure activities, e.g. DateTime.Now) for the other be deterministic (pure) and hence - testable.
3. Can the whole program/system be as pure as this:
INPUT -> PURE_CODE -> OUTPUTI'm afraid not as it'd mean the pure code needed to know all the required input data upfront. That's impossible most of times. So, when it comes to measures, I'd argue that the number of pure code lines is enough to tell how pure the codebase is. I'd accompany this with e.g. percentile distribution of pure chunk length (functions/blocks of contingent im/purity etc.). E.g. I'd personally favour 1) over 2) in the following:
1. INPUT -> 3 x LONG_PURE_CHUNK + 2 x LONG_IMPURE_CHUNK -> OUTPUT 2. INPUT -> 10 x SHORT_PURE_CHUNK + 7 x SHORT_IMPURE_CHUNK -> OUTPUT
4. I'd love to see such tools too :) I believe the purity concept does not pertain only to FP nor OO and is related to the early foundational days of computer programming with mathematical proofs they had.
Marcin, thank you for writing. To be clear, you can perform side effects or non-deterministic behaviour in C# delegates, so delegates aren't guaranteed to be referentially transparent. In fact, delegates, and particularly closures, are isomorphic to objects. In C#, they even compile to classes.
I'm aware that some people think that they're doing functional programming when they use lambda expressions in C#, but I disagree.
I'll see if I can address your other comments below.
Re: 1. #
Some functions are certainly ad-hoc, while others are grounded in mathematics. I agree that pure functions 'fit better in your brain', mostly because it's clear that the only stimuli that can affect the outcome of the function is the input. Granted, if we imagine a concrete, ad-hoc function that takes 23 function arguments, we might still consider it bad code. Small functions, though, tend to be easy to reason about.
I've previously written about the relationship between types and tests, and I believe that there's some sort of linearity in that relationship. The better the type system, the fewer tests you need. The weaker the type system, the more tests you need. It's no wonder that the unit testing culture related to languages like Ruby seems stronger than in the Haskell community.
Re: 2. #
In my experience, most people make legacy code more testable by introducing some variation of Dependency Injection. This may enable you to control some otherwise non-deterministic behaviour from tests, but it doesn't make the design more functional. Those types of dependencies (e.g. on DateTime.Now) are inherently impure, and therefore they make everything that invokes them impure as well. The above functional interaction law excludes such a design from being considered functional.
Functional code, on the other hand, is intrinsically testable. Watch out for a future series of articles that show how to move an object-oriented architecture towards something both more functional, more sustainable, and more testable.
Re: 3. #
A command-line utility could be as pure as you suggest, but most other programs will need to at least
- load some more data from impure sources, such as files, databases, or the current time,
- run some pure functions,
- output the results to some impure destinations, such as files, databases, UI, email, and so on.
Re: 4. #
I'm not sure I understand what you mean by that comment, but the mathematical proofs about computability pre-date computer programming. Gödel's work on recursive functions is from 1933, Church's work on lambda calculus is from 1936, and Turing's paper On Computable Numbers, with an Application to the Entscheidungsproblem is from later in 1936. Turing and Church later showed that all three definitions of computability are equivalent.
I don't know much about Gödel's work, but lambda calculus is defined entirely on the foundation of functions, while the Turing machines described in Turing's paper have nothing to do with functions in the mathematical sense.
Mathematical functions are, however, referentially transparent. They're also total, meaning that they always return a result for any input in the function's domain. Due to the halting problem, a Turing-complete language can't guarantee that all functions are total.
Mathematical functions are not always defined for all input, as seen with division (since it's only defined in ℝ ∖ {0}, real numbers without 0). We see for instance the term partial applied instead of total. You could say that the domain of division in ℝ is ℝ ∖ {0}.
Having total functions for some space S where the domain of the function is the same as S are nice to have, but not we are not always that fortunate.
Oskar, yes, you're right. I admit that what I wrote about totality above was a bit too sweeping. If we really start to dissect what I wrote, it's wrong on more levels. Clearly, mathematical functions (or, at least, algorithms) that never return exist; an algorithm to calculate all the decimals of π would be an example.
If I understand the results that both Church and Gödel arrived at, such algorithms can be encoded in such a way that we can also consider them mathematical functions. If so, then not all mathematical functions are total.
As you may be able to tell, it wasn't entirely clear to me what I was supposed to respond to, and it seems (now that I reread what I wrote) that I managed to write a few sentences that don't make clear sense. My main point, however, seems to have been that we can't write a general-purpose tool that'll be able to determine whether or not any arbitrary function is total or not. Does that part seem reasonable?
Thanks for this article. I feel there is a huge benefit of having a precise definition like that.
I want to point out that there is one more dimension in deciding how far a piece of code is from ‘the ideal functional architecture’. And that is developer's intention. I know, that sound stupid. And technically that code is not pure. But we are talking about how close to the ideal it is.
This is a problem I discovered some time ago. Especially in dynamic languages even the code that looks pure might not be strictly speaking pure because of some dynamic behaviour of the language and other quirks. There are some examples in JavaScript in this article: Do pure functions exist in JavaScript?.
Why is this a different dimention? For F# code there could exist a static analysis tool that would discover usage of impure function down in the code base. That is simply impossible in e.g. JavaScript. So I suggest that the intention the developer had and which is manifested in the code (assuming no harmful behaviour) should also play its role.
What do you and others think? Should such a soft view be considered?
Robin, thank you for writing. If I understand you correctly, you're asking whether we should consider code functional if the programmer intended it to be functional?
To be clear, I don't think that a static analysis tool like the one you suggest could be made for a language like F#. Not only do you need to analyse all of your own code, but if your code calls other libraries, you need to know whether or not these other libraries are pure as well. That's not a trivial undertaking.
My point is that even in F#, a programmer could intend to write pure code, yet still inadvertently fail to do so. Should we still consider it functional?
I admit that I haven't thought deeply about this, but I'd be inclined to say no. I'm sure that you can think of many examples, from other walks of life, where good intentions led to bad outcomes.
The goal of functional architecture is ultimately larger than just purity for the sake of purity. Why is functional programming valuable? I believe that it's valuable because a pure function holds few surprises. When you call a pure function, it doesn't have unintended side-effects. The lack of state mutation eradicates aliasing bugs.
If a programmer intends to write functional code, but nevertheless leaves behind many surprises in the code, the potential of functional programming remains unfulfilled.
Perhaps I misunderstood what you meant, so please elaborate if I missed your point.
You mention, that most languages provide no way to determine whatever or not, a function is pure. I agree, that this is an oversight in functional programming and while FSharp is my most favorite language, is there one that is, you could say, quite surprisingly well defined in this regard. Surprisingly because it is not a functional language per se. It supports nearly all the important concepts, while not something like an HMD type system and immutable data structures.
I am speaking about Nim. It has the keyword func for pure functions and opposite to this the keyword proc in order to perform procedures. In that context is it already obvious, what is the cause for all this confusion:
Calling one thing function, while it is actually something impure, has let to the acceptance that functions can be impure.
And this is the cause of all this trouble: Both in programming, and as well about this specific topic. Talking about implicit versus explicit as well.Matthias, thank you for writing. I didn't know about Nim.
I agree that it's confusing to call an impure procedure a function. These days, I try to stay away form that word in that context, and instead talk about impure actions or, as I did in this article, impure activities.
What to test and not to test
Should you unit test everything? Hardly surprising, the answer is that It Depends™. This article outlines some of the circumstances you might consider.
Some years ago, I, somewhat to my own surprise, found myself on the wrong side of a controversy about whether one should test trivial code. The context was a discussion about Test-Driven Development (TDD), and for reasons that I still stand behind today, I argued that you should test all code, including trivial code, such as property getters.
Most of the 'TDD community' reacted quite negatively to that article, some in not-so-nice ways. Some people reacted, I believe, based on their dislike of the conclusion, without responding to my arguments. Others, however, gave reasoned rebuttals. When people like Derick Bailey and Mark Rendle disagree with me, in a reasoned matter, even, I consider that a good reason to revisit my thinking.
Could I have been wrong? That certainly wouldn't be the first time, but even re-reading the article today, I find my logic sound. Yet, I've substantially nuanced my position since then.
It took me some time to understand how I could disagree so radically with people I respect. It didn't take me five years, though, but while I've been at peace with the apparent conflict for years, I've never written a coherent description of my current understanding of this problem space. This article is my attempt to remedy that omission.
Context matters #
Whenever you consult an expert about how to address a problem, you'll invariably get the answer that it depends. I'd suggest that if you don't get that answer, the person is probably not an expert, after all. A useful expert will also be able to tell you on what 'it' depends.
In an abstract sense, what 'it' depends on is the context.
I wrote my original piece from a particular context. Part of that context is explicitly present in the article, but another part is entirely implicit. People read the article from within their own contexts, which in many cases turned out to be incongruent with mine. No wonder people disagreed.
Watching the wildlife #
My context at that time was that I had some success with AutoFixture, an open source library, which is what I consider wildlife software. Once you've released a version of the software, you have no control of where it's installed, or how it's used.
This means that backwards compatibility becomes important. If I broke something, I would inconvenience the users of my software. Making sure that compatibility didn't break became one of my highest priorities. I used unit tests for regression tests, and I did, indeed, test the entire public API of AutoFixture, to make sure that no breaking changes were introduced.
That was my implicit context. Read in that light, my dogmatic insistence on testing everything hopefully makes a little more sense.
Does that mean that my conclusion transfers to other circumstances? No, of course it doesn't. If you're developing and maintaining zoo software, breaking changes are of less concern. From that perspective, my article could easily look like the creation of an unhinged mind.
The purpose of tests #
In order to figure out what to test, and what not to test, you should ask yourself the question: what's the purpose of testing?
At first glance, that may seem like an inane question, but there's actually more than one purpose of a unit test. When doing TDD, the purpose of a test is to provide feedback about the API you're developing. A unit test is the first client of the production API. If a test is difficult to write, the production API is difficult to use. More on TDD later, though.
You may say that another purpose of automated tests is that they prevent errors. That's not the case, though. Automated tests prevent regressions.
If you wrote the correct test, your test suite may also help to prevent errors, but a unit test is only as good as the programmer who wrote it. You could have made a mistake when you wrote the test. Or perhaps you misunderstood the specification of what you were trying to implement. Why do you even trust tests?
The cost of regressions #
Why do you want to prevent regressions? Because they're costly?
Based on the little risk management I know about, you operate with two dimensions of risk: the impact of an event, should it occur, and the probability that the event occurs.
Should we all be worried that an asteroid will hit the Earth and wipe out most life? The impact of such an event is truly catastrophic, yet the probability is diminishingly small, so the risk is insignificant. The risk of going for a drive in a car is much higher.
How do you reduce risk? You either decrease the probability that the adverse event will happen, or you reduce the impact of it, should it happen.
Steve Freeman once wrote a nice article about the distinction between fail-safe software, and software that could safely fail. Unfortunately, that article seems to have disappeared from the internet. The point, however, was that with unit tests, we attempt to make our software fail-safe. The unit tests act as a gate that prevents bad versions of the software from being released. That's not a bad strategy for managing risk, but only half of the strategies available.
For example, Continuous Delivery describes how you can use Canary Releases and automated rollbacks to reduce the impact of errors. That's what Steve Freeman called safe fail.
I apologise for this detour around risk management, but I think that it's important that you make an explicit decision about automated testing. You can use unit tests to prevent regressions. What's the impact of an error in production, though?
This depends on the type of software you're developing. When considering alternatives, I often envision the various options as inhabiting a continuum:

For some types of software, an error 'in production' could be fatal. This would be the case for guidance software for Voyager 1, 2, other guidance software, software for medical devices, and so on. If you deploy a defect to Voyager 2, you've probably lost the craft for ever.
(I'd be surprised if the Voyager guidance software is actually covered by unit tests, but I'd expect that other quality assurance checks are in place. For comparison, the space shuttle software development process has been appraised at CMMI level 5.)
On the other side of the continuum, as a software developer, you probably write small ad-hoc development tools for your own use. For example, a few years ago I did a lot of REST API development, and many of the APIs I worked with required OAuth authentication. I wrote a little command-line program that I could use to log on to an internal system and exchange that to a token. I don't think that I wrote any tests for that program. If there were problems with it, I'd just open the source code and fix the problem. Errors were cheap in that situation.
Most software probably falls somewhere in the middle of those extremes. The cost of errors in wildlife software is probably higher than it is for zoo software, but most software can get by with less coverage than everything.
Cyclomatic complexity #
How do you know that your software works? You test it. If you want to automate your testing efforts, you write unit tests... but a unit test suite is software. How do you know that your tests work? Is it going to be turtles all the way down?
I think that we can trust tests for other reasons, but one of them is that each test case exercises a deterministic path through a unit that supports many paths of execution.
In other words, each unit test is an example of a singular execution path. Tests, then, should have a cyclomatic complexity of 1. In other words, you write (test) code with a cyclomatic complexity of 1 in order to test code with a higher cyclomatic complexity.
Should you test code that has a cyclomatic complexity of 1?
What would be the point of that? Why would you write a unit test with a cyclomatic complexity of 1 to test a piece of code with a cyclomatic complexity of 1? Wouldn't you just be adding more code?
From the perspective of trusting the code, there's no reason to trust such a test more than the code that it exercises. In that light, I think it makes sense to not write that test.
To be clear, there could be other reasons to test code with a cyclomatic complexity of 1. One reason, that I pointed out in my original article, is that you don't know if the simple piece of code will stay simple. Another reason is to prevent regressions. A common metaphor for unit testing is double-entry bookkeeping. If you write the unit test in a different way than the implementation, the two views on that behaviour may keep each other in check. You could do that with triangulation using parametrised tests, or perhaps with property-based testing.
I tend to use a heuristic where the farther to the left I am on the above continuum, the more I'm inclined to skip testing of simple functionality. Code with a cyclomatic complexity of 1 falls into that bucket.
TDD #
Let's return our attention to TDD. The previous paragraphs have mostly discussed automated tests as a way to prevent regressions. TDD gives us an entirely different motivation for writing tests: the tests provide feedback on the design of our production code.
Viewed like this, the tests themselves are only artefacts of the TDD process. It's usually a good idea to keep them around after the standard red-green-refactor cycle, because they serve double-duty as regression tests.
Should you test-drive everything? If you're inexperienced with TDD, you get the best exercise by test-driving as much as possible. This still doesn't have to mean that you must write a an explicit test case for each class member. That's what both Mark Rendle and Derick Bailey pointed out. It's often enough if the tests somehow exercise those members.
Revisiting my old article, my mistake was that I conflated TDD with regression testing. My motivation for writing an explicit test case for each member, no matter how trivial, was to preserve backwards compatibility. It really had nothing to do with TDD.
When in doubt #
Despite all other rules of thumb I've so far listed, I'll suggest a few exceptions.
Even if a piece of code theoretically has a cyclomatic complexity of 1, if you're in doubt of how it works, then write a test.
If you have a defect in production, then reproduce that defect with one or more tests, even if the code in question is 'trivial'. Obviously, it wasn't trivial after all, if it caused a bug in production.
Pragmatism #
When you're learning something new, you're typically struggling with even the most basic concepts. That's just how learning works. In that phase of learning, it often pays to follow explicit rules. A way to think about this is the Dreyfus model of skill acquisition. Once you gain some experience, you can start deviating from the rules. We could call this pragmatism.
I often discuss TDD with people who plead for pragmatism. Those people have typically practised TDD for years, if not decades. So have I, and, believe it or not, I'm often quite pragmatic when I practice TDD 'for real'. This is, however, a prerogative of experience.
You can only be pragmatic if you know how to be dogmatic.I use the concept of dogmatism as an antonym to pragmatism. I view pragmatism in programming as the choice of practical solutions over theoretical principles. It's a choice, which means that you must be aware of alternatives.
If you don't know the (principled) alternative, there's no choice.
When you're learning something new, you're still not aware of how to do things according to principle. That's natural. I find myself in that situation all the time. If you keep at it, though, eventually you'll have gained enough experience that you can make actual choices.
This applies to TDD as well. When you're still learning TDD, stick to the principles, particularly when it's inconvenient. Once you've done TDD for a few years, you've earned the right to be pragmatic.
Conclusion #
Which parts of your code base should you (unit) test? It Depends™.
It depends on why you are unit testing, and on the cost of defects in production, and probably many other things I didn't think of.
What's the purpose of tests? Are you using TDD to get feedback on your API design ideas? Or is the main purpose of tests to prevent regressions? Your answers to such questions should guide your decisions on how much to test.
Recently, I've mostly been writing about topics related to computer science, such as the relationships between various branches of mathematics to computation. In such realms, laws apply, and answers tend to be either right or wrong. A piece like this article is different.
This is fundamentally a deeply subjective essay. It's based on my experience with writing automated tests in various circumstances since 2003. I've tried to be as explicit about my context as possible, but I've most likely failed to identify one or more implicit assumptions or biases. I do, therefore, encourage comments.
I wrote this commentary because people keep asking me about how much to test, and when. I suppose it's because they wish to learn from me, and I'm happy to share what I know, to the best of my ability. I have much to learn myself, though, so read this only as the partial, flawed, personal answer that it is.
Applicative validation
Validate input in applicative style for superior readability and composability.
This article is an instalment in an article series about applicative functors. It demonstrates how applicative style can be used to compose small validation functions to a larger validation function in such a way that no validation messages are lost, and the composition remains readable.
All example code in this article is given in Haskell. No F# translation is offered, because Scott Wlaschin has an equivalent example covering input validation in F#.
JSON validation #
In my Pluralsight course about a functional architecture in F#, you can see an example of an on-line restaurant reservation system. I often return to that example scenario, so for regular readers of this blog, it should be known territory. For newcomers, imagine that you've been asked to develop an HTTP-based API that accepts JSON documents containing restaurant reservations. Such a JSON document could look like this:
{
"date": "2017-06-27 18:30:00+02:00",
"name": "Mark Seemann",
"email": "mark@example.com",
"quantity": 4
}
It contains the date and time of the (requested) reservation, the email address and name of the person making the reservation, as well as the number of people who will be dining. Particularly, notice that the date and time is represented as a string value (specifically, in ISO 8601 format), since JSON has no built-in date and time data type.
In Haskell, you can represent such a JSON document using a type like this:
data ReservationJson = ReservationJson { jsonDate :: String, jsonQuantity :: Double, jsonName :: String, jsonEmail :: String } deriving (Eq, Show, Read, Generic)
Haskell's strength is in its type system, so you should prefer to model a reservation using a strong type:
data Reservation = Reservation { reservationDate :: ZonedTime, reservationQuantity :: Int, reservationName :: String, reservationEmail :: String } deriving (Show, Read)
Instead of modelling the date and time as a string, you model it as a ZonedTime value. Additionally, you should model quantity as an integer, since a floating point value doesn't make much sense.
While you can always translate a Reservation value to a ReservationJson value, the converse doesn't hold. There are ReservationJson values that you can't translate to Reservation. Such ReservationJson values are invalid.
You should write code to validate and translate ReservationJson values to Reservation values, if possible.
Specialised validations #
The ReservationJson type is a complex type, because it's composed of multiple (four) elements of different types. You can easily define at least three validation rules that ought to hold:
- You should be able to convert the
jsonDatevalue to aZonedTimevalue. jsonQuantitymust be a positive integer.jsonEmailshould look believably like an email address.
In Haskell, people often use Either for validation, but instead of using Either directly, I'll introduce a specialised Validation type:
newtype Validation e r = Validation (Either e r) deriving (Eq, Show, Functor)
You'll notice that this is simply a redefinition of Either. Haskell can automatically derive its Functor instance with the DeriveFunctor language extension.
My motivation for introducing a new type is that the way that Either is Applicative is not quite how I'd like it to be. Introducing a newtype enables you to change how a type behaves. More on that later. First, you can implement the three individual validation functions.
Date validation #
If the JSON date value is an ISO 8601-formatted string, then you can parse it as a ZonedTime. In that case, you should return the Right case of Validation. If you can't parse the string into a ZonedTime value, you should return a Left value containing a helpful error message.
validateDate :: String -> Validation [String] ZonedTime validateDate candidate = case readMaybe candidate of Just d -> Validation $ Right d Nothing -> Validation $ Left ["Not a date."]
This function uses readMaybe from Text.Read to attempt to parse the candidate String. When readMaybe can read the String value, it returns a Just value with the parsed value inside; otherwise, it returns Nothing. The function pattern-matches on those two cases and returns the appropriate value in each case.
Notice that errors are represented as a list of String values, although this particular function only returns a single message in its list of error messages. The reason for that is that you should be able to collect multiple validation issues for a complex value such as ReservationJson, and keeping track of errors in a list makes that possible.
Haskell golfers may argue that this implementation is overly verbose, and it could, for instance, instead be written as:
validateDate = Validation . maybe (Left ["Not a date."]) Right . readMaybe
which is true, but not as readable. Both versions get the job done, though, as these GCHi-based ad-hoc tests demonstrate:
λ> validateDate "2017/27/06 18:30:00 UTC+2" Validation (Left ["Not a date."]) λ> validateDate "2017-06-27 18:30:00+02:00" Validation (Right 2017-06-27 18:30:00 +0200)
That takes care of parsing dates. On to the next validation function.
Quantity validation #
JSON numbers aren't guaranteed to be integers, so it's possible that even a well-formed Reservation JSON document could contain a quantity property of 9.7, -11.9463, or similar. When handling restaurant reservations, however, it only makes sense to handle positive integers. Even 0 is useless in this context. Thus, validation must check for two conditions, so in principle, you could write two separate functions for that. In order to keep the example simple, though, I've included both tests in the same function:
validateQuantity :: Double -> Validation [String] Int validateQuantity candidate = if isInt candidate && candidate > 0 then Validation $ Right $ round candidate else Validation $ Left ["Not a positive integer."] where isInt x = x == fromInteger (round x)
If candidate is both an integer, and greater than zero, then validateQuantity returns Right; otherwise, it returns a Left value containing an error message. Like validateDate, you can easily test validateQuantity in GHCi:
λ> validateQuantity 4 Validation (Right 4) λ> validateQuantity (-1) Validation (Left ["Not a positive integer."]) λ> validateQuantity 2.32 Validation (Left ["Not a positive integer."])
Perhaps you can think of rules for names, but I can't, so we'll leave the name be and move on to validating email addresses.
Email validation #
It's notoriously difficult to validate SMTP addresses, so you shouldn't even try. It seems fairly safe to assume, however, that an email address must contain at least one @ character, so that's going to be all the validation you have to implement:
validateEmail :: String -> Validation [String] String validateEmail candidate = if '@' `elem` candidate then Validation $ Right candidate else Validation $ Left ["Not an email address."]
Straightforward. Try it out in GHCI:
λ> validateEmail "foo" Validation (Left ["Not an email address."]) λ> validateEmail "foo@example.org" Validation (Right "foo@example.org")
Indeed, that works.
Applicative composition #
What you really should be doing is to validate a ReservationJson value. You have the three validation rules implemented, so now you have to compose them. There is, however, a catch: you must evaluate all rules, and return a list of all the errors you encountered. That's probably going to be a better user experience for a user.
That's the reason you can't use Either. While it's Applicative, it doesn't behave like you'd like it to behave in this scenario. Particularly, the problem is that it throws away all but the first Left value it finds:
λ> Right (,,) <*> Right 42 <*> Left "foo" <*> Left "bar" Left "foo"
Notice how Left "bar" is ignored.
With the new type Validation based on Either, you can now define how it behaves as an applicative functor:
instance Monoid m => Applicative (Validation m) where pure = Validation . pure Validation (Left x) <*> Validation (Left y) = Validation (Left (mappend x y)) Validation f <*> Validation r = Validation (f <*> r)
This instance is restricted to Monoid Left types. It has special behaviour for the case where both expressions passed to <*> are Left values. In that case, it uses mappend (from Monoid) to 'add' the two Left values together in a new Left value.
For all other cases, this instance of Applicative delegates to the behaviour defined for Either. It also uses pure from Either to implement its own pure function.
Lists ([]) form a monoid, and since all the above validation functions return lists of errors, it means that you can compose them using this definition of Applicative:
validateReservation :: ReservationJson -> Validation [String] Reservation validateReservation candidate = pure Reservation <*> vDate <*> vQuantity <*> vName <*> vEmail where vDate = validateDate $ jsonDate candidate vQuantity = validateQuantity $ jsonQuantity candidate vName = pure $ jsonName candidate vEmail = validateEmail $ jsonEmail candidate
The candidate is a ReservationJson value, but each of the validation functions work on either String or Double, so you'll have to use the ReservationJson type's access functions (jsonDate, jsonQuantity, and so on) to pull the relevant values out of it. Once you have those, you can pass them as arguments to the appropriate validation function.
Since there's no rule for jsonName, you can use pure to create a Validation value. All four resulting values (vDate, vQuantity, vName, and vEmail) are Validation [String] values; only their Right types differ.
The Reservation record constructor is a function of the type ZonedTime -> Int -> String -> String -> Reservation, so when you arrange the four v* values correctly between the <*> operator, you have the desired composition.
Try it in GHCi:
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" 4 "Jane Doe" "j@example.com"
Validation (Right (Reservation {
reservationDate = 2017-06-30 19:00:00 +0200,
reservationQuantity = 4,
reservationName = "Jane Doe",
reservationEmail = "j@example.com"}))
λ> validateReservation $ ReservationJson "2017/14/12 6pm" 4.1 "Jane Doe" "jane.example.com"
Validation (Left ["Not a date.","Not a positive integer.","Not an email address."])
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" (-3) "Jane Doe" "j@example.com"
Validation (Left ["Not a positive integer."])
The first ReservationJson value passed to validateReservation is valid, so the return value is a Right value.
The next ReservationJson value is about as wrong as it can be, so three different error messages are returned in a Left value. This demonstrates that Validation doesn't give up the first time it encounters a Left value, but rather collects them all.
The third example demonstrates that even a single invalid value (in this case a negative quantity) is enough to make the entire input invalid, but as expected, there's only a single error message.
Summary #
Validation may be the poster child of applicative functors, but it is a convenient way to solve the problem. In this article you saw how to validate a complex data type, collecting and reporting on all problems, if any.
In order to collect all errors, instead of immediately short-circuiting on the first error, you have to deviate from the standard Either implementation of <*>. If you go back to read Scott Wlaschin's article, you should be aware that it specifically implements its applicative functor in that way, instead of the normal behaviour of Either.
More applicative functors exist. This article series has, I think, room for more examples.
The Maybe applicative functor
An introduction to the Maybe applicative functor for object-oriented programmers.
This article is an instalment in an article series about applicative functors. Previously, in a related series, you got an introduction to Maybe as a functor. Not all functors are applicative, but some are, and Maybe is one of them (like list).
In this article, you'll see how to make a C# Maybe class applicative. While I'm going to start with F# and Haskell, you can skip to the C# section if you'd like.
F# #
A few years ago, I did the Roman numerals kata in F#. This is an exercise where you have to convert between normal base 10 integers and Roman numerals. Conversions can fail in both directions, because Roman numerals don't support negative numbers, zero, or numbers greater than 3,999, and Roman numerals represented as strings could be malformed.
Some Roman numbers are written in a subtractive style, e.g. "IV" means subtract 1 (I) from 5 (V). It's easy enough to subtract two numbers, but because parsing isn't guaranteed to succeed, I didn't have two numbers; I had two number options (recall that in F#, Maybe is called option).
How do you subtract one int option from another int option?
Both of these values could be Some, or they could be None. What should happen in each case? With Maybe, only four combinations are possible, so you can put them in a table:
Some x |
None |
|
|---|---|---|
Some y |
Some (x - y) |
None |
None |
None |
None |
Some cases should you return a Some case with the result of the subtraction; in all other cases, you should return None.
You can do this with regular pattern matching, but it's hardly the most elegant solution:
// int option let difference = match minuend, subtrahend with | Some m, Some s -> Some (m - s) | _ -> None
You could attempt to solve this with a specialised helper function like this:
module Option = // ('a -> 'b -> 'c) -> 'a option -> 'b option -> 'c option let map2 f xo yo = match xo, yo with | Some x, Some y -> Some (f x y) | _ -> None
which you could use like this:
let difference = Option.map2 (-) minuend subtrahend
It doesn't, however, generalise well... What if you need to operate on three option values, instead of two? Or four? Should you add map3 and map4 functions as well?
Making option an applicative functor addresses that problem. Here's one possible implementation of <*>:
// ('a -> 'b) option -> 'a option -> 'b option let (<*>) fo xo = match fo, xo with | Some f, Some x -> Some (f x) | _ -> None
This enables you two write the subtraction like this:
let difference = Some (-) <*> minuend <*> subtrahend
For a detailed explanation on how that works, see the previous explanation for lists; it works the same way for Maybe as it does for List.
In the end, however, I didn't think that this was the most readable code, so in the Roman numeral exercise, I chose to use a computation expression instead.
Haskell #
In Haskell, Maybe is already Applicative as part of the language. Without further ado, you can simply write:
difference = pure (-) <*> minuend <*> subtrahend
As is the case with the F# code, I don't consider this the most readable way to express the subtraction of two integers. In F#, I ultimately decided to use a computation expression. In Haskell, that's equivalent to using do notation:
difference :: Maybe Integer difference = do m <- minuend s <- subtrahend return $ m - s
While more verbose, I think it's clearer that one number is being subtracted from another number.
This works for Maybe because not only is Maybe Applicative, it's also a Monad. It's its monadness that enables the do notation. Not all applicative functors are monads, but Maybe is.
C# #
In a previous article you saw how to implement the Maybe functor in C#. You can extend it so that it also becomes an applicative functor:
public static Maybe<TResult> Apply<T, TResult>( this Maybe<Func<T, TResult>> selector, Maybe<T> source) { if (selector.HasItem && source.HasItem) return new Maybe<TResult>(selector.Item(source.Item)); else return new Maybe<TResult>(); } public static Maybe<Func<T2, TResult>> Apply<T1, T2, TResult>( this Maybe<Func<T1, T2, TResult>> selector, Maybe<T1> source) { if (selector.HasItem && source.HasItem) { Func<T2, TResult> g = x => selector.Item(source.Item, x); return new Maybe<Func<T2, TResult>>(g); } else return new Maybe<Func<T2, TResult>>(); }
As was the case for making sequences applicative in C#, you need overloads of the Apply method, because C#'s type inference is inadequate for this task.
If you have two Maybe<int> values, minuend and subtrahend, you can now perform the subtraction:
Func<int, int, int> subtract = (x, y) => x - y; Maybe<int> difference = subtract.ToMaybe().Apply(minuend).Apply(subtrahend);
Like in F# and Haskell, applicative style is hardly the most readable way to express subtraction. It'd be nice if you could write it like Haskell's do notation. You can, but to do that, you must make Maybe a monad, and this isn't a monad tutorial. Mike Hadlow has a good monad tutorial for C# developers, the gist of which is that you must implement SelectMany in order to turn your generic type into a monad. For now, I'll leave this as an exercise for you, but if you add an appropriate SelectMany method, you'd be able to write the subtraction like this:
Maybe<int> difference = from m in minuend from s in subtrahend select m - s;
Again, I think this is more readable, but it does require that the type in question is a monad, and not all applicative functors are (but Maybe is).
Summary #
This article demonstrates that lists or sequences aren't the only applicative functors. Maybe is also an applicative functor, but more exist. The next article will give you another example.
Next: Applicative validation.
Comments
As was the case for making sequences applicative in C#, you need overloads of the Apply method, because C#'s type inference is inadequate for this task.
I think we agreed that the issue is not C#'s weak type inference but its lack of default function currying? My guess is that you wrote this quoted part of this article before my comment on your previous article.
Tyson, thank you for writing.
"My guess is that you wrote this quoted part of this article before my comment on your previous article."Yes, June 27, 2017, in fact...
You're correct that this particular issue is related to the uncurried nature of C# methods.
I do, however, maintain that C#'s type inference capabilities are weaker than F#'s or Haskell's. To be clear, I view this as the result of priorities. I don't think that the people who designed and wrote the C# compiler are less skilled than the designers of F# or Haskell. The C# compiler has to solve many other problems, such as for example overload resolution, which is a language feature in direct opposition to currying. The C# compiler is excellent at overload resolution, a task with which the F# compiler sometimes struggle (and is not even a language feature in Haskell).
Your comment is, however, a reminder that I should consider how I phrase such notions in the future. Thank you for pointing that out. As I'm publishing and get feedback, I constantly learn new things. I'm always grateful when someone like you take the time to educate me.
I'll see if I can improve in the future. I do, however, still have a backlog of articles I wrote months, or even more than a year, ago, so it's possible that more errors escape my attention when I proof read them before publication. If that happens, I'll appreciate more corrections.
Thank you very much for your kind reply. I agree with everything you said.
I will expand my comment a bit to give a clearer picture of my understanding.
First, very little is "needed"; most things are merely sufficient. In particular, we don't need to overload your Apply method to achieve your goal. As I mentioned before, it sufficies to have a single Apply method and instead create overloads of a function called curry that explicitly curries a given function. Furthermore, I think there is a sense in which this latter approach to overcome the lack of default currying is somehow minimal or most abstract or most general.
Second, compared to languages like F# or Haskell, type inference is definitely weaker in C#. This issue was also present (in a subtle way) in your previous article, but I decided to largely ignore it in order to keep my comment more focused. In your previous article, you expliciltly defined the local variable concat like this
In particular, you explicitly told the C# compiler that the type of all of these six variable isFunc<string, string, string, string, string, string, string> concat = (x, y, z, æ, ø, å) => x + y + z + æ + ø + å;
string. That part was necessary; the type inference in C# is not strong enough to innfer (possibily in some use of concat) that the types could be string.
Suppose instead of defining concat as a local variable (with Func<string, string, string, string, string, string, string> as its type) you had defined it as a member method on a class. Then its type in C# is some kind "method group". The method group of a method essentially corresponds to the set of methods containing itself and its overloads. Then in order to pass concat into curry, there needs to be a type conversion (or cast) from its method group to Func<string, string, string, string, string, string, string>. This is also something that the C# system cannot do, and so Language Ext has overloads of a function called fun to do this explicitly. Using it on our hypothetical member function concat would look like
fun<string, string, string, string, string, string, string>(concat)Again, I think there is a sense in which this explicit way to specify non-inferable types is somehow minimal or most abstract or most general.
My impression is that there is some low hanging fruit here for strengthing the type inference of the C# compiler. If a method group correpsonds to a singleton set (and that method has no ref or out arguments), then I would think it would be straight forward to consider an implicit cast from the method group to the corresponding Func or Action delegate.
Applicative combinations of functions
Applicative lists and sequences enable you to create combinations of functions as well as values.
This article is an instalment in an article series about applicative functors. In the previous article, you saw how you can use applicative lists and sequences to generate combinations of values; specifically, the example demonstrated how to generate various password character combinations.
People often create passwords by using a common word as basis, and then turn characters into upper- or lower case. Someone feeling particularly tech-savvy may replace certain characters with digits, in an imitation of 1337. While this isn't secure, let's look at how to create various combinations of transformations using applicative lists and sequences.
List of functions #
In the previous article, I mentioned that there was a feature of applicative lists that I had, so far, deliberately ignored.
If you consider an example like this:
let passwordCombinations = [sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"] <*> ["a"; "4"] <*> ["ssw"] <*> ["o"; "0"] <*> ["rd"] <*> [""; "!"]
you may have already noticed that while the left side of the <*> operator is a list of functions, it contains only a single function. What happens if you supply more than a single function?
You get a combination of each function and each list element.
Assume that you have three functions to convert characters:
module Char = // char -> char let toUpper c = System.Char.ToUpperInvariant c // char -> char let toLower c = System.Char.ToLowerInvariant c // Not even trying to be complete: // char -> char let to1337 = function | 'a' | 'A' -> '4' | 'b' -> '6' | 'E' -> '3' | 'H' -> '#' | 'i' -> '!' | 'l' -> '1' | 'o' | 'O' -> '0' | 't' -> '+' | c -> c
All three are functions that convert one char value to another, although many values could pass through without being modified. Since they all have the same type, you can create a list of them:
> List.map String.map [Char.toUpper; Char.toLower; Char.to1337] <*> ["Hello"; "World"];; val it : string list = ["HELLO"; "WORLD"; "hello"; "world"; "#e110"; "W0r1d"]
There's a bit to unpack there. Recall that all three functions in the Char module have the same type: char -> char. Making a list of them gives you a (char -> char) list, but you really need a (string -> string) list. Fortunately, the built-in String.map function takes a char -> char function and uses it to map each char values in a string. Thus, List.map String.map [Char.toUpper; Char.toLower; Char.to1337] gives you a (string -> string) list.
When you apply (<*>) that list of functions with a list of string values, you get all possible combinations of each function used with each string. Both "Hello" and "World" are converted to upper case, lower case, and 1337.
Combinations of functions #
Perhaps you're happy with the above combinations, but can we do better? As an example, you'll notice that to1337 only converts an upper-case 'E' to '3', but ignores a lower-case 'e'. What if you also want the combination where 'e' is first converted to upper case, and then to 1337? You'd like that, but you still want to retain the combinations where each of these transformations are applied without the other.
Fear not; functions are values, so you can combine them as well!
In the previous article, did you notice how you could model the presence or absence of a particular value? Specifically, the last character in the potential password could be '!', but '!' could also be omitted.
Consider, again, the expression for all password combinations:
let passwordCombinations = [sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"] <*> ["a"; "4"] <*> ["ssw"] <*> ["o"; "0"] <*> ["rd"] <*> [""; "!"]
Notice that the last list contains two options: "!" and the empty string (""). You can read about this in another article series, but character strings are monoids, and one of the characteristics of monoids is that they have an identity element - a 'neutral' element, if you will. For strings, it's ""; you can append or prepend the empty string as much as you'd like, but it's not going to change the other string.
If you have a set of functions of the type 'a -> 'a, then the built-in function id is the identity element. You can compose any 'a -> 'a function with id, and it's not going to change the other function.
Since functions are values, then, you can create combinations of functions:
// (char -> char) list let maps = [fun f g h -> f >> g >> h] <*> [Char.toUpper; id] <*> [Char.toLower; id] <*> [Char.to1337; id]
Here, maps is a list of functions, but it's not only three functions as in the above example. It's eight functions:
> List.length maps;; val it : int = 8
The above applicative composition of maps combines three lists of functions. Each list presents two alternatives: a function (e.g. Char.toUpper), and id. In other words, a choice between doing something, and doing nothing. The lambda expression fun f g h -> f >> g >> h takes three (curried) arguments, and returns the composition of calling f, then passing the result of that to g, and again passing the result of that to h. f is either Char.toUpper or id, g is either Char.toLower or id, and h is either Char.to1337 or id. That's eight possible combinations.
Combine eight functions with two string values, and you get sixteen alternatives back:
> List.map String.map maps <*> ["Hello"; "World"];; val it : string list = ["he110"; "w0r1d"; "hello"; "world"; "#3LL0"; "W0RLD"; "HELLO"; "WORLD"; "he110"; "w0r1d"; "hello"; "world"; "#e110"; "W0r1d"; "Hello"; "World"]
Notice, for example, how one of the suggested alternatives is "#3LL0". Previously, there was no translation from 'e' to '3', but now there is, via Char.toUpper >> id >> Char.to1337.
Some of the combinations are redundant. For example, "hello" is generated twice, by Char.toUpper >> Char.toLower >> id and id >> Char.toLower >> id, respectively. You can reduce the output with List.distinct:
> List.map String.map maps <*> ["Hello"; "World"] |> List.distinct;; val it : string list = ["he110"; "w0r1d"; "hello"; "world"; "#3LL0"; "W0RLD"; "HELLO"; "WORLD"; "#e110"; "W0r1d"; "Hello"; "World"]
You can write equivalent code in Haskell, but it's so similar to the F# code that there's no reason to show it.
Translation to C# #
Using the Apply extension methods from the previous article, you can translate the above code to C#.
While you can use the .NET Base Class Library's Char.ToUpperInvariant and Char.ToLowerInvariant methods as is, you'll need to supply a to1337 function. You can write it as a named static method, but you can also write it as a delegate:
Func<char, char> to1337 = c => { switch (c) { case 'A': case 'a': return '4'; case 'b': return '6'; case 'E': return '3'; case 'H': return '#'; case 'i': return '!'; case 'l': return '1'; case 'o': case 'O': return '0'; case 't': return '+'; default: return c; } };
You're also going to need an id function:
Func<char, char> id = c => c;
In order to compose three functions to one, you can write something like this:
Func<Func<char, char>, Func<char, char>, Func<char, char>, Func<char, char>> compose3 = (f, g, h) => x => h(g(f(x)));
That's going to be a contender for some of the most obscure C# code I've written in a while. By the double use of =>, you can tell that it's a delegate that returns a delegate. That's not even the worst part: check out the type of the thing! In reality, nothing happens here that doesn't also happen in the above F# code, but it's an example of the superiority of Hindley–Milner type inference: in F#, you don't have to explicitly type out the type.
With a function to compose three other functions, you can now apply the three alternative functions:
IEnumerable<Func<char, char>> maps = new[] { compose3 } .Apply(new[] { Char.ToUpperInvariant, id }) .Apply(new[] { Char.ToLowerInvariant, id }) .Apply(new[] { to1337, id });
Now you have a sequence of functions that translate char values to char values. What you really need, though, is a sequence of functions that translate string values to string values.
The F# core library defines the built-in String.map function, but as far as I can tell, there's no equivalent method in the .NET Base Class Library. Therefore, you must implement it yourself:
Func<Func<char, char>, Func<string, string>> stringMap = f => (string s) => new string(s.Select(f).ToArray());
This is a function that takes a Func<char, char> as input and returns a Func<string, string>. Again, the type declaration isn't the prettiest.
You can now apply maps to some string values, using the Apply extension method:
IEnumerable<string> hellos = maps.Select(stringMap).Apply(new[] { "Hello", "World" });
This produces exactly the same output as the above F# example, even in the same order.
Applicative functors are elegant in F# and Haskell, but awkward in a language like C# - mostly because of its inferior type inference engine.
Summary #
Previous articles demonstrated how applicative lists can be used to compose several lists into a list that contains all possible combinations. In this article you saw how this also extends to combinations of functions.
The last three articles (including the present) focus on lists as applicative functors, but lists aren't the only type of applicative functor. In the next articles, you'll encounter some other applicative functors.

Comments
Great post, a very good read! Interestingly enough we recently made an F# implementation for the swedish personal identification number. In fact v1.0.0 will be published any day now. Interesting to see how the problem with four-digit years are handled differently in Denmark and Sweden.
I really like the Between Active pattern of your solution, we did not really take as a generic approach, instead we modeled with types for Year, Month, Day, etc. But I find your solution to be very concise and clear. Also we worked with the Result type instead of Option to be able to provide the client with helpful error messages. For our Object Oriented friends we are also exposing a C#-friendly facade which adds a bit of boiler plate code.
Viktor, thank you for your kind words. The
Result(or Either) type does, indeed, provide more information when things go wrong. This can be useful when client code needs to handle different error cases in different ways. Sometimes, it may also be useful, as you write, when you want to provide more helpful error messages.Particularly when it comes to parsing or input validation, Either can be useful.
The main reason I chose to model with
optionin this article was that I wanted to demonstrate how to use the applicative nature ofoption, but I suppose I could have equally done so withResult.