ploeh blog danish software design
Either catamorphism
The catamorphism for Either is a generalisation of its fold. The catamorphism enables operations not available via fold.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for Either (also known as Result), as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
Either is a data container that models two mutually exclusive results. It's often used to return values that may be either correct (right), or incorrect (left). In statically typed functional programming with a preference for total functions, Either offers a saner, more reasonable way to model success and error results than throwing exceptions.
C# catamorphism #
This article uses the Church encoding of Either. The catamorphism for Either is the Match method:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Until this article, all previous catamorphisms have been a pair made from an initial value and a function. The Either catamorphism is a generalisation, since it's a pair of functions. One function handles the case where there's a left value, and the other function handles the case where there's a right value. Both functions must return the same, unifying type, which is often a string or something similar that can be shown in a user interface:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3)); > e.Match(ts => ts.ToString(), i => i.ToString()) "00:03:00" > IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42); > e.Match(ts => ts.ToString(), i => i.ToString()) "42"
You'll often see examples like the above that turns both left and right cases into strings or something that can be represented as a unifying response type, but this is in no way required. If you can come up with a unifying type, you can convert both cases to that type:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid()); > e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length) 12 > IEither<Guid, string> e = new Right<Guid, string>("foo"); > e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length) 3
In the two above examples, you use two different functions that both reduce respectively Guid and string values to a number. The function that turns Guid values into a number counts how many of the hexadecimal digits that are greater than or equal to A (10). The other function simply returns the length of the string, if it's there. That example makes little sense, but the Match method doesn't care about that.
In practical use, Either is often used for error handling. The article on the Church encoding of Either contains an example.
Either F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
While F-Algebras and fixed points are mostly used for recursive data structures, you can also define an F-Algebra for a non-recursive data structure. You already saw an example of that in the articles about Boolean catamorphism and Maybe catamorphism. The difference between e.g. Maybe values and Either is that both cases of Either carry a value. You can model this as a Functor with both a carrier type and two type arguments for the data that Either may contain:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
I chose to call the 'data types' l (for left) and r (for right), and the carrier type c (for carrier). As was also the case with BoolF and MaybeF, the Functor instance ignores the map function because the carrier type is missing from both the LeftF case and the RightF case. Like the Functor instances for BoolF and MaybeF, it'd seem that nothing happens, but at the type level, this is still a translation from EitherF l r c to EitherF l r c1. Not much of a function, perhaps, but definitely an endofunctor.
As was also the case when deducing the Maybe and List catamorphisms, Haskell isn't too happy about defining instances for a type like Fix (EitherF l r). To address that problem, you can introduce a newtype wrapper:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
You can define Functor, Applicative, Monad, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A pair of helper functions make it easier to define EitherFix values:
leftF :: l -> EitherFix l r leftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l r rightF = EitherFix . Fix . RightF
With those functions, you can create EitherFix values:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandom
EitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}
Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"
EitherFix {unEitherFix = Fix (RightF "foo")}
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (EitherF l r), and an object c, but you still need to find a morphism EitherF l r c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data types' l and r. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore l and r, as you'll see.
As in the previous articles, start by writing a function that will become the catamorphism, based on cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the LeftF case? You could pass an argument to the eitherF function:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
While you could, technically, pass an argument of the type c to eitherF and then return that value from the LeftF case, that would mean that you would ignore the l value. This would be incorrect, so instead, make the argument a function and call it with l. Likewise, you can deal with the RightF case in the same way:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> c eitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of EitherF, the compiler infers that the alg function has the type EitherF l r c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
This, then, is the catamorphism for Either. As has been consistent so far, it's a pair, but now made from two functions. As you've seen repeatedly, this isn't the only possible catamorphism, since you can, for example, trivially flip the arguments to eitherF.
I've chosen the representation shown here because it's isomorphic to the either function from Haskell's built-in Data.Either module, which calls the function the "Case analysis for the Either type". Both of these functions (eitherF and either) are equivalent to the above C# Match method.
Basis #
You can implement most other useful functionality with eitherF. Here's the Bifunctor instance:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
From that instance, the Functor instance trivially follows:
instance Functor (EitherFix l) where fmap = second
On top of Functor you can add Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Notice that the <*> implementation is similar to to the <*> implementation for MaybeFix. The same is the case for the Monad instance:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Not only is EitherFix Foldable, it's Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Notice, interestingly, that bifoldMap is identical to eitherF.
The Bifoldable instance enables you to trivially implement the Foldable instance:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
You may find the presence of mempty puzzling, since bifoldMap (or eitherF; they're identical) takes as arguments two functions. Is mempty a function?
Yes, mempty can be a function. Here, it is. There's a Monoid instance for any function a -> m, where m is a Monoid instance, and mempty is the identity for that monoid. That's the instance in use here.
Just as EitherFix is Bifoldable, it's also Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
You can comfortably implement the Traversable instance based on the Bitraversable instance:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Finally, you can implement conversions to and from the standard Either type, using ana as the dual of cata:
toEither :: EitherFix l r -> Either l r toEither = eitherF Left Right fromEither :: Either a b -> EitherFix a b fromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
This demonstrates that EitherFix is isomorphic to Either, which again establishes that eitherF and either are equivalent.
Relationships #
In this series, you've seen various examples of catamorphisms of structures that have no folds, catamorphisms that coincide with folds, and now a catamorphism that is more general than the fold. The introduction to the series included this diagram:
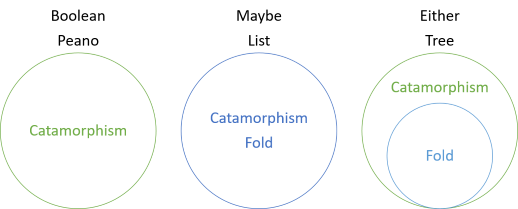
This shows that Boolean values and Peano numbers have catamorphisms, but no folds, whereas for Maybe and List, the fold and the catamorphism is the same. For Either, however, the fold is a special case of the catamorphism. The fold for Either 'pretends' that the left side doesn't exist. Instead, the left value is interpreted as a missing right value. Thus, in order to fold Either values, you must supply a 'fallback' value that will be used in case an Either value isn't a right value:
Prelude Fix Either> e = rightF LT :: EitherFix Integer Ordering Prelude Fix Either> foldr (const . show) "" e "LT" Prelude Fix Either> e = leftF 42 :: EitherFix Integer Ordering Prelude Fix Either> foldr (const . show) "" e ""
In a GHCi session like the above, you can create two Either values of the same type. The right case is an Ordering value, while the left case is an Integer value.
With foldr, there's no way to access the left case. While you can access and transform the right Ordering value, the number 42 is simply ignored during the fold. Instead, the default value "" is returned.
Contrast this with the catamorphism, which can access both cases:
Prelude Fix Either> e = rightF LT :: EitherFix Integer Ordering Prelude Fix Either> eitherF show show e "LT" Prelude Fix Either> e = leftF 42 :: EitherFix Integer Ordering Prelude Fix Either> eitherF show show e "42"
In a session like this, you recreate the same values, but using the catamorphism eitherF, you can now access and transform both the left and the right cases. In other words, the catamorphism enables you to perform operations not possible with the fold.
It's interesting, however, to note that while the fold is a specialisation of the catamorphism, the bifold is identical to the catamorphism.
Summary #
The catamorphism for Either is a pair of functions. One function transforms the left case, while the other function transforms the right case. For any Either value, only one of those functions will be used.
When I originally encountered the concept of a catamorphism, I found it difficult to distinguish between catamorphism and fold. My problem was, I think, that the tutorials I ran into mostly used linked lists to demonstrate how, in that case, the fold is the catamorphism. It turns out, however, that this isn't always the case. A catamorphism is a general abstraction. A fold, on the other hand, seems to me to be mostly related to collections.
In this article you saw the first example of a catamorphism that can do more than the fold. For Either, the fold is just a special case of the catamorphism. You also saw, however, how the catamorphism was identical to the bifold. Thus, it's still not entirely clear how these concepts relate. Therefore, in the next article, you'll get an example of a container where there's no bifold, and where the catamorphism is, indeed, a generalisation of the fold.
Next: Tree catamorphism.
List catamorphism
The catamorphism for a list is the same as its fold.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for (linked) lists, and other collections in general. It also shows how to identify it. The beginning of this article presents the catamorphism in C#, with an example. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
The C# part of the article will discuss IEnumerable<T>, while the Haskell part will deal specifically with linked lists. Since C# is a less strict language anyway, we have to make some concessions when we consider how concepts translate. In my experience, the functionality of IEnumerable<T> closely mirrors that of Haskell lists.
C# catamorphism #
The .NET base class library defines this Aggregate overload:
public static TAccumulate Aggregate<TSource, TAccumulate>( this IEnumerable<TSource> source, TAccumulate seed, Func<TAccumulate, TSource, TAccumulate> func);
This is the catamorphism for linked lists (and, I'll conjecture, for IEnumerable<T> in general). The introductory article already used it to show several motivating examples, of which I'll only repeat the last:
> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 } . .Aggregate(Angle.Identity, (a, i) => a.Add(Angle.FromDegrees(i))) [{ Angle = 207° }]
In short, the catamorphism is, similar to the previous catamorphisms covered in this article series, a pair made from an initial value and a function. This has been true for both the Peano catamorphism and the Maybe catamorphism. An initial value is just a value in all three cases, but you may notice that the function in question becomes increasingly elaborate. For IEnumerable<T>, it's a function that takes two values. One of the values are of the type of the input list, i.e. for IEnumerable<TSource> it would be TSource. By elimination you can deduce that this value must come from the input list. The other value is of the type TAccumulate, which implies that it could be the seed, or the result from a previous call to func.
List F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras. The ListF type comes from his article as well, although I've renamed the type arguments:
data ListF a c = NilF | ConsF a c deriving (Show, Eq, Read) instance Functor (ListF a) where fmap _ NilF = NilF fmap f (ConsF a c) = ConsF a $ f c
Like I did with MaybeF, I've named the 'data' type argument a, and the carrier type c (for carrier). Once again, notice that the Functor instance maps over the carrier type c; not over the 'data' type a.
As was also the case when deducing the Maybe catamorphism, Haskell isn't too happy about defining instances for a type like Fix (ListF a). To address that problem, you can introduce a newtype wrapper:
newtype ListFix a = ListFix { unListFix :: Fix (ListF a) } deriving (Show, Eq, Read)
You can define Functor, Applicative, Monad, etc. instances for this type without resorting to any funky GHC extensions. Keep in mind that ultimately, the purpose of all this code is just to figure out what the catamorphism looks like. This code isn't intended for actual use.
A few helper functions make it easier to define ListFix values:
nilF :: ListFix a nilF = ListFix $ Fix NilF consF :: a -> ListFix a -> ListFix a consF x = ListFix . Fix . ConsF x . unListFix
With those functions, you can create ListFix linked lists:
Prelude Fix List> nilF
ListFix {unListFix = Fix NilF}
Prelude Fix List> consF 42 $ consF 1337 $ consF 2112 nilF
ListFix {unListFix = Fix (ConsF 42 (Fix (ConsF 1337 (Fix (ConsF 2112 (Fix NilF))))))}
The first example creates an empty list, whereas the second creates a list of three integers, corresponding to [42,1337,2112].
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (ListF), and an object a, but you still need to find a morphism ListF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.
As in the previous article, start by writing a function that will become the catamorphism, based on cata:
listF = cata alg . unListFix where alg NilF = undefined alg (ConsF h t) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the NilF case? You could pass an argument to the listF function:
listF n = cata alg . unListFix where alg NilF = n alg (ConsF h t) = undefined
The ConsF case, contrary to NilF, contains both a head h (of type a) and a tail t (of type c). While you could make the code compile by simply returning t, it'd be incorrect to ignore h. In order to deal with both, you'll need a function that turns both h and t into a value of the type c. You can do this by passing a function to listF and using it:
listF :: (a -> c -> c) -> c -> ListFix a -> c listF f n = cata alg . unListFix where alg NilF = n alg (ConsF h t) = f h t
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of ListF, the compiler infers that the alg function has the type ListF a c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
This, then, is the catamorphism for lists. As has been consistent so far, it's a pair made from an initial value and a function. Once more, this isn't the only possible catamorphism, since you can, for example, trivially flip the arguments to listF:
listF :: c -> (a -> c -> c) -> ListFix a -> c listF n f = cata alg . unListFix where alg NilF = n alg (ConsF h t) = f h t
You can also flip the arguments of f:
listF :: c -> (c -> a -> c) -> ListFix a -> c listF n f = cata alg . unListFix where alg NilF = n alg (ConsF h t) = f t h
These representations are all isomorphic to each other, but notice that the last variation is similar to the above C# Aggregate overload. The initial n value is the seed, and the function f has the same shape as func. Thus, I consider it reasonable to conjecture that that Aggregate overload is the catamorphism for IEnumerable<T>.
Basis #
You can implement most other useful functionality with listF. The rest of this article uses the first of the variations shown above, with the type (a -> c -> c) -> c -> ListFix a -> c. Here's the Semigroup instance:
instance Semigroup (ListFix a) where xs <> ys = listF consF ys xs
The initial value passed to listF is ys, and the function to apply is simply the consF function, thus 'consing' the two lists together. Here's an example of the operation in action:
Prelude Fix List> consF 42 $ consF 1337 nilF <> (consF 2112 $ consF 1 nilF)
ListFix {unListFix = Fix (ConsF 42 (Fix (ConsF 1337 (Fix (ConsF 2112 (Fix (ConsF 1 (Fix NilF))))))))}
With a Semigroup instance, it's trivial to also implement the Monoid instance:
instance Monoid (ListFix a) where mempty = nilF
While you could implement mempty with listF (mempty = listF (const id) nilF nilF), that'd be overcomplicated. Just because you can implement all functionality using listF, it doesn't mean that you should, if a simpler alternative exists.
You can, on the other hand, use listF for the Functor instance:
instance Functor ListFix where fmap f = listF (\h l -> consF (f h) l) nilF
You could write the function you pass to listF in a point-free fashion as consF . f, but I thought it'd be easier to follow what happens when written as an explicit lambda expression. The function receives a 'current value' h, as well as the part of the list which has already been translated l. Use f to translate h, and consF the result unto l.
You can add Applicative and Monad instances in a similar fashion:
instance Applicative ListFix where pure x = consF x nilF fs <*> xs = listF (\f acc -> (f <$> xs) <> acc) nilF fs instance Monad ListFix where xs >>= f = listF (\x acc -> f x <> acc) nilF xs
What may be more interesting, however, is the Foldable instance:
instance Foldable ListFix where foldr = listF
The demonstrates that listF and foldr is the same.
Next, you can also add a Traversable instance:
instance Traversable ListFix where sequenceA = listF (\x acc -> consF <$> x <*> acc) (pure nilF)
Finally, you can implement conversions to and from the standard list [] type, using ana as the dual of cata:
toList :: ListFix a -> [a] toList = listF (:) [] fromList :: [a] -> ListFix a fromList = ListFix . ana coalg where coalg [] = NilF coalg (h:t) = ConsF h t
This demonstrates that ListFix is isomorphic to [], which again establishes that listF and foldr are equivalent.
Summary #
The catamorphism for lists is a pair made from an initial value and a function. One variation is equal to foldr. Like Maybe, the catamorphism is the same as the fold.
In C#, this function corresponds to the Aggregate extension method identified above.
You've now seen two examples where the catamorphism coincides with the fold. You've also seen examples (Boolean catamorphism and Peano catamorphism) where there's a catamorphism, but no fold at all. In a subsequent article, you'll see an example of a container that has both catamorphism and fold, but where the catamorphism is more general than the fold.
Next: NonEmpty catamorphism.
Maybe catamorphism
The catamorphism for Maybe is just a simplification of its fold.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for Maybe, as well as how to identify it. The beginning of this article presents the catamorphism in C#, with examples. The rest of the article describes how to deduce the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
Maybe is a data container that models the absence or presence of a value. Contrary to null, Maybe has a type, so offers a sane and reasonable way to model that situation.
C# catamorphism #
This article uses Church-encoded Maybe. Other, alternative implementations of Maybe are possible. The catamorphism for Maybe is the Match method:
TResult Match<TResult>(TResult nothing, Func<T, TResult> just);
Like the Peano catamorphism, the Maybe catamorphism is a pair of a value and a function. The nothing value corresponds to the absence of data, whereas the just function handles the presence of data.
Given, for example, a Maybe containing a number, you can use Match to get the value out of the Maybe:
> IMaybe<int> maybe = new Just<int>(42); > maybe.Match(0, x => x) 42 > IMaybe<int> maybe = new Nothing<int>(); > maybe.Match(0, x => x) 0
The functionality is, however, more useful than a simple get-value-or-default operation. Often, you don't have a good default value for the type potentially wrapped in a Maybe object. In the core of your application architecture, it may not be clear how to deal with, say, the absence of a Reservation object, whereas at the boundary of your system, it's evident how to convert both absence and presence of data into a unifying type, such as an HTTP response:
Maybe<Reservation> maybe = // ... return maybe .Select(r => Repository.Create(r)) .Match<IHttpActionResult>( nothing: Content( HttpStatusCode.InternalServerError, new HttpError("Couldn't accept.")), just: id => Ok(id));
This enables you to avoid special cases, such as null Reservation objects, or magic numbers like -1 to indicate the absence of id values. At the boundary of an HTTP-based application, you know that you must return an HTTP response. That's the unifying type, so you can return 200 OK with a reservation ID in the response body when data is present, and 500 Internal Server Error when data is absent.
Maybe F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras.
While F-Algebras and fixed points are mostly used for recursive data structures, you can also define an F-Algebra for a non-recursive data structure. You already saw an example of that in the article about Boolean catamorphism. The difference between Boolean values and Maybe is that the just case of Maybe carries a value. You can model this as a Functor with both a carrier type and a type argument for the data that Maybe may contain:
data MaybeF a c = NothingF | JustF a deriving (Show, Eq, Read) instance Functor (MaybeF a) where fmap _ NothingF = NothingF fmap _ (JustF x) = JustF x
I chose to call the 'data type' a and the carrier type c (for carrier). As was also the case with BoolF, the Functor instance ignores the map function because the carrier type is missing from both the NothingF case and the JustF case. Like the Functor instance for BoolF, it'd seem that nothing happens, but at the type level, this is still a translation from MaybeF a c to MaybeF a c1. Not much of a function, perhaps, but definitely an endofunctor.
In the previous articles, it was possible to work directly with the fixed points of both functors; i.e. Fix BoolF and Fix NatF. Haskell isn't happy about attempts to define various instances for Fix (MaybeF a), so in order to make this easier, you can define a newtype wrapper:
newtype MaybeFix a = MaybeFix { unMaybeFix :: Fix (MaybeF a) } deriving (Show, Eq, Read)
In order to make it easier to work with MaybeFix you can add helper functions to create values:
nothingF :: MaybeFix a nothingF = MaybeFix $ Fix NothingF justF :: a -> MaybeFix a justF = MaybeFix . Fix . JustF
You can now create MaybeFix values to your heart's content:
Prelude Fix Maybe> justF 42
MaybeFix {unMaybeFix = Fix (JustF 42)}
Prelude Fix Maybe> nothingF
MaybeFix {unMaybeFix = Fix NothingF}
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (MaybeF), and an object a, but you still need to find a morphism MaybeF a c -> c. Notice that the algebra you have to find is the function that reduces the functor to its carrier type c, not the 'data type' a. This takes some time to get used to, but that's how catamorphisms work. This doesn't mean, however, that you get to ignore a, as you'll see.
As in the previous article, start by writing a function that will become the catamorphism, based on cata:
maybeF = cata alg . unMaybeFix where alg NothingF = undefined alg (JustF x) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type c from the NothingF case? You could pass an argument to the maybeF function:
maybeF n = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = undefined
The JustF case, contrary to NothingF, already contains a value, and it'd be incorrect to ignore it. On the other hand, x is a value of type a, and you need to return a value of type c. You'll need a function to perform the conversion, so pass such a function as an argument to maybeF as well:
maybeF :: c -> (a -> c) -> MaybeFix a -> c maybeF n f = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = f x
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of MaybeF, the compiler infers that the alg function has the type MaybeF a c -> c, which is just what you need!
You can now see what the carrier type c is for. It's the type that the algebra extracts, and thus the type that the catamorphism returns.
Notice that maybeF, like the above C# Match method, takes as arguments a pair of a value and a function (together with the Maybe value itself). Those are two representations of the same idea. Furthermore, this is nearly identical to the maybe function in Haskell's Data.Maybe module. I found it fitting, therefore, to name the function maybeF.
Basis #
You can implement most other useful functionality with maybeF. Here's the Functor instance:
instance Functor MaybeFix where fmap f = maybeF nothingF (justF . f)
Since fmap should be a structure-preserving map, you'll have to map the nothing case to the nothing case, and just to just. When calling maybeF, you must supply a value for the nothing case and a function to deal with the just case. The nothing case is easy to handle: just use nothingF.
In the just case, first apply the function f to map from a to b, and then use justF to wrap the b value in a new MaybeFix container to get MaybeFix b.
Applicative is a little harder, but not much:
instance Applicative MaybeFix where pure = justF f <*> x = maybeF nothingF (<$> x) f
The pure function is just justF (pun intended). The apply operator <*> is more complex.
Both f and x surrounding <*> are MaybeFix values: f is MaybeFix (a -> b), and x is MaybeFix a. While it's becoming increasingly clear that you can use a catamorphism like maybeF to implement most other functionality, to which MaybeFix value should you apply it? To f or x?
Both are possible, but the code looks (in my opinion) more readable if you apply it to f. Again, when f is nothing, return nothingF. When f is just, use the functor instance to map x (using the infix fmap alias <$>).
The Monad instance, on the other hand, is almost trivial:
instance Monad MaybeFix where x >>= f = maybeF nothingF f x
As usual, map nothing to nothing by supplying nothingF. f is already a function that returns a MaybeFix b value, so just use that.
The Foldable instance is likewise trivial (although, as you'll see below, you can make it even more trivial):
instance Foldable MaybeFix where foldMap = maybeF mempty
The foldMap function must return a Monoid instance, so for the nothing case, simply return the identity, mempty. Furthermore, foldMap takes a function a -> m, but since the foldMap implementation is point-free, you can't 'see' that function as an argument.
Finally, for the sake of completeness, here's the Traversable instance:
instance Traversable MaybeFix where sequenceA = maybeF (pure nothingF) (justF <$>)
In the nothing case, you can put nothingF into the desired Applicative with pure. In the just case you can take advantage of the desired Applicative being also a Functor by simply mapping the inner value(s) with justF.
Since the Applicative instance for MaybeFix equals pure to justF, you could alternatively write the Traversable instance like this:
instance Traversable MaybeFix where sequenceA = maybeF (pure nothingF) (pure <$>)
I like this alternative less, since I find it confusing. The two appearances of pure relate to two different types. The pure in pure nothingF has the type MaybeFix a -> f (MaybeFix a), while the pure in pure <$> has the type a -> MaybeFix a!
Both implementations work the same, though:
Prelude Fix Maybe> sequenceA (justF ("foo", 42))
("foo",MaybeFix {unMaybeFix = Fix (JustF 42)})
Here, I'm using the Applicative instance of (,) String.
Finally, you can implement conversions to and from the standard Maybe type, using ana as the dual of cata:
toMaybe :: MaybeFix a -> Maybe a toMaybe = maybeF Nothing return fromMaybe :: Maybe a -> MaybeFix a fromMaybe = MaybeFix . ana coalg where coalg Nothing = NothingF coalg (Just x) = JustF x
This demonstrates that MaybeFix is isomorphic to Maybe, which again establishes that maybeF and maybe are equivalent.
Alternatives #
As usual, the above maybeF isn't the only possible catamorphism. A trivial variation is to flip its arguments, but other variations exist.
It's a recurring observation that a catamorphism is just a generalisation of a fold. In the above code, the Foldable instance already looked as simple as anyone could desire, but another variation of a catamorphism for Maybe is this gratuitously embellished definition:
maybeF :: (a -> c -> c) -> c -> MaybeFix a -> c maybeF f n = cata alg . unMaybeFix where alg NothingF = n alg (JustF x) = f x n
This variation redundantly passes n as an argument to f, thereby changing the type of f to a -> c -> c. There's no particular motivation for doing this, apart from establishing that this catamorphism is exactly the same as the fold:
instance Foldable MaybeFix where foldr = maybeF
You can still implement the other instances as well, but the rest of the code suffers in clarity. Here's a few examples:
instance Functor MaybeFix where fmap f = maybeF (const . justF . f) nothingF instance Applicative MaybeFix where pure = justF f <*> x = maybeF (const . (<$> x)) nothingF f instance Monad MaybeFix where x >>= f = maybeF (const . f) nothingF x
I find that the need to compose with const does nothing to improve the readability of the code, so this variation is mostly, I think, of academic interest. It does show, though, that the catamorphism of Maybe is isomorphic to its fold, as the diagram in the overview article indicated:

You can demonstrate that this variation, too, is isomorphic to Maybe with a set of conversion:
toMaybe :: MaybeFix a -> Maybe a toMaybe = maybeF (const . return) Nothing fromMaybe :: Maybe a -> MaybeFix a fromMaybe = MaybeFix . ana coalg where coalg Nothing = NothingF coalg (Just x) = JustF x
Only toMaybe has changed, compared to above; the fromMaybe function remains the same. The only change to toMaybe is that the arguments have been flipped, and return is now composed with const.
Since (according to Conceptual Mathematics) isomorphisms are transitive this means that the two variations of maybeF are isomorphic. The latter, more complex, variation of maybeF is identical foldr, so we can consider the simpler, more frequently encountered variation a simplification of fold.
Summary #
The catamorphism for Maybe is the same as its Church encoding: a pair made from a default value and a function. In Haskell's base library, this is simply called maybe. In the above C# code, it's called Match.
This function is total, and you can implement any other functionality you need with it. I therefore consider it the canonical representation of Maybe, which is also why it annoys me that most Maybe implementations come equipped with partial functions like fromJust, or F#'s Option.get. Those functions shouldn't be part of a sane and reasonable Maybe API. You shouldn't need them.
In this series of articles about catamorphisms, you've now seen the first example of catamorphism and fold coinciding. In the next article, you'll see another such example - probably the most well-known catamorphism example of them all.
Next: List catamorphism.
Peano catamorphism
The catamorphism for Peano numbers involves a base value and a successor function.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for natural numbers, as well as how to identify it. The beginning of the article presents the catamorphism in C#, with examples. The rest of the article describes how I deduced the catamorphism. This part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
C# catamorphism #
In this article, I model natural numbers using Peano's model, and I'll reuse the Church-encoded implementation you've seen before. The catamorphism for INaturalNumber is:
public static T Cata<T>(this INaturalNumber n, T zero, Func<T, T> succ) { return n.Match(zero, p => p.Cata(succ(zero), succ)); }
Notice that this is an extension method on INaturalNumber, taking two other arguments: a zero argument which will be returned when the number is zero, and a successor function to return the 'next' value based on a previous value.
The zero argument is the easiest to understand. It's simply passed to Match so that this is the value that Cata returns when n is zero.
The other argument to Match must be a Func<INaturalNumber, T>; that is, a function that takes an INaturalNumber as input and returns a value of the type T. You can supply such a function by using a lambda expression. This expression receives a predecessor p as input, and has to return a value of the type T. The only function available in this context, however, is succ, which has the type Func<T, T>. How can you make that work?
As is often the case when programming with generics, it pays to follow the types. A Func<T, T> requires an input of the type T. Do you have any T objects around?
The only available T object is zero, so you could call succ(zero) to produce another T value. While you could return that immediately, that'd ignore the predecessor p, so that's not going to work. Another option, which is the one that works, is to recursively call Cata with succ(zero) as the zero value, and succ as the second argument.
What this accomplishes is that Cata keeps recursively calling itself until n is zero. The zero object, however, will be the result of repeated applications of succ(zero). In other words, succ will be called as many times as the natural number. If n is 7, then succ will be called seven times, the first time with the original zero value, the next time with the result of succ(zero), the third time with the result of succ(succ(zero)), and so on. If the number is 42, succ will be called 42 times.
Arithmetic #
You can implement all the functionality you saw in the article on Church-encoded natural numbers. You can start gently by converting a Peano number into a normal C# int:
public static int Count(this INaturalNumber n) { return n.Cata(0, x => 1 + x); }
You can play with the functionality in C# Interactive to get a feel for how it works:
> NaturalNumber.Eight.Count() 8 > NaturalNumber.Five.Count() 5
The Count extension method uses Cata to count the level of recursion. The zero value is, not surprisingly, 0, and the successor function simply adds one to the previous number. Since the successor function runs as many times as encoded by the Peano number, and since the initial value is 0, you get the integer value of the number when Cata exits.
A useful building block you can write using Cata is a function to increment a natural number by one:
public static INaturalNumber Increment(this INaturalNumber n) { return n.Cata(One, p => new Successor(p)); }
This, again, works as you'd expect:
> NaturalNumber.Zero.Increment().Count() 1 > NaturalNumber.Eight.Increment().Count() 9
With the Increment method and Cata, you can easily implement addition:
public static INaturalNumber Add(this INaturalNumber x, INaturalNumber y) { return x.Cata(y, p => p.Increment()); }
The trick here is to use y as the zero case for x. In other words, if x is zero, then Add should return y. If x isn't zero, then Increment it as many times as the number encodes, but starting at y. In other words, start with y and Increment x times.
The catamorphism makes it much easier to implement arithmetic operation. Just consider multiplication, which wasn't the simplest implementation in the previous article. Now, it's as simple as this:
public static INaturalNumber Multiply(this INaturalNumber x, INaturalNumber y) { return x.Cata(Zero, p => p.Add(y)); }
Start at 0 and simply Add(y) x times.
> NaturalNumber.Nine.Multiply(NaturalNumber.Four).Count() 36
Finally, you can also implement some common predicates:
public static IChurchBoolean IsZero(this INaturalNumber n) { return n.Cata<IChurchBoolean>(new ChurchTrue(), _ => new ChurchFalse()); } public static IChurchBoolean IsEven(this INaturalNumber n) { return n.Cata<IChurchBoolean>(new ChurchTrue(), b => new ChurchNot(b)); } public static IChurchBoolean IsOdd(this INaturalNumber n) { return new ChurchNot(n.IsEven()); }
Particularly IsEven is elegant: It considers zero even, so simply uses a new ChurchTrue() object for that case. In all other cases, it alternates between false and true by negating the predecessor.
> NaturalNumber.Three.IsEven().ToBool()
false
It seems convincing that we can use Cata to implement all the other functionality we need. That seems to be a characteristic of a catamorphism. Still, how do we know that Cata is, in fact, the catamorphism for natural numbers?
Peano F-Algebra #
As in the previous article, I'll use Fix and cata as explained in Bartosz Milewski's excellent article on F-Algebras. The NatF type comes from his article as well:
data NatF a = ZeroF | SuccF a deriving (Show, Eq, Read) instance Functor NatF where fmap _ ZeroF = ZeroF fmap f (SuccF x) = SuccF $ f x
You can use the fixed point of this functor to define numbers with a shared type. Here's just the first ten:
zeroF, oneF, twoF, threeF, fourF, fiveF, sixF, sevenF, eightF, nineF :: Fix NatF zeroF = Fix ZeroF oneF = Fix $ SuccF zeroF twoF = Fix $ SuccF oneF threeF = Fix $ SuccF twoF fourF = Fix $ SuccF threeF fiveF = Fix $ SuccF fourF sixF = Fix $ SuccF fiveF sevenF = Fix $ SuccF sixF eightF = Fix $ SuccF sevenF nineF = Fix $ SuccF eightF
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (NatF), and an object a, but you still need to find a morphism NatF a -> a.
As in the previous article, start by writing a function that will become the catamorphism, based on cata:
natF = cata alg where alg ZeroF = undefined alg (SuccF predecessor) = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type a from the ZeroF case? You could pass an argument to the natF function:
natF z = cata alg where alg ZeroF = z alg (SuccF predecessor) = undefined
In the SuccF case, predecessor is already of the polymorphic type a, so instead of returning a constant value, you can supply a function as an argument to natF and use it in that case:
natF :: a -> (a -> a) -> Fix NatF -> a natF z next = cata alg where alg ZeroF = z alg (SuccF predecessor) = next predecessor
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of NatF, the compiler infers that the alg function has the type NatF a -> a, which is just what you need!
For good measure, I should point out that, as usual, the above natF function isn't the only possible catamorphism. Trivially, you can flip the order of the arguments, and this would also be a catamorphism. These two alternatives are isomorphic.
The natF function identifies the Peano number catamorphism, which is equivalent to the C# representation in the beginning of the article. I called the function natF, because there's a tendency in Haskell to name the 'case analysis' or catamorphism after the type, just with a lower-case initial letter.
Basis #
A catamorphism can be used to implement most (if not all) other useful functionality, like all of the above C# functionality. In fact, I wrote the Haskell code first, and then translated my implementations into the above C# extension methods. This means that the following functions apply the same reasoning:
evenF :: Fix NatF -> Fix BoolF evenF = natF trueF notF oddF :: Fix NatF -> Fix BoolF oddF = notF . evenF incF :: Fix NatF -> Fix NatF incF = natF oneF $ Fix . SuccF addF :: Fix NatF -> Fix NatF -> Fix NatF addF x y = natF y incF x multiplyF :: Fix NatF -> Fix NatF -> Fix NatF multiplyF x y = natF zeroF (addF y) x
Here are some GHCi usage examples:
Prelude Boolean Nat> evenF eightF Fix TrueF Prelude Boolean Nat> toNum $ multiplyF sevenF sixF 42
The toNum function corresponds to the above Count C# method. It is, again, based on cata. You can use ana to convert the other way:
toNum :: Num a => Fix NatF -> a toNum = natF 0 (+ 1) fromNum :: (Eq a, Num a) => a -> Fix NatF fromNum = ana coalg where coalg 0 = ZeroF coalg x = SuccF $ x - 1
This demonstrates that Fix NatF is isomorphic to Num instances, such as Integer.
Summary #
The catamorphism for Peano numbers is a pair consisting of a zero value and a successor function. The most common description of catamorphisms that I've found emphasise how a catamorphism is like a fold; an operation you can use to reduce a data structure like a list or a tree to a single value. This is what happens here, but even so, the Fix NatF type isn't a Foldable instance. The reason is that while NatF is a polymorphic type, its fixed point Fix NatF isn't. Haskell's Foldable type class requires foldable containers to be polymorphic (what C# programmers would call 'generic').
When I first ran into the concept of a catamorphism, it was invariably described as a 'generalisation of fold'. The examples shown were always how the catamorphism for linked list is the same as its fold. I found such explanations unhelpful, because I couldn't understand how those two concepts differ.
The purpose with this article series is to show just how much more general the abstraction of a catamorphism is. In this article you saw how an infinitely recursive data structure like Peano numbers have a catamorphism, even though it isn't a parametrically polymorphic type. In the next article, though, you'll see the first example of a polymorphic type where the catamorphism coincides with the fold.
Next: Maybe catamorphism.
Boolean catamorphism
The catamorphism for Boolean values is just the common ternary operator.
This article is part of an article series about catamorphisms. A catamorphism is a universal abstraction that describes how to digest a data structure into a potentially more compact value.
This article presents the catamorphism for Boolean values, as well as how you identify it. The beginning of this article presents the catamorphism in C#, with a simple example. The rest of the article describes how I deduced the catamorphism. That part of the article presents my work in Haskell. Readers not comfortable with Haskell can just read the first part, and consider the rest of the article as an optional appendix.
C# catamorphism #
The catamorphism for Boolean values is the familiar ternary conditional operator:
> DateTime.Now.Day % 2 == 0 ? "Even date" : "Odd date" "Odd date"
Given a Boolean expression, you basically provide two values: one to use in case the Boolean expression is true, and one to use in case it's false.
For Church-encoded Boolean values, the catamorphism looks like this:
T Match<T>(T trueCase, T falseCase);
This is an instance method where you must, again, supply two alternatives. When the instance represents true, you'll get the left-most value trueCase; otherwise, when the instance represents false, you'll get the right-most value falseCase.
The catamorphism turns out to be the same as the Church encoding. This seems to be a recurring pattern.
Alternatives #
To be accurate, there's more than one catamorphism for Boolean values. It's only by convention that the value corresponding to true goes on the left, and the false value goes to the right. You could flip the arguments, and it would still be a catamorphism. This is, in fact, what Haskell's Data.Bool module does:
Prelude Data.Bool> bool "Odd date" "Even date" $ even date "Odd date"
The module documentation calls this the "Case analysis for the Bool type", instead of a catamorphism, but the two representations are isomorphic:
"This is equivalent to if p then y else x; that is, one can think of it as an if-then-else construct with its arguments reordered."
This is another recurring result. There's typically more than one catamorphism, but the alternatives are isomorphic. In this article series, I'll mostly present the alternative that strikes me as the one you'll encounter most frequently.
Fix #
In this and future articles, I'll derive the catamorphism from an F-Algebra. For an introduction to F-Algebras and fixed points, I'll refer you to Bartosz Milewski's excellent article on the topic. In it, he presents a generic data type for a fixed point, as well as polymorphic functions for catamorphisms and anamorphisms. While they're available in his article, I'll repeat them here for good measure:
newtype Fix f = Fix { unFix :: f (Fix f) } cata :: Functor f => (f a -> a) -> Fix f -> a cata alg = alg . fmap (cata alg) . unFix ana :: Functor f => (a -> f a) -> a -> Fix f ana coalg = Fix . fmap (ana coalg) . coalg
This should be recognisable from Bartosz Milewski's article. With one small exception, this is just a copy of the code shown there.
Boolean F-Algebra #
While F-Algebras and fixed points are mostly used for recursive data structures, you can also define an F-Algebra for a non-recursive data structure. As data types go, they don't get much simpler than Boolean values, which are just two mutually exclusive cases. In order to make a Functor out of the definition, though, you can equip it with a carrier type:
data BoolF a = TrueF | FalseF deriving (Show, Eq, Read) instance Functor BoolF where fmap _ TrueF = TrueF fmap _ FalseF = FalseF
The Functor instance simply ignores the carrier type and just returns TrueF and FalseF, respectively. It'd seem that nothing happens, but at the type level, this is still a translation from BoolF a to BoolF b. Not much of a function, perhaps, but definitely an endofunctor.
Another note that may be in order here, as well as for all future articles in this series, is that you'll notice that most types and custom functions come with the F suffix. This is simply a suffix I've added to avoid conflicts with built-in types, values, and functions, such as Bool, True, and, and so on. The F is for F-Algebra.
You can lift these values into Fix in order to make it fit with the cata function:
trueF, falseF :: Fix BoolF trueF = Fix TrueF falseF = Fix FalseF
That's all you need to identify the catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. You have an endofunctor (BoolF), and an object a, but you still need to find a morphism BoolF a -> a. At first glance, this seems impossible, because neither TrueF nor FalseF actually contain a value of the type a. How, then, can you conjure an a value out of thin air?
The cata function has the answer.
What you can do is to start writing the function that will become the catamorphism, basing it on cata:
boolF = cata alg where alg TrueF = undefined alg FalseF = undefined
While this compiles, with its undefined implementations, it obviously doesn't do anything useful. I find, however, that it helps me think. How can you return a value of the type a from the TrueF case? You could pass an argument to the boolF function:
boolF x = cata alg where alg TrueF = x alg FalseF = undefined
That seems promising, so do that for the FalseF case as well:
boolF :: a -> a -> Fix BoolF -> a boolF x y = cata alg where alg TrueF = x alg FalseF = y
This works. Since cata has the type Functor f => (f a -> a) -> Fix f -> a, that means that alg has the type f a -> a. In the case of BoolF, the compiler infers that the alg function has the type BoolF a -> a, which is just what you need!
The boolF function identifies the Boolean catamorphism, which is equivalent to representations in the beginning of the article. I called the function boolF, because there's a tendency in Haskell to name the 'case analysis' or catamorphism after the type, just with a lower-case initial letter.
You can use the boolF function just like the above ternary operator:
Prelude Boolean Nat> boolF "Even date" "Odd date" $ evenF dateF "Odd date"
Here, I've also used evenF from the Nat module shown in the next article in the series.
From the above definition of boolF, it should also be clear that you can arrive at the alternative catamorphism defined by Data.Bool.bool by simply flipping x and y.
Basis #
A catamorphism can be used to implement most (if not all) other useful functionality. For Boolean values, that would be the standard Boolean operations and, or, and not:
andF :: Fix BoolF -> Fix BoolF -> Fix BoolF andF x y = boolF y falseF x orF :: Fix BoolF -> Fix BoolF -> Fix BoolF orF x y = boolF trueF y x notF :: Fix BoolF -> Fix BoolF notF = boolF falseF trueF
They work as you'd expect them to work:
Prelude Boolean> andF trueF falseF Fix FalseF Prelude Boolean> orF trueF falseF Fix TrueF Prelude Boolean> orF (notF trueF) falseF Fix FalseF
You can also implement conversion to and from the built-in Bool type:
toBool :: Fix BoolF -> Bool toBool = boolF True False fromBool :: Bool -> Fix BoolF fromBool = ana coalg where coalg True = TrueF coalg False = FalseF
This demonstrates that Fix BoolF is isomorphic to Bool.
Summary #
The catamorphism for Boolean values is a function, method, or operator akin to the familiar ternary conditional operator. The most common descriptions of catamorphisms that I've found emphasise how a catamorphism is like a fold; an operation you can use to reduce a data structure like a list or a tree to a single value. In that light, it may be surprising that something as simple as Boolean values have an associated catamorphism.
Since Fix BoolF is isomorphic to Bool, you may wonder what the point is. Why define this data type, and implement functions like andF, orF, and notF?
The code presented here is nothing but an analysis tool. It's a way to identify the catamorphism for Boolean values.
Next: Peano catamorphism.
Catamorphisms
A catamorphism is a general abstraction that enables you to handle multiple values, for example in order to reduce them to a single value.
This article series is part of an even larger series of articles about the relationship between design patterns and category theory. In another article series in this big series of articles, you learned about functors, applicatives, and other types of data containers.
You may have heard about map-reduce architectures. Much software can be designed around two general types of operations: those that map data, and those that reduce data. A functor is a container of data that supports structure-preserving maps. Thus, you can think of functors as the general abstraction for map operations (also sometimes called projections). Does a similar universal abstraction exist for operations that reduce data?
Yes, that abstraction is called a catamorphism.
Aggregation #
Catamorphism is an intimidating word, so let's start with an example. You often have a collection of values that you'd like to reduce to a single value. Such a collection can contain arbitrarily complex objects, but I'll keep it simple and start with a collection of numbers:
new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 };
This particular list of numbers is an array, but that's not important. What comes next works for any IEnumerable<T>, including arrays. I only chose an array because the C# syntax for array creation is more compact than for other collection types.
How do you reduce those seven numbers to a single number? That depends on what you want that number to tell you. One option is to add the numbers together. There's a specific, built-in function for that:
> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 }.Sum();
100647
The Sum extension method is a one of many built-in functions that enable you to reduce a list of numbers to a single number: Average, Max, Count, and so on.
What do you do, though, if you need to reduce many values to one, and there's no existing function for that? What if, for example, you need to add all the numbers using modulo 360 addition?
In that case, you use Aggregate:
> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 }.Aggregate((x, y) => (x + y) % 360)
207
The way to interpret this result is that the initial array represents a sequence of rotations (measured in degrees), and the result is the final angle after all the rotations have completed.
In other (functional) languages, such a 'reduce' operation is called a fold. The metaphor, I suppose, is that you fold multiple values together, two by two.
A fold is a catamorphism, but a catamorphism is a more general abstraction. For some data structures, the catamorphism is more powerful than the fold, but for collections, there's no difference.
There's one edge case we need to be aware of, though. What if the collection is empty?
Aggregation of empty containers #
What happens if you attempt to aggregate an empty collection?
> new int[0].Aggregate((x, y) => (x + y) % 360) Sequence contains no elements + System.Linq.Enumerable.Aggregate<TSource>(IEnumerable<TSource>, Func<TSource, TSource, TSource>)
The Aggregate method throws an exception because it doesn't know how to deal with empty collections. The lambda expression you supply tells the Aggregate method how to combine two values into one. This is, for instance, how semigroups accumulate.
The lambda expression handles all cases where you have two or more values. If you have only a single value, then that's no problem either:
> new[] { 1337 }.Aggregate((x, y) => (x + y) % 360)
1337
In that case, the lambda expression isn't involved at all, because the single value is simply returned without modification. In this example, this could even be interpreted as being incorrect, since you'd expect the result to be 257 (1337 % 360).
It's safer to use the Aggregate overload that takes a seed value:
> new int[0].Aggregate(0, (x, y) => (x + y) % 360) 0
Not only does that gracefully handle empty collections, it also gives you a 'better' result for a single value:
> new[] { 1337 }.Aggregate(0, (x, y) => (x + y) % 360)
257
This works better because the method always starts with the seed value, which means that even if there's only a single value (1337), the lambda expression still runs ((0 + 1337) % 360).
This overload of Aggregate has a different type, though:
public static TAccumulate Aggregate<TSource, TAccumulate>( this IEnumerable<TSource> source, TAccumulate seed, Func<TAccumulate, TSource, TAccumulate> func);
Notice that the func doesn't require the accumulator to have the same type as elements from the source collection. This enables you to translate on the fly, so to speak. You can still use binary operations like the above modulo 360 addition, because that just implies that both TSource and TAccumulate are int.
With this overload, you could, for example, use the Angle class to perform the work:
> new[] { 42, 1337, 2112, 90125, 5040, 7, 1984 } . .Aggregate(Angle.Identity, (a, i) => a.Add(Angle.FromDegrees(i))) [{ Angle = 207° }]
Now the seed argument is Angle.Identity, which implies that TAccumulate is Angle. The source is still a collection of numbers, so TSource is int. Hence, I called the angle a and the integer i in the lambda expression. The output is an Angle object that represents 207°.
That Aggregate overload is the catamorphism for collections. It reduces a collection to an object.
Catamorphisms and folds #
Is catamorphism just an intimidating word for aggregate, accumulate, fold, or reduce?
It took me a long time to be able to tell the difference, because in many cases, it seems that there's no difference. The purpose of this article series is to make the distinction clearer. In short, a catamorphism is a more general concept.

For some data structures, such as Boolean values, or Peano numbers, the catamorphism is all there is; no fold exists. For other data structures, such as Maybe or collections, the catamorphism and the fold coincide. Still other data structures, such as Either and trees, support folding, but the fold is based on the catamorphism. For those types, there are operations you can do with the catamorphism that are impossible to implement with the fold function. One example is that a tree's catamorphism enables you to count its leaves; you can't do that with its fold function.
You'll see plenty of examples in this article series:
- Boolean catamorphism
- Peano catamorphism
- Maybe catamorphism
- List catamorphism
- NonEmpty catamorphism
- Either catamorphism
- Tree catamorphism
- Rose tree catamorphism
- Full binary tree catamorphism
- Payment types catamorphism
Each of these articles will contain a fair amount of Haskell code, but even if you're an object-oriented programmer who doesn't read Haskell, you should still scan them, as I'll start each with some C# examples. The Haskell code, by the way, is available on GitHub.
Greek #
When encountering a word like catamorphism, your reaction might be:
"Catamorphism?! What does that even mean? It's all Greek to me."Indeed, it's Greek, as is so much of mathematical terminology. The cata prefix means 'down'; lots of words start with cata, like catastrophe, catalogue, catatonia, catacomb, etc.
The morph suffix generally means 'shape'. While the cata prefix appears in common words like catastrophe, the morph suffix mostly appears in more academic contexts. Programmers will probably have encountered polymorphism and skeuomorphism, not to mention isomorphism. While morphism is heavily used in mathematics, other sciences use the suffix too, like dimorphism in biology.
In category theory, a morphism is basically just an arrow that points from one object to another. Think of it as a function.
If a morphism is just a function, why don't we just call it that, then? Is it really necessary with this intimidating terminology? Yes and no.
If someone had originally figured all of this out in the context of mainstream programming, he or she would probably have used friendlier names, like condense, reduce, fold, and so on. This would have been more encouraging, although I'm not sure it would have been better.
In software architecture we use many overloaded terms. For example, what's a service, or a client? What does tier mean? Is it the same as a layer, or is it something different? What's the difference between a library and a framework?
At least a word like catamorphism is concise. It's not in common use, so isn't overloaded and vague.
Another, more pragmatic, concern is that whether you like it or not, the terminology is already established. Mathematicians decided to name the concept catamorphism. While the name may seem intimidating, I prefer to teach concepts like these using established terminology. This means that if my articles are unclear, you can do further research with other resources. That's the benefit of established terminology, whether you like the specific words or not.
Summary #
You can compose entire applications based on the abstractions of map and reduce. You can see one example of such a system in my A Functional Architecture with F# Pluralsight course.
The terms map and reduce may, however, not be helpful, because it may not be clear exactly what types of data you can map, and what types you can reduce. One of the most important goals of this overall article series about universal abstractions is to help you identify when such software architectures apply. This is more often that you think.
What sort of data can you map? You can map functors. While hardly finite, there's a catalogue of well-known functors, of which I've covered some, but not all. That catalogue contains data containers like Maybe, Tree, lazy computations, tasks, and perhaps a score more. The catalogue of (actually useful) functors has, in my experience, a manageable size.
Likewise you could ask: What sort of data can you reduce? How do you implement that reduction? Again, there's a compact set of well-known catamorphisms. How do you reduce a collection? You use its catamorphism (which is equal to a fold). How do you reduce a tree? You use its catamorphism. How do you reduce an Either object? You use its catamorphism.
When we learn new programming languages, new libraries, new frameworks, we gladly invest time in learning hundreds, if not thousands, of keywords, APIs, extensibility points, and so on. May I offer, for your consideration, that your mental resources are better spent learning only a handful of universal abstractions?
Next: Boolean catamorphism.
Applicative monoids
An applicative functor containing monoidal values itself forms a monoid.
This article is an instalment in an article series about applicative functors. An applicative functor is a data container that supports combinations. If an applicative functor contains values of a type that gives rise to a monoid, then the functor itself forms a monoid.
In a previous article you learned that lazy computations of monoids remain monoids. Furthermore, a lazy computation is an applicative functor, and it turns out that the result generalises. The result regarding lazy computation is just a special case.
Monap #
Since version 4.11 of Haskell's base library, Monoid is a subset of Semigroup, so in order to create a Monoid instance, you must first define a Semigroup instance.
In order to escape the need for flexible contexts, you'll have to define a wrapper newtype that'll be the instance. What should you call it? It's going to be an applicative functor of monoids, so perhaps something like ApplicativeMonoid? Nah, that's too long. AppMon, then? Sure, but how about flipping the terms: MonApp? That's better. Let's drop the last p and dispense with the Pascal case: Monap.
Monap almost looks like Monad, only with the last letter rotated half a revolution. This should allow for maximum confusion.
To be clear, I normally don't advocate for droll word play when writing production code, but I occasionally do it in articles and presentations. The Monap in this article exists only to illustrate a point. It's not intended to be used. Furthermore, this article doesn't discuss monads at all, so the risk of confusion should, hopefully, be minimised. I may, however, regret this decision...
Applicative semigroup #
First, introduce the wrapper newtype:
newtype Monap f a = Monap { runMonap :: f a } deriving (Show, Eq)
This only states that there's a type called Monap that wraps some higher-kinded type f a; that is, a container f of values of the type a. The intent is that f is an applicative functor, hence the use of the letter f, but the type itself doesn't constrain f to any type class.
The Semigroup instance does, though:
instance (Applicative f, Semigroup a) => Semigroup (Monap f a) where (Monap x) <> (Monap y) = Monap $ liftA2 (<>) x y
This states that when f is a Applicative instance, and a is a Semigroup instance, then Monap f a is also a Semigroup instance.
Here's an example of combining two applicative semigroups:
λ> Monap (Just (Max 42)) <> Monap (Just (Max 1337))
Monap {runMonap = Just (Max {getMax = 1337})}
This example uses the Max semigroup container, and Maybe as the applicative functor. For Max, the <> operator returns the value that contains the highest value, which in this case is 1337.
It even works when the applicative functor in question is IO:
λ> runMonap $ Monap (Sum <$> randomIO @Word8) <> Monap (Sum <$> randomIO @Word8)
Sum {getSum = 165}
This example uses randomIO to generate two random values. It uses the TypeApplications GHC extension to make randomIO generate Word8 values. Each random number is projected into the Sum container, which means that <> will add the numbers together. In the above example, the result is 165, but if you evaluate the expression a second time, you'll most likely get another result:
λ> runMonap $ Monap (Sum <$> randomIO @Word8) <> Monap (Sum <$> randomIO @Word8)
Sum {getSum = 246}
You can also use linked list ([]) as the applicative functor. In this case, the result may be surprising (depending on what you expect):
λ> Monap [Product 2, Product 3] <> Monap [Product 4, Product 5, Product 6]
Monap {runMonap = [Product {getProduct = 8},Product {getProduct = 10},Product {getProduct = 12},
Product {getProduct = 12},Product {getProduct = 15},Product {getProduct = 18}]}
Notice that we get all the combinations of products: 2 multiplied with each element in the second list, followed by 3 multiplied by each of the elements in the second list. This shouldn't be that startling, though, since you've already, previously in this article series, seen several examples of how an applicative functor implies combinations.
Applicative monoid #
With the Semigroup instance in place, you can now add the Monoid instance:
instance (Applicative f, Monoid a) => Monoid (Monap f a) where mempty = Monap $ pure $ mempty
This is straightforward: you take the identity (mempty) of the monoid a, promote it to the applicative functor f with pure, and finally put that value into the Monap wrapper.
This works fine as well:
λ> mempty :: Monap Maybe (Sum Integer)
Monap {runMonap = Just (Sum {getSum = 0})}
λ> mempty :: Monap [] (Product Word8)
Monap {runMonap = [Product {getProduct = 1}]}
The identity laws also seem to hold:
λ> Monap (Right mempty) <> Monap (Right (Sum 2112))
Monap {runMonap = Right (Sum {getSum = 2112})}
λ> Monap ("foo", All False) <> Monap mempty
Monap {runMonap = ("foo",All {getAll = False})}
The last, right-identity example is interesting, because the applicative functor in question is a tuple. Tuples are Applicative instances when the first, or left, element is a Monoid instance. In other words, f is, in this case, (,) String. The Monoid instance that Monap sees as a, on the other hand, is All.
Since tuples of monoids are themselves monoids, however, I can get away with writing Monap mempty on the right-hand side, instead of the more elaborate template the other examples use:
λ> Monap ("foo", All False) <> Monap ("", mempty)
Monap {runMonap = ("foo",All {getAll = False})}
or perhaps even:
λ> Monap ("foo", All False) <> Monap (mempty, mempty)
Monap {runMonap = ("foo",All {getAll = False})}
Ultimately, all three alternatives mean the same.
Associativity #
As usual, I'm not going to do the work of formally proving that the monoid laws hold for the Monap instances, but I'd like to share some QuickCheck properties that indicate that they do, starting with a property that verifies associativity:
assocLaw :: (Eq a, Show a, Semigroup a) => a -> a -> a -> Property assocLaw x y z = (x <> y) <> z === x <> (y <> z)
This property is entirely generic. It'll verify associativity for any Semigroup a, not only for Monap. You can, however, run it for various Monap types, as well. You'll see how this is done a little later.
Identity #
Likewise, you can write two properties that check left and right identity, respectively.
leftIdLaw :: (Eq a, Show a, Monoid a) => a -> Property leftIdLaw x = x === mempty <> x rightIdLaw :: (Eq a, Show a, Monoid a) => a -> Property rightIdLaw x = x === x <> mempty
Again, this is entirely generic. These properties can be used to test the identity laws for any monoid, including Monap.
Properties #
You can run each of these properties multiple time, for various different functors and monoids. As Applicative instances, I've used Maybe, [], (,) Any, and Identity. As Monoid instances, I've used String, Sum Integer, Max Int16, and [Float]. Notice that a list ([]) is both an applicative functor as well as a monoid. In this test set, I've used it in both roles.
tests = [ testGroup "Properties" [ testProperty "Associativity law, Maybe String" (assocLaw @(Monap Maybe String)), testProperty "Left identity law, Maybe String" (leftIdLaw @(Monap Maybe String)), testProperty "Right identity law, Maybe String" (rightIdLaw @(Monap Maybe String)), testProperty "Associativity law, [Sum Integer]" (assocLaw @(Monap [] (Sum Integer))), testProperty "Left identity law, [Sum Integer]" (leftIdLaw @(Monap [] (Sum Integer))), testProperty "Right identity law, [Sum Integer]" (rightIdLaw @(Monap [] (Sum Integer))), testProperty "Associativity law, (Any, Max Int8)" (assocLaw @(Monap ((,) Any) (Max Int8))), testProperty "Left identity law, (Any, Max Int8)" (leftIdLaw @(Monap ((,) Any) (Max Int8))), testProperty "Right identity law, (Any, Max Int8)" (rightIdLaw @(Monap ((,) Any) (Max Int8))), testProperty "Associativity law, Identity [Float]" (assocLaw @(Monap Identity [Float])), testProperty "Left identity law, Identity [Float]" (leftIdLaw @(Monap Identity [Float])), testProperty "Right identity law, Identity [Float]" (rightIdLaw @(Monap Identity [Float])) ] ]
All of these properties pass.
Summary #
It seems that any applicative functor that contains monoidal values itself forms a monoid. The Monap type presented in this article only exists to demonstrate this conjecture; it's not intended to be used.
If it holds, I think it's an interesting result, because it further enables you to reason about the properties of complex systems, based on the properties of simpler systems.
Next: Bifunctors.
Comments
It seems that any applicative functor that contains monoidal values itself forms a monoid.
Is it necessary for the functor to be applicative? Do you know of a functor that contains monoidal values for which itself does not form a monoid?
Tyson, thank you for writing. Yes, it's necessary for the functor to be applicative, because you need the applicative combination operator <*> in order to implement the combination. In C#, you'd need an Apply method as shown here.
Technically, the monoidal <> operator for Monap is, as you can see, implemented with a call to liftA2. In Haskell, you can implement an instance of Applicative by implementing either liftA2 or <*>, as well as pure. You usually see Applicative described by <*>, which is what I've done in my article series on applicative functors. If you do that, you can define liftA2 by a combination of <*> and fmap (the Select method that defines functors).
If you want to put this in C# terms, you need both Select and Apply in order to be able to lift a monoid into a functor.
Is there a functor that contains monoidal values that itself doesn't form a monoid?
Yes, indeed. In order to answer that question, we 'just' need to identify a functor that's not an applicative functor. Tuples are good examples.
A tuple forms a functor, but in general nothing more than that. Consider a tuple where the first element is a Guid. It's a functor, but can you implement the following function?
public static Tuple<Guid, TResult> Apply<TResult, T>( this Tuple<Guid, Func<T, TResult>> selector, Tuple<Guid, T> source) { throw new NotImplementedException("What would you write here?"); }
You can pull the T value out of source and project it to a TResult value with selector, but you'll need to put it back in a Tuple<Guid, TResult>. Which Guid value are you going to use for that tuple?
There's no clear answer to that question.
More specifically, consider Tuple<Guid, int>. This is a functor that contains monoidal values. Let's say that we want to use the addition monoid over integers. How would you implement the following method?
public static Tuple<Guid, int> Add(this Tuple<Guid, int> x, Tuple<Guid, int> y) { throw new NotImplementedException("What would you write here?"); }
Again, you run into the issue that while you can pull the integers out of the tuples and add them together, there's no clear way to figure out which Guid value to put into the tuple that contains the sum.
The issue particularly with tuples is that there's no general way to combine the leftmost values of the tuples. If there is - that is, if leftmost values form a monoid - then the tuple is also an applicative functor. For example, Tuple<string, int> is applicative and forms a monoid over addition:
public static Tuple<string, TResult> Apply<TResult, T>( this Tuple<string, Func<T, TResult>> selector, Tuple<string, T> source) { return Tuple.Create( selector.Item1 + source.Item1, selector.Item2(source.Item2)); } public static Tuple<string, int> Add(this Tuple<string, int> x, Tuple<string, int> y) { return Tuple.Create(x.Item1 + y.Item1, x.Item2 + y.Item2); }
You can also implement Add with Apply, but you're going to need two Apply overloads to make it work.
Incidentally, unbeknownst to me, the Ap wrapper was added to Haskell's Data.Monoid module 12 days before I wrote this article. In all but name, it's equivalent to the Monap wrapper presented here.
...if leftmost values form a monoid - then the tuple is also an applicative functor. For example,
Tuple<string, int>is applicative...
I want to add some prepositional phrases to our statements like I commented here to help claify things. I don't think that Tuple<string, int> can be applicative because there are no type parameters in which it could be applicative. Were you trying to say that Tuple<string, B> is applicative in B? This seems to match your Apply function, which doesn't depend on int.
Tyson, you're quite right; good catch. My wording was incorrect (I was probably either tired or in a hurry when I wrote that), but fortunately, the code looks like it's correct.
That you for pointing out my error.
...
Tuple<string, int>is applicative and forms a monoid over addition...
I do agree with the monoid part, where "addition" means string concatenation for the first item and integer addition for the second item.
Tuple<string, B>is applicative inB
Now I am trying to improve my understanding of this statement. In Haskell, my understanding the definition of the Applicative type class applied to Tuple<string, B> requires a function pure from B to Tuple<string, B>. What it the definition of this funciton? Does it use the empty string in order to make an instance of Tuple<string, B>? If so, what is the justification for this? Or maybe my reasoning here is mistaken.
Tyson, thank you for writing. In Haskell, it's true that applicative functors must also define pure. In this article series, I've glosssed over that constraint, since I'm not aware of any data containers that can lawfully implement <*> or liftA2, but can't define pure.
The applicative instance for tuples is, however, constrained:
Monoid a => Applicative ((,) a)
The construct ((,) a) means any tuple where the first element has the generic type a. The entire expression means that tuples are applicative functors when the first element forms a monoid; that's the restriction on a. The definition of pure, then, is:
pure x = (mempty, x)
That is, use the monoidal identity (mempty) for the first element, and use x as the second element. For strings, since the identity for string concatenation is the empty string, yes, it does exactly mean that pure for Tuple<string, B> would return a tuple with the empty string, and the input argument as the second element:
public static Tuple<string, T> Pure<T>(this T x) { return Tuple.Create("", x); }
That's the behaviour you get from Haskell as well:
Prelude Data.Monoid> pure 42 :: (String, Int)
("",42)
Lazy monoids
Lazy monoids are monoids. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity). Previous articles have shown how more complex monoids arise from simpler monoids, such as tuple monoids, function monoids, and Maybe monoids. This article shows another such result: how lazy computations of monoids itself form monoids.
You'll see how simple this is through a series of examples. Specifically, you'll revisit several of the examples you've already seen in this article series.
Lazy addition #
Perhaps the most intuitive monoid is addition. Lazy addition forms a monoid as well. In C#, you can implement this with a simple extension method:
public static Lazy<int> Add(this Lazy<int> x, Lazy<int> y) { return new Lazy<int>(() => x.Value + y.Value); }
This Add method simply adds two lazy integers together in a lazy computation. You use it like any other extension method:
Lazy<int> x = // ... Lazy<int> y = // ... Lazy<int> sum = x.Add(y);
I'll spare you the tedious listing of FsCheck-based properties that demonstrate that the monoid laws hold. We'll look at an example of such a set of properties later in this article, for one of the other monoids.
Lazy multiplication #
Not surprisingly, I hope, you can implement multiplication over lazy numbers in the same way:
public static Lazy<int> Multiply(this Lazy<int> x, Lazy<int> y) { return new Lazy<int>(() => x.Value * y.Value); }
Usage is similar to lazy addition:
Lazy<int> x = // ... Lazy<int> y = // ... Lazy<int> product = x.Multiply(y);
As is the case with lazy addition, this Multiply method currently only works with lazy int values. If you also want it to work with long, short, or other types of numbers, you'll have to add method overloads.
Lazy Boolean monoids #
There are four monoids over Boolean values, although I've customarily only shown two of them: and and or. These also, trivially, work with lazy Boolean values:
public static Lazy<bool> And(this Lazy<bool> x, Lazy<bool> y) { return new Lazy<bool>(() => x.Value && y.Value); } public static Lazy<bool> Or(this Lazy<bool> x, Lazy<bool> y) { return new Lazy<bool>(() => x.Value || y.Value); }
Given the previous examples, you'll hardly be surprised to see how you can use one of these extension methods:
Lazy<bool> x = // ... Lazy<bool> y = // ... Lazy<bool> b = x.And(y);
Have you noticed a pattern in how the lazy binary operations Add, Multiply, And, and Or are implemented? Could this be generalised?
Lazy angular addition #
In a previous article you saw how angular addition forms a monoid. Lazy angular addition forms a monoid as well, which you can implement with another extension method:
public static Lazy<Angle> Add(this Lazy<Angle> x, Lazy<Angle> y) { return new Lazy<Angle>(() => x.Value.Add(y.Value)); }
Until now, you may have noticed that all the extension methods seemed to follow a common pattern that looks like this:
return new Lazy<Foo>(() => x.Value ⋄ y.Value);
I've here used the diamond operator ⋄ as a place-holder for any sort of binary operation. My choice of that particular character is strongly influenced by Haskell, where semigroups and monoids polymorphically are modelled with (among other options) the <> operator.
The lazy angular addition implementation looks a bit different, though. This is because the original example uses an instance method to model the binary operation, instead of an infix operator such as +, &&, and so on. Given that the implementation of a lazy binary operation can also look like this, can you still imagine a generalisation?
Lazy string concatenation #
If we follow the rough ordering of examples introduced in this article series about monoids, we've now reached concatenation as a monoid. While various lists, arrays, and other sorts of collections also form a monoid over concatenation, in .NET, IEnumerable<T> already enables lazy evaluation, so I think it's more interesting to consider lazy string concatenation.
The implementation, however, holds few surprises:
public static Lazy<string> Concat(this Lazy<string> x, Lazy<string> y) { return new Lazy<string>(() => x.Value + y.Value); }
The overall result, so far, seems encouraging. All the basic monoids we've covered are also monoids when lazily computed.
Lazy money addition #
The portfolio example from Kent Beck's book Test-Driven Development By Example also forms a monoid. You can, again, implement an extension method that enables you to add lazy expressions together:
public static Lazy<IExpression> Plus( this Lazy<IExpression> source, Lazy<IExpression> addend) { return new Lazy<IExpression>(() => source.Value.Plus(addend.Value)); }
So far, you've seen several examples of implementations, but are they really monoids? All are clearly binary operations, but are they associative? Do identities exist? In other words, do the lazy binary operations obey the monoid laws?
As usual, I'm not going to prove that they do, but I do want to share a set of FsCheck properties that demonstrate that the monoid laws hold. As an example, I'll share the properties for this lazy Plus method, but you can write similar properties for all of the above methods as well.
You can verify the associativity law like this:
public void LazyPlusIsAssociative( Lazy<IExpression> x, Lazy<IExpression> y, Lazy<IExpression> z) { Assert.Equal( x.Plus(y).Plus(z), x.Plus(y.Plus(z)), Compare.UsingBank); }
Here, Compare.UsingBank is just a test utility API to make the code more readable:
public static class Compare { public static ExpressionEqualityComparer UsingBank = new ExpressionEqualityComparer(); }
This takes advantage of the overloads for xUnit.net's Assert methods that take custom equality comparers as an extra, optional argument. ExpressionEqualityComparer is implemented in the test code base:
public class ExpressionEqualityComparer : IEqualityComparer<IExpression>, IEqualityComparer<Lazy<IExpression>> { private readonly Bank bank; public ExpressionEqualityComparer() { bank = new Bank(); bank.AddRate("CHF", "USD", 2); } public bool Equals(IExpression x, IExpression y) { var xm = bank.Reduce(x, "USD"); var ym = bank.Reduce(y, "USD"); return object.Equals(xm, ym); } public int GetHashCode(IExpression obj) { return bank.Reduce(obj, "USD").GetHashCode(); } public bool Equals(Lazy<IExpression> x, Lazy<IExpression> y) { return Equals(x.Value, y.Value); } public int GetHashCode(Lazy<IExpression> obj) { return GetHashCode(obj.Value); } }
If you think that the exchange rate between Dollars and Swiss Francs looks ridiculous, it's because I'm using the rate that Kent Beck used in his book, which is from 2002 (but otherwise timeless).
The above property passes for hundreds of randomly generated input values, as is the case for this property, which verifies the left and right identity:
public void LazyPlusHasIdentity(Lazy<IExpression> x) { Assert.Equal(x, x.Plus(Plus.Identity.ToLazy()), Compare.UsingBank); Assert.Equal(x, Plus.Identity.ToLazy().Plus(x), Compare.UsingBank); }
These properties are just examples, not proofs. Still, they give confidence that lazy computations of monoids are themselves monoids.
Lazy Roster combinations #
The last example you'll get in this article is the Roster example from the article on tuple monoids. Here's yet another extension method that enables you to combine two lazy rosters:
public static Lazy<Roster> Combine(this Lazy<Roster> x, Lazy<Roster> y) { return new Lazy<Roster>(() => x.Value.Combine(y.Value)); }
At this point it should be clear that there's essentially two variations in how the above extension methods are implemented. One variation is when the binary operation is implemented with an infix operator (like +, ||, and so on), and another variation is when it's modelled as an instance method. How do these implementations generalise?
I'm sure you could come up with an ad-hoc higher-order function, abstract base class, or interface to model such a generalisation, but I'm not motivated by saving keystrokes. What I'm trying to uncover with this overall article series is how universal abstractions apply to programming.
Which universal abstraction is in play here?
Lazy monoids as applicative operations #
Lazy<T> forms an applicative functor. Using appropriate Apply overloads, you can rewrite all the above implementations in applicative style. Here's lazy addition:
public static Lazy<int> Add(this Lazy<int> x, Lazy<int> y) { Func<int, int, int> f = (i, j) => i + j; return f.Apply(x).Apply(y); }
This first declares a Func value f that invokes the non-lazy binary operation, in this case +. Next, you can leverage the applicative nature of Lazy<T> to apply f to the two lazy values x and y.
Multiplication, as well as the Boolean operations, follow the exact same template:
public static Lazy<int> Multiply(this Lazy<int> x, Lazy<int> y) { Func<int, int, int> f = (i, j) => i * j; return f.Apply(x).Apply(y); } public static Lazy<bool> And(this Lazy<bool> x, Lazy<bool> y) { Func<bool, bool, bool> f = (b1, b2) => b1 && b2; return f.Apply(x).Apply(y); } public static Lazy<bool> Or(this Lazy<bool> x, Lazy<bool> y) { Func<bool, bool, bool> f = (b1, b2) => b1 || b2; return f.Apply(x).Apply(y); }
Notice that in all four implementations, the second line of code is verbatim the same: return f.Apply(x).Apply(y);
Does this generalisation also hold when the underlying, non-lazy binary operation is modelled as an instance method, as is the case of e.g. angular addition? Yes, indeed:
public static Lazy<Angle> Add(this Lazy<Angle> x, Lazy<Angle> y) { Func<Angle, Angle, Angle> f = (i, j) => i.Add(j); return f.Apply(x).Apply(y); }
You can implement the Combine method for lazy Roster objects in the same way, as well as Plus for lazy monetary expressions. The latter is worth revisiting.
Using the Lazy functor over portfolio expressions #
The lazy Plus implementation looks like all of the above Apply-based implementations:
public static Lazy<IExpression> Plus( this Lazy<IExpression> source, Lazy<IExpression> addend) { Func<IExpression, IExpression, IExpression> f = (x, y) => x.Plus(y); return f.Apply(source).Apply(addend); }
In my article, however, you saw how, when Plus is a monoid, you can implement Times as an extension method. Can you implement a lazy version of Times as well? Must it be another extension method?
Yes, but instead of an ad-hoc implementation, you can take advantage of the functor nature of Lazy:
public static Lazy<IExpression> Times(this Lazy<IExpression> exp, int multiplier) { return exp.Select(x => x.Times(multiplier)); }
Notice that instead of explicitly reaching into the lazy Value, you can simply call Select on exp. This lazily projects the Times operation, while preserving the invariants of Lazy<T> (i.e. that the computation is deferred until you ultimately access the Value property).
You can implement a lazy version of Reduce in the same way:
public static Lazy<Money> Reduce(this Lazy<IExpression> exp, Bank bank, string to) { return exp.Select(x => x.Reduce(bank, to)); }
The question is, however, is it even worthwhile? Do you need to create all these overloads, or could you just leverage Select when you have a lazy value?
For example, if the above Reduce overload didn't exist, you'd still be able to work with the portfolio API like this:
Lazy<IExpression> portfolio = // ... Lazy<Money> result = portfolio.Select(x => x.Reduce(bank, "USD"));
If you only occasionally use Reduce, then perhaps this is good enough. If you frequently call Reduce, however, it might be worth to add the above overload, in which case you could then instead write:
Lazy<IExpression> portfolio = // ... Lazy<Money> result = portfolio.Reduce(bank, "USD");
In both cases, however, I think that you'd be putting the concept of an applicative functor to good use.
Towards generalisation #
Is the applicative style better than the initial ad-hoc implementations? That depends on how you evaluate 'better'. If you count lines of code, then the applicative style is twice as verbose as the ad-hoc implementations. In other words, this:
return new Lazy<int>(() => x.Value + y.Value);
seems simpler than this:
Func<int, int, int> f = (i, j) => i + j; return f.Apply(x).Apply(y);
This is, however, mostly because C# is too weak to express such abstractions in an elegant way. In F#, using the custom <*> operator from the article on the Lazy applicative functor, you could express the lazy addition as simply as:
lazy (+) <*> x <*> y
In Haskell (if we, once more, pretend that Identity is equivalent to Lazy), you can simplify even further to:
(+) <$> x <*> y
Or rather, if you want it in point-free style, liftA2 (+).
Summary #
The point of this article series isn't to save keystrokes, but to identify universal laws of computing, even as they relate to object-oriented programming. The pattern seems clear enough that I dare propose the following:
All monoids remain monoids under lazy computation.
In a future article I'll offer further support for that proposition.
Next: Monoids accumulate.
Comments
In the Lazy monoids as applicative operations section, you mention "Apply overloads".
In pondering what those might look like, I found the two examples in the A C# perspective
section of your post on applicative functors, and from those, drew the conclusion that Apply for Lazy<T> would look like this:
public static Lazy<TResult> Apply<T, TResult>( this Lazy<Func<T, TResult>> selector, Lazy<T> source) { return new Lazy<TResult>(() => selector.Value(source.Value)); }
You want to be able to use Apply against a two-argument function, and since C# doesn't curry functions, we've got a couple of options. We could define an additional Apply overload to handle
two-argument functions. But since we're going to need to wrap up the function in a Lazy anyway, we could just curry while doing that:
Func<int, int, int> f = (i, j) => i + j; return new Lazy<Func<int, Func<int, int>>>(x => y => f(x, y)).Apply(x).Apply(y);
That seems in line not only with your formulation in the article on applicative functors, but also with how they look in Haskell: Applicative defines the first argument to <*> as being f (a -> b).
In other words, the first argument to Apply is not a function, it's a function wrapped in a functor. In Haskell, that means doing something like this:
((Just (+)) <*> (Just 10)) <*> (Just 32)
But that's apparently not what you've done here. You've called Apply directly on a function (and not a function wrapped in Lazy). But isn't the point of applicative functors that it's not just values that are wrapped up in
a functor: so, too, are the functions we might want to map over them, right? If you merely want to map a bare function over a functor, then you can just do that with fmap (or Select, as we normally call it in .NET).
(That said, your definition is consistent with liftA2. But my understanding is that the ability to define an applicative
in terms of liftA2 is an optimization rather than a fundamental feature; originally only <*> was part of the typeclass, with liftA2 being defined in terms of <*> and fmap.)
Not that Select alone would be sufficient here. If you are starting with an unwrapped function, you'd use Select to apply the first argument, but the result would be a Lazy<Func<int, int>>,
so you would actually need to use Apply for the second step. So you'd end up with this oddity:
Func<int, int, int> f = (i, j) => i + j; Func<int, Func<int, int>> curried = x => y => f(x, y); return curried.Select(x).Apply(y);
In Haskell, that would be equivalent to ((fmap (+)) (Just 10)) <*> (Just 32). Just like in the C# version, I'm using a plain function ((+)), not wrapped in a functor, and so I have to
use fmap (aka Select) to apply that unwrapped function to the value in the Maybe.
Obviously we could avoid the manual currying in C# by defining overloads that work with 2-argument functions, but I don't think it would change the fundamental fact that with applicative functors, you
apply a function wrapper in the functor, whereas if you just want to apply a function directly, that's ordinary functor fmap (aka Select).
Weird though this look, it makes plain something that I think is obscured in your ...Apply(x).Apply(y) examples: the application of the first argument is a quite different operation, because you're applying
a lazy argument to a non-lazy function, but since the result is a lazy function, the application of the second argument needs to do something different: applying a lazy argument to a lazy function. Weird though
f.Select(x).Apply(x) looks, it does make it clear that the two stages are not the same thing.
Ian, thank you for writing. I agree that there's some hand-waving going on in that article. To make a long story short, that particular code base also includes this overload of Apply:
public static Lazy<Func<T2, TResult>> Apply<T1, T2, TResult>( this Func<T1, T2, TResult> selector, Lazy<T1> source) { return new Lazy<Func<T2, TResult>>( () => y => selector(source.Value, y)); }
I keep learning during and after writing these articles, and it's possible that some of the connections you point out weren't entirely clear to me when I wrote. Or perhaps I was driven by a didactic motivation of presenting the concept in as clean a way as possible. Sometimes, I gloss over some details in order to get an overall point across. I honestly no longer remember exactly what motivated me to leave out that detail back then, but it was probably some combination of the above.
You are correct that currying is the key to making this simpler. Tyson Williams pointed this out to me in 2018.
FWIW, until recently I had a tendency to forget about liftA2 and its cousins, so I developed a habit of writing Haskell expressions like (+) <$> (Just 10) <*> (Just 32), as witnessed by, among others, this article.
Is your final C# example to be preferred? I'm not sure. I haven't tried to actually write it out, so perhaps I'm missing something, but as far as I can tell, it's an extension method on Func that takes a single 'applicative value' as an argument. If so, isn't it more or less the above Apply overload with a different name?
As far as I can tell, that's not the idiomatic Select shape that most C# developers are used to, since it has its arguments swapped. You and I may realize that this is still isomorphic to the 'standard' Select signature, but I think that we've now moved beyond what most professional C# developers are willing to grapple with.
I don't mean that as an attack on your comments. I think that you are correct. Rather, during and after writing this article series on applicative functors, I've come to appreciate that however useful that abstraction is, it's not a good fit in C#.
A pure Test Spy
Ad-hoc Test Spies can be implemented in Haskell using the Writer monad.
In a previous article on state-based testing in Haskell, I made the following throw-away statement:
"you could write an ad-hoc Mock using, for example, the Writer monad"In that article, I didn't pursue that thought, since the theme was another. Instead, I'll expand on it here.
Test Double continuum #
More than a decade ago, I wrote an MSDN Magazine article called Exploring The Continuum Of Test Doubles. It was in the September 2007 issue, and you can also download the entire issue as a single file and read the article offline, should you want to.
In the article, I made the argument that the classification of Test Doubles presented in the excellent xUnit Test Patterns should be thought of more as a continuum with vague and fuzzy transitions, rather than discrete categories.
This figure appeared in the original article. Given that the entire MSDN Magazine issue is available for free, and that I'm the original author of the article, I consider it fair use to repeat it here.
The point is that it's not always clear whether a Test Double is, say, a Mock, or a Spy. What I'll show you in this article is closer to a Test Spy than to a Mock, but since the distinction is blurred anyway, I think that I can get away with it.
Test Spy #
xUnit Test Patterns defines a Test Spy as a Test Double that captures "the indirect output calls made to another component by the SUT [System Under Test] for later verification by the test." When, as shown in a previous article, you use Mock<T>.Verify to assert than an interaction took place, you're using the Test Double more as a Spy than a Mock:
repoTD.Verify(r => r.Update(user));
Strictly speaking, a Mock is a Test Double that immediately fails the test if any unexpected interaction takes place. People often call those Strict Mocks, but according to the book, that's a Mock. If the Test Double only records what happens, so that you can later query it to verify whether some interaction took place, it's closer to being a Test Spy.
Whether you call it a Mock or a Spy, you can implement verification similar to the above Verify method in functional programming using the Writer monad.
Writer-based Spy #
I'll show you a single example in Haskell. In a previous article, you saw a simplified function to implement a restaurant reservation feature, repeated here for your convenience:
tryAccept :: Int -> Reservation -> MaybeT ReservationsProgram Int tryAccept capacity reservation = do guard =<< isReservationInFuture reservation reservations <- readReservations $ reservationDate reservation let reservedSeats = sum $ reservationQuantity <$> reservations guard $ reservedSeats + reservationQuantity reservation <= capacity create $ reservation { reservationIsAccepted = True }
This function runs in the MaybeT monad, so the two guard functions could easily prevent if from running 'to completion'. In the happy path, though, execution should reach 'the end' of the function and call the create function.
In order to test this happy path, you'll need to not only run a test-specific interpreter over the ReservationsProgram free monad, you should also verify that reservationIsAccepted is True.
You can do this using the Writer monad to implement a Test Spy:
testProperty "tryAccept, happy path" $ \ (NonNegative i) (fmap getReservation -> reservations) (ArbReservation reservation) expected -> let spy (IsReservationInFuture _ next) = return $ next True spy (ReadReservations _ next) = return $ next reservations spy (Create r next) = tell [r] >> return (next expected) reservedSeats = sum $ reservationQuantity <$> reservations capacity = reservedSeats + reservationQuantity reservation + i (actual, observedReservations) = runWriter $ foldFreeT spy $ runMaybeT $ tryAccept capacity reservation in Just expected == actual && [True] == (reservationIsAccepted <$> observedReservations)
This test is an inlined QuickCheck-based property. The entire source code is available on GitHub.
Notice the spy function. As the name implies, it's the Test Spy for the test. Its full type is:
spy :: Monad m => ReservationsInstruction a -> WriterT [Reservation] m a
This is a function that, for a given ReservationsInstruction value returns a WriterT value where the type of data being written is [Reservation]. The function only writes to the writer context in one of the three cases: the Create case. The Create case carries with it a Reservation value here named r. Before returning the next step in interpreting the free monad, the spy function calls tell, thereby writing a singleton list of [r] to the writer context.
In the Act phase of the test, it calls the tryAccept function and proceeds to interpret the result, which is a MaybeT ReservationsProgram Int value. Calling runMaybeT produces a ReservationsProgram (Maybe Int), which you can then interpret with foldFreeT spy. This returns a Writer [Reservation] (Maybe Int), which you can finally run with runWriter to get a (Maybe Int, [Reservation]) tuple. Thus, actual is a Maybe Int value, and observedReservations is a [Reservation] value - the reservation that was written by spy using tell.
The Assert phase of the test is a Boolean expression that checks that actual is as expected, and that reservationIsAccepted of the observed reservation is True.
It takes a little while to make the pieces of the puzzle fit, but it's basically just standard Haskell library functions clicked together.
Summary #
People sometimes ask me: How do Mocks and Stubs work in functional programming?
In general, my answer is that you don't need Mocks and Stubs because when functions are pure, you don't need to to test interactions. Sooner or later, though, you may run into higher-level interactions, even if they're pure interactions, and you'll likely want to unit test those.
In a previous article you saw how to apply state-based testing in Haskell, using the State monad. In this article you've seen how you can create ad-hoc Mocks or Spies with the Writer monad. No auto-magical test-specific 'isolation frameworks' are required.
An example of state-based testing in C#
An example of avoiding Mocks and Stubs in C# unit testing.
This article is an instalment in an article series about how to move from interaction-based testing to state-based testing. In the previous article, you saw an example of a pragmatic state-based test in F#. You can now take your new-found knowledge and apply it to the original C# example.
In the spirit of xUnit Test Patterns, in this article you'll see how to refactor the tests while keeping the implementation code constant.
The code shown in this article is available on GitHub.
Connect two users #
The previous article provides more details on the System Under Test (SUT), but here it is, repeated, for your convenience:
public class ConnectionsController : ApiController { public ConnectionsController( IUserReader userReader, IUserRepository userRepository) { UserReader = userReader; UserRepository = userRepository; } public IUserReader UserReader { get; } public IUserRepository UserRepository { get; } public IHttpActionResult Post(string userId, string otherUserId) { var userRes = UserReader.Lookup(userId).SelectError( error => error.Accept(UserLookupError.Switch( onInvalidId: "Invalid user ID.", onNotFound: "User not found."))); var otherUserRes = UserReader.Lookup(otherUserId).SelectError( error => error.Accept(UserLookupError.Switch( onInvalidId: "Invalid ID for other user.", onNotFound: "Other user not found."))); var connect = from user in userRes from otherUser in otherUserRes select Connect(user, otherUser); return connect.SelectBoth(Ok, BadRequest).Bifold(); } private User Connect(User user, User otherUser) { user.Connect(otherUser); UserRepository.Update(user); return otherUser; } }
This implementation code is a simplification of the code example that serves as an example running through my two Clean Coders videos, Church Visitor and Preserved in translation.
A Fake database #
As in the previous article, you can define a test-specific Fake database:
public class FakeDB : Collection<User>, IUserReader, IUserRepository { public IResult<User, IUserLookupError> Lookup(string id) { if (!(int.TryParse(id, out int i))) return Result.Error<User, IUserLookupError>(UserLookupError.InvalidId); var user = this.FirstOrDefault(u => u.Id == i); if (user == null) return Result.Error<User, IUserLookupError>(UserLookupError.NotFound); return Result.Success<User, IUserLookupError>(user); } public bool IsDirty { get; set; } public void Update(User user) { IsDirty = true; if (!Contains(user)) Add(user); } }
This is one of the few cases where I find inheritance more convenient than composition. By deriving from Collection<User>, you don't have to explicitly write code to expose a Retrieval Interface. The entirety of a standard collection API is already available via the base class. Had this class been part of a public API, I'd be concerned that inheritance could introduce future breaking changes, but as part of a suite of unit tests, I hope that I've made the right decision.
Although you can derive a Fake database from a base class, you can still implement required interfaces - in this case IUserReader and IUserRepository. The Update method is the easiest one to implement, since it simply sets the IsDirty flag to true and adds the user if it's not already part of the collection.
The IsDirty flag is the only custom Retrieval Interface added to the FakeDB class. As the previous article explains, this flag provides a convenient was to verify whether or not the database has changed.
The Lookup method is a bit more involved, since it has to support all three outcomes implied by the protocol:
- If the
idis invalid, a result to that effect is returned. - If the user isn't found, a result to that effect is returned.
- If the user with the requested
idis found, then that user is returned.
Happy path test case #
This is all you need in terms of Test Doubles. You now have a test-specific IUserReader and IUserRepository implementation that you can pass to the Post method. Notice that a single class implements multiple interfaces. This is often key to be able to implement a Fake object in the first place.
Like in the previous article, you can start by exercising the happy path where a user successfully connects with another user:
[Theory, UserManagementTestConventions] public void UsersSuccessfullyConnect( [Frozen(Matching.ImplementedInterfaces)]FakeDB db, User user, User otherUser, ConnectionsController sut) { db.Add(user); db.Add(otherUser); db.IsDirty = false; var actual = sut.Post(user.Id.ToString(), otherUser.Id.ToString()); var ok = Assert.IsAssignableFrom<OkNegotiatedContentResult<User>>(actual); Assert.Equal(otherUser, ok.Content); Assert.True(db.IsDirty); Assert.Contains(otherUser.Id, user.Connections); }
This, and all other tests in this article use xUnit.net 2.3.1 and AutoFixture 4.1.0.
The test is organised according to my standard heuristic for formatting tests according to the Arrange Act Assert pattern. In the Arrange phase, it adds the two valid User objects to the Fake db and sets the IsDirty flag to false.
Setting the flag is necessary because this is object-oriented code, where objects have mutable state. In the previous articles with examples in F# and Haskell, the User types were immutable. Connecting two users didn't mutate one of the users, but rather returned a new User value, as this F# example demonstrates:
// User -> User -> User let addConnection user otherUser = { user with ConnectedUsers = otherUser :: user.ConnectedUsers }
In the current object-oriented code base, however, connecting one user to another is an instance method on the User class that mutates its state:
public void Connect(User otherUser) { connections.Add(otherUser.Id); }
As a consequence, the Post method could, if someone made a mistake in its implementation, call user.Connect, but forget to invoke UserRepository.Update. Even if that happened, then all the other assertions would pass. This is the reason that you need the Assert.True(db.IsDirty) assertion in the Assert phase of the test.
While we can apply to object-oriented code what we've learned from functional programming, the latter remains simpler.
Error test cases #
While there's one happy path, there's four distinct error paths that you ought to cover. You can use the Fake database for that as well:
[Theory, UserManagementTestConventions] public void UsersFailToConnectWhenUserIdIsInvalid( [Frozen(Matching.ImplementedInterfaces)]FakeDB db, string userId, User otherUser, ConnectionsController sut) { Assert.False(int.TryParse(userId, out var _)); db.Add(otherUser); db.IsDirty = false; var actual = sut.Post(userId, otherUser.Id.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Invalid user ID.", err.Message); Assert.False(db.IsDirty); } [Theory, UserManagementTestConventions] public void UsersFailToConnectWhenOtherUserIdIsInvalid( [Frozen(Matching.ImplementedInterfaces)]FakeDB db, User user, string otherUserId, ConnectionsController sut) { Assert.False(int.TryParse(otherUserId, out var _)); db.Add(user); db.IsDirty = false; var actual = sut.Post(user.Id.ToString(), otherUserId); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Invalid ID for other user.", err.Message); Assert.False(db.IsDirty); } [Theory, UserManagementTestConventions] public void UsersDoNotConnectWhenUserDoesNotExist( [Frozen(Matching.ImplementedInterfaces)]FakeDB db, int userId, User otherUser, ConnectionsController sut) { db.Add(otherUser); db.IsDirty = false; var actual = sut.Post(userId.ToString(), otherUser.Id.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("User not found.", err.Message); Assert.False(db.IsDirty); } [Theory, UserManagementTestConventions] public void UsersDoNotConnectWhenOtherUserDoesNotExist( [Frozen(Matching.ImplementedInterfaces)]FakeDB db, User user, int otherUserId, ConnectionsController sut) { db.Add(user); db.IsDirty = false; var actual = sut.Post(user.Id.ToString(), otherUserId.ToString()); var err = Assert.IsAssignableFrom<BadRequestErrorMessageResult>(actual); Assert.Equal("Other user not found.", err.Message); Assert.False(db.IsDirty); }
There's little to say about these tests that hasn't already been said in at least one of the previous articles. All tests inspect the state of the Fake database after calling the Post method. The exact interactions between Post and db aren't specified. Instead, these tests rely on setting up the initial state, exercising the SUT, and verifying the final state. These are all state-based tests that avoid over-specifying the interactions.
Specifically, none of these tests use Mocks and Stubs. In fact, at this incarnation of the test code, I was able to entirely remove the reference to Moq.
Summary #
The premise of Refactoring is that in order to be able to refactor, the "precondition is [...] solid tests". In reality, many development organisations have the opposite experience. When programmers attempt to make changes to how their code is organised, tests break. In xUnit Test Patterns this problem is called Fragile Tests, and the cause is often Overspecified Software. This means that tests are tightly coupled to implementation details of the SUT.
It's easy to inadvertently fall into this trap when you use Mocks and Stubs, even when you follow the rule of using Mocks for Commands and Stubs for Queries. Refactoring tests towards state-based testing with Fake objects, instead of interaction-based testing, could make test suites more robust to changes.
It's intriguing, though, that state-based testing is simpler in functional programming. In Haskell, you can simply write your tests in the State monad and compare the expected outcome to the actual outcome. Since state in Haskell is immutable, it's trivial to compare the expected with the actual state.
As soon as you introduce mutable state, structural equality is no longer safe, and instead you have to rely on other inspection mechanisms, such as the IsDirty flag seen in this, and the previous, article. This makes the tests slightly more brittle, because it tends to pull towards interaction-based testing.
While you can implement the State monad in both F# and C#, it's probably more pragmatic to express state-based tests using mutable state and the occasional IsDirty flag. As always, there's no panacea.
While this article concludes the series on moving towards state-based testing, I think that an appendix on Test Spies is in order.
Next: A pure Test Spy.
Comments
If we had checked the FakeDB contains to user (by retrieving, similar as in the F# case), and assert Connections property on the retrieved objects, would we still need the IsDirty flag? I think it would be good to create a couple of cases which demonstrates refactoring, and how overspecified tests break with the interaction based tests, while works nicely here.
ladeak, thank you for writing. The IsDirty flag is essentially a hack to work around the mutable nature of the FakeDB. As the previous article describes:
"In the previous article, the Fake database was simply an immutable dictionary. This meant that tests could easily compare expected and actual values, since they were immutable. When you use a mutable object, like the above dictionary, this is harder. Instead, what I chose to do here was to introduce an IsDirty flag. This enables easy verification of whether or not the database changed."
The Haskell example demonstrates how no IsDirty flag is required, because you can simply compare the state before and after the SUT was exercised.
You could do something similar in C# or F#, but that would require you to take an immutable snapshot of the Fake database before exercising the SUT, and then compare that snapshot with the state of the Fake database after the SUT was exercised. This is definitely also doable (as the Haskell example demonstrates), but a bit more work, which is the (unprincipled, pragmatic) reason I instead chose to use an IsDirty flag.
Regarding more examples, I originally wrote another sample code base to support this talk. That sample code base contains examples that demonstrate how overspecified tests break even when you make small internal changes. I haven't yet, however, found a good home for that code base.
First of all, thank you for yet another awesome series.
The fragility of my various employers' unit tests has always bothered me, but I couldn't necessarily offer an alternative that reduced/removed that. After further thought, I initially came up with two objections to this approach (based on actual enterprise experience), but was easily able to dismiss them:
- What if the SUT has a lot of dependencies?
- Then--following best practices--the SUT is doing too much
- What if the dependency has a lot of methods
- Then--following best practices--the dependency is doing too much
After reading this series I was trying to imagine how I could introduce this into my team's codebase where both of the objections I listed above are very real problems (I am new to the team and trying to wrangle with these issues). I imagine a pragmatic first step would be to define multiple fakes for a given large SUT that attempt to group dependency behavior in some logical fashion. Per usual, you've given me a lot to think about and some motivation to clean up some code!
Sven, thank you for writing. I think that your summary of my position is accurate. A Fake affords a 'one-stop' place where you can go and address changes in you SUT APIs. You'll still need to edit test code (your Fake implementation), but in single place.
We can, on the other hand, view multiple Setup/Verify changes as a violation of the DRY principle.
I don't understand, however, why you want to involve the concept of a Fixture, one way or another. A Fake is Fake, regardless of the Fixture in which it appears.
I don't understand, however, why you want to involve the concept of a Fixture, one way or another. A Fake is Fake, regardless of the Fixture in which it appears.Mark, you are right and I had intended to remove that reference to fixtures but forgot to. I could easily see fakes living completely outside of any specific fixture.

Comments
My impression is that part of the functional programming style is to avoid function overloading. Consistent with that is the naming used by Language Ext for these concepts. In Language Ext, the function with type (in F# notation)
seq<'a> -> ('a -> 'a -> 'a) -> 'ais called Reduce and the function with type (in F# notation)seq<'a> -> 'b -> ('b -> 'a -> 'b) -> 'bis called Fold.I don't know the origin of these two names, but I remember the difference by thinking about preparing food. In cooking, reduction increases the concentration of a liquid by boiling away some of its water. I think of the returned
'aas being a highly concentrated form of the input sequence since every sequence element (and only those elements) was used to create that return value. In baking, folding is a technique that carefully combines two mixtures into one. This reminds me of how the seed value'band the sequence of'aare (typically) two different types and are combined by the given function. They are not perfect analogies, but they work for me.On a related note, I dislike that Reduce returns
'ainstead ofOption<'a>.Tyson, thank you for writing. As you may know, my book liberally employs cooking analogies, but I admit that I've never thought about reduction and fold in that light before. Good analogies, although perhaps a bit strained (pun intended).
They do work well, though, for the reasons you give.
As far as I can tell, this has more to do with the combination of Hindley–Milner type inference and currying you encounter in Haskell and ML-derived languages than it has to do with functional programming in itself. If I recall correctly, Clojure makes copious use of overloading.The problem with overloading in a language like F# is that if you imagine that the function you refer to as
foldwas also calledreduce, a partially applied expression like this would be ambiguous:What is
bar, here? Ifreduceis overloaded, is it a function, or is it a 'seed value'?As far as I can tell, the compiler can't infer that, so instead of compromising on type inference, the languages in question disallow function overloading.
Notice, additionally, that F# does allow method overloading, for the part of the language that enables interoperability with the rest of .NET. In that part of the language, type inference rarely works anyway. I'm not an expert in how the F# compiler works, but I've always understood this to indicate that the interop part of F# isn't based on Hindley-Milner. I don't see how it could be, since the .NET/IL type system isn't a Hindley-Milner type system.
The
reducefunction you refer to is, by the way, based on a semigroup instance. More specifically, it's simply how semigroups accumulate. I agree thatreduceis partial, and therefore not as pretty as one could wish, but I think a more appropriate solution is to define it onNotEmptyCollection<T>, instead of onIEnumerable<T>, as shown in that article.In other words, I don't think
reducebelongs onIEnumerable<T>at all. I know it's in both F# and Haskell, but my personal opinion is that it shouldn't be, just like Haskell'sheadfunction ought not to exist either...