ploeh blog danish software design
Semigroups
Introduction to semigroups for object-oriented programmers.
This article is part of a larger series about monoids, semigroups, and other group-like algebraic structures. In this article, you'll learn what a semigroup is, and what distinguishes it from a monoid.

Semigroups form a superset of monoids. They are associative binary operations. While monoids additionally require that an identity element exists, no such requirement exist for semigroups. In other words, all monoids are semigroups, but not all semigroups are monoids.
This article gives you an overview of semigroups, as well as a few small examples. A supplemental article will show a more elaborate example.
Minimum #
An operation that returns the smallest of two values form a semigroup. In the .NET Base Class Library, such an operation is already defined for many numbers, for example 32-bit integers. Since associativity is a property of a semigroup, it makes sense to demonstrate it with a property-based test, here using FsCheck:
[Property(QuietOnSuccess = true)] public void IntMinimumIsAssociative(int x, int y, int z) { Assert.Equal( Math.Min(Math.Min(x, y), z), Math.Min(x, Math.Min(y, z))); }
This example uses the FsCheck.Xunit glue library for xUnit.net. Notice that although FsCheck is written in F#, you can also use it from C#. This test (as well as all other tests in this article) passes.
For mathematical integers, no identity element exists, so the minimum operation doesn't form a monoid. In practice, however, .NET 32-bit integers do have an identity element:
[Property(QuietOnSuccess = true)] public void MimimumIntHasIdentity(int x) { Assert.Equal(x, Math.Min(int.MaxValue, x)); Assert.Equal(x, Math.Min(x, int.MaxValue)); }
Int32.MaxValue is the maximum possible 32-bit integer value, so it effectively behaves as the identity for the 32-bit integer minimum operation. All 32-bit numbers are smaller than, or equal to, Int32.MaxValue. This effectively makes Math.Min(int, int) a monoid, but conceptually, it's not.
This may be clearer if, instead of 32-bit integers, you consider BigInteger, which is an arbitrarily large (or small) integer. The minimum operation is still associative:
[Property(QuietOnSuccess = true)] public void BigIntMinimumIsAssociative( BigInteger x, BigInteger y, BigInteger z) { Assert.Equal( BigInteger.Min(BigInteger.Min(x, y), z), BigInteger.Min(x, BigInteger.Min(y, z))); }
No identity element exists, however, because no matter which integer you have, you can always find one that's bigger: no maximum value exists. This makes BigInteger.Min a semigroup, but not a monoid.
Maximum #
Like minimum, the maximum operation forms a semigroup, here demonstrated by BigInteger.Max:
[Property(QuietOnSuccess = true)] public void BigIntMaximumIsAssociative( BigInteger x, BigInteger y, BigInteger z) { Assert.Equal( BigInteger.Max(BigInteger.Max(x, y), z), BigInteger.Max(x, BigInteger.Max(y, z))); }
Again, like minimum, no identity element exists because the set of integers is infinite; you can always find a bigger or smaller number.
Minimum and maximum operations aren't limited to primitive numbers. If values can be compared, you can always find the smallest or largest of two values, here demonstrated with DateTime values:
[Property(QuietOnSuccess = true)] public void DateTimeMaximumIsAssociative( DateTime x, DateTime y, DateTime z) { Func<DateTime, DateTime, DateTime> dtMax = (dt1, dt2) => dt1 > dt2 ? dt1 : dt2; Assert.Equal( dtMax(dtMax(x, y), z), dtMax(x, dtMax(y, z))); }
As was the case with 32-bit integers, however, the presence of DateTime.MinValue effectively makes dtMax a monoid, but conceptually, no identity element exists, because dates are infinite.
First #
Another binary operation simply returns the first of two values:
public static T First<T>(T x, T y) { return x; }
This may seem pointless, but First is associative:
[Property(QuietOnSuccess = true)] public void FirstIsAssociative(Guid x, Guid y, Guid z) { Assert.Equal( First(First(x, y), z), First(x, First(y, z))); }
On the other hand, there's no identity element, because there's no left identity. The left identity is an element e such that First(e, x) == x for any x. Clearly, for any generic type T, no such element exists because First(e, x) will only return x when x is equal to e. (There are, however, degenerate types for which an identity exists for First. Can you find an example?)
Last #
Like First, a binary operation that returns the last (second) of two values also forms a semigroup:
public static T Last<T>(T x, T y) { return y; }
Similar to First, Last is associative:
[Property(QuietOnSuccess = true)] public void LastIsAssociative(String x, String y, String z) { Assert.Equal( Last(Last(x, y), z), Last(x, Last(y, z))); }
As is also the case for First, no identity exists for Last, but here the problem is the lack of a right identity. The right identity is an element e for which Last(x, e) == x for all x. Clearly, Last(x, e) can only be equal to x if e is equal to x.
Aggregation #
Perhaps you think that operations like First and Last seem useless in practice, but when you have a semigroup, you can reduce any non-empty sequence to a single value. In C#, you can use the Aggregate LINQ method for this. For example
var a = new[] { 1, 0, 1337, -10, 42 }.Aggregate(Math.Min);
returns -10, while
var a = new[] { 1, 0, 1337, -10, 42 }.Aggregate(Math.Max);
returns 1337. Notice that the input sequence is the same in both examples, but the semigroup differs. Likewise, you can use Aggregate with First:
var a = new[] { 1, 0, 1337, -10, 42 }.Aggregate(First);
Here, a is 1, while
var a = new[] { 1, 0, 1337, -10, 42 }.Aggregate(Last);
returns 42.
LINQ has specialised methods like Min, Last, and so on, but from the perspective of behaviour, Aggregate would have been enough. While there may be performance reasons why some of those specialised methods exist, you can think of all of them as being based on the same abstraction: that of a semigroup.
Aggregate, and many of the specialised methods, throw an exception if the input sequence is empty. This is because there's no identity element in a semigroup. The method doesn't know how to create a value of the type T from an empty list.
If, on the other hand, you have a monoid, you can return the identity element in case of an empty sequence. Haskell explicitly makes this distinction with sconcat and mconcat, but I'm not going to go into that now.
Summary #
Semigroups are associative binary operations. In the previous article series about monoids you saw plenty of examples, and since all monoids are semigroups, you've already seen more than one semigroup example. In this article, however, you saw four examples of semigroups that are not monoids.
All four examples in this article are simple, and may not seem like 'real-world' examples. In the next article, then, you'll get a more realistic example of a semigroup that's not a monoid.
Next: Bounding box semigroup.
Monoids accumulate
You can accumulate an arbitrary number of monoidal values to a single value. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
Recall that a binary operation is an operation involving two arguments of the same type, and returning a value of that type.
public static Foo Op(Foo x, Foo y)
Notice that such an operation reduces two Foo values to a single Foo value.
Accumulation #
Since you have an operation that can reduce two values to a single value, you can use that single value as the input for yet another binary operation. This enables you to accumulate, or aggregate, an arbitrary number of values.
Consider the instance variation of the above Op method:
public Foo Op(Foo foo)
This is another representation of the operation, but instead of being a static method, it's an instance method on the Foo class.
When Op is a monoid, you can easily write a function that accumulates an arbitrary number of Foo values:
public static Foo Accumulate(IReadOnlyCollection<Foo> foos) { var acc = Identity; foreach (var f in foos) acc = acc.Op(f); return acc; }
You start with the Identity value, which also becomes the return value if foos is empty. Then you simply loop over each value in foos and use Op with the value accumulated so far (acc) and the current element in the sequence.
Once you're done looping, you return the accumulator.
This implementation isn't always guaranteed to be the most efficient, but you can always write accumulation like that. Sometimes, a more efficient algorithm exists, but that doesn't change the overall result that you can always reduce an arbitrary number of values whenever a monoid exists for those values.
Generalisation #
You can do this with any monoid. In Haskell, this function is called mconcat, and it has this type:
mconcat :: Monoid a => [a] -> a
The way you can read this is that for any monoid a, mconcat is a function that takes a linked list of a values as input, and returns a single a value as output.
This function seems both more general, and more constrained, than the above C# example. It's more general than the C# example because it works on any monoid, instead of just Foo.Op. On the other hand, it seems more limited because it works only on Haskell lists. The C# example, in contrast, can accumulate any IReadOnlyCollection<Foo>. Could you somehow combine those two generalisations?
Nothing stops you from doing that, but it's already in Haskell's Data.Foldable module:
fold :: (Monoid m, Foldable t) => t m -> m
The way to read this is that there's a function called fold, and it accumulates any monoid m contained in any 'foldable' data container t. That a data container is 'foldable' means that there's a way to somehow fold, or aggregate, the element(s) in the container into a value.
Linked lists, arrays, and other types of sequences are foldable, as are Maybe and trees.
In fact, there's little difference between Haskell's Foldable type class and .NET's IEnumerable<T>, but as the names suggest, their foci are different. In Haskell, the focus is being able to fold, accumulate, or aggregate a data structure, whereas on .NET the focus is on being able to enumerate the values inside the data structure. Ultimately, though, both abstractions afford the same capabilities.
In .NET, the focal abstraction is the Iterator pattern, which enables you to enumerate the values in the data container. On top of that abstraction, you can derive other behaviour, such as the ability to Aggregate data.
In Haskell, the focus is on the ability to fold, but from that central abstraction follows the ability to convert the data container into a linked list, which you can then enumerate.
Summary #
You can accumulate an arbitrary number of monoidal values as long as they're held in a container that enables you to 'fold' it. This includes all sorts of lists and arrays.
This article concludes the article series about monoids. In the next series of articles, you'll learn about a related category of operations.
Next: Semigroups.
Endomorphism monoid
A method that returns the same type of output as its input forms a monoid. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity). Methods that return the same type of value as their input form monoids over composition. The formal term for such an operation is an endomorphism.
Scheduling example #
Imagine that you have to develop some functionality for scheduling events in the future. As a concrete example, I recently wrote about adjusting dates while taking bank holidays into account. For instance, if you want to find the latest bank day before a given date, you could call the AdjustToLatestPrecedingDutchBankDay method. If you give it a normal bank day (say, a Thursday), it'll simply return the input date, but if you give it a Sunday, it'll return the preceding Friday. That is, unless that particular Friday is a bank holiday, in which case it'll return the Thursday before - as long as that's not also a bank holiday, and so on.
In that previous article, the AdjustToLatestPrecedingDutchBankDay method is an extension method, but you can also model it as an instance method, like this:
public DateTimeOffset Adjust(DateTimeOffset value) { var candidate = value; while (!(IsDutchBankDay(candidate.DateTime))) candidate = candidate.AddDays(-1); return candidate; }
This method would be part of a class that implements an interface:
public interface IDateTimeOffsetAdjustment { DateTimeOffset Adjust(DateTimeOffset value); }
You can make other implementations of this interface. Here's one that adjusts a date and time to business hours:
public class BusinessHoursAdjustment : IDateTimeOffsetAdjustment { private readonly static TimeSpan startOfBussiness = TimeSpan.FromHours(9); private readonly static TimeSpan endOfBusiness = TimeSpan.FromHours(17); public DateTimeOffset Adjust(DateTimeOffset value) { // Warning: May not handle DST changes appropriately! // It's only example code... if (value.TimeOfDay < startOfBussiness) return value - value.TimeOfDay + startOfBussiness; if (endOfBusiness < value.TimeOfDay) return (value - value.TimeOfDay + startOfBussiness).AddDays(1); return value; } }
To keep the example simple, business hours are hard-coded to 9-17.
You could also adapt conversion to UTC:
public class UtcAdjustment : IDateTimeOffsetAdjustment { public DateTimeOffset Adjust(DateTimeOffset value) { return value.ToUniversalTime(); } }
Or add a month:
public class NextMonthAdjustment : IDateTimeOffsetAdjustment { public DateTimeOffset Adjust(DateTimeOffset value) { return value.AddMonths(1); } }
Notice that the Adjust method returns a value of the same type as its input. So far when discussing monoids, we've been looking at binary operations, but Adjust is a unary operation.
An operation that returns the same type as its input is called an endomorphism. Those form monoids.
Composing adjustments #
It's easy to connect two adjustments. Perhaps, for example, you'd like to first use BusinessHoursAdjustment, followed by the bank day adjustment. This will adjust an original input date and time to a date and time that falls on a bank day, within business hours.
You can do this in a general-purpose, reusable way:
public static IDateTimeOffsetAdjustment Append( this IDateTimeOffsetAdjustment x, IDateTimeOffsetAdjustment y) { return new AppendedAdjustment(x, y); } private class AppendedAdjustment : IDateTimeOffsetAdjustment { private readonly IDateTimeOffsetAdjustment x; private readonly IDateTimeOffsetAdjustment y; public AppendedAdjustment( IDateTimeOffsetAdjustment x, IDateTimeOffsetAdjustment y) { this.x = x; this.y = y; } public DateTimeOffset Adjust(DateTimeOffset value) { return y.Adjust(x.Adjust(value)); } }
The Append method takes two IDateTimeOffsetAdjustment values and combines them by wrapping them in a private implementation of IDateTimeOffsetAdjustment. When AppendedAdjustment.Adjust is called, it first calls Adjust on x, and then calls Adjust on y with the return value from the first call.
In order to keep the example simple, I omitted null guards, but apart from that, Append should work with any two implementations of IDateTimeOffsetAdjustment. In other words, it obeys the Liskov Substitution Principle.
Associativity #
The Append method is a binary operation. It takes two IDateTimeOffsetAdjustment values and returns an IDateTimeOffsetAdjustment. It's also associative, as a test like this demonstrates:
private void AppendIsAssociative( IDateTimeOffsetAdjustment x, IDateTimeOffsetAdjustment y, IDateTimeOffsetAdjustment z) { Assert.Equal( x.Append(y).Append(z), x.Append(y.Append(z))); }
As usual in this article series, such a test doesn't prove that Append is associative for all values of IDateTimeOffsetAdjustment, but if you run it as a property-based test, it demonstrates that it's quite likely.
Identity #
In true monoidal fashion, IDateTimeOffsetAdjustment also has an identity element:
public class IdentityDateTimeOffsetAdjustment : IDateTimeOffsetAdjustment { public DateTimeOffset Adjust(DateTimeOffset value) { return value; } }
This implementation simply returns the input value without modifying it. That's a neutral operation, as a test like this demonstrates:
private void AppendHasIdentity(IDateTimeOffsetAdjustment x) { Assert.Equal( x.Append(new IdentityDateTimeOffsetAdjustment()), x); Assert.Equal( new IdentityDateTimeOffsetAdjustment().Append(x), x); }
These two assertions verify that left and right identity holds.
Since Append is associative and has identity, it's a monoid.
This holds generally for any method (or function) that returns the same type as it takes as input, i.e. T SomeOperation(T x). This matches the built-in library in Haskell, where Endo is a Monoid.
Conclusion #
A method that returns a value of the same type as its (singular) input argument is called an endomorphism. You can compose two such unary operations together in order to get a composed operation. You simply take the output of the first method and use it as the input argument for the second method. That composition is a monoid. Endomorphisms form monoids.
Next: Maybe monoids.
Comments
Hi, Mark!
I'm really enjoing your series on category theory. I think you're doing a great job in making such abstract concepts accessible to us programmers. However, I found this particular episode puzzling. You claim that any composition of endomorphisms is a monoid, and you also claim to have tested that your Append method is associative. However, it is not hard to come up with a counter-example:
[Fact]
public void CounterExample()
{
IDateTimeOffsetAdjustment weekend = new WeekendAdjustment();
IDateTimeOffsetAdjustment nextMonth = new NextMonthAdjustment();
var a = new AppendedAdjustment(weekend, nextMonth);
var b = new AppendedAdjustment(nextMonth, weekend);
var startDate = new DateTimeOffset(2019, 1, 5, 0, 0, 0, TimeSpan.Zero);
Assert.Equal(a.Adjust(startDate), b.Adjust(startDate));
}
Here, WeekendAdjustment is just a simplified DutchBankDayAdjustment.
It would also be interesting to see how you can do property based testing on this, i.e. how to automatically generate meaningful instances of IDateTimeOffsetAdjustment. When I try to run your test, I get: "IDateTimeOffsetAdjustment is not handled automatically by FsCheck. Consider using another type or writing and registering a generator for it."
Tor, thank you for writing, and for your kind words. I suppose that the CounterExample test fails when one executes it; you don't explicitly write that, but that's what I expect would happen.
The Append operation is, indeed, not commutative. This is, however, not a requirement for monoids, or even for groups. Some monoids, such as addition and multiplication, are also commutative, while others, like list concatenation or, here, the endomorphism monoid, aren't.
When it comes to the FsCheck properties, I admit that I cheated slightly with the code listing in the article. I did this because the properties are a bit more complicated than what I show, and I was concerned that the extra infrastructure surrounding those tests would detract from the overall message.
The associativity property in its entirety looks like this:
[Property(QuietOnSuccess = true)] public Property AppendIsAssociative() { return Prop.ForAll( GenerateAdjustment().Three().ToArbitrary(), t => AppendIsAssociative(t.Item1, t.Item2, t.Item3)); } private void AppendIsAssociative( IDateTimeOffsetAdjustment x, IDateTimeOffsetAdjustment y, IDateTimeOffsetAdjustment z) { Assert.Equal( x.Append(y).Append(z), x.Append(y.Append(z)), new DateTimeOffsetAdjustmentComparer()); }
Where GenerateAdjustment is defined like this:
private static Gen<IDateTimeOffsetAdjustment> GenerateAdjustment() { return Gen.Elements<IDateTimeOffsetAdjustment>( new IdentityDateTimeOffsetAdjustment(), new BusinessHoursAdjustment(), new DutchBankDayAdjustment(), new NextMonthAdjustment(), new UtcAdjustment()); }
Not only did I omit all that extra scaffolding, I also pretended that IDateTimeOffsetAdjustment objects could be compared using their default implementations of Equals, which they meaningfully can't. Notice that the full property listed here also asserts using a custom equality comparer:
private class DateTimeOffsetAdjustmentComparer : IEqualityComparer<IDateTimeOffsetAdjustment> { public bool Equals(IDateTimeOffsetAdjustment x, IDateTimeOffsetAdjustment y) { var rnd = new System.Random(); var dt = new DateTimeOffset(rnd.Next(), TimeSpan.Zero); return x.Adjust(dt) == y.Adjust(dt); } public int GetHashCode(IDateTimeOffsetAdjustment obj) { return 0; } }
The custom comparer's Equals method creates a random number of ticks and uses it to create a DateTimeOffset value. It then calls Adjust on both objects, which are considered equal if they produce the same result.
The test for identity is defined in a similar fashion; it also uses GenerateAdjustment and DateTimeOffsetAdjustmentComparer.
Thank you for such a prompt and thorough reply. You are of course correct, I have been confusing associativity with commutativity. I didn't run into the same mistake during the list concatenation article, though, maybe because list concatenation more obviously is associative and not commutative. In the current article, however, I intuitively felt that the operations needed to be commutative, but your reply clears that up.
It is also helpful to see the extra scaffolding around your property based test. The article itself seemed to imply that instances of IDateTimeOffsetAdjustment could be automatically generated. Your approach to set up such a test will come in handy now that I'm convinced that I should let more of my tests be property based, even in C#!
Tor, I made the same mistake several times when I started researching all of this. I think that there's something intuitive and fundamental about commutativity, so at a superficial glance, it seems odd that we can do without it, while at the same time requiring a less intuitive property like associativity.
When it comes to computation, though, I think that it's exactly the nature of associativity that enables us to decompose big problems into several small problems. The order of how you deal with those small problems doesn't matter, as long as you apply the intermediate results in the correct order.
Dear Mark!
These additional explanations and contextual information in the comment sections deserve a place in the original text. To keep the text uncluttered this site uses clickable popups: . If you click on some of the numbers, you'll see what I mean. You might consider adding this feature to the text.
Best regards, Norbert.
Dear Mark,
Although late to the game I really enjoy and appreciate your series here explaining monoids. Your examples are quite helful in getting to a deeper understanding.
This one however have me puzzled.
As I see it, it's fairly easy to produce a counterexample to your claim (if I understand it correctly) that composition of functions with similar domain and codomain forms a monoid. To make it simple I'll use the domain of integers and define a function f(x) = x + 1 and g(x) = x * 6. They both return the same type as they take as input and yet, the composition is clearly not associative.
The possible explanation I've been able to dig out, is if we assume the set of functions we talk about and the composition operator forms a category. However in this case, it's part of the definition of a category that an identity element exist and composition is associative. But then the claim seems circular.
Am I missing anything here?
Michael, thank you for writing. Can you share a counterexample?
I've tried some casual examples with your f and g functions, but associativity seems to hold:
Prelude> (f . (g . f)) (-1) 1 Prelude> ((f . g) . f) (-1) 1 Prelude> (f . (g . f)) 0 7 Prelude> ((f . g) . f) 0 7 Prelude> (f . (g . f)) 1 13 Prelude> ((f . g) . f) 1 13 Prelude> (f . (g . f)) 2 19 Prelude> ((f . g) . f) 2 19
Casual experiments with f . f . g also indicates associativity.
I've also tried with QuickCheck:
Prelude> import Test.QuickCheck
Prelude Test.QuickCheck> f x = x + 1
Prelude Test.QuickCheck> g x = x * 6
Prelude Test.QuickCheck> :{
Prelude Test.QuickCheck| endoIsAssociative :: Int -> Bool
Prelude Test.QuickCheck| endoIsAssociative x = ((f . g) . f) x == (f . (g . f)) x
Prelude Test.QuickCheck| :}
Prelude Test.QuickCheck> quickCheck $ withMaxSuccess 100000 endoIsAssociative
+++ OK, passed 100000 tests.
The composition f . g . f doesn't seem to easily produce any counterexamples. I haven't, however, tried all possible permutations of f and g, so that's no proof.
If I recall correctly, however, associativity of endomorphisms is a property that one can prove with equational reasoning, so I'd be surprised if a counterexample exists.
Mark, thanks for a quick and quite elaborate reply.
I'm slightly embarrased. First of all, my example attempting to disprove associativity should of course contain 3 functions, not 2 as I did. And second of all I could have / should have done exactly what you did and coded up an example - and then seen the error of my assumptions without taking your time. I apologise for the inconvenience. Lesson learned!
I do appreciate your answer - and clearly I was wrong.
Something still bothers my intuition around this. I trust your statement that it actually can be proven, so clearly my intuition have got it wrong. I'll continue to work on understanding this "associativity of endomorphisms", so I can develop a stronger intuition around monoids as well as associativity.
Thank you for your help :)
Michael, being wrong is rarely a pleasant experience, but it might be a symptom that you're learning. Admitting one's mistake in public is, I believe, a sign of maturity and personal integrity. Thank you for doing that.
I don't know if I can help your intuition along, but the proof isn't that hard. I originally learned equational reasoning from this article by Bartosz Milewski, so I'm using that notation. The goal is to prove that:
(f . g) . h == f . (g . h)
for any three (pure) functions f, g, and h, where the binary operation is question is the composition operator (.) given as:
(f . g) x = f (g x)
This is Haskell syntax, where a function call is simply written as f x or g x, meaning that you call the function f or g with the value x. Brackets in Haskell work the same way as brackets in F#, which again work like in mathematics. Thus, (f . g) x means 'the composed function (f . g) called with the argument x'.
The proof might go like this:
(f . g) . h
= { eta expansion }
(\x -> (f . g) x) . h
= { definition of (.) }
(\x -> f (g x)) . h
= { eta expansion }
\y -> ((\x -> f (g x)) . h) y
= { definition of (.) }
\y -> (\x -> f (g x)) (h y)
= { substitution (x = (h y)) }
\y -> f (g (h y))
= { definition of (.) }
\y -> f ((g . h) y)
= { definition of (.) }
\y -> (f . (g . h)) y
= { eta reduction }
f . (g . h)
Writing out a proof like this isn't something I do every day, so I may have made a mistake or two. Also, I can't shake the feeling that a simpler proof is available, but on the other hand, I found it a good exercise.
Mark, thank you for the kind words!
And thank you for taking the time to write down a proof. Yes, the proof is indeed helpful. Seeing it made it clear that all function composition is associative. I think your comment about this being about pure functions (which really is quite obvious) also helped. It triggered one of the original insights that has moved me towards functional programming, which is Referential Transparency. Suddenly it was blinding obvious that functional composition of pure functions really is just term substitution - so of course it's associative.
It feels good to have my intuition up to speed :)
This has been quite a fun and valuable exchange. Thank you for taking your time. I've learned something new and that's always a source of joy.
Onwards and upwards!
Function monoids
Methods are monoids if they return monoids. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
Functions #
In statically typed C-languages, like C# or Java, methods are typically declared like this:
public Foo Bar(Baz baz, Qux qux)
As you'll see in another article, however, you can refactor any method to a method that takes a single argument as input, and returns a single (possibly complex) value as output. In abstract form, we can write it like this:
public Out1 Op1(In1 arg)
Another way to abstract a method is by using generics:
public T Op1<T1, T>(T1 x)
Another article demonstrates how this is similar to a generic function. In F#, for instance, the type of the function would be written as 'a -> 'b, whereas in Haskell it'd be written a -> b. The way to read this is that the function takes a value of the generic type T1/'a/a as input, and returns a value of the generic type T/'b/b as output. For the rest of this article, I'll favour the Haskell syntax, since it has minimal noise.
To be clear, however, although I favour the Haskell syntax because of its succinctness, I don't mean to imply that the functions that I discuss are exclusively pure - think of an F# function 'a -> 'b which may or may not be pure.
Binary combination of functions #
A function a -> b is a monoid if b is a monoid. This means that you can combine two functions with the same type. In an object-oriented context, it means that you can combine two methods with the same signature into one method as long as the return type forms a monoid.
Consider the following (facetious) C# example. You're trying to establish how secure a GUID is. Primes are important in cryptography, so the more primes a GUID contains, the better... right?
private const string primes = "2357bd"; public static int CountPrimes(Guid g) { return g.ToString("N").Count(primes.Contains); }
The CountPrimes method counts the number of prime digits in a given GUID. So far so good, but you also think that hexadecimal notation is more exotic than decimal notation, so surely, the digits A-F are somehow more secure, being more unfamiliar. Thus, you have a method to count those as well:
private const string letters = "abcdef"; public static int CountLetters(Guid g) { return g.ToString("N").Count(letters.Contains); }
Good, but both of these numbers are, clearly, excellent indicators of how secure a GUID is. Which one should you choose? Both of them, of course!
Can you combine CountPrimes and CountLetters? Yes, you can, because, while GUIDs don't form a monoid, the return type int forms a monoid over addition. This enables you to write a Combine method:
public static Func<Guid, int> Combine( Func<Guid, int> f, Func<Guid, int> g) { return x => f(x) + g(x); }
Notice that Combine takes two Func<Guid, int> values and return a new Func<Guid, int> value. It's a binary operation. Here's an example of how to use it:
var calculateSecurity = Combine(CountPrimes, CountLetters); var actual = calculateSecurity(new Guid("10763FF5-E3C8-46D1-A70F-6C1D9EDA8120")); Assert.Equal(21, actual);
Now you have an excellent measure of the security strength of GUIDs! 21 isn't that good, though, is it?
Antics aside, Combine is a binary function. Is it a monoid?
Monoid laws #
In order to be a monoid, Combine must be associative, and it is, as the following FsCheck property demonstrates:
[Property(QuietOnSuccess = true)] public void CombineIsAssociative( Func<Guid, int> f, Func<Guid, int> g, Func<Guid, int> h, Guid guid) { Assert.Equal( Combine(Combine(f, g), h)(guid), Combine(f, Combine(g, h))(guid)); }
In this property-based test, FsCheck generates three functions with the same signature. Since functions don't have structural equality, the easiest way to compare them is to call them and see whether they return the same result. This explains why the assertion invokes both associative combinations with guid. The test passes.
In order to be a monoid, Combine must also have an identity element. It does:
public static Func<Guid, int> FuncIdentity = _ => 0;
This is simply a function that ignores its input and always returns 0, which is the identity value for addition. The following test demonstrates that it behaves as expected:
[Property(QuietOnSuccess = true)] public void CombineHasIdentity(Func<Guid, int> f, Guid guid) { Assert.Equal(f(guid), Combine(FuncIdentity, f)(guid)); Assert.Equal(f(guid), Combine(f, FuncIdentity)(guid)); }
As was the case with CombineIsAssociative, in order to assert that the combined functions behave correctly, you have to call them. This, again, explains why the assertion invokes the combined functions with guid. This test passes as well.
Combine is a monoid.
Generalisation #
While the above C# code is only an example, the general rule is that any function that returns a monoid is itself a monoid. In Haskell, this rule is articulated in the standard library:
instance Monoid b => Monoid (a -> b)
This means that for any monoid b, a function a -> b is also (automatically) a monoid.
Summary #
A function or method with a return type that forms a monoid is itself a monoid.
Next: Endomorphism monoid.
Tuple monoids
Tuples of monoids form monoids. Data objects of monoids also form monoids. An article for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity). This article starts off with some easy-to-understand, but abstract results. Once these are established, however, you'll see how to use them in a relatable example, so keep reading!
Tuples #
A tuple is a group of elements. In statically typed programming languages, each element has a type, and the types don't have to be the same. As an example, in C#, you can create a tuple like this:
Tuple<int, string> pair = Tuple.Create(42, "Foo");
This creates a tuple where the first element must be an int and the second element a string. In the example, I've explicitly declared the type instead of using the var keyword, but this is only to make the type clearer (since you don't have an IDE in which to read the code).
The pair tuple is a two-tuple, which means that it must have exactly two elements, of the types given, but you can also create larger tuples:
Tuple<string, bool, int> triple = Tuple.Create("Bar", false, 42);
This is a three-tuple, but conceptually, tuples can have any size.
Pairs of monoids #
A pair (a two-tuple) forms a monoid if both elements form a monoid. Haskell formalises this by stating:
instance (Monoid a, Monoid b) => Monoid (a, b)
The way to read this is that for any monoid a and any monoid b, the pair (a, b) is also a monoid.
Perhaps this is easiest to understand with a C# example. Consider a tuple of the type Tuple<int, string>. Integers form monoids under both addition and multiplication, and strings are monoids under concatenation. Thus, you can make Tuple<int, string> form a monoid as well. For instance, use the multiplication monoid to define this binary operation:
public static Tuple<int, string> CombinePair( Tuple<int, string> x, Tuple<int, string> y) { return Tuple.Create(x.Item1 * y.Item1, x.Item2 + y.Item2); }
For this particular example, I've chosen multiplication as the binary operation for int, and the string concatenation operator + for string. The point is that since both elements are monoids, you can use their respective binary operations to return a new tuple with the combined values.
This operation is associative, as the following FsCheck property demonstrates:
[Property(QuietOnSuccess = true)] public void CombinePairIsAssociative( Tuple<int, string> x, Tuple<int, string> y, Tuple<int, string> z) { Assert.Equal( CombinePair(CombinePair(x, y), z), CombinePair(x, CombinePair(y, z))); }
This property passes for all the x, y, and z values that FsCheck generates.
The CombinePair operation has identity as well:
public static Tuple<int, string> PairIdentity = Tuple.Create(1, "");
Again, you can use the identity value for each of the elements in the tuple: 1 for the multiplication monoid, and "" for string concatenation.
This value behaves as the identity for CombinePair, at least for all non-null string values:
[Property(QuietOnSuccess = true)] public void CombinePairHasIdentity(Tuple<int, NonNull<string>> seed) { var x = Tuple.Create(seed.Item1, seed.Item2.Get); Assert.Equal(CombinePair(PairIdentity, x), CombinePair(x, PairIdentity)); Assert.Equal(x, CombinePair(x, PairIdentity)); }
Again, this test passes for all seed values generated by FsCheck.
The C# code here is only an example, but I hope it's clear how the result generalises.
Triples of monoids #
In the above section, you saw how pairs of monoids form a monoid. Not surprisingly, triples of monoids also form monoids. Here's another C# example:
public static Tuple<string, bool, int> CombineTriple( Tuple<string, bool, int> x, Tuple<string, bool, int> y) { return Tuple.Create( x.Item1 + y.Item1, x.Item2 || y.Item2, x.Item3 * y.Item3); }
The CombineTriple method is another binary operation. This time it combines two triples to a single triple. Since both string, bool, and int form monoids, it's possible to combine each element in the two tuples to create a new tuple. There's more than one monoid for integers, and the same goes for Boolean values, but here I've chosen multiplication and Boolean or, so the identity is this:
public static Tuple<string, bool, int> TripleIdentity = Tuple.Create("", false, 1);
This triple simply contains the identities for string concatenation, Boolean or, and multiplication. The operation is associative, but I'm not going to show this with a property-based test. Both tests for associativity and identity are similar to the above tests; you could consider writing them as an exercise, if you'd like.
This triple example only demonstrates a particular triple, but you can find the generalisation in Haskell:
instance (Monoid a, Monoid b, Monoid c) => Monoid (a, b, c)
This simply states that for monoids a, b, and c, the tuple (a, b, c) is also a monoid.
Generalisation #
At this point, it can hardly come as a surprise that quadruples and pentuples of monoids are also monoids. From Haskell:
instance (Monoid a, Monoid b, Monoid c, Monoid d) => Monoid (a, b, c, d) instance (Monoid a, Monoid b, Monoid c, Monoid d, Monoid e) => Monoid (a, b, c, d, e)
The Haskell standard library stops at pentuples (five-tuples), because it has to stop somewhere, but I'm sure you can see how this is a general rule.
Data objects as monoids #
If you're an object-oriented programmer, you probably don't use tuples much in your day-to-day work. I'd even suggest that you shouldn't, because tuples carry too little information to make good domain objects. For example, if you have Tuple<int, string, string>, what do the elements mean? A better design would be to introduce a small Value Object called Customer, with Id, FirstName, and LastName properties.
(In functional programming, you frequently use tuples, because they're useful for 'gluing' generic functions together. A Haskell programmer may instead say that they are useful for composing parametrically polymorphic functions, but the meaning would be the same.)
As on object-oriented developer, then why should you care that tuples of monoids are monoids?
The reason this is interesting in object-oriented programming is that there's a strong relationship between tuples and data objects (Value Objects or Data Transfer Objects). Consider the Customer examples that I sketched out a few paragraphs above. As you'll learn in a future article, you can refactor a tuple to a class, or a class to a tuple.
Example: Roster #
In Denmark, where I live, learning to swim is a mandatory part of the school curriculum. Teachers take the children to the nearby swimming stadium and teach them to swim. Since this is an activity outside of school, teachers would be prudent to keep a roster of the children. Modelled as a class, it might look like this:
public class Roster { public int Girls { get; } public int Boys { get; } public IReadOnlyCollection<string> Exemptions { get; } public Roster(int girls, int boys, params string[] exemptions) { Girls = girls; Boys = boys; Exemptions = exemptions; } // ... }
Some children may be temporarily exempt from a swimming lesson, perhaps because of a passing medical condition. This changes from lesson to lesson, so the roster keeps track of them separately. Additionally, the boys will need to go in the men's changing rooms, and the girls in the women's changing rooms. This is the reason the roster keeps track of the number of boys and girls separately.
This, however, presents a logistical problem, because there's only one teacher for a class. The children are small, so need the company of an adult.
The way my children's school solved that problem was to combine two groups of children (in Danish, en klasse, a class), each with their own teacher - one female, and one male.
To model that, the Roster class should have a Combine method:
public Roster Combine(Roster other) { return new Roster( this.Girls + other.Girls, this.Boys + other.Boys, this.Exemptions.Concat(other.Exemptions).ToArray()); }
Clearly, this is easy to implement. Just add the number of girls together, add the number of boys together, and concatenate the two lists of exemptions.
Here's an example of using the method:
[Fact] public void UsageExample() { var x = new Roster(11, 10, "Susan", "George"); var y = new Roster(12, 9, "Edward"); var roster = x.Combine(y); var expected = new Roster(23, 19, "Susan", "George", "Edward"); Assert.Equal(expected, roster); }
The Combine method is an instance method on the Roster class, taking a second Roster as input, and returning a new Roster value. It's a binary operation. Does it also have identity?
Yes, it does:
public static readonly Roster Identity = new Roster(0, 0);
Notice that the exemptions constructor argument is a params array, so omitting it means passing an empty array as the third argument.
The following properties demonstrate that the Combine operation is both associative and has identity:
[Property(QuietOnSuccess = true)] public void CombineIsAssociative(Roster x, Roster y, Roster z) { Assert.Equal( x.Combine(y).Combine(z), x.Combine(y.Combine(z))); } [Property(QuietOnSuccess = true)] public void CombineHasIdentity(Roster x) { Assert.Equal(x, Roster.Identity.Combine(x)); Assert.Equal(x, x.Combine(Roster.Identity)); }
In other words, Combine is a monoid.
This shouldn't surprise us in the least, since we've already established that tuples of monoids are monoids, and that a data class is more or less 'just' a tuple with named elements. Specifically, the Roster class is a 'tuple' of two addition monoids and the sequence concatenation monoid, so it follows that the Combine method is a monoid as well.
Roster isomorphism #
In future articles, you'll learn more about isomorphisms between various representations of objects, but in this context, I think it's relevant to show how the Roster example is isomorphic to a tuple. It's trivial, really:
public Tuple<int, int, string[]> ToTriple() { return Tuple.Create(this.Girls, this.Boys, this.Exemptions.ToArray()); } public static Roster FromTriple(Tuple<int, int, string[]> triple) { return new Roster(triple.Item1, triple.Item2, triple.Item3); }
This pair of methods turn a Roster into a triple, and a corresponding triple back into a Roster value. As the following two FsCheck properties demonstrate, these methods form an isomorphism:
[Property(QuietOnSuccess = true)] public void ToTripleRoundTrips(Roster x) { var triple = x.ToTriple(); Assert.Equal(x, Roster.FromTriple(triple)); } [Property(QuietOnSuccess = true)] public void FromTripleRoundTrips(Tuple<int, int, string[]> triple) { var roster = Roster.FromTriple(triple); Assert.Equal(triple, roster.ToTriple()); }
This isn't the only possible isomorphism between triples and Roster objects. You could create another one where the string[] element goes first, instead of last; where boys go before girls; and so on.
Summary #
Tuples of monoids are also monoids. This holds for tuples of any size, but all of the elements have to be monoids. By isomorphism, this result also applies to data objects.
Next: Function monoids.
Comments
Hi Mark, I have trouble understanding your usage of the term 'monoid' in this post. You apply it to the types string, bool, and int when you say that a tuple of those "monoids" is a monoid as well. But up to this point you made it very clear, that a type is NOT a monoid. A function can be a monoid. So, would it be more correct to say that a tuple of certain functions, which are monoids, is a monoid as well?
Punkislamist, thank you for writing. You're entirely correct that a monoid is an associative binary operation with identity. It's a function, not a type. If this article is unclear, the fault is all mine.
Not surprisingly, this topic is difficult to write about. The text has to be exact in order to avoid confusion, but since I'm only human, I sometimes make mistakes in how I phrase my explanations. While I've tried to favour the phrase that a type forms a monoid, I can see that I've slipped up once or twice in this article.
Some types form more than a single monoid. Boolean values, for instance, form exactly four monoids. Other types, like integers, form an infinite set of monoids, but the most commonly used integer monoids are addition and multiplication. Other types, particularly unit, only form a single monoid.
Why do I talk about types, then? There's at least two reasons. The first is the practical reason that most statically typed languages naturally come with a notion of types embedded. One could argue, I think, that types are a more fundamental concept than functions, since even functions have types (for instance, in Haskell, we'd characterise a binary operation with the type a -> a -> a).
A more abstract reason is that category theory mostly operates with the concepts of objects and morphisms. Such objects aren't objects in the sense of object-oriented programming, but rather correspond to types in programming languages. (Actually, a category theory object is a more fluffy concept than that, but that's the closest analogy that I'm aware of.)
In category theory, a particular monoid is an object in the category of monoids. For example, the integer addition monoid is an object in the category of monoids, as is the string concatenation monoid, etcetera.
When you consider a 'raw' programming language type like C#'s int, you're correct that it's not a monoid. It's just a type. The same goes for Haskell's corresponding Int32 type. As primitive values, we could say that the type of 32-bit integers is an object in some category (for example, the category of number representations). Such an object is not a monoid.
There exists, however, a morphism (a 'map') from the 32-bit integer object to the addition monoid (which is an object in the category of monoids). In Haskell, this morphism is the data constructor Sum:
Prelude Data.Monoid> :t Sum Sum :: a -> Sum a
What this states is that Sum is a function (i.e. a morphism) that takes an object a and turns it into an object Sum a. We have to be careful here, because Sum a is a Haskell type, whereas Sum is the function that 'elevates' an object a to Sum a. The names are similar, but the roles are different. This is a common idiom in Haskell, and has some mnemonic advantages, but it may be confusing until you get the hang of it.
We can think of Sum a as equivalent to the category theory object addition in the category of monoids. That's also how it works in Haskell: Sum a is a monoid:
Prelude Data.Monoid> Sum 40 <> Sum 2
Sum {getSum = 42}
In Haskell, <> is the polymorphic binary operation; exactly what it does depends on the object (that is: the type) on which it operates. When applied to two values of Sum a, the result of combining 40 and 2 is 42.
To be clear, Sum isn't the only morphism from the category of number representations to the category of monoids. Product is another:
Prelude Data.Monoid> :t Product
Product :: a -> Product a
Prelude Data.Monoid> Product 6 <> Product 7
Product {getProduct = 42}
Thus, there is a relationship between types and monoids, but it's most apparent in programming languages that are geared towards that way of thinking (like Haskell). In C#, it's difficult to translate some of these concepts into code, because C#'s type system isn't up to the task. Instead, when we consider a type like int, I think it's pragmatic to state that the type forms one or more monoids. I've also encountered the phrase that it gives rise to a monoid.
While you can represent a monoid with a C# interface, I've so far tried to avoid doing so, as I'm not sure whether or not it's helpful.
Hi Mark, I did not expect to recieve such an exhaustive answer. That is incredible, thank you so much! It did clear up my confusion as well. Since most of these terms and concepts are new to me, even a slight inconsistency can be really confusing. But with your additional explanation I think I got a good understanding of the terms again.
Your explanations of these concepts in general are very well written and make it easy for people unfamiliar with this topic to understand the terms and their significance. Thanks again for writing!
Punkislamist, thank you for those kind words. I'm happy to hear that what I wrote made sense to you; it makes sense to me, but I forgot to point out that I'm hardly an expert in category theory. Writing out the above answer helped clarify some things for me as well; as is common wisdom: you only really understand a topic when you teach it.
Convex hull monoid
The union of convex hulls form a monoid. Yet another non-trivial monoid example, this time in F#.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
If you're reading the series as an object-oriented programmer, I apologise for the digression, but this article exclusively contains F# code. The next article will return with more C# examples.
Convex hull #
In a past article I've described my adventures with finding convex hulls in F#. The convex hulls I've been looking at form the external convex boundary of a set of two-dimensional points. While you can generalise the concept of convex hulls to n dimensions, we're going to stick to two-dimensional hulls here.
If you have two convex hulls, you can find the convex hull of both:
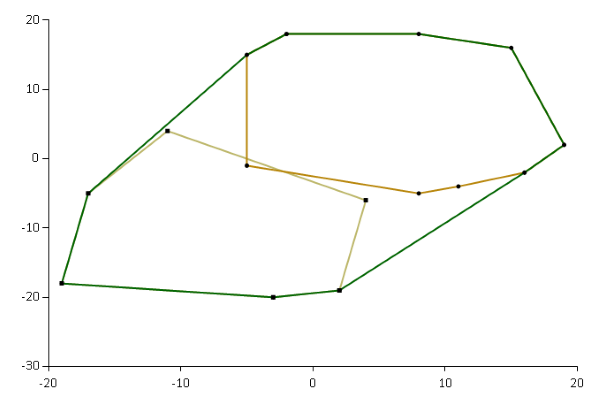
Here, the dark green outline is the convex hull of the two lighter-coloured hulls.
Finding the convex hull of two other hulls is a binary operation. Is it a monoid?
In order to examine that, I'm going to make some changes to my existing code base, the most important of which is that I'm going to introduce a Hull type. The intent is that if points are contained within this type, then only the convex hull remains. It'd be better if it was possible to make the
case constructor private, but if one does that, then the hull function can no longer be inlined and generic.
type Hull<'a> = Hull of ('a * 'a) list
With the addition of the Hull type, you can now add a binary operation:
// Hull<'a> -> Hull<'a> -> Hull<'a> let inline (+) (Hull x) (Hull y) = hull (x @ y)
This operation explicitly uses the + operator, so I'm clearly anticipating the turn of events here. Nothing much is going on, though. The function pattern-matches the points out of two Hull values. x and y are two lists of points. The + function concatenates the two lists with the @ operator, and finds the convex hull of this new list of points.
Associativity #
My choice of operator strongly suggests that the + operation is a monoid. If you have three hulls, the order in which you find the hulls doesn't matter. One way to demonstrate that property is with property-based testing. In this article, I'm using Hedgehog.
[<Fact>] let ``Hull addition is associative`` () = Property.check <| property { let! (x, y, z) = Range.linear -10000 10000 |> Gen.int |> Gen.tuple |> Gen.list (Range.linear 0 100) |> Gen.tuple3 (hull x + hull y) + hull z =! hull x + (hull y + hull z) }
This automated test generates three lists of points, x, y, and z. The hull function uses the Graham Scan algorithm to find the hull, and part of that algorithm includes calculating the cross product of three points. For large enough integers, the cross product will overflow, so the property constrains the point coordinates to stay within -10,000 and 10,000. The implication of that is that although + is associative, it's only associative for a subset of all 32-bit integers. I could probably change the internal implementation so that it calculates the cross product using bigint, but I'll leave that as an exercise to you.
For performance reasons, I also arbitrarily decided to constrain the size of each set of points to between 0 and 100 elements. If I change the maximum count to 1,000, it takes my laptop 9 seconds to run the test.
In addition to Hedgehog, this test also uses xUnit.net, and Unquote for assertions. The =! operator is the Unquote way of saying must equal. It's an assertion.
This property passes, which demonstrates that the + operator for convex hulls is associative.
Identity #
Likewise, you can write a property-based test that demonstrates that an identity element exists for the + operator:
[<Fact>] let `` Hull addition has identity`` () = Property.check <| property { let! x = Range.linear -10000 10000 |> Gen.int |> Gen.tuple |> Gen.list (Range.linear 0 100) let hasIdentity = Hull.identity + hull x = hull x + Hull.identity && hull x + Hull.identity = hull x test <@ hasIdentity @> }
This test generates a list of integer pairs (x) and applies the + operator to x and Hull.identity. The test passes for all x that Hedgehog generates.
What's Hull.identity?
It's simply the empty hull:
module Hull = let identity = Hull []
If you have a set of zero 2D points, then the convex hull is empty as well.
The + operator for convex hulls is a monoid for the set of coordinates where the cross product doesn't overflow.
Summary #
If you consider that the Hull type is nothing but a container for a list, it should come as no surprise that a monoid exists. After all, list concatenation is a monoid, and the + operator shown here is a combination of list concatenation (@) and a Graham Scan.
The point of this article was mostly to demonstrate that monoids exist not only for primitive types, but also for (some) more complex types. The + operator shown here is really a set union operation. What about intersections of convex hulls? Is that a monoid as well? I'll leave that as an exercise.
Next: Tuple monoids.
Comments
Is that true that you could replace hull with any other function, and (+) operator would still be a monoid? Since the operator is based on list concatenation, the "monoidness" is probably derived from there, not from function implementation.
Mikhail, thank you for writing. You can't replace hull with any other function and expect list concatenation to remain a monoid. I'm sorry if my turn of phrase gave that impression. I can see how one could interpret my summary in that way, but it wasn't my intention to imply that this relationship holds in general. It doesn't, and it's not hard to show, because we only need to come up with a single counter-example.
One counter example is a function that always removes the first element in a list - unless the list is empty, in which case it simply returns the empty list. In Haskell, we can define a newtype with this behaviour in mind:
Prelude Data.Monoid Data.List> newtype Drop1 a = Drop1 [a] deriving (Show, Eq)
For my own convenience, I wrote the entire counter-example in GHCi (the Haskell REPL), but imagine that the Drop1 data constructor is hidden from clients. The normal way to do that is to not export the data constructor from the module. In GHCi, we can't do that, but just pretend that the Drop1 data constructor is unavailable to clients. Instead, we'll have to use this function:
Prelude Data.Monoid Data.List> drop1 = Drop1 . drop 1
The drop1 function has the type [a] -> Drop1 a; it takes a list, and returns a Drop1 value, which contains the input list, apart from its first element.
We can attempt to make Drop 1 a monoid:
Prelude Data.Monoid Data.List> :{
Prelude Data.Monoid Data.List| instance Monoid (Drop1 a) where
Prelude Data.Monoid Data.List| mempty = drop1 []
Prelude Data.Monoid Data.List| mappend (Drop1 xs) (Drop1 ys) = drop1 (xs ++ ys)
Prelude Data.Monoid Data.List| :}
Hopefully, you can see that the implementation of mappend is similar to the above F# implementation of + for convex hulls. In F#, the list concatenation operator is @, whereas in Haskell, it's ++.
This compiles, but it's easy to come up with some counter-examples that demonstrate that the monoid laws don't hold. First, associativity:
Prelude Data.Monoid Data.List> (drop1 [1..3] <> drop1 [4..6]) <> drop1 [7..9] Drop1 [5,6,8,9] Prelude Data.Monoid Data.List> drop1 [1..3] <> (drop1 [4..6] <> drop1 [7..9]) Drop1 [3,6,8,9]
(The <> operator is an infix alias for mappend.)
Clearly, [5,6,8,9] is different from [3,6,8,9], so the operation isn't associative.
Equivalently, identity fails as well:
Prelude Data.Monoid Data.List> mempty <> drop1 [1..3] Drop1 [3] Prelude Data.Monoid Data.List> drop1 [1..3] Drop1 [2,3]
Again, [3] is different from [2,3], so mempty isn't a proper identity element.
It was easy to come up with this counter-example. I haven't attempted to come up with more, but I'd be surprised if I accidentally happened to pick the only counter-example there is. Rather, I conjecture that there are infinitely many counter-examples that each proves that there's no general rule about 'wrapped' lists operations being monoids.
Money monoid
Kent Beck's money TDD example has some interesting properties.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
In the first half of Test-Driven Development By Example Kent Beck explores how to develop a simple and flexible Money API using test-driven development. Towards the end, he arrives at a design that warrants further investigation.
Kent Beck's API #
The following treatment of Kent Beck's code is based on Yawar Amin's C# reproduction of Kent Beck's original Java code, further forked and manipulated by me.
The goal of Kent Beck's exercise is to develop an object-oriented API able to handle money of multiple currencies, and for example be able to express operations such as 5 USD + 10 CHF. Towards the end of the example, he arrives at an interface that, translated to C#, looks like this:
public interface IExpression { Money Reduce(Bank bank, string to); IExpression Plus(IExpression addend); IExpression Times(int multiplier); }
The Reduce method reduces an IExpression object to a single currency (to), represented as a Money object. This is useful if you have an IExpression object that contains several currencies.
The Plus method adds another IExpression object to the current object, and returns a new IExpression. This could be money in a single currency, but could also represent money held in more than one currency.
The Times method multiplies an IExpression with a multiplier. You'll notice that, throughout this example code base, both multiplier and amounts are modelled as integers. I think that Kent Beck did this as a simplification, but a more realistic example should use decimal values.
The metaphor is that you can model money as one or more expressions. A simple expression would be 5 USD, but you could also have 5 USD + 10 CHF or 5 USD + 10 CHF + 10 USD. While you can reduce some expressions, such as 5 CHF + 7 CHF, you can't reduce an expression like 5 USD + 10 CHF unless you have an exchange rate. Instead of attempting to reduce monetary values, this particular design builds an expression tree until you decide to evaluate it. (Sounds familiar?)
Kent Beck implements IExpression twice:
Moneymodels an amount in a single currency. It contains anAmountand aCurrencyread-only property. It's the quintessential Value Object.Summodels the sum of two otherIExpressionobjects. It contains two otherIExpressionobjects, calledAugendandAddend.
IExpression sum = new Sum(Money.Dollar(5), Money.Franc(10));
where Money.Dollar and Money.Franc are two static factory methods that return Money values.
Associativity #
Did you notice that Plus is a binary operation? Could it be a monoid as well?
In order to be a monoid, it must obey the monoid laws, the first of which is that the operation must be associative. This means that for three IExpression objects, x, y, and z, x.Plus(y).Plus(z) must be equal to x.Plus(y.Plus(z)). How should you interpret equality here? The return value from Plus is another IExpression value, and interfaces don't have custom equality behaviour. Either, it's up to the individual implementations (Money and Sum) to override and implement equality, or you can use test-specific equality.
The xUnit.net assertion library supports test-specific equality via custom comparers (for more details, see my Advanced Unit Testing Pluralsight course). The original Money API does, however, already include a way to compare expressions!
The Reduce method can reduce any IExpression to a single Money object (that is, to a single currency), and since Money is a Value Object, it has structural equality. You can use this to compare the values of IExpression objects. All you need is an exchange rate.
In the book, Kent Beck uses a 2:1 exchange rate between CHF and USD. As I'm writing this, the exchange rate is 0.96 Swiss Franc to a Dollar, but since the example code consistently models money as integers, that rounds to a 1:1 exchange rate. This is, however, a degenerate case, so instead, I'm going to stick to the book's original 2:1 exchange rate.
You can now add an Adapter between Reduce and xUnit.net in the form of an IEqualityComparer<IExpression>:
public class ExpressionEqualityComparer : IEqualityComparer<IExpression> { private readonly Bank bank; public ExpressionEqualityComparer() { bank = new Bank(); bank.AddRate("CHF", "USD", 2); } public bool Equals(IExpression x, IExpression y) { var xm = bank.Reduce(x, "USD"); var ym = bank.Reduce(y, "USD"); return object.Equals(xm, ym); } public int GetHashCode(IExpression obj) { return bank.Reduce(obj, "USD").GetHashCode(); } }
You'll notice that this custom equality comparer uses a Bank object with a 2:1 exchange rate. Bank is another object from the Test-Driven Development example. It doesn't implement any interface itself, but it does appear as an argument in the Reduce method.
In order to make your test code more readable, you can add a static helper class:
public static class Compare { public static ExpressionEqualityComparer UsingBank = new ExpressionEqualityComparer(); }
This enables you to write an assertion for associativity like this:
Assert.Equal( x.Plus(y).Plus(z), x.Plus(y.Plus(z)), Compare.UsingBank);
In my fork of Yawar Amin's code base, I added this assertion to an FsCheck-based automated test, and it holds for all the Sum and Money objects that FsCheck generates.
In its present incarnation, IExpression.Plus is associative, but it's worth noting that this isn't guaranteed to last. An interface like IExpression is an extensibility point, so someone could easily add a third implementation that would violate associativity. We can tentatively conclude that Plus is currently associative, but that the situation is delicate.
Identity #
If you accept that IExpression.Plus is associative, it's a monoid candidate. If an identity element exists, then it's a monoid.
Kent Beck never adds an identity element in his book, but you can add one yourself:
public static class Plus { public readonly static IExpression Identity = new PlusIdentity(); private class PlusIdentity : IExpression { public IExpression Plus(IExpression addend) { return addend; } public Money Reduce(Bank bank, string to) { return new Money(0, to); } public IExpression Times(int multiplier) { return this; } } }
There's only a single identity element, so it makes sense to make it a Singleton. The private PlusIdentity class is a new IExpression implementation that deliberately doesn't do anything.
In Plus, it simply returns the input expression. This is the same behaviour as zero has for integer addition. When adding numbers together, zero is the identity element, and the same is the case here. This is more explicitly visible in the Reduce method, where the identity expression simply reduces to zero in the requested currency. Finally, if you multiply the identity element, you still get the identity element. Here, interestingly,
PlusIdentity behaves similar to the identity element for multiplication (1).
You can now write the following assertions for any IExpression x:
Assert.Equal(x, x.Plus(Plus.Identity), Compare.UsingBank); Assert.Equal(x, Plus.Identity.Plus(x), Compare.UsingBank);
Running this as a property-based test, it holds for all x generated by FsCheck. The same caution that applies to associativity also applies here: IExpression is an extensibility point, so you can't be sure that Plus.Identity will be the identity element for all IExpression implementations someone could create, but for the three implementations that now exist, the monoid laws hold.
IExpression.Plus is a monoid.
Multiplication #
In basic arithmetic, the multiplication operator is called times. When you write 3 * 5, it literally means that you have 3 five times (or do you have 5 three times?). In other words:
3 * 5 = 3 + 3 + 3 + 3 + 3
Does a similar relationship exist for IExpression?
Perhaps, we can take a hint from Haskell, where monoids and semigroups are explicit parts of the core library. You're going to learn about semigroups later, but for now, it's interesting to observe that the Semigroup typeclass defines a function called stimes, which has the type Integral b => b -> a -> a. Basically, what this means that for any integer type (16-bit integer, 32-bit integer, etc.) stimes takes an integer and a value a and 'multiplies' the value. Here, a is a type for which a binary operation exists.
In C# syntax, stimes would look like this as an instance method on a Foo class:
public Foo Times(int multiplier)
I named the method Times instead of STimes, since I strongly suspect that the s in Haskell's stimes stands for Semigroup.
Notice how this is the same type of signature as IExpression.Times.
If it's possible to define a universal implementation of such a function in Haskell, could you do the same in C#? In Money, you can implement Times based on Plus:
public IExpression Times(int multiplier) { return Enumerable .Repeat((IExpression)this, multiplier) .Aggregate((x, y) => x.Plus(y)); }
The static Repeat LINQ method returns this as many times as requested by multiplier. The return value is an IEnumerable<IExpression>, but according to the IExpression interface, Times must return a single IExpression value. You can use the Aggregate LINQ method to repeatedly combine two IExpression values (x and y) to one, using the Plus method.
This implementation is hardly as efficient as the previous, individual implementation, but the point here isn't about efficiency, but about a common, reusable abstraction. The exact same implementation can be used to implement Sum.Times:
public IExpression Times(int multiplier) { return Enumerable .Repeat((IExpression)this, multiplier) .Aggregate((x, y) => x.Plus(y)); }
This is literally the same code as for Money.Times. You can also copy and paste this code to PlusIdentity.Times, but I'm not going to repeat it here, because it's the same code as above.
This means that you can remove the Times method from IExpression:
public interface IExpression { Money Reduce(Bank bank, string to); IExpression Plus(IExpression addend); }
Instead, you can implement it as an extension method:
public static class Expression { public static IExpression Times(this IExpression exp, int multiplier) { return Enumerable .Repeat(exp, multiplier) .Aggregate((x, y) => x.Plus(y)); } }
This works because any IExpression object has a Plus method.
As I've already admitted, this is likely to be less efficient than specialised implementations of Times. In Haskell, this is addressed by making stimes part of the typeclass, so that implementers can implement a more efficient algorithm than the default implementation. In C#, the same effect could be achieved by refactoring IExpression to an abstract base class, with Times as a public virtual (overridable) method.
Haskell sanity check #
Since Haskell has a more formal definition of a monoid, you may want to try to port Kent Beck's API to Haskell, as a proof of concept. In its final modification, my C# fork has three implementations of IExpression:
MoneySumPlusIdentity
data Expression = Money { amount :: Int, currency :: String } | Sum { augend :: Expression, addend :: Expression } | MoneyIdentity deriving (Show)
You can formally make this a Monoid:
instance Monoid Expression where mempty = MoneyIdentity mappend MoneyIdentity y = y mappend x MoneyIdentity = x mappend x y = Sum x y
The C# Plus method is here implemented by the mappend function. The only remaining member of IExpression is Reduce, which you can implement like this:
import Data.Map.Strict (Map, (!)) reduce :: Ord a => Map (String, a) Int -> a -> Expression -> Int reduce bank to (Money amt cur) = amt `div` rate where rate = bank ! (cur, to) reduce bank to (Sum x y) = reduce bank to x + reduce bank to y reduce _ _ MoneyIdentity = 0
Haskell's typeclass mechanism takes care of the rest, so that, for example, you can reproduce one of Kent Beck's original tests like this:
λ> let bank = fromList [(("CHF","USD"),2), (("USD", "USD"),1)]
λ> let sum = stimesMonoid 2 $ MoneyPort.Sum (Money 5 "USD") (Money 10 "CHF")
λ> reduce bank "USD" sum
20
Just like stimes works for any Semigroup, stimesMonoid is defined for any Monoid, and therefore you can also use it with Expression.
With the historical 2:1 exchange rate, 5 Dollars + 10 Swiss Franc, times 2, is equivalent to 20 Dollars.
Summary #
In chapter 17 of his book, Kent Beck describes that he'd been TDD'ing a Money API many times before trying out the expression-based API he ultimately used in the book. In other words, he had much experience, both with this particular problem, and with programming in general. Clearly this is a highly skilled programmer at work.
I find it interesting that he seems to intuitively arrive at a design involving a monoid and an interpreter. If he did this on purpose, he doesn't say so in the book, so I rather speculate that he arrived at the design simply because he recognised its superiority. This is the reason that I find it interesting to identify this, an existing example, as a monoid, because it indicates that there's something supremely comprehensible about monoid-based APIs. It's conceptually 'just like addition'.
In this article, we returned to a decade-old code example in order to identify it as a monoid. In the next article, I'm going to revisit an example code base of mine from 2015.
Next: Convex hull monoid.
Comments
You'll notice that, throughout this example code base, both multiplier and amounts are modelled as integers. I think that Kent Beck did this as a simplification, but a more realistic example should use decimal values.
Actually, in a lot of financial systems money is stored in cents, and therefore as integers, because it avoids rounding errors.
Great articles btw! :)
Hrvoje, thank you for writing. Yes, it's a good point that you could model the values as cents and rappen, but I think I recall that Kent Beck's text distinctly discusses dollars and francs. I am, however, currently travelling, without access to the book, so I can't check.
The scenario, as simplistic as it may be, involves currency exchange, and exchange rates tend to involve much smaller fractions. As an example, right now, one currency exchange web site reports that 1 CHF is 1.01950 USD. Clearly, representing the U.S. currency with cents would incur a loss of precision, because that would imply an exchange rate of 102 cents to 100 rappen. I'm sure arbitrage opportunities would be legion if you ever wrote code like that.
If I remember number theory correctly, you can always scale any rational number to an integer. I.e. in this case, you could scale 1.01950 to 101,950. There's little reason to do that, because you have the decimal struct for that purpose:
"The Decimal value type is appropriate for financial calculations that require large numbers of significant integral and fractional digits and no round-off errors."All of this, however, is just idle speculation on my point. I admit that I've never had to implement complex financial calculations, so there may be some edge cases of which I'm not aware. For all the run-of-the-mill eCommerce and payment solutions I've implemented over the years,
decimal has always been more than adequate.
Although exchange rates are typically represented as decimal fractions, it does not follow that amounts of money should be, even if the amounts were determined by calculations involving that exchange rate.
The oversimplified representation of foreign exchange (FX) in Kent Beck's money examples has always struck me as a particularly weak aspect (and not simply because they are integers; that's the least of the problems). You could argue that the very poor modelling of FX is tolerable because that aspect of the problem domain is not the focus in his example. But I think it's problematic because it can lead you to the wrong conclusion about the design of the central parts of the model. Your conclusion that it might be a good idea not to represent a money amount as an integer is an example - I believe it's the wrong conclusion, and that you've been led to it by the completely wrong-headed way his example represents FX.
The nature of foreign exchange is that it is a transaction with a third party. Some entity (perhaps a bank, or the FX trading desk within an company that may or may not be a financial institution (large multinational firms sometimes have their own FX desks) or maybe a friend who has some of the kind of currency you need in her purse) agrees to give you a specific amount of one currency if you give them a specific amount of some other currency, and there is usually an accompanying agreement on the timescale in which the actual monies are to be transferred. (There will sometimes be more than two currencies involved, either because you're doing something complex, or just because you agree to pay a commission fee in some currency that is different from either the 'to' or 'from' currency.) The amounts of actual money that changes hands will invariably be some integer multiple of the smallest available denomination of the currencies in question.
There may well be a published exchange rate. It might even form part of some contract, although such an advertised rate is very often not binding because markets can move fast, and the exchange rate posted when you started negotiation could change at any moment, and might not be available by the time you attempt to reach an agreement. In cases where a published exchange rate has some reliable meaning, it will necessarily come with a time limit (and unless this time limit is pretty short, the time window itself may come at a price - if someone has agreed to sell you currency for a specific price within some time window, what you have there is in effect either a future or an option, depending on whether you are allowed to decide not to complete the transaction).
One very common case where a 'current' exchange rate does in fact apply is when using a credit or debit card abroad. In this case, somewhere in the terms and conditions that you agreed to at some point in the past, it will say that the bank gets to apply the current rate for some definition of current. (The bank will generally have freedom to define what it means by 'current', which is one of the reasons you tend not to get a very good deal on such transactions.) And there will be rules (often generally accepted conventions, instead of being explicitly set out in the contract) about how the rate is applied. It will necessarily involve some amount of rounding. When you bought something on your credit card in a foreign currency, it will have been for a precise amount in that currency - merchants don't get to charge you Pi dollars for something. And when the bank debits your account, they will also do so by a precise amount - if you've ever used a card in this way you'll know that you didn't end up with some fractional number of cents or pennies or whatever in your account afterwards. So the exchange rate you got in practice will very rarely be exactly the advertised one (unless it's such a large transaction that the amounts involved have more decimal places than the 'current' exchange rate, or, by sheer coincidence, the numbers worked out in such a way that you happened to get the exact exchange rate advertised.).
So although you will often see published exchange rates with multiple decimal places, the actual exchange rate depends entirely on the agreement you strike with whoever it is that is going to give you money in the currency you want in exchange for money in the currency you have. The actual exchanges that result from such agreements do not involve fractional amounts.
Where does this leave Kent's example? Fundamentally, 'reducing' a multi-currency expression to a single-currency result will need to create at least one FX transaction (possibly several). So you'll need some sort of mechanism for agreeing the terms of those transactions with the other party or parties. And realistically you'd want to do something to minimize transaction costs (e.g., if you perform multiple USD to GBP conversions, you'll want to handle that with a single FX transaction), so you'll need some sort of logic for managing that too. It's certainly not going to be as simple as looking up the bank's rate.
Ian, thank you for writing. Much of what you write about foreign exchange matches the little I know. What interested me about Kent Beck's example was that his intuition about good programming lead him to a monoidal design.
It seems to me that your criticism mostly targets how the exchange itself is implemented, i.e. the Reduce method, or rather, its bank argument. In its current form, the Bank implementation is indisputably naive.
Would a more sophisticated Bank implementation address some of the problems? What if, instead of calling it Bank, we called it Exchange?
Already in its current form, the Bank implementation is nothing but a dictionary of exchange rates, defined by a from and a to currency. It follow that the USD/CHF entry isn't the same as the CHF/USD entry. They don't have to be each others' inverses. Doesn't this, already, enable arbitrage?
Another change that we could add to a hypothetical more sophisticated Exchange class would be to subtract a fee from the returned value. Would that address one of the other concerns?
Furthermore, we could add a time limit to each dictionary of exchange rates.
It's not my intent to claim that such a model would be sufficient to implement an international bank's foreign exchange business, but that's not the scenario that Kent Beck had in mind. The introduction to Test-Driven Development By Example explicitly explains that the scenario is a bond portfolio management system. Doesn't the overall API he outlines sufficiently address that?
Hi Mark, thanks for the code examples here. I do have a few clarifying questions:
-
When you mention the identity element, you write, "Finally, if you multiply the identity element, you still get the identity element. Here, interestingly,
PlusIdentitybehaves similar to the identity element for multiplication (1)". But with multiplication, when you multiply the identity element with another factor, you get the other factor, not the identity element. Am I misreading you here? -
Your C# example has
Money Reduce(Bank bank, string to);, but your Haskell example hasreduce :: Ord a => Map (String, a) Int -> a -> Expression -> Int. The return types here are different, right? C# returns aMoneyobject. Haskell seems to return anIntfrom the code signature and sample output. Was this intentional?
I know I'm often focused on little details, I just want to make sure it's not a sign of me misunderstanding the main concept. The rest of the article is very clear :)
Mark, thank you for writing. You're right about the first quote - it does look a little odd. The first sentence, however, looks good enough to me. The Times method does, indeed, return this - itself. The second sentence, on the other hand, looks wrong. I'm not sure what I had in mind when I wrote that four years ago, but now that you ask, it does look incorrect. It still behaves like zero. I think I'm going to strike out that sentence. Thank you for pointing that out.
You're also right about the Haskell example. For better parity, I should have wrapped the result of reduce in a new Expression value. This is trivially possible like this:
reduce' :: Map (String, String) Int -> String -> Expression -> Expression reduce' bank to exp = Money (reduce bank to exp) to
This new 'overload' calls the above reduce function and wraps the resulting Int in a new Expression value.
After the article was written, a proposal to make Semigroup as a superclass of Monoid came out and eventually made it into GHC 8+. The changes so that the Haskell part of the article compiles (with GHC 8+) are:
{-# LANGUAGE CPP #-}
import Data.Semigroup (stimesMonoid)
#if !MIN_VERSION_base(4,11,0)
import qualified Data.Semigroup as Semigroup
#endif
instance Monoid Expression where
#if !MIN_VERSION_base(4,11,0)
mappend =
(Semigroup.<>)
#endif
mempty =
MoneyIdentity
instance Semigroup Expression where
MoneyIdentity <> y =
y
x <> MoneyIdentity =
x
x <> y =
Sum x y
Strings, lists, and sequences as a monoid
Strings, lists, and sequences are essentially the same monoid. An introduction for object-oriented programmers.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
Sequences #
C# models a lazily evaluated sequence of values as IEnumerable<T>. You can combine two sequences by appending one to the other:
xs.Concat(ys);
Here, xs and ys are instances of IEnumerable<T>. The Concat extension method concatenates two sequences together. It has the signature IEnumerable<T> Concat<T>(IEnumerable<T>, IEnumerable<T>), so it's a binary operation. If it's also associative and has identity, then it's a monoid.
Sequences are associative, because the order of evaluation doesn't change the outcome. Associativity is a property of a monoid, so one way to demonstrate this is with property-based testing:
[Property(QuietOnSuccess = true)] public void ConcatIsAssociative(int[] xs, int[] ys, int[] zs) { Assert.Equal( xs.Concat(ys).Concat(zs), xs.Concat(ys.Concat(zs))); }
This automated test uses FsCheck (yes, it also works from C#!) to demonstrate that Concat is associative. For simplicity's sake, the test declares xs, ys, and zs as arrays. This is because FsCheck natively knows how to create arrays, whereas it doesn't have built-in support for IEnumerable<T>. While you can use FsCheck's API to define how IEnumerable<T> objects should be created, I didn't want to add this extra complexity to the example. The associativity property holds for other pure implementations of IEnumerable<T> as well. Try it, if you need to convince yourself.
The Concat operation also has identity. The identity element is the empty sequence, as this FsCheck-based test demonstrates:
[Property(QuietOnSuccess = true)] public void ConcatHasIdentity(int[] xs) { Assert.Equal( Enumerable.Empty<int>().Concat(xs), xs.Concat(Enumerable.Empty<int>())); Assert.Equal( xs, xs.Concat(Enumerable.Empty<int>())); }
Appending an empty sequence before or after another sequence doesn't change the other sequence.
Since Concat is an associative binary operation with identity, it's a monoid.
Linked lists and other collections #
The above FsCheck-based tests demonstrate that Concat is a monoid for arrays. The properties hold for all pure implementations of IEnumerable<T>.
In Haskell, lazily evaluated sequences are modelled as linked lists. These are lazy because all Haskell expressions are lazily evaluated by default. The monoid laws hold for Haskell lists as well:
λ> ([1,2,3] ++ [4,5,6]) ++ [7,8,9] [1,2,3,4,5,6,7,8,9] λ> [1,2,3] ++ ([4,5,6] ++ [7,8,9]) [1,2,3,4,5,6,7,8,9] λ> [] ++ [1,2,3] [1,2,3] λ> [1,2,3] ++ [] [1,2,3]
In Haskell, ++ is the operator that corresponds to Concat in C#, but the operation is normally called append instead of concat.
In F#, linked lists are eagerly evaluated, because all F# expressions are eagerly evaluated by default. Lists are still monoids, though, because the monoid laws still hold:
> ([1; 2; 3] @ [4; 5; 6]) @ [7; 8; 9];; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [1; 2; 3] @ ([4; 5; 6] @ [7; 8; 9]);; val it : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9] > [] @ [1; 2; 3];; val it : int list = [1; 2; 3] > [1; 2; 3] @ [];; val it : int list = [1; 2; 3]
In F#, the list concatenation operator is @, instead of ++, but the behaviour is the same.
Strings #
Have you ever wondered why text values are called strings in most programming languages? After all, for most people, a string is a long flexible structure made from fibres. What does that have to do with text?
In programming, text is often arranged in memory as a consecutive block of characters, one after the other. Thus, you could think of text as characters like pearls on a string. A program often reads such a consecutive block of memory until it reaches a terminator of some kind. Thus, strings of characters have an order to them. They are similar to sequences and lists.
In fact, in Haskell, the type String is nothing but a synonym for [Char] (meaning: a list of Char values). Thus, anything you can do with lists of other values, you can do with String values:
λ> "foo" ++ []
"foo"
λ> [] ++ "foo"
"foo"
λ> ("foo" ++ "bar") ++ "baz"
"foobarbaz"
λ> "foo" ++ ("bar" ++ "baz")
"foobarbaz"
Clearly, ++ over String is a monoid in Haskell.
Likewise, in .NET, System.String implements IEnumerable<char>, so you'd expect it to be a monoid here as well - and it almost is. It's certainly associative:
[Property(QuietOnSuccess = true)] public void PlusIsAssociative(string x, string y, string z) { Assert.Equal( (x + y) + z, x + (y + z)); }
In C#, the + operator is actually defined for string, and as the FsCheck test demonstrates, it's associative. It almost also has identity. What's the equivalent of an empty list for strings? The empty string:
[Property(QuietOnSuccess = true)] public void PlusHasIdentity(NonNull<string> x) { Assert.Equal("" + x.Get, x.Get + ""); Assert.Equal(x.Get, x.Get + ""); }
Here, I had to tell FsCheck to avoid null values, because, as usual, null throws a big wrench into our attempts at being able to reason about the code.
The problem here is that "" + null and null + "" both return "", which is not equal to the input value (null). In other words, "" is not a true identity element for +, because of this single special case. (And by the way, null isn't the identity element either, because null + null returns... ""! Of course it does.) This is, however, an implementation detail. As an exercise, consider writing an (extension) method in C# that makes string a proper monoid, even for null values. If you can do that, you'll have demonstrated that string concatenation is a monoid in .NET, just as it is in Haskell.
Free monoid #
Recall that in the previous article, you learned how both addition and multiplication of numbers form monoids. There's at least one more monoid for numbers, and that's a sequence. If you have a generic sequence (IEnumerable<T>), it can contain anything, including numbers.
Imagine that you have two numbers, 3 and 4, and you want to combine them, but you haven't yet made up your mind about how you want to combine them. In order to postpone the decision, you can put both numbers in a singleton array (that is, an array with a single element, not to be confused with the Singleton design pattern):
var three = new[] { 3 }; var four = new[] { 4 };
Since sequences are monoids, you can combine them:
var combination = three.Concat(four);
This gives you a new sequence that contains both numbers. At this point, you haven't lost any information, so once you've decided how to combine the numbers, you can evaluate the data that you've collected so far. This is called the free monoid.
If you need the sum of the numbers, you can add them together:
var sum = combination.Aggregate(0, (x, y) => x + y);
(Yes, I'm aware that the Sum method exists, but I want you to see the details.) This Aggregate overloads takes a seed value as the first argument, and a function to combine two values as the second.
Here's how to get the product:
var product = combination.Aggregate(1, (x, y) => x * y);
Notice how in both cases, the seed value is the identity for the monoidal operation: 0 for addition, and 1 for multiplication. Likewise, the aggregator function uses the binary operation associated with that particular monoid.
I think it's interesting that this is called the free monoid, similar to free monads. In both cases, you collect data without initially interpreting it, and then later you can submit the collected data to one of several evaluators.
Summary #
Various collection types, like .NET sequences, arrays, or Haskell and F# lists, are monoids over concatenation. In Haskell, strings are lists, so string concatenation is a monoid as well. In .NET, the + operator for strings is a monoid if you pretend that null strings don't exist. Still, all of these are essentially variations of the same monoid.
It makes sense that C# uses + for string concatenation, because, as the previous article described, addition is the most intuitive and 'natural' of all monoids. Because you know first-grade arithmetic, you can immediately grasp the concept of addition as a metaphor. A monoid, however, is more than a metaphor; it's an abstraction that describes well-behaved binary operations, where one of those operations just happen to be addition. It's a generalisation of the concept. It's an abstraction that you already understand.
Next: Money monoid.
Comments
Thanks for this article series! Best regards, Manuel
Manuel, thank you for writing. The confusion is entirely caused by my sloppy writing. A monoid is an associative binary operation with identity. Since the free monoid essentially elevates each number to a singleton list, the binary operation in question is list concatenation.
The Aggregate method is a built-in BCL method that aggregates values. I'll have more to say about that in later articles, but aggregation in itself is not a monoid; it follows from monoids.
I've yet to find a source that explains the etymology of the 'free' terminology, but as far as I can tell, free monoids, as well as free monads, are instances of a particular abstraction that you 'get for free', so to speak. You can always put values into singleton lists, just like you can always create a free monad from any functor. These instances are lossless in the sense that performing operations on them never erase data. For the free monoid, you just keep on concatenating more values to your list of values.
This decouples the collection of data from evaluation. Data collection is lossless. Only when you want to evaluate the result must you decide on a particular type of evaluation. For integers, for example, you could choose between addition and multiplication. Once you perform the evaluation, the result is lossy.
In Haskell, the Data.Monoid module defines an <> infix operator that you can use as the binary operation associated with a particular type. For lists, you can use it like this:
Prelude Data.Monoid Data.Foldable> xs = [3] <> [4] <> [5] Prelude Data.Monoid Data.Foldable> xs [3,4,5]
Notice how the operation isn't lossy. This means you can defer the decision on how to evaluate it until later:
Prelude Data.Monoid Data.Foldable> getSum $ fold $ Sum <$> xs 12 Prelude Data.Monoid Data.Foldable> getProduct $ fold $ Product <$> xs 60
Notice how you can choose to evaluate xs to calculate the sum, or the product.
I think the word free is used in algebraic structures to suggest that all possible interpretations are left open. This is because they are not constrained by additional specific laws which would allow to further evaluate (reduce, simplify) expressions.
For example,
2+0can be simplified to
2due to Monoid laws (identity) while
2+3can be reduced to
5due to specific arithmetic laws.
Freedom from further constraints also mean that we can always devise automatically (hence free
as in free beer
) an instance from a signature.
This construction is called term algebra;
its values are essentially the syntactic structures (AST) of the expressions allowed by the signature
and the sole simplifications permitted are those specified by the general laws.
In the case of a Monoid, thanks to associativity (which is a Monoid law, not specific to any particular instance), if we consider complex expressions like
(1+3)+2we can flatten their AST to a list
[1,3,2]without losing information and still without committing yet to any specific interpretation. And for atomic expressions like
3the single node AST becomes a singleton list.
Monoids
Introduction to monoids for object-oriented programmers.
This article is part of a larger series about monoids, semigroups, and related concepts. In this article, you'll learn what a monoid is, and what distinguishes it from a semigroup.

Monoids form a subset of semigroups. The rules that govern monoids are stricter than those for semigroups, so you'd be forgiven for thinking that it would make sense to start with semigroups, and then build upon that definition to learn about monoids. From a strictly hierarchical perspective, that would make sense, but I think that monoids are more intuitive. When you see the most obvious monoid example, you'll see that they cover operations from everyday life. It's easy to think of examples of monoids, while you have to think harder to find some good semigroup examples. That's the reason I think that you should start with monoids.
Monoid laws #
What do addition (40 + 2) and multiplication (6 * 7) have in common?
They're both
- associative
- binary operations
- with a neutral element.
Binary operation #
Let's start with the most basic property. That an operation is binary means that it works on two values. Perhaps you mostly associate the word binary with binary numbers, such as 101010, but the word originates from Latin and means something like of two. Astronomers talk about binary stars, but the word is dominantly used in computing context: apart from binary numbers, you may also have heard about binary trees. When talking about binary operations, it's implied that both input values are of the same type, and that the return type is the same as the input type. In other words, a C# method like this is a proper binary operation:
public static Foo Op(Foo x, Foo y)
Sometimes, if Op is an instance method on the Foo class, it can also look like this:
public Foo Op (Foo foo)
On the other hand, this isn't a binary operation:
public static Baz Op(Foo f, Bar b)
Although it takes two input arguments, they're of different types, and the return type is a third type.
Since all involved arguments and return values are of the same type, a binary operation exhibits what Eric Evans in Domain-Driven Design calls Closure of Operations.
Associative #
In order to form a monoid, the binary operation must be associative. This simply means that the order of evaluation doesn't matter. For example, for addition, it means that
(2 + 3) + 4 = 2 + (3 + 4) = 2 + 3 + 4 = 9
Likewise, for multiplication
(2 * 3) * 4 = 2 * (3 * 4) = 2 * 3 * 4 = 24
Expressed as the above Op instance method, associativity would require that areEqual is true in the following code:
var areEqual = foo1.Op(foo2).Op(foo3) == foo1.Op(foo2.Op(foo3));
On the left-hand side, foo1.Op(foo2) is evaluated first, and the result then evaluated with foo3. On the right-hand side, foo2.Op(foo3) is evaluated first, and then used as an input argument to foo1.Op. Since the left-hand side and the right-hand side are compared with the == operator, associativity requires that areEqual is true.
In C#, if you have a custom monoid like Foo, you'll have to override Equals and implement the == operator in order to make all of this work.
Neutral element #
The third rule for monoids is that there must exist a neutral value. In the normal jargon, this is called the identity element, and this is what I'm going to be calling it from now on. I only wanted to introduce the concept using a friendlier name.
The identity element is a value that doesn't 'do' anything. For addition, for example, it's zero, because adding zero to a value doesn't change the value:
0 + 42 = 42 + 0 = 42
As an easy exercise, see if you can figure out the identity value for multiplication.
As implied by the above sum, the identity element must act neutrally both when applied to the left-hand side and the right-hand side of another value. For our Foo objects, it could look like this:
var hasIdentity = Foo.Identity.Op(foo) == foo.Op(Foo.Identity) && foo.Op(Foo.Identity) == foo;
Here, Foo.Identity is a static read-only field of the type Foo.
Examples #
There are plenty of examples of monoids. The most obvious examples are addition and multiplication, but there are more. Depending on your perspective, you could even say that there's more than one addition monoid, because there's one for integers, one for real numbers, and so on. The same can be said for multiplication.
There are also two monoids over boolean values called all and any. If you have a binary operation over boolean values called all, how do you think it works? What would be the identity value? What about any?
I'll leave you to ponder (or look up) all and any, and instead, in the next articles, show you some slightly more interesting monoids.
- Angular addition monoid
- Strings, lists, and sequences as a monoid
- Money monoid
- Convex hull monoid
- Tuple monoids
- Function monoids
- Endomorphism monoid
- Maybe monoids
- Lazy monoids
- Monoids accumulate
== operator. On the other hand, there's no Multiply method for TimeSpan, because what does it mean to multiply two durations? What would the dimension be? Time squared?
Summary #
A monoid (not to be confused with a monad) is a set (a type) equipped with a binary operation that satisfies the two monoid laws: that the operation is associative, and that an identity element exists. Addition and multiplication are prime examples, but several others exist.
(By the way, the identity element for multiplication is one (1), the all monoid is boolean and, and the any monoid is boolean or.)
Next: Angular addition monoid
Comments
Great series! I'm a big fan of intuitive abstractions and composition. Can't wait for the remaining parts.
I first heard of the closure property in SICP, where it's mentioned that:
In general, an operation for combining data objects satisfies the closure property if the results of combining things with that operation can themselves be combined using the same operation.Also, a reference to the algebraic origin of this concept is made in the foot note for this sentence:
The use of the word "closure" here comes from abstract algebra, where a set of elements is said to be closed under an operation if applying the operation to elements in the set produces an element that is again an element of the set.
It's interesting to see this concept come up over and over, although it hasn't been widely socialized as a formal construct to software composition.
This looks like it's going to be a fantastic series - I'm really looking forwards to reading the rest!
So, as we are talking about forming a vocabulary and reducing ambiguity, I have a question about the use of the word closure, which I think has more than one common meaning in this context.
In Eric Evans' "Closure of Operations", closure refers to the fact that the operation is "closed" over it's set of possible values - in other words, the set is closed under the operation.
Closure is also used to describe a function with a bound value (as in the poor man's object").
These are two separate concepts as far as I am aware. Also, I suspect that the latter meaning is likely more well known to C# devs reading this series, especially ReSharper users who have come across it's "implicitly captured closure" detection. So, if I am correct, do you think it is worth making this distinction clear to avoid potential confusion?
Sean, thank you for writing. That's a great observation, and one that I frankly admit that I hadn't made myself. In an ideal world, one of those concepts would have a different name, so that we'd be able to distinguish them from each other.
In my experience, I find that the context in which I'm using those words tend to make the usage unambiguous, but I think that you have a good point that some readers may be more familiar with closure as a captured outer value, rather than the concept of an operation where the domain and the codomain is the same. I'll see if I can make this clearer when I revisit Evans' example.
I'm recently learning category theory, and happened to read this blog. Great post! I'll follow up the series.
I find it a little confusing:
(By the way, the identity element for multiplication is one (1), all is boolean and, and any is boolean or.)
Identity element should be the element of the collection rather than operation, right? So, the id for all should be True, and that of any should be False.
Vitrun, thank you for writing. Yes, the identity for any is false, and for all it's true. There are two other monoids over Boolean values. Can you figure out what they are?
I don't understand this:
"Identity element should be the element of the collection rather than operation"Can you elaborate what you mean by that?
A monoid is a sequence (M, e, ⋆), where M is a set, e ∈ M is the identity, and ⋆ is the function/operator.
To be clear. I mean, the identity should be the element of the set, rather than the operator
Are the other two and and or?
I found you good at bridging the gap between programming practice and ivory-tower concepts. How do you do that?
Vitrun, thank you for your kind words. I don't know if I have a particular way of 'bridging the gap'; I try to identify patterns in the problems I run into, and then communicate those patterns in as simple a language as I can, with as helpful examples as I can think of...
the identity should be the element of the setYes.
Regarding monoids over Boolean values, any is another name for Boolean or, and all is another name for Boolean and. That's two monoids (any and all); in addition to those, there are two more monoids over Booleans. I could tell you what they are, but it's a good exercise if you can figure them out by yourself. If not, you can easily Google them.
Hi Mark. Thank you for these articles.
Are the other two boolean monoids not and xor? ... And the identity value for not is the input value. And the identity value for xor is any of the two input values. I did not google for them. I will just wait for your answer so that there will be thrill, and so I remember what the answer is :)
I just realized that not is not a monoid because it does not operate on two values hehe. Sorry about that.
I googled it already :)
I gave answers too soon. I just realized that I was confused about the definition of an identity value.
This is another lesson for me to read a technical writing at least two or three times before thinking that I already understood it.
Jeremiah, thank you for writing, and please accept my apologies that I didn't respond right away. Not only do I write technical content, but I also read a fair bit of it, and my experience is that I often have to work with the topic in question in order to fully grasp it. Reading a text more than once is one way of doing it. When it comes to Boolean monoids, another way is to draw up some truth tables. A third way would be to simply play with Boolean expressions in your programming language of choice. Whatever it takes; if you learned something, then I'm happy.
Thanks for this great series. I know you've specified twice that a monoid is a set equipped with a binary operation, and that's consistent with other sources. However, I'm confused when you say addition and multiplication are monoids. Is it more technically correct to say "the set of integers under addition is a monoid"?
Mark, thank you for writing. It's almost impossible to be explicitly correct all the time when discussing matters like these. It'd tend to make the text verbose, bordering on unreadable. I'm no mathematician, but I think that you're right that it's technically more correct to say that the set of integers under addition forms a monoid, or gives rise to a monoid.
If you were to insist on precision, however, then I believe that your formulation is also incorrect. Mathematically, monoids are triples consisting of 1. a set, 2. a binary, associative operation, and 3. an identity. You didn't mention the identity, which under addition is zero.
I'm not writing this to insist that 'you're wrong, and therefore I'm right'. My language is imprecise, too. I do point this out, however, to highlight just how difficult it is to be absolutely precise when discussing such concepts in prose.
Other aspects to be aware of are these:
- Addition also gives rise to a monoid on the set of rational numbers and real numbers. On complex numbers, too, I think...
- In programming, addition isn't really addition because of overflow/underflow. Exceptions to that rule are unbounded numbers like .NET's BigInteger or Haskell's Integer and Rational. (Interestingly, even in the face of overflow, 'addition' may still form a monoid, but I'll leave that as an exercise.)
- Floating-point arithmetic, as yet another consideration, in general requires some hand-waving. As far as I recall, floating-point addition isn't associative. Is it really addition, then? In practice, however, we still call it addition. Would we say that it forms a monoid?
Being precise in language can be useful when trying to learn an unfamiliar concept, but my experience with writing this series of articles is that I've been unable to keep up the rigour in my prose at all times.
Monoids, semigroups, and friends
Introduction to monoids, semigroups, and similar concepts, for object-oriented programmers.
This article series is part of an even larger series of articles about the relationship between design patterns and category theory.
Functional programming has often been criticised for its abstruse jargon. Terminology like zygohistomorphic prepromorphism doesn't help sell the message, but before we start throwing stones, we should first exit our own glass house. In object-oriented design, we have names like Bridge, Visitor, SOLID, cohesion, and so on. The words sound familiar, but can you actually explain or implement the Visitor design pattern, or characterise cohesion?
That Bridge is a word you know doesn't make object-oriented terminology better. Perhaps it even makes it worse. After all, now the word has become ambiguous: did you mean a physical structure connecting two places, or are you talking about the design pattern? Granted, in practical use, it will often be clear from the context, but it doesn't change that if someone talks about the Bridge pattern, you'll have no idea what it is, unless you've actually learned it. Thus, that the word is familiar doesn't make it better.
More than one object-oriented programmer have extolled the virtues of 'operations whose return type is the same as the type of its argument(s)'. Such vocabulary, however, is inconvenient. Wouldn't it be nice to have a single, well-defined word for this? Perhaps monoid, or semigroup?
Object-oriented hunches #
In Domain-Driven Design, Eric Evans discusses the notion of Closure of Operations, that is, operations "whose return type is the same as the type of its argument(s)." In C#, it could be a method with the signature public Foo Bar(Foo f1, Foo f2). This method takes two Foo objects as input, and returns a new Foo object as output.
As Evans points out, object designs with that quality begins to look like arithmetic. If you have an operation that takes two Foo and returns a Foo, what could it be? Could it be like addition? Multiplication? Another mathematical operation?
Some enterprise developers just 'want to get stuff done', and don't care about mathematics. To them, the value of making code more mathematical is disputable. Still, even if you 'don't like maths', you understand addition, multiplication, and so on. Arithmetic is a powerful metaphor, because all programmers understand it.
In his book Test-Driven Development: By Example, Kent Beck seems to have the same hunch, although I don't think he ever explicitly calls it out.
What Evans describes are monoids, semigroups, and similar concepts from abstract algebra. To be fair, I recently had the opportunity to discuss the matter with him, and he's perfectly aware of those concepts today. Whether he was aware of them when he wrote DDD in 2003 I don't know, but I certainly wasn't; my errand isn't to point fingers, but to point out that clever people have found this design principle valuable in object-oriented design long before they gave it a distinct name.
Relationships #
Monoids and semigroups belong to a larger group of operations called magmas. You'll learn about those later, but we'll start with monoids, move on to semigroups, and then explore other magmas. All monoids are semigroups, while the inverse doesn't hold. In other words, monoids form a subset of semigroups.
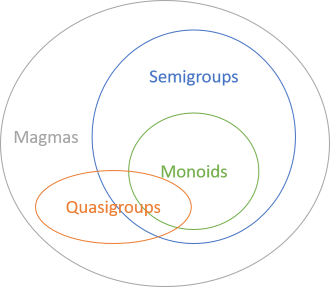
All magmas describe binary operations of the form: an operation takes two Foo values as input and returns a Foo value as output. Both categories are governed by (intuitive) laws. The difference is that the laws governing monoids are stricter than the laws governing semigroups. Don't be put off by the terminology; 'law' may sound like you have to get involved in complicated maths, but these laws are simple and intuitive. You'll learn them as you read on.
Summary #
To the average object-oriented programmer, terms like monoid and semigroup smell of mathematics, academia, and ivory-tower astronaut architects, but they're plain and simple concepts that anyone can understand, if they wish to invest 15 minutes of their time.
Whether or not an object is a magma tells us whether Evans' Closure of Operations is possible. It might teach us other things about our code, as well.
Next: Monoids.
Comments
Hi Mark,
Thank you for taking the time to write such interesting articles. I'm personally fascinated by the relationship between ancient subjects like algebra and modern ones like programming. I can't wait to read more.
That said, I understand the feeling of being put off by some of the terms used in functional programming (I'm looking at you, "zygohistomorphic"). I think the reason for it is that the vast majority of those words come from Greek or Latin, and to many people (me included) Greek is exactly what it sounds like — Greek.
Granted, things aren't much better in the object-oriented programming world, where a Visitor isn't necessarily what you think it is, even if you recognize the word.
However, in my experience, knowing the etymology of a word is the first step in understanding it. I think that including a translation for every new term would make the subjects of these articles feel less alien. It would be a way to "break the ice", so to speak.
One example I came to think of is the word polymorphism — perhaps one of the most "academic-sounding" words thrown around in object-oriented programming conversations. It may feel intimidating at first, but it quickly falls off the ivory tower once you know that it literally means "when things can take many shapes" (from the Greek polys, "many", morphē, "shape" and "ismós", the general concept).
/Enrico
Enrico, thank you for writing. Funny you should write that, because leading with an explanation of monoid is exactly what I do in my new Clean Coders episode Composite as Universal Abstraction. In short, monoid means 'one-like'. In the video, I go into more details on why that's a useful name.
Hey, Mark, what a great start on a very promising series! One more accessibility suggestion along the same lines as Enrico's: You might consider including pronunciation for new terms that aren't obvious.
Eagerly anticipating future installments!

Comments
@ploeh as always I loved your blog post but I don't 100% agree on your comparison of the iterator pattern with Foldable - the iterator pattern allows usually sideeffects and you have Traversable for that - you might also like this: http://www.cs.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf …
(Comment submitted via Twitter)