ploeh blog danish software design
An F# demo of validation with partial data round trip
An F# port of the previous Haskell proof of concept.
This article is part of a short article series on applicative validation with a twist. The twist is that validation, when it fails, should return not only a list of error messages; it should also retain that part of the input that was valid.
In the previous article you saw a Haskell proof of concept that demonstrated how to compose the appropriate applicative functor with a suitable semigroup to make validation work as desired. In this article, you'll see how to port that proof of concept to F#.
Data definitions #
Like in the previous article, we're going to need some types. These are essentially direct translations of the corresponding Haskell types:
type Input = { Name : string option; DoB : DateTime option; Address : string option} type ValidInput = { Name : string; DoB : DateTime; Address : string }
The Input type plays the role of the input we'd like to validate, while ValidInput presents validated data.
If you're an F# fan, you can bask in the reality that F# records are terser than Haskell records. I like both languages, so I have mixed feelings about this.
Computation expression #
Haskell's main workhorse is its type class system. F# doesn't have that, but it has computation expressions, which in F# 5 got support for applicative functors. That's just what we need, and it turns out that there isn't a lot of code we have to write to make all of this work.
To recap from the Haskell proof of concept: We need a Result-like container that returns a tuple for errors. One element of the tuple should be a an endomorphism, which forms a monoid (and therefore also a semigroup). The other element should be a list of error messages - another monoid. In F# terms we'll write it as (('b -> 'b) * 'c list).
That's a tuple, and since tuples form monoids when their elements do the Error part of Result supports accumulation.
To support an applicative computation expression, we're going to need a a way to merge two results together. This is by far the most complicated piece of code in this article, all six lines of code:
module Result = // Result<'a ,(('b -> 'b) * 'c list)> -> // Result<'d ,(('b -> 'b) * 'c list)> -> // Result<('a * 'd),(('b -> 'b) * 'c list)> let merge x y = match x, y with | Ok xres, Ok yres -> Ok (xres, yres) | Error (f, e1s), Error (g, e2s) -> Error (f >> g, e2s @ e1s) | Error e, Ok _ -> Error e | Ok _, Error e -> Error e
The merge function composes two input results together. The results have Ok types called 'a and 'd, and if they're both Ok values, the return value is an Ok tuple of 'a and 'd.
If one of the results is an Error value, it beats an Ok value. The only moderately complex operations is when both are Error values.
Keep in mind that an Error value in this instance contains a tuple of the type (('b -> 'b) * 'c list). The first element is an endomorphism 'b -> 'b and the other element is a list. The merge function composes the endomorphism f and g by standard function composition (the >> operator), and concatenates the lists with the standard @ list concatenation operator.
Because I'm emulating how the original forum post's code behaves, I'm concatenating the two lists with the rightmost going before the leftmost. It doesn't make any other difference than determining the order of the error list.
With the merge function in place, the computation expression is a simple matter:
type ValidationBuilder () = member _.BindReturn (x, f) = Result.map f x member _.MergeSources (x, y) = Result.merge x y
The last piece is a ValidationBuilder value:
[<AutoOpen>] module ComputationExpressions = let validation = ValidationBuilder ()
Now, whenever you use the validation computation expression, you get the desired functionality.
Validators #
Before we can compose some validation functions, we'll need to have some validators in place. These are straightforward translations of the Haskell validation functions, starting with the name validator:
// Input -> Result<string,((Input -> Input) * string list)> let validateName ({ Name = name } : Input) = match name with | Some n when n.Length > 3 -> Ok n | Some _ -> Error ( (fun (args : Input) -> { args with Name = None }), ["no bob and toms allowed"]) | None -> Error (id, ["name is required"])
When the name is too short, the endomorphism resets the Name field to None.
The date-of-birth validation function works the same way:
// DateTime -> Input -> Result<DateTime,((Input -> Input) * string list)> let validateDoB (now : DateTime) ({ DoB = dob } : Input) = match dob with | Some d when d > now.AddYears -12 -> Ok d | Some _ -> Error ( (fun (args : Input) -> { args with DoB = None }), ["get off my lawn"]) | None -> Error (id, ["dob is required"])
Again, like in the Haskell proof of concept, instead of calling DateTime.Now from within the function, I'm passing now as an argument to keep the function pure.
The address validation concludes the set of validators:
// Input -> Result<string,(('a -> 'a) * string list)> let validateAddress ({ Address = address }: Input) = match address with | Some a -> Ok a | None -> Error (id, ["add1 is required"])
The inferred endomorphism type here is the more general 'a -> 'a, but it's compatible with Input -> Input.
Composition #
All three functions have compatible Error types, so they ought to compose with the applicative computation expression to produce the desired behaviour:
// DateTime -> Input -> Result<ValidInput,(Input * string list)> let validateInput now args = validation { let! name = validateName args and! dob = validateDoB now args and! address = validateAddress args return { Name = name; DoB = dob; Address = address } } |> Result.mapError (fun (f, msgs) -> f args, msgs)
The validation expression alone produces a Result<ValidInput,((Input -> Input) * string list)> value. To get an Input value in the Error tuple, we need to 'run' the Input -> Input endomorphism. The validateInput function does that by applying the endomorphism f to args when mapping the error with Result.mapError.
Tests #
To test that the validateInput works as intended, I first copied all the code from the original forum post. I then wrote eight characterisation tests against that code to make sure that I could reproduce the desired functionality.
I then wrote a parametrised test against the new function:
[<Theory; ClassData(typeof<ValidationTestCases>)>] let ``Validation works`` input expected = let now = DateTime.Now let actual = validateInput now input expected =! actual
The ValidationTestCases class is defined like this:
type ValidationTestCases () as this = inherit TheoryData<Input, Result<ValidInput, Input * string list>> ()
This class produces a set of test cases, where each test case contains an input value and the expected output. To define the test cases, I copied the eight characterisation tests I'd already produced and adjusted them so that they fit the simpler API of the validateInput function. Here's a few examples:
let eightYearsAgo = DateTime.Now.AddYears -8 do this.Add ( { Name = Some "Alice"; DoB = Some eightYearsAgo; Address = None }, Error ( { Name = Some "Alice"; DoB = Some eightYearsAgo; Address = None }, ["add1 is required"])) do this.Add ( { Name = Some "Alice"; DoB = Some eightYearsAgo; Address = Some "x" }, Ok ({ Name = "Alice"; DoB = eightYearsAgo; Address = "x" }))
The first case expects an Error value because the Input value has no address. The other test case expects an Ok value because all input is fine.
I copied all eight characterisation tests over, so now I have those eight tests, as well as the modified eight tests for the applicative-based API shown here. All sixteen tests pass.
Conclusion #
I find this solution to the problem elegant. It's always satisfying when you can implement what at first glance looks like custom behaviour using universal abstractions.
Besides the aesthetic value, I also believe that this keeps a team more productive. These concepts of monoids, semigroups, applicative functors, and so on, are concepts that you only have to learn once. Once you know them, you'll recognise them when you run into them. This means that there's less code to understand.
An ad-hoc implementation as the original forum post suggested (even though it looked quite decent) always puts the onus on a maintenance developer to read and understand even more one-off infrastructure code.
With an architecture based on universal abstractions and well-documented language features, a functional programmer that knows these things will be able to pick up what's going on without much trouble. Specifically, (s)he will recognise that this is 'just' applicative validation with a twist.
This article is the December 28 entry in the F# Advent Calendar in English 2020.
A Haskell proof of concept of validation with partial data round trip
Which Semigroup best addresses the twist in the previous article?
This article is part of a short article series on applicative validation with a twist. The twist is that validation, when it fails, should return not only a list of error messages; it should also retain that part of the input that was valid.
In this article, I'll show how I did a quick proof of concept in Haskell.
Data definitions #
You can't use the regular Either instance of Applicative for validation because it short-circuits on the first error. In other words, you can't collect multiple error messages, even if the input has multiple issues. Instead, you need a custom Applicative instance. You can easily write such an instance yourself, but there are a couple of libraries that already do this. For this prototype, I chose the validation package.
import Data.Bifunctor import Data.Time import Data.Semigroup import Data.Validation
Apart from importing Data.Validation, I also need a few other imports for the proof of concept. All of them are well-known. I used no language extensions.
For the proof of concept, the input is a triple of a name, a date of birth, and an address:
data Input = Input { inputName :: Maybe String, inputDoB :: Maybe Day, inputAddress :: Maybe String } deriving (Eq, Show)
The goal is actually to parse (not validate) Input into a safer data type:
data ValidInput = ValidInput { validName :: String, validDoB :: Day, validAddress :: String } deriving (Eq, Show)
If parsing/validation fails, the output should report a collection of error messages and return the Input value with any valid data retained.
Looking for a Semigroup #
My hypothesis was that validation, even with that twist, can be implemented elegantly with an Applicative instance. The validation package defines its Validation data type such that it's an Applicative instance as long as its error type is a Semigroup instance:
Semigroup err => Applicative (Validation err)
The question is: which Semigroup can we use?
Since we need to return both a list of error messages and a modified Input value, it sounds like we'll need a product type of some sorts. A tuple will do; something like (Input, [String]). Is that a Semigroup instance, though?
Tuples only form semigroups if both elements give rise to a semigroup:
(Semigroup a, Semigroup b) => Semigroup (a, b)
The second element of my candidate is [String], which is fine. Lists are Semigroup instances. But what about Input? Can we somehow combine two Input values into one? It's not entirely clear how we should do that, so that doesn't seem too promising.
What we need to do, however, is to take the original Input and modify it by (optionally) resetting one or more fields. In other words, a series of functions of the type Input -> Input. Aha! There's the semigroup we need: Endo Input.
So the Semigroup instance we need is (Endo Input, [String]), and the validation output should be of the type Validation (Endo Input, [String]) a.
Validators #
Cool, we can now implement the validation logic; a function for each field, starting with the name:
validateName :: Input -> Validation (Endo Input, [String]) String validateName (Input (Just name) _ _) | length name > 3 = Success name validateName (Input (Just _) _ _) = Failure (Endo $ \x -> x { inputName = Nothing }, ["no bob and toms allowed"]) validateName _ = Failure (mempty, ["name is required"])
This function reproduces the validation logic implied by the forum question that started it all. Notice, particularly, that when the name is too short, the endomorphism resets inputName to Nothing.
The date-of-birth validation function works the same way:
validateDoB :: Day -> Input -> Validation (Endo Input, [String]) Day validateDoB now (Input _ (Just dob) _) | addGregorianYearsRollOver (-12) now < dob = Success dob validateDoB _ (Input _ (Just _) _) = Failure (Endo $ \x -> x { inputDoB = Nothing }, ["get off my lawn"]) validateDoB _ _ = Failure (mempty, ["dob is required"])
Again, the validation logic is inferred from the forum question, although I found it better keep the function pure by requiring a now argument.
The address validation is the simplest of the three validators:
validateAddress :: Monoid a => Input -> Validation (a, [String]) String validateAddress (Input _ _ (Just a)) = Success a validateAddress _ = Failure (mempty, ["add1 is required"])
This one's return type is actually more general than required, since I used mempty instead of Endo id. This means that it actually works for any Monoid a, which also includes Endo Input.
Composition #
All three functions return Validation (Endo Input, [String]), which has an Applicative instance. This means that we should be able to compose them together to get the behaviour we're looking for:
validateInput :: Day -> Input -> Either (Input, [String]) ValidInput validateInput now args = toEither $ first (first (`appEndo` args)) $ ValidInput <$> validateName args <*> validateDoB now args <*> validateAddress args
That compiles, so it probably works.
Sanity check #
Still, it'd be prudent to check. Since this is only a proof of concept, I'm not going to set up a test suite. Instead, I'll just start GHCi for some ad-hoc testing:
λ> now <- localDay <&> zonedTimeToLocalTime <&> getZonedTime
λ> validateInput now & Input Nothing Nothing Nothing
Left (Input {inputName = Nothing, inputDoB = Nothing, inputAddress = Nothing},
["name is required","dob is required","add1 is required"])
λ> validateInput now & Input (Just "Bob") Nothing Nothing
Left (Input {inputName = Nothing, inputDoB = Nothing, inputAddress = Nothing},
["no bob and toms allowed","dob is required","add1 is required"])
λ> validateInput now & Input (Just "Alice") Nothing Nothing
Left (Input {inputName = Just "Alice", inputDoB = Nothing, inputAddress = Nothing},
["dob is required","add1 is required"])
λ> validateInput now & Input (Just "Alice") (Just & fromGregorian 2002 10 12) Nothing
Left (Input {inputName = Just "Alice", inputDoB = Nothing, inputAddress = Nothing},
["get off my lawn","add1 is required"])
λ> validateInput now & Input (Just "Alice") (Just & fromGregorian 2012 4 21) Nothing
Left (Input {inputName = Just "Alice", inputDoB = Just 2012-04-21, inputAddress = Nothing},
["add1 is required"])
λ> validateInput now & Input (Just "Alice") (Just & fromGregorian 2012 4 21) (Just "x")
Right (ValidInput {validName = "Alice", validDoB = 2012-04-21, validAddress = "x"})
In order to make the output more readable, I've manually edited the GHCi session by adding line breaks to the output.
It looks like it's working like it's supposed to. Only the last line successfully parses the input and returns a Right value.
Conclusion #
Before I started this proof of concept, I had an inkling of the way this would go. Instead of making the prototype in F#, I found it more productive to do it in Haskell, since Haskell enables me to compose things together. I particularly appreciate how a composition of types like (Endo Input, [String]) is automatically a Semigroup instance. I don't have to do anything. That makes the language great for prototyping things like this.
Now that I've found the appropriate semigroup, I know how to convert the code to F#. That's in the next article.
Next: An F# demo of validation with partial data round trip.
Validation, a solved problem?
A validation problem with a twist.
Until recently, I thought that data validation was a solved problem: Use an applicative functor. I then encountered a forum question that for a few minutes shook my faith.
After brief consideration, though, I realised that all is good. Validation, even with a twist, is successfully modelled with an applicative functor. Faith in computer science restored.
The twist #
Usually, when you see a demo of applicative validation, the result of validating is one of two: either a parsed result, or a collection of error messages.
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" 4 "Jane Doe" "j@example.com"
Validation (Right (Reservation {
reservationDate = 2017-06-30 19:00:00 +0200,
reservationQuantity = 4,
reservationName = "Jane Doe",
reservationEmail = "j@example.com"}))
λ> validateReservation $ ReservationJson "2017/14/12 6pm" 4.1 "Jane Doe" "jane.example.com"
Validation (Left ["Not a date.","Not a positive integer.","Not an email address."])
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" (-3) "Jane Doe" "j@example.com"
Validation (Left ["Not a positive integer."])
(Example from Applicative validation.)
What if, instead, you're displaying an input form? When users enter data, you want to validate it. Imagine, for the rest of this short series of articles that the input form has three fields: name, date of birth, and address. Each piece of data has associated validation rules.
If you enter a valid name, but an invalid date of birth, you want to clear the input form's date of birth, but not the name. It's such a bother for a user having to retype valid data just because a single field turned out to be invalid.
Imagine, for example, that you want to bind the form to a data model like this F# record type:
type Input = { Name : string option; DoB : DateTime option; Address : string option}
Each of these three fields is optional. We'd like validation to work in the following way: If validation fails, the function should return both a list of error messages, and also the Input object, with valid data retained, but invalid data cleared.
One of the rules implied in the forum question is that names must be more than three characters long. Thus, input like this is invalid:
{ Name = Some "Tom"; DoB = Some eightYearsAgo; Address = Some "x" }
Both the DoB and Address fields, however, are valid, so, along with error messages, we'd like our validation function to return a partially wiped Input value:
{ Name = None; DoB = Some eightYearsAgo; Address = Some "x" }
Notice that both DoB and Address field values are retained, while Name has been reset.
A final requirement: If validation succeeds, the return value should be a parsed value that captures that validation took place:
type ValidInput = { Name : string; DoB : DateTime; Address : string }
That requirement is straightforward. That's how you'd usually implement application validation. It's the partial data round-trip that seems to throw a spanner in the works.
How should we model such validation?
Theory, applied #
There's a subculture of functional programming that draws heavily on category theory. This is most prevalent in Haskell. I've been studying category theory in an attempt to understand what it's all about. I even wrote a substantial article series about some design patterns and how they relate to theory.
One thing I learned after I'd named that article series is that most of the useful theoretical concepts come from abstract algebra, with the possible exception of monads.
People often ask me: does all that theory have any practical use?
Yes, it does, as it turns out. It did, for example, enable me to identify a solution to the above twist in five to ten minutes.
It's a discussion that I often have, particularly with the always friendly F# community. Do you have to understand functors, monads, etcetera to be a productive F# developer?
To anyone who wants to learn F# I'd respond: Don't worry about that at the gate. Find a good learning resource and dive right in. It's a friendly language that you can learn gradually.
Sooner or later, though, you'll run into knotty problems that you may struggle to address. I've seen this enough times that it looks like a pattern. The present forum question is just one example. A beginner or intermediate F# programmer will typically attempt to solve the problem in an ad-hoc manner that may or may not be easy to maintain. (The solution proposed by the author of that forum question doesn't, by the way, look half bad.)
To be clear: there's nothing wrong with being a beginner. I was once a beginner programmer, and I'm still a beginner in multiple ways. What I'm trying to argue here is that there is value in knowing theory. With my knowledge of abstract algebra and how it applies to functional programming, it didn't take me long to identify a solution. I'll get to that later.
Before I outline a solution, I'd like to round off the discussion of applied theory. That question about monads comes up a lot. Do I have to understand functors, monads, etcetera to be a good F# developer?
I think it's like asking Do I have to understand polymorphism, design patterns, the SOLID principles, etcetera to be a good object-oriented programmer?
Those are typically not the first topics people are taught about OOD. I would assert, however, that understanding such topics do help. They may not be required to get started with OOP, but knowing them makes you a better programmer.
I think the same is true for functional programming. It's just a different skill set that makes you better in that paradigm.
Solution outline #
When you know a bit of theory, you may know that validation can be implemented with an applicative sum type like Either (AKA Option), with one extra requirement.
Either has two dimensions, left or right (success or failure, ok or error, etcetera). The applicative nature of it already supplies a way to compose the successes, but what if there's more than one validation error?
In my article about applicative validation I showed how to collect multiple error messages in a list. Lists, however, form a monoid, so I typed the validation API to be that flexible.
In fact, all you need is a semigroup. When I wrote the article on applicative validation, Haskell's Semigroup type class wasn't yet a supertype of Monoid, and I (perhaps without sufficient contemplation) just went with Monoid.
What remains is that applicative validation can collect errors for any semigroup of errors. All we need to solve the above validation problem with a twist, then, is to identify a suitable semigroup.
I don't want to give away everything in this article, so I'm going to leave you with this cliffhanger. Which semigroup solves the problem? Read on.
- A Haskell proof of concept of validation with partial data round trip
- An F# demo of validation with partial data round trip
- A C# port of validation with partial round trip
After the Haskell article, I'll show how it translates to F#. You can skip the Haskell article if you like.
Conclusion #
I still think that validation is a solved problem. It's always interesting when such a belief for a moment is challenged, and satisfying to discover that it still holds.
This is, after all, not proof of anything. Perhaps tomorrow, someone will throw another curve ball that I can't catch. If that happens, I'll have to update my beliefs. Until then, I'll consider validation a solved problem.
Next: A Haskell proof of concept of validation with partial data round trip.
Branching tests
Is it ever okay to branch and loop in a unit test?
When I coach development organisations about unit testing and test-driven development, there's often a sizeable group of developers who don't see the value of unit testing. Some of the arguments they typically use are worth considering.
A common complaint is that it's difficult to see the wisdom in writing code to prevent defects in code. That's not an unreasonable objection.
We have scant scientific knowledge about software engineering, but the little we know suggests that the number of defects is proportional to lines of code. The more lines of code, the more defects.
If that's true, adding more code - even when it's test code - seems like a bad idea.
Reasons to trust test code #
First, we should consider the possibility that the correlation between lines of code and defects doesn't mean that defects are evenly distributed. As Adam Tornhill argues in Your Code as a Crime Scene, defects tend to cluster in hotspots.
You can have a large proportion of your code base which is, for all intents and purpose, bug-free, and hotspots where defects keep spawning.
If this is true, adding test code isn't a problem if you can keep it bug-free.
That, however, sounds like a chicken-and-the-egg kind of problem. How can you know that test code is bug-free without tests?
I've previously answered that question. In short, you can trust a test for two reasons:
- You've seen it fail (haven't you?)
- It's simple
That's what this article is actually about.
What's in a name? #
I was working with an online restaurant reservation system (example code), and had written this test:
[Theory] [InlineData("2023-11-24 19:00", "juliad@example.net", "Julia Domna", 5)] [InlineData("2024-02-13 18:15", "x@example.com", "Xenia Ng", 9)] public async Task PostValidReservationWhenDatabaseIsEmpty( string at, string email, string name, int quantity) { var db = new FakeDatabase(); var sut = new ReservationsController(db); var dto = new ReservationDto { At = at, Email = email, Name = name, Quantity = quantity }; await sut.Post(dto); var expected = new Reservation( DateTime.Parse(dto.At, CultureInfo.InvariantCulture), dto.Email, dto.Name, dto.Quantity); Assert.Contains(expected, db); }
This is a state-based test that verifies that a valid reservation makes it to the database. The test has a cyclomatic complexity of 1, and I've seen it fail, so all is good. (It may, in fact, contain a future maintenance problem, but that's a topic for another article.)
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
What constitutes a valid reservation? At the very least, we should demand that At is a valid date and time, and that Quantity is a positive number. The restaurant would like to be able to email a confirmation to the user, so an email address is also required. Email addresses are notoriously difficult to validate, so we'll just require that the the string isn't null.
What about the Name? I thought about this a bit and decided that, according to Postel's law, the system should accept null names. The name is only a convenience; the system doesn't need it, it's just there so that when you arrive at the restaurant, you can say "I have a reservation for Julia" instead of giving an email address to the maître d'hôtel. But then, if you didn't supply a name when you made the reservation, you can always state your email address when you arrive. To summarise, the name is just a convenience, not a requirement.
This decision meant that I ought to write a test case with a null name.
That turned out to present a problem. I'd defined the Reservation class so that it didn't accept null arguments, and I think that's the appropriate design. Null is just evil and has no place in my domain models.
That's not a problem in itself. In this case, I think it's acceptable to convert a null name to the empty string.
Copy and paste #
Allow me to summarise. If you consider the above unit test, I needed a third test case with a null name. In that case, expected should be a Reservation value with the name "". Not null, but "".
As far as I can tell, you can't easily express that in PostValidReservationWhenDatabaseIsEmpty without increasing its cyclomatic complexity. Based on the above introduction, that seems like a no-no.
What's the alternative? Should I copy the test and adjust the single line of code that differs? If I did, it would look like this:
[Theory] [InlineData("2023-08-23 16:55", "kite@example.edu", null, 2)] public async Task PostValidReservationWithNullNameWhenDatabaseIsEmpty( string at, string email, string name, int quantity) { var db = new FakeDatabase(); var sut = new ReservationsController(db); var dto = new ReservationDto { At = at, Email = email, Name = name, Quantity = quantity }; await sut.Post(dto); var expected = new Reservation( DateTime.Parse(dto.At, CultureInfo.InvariantCulture), dto.Email, "", dto.Quantity); Assert.Contains(expected, db); }
Apart from the values in the [InlineData] attribute and the method name, the only difference from PostValidReservationWhenDatabaseIsEmpty is that expected has a hard-coded name of "".
This is not acceptable.
There's a common misconception that the DRY principle doesn't apply to unit tests. I don't see why this should be true. The DRY principle exists because copy-and-paste code is difficult to maintain. Unit test code is also code that you have to maintain. All the rules about writing maintainable code also apply to unit test code.
Branching in test #
What's the alternative? One option (that shouldn't be easily dismissed) is to introduce a Test Helper to perform the conversion from a nullable name to a non-nullable name. Such a helper would have a cyclomatic complexity of 2, but could be unit tested in isolation. It might even turn out that it'd be useful in the production code.
Still, that seems like overkill, so I instead made the taboo move and added branching logic to the existing test to see how it'd look:
[Theory] [InlineData("2023-11-24 19:00", "juliad@example.net", "Julia Domna", 5)] [InlineData("2024-02-13 18:15", "x@example.com", "Xenia Ng", 9)] [InlineData("2023-08-23 16:55", "kite@example.edu", null, 2)] public async Task PostValidReservationWhenDatabaseIsEmpty( string at, string email, string name, int quantity) { var db = new FakeDatabase(); var sut = new ReservationsController(db); var dto = new ReservationDto { At = at, Email = email, Name = name, Quantity = quantity }; await sut.Post(dto); var expected = new Reservation( DateTime.Parse(dto.At, CultureInfo.InvariantCulture), dto.Email, dto.Name ?? "", dto.Quantity); Assert.Contains(expected, db); }
Notice that the expected name is now computed as dto.Name ?? "". Perhaps you think about branching instructions as relating exclusively to keywords such as if or switch, but the ?? operator is also a branching instruction. The test now has a cyclomatic complexity of 2.
Is that okay?
To branch or not to branch #
I think that in this case, it's okay to slightly increase the cyclomatic complexity of the test. It's not something I just pull out of my hat, though. I think it's possible to adjust the above heuristics to embrace this sort of variation.
To be clear, I consider this an advanced practice. If you're just getting started with unit testing, try to keep tests simple. Keep the cyclomatic complexity at 1.
Had I been in the above situation a couple of years ago, I might not have considered this option. About a year ago, though, I watched John Hughes' presentation Building on developers' intuitions to create effective property-based tests. When he, about 15 minutes in, wrote a test with a branching instruction, I remember becoming quite uncomfortable. This lasted for a while until I understood where he was going with it. It's truly an inspiring and illuminating talk; I highly recommend it.
How it relates to the problem presented here is through coverage. While the PostValidReservationWhenDatabaseIsEmpty test now has a cyclomatic complexity of 2, it's a parametrised test with three test cases. Two of these cover one branch, and the third covers the other.
What's more important is the process that produced the test. I added one test case at a time, and for each case, I saw the test fail.
Specifically, when I added the third test case with the null name, I first added the branching expression dto.Name ?? "" and ran the two existing tests. They still both passed, which bolstered my belief that they both exercised the left branch of that expression. I then added the third case and saw that it (and only it) failed. This supported my belief that the third case exercised the right branch of ??.
Branching in unit tests isn't something I do lightly. I still believe that it could make the test more vulnerable to future changes. I'm particularly worried about making a future change that might shift one or more of these test cases into false negatives in the form of tautological assertions.
Conclusion #
As you can tell, when I feel that I'm moving onto thin ice, I move deliberately. If there's one thing I've learned from decades of professional programming it's that my brain loves jumping to conclusions. Moving slowly and deliberately is my attempt at countering this tendency. I believe that it enables me to go faster in the long run.
I don't think that branching in unit tests should be common, but I believe that it may be occasionally valid. The key, I think, is to guarantee that each branch in the test is covered by a test case. The implication is that there must be at least as many test cases as the cyclomatic complexity. In other words, the test must be a parametrised test.
Comments
Hi Mark, I guess there is
implicit cyclomatic complexity in the testing framework itself (For example,
it loops through the InlineData records). That feels fine though, does this
somehow have less cost than cyclomatic complexity in the test code itself?
I guess, as you mentioned, it's acceptable because the alternative is violation of DRY.
With this in mind, I wonder how you feel about adding
an expectedName parameter to the InlineData
attributes, instead of the conditional in the test code? Maybe it's
harder to read though when the test data includes input and output.
James, thank you for writing. I consider the cyclomatic complexity of a method call to be 1, and Visual Studio code metrics agree with me. Whatever happens in a framework should, in my opinion, likewise be considered as encapsulated abstraction that's none of our business.
Adding an expectedName parameter to the method is definitely an option. I sometimes do that, and I could have done that here, too. In this situation, I think it's a toss-up. It'd make it harder for a later reader of the code to parse the test cases, but would simplify the test code itself, so that alternative comes with both advantages and disadvantages.
Hi Mark. To build up on the additional expectedName parameter, instead of keeping a single test with the 3 cases but the last being a edge case, I prefer introduce a specific test for the last case.
Then, to remove the duplication, we can extract a common method which will take this additional expectedName parameter:
[Theory] [InlineData("2023-11-24 19:00", "juliad@example.net", "Julia Domna", 5)] [InlineData("2024-02-13 18:15", "x@example.com", "Xenia Ng", 9)] public async Task PostValidReservationWithNameWhenDatabaseIsEmpty (string at, string email, string name, int quantity) => PostValidReservationWhenDatabaseIsEmpty(at, email, name, expectedName: name, quantity); [Fact] public async Task PostValidReservationWithoutNameWhenDatabaseIsEmpty() => PostValidReservationWhenDatabaseIsEmpty( at : "2023-11-24 19:00", email : "juliad@example.net", name : null, expectedName: "", quantity : 5); private async Task PostValidReservationWhenDatabaseIsEmpty( string at, string email, string name, string expectedName, int quantity) { var db = new FakeDatabase(); var sut = new ReservationsController(db); var dto = new ReservationDto { At = at, Email = email, Name = name, Quantity = quantity, }; await sut.Post(dto); var expected = new Reservation( DateTime.Parse(dto.At, CultureInfo.InvariantCulture), dto.Email, expectedName, // /!\ Not `dto.Name`, dto.Quantity); Assert.Contains(expected, db); }
Romain, thank you for writing. There are, indeed, many ways to skin that cat. If you're comfortable with distributing a test over more than one method, I instead prefer to use another data source for the [Theory] attribute:
private class PostValidReservationWhenDatabaseIsEmptyTestCases : TheoryData<ReservationDto, Reservation> { public PostValidReservationWhenDatabaseIsEmptyTestCases() { AddWithName(new DateTime(2023, 11, 24, 19, 0, 0), "juliad@example.net", "Julia Domna", 5); AddWithName(new DateTime(2024, 2, 13, 18, 15, 0), "x@example.com", "Xenia Ng", 9); AddWithoutName(new DateTime(2023, 8, 23, 16, 55, 0), "kite@example.edu", 2); } private void AddWithName(DateTime at, string email, string name, int quantity) { Add(new ReservationDto { At = at.ToString("O"), Email = email, Name = name, Quantity = quantity }, new Reservation(at, email, name, quantity)); } private void AddWithoutName(DateTime at, string email, int quantity) { Add(new ReservationDto { At = at.ToString("O"), Email = email, Quantity = quantity }, new Reservation(at, email, "", quantity)); } } [Theory, ClassData(typeof(PostValidReservationWhenDatabaseIsEmptyTestCases))] public async Task PostValidReservationWhenDatabaseIsEmpty( ReservationDto dto, Reservation expected) { var db = new FakeDatabase(); var sut = new ReservationsController(db); await sut.Post(dto); Assert.Contains(expected, db); }
Whether you prefer one over the other is, I think, subjective. I like my alternative, using a [ClassData] source, better, because I find it a bit more principled and 'pattern-based', if you will. I also like how small the actual test method becomes.
Your solution, on the other hand, is more portable, in the sense that you could also apply it in a testing framework that doesn't have the sort of capability that xUnit.net has. That's a definite benefit with your suggestion.
Name by role
Consider naming variables according to their role, instead of their type.
My recent article on good names might leave you with the impression that I consider good names unimportant. Not at all. That article was an attempt at delineating the limits of naming. Good names aren't the panacea some people seem to imply, but they're still important.
As the cliché goes, naming is one of the hardest problems in software development. Perhaps it's hard because you have to do it so frequently. Every time you create a variable, you have to name it. It's also an opportunity to add clarity to a code base.
A common naming strategy is to name objects after their type:
Reservation? reservation = dto.Validate(id);
or:
Restaurant? restaurant = await RestaurantDatabase.GetRestaurant(restaurantId);
There's nothing inherently wrong with a naming scheme like this. It often makes sense. The reservation variable is a Reservation object, and there's not that much more to say about it. The same goes for the restaurant object.
In some contexts, however, objects play specific roles. This is particularly prevalent with primitive types, but can happen to any type of object. It may help the reader if you name the variables according to such roles.
In this article, I'll show you several examples. I hope these examples are so plentiful and varied that they can inspire you to come up with good names. Most of the code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
A variable introduced only to be named #
In a recent article I showed this code snippet:
private bool SignatureIsValid(string candidate, ActionExecutingContext context) { var sig = context.HttpContext.Request.Query["sig"]; var receivedSignature = Convert.FromBase64String(sig.ToString()); using var hmac = new HMACSHA256(urlSigningKey); var computedSignature = hmac.ComputeHash(Encoding.ASCII.GetBytes(candidate)); var signaturesMatch = computedSignature.SequenceEqual(receivedSignature); return signaturesMatch; }
Did you wonder about the signaturesMatch variable? Why didn't I just return the result of SequenceEqual, like the following?
private bool SignatureIsValid(string candidate, ActionExecutingContext context) { var sig = context.HttpContext.Request.Query["sig"]; var receivedSignature = Convert.FromBase64String(sig.ToString()); using var hmac = new HMACSHA256(urlSigningKey); var computedSignature = hmac.ComputeHash(Encoding.ASCII.GetBytes(candidate)); return computedSignature.SequenceEqual(receivedSignature); }
Visual Studio even offers this as a possible refactoring that it'll do for you.
The inclusion of the signaturesMatch variable was a conscious decision of mine. I felt that directly returning the result of SequenceEqual was a bit too implicit. It forces readers to make the inference themselves: Ah, the two arrays contain the same sequence of bytes; that must mean that the signatures match!
Instead of asking readers to do that work themselves, I decided to do it for them. I hope that it improves readability. It doesn't change the behaviour of the code one bit.
Test roles #
When it comes to unit testing, there's plenty of inconsistent terminology. One man's mock object is another woman's test double. Most of the jargon isn't even internally consistent. Do yourself a favour and adopt a consistent pattern language. I use the one presented in xUnit Test Patterns.
For instance, the thing that you're testing is the System Under Test (SUT). This can be a pure function or a static method, but when it's an object, you're going to create a variable. Consider naming it sut. A typical test also defines other variables. Naming one of them sut clearly identifies which of them is the SUT. It also protects the tests against the class in question being renamed.
[Fact] public void ScheduleSingleReservationCommunalTable() { var table = Table.Communal(12); var sut = new MaitreD( TimeSpan.FromHours(18), TimeSpan.FromHours(21), TimeSpan.FromHours(6), table); var r = Some.Reservation; var actual = sut.Schedule(new[] { r }); var expected = new[] { new TimeSlot(r.At, table.Reserve(r)) }; Assert.Equal(expected, actual); }
The above test follows my AAA.formatting heuristic. In all, it defines five variables, but there can be little doubt about which one is the sut.
The table and r variables follow the mainstream practice of naming variables after their type. They play no special role, so that's okay. You may balk at such a short variable name as r, and that's okay. In my defence, I follow Clean Code's N5 heuristic for long and short scopes. A variable name like r is fine when it only spans three lines of code (four, if you also count the blank line).
Consider also using the variable names expected and actual, as in the above example. In many unit testing frameworks, those are the argument names for the assertion. For instance, in xUnit.net (which the above test uses) the Assert.Equals overloads are defined as Equal<T>(T expected, T actual). Using these names for variables makes the roles clearer, I think.
The other #
The above assertion relies on structural equality. The TimeSlot class is immutable, so it can safely override Equals (and GetHashCode) to implement structural equality:
public override bool Equals(object? obj) { return obj is TimeSlot other && At == other.At && Tables.SequenceEqual(other.Tables); }
I usually call the downcast variable other because, from the perspective of the instance, it's the other object. I usually use that convention whenever an instance interacts with another object of the same type. Among other examples, this happens when you model objects as semigroups and monoids. The Angle struct, for example, defines this binary operation:
public Angle Add(Angle other) { return new Angle(this.degrees + other.degrees); }
Again, the method argument is in the role as the other object, so naming it other seems natural.
Here's another example from a restaurant reservation code base:
public bool Overlaps(Seating other) { if (other is null) throw new ArgumentNullException(nameof(other)); return Start < other.End && other.Start < End; }
The Overlaps method is an instance method on the Seating class. Again, other seems natural.
Candidates #
The Overlaps method looks like a predicate, i.e. a function that returns a Boolean value. In the case of that method, other indicates the role of being the other object, but it also plays another role. It makes sense to me to call predicate input candidates. Typically, you have some input that you want to evaluate as either true or false. I think it makes sense to think of such a parameter as a 'truth candidate'. You can see one example of that in the above SignatureIsValid method.
There, the string parameter is a candidate for having a valid signature.
Here's another restaurant-related example:
public bool WillAccept( DateTime now, IEnumerable<Reservation> existingReservations, Reservation candidate) { if (existingReservations is null) throw new ArgumentNullException(nameof(existingReservations)); if (candidate is null) throw new ArgumentNullException(nameof(candidate)); if (candidate.At < now) return false; if (IsOutsideOfOpeningHours(candidate)) return false; var seating = new Seating(SeatingDuration, candidate.At); var relevantReservations = existingReservations.Where(seating.Overlaps); var availableTables = Allocate(relevantReservations); return availableTables.Any(t => t.Fits(candidate.Quantity)); }
Here, the reservation in question is actually not yet a reservation. It might be rejected, so it's a candidate reservation.
You can also use that name in TryParse methods, as shown in this article.
Data Transfer Objects #
Another name that I like to use is dto for Data Transfer Objects (DTOs). The benefit here is that as long as dto is unambiguous in context, it makes it easier to distinguish between a DTO and the domain model you might want to turn it into:
[HttpPost("restaurants/{restaurantId}/reservations")] public async Task<ActionResult> Post(int restaurantId, ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); var id = dto.ParseId() ?? Guid.NewGuid(); Reservation? reservation = dto.Validate(id); if (reservation is null) return new BadRequestResult(); var restaurant = await RestaurantDatabase.GetRestaurant(restaurantId); if (restaurant is null) return new NotFoundResult(); return await TryCreate(restaurant, reservation); }
By naming the input parameter dto, I keep the name reservation free for the domain object, which ought to be the more important object of the two.
I could have named the input parameter"A Data Transfer Object is one of those objects our mothers told us never to write."
reservationDto instead of dto, but that would diminish the 'mental distance' between reservationDto and reservation. I like to keep that distance, so that the roles are more explicit.
Time #
You often need to make decisions based on the current time or date. In .NET the return value from DateTime.Now is a DateTime value. Typical variable names are dateTime, date, time, or dt, but why not call it now?
private async Task<ActionResult> TryCreate(Restaurant restaurant, Reservation reservation) { using var scope = new TransactionScope(TransactionScopeAsyncFlowOption.Enabled); var reservations = await Repository.ReadReservations(restaurant.Id, reservation.At); var now = Clock.GetCurrentDateTime(); if (!restaurant.MaitreD.WillAccept(now, reservations, reservation)) return NoTables500InternalServerError(); await Repository.Create(restaurant.Id, reservation).ConfigureAwait(false); scope.Complete(); return Reservation201Created(restaurant.Id, reservation); }
This is the TryCreate method called by the above Post method. Here, DateTime.Now is hidden behind Clock.GetCurrentDateTime() in order to make execution repeatable, but the idea remains: the variable represents the current time or date, or, with a bit of good will, now.
Notice that the WillAccept method (shown above) also uses now as a parameter name. That value's role is to represent now as a concept.
When working with time, I also sometimes use the variable names before and after. This is mostly useful in integration tests:
[Fact] public async Task GetCurrentYear() { using var api = new LegacyApi(); var before = DateTime.Now; var response = await api.GetCurrentYear(); var after = DateTime.Now; response.EnsureSuccessStatusCode(); var actual = await response.ParseJsonContent<CalendarDto>(); AssertOneOf(before.Year, after.Year, actual.Year); Assert.Null(actual.Month); Assert.Null(actual.Day); AssertLinks(actual); }
While you can inject something like a Clock dependency in order to make your SUT deterministic, in integration tests you might want to see behaviour when using the system clock. You can often verify such behaviour by surrounding the test's Act phase with two calls to DateTime.Now. This gives you the time before and after the test exercised the SUT.
When you do that, however, be careful with the assertions. If such a test runs at midnight, before and after might be two different dates. If it runs on midnight December 31, it might actually be two different years! That's the reason that the test passes as long as the actual.Year is either of before.Year and after.Year.
Invalid values #
While integration tests often test happy paths, unit tests should also exercise error paths. What happens when you supply invalid input to a method? When you write such tests, you can identify the invalid values by naming the variables or parameters accordingly:
[Theory] [InlineData(null)] [InlineData("")] [InlineData("bas")] public async Task PutInvalidId(string invalidId) { var db = new FakeDatabase(); var sut = new ReservationsController( new SystemClock(), new InMemoryRestaurantDatabase(Some.Restaurant), db); var dummyDto = new ReservationDto { At = "2024-06-25 18:19", Email = "colera@example.com", Name = "Cole Aera", Quantity = 2 }; var actual = await sut.Put(invalidId, dummyDto); Assert.IsAssignableFrom<NotFoundResult>(actual); }
Here, the invalid input represent an ID. To indicate that, I called the parameter invalidId.
The system under test is the Put method, which takes two arguments:
public Task<ActionResult> Put(string id, ReservationDto dto)
When testing an error path, it's important to keep other arguments well-behaved. In this example, I want to make sure that it's the invalidId that causes the NotFoundResult result. Thus, the dto argument should be as well-behaved as possible, so that it isn't going to be the source of divergence.
Apart from being well-behaved, that object plays no role in the test. It just needs to be there to make the code compile. xUnit Test Patterns calls such an object a Dummy Object, so I named the variable dummyDto as information to any reader familiar with that pattern language.
Derived class names #
The thrust of all of these examples is that you don't have to name variables after their types. You can extend this line of reasoning to class inheritance. Just because a base class is called Foo it doesn't mean that you have to call a derived class SomethingFoo.
This is something of which I have to remind myself. For example, to support integration testing with ASP.NET you'll need a WebApplicationFactory<TEntryPoint>. To override the default DI Container configuration, you'll have to derive from this class and override its ConfigureWebHost method. In an example I've previously published I didn't spend much time thinking about the class name, so RestaurantApiFactory it was.
At first, I named the variables of this type factory, or something equally devoid of information. That bothered me, so instead tried service, which I felt was an improvement, but still too vapid. I then adopted api as a variable name, but then realised that that also suggested a better class name. So currently, this defines my self-hosting API:
public sealed class SelfHostedApi : WebApplicationFactory<Startup>
Here's how I use it:
[Fact] public async Task ReserveTableAtNono() { using var api = new SelfHostedApi(); var client = api.CreateClient(); var dto = Some.Reservation.ToDto(); dto.Quantity = 6; var response = await client.PostReservation("Nono", dto); var at = Some.Reservation.At; await AssertRemainingCapacity(client, at, "Nono", 4); await AssertRemainingCapacity(client, at, "Hipgnosta", 10); }
The variable is just called api, but the reader can tell from the initialisation that this is an instance of the SelfHostedApi class. I like how that communicates that this is an integration test that uses a self-hosted API. It literally says that.
This test also uses the dto naming convention. Additionally, you may take note of the variable and property called at. That's another name for a date and time. I struggled with naming this value, until Karsten Strøbæk suggested that I used the simple word at: reservation.At indicates the date and time of the reservation without being encumbered by awkward details about date and time. Should we call it date? time? dateTime? No, just call it at. I find it elegant.
Conclusion #
Sometimes, a Reservation object is just a reservation, and that's okay. At other times, it's the actual value, or the expected value. If it represents an invalid reservation in a test case, it makes sense to call the variable invalidResevation.
Giving variables descriptive names improves code quality. You don't have to write comments as apologies for poor readability if a better name communicates what the comment would have said.
Consider naming variables (and classes) for the roles they play, rather than their types.
On the other hand, when variable names are in the way, consider point-free code.
Comments
Excellent name suggestions. Thanks for sharing them :)
I usually call the downcast variable other because, from the perspective of the instance, it's the other object. I usually use that convention whenever an instance interacts with another object of the same type.
The name other is good, but I prefer that because I think it is a better antonym of this (the keyword for the current instance) and because it has the same number of letters as this.
It makes sense to me to call predicate input candidates. Typically, you have some input that you want to evaluate as either true or false. I think it makes sense to think of such a parameter as a 'truth candidate'. You can see one example of that in the above
SignatureIsValidmethod....
Here, the reservation in question is actually not yet a reservation. It might be rejected, so it's a
candidatereservation.
I typically try to avoid turning some input into either true or false. In particular, I find it confusing for the syntax to say that some instance is a Reservation while the semantics says that it "is actually not yet a reservation". I think of this as an example of primitive obsession. Strictly speaking, I think "Primitive Obsession is when the code relies too much on primitives." (aka, on primitive types). In my mind though, I have generalized this to cover any code that relies too much on weaker types. Separate types Reservation and bool are weaker than separate types Reservation and CandidateReservation. I think Alexis King summarized this well with a blog post titled Parse, don’t validate.
And yet, my coworkers and I have engaged in friendly but serious debates for years about which of those two approaches is better. My argument, essentially as given above, is for separate types Reservation and CandidateReservation. The main counterargument is that these types are the same except for a database-generated ID, so just represent both using one type with an optional ID.
Have you thought about this before?
By naming the input parameter
dto, I keep the namereservationfree for the domain object, which ought to be the more important object of the two....
I could have named the input parameter
reservationDtoinstead ofdto, but that would diminish the 'mental distance' betweenreservationDtoandreservation. I like to keep that distance, so that the roles are more explicit.
I prefer to emphasize the roles even more by using the names dto and model. We are in the implementation of the (Post) route for "restaurants/{restaurantId}/reservations", so I think it is clear from context that the dto and model are really a reservation DTO and a reservation model.
Tyson, thank you for writing. Certainly, I didn't intent my article to dictate names. As you imply, there's room for both creativity and subjectivity, and that's fine. My suggestions were meant only for inspiration.
Yes; I would think twice before deciding to model a domain type with a database-generated ID. A server-generated ID is an implementation detail that shouldn't escape the data access layer. If it does, you have a leaky abstraction at hand. Sooner or later, it's going to bite you.The main counterargument is that these types are the same except for a database-generated ID, so just represent both using one type with an optional ID.
Have you thought about this before?
The Reservation class in the above examples has this sole constructor:
public Reservation(Guid id, DateTime at, Email email, Name name, int quantity)
You can't create an instance without supplying an ID. On the other hand, any code can conjure up a GUID, so no server is required. At the type-level, there's no compelling reason to distinguish between a reservation and a candidate reservation.
Granted, you could define two types, Reservation and CandidateReservation, but they'd be isomorphic. In Haskell, you'd probably use a newtype for one of these types, and then you're back at Alexis King's blog.
...naming is one of the hardest problems in software development. Perhaps it's hard because you have to do it so frequently.
Usually, doing things frequently means mastering them pretty quickly. Not so for naming. I guess, there are multiple issues:
- Words are ambiguous. The key is, not to do naming in isolation, the context matters. For example, it's difficult to come up with a good name for a method when we don't have a good name for its class, the whole component, etc. Similar with Clean Code's N5: the meaning of a short variable is clear in a small scope, closed context.
- Good naming requires deep understanding of the domain. Developers are usualy not good at the business they model. Sadly, it often means "necessary evil" for them.
Naming variables by their roles is a great idea!
Many thanks for another awesome post, I enjoyed reading it.
Tomas, thank you for writing.
Good point; I hadn't thought about that. I think that the reasons you list are valid.doing things frequently means mastering them pretty quickly. Not so for naming. I guess
As an additional observation, it may be that there's a connection to the notion of deliberate practice. As the catch-phrase about professional experience puts it, there's a difference between 20 years of experience and one year of experience repeated 20 times.
Doing a thing again and again generates little improvement if one does it by rote. One has to deliberately practice. In this case, it implies that a programmer should explicitly reflect on variable names, and consider more than one option.
I haven't met many software developers who do that.
Good names are skin-deep
Good names are important, but insufficient, for code maintainability.
You should give the building blocks of your code bases descriptive names. It's easier to understand the purpose of a library, module, class, method, function, etcetera if the name contains a clue about the artefact's purpose. This is hardly controversial, and while naming is hard, most teams I visit agree that names are important.
Still, despite good intentions and efforts to name things well, code bases deteriorate into unmaintainable clutter.
Clearly, good names aren't enough.
Tenuousness of names #
A good name is tenuous. First, naming is hard, so while you may have spent some effort coming up with a good name, other people may misinterpret it. Because they originate from natural language, names are as ambiguous as language. (Terse operators, on the other hand...)
Another maintainability problem with names is that implementation may change over time, but the names remain constant. Granted, modern IDEs make it easy to rename methods, but developers rarely adjust names when they adjust behaviour. Even the best names may become misleading over time.
These weakness aren't the worst, though. In my experience, a more fundamental problem is that all it takes is one badly named 'wrapper object' before the information in a good name is lost.

In the figure, the inner object is well-named. It has a clear name and descriptive method names. All it takes before this information is lost, however, is another object with vague names to 'encapsulate' it.
An attempt at a descriptive method name #
Here's an example. Imagine an online restaurant reservation system. One of the features of this system is to take reservations and save them in the database.
A restaurant, however, is a finite resource. It can only accommodate a certain number of guests at the same time. Whenever the system receives a reservation request, it'll have to retrieve the existing reservations for that time and make a decision. Can it accept the reservation? Only if it can should it save the reservation.
How do you model such an interaction? How about a descriptive name? How about TrySave? Here's a possible implementation:
public async Task<bool> TrySave(Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); var reservations = await Repository .ReadReservations( reservation.At, reservation.At + SeatingDuration) .ConfigureAwait(false); var availableTables = Allocate(reservations); if (!availableTables.Any(t => reservation.Quantity <= t.Seats)) return false; await Repository.Create(reservation).ConfigureAwait(false); return true; }
There's an implicit naming convention in .NET that methods with the Try prefix indicate an operation that may or may not succeed. The return value of such methods is either true or false, and they may also have out parameters if they optionally produce a value. That's not the case here, but I think one could make the case that TrySave succinctly describes what's going on.
All is good, then?
A vague wrapper #
After our conscientious programmer meticulously designed and named the above TrySave method, it turns out that it doesn't meet all requirements. Users of the system file a bug: the system accepts reservations outside the restaurant's opening hours.
The original programmer has moved on to greener pastures, so fixing the bug falls on a poor maintenance developer with too much to do. Having recently learned about the open-closed principle, our new protagonist decides to wrap the existing TrySave in a new method:
public async Task<bool> Check(Reservation reservation) { if (reservation is null) throw new ArgumentNullException(nameof(reservation)); if (reservation.At < DateTime.Now) return false; if (reservation.At.TimeOfDay < OpensAt) return false; if (LastSeating < reservation.At.TimeOfDay) return false; return await Manager.TrySave(reservation).ConfigureAwait(false); }
This new method first checks whether the reservation is within opening hours and in the future. If that's not the case, it returns false. Only if these preconditions are fulfilled does it delegate the decision to that TrySave method.
Notice, however, the name. The bug was urgent, and our poor programmer didn't have time to think of a good name, so Check it is.
Caller's perspective #
How does this look from the perspective of calling code? Here's the Controller action that handles the pertinent HTTP request:
public async Task<ActionResult> Post(ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); Reservation? r = dto.Validate(); if (r is null) return new BadRequestResult(); var isOk = await Manager.Check(r).ConfigureAwait(false); if (!isOk) return new StatusCodeResult(StatusCodes.Status500InternalServerError); return new NoContentResult(); }
Try to forget the code you've just seen and imagine that you're looking at this code first. You'd be excused if you miss what's going on. It looks as though the method just does a bit of validation and then checks 'something' concerning the reservation.
There's no hint that the Check method might perform the significant side effect of saving the reservation in the database.
You'll only learn that if you read the implementation details of Check. As I argue in my Humane Code video, if you have to read the source code of an object, encapsulation is broken.
Such code doesn't fit in your brain. You'll struggle as you try keep track of all the things that are going on in the code, all the way from the outer boundary of the application to implementation details that relate to databases, third-party services, etcetera.
Straw man? #
You may think that this is a straw man argument. After all, wouldn't it be better to edit the original TrySave method?
Perhaps, but it would make that class more complex. The TrySave method has a cyclomatic complexity of only 3, while the Check method has a complexity of 5. Combining them might easily take them over some threshold.
Additionally, each of these two classes have different dependencies. As the TrySave method implies, it relies on both Repository and SeatingDuration, and the Allocate helper method (not shown) uses a third dependency: the restaurant's table configuration.
Likewise, the Check method relies on OpensAt and LastSeating. If you find it better to edit the original TrySave method, you'd have to combine these dependencies as well. Each time you do that, the class grows until it becomes a God object.
It's rational to attempt to separate things in multiple classes. It also, on the surface, seems to make unit testing easier. For example, here's a test that verifies that the Check method rejects reservations before the restaurant's opening time:
[Fact] public async Task RejectReservationBeforeOpeningTime() { var r = new Reservation( DateTime.Now.AddDays(10).Date.AddHours(17), "colaera@example.com", "Cole Aera", 1); var mgrTD = new Mock<IReservationsManager>(); mgrTD.Setup(mgr => mgr.TrySave(r)).ReturnsAsync(true); var sut = new RestaurantManager( TimeSpan.FromHours(18), TimeSpan.FromHours(21), mgrTD.Object); var actual = await sut.Check(r); Assert.False(actual); }
By replacing the TrySave method by a test double, you've ostensibly decoupled the Check method from all the complexity of the TrySave method.
To be clear, this style of programming, with lots of nested interfaces and tests with mocks and stubs is far from ideal, but I still find it better than a big ball of mud.
Alternative #
A better alternative is Functional Core, Imperative Shell, AKA impureim sandwich. Move all impure actions to the edge of the system, leaving only referentially transparent functions as the main implementers of logic. It could look like this:
[HttpPost] public async Task<ActionResult> Post(ReservationDto dto) { if (dto is null) throw new ArgumentNullException(nameof(dto)); var id = dto.ParseId() ?? Guid.NewGuid(); Reservation? r = dto.Validate(id); if (r is null) return new BadRequestResult(); var reservations = await Repository.ReadReservations(r.At).ConfigureAwait(false); if (!MaitreD.WillAccept(DateTime.Now, reservations, r)) return NoTables500InternalServerError(); await Repository.Create(r).ConfigureAwait(false); return Reservation201Created(r); }
Nothing is swept under the rug here. WillAccept is a pure function, and while it encapsulates significant complexity, the only thing you need to understand when you're trying to understand the above Post code is that it returns either true or false.
Another advantage of pure functions is that they are intrinsically testable. That makes unit testing and test-driven development easier.
Even with a functional core, you'll also have an imperative shell. You can still test that, too, such as the Post method. It isn't referentially transparent, so you might be inclined to use mocks and stubs, but I instead recommend state-based testing with a Fake database.
Conclusion #
Good names are important, but don't let good names, alone, lull you into a false sense of security. All it takes is one vaguely named wrapper object, and all the information in your meticulously named methods is lost.
This is one of many reasons I try to design with static types instead of names. Not that I dismiss the value of good names. After all, you'll have to give your types good names as well.
Types are more robust in the face of inadvertent changes; or, rather, they tend to resist when we try to do something stupid. I suppose that's what lovers of dynamically typed languages feel as 'friction'. In my mind, it's entirely opposite. Types keep me honest.
Unfortunately, most type systems don't offer an adequate degree of safety. Even in F#, which has a great type system, you can introduce impure actions into what you thought was a pure function, and you'd be none the wiser. That's one of the reasons I find Haskell so interesting. Because of the way IO works, you can't inadvertently sweep surprises under the rug.
Comments
I find the idea of the impure/pure/impure sandwich rather interesting and I agree with the benefits that it yields. However, I was wondering about where to move synchronization logic, i.e. the reservation system should avoid double bookings. With the initial TrySave approach it would be clear for me where to put this logic: the synchonrization mechanism should be part of the TrySave method. With the impure/pure/impure sandwich, it will move out to the most outer layern (HTTP Controller) - at least this is how I'd see it. My feelings tells me that this is a bit smelly, but I can't really pin point why I think so. Can you give some advice on this? How would you solve that?
Johannes, thank you for writing. There are several ways to address that issue, depending on what sort of trade-off you're looking for. There's always a trade-off.
You can address the issue with a lock-free architecture. This typically involves expressing the desired action as a Command and putting it on a durable queue. If you combine that with a single-threaded, single-instance Actor that pulls Commands off the queue, you need no further transaction processing, because the architecture itself serialises writes. You can find plenty of examples of such an architecture on the internet, including (IIRC) my Pluralsight course Functional Architecture with F#.
Another option is to simply surround the impureim sandwich with a TransactionScope (if you're on .NET, that is).
Redirect legacy URLs
Evolving REST API URLs when cool URIs don't change.
More than one reader reacted to my article on fit URLs by asking about bookmarks and original URLs. Daniel Sklenitzka's question is a good example:
While I answered the question on the same page, I think that it's worthwhile to expand it."I see how signing the URLs prevents clients from retro-engineering the URL templates, but how does it help preventing breaking changes? If the client stores the whole URL instead of just the ID and later the URL changes because a restaurant ID is added, the original URL is still broken, isn't it?"
The rules of HTTP #
I agree with the implicit assumption that clients are allowed to bookmark links. It seems, then, like a breaking change if you later change your internal URL scheme. That seems to imply that the bookmarked URL is gone, breaking a tenet of the HTTP protocol: Cool URIs don't change.
REST APIs are supposed to play by the rules of HTTP, so it'd seem that once you've published a URL, you can never retire it. You can, on the other hand, change its behaviour.
Let's call such URLs legacy URLs. Keep them around, but change them to return 301 Moved Permanently responses.
The rules of REST go both ways. The API is expected to play by the rules of HTTP, and so are the clients. Clients are not only expected to follow links, but also redirects. If a legacy URL starts returning a 301 Moved Permanently response, a well-behaved client doesn't break.
Reverse proxy #
As I've previously described, one of the many benefits of HTTP-based services is that you can put a reverse proxy in front of your application servers. I've no idea how to configure or operate NGINX or Varnish, but from talking to people who do know, I get the impression that they're quite scriptable.
Since the above ideas are independent of actual service implementation or behaviour, it's a generic problem that you should seek to address with general-purpose software.
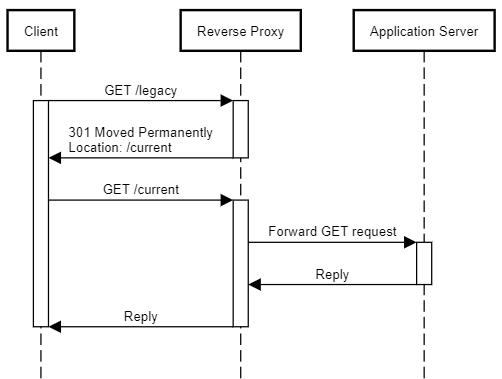
Imagine that a reverse proxy is configured with a set of rules that detects legacy URLs and knows how to forward them. Clearly, the reverse proxy must know of the REST API's current URL scheme to be able to do that. You might think that this would entail leaking an implementation detail, but just as I consider any database used by the API as part of the overall system, I'd consider the reverse proxy as just another part.
Redirecting with ASP.NET #
If you don't have a reverse proxy, you can also implement redirects in code. It'd be better to use something like a reverse proxy, because that would mean that you get to delete code from your code base, but sometimes that's not possible.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
In ASP.NET, you can return 301 Moved Permanently responses just like any other kind of HTTP response:
[Obsolete("Use Get method with restaurant ID.")] [HttpGet("calendar/{year}/{month}")] public ActionResult LegacyGet(int year, int month) { return new RedirectToActionResult( nameof(Get), null, new { restaurantId = Grandfather.Id, year, month }, permanent: true); }
This LegacyGet method redirects to the current Controller action called Get by supplying the arguments that the new method requires. The Get method has this signature:
[HttpGet("restaurants/{restaurantId}/calendar/{year}/{month}")] public async Task<ActionResult> Get(int restaurantId, int year, int month)
When I expanded the API from a single restaurant to a multi-tenant system, I had to grandfather in the original restaurant. I gave it a restaurantId, but in order to not put magic constants in the code, I defined it as the named constant Grandfather.Id.
Notice that I also adorned the LegacyGet method with an [Obsolete] attribute to make it clear to maintenance programmers that this is legacy code. You might argue that the Legacy prefix already does that, but the [Obsolete] attribute will make the compiler emit a warning, which is even better feedback.
Regression test #
While legacy URLs may be just that: legacy, that doesn't mean that it doesn't matter whether or not they work. You may want to add regression tests.
If you implement redirects in code (as opposed to a reverse proxy), you should also add automated tests that verify that the redirects work:
[Theory] [InlineData("http://localhost/calendar/2020?sig=ePBoUg5gDw2RKMVWz8KIVzF%2Fgq74RL6ynECiPpDwVks%3D")] [InlineData("http://localhost/calendar/2020/9?sig=ZgxaZqg5ubDp0Z7IUx4dkqTzS%2Fyjv6veDUc2swdysDU%3D")] public async Task BookmarksStillWork(string bookmarkedAddress) { using var api = new LegacyApi(); var actual = await api.CreateDefaultClient().GetAsync(new Uri(bookmarkedAddress)); Assert.Equal(HttpStatusCode.MovedPermanently, actual.StatusCode); var follow = await api.CreateClient().GetAsync(actual.Headers.Location); follow.EnsureSuccessStatusCode(); }
This test interacts with a self-hosted service at the HTTP level. LegacyApi is a test-specific helper class that derives from WebApplicationFactory<Startup>.
The test uses URLs that I 'bookmarked' before I evolved the URLs to a multi-tenant system. As you can tell from the host name (localhost), these are bookmarks against the self-hosted service. The test first verifies that the response is 301 Moved Permanently. It then requests the new address and uses EnsureSuccessStatusCode as an assertion.
Conclusion #
When you evolve fit URLs, it could break clients that may have bookmarked legacy URLs. Consider leaving 301 Moved Permanently responses at those addresses.
Checking signed URLs with ASP.NET
Use a filter to check all requested URL signatures.
This article is part of a short series on fit URLs. In the overview article, I argued that you should be signing URLs in order to prevent your REST APIs from becoming victims of Hyrum's law. In the previous article you saw how to sign URLs with ASP.NET.
In this article you'll see how to check the URLs of all HTTP requests to the API and reject those that aren't up to snuff.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
Filter #
If you want to intercept all incoming HTTP requests in ASP.NET Core, an IAsyncActionFilter is a good option. This one should look at the URL of all incoming HTTP requests and detect if the client tried to tamper with it.
internal sealed class UrlIntegrityFilter : IAsyncActionFilter { private readonly byte[] urlSigningKey; public UrlIntegrityFilter(byte[] urlSigningKey) { this.urlSigningKey = urlSigningKey; } // More code comes here...
The interface only defines a single method:
public async Task OnActionExecutionAsync( ActionExecutingContext context, ActionExecutionDelegate next) { if (IsGetHomeRequest(context)) { await next().ConfigureAwait(false); return; } var strippedUrl = GetUrlWithoutSignature(context); if (SignatureIsValid(strippedUrl, context)) { await next().ConfigureAwait(false); return; } context.Result = new NotFoundResult(); }
While the rule is to reject requests with invalid signatures, there's one exception. The 'home' resource requires no signature, as this is the only publicly documented URL for the API. Thus, if IsGetHomeRequest returns true, the filter invokes the next delegate and returns.
Otherwise, it strips the signature off the URL and checks if the signature is valid. If it is, it again invokes the next delegate and returns.
If the signature is invalid, on the other hand, the filter stops further execution by not invoking next. Instead, it sets the response to a 404 Not Found result.
It may seem odd to return 404 Not Found if the signature is invalid. Wouldn't 401 Unauthorized or 403 Forbidden be more appropriate?
Not really. Keep in mind that while this behaviour may use encryption technology, it's not a security feature. The purpose is to make it impossible for clients to 'retro-engineer' an implied interface. This protects them from breaking changes in the future. Clients are supposed to follow links, and the URLs given by the API itself are proper, existing URLs. If you try to edit a URL, then that URL doesn't work. It represents a resource that doesn't exist. While it may seem surprising at first, I find that a 404 Not Found result is the most appropriate status code to return.
Detecting a home request #
The IsGetHomeRequest helper method is straightforward:
private static bool IsGetHomeRequest(ActionExecutingContext context) { return context.HttpContext.Request.Path == "/" && context.HttpContext.Request.Method == "GET"; }
This predicate only looks at the Path and Method of the incoming request. Perhaps it also ought to check that the URL has no query string parameters, but I'm not sure if that actually matters.
Stripping off the signature #
The GetUrlWithoutSignature method strips off the signature query string variable from the URL, but leaves everything else intact:
private static string GetUrlWithoutSignature(ActionExecutingContext context) { var restOfQuery = QueryString.Create( context.HttpContext.Request.Query.Where(x => x.Key != "sig")); var url = context.HttpContext.Request.GetEncodedUrl(); var ub = new UriBuilder(url); ub.Query = restOfQuery.ToString(); return ub.Uri.AbsoluteUri; }
The purpose of removing only the sig query string parameter is that it restores the rest of the URL to the value that it had when it was signed. This enables the SignatureIsValid method to recalculate the HMAC.
Validating the signature #
The SignatureIsValid method validates the signature:
private bool SignatureIsValid(string candidate, ActionExecutingContext context) { var sig = context.HttpContext.Request.Query["sig"]; var receivedSignature = Convert.FromBase64String(sig.ToString()); using var hmac = new HMACSHA256(urlSigningKey); var computedSignature = hmac.ComputeHash(Encoding.ASCII.GetBytes(candidate)); var signaturesMatch = computedSignature.SequenceEqual(receivedSignature); return signaturesMatch; }
If the receivedSignature equals the computedSignature the signature is valid.
This prevents clients from creating URLs based on implied templates. Since clients don't have the signing key, they can't compute a valid HMAC, and therefore the URLs they'll produce will fail the integrity test.
Configuration #
As is the case for the URL-signing feature, you'll first need to read the signing key from the configuration system. This is the same key used to sign URLs:
var urlSigningKey = Encoding.ASCII.GetBytes( Configuration.GetValue<string>("UrlSigningKey"));
Next, you'll need to register the filter with the ASP.NET framework:
services.AddControllers(opts => opts.Filters.Add(new UrlIntegrityFilter(urlSigningKey)));
This is typically done in the ConfigureServices method of the Startup class.
Conclusion #
With a filter like UrlIntegrityFilter you can check the integrity of URLs on all incoming requests to your REST API. This prevents clients from making up URLs based on an implied interface. This may seem restrictive, but is actually for their own benefit. When they can't assemble URLs from scratch, the only remaining option is to follow the links that the API provides.
This enables you to evolve the API without breaking existing clients. While client developers may not initially appreciate having to follow links instead of building URLs out of templates, they may value that their clients don't break as you evolve the API.
Next: Redirect legacy URLs.
Signing URLs with ASP.NET
A few Decorators is all it takes.
This article is part of a short series on fit URLs. In the overview article, I argued that you should be signing URLs in order to prevent your REST APIs from becoming victims of Hyrum's law.
In this article, you'll see how to do this with ASP.NET Core 3.1, and in the next article you'll see how to check URL integrity.
The code shown here is part of the sample code base that accompanies my book Code That Fits in Your Head.
SigningUrlHelper #
I wanted the URL-signing functionality to slot into the ASP.NET framework, which supplies the IUrlHelper interface for the purpose of creating URLs. (For example, the UrlBuilder I recently described relies on that interface.)
Since it's an interface, you can define a Decorator around it:
internal sealed class SigningUrlHelper : IUrlHelper { private readonly IUrlHelper inner; private readonly byte[] urlSigningKey; public SigningUrlHelper(IUrlHelper inner, byte[] urlSigningKey) { this.inner = inner; this.urlSigningKey = urlSigningKey; } // More code comes here...
As you can tell, this Decorator requires an inner IUrlHelper and a urlSigningKey. Most of the members just delegate to the inner implementation:
public bool IsLocalUrl(string url) { return inner.IsLocalUrl(url); }
The Action method creates URLs, so this is the method to modify:
public string Action(UrlActionContext actionContext) { var url = inner.Action(actionContext); if (IsLocalUrl(url)) { var b = new UriBuilder( ActionContext.HttpContext.Request.Scheme, ActionContext.HttpContext.Request.Host.ToUriComponent()); url = new Uri(b.Uri, url).AbsoluteUri; } var ub = new UriBuilder(url); using var hmac = new HMACSHA256(urlSigningKey); var sig = Convert.ToBase64String( hmac.ComputeHash(Encoding.ASCII.GetBytes(url))); ub.Query = new QueryString(ub.Query).Add("sig", sig).ToString(); return ub.ToString(); }
The actionContext may sometimes indicate a local (relative) URL, in which case I wanted to convert it to an absolute URL. Once that's taken care of, the method calculates an HMAC and adds it as a query string variable.
SigningUrlHelperFactory #
While it's possible take ASP.NET's default IUrlHelper instance (e.g. from ControllerBase.Url) and manually decorate it with SigningUrlHelper, that doesn't slot seamlessly into the framework.
For example, to add the Location header that you saw in the previous article, the code is this:
private static ActionResult Reservation201Created( int restaurantId, Reservation r) { return new CreatedAtActionResult( nameof(Get), null, new { restaurantId, id = r.Id.ToString("N") }, r.ToDto()); }
The method just returns a new CreatedAtActionResult object, and the framework takes care of the rest. No explicit IUrlHelper object is used, so there's nothing to manually decorate. By default, then, the URLs created from such CreatedAtActionResult objects aren't signed.
It turns out that the ASP.NET framework uses an interface called IUrlHelperFactory to create IUrlHelper objects. Decorate that as well:
public sealed class SigningUrlHelperFactory : IUrlHelperFactory { private readonly IUrlHelperFactory inner; private readonly byte[] urlSigningKey; public SigningUrlHelperFactory(IUrlHelperFactory inner, byte[] urlSigningKey) { this.inner = inner; this.urlSigningKey = urlSigningKey; } public IUrlHelper GetUrlHelper(ActionContext context) { var url = inner.GetUrlHelper(context); return new SigningUrlHelper(url, urlSigningKey); } }
Straightforward: use the inner object to get an IUrlHelper object, and decorate it with SigningUrlHelper.
Configuration #
The final piece of the puzzle is to tell the framework about the SigningUrlHelperFactory. You can do this in the Startup class' ConfigureServices method.
First, read the signing key from the configuration system (e.g. a configuration file):
var urlSigningKey = Encoding.ASCII.GetBytes( Configuration.GetValue<string>("UrlSigningKey"));
Then use the signing key to configure the SigningUrlHelperFactory service. Here, I wrapped that in a little helper method:
private static void ConfigureUrSigning( IServiceCollection services, byte[] urlSigningKey) { services.RemoveAll<IUrlHelperFactory>(); services.AddSingleton<IUrlHelperFactory>( new SigningUrlHelperFactory( new UrlHelperFactory(), urlSigningKey)); }
This method first removes the default IUrlHelperFactory service and then adds the SigningUrlHelperFactory instead. It decorates UrlHelperFactory, which is the default built-in implementation of the interface.
Conclusion #
You can extend the ASP.NET framework to add a signature to all the URLs it generates. All it takes is two simple Decorators.
Fit URLs
Keep REST API URLs evolvable. A way to address Hyrum's law.
Publishing and maintaining a true (level 3) RESTful API is difficult. This is the style of REST design where clients are expected to follow links to perform the work they want to accomplish; not assemble URLs from templates.
Have you ever designed a URL scheme and published it, only to later discover that you wished you'd come up with a different structure? If you've published a set of URL templates, changing your mind constitutes a breaking change. If clients follow links, however, URLs are opaque and you can redesign the URLs without breaking existing clients.
You can try to document this design principle all you want, to no avail. You can tell client developers that they're supposed to follow links, not try to retro-engineer the URLs, and still they'll do it.
I know; I've experienced it. When we later changed the URL structure, it didn't take long for the client developers to complain that we broke their code.
Hyrum's law #
This is an example of Hyrum's law in action, albeit on the scale of web service interactions, rather than low-level APIs. The presence of a discernible system to URLs suggests an implicit interface.
Consider this 'home' resource for an online restaurant reservation system:
GET / HTTP/1.1
HTTP/1.1 200 OK
Content-Type: application/json; charset=utf-8
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/reservations"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/calendar/2020"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/calendar/2020/10"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/calendar/2020/10/23"
}
]
}
It doesn't take much interaction with the API before you realise that there's a system to the URLs provided in the links. If you want to see the calendar for a specific date, you can easily retro-engineer the URL template /calendar/{yyyy}/{MM}/{dd}, and /calendar/{yyyy}/{MM} for a month, and so on.
The same is likely to happen with the reservations link. You can POST to this link to make a new reservation:
POST /reservations HTTP/1.1
Content-Type: application/json
{
"at": "2020-12-09 19:15",
"email": "rainboughs@example.com",
"name": "Raine Burroughs",
"quantity": 5
}
HTTP/1.1 201 Created
Content-Type: application/json
Location: http://localhost:53568/reservations/fabc5bf63a1a4db38b95deaa89c01178
{
"id": "fabc5bf63a1a4db38b95deaa89c01178",
"at": "2020-12-09T19:15:00.0000000",
"email": "rainboughs@example.com",
"name": "Raine Burroughs",
"quantity": 5
}
Notice that when the API responds, its Location header gives you the URL for that particular reservation. It doesn't take long to figure out that there's a template there, as well: /reservations/{id}.
So client developers may just store the ID (fabc5bf63a1a4db38b95deaa89c01178) and use the implied template to construct URLs on the fly. And who can blame them?
That, however, misses the point of REST. The ID of that reservation isn't fabc5bf63a1a4db38b95deaa89c01178, but rather http://localhost:53568/reservations/fabc5bf63a1a4db38b95deaa89c01178. Yes, the URL, all of it, is the ID.
Evolving URLs #
Why does that matter?
It matters because you're human, and you make mistakes. Or, rather, it's intrinsic to software development that you learn as you work. You'll make decisions at the beginning that you'll want to change as you gain more insight.
Also, requirements change. Consider the URL template scheme implied by the above examples. Can you spot any problems? Would you want to change anything?
Imagine, for example, that you've already deployed the first version of the API. It's a big success. Now the product owner wants to expand the market to more restaurants. She wants to make the service a multi-tenant API. How does that affect URLs?
In that new context, perhaps URLs like /restaurants/1/reservations or /restaurants/90125/calendar/2020/10 would be better.
That, however, would be a breaking change if clients construct URLs based on implied templates.
Couldn't you just pass the restaurant ID as an HTTP header instead of in the URL? Yes, technically you could do that, but that doesn't work well with HTTP caching. It's not a RESTful thing to do, for that, and other, reasons.
Fitness #
Do we just give up in the face of Hyrum's law? Or can we keep URLs evolvable? In evolution, organisms evolve according to a 'fitness function', so to name such URLs, we could call them fit URLs.
To keep URLs fit, we must prevent client developers from retro-engineering the implied interface. My original thought was to give each URL an opaque ID, such as a GUID, but in 2015 Dan Kubb instead suggested to sign the URLs. What a great idea!
If you do that, then the above home resource might look like this:
{
"links": [
{
"rel": "urn:reservations",
"href": "http://localhost:53568/restaurants/1/reservations?sig=1WiLlS5705bfsffPzaFYLwntrS4FCjE5CLdaeYTHxxg%3D"
},
{
"rel": "urn:year",
"href": "http://localhost:53568/restaurants/1/calendar/2020?sig=eIFuUkb6WprPrp%2B4HPSPaavcUdwVjeG%2BKVrIRqDs9OI%3D"
},
{
"rel": "urn:month",
"href": "http://localhost:53568/restaurants/1/calendar/2020/10?sig=mGqkAjY7vMbC5Fr7UiRXWWnjn3pFn21MYrMagpdWaU0%3D"
},
{
"rel": "urn:day",
"href": "http://localhost:53568/restaurants/1/calendar/2020/10/23?sig=Ua5F%2FucP6zmAy219cHa4WG7zIcCa0hgVD5ModXcNQuo%3D"
}
]
}
Even if you can still figure out what the URL templates are, it doesn't avail you. Creating a new reservation may return a URL like https://localhost:53568/restaurants/1/reservations/fabc5bf63a1a4db38b95deaa89c01178?sig=8e80PmVi8aSS1UH6iSJ73nHmOsCLrUMs7yggEOkvEqo%3D, but you can't just replace the ID with another ID and expect it to work:
GET /restaurants/1/reservations/79520877ef4f4acdb69838e22ad04510?sig=8e80PmVi8aSS1UH6iSJ73nHmOsCLrUMs7yggEOkvEqo%3D HTTP/1.1 HTTP/1.1 404 Not Found
You're requesting a URL that doesn't exist, so the result is 404 Not Found. To be clear: yes, there is a reservation with the ID 79520877ef4f4acdb69838e22ad04510, but its URL isn't the above URL.
ASP.NET implementation #
In two articles, I'll show you how to implement fit URLs in ASP.NET Core.
The ASP.NET framework comes with enough extensibility points to make this a non-intrusive operation. I implemented this using a filter and a few Decorators in a way so that you can easily turn the feature on or off.Conclusion #
One of the major benefits of true RESTful API design is that it's evolvable. It enables you to learn and improve as you go, without breaking existing clients.
You have to take care, however, that clients don't retro-engineer the URL templates that you may be using for implementation purposes. You want to be able to change URLs in the future.
Hyrum's law suggests that clients will rely on undocumented features if they can. By signing the URLs you keep them fit to evolve.
Next: Signing URLs with ASP.NET.
Comments
I see how signing the URLs prevents clients from retro-engineering the URL templates, but how does it help preventing breaking changes? If the client stores the whole URL instead of just the ID and later the URL changes because a restaurant ID is added, the original URL is still broken, isn't it?
Daniel, thank you for writing. You're correct when assuming that clients are allowed to 'bookmark' URLs. An implicit assumption that I didn't explicitly state is that clients are supposed to follow not only links, but also redirects. Thus, to avoid breaking changes, it's the API's responsibility to leave a 301 Moved Permanently response behind at the old address.
As a service owner, though, you have some flexibility in how to achieve this. You can code this into the service code itself, but another option might be to use a reverse proxy for such purposes. One of the many advantages of REST is that you can offload a lot HTTP-level behaviour on standard networking software; here's another example.
I think I have the same confusion as Daniel.
If you've published a set of URL templates, changing your mind constitutes a breaking change. If clients follow links, however, URLs are opaque and you can redesign the URLs without breaking existing clients.
...
You're correct when assuming that clients are allowed to 'bookmark' URLs. An implicit assumption that I didn't explicitly state is that clients are supposed to follow not only links, but also redirects. Thus, to avoid breaking changes, it's the API's responsibility to leave a
301 Moved Permanentlyresponse behind at the old address.
Is there a certain kind of breaking change that exists for a level 2 API that doesn't exist for a level 3 API?
Tyson, thank you for writing. I haven't thought much about whether there are categories of errors that differ between the levels, but I think that in practice, there's a difference in mindset.
With a level 2 API, I think most people are still caught in a mindset that's largely a projection of RPC. URL templates map easily to programming procedures (e.g. object-oriented methods). Thus, you have a mental model that includes PostReservation, GetCalendar, etc. People think of that as being the API. With that mindset, I don't think that many client developers configure their HTTP clients to follow redirects. Thus, one could argue that changing URLs are breaking changes for a level 2 API, even if you leave 301 Moved Permanently responses behind.
With level 3 APIs, you encourage client developers to think in terms of 'the web'. That includes following links and redirects. I believe that there's a difference in perception, even if there may not be any technical difference.
I do believe, however, that the real advantage is that you impose a smaller maintenance burden on client developers with a level 3 API. Granted, a client developer may have to spend a little more effort up front to follow links, but once a compliant client is in place, it needs no more maintenance. It'll just keep working.
Not so with published URL templates. Here you have to entice client developers to actively update their code. This may be impossible if you don't know who the clients are, or if the client software is in maintenance mode. This may make it harder to retire old versions. You may be stuck with these old versions forever.

Comments
Great work and excellent post. I just had a few clarification quesitons.
How rhetorical are those questions? Whatever the case, I will take the bait.
Any product type forms a semigroup if all of its elements do. You explicitly stated this for tuples of length 2; it also holds for records such as
Input. Each field on that record has typeMaybe afor somea, so it suffices to select a semigroup involvingMaybe a. There are few different semigropus involvingMaybethat have different functions.I think the most common semigroup for
Maybe ahas the function that returns the firstJust _if one exists or else returnsNothing. Combining that withNothingas the identity element gives the monoid that is typically associated withMaybe a(and I know by the name monoidal plus). Another monoid, and therefore a semigroup, is to return the lastJust _instead of the first.Instead of the having a preference for
Just _, the function could have a preference forNothing. As before, when both inputs areJust _, the output could be either of the inputs.I think either of those last two semigroups will achieved the desired behavior in the problem at hand. Your code never replaces an instace of
Just awith a different instance, so we don't need a preference for some input when they are bothJust _.In the end though, I think the semigroup you derived from
Endoleads to simpler code.At the end of the type signature for
validateName/validateDoB/validateAddress, what doesString/Day/Stringmean?Why did you pass all three arguments into every parsing/validation function? I think it is a bit simpler to only pass in the needed argument. Maybe you thought this was good enough for prototype code.
Why did you use
add1in your error message instead ofaddress? Was it only for prototype code to make the message a bit shorter?Tyson, thank you for writing. The semigroup you suggest, I take it, would look something like this:
That might work, but it's an atypical semigroup. I think that it's lawful - at least, I can't come up with a counterexample against associativity. It seems reminiscent of Boolean and (the All monoid), but it isn't a monoid, as far as I can tell.
Granted, a
Monoidconstraint isn't required to make the validation code work, but following the principle of least surprise, I still think that picking a well-known semigroup such asEndois preferable.Regarding your second question, the type signature of e.g.
validateNameis:Like
Either,Validationhas two type arguments:erranda; it's defined asdata Validation err a. In the above function type, the return value is aValidationvalue where theerrtype is(Endo Input, [String])andaisString.All three validation functions share a common
errtype:(Endo Input, [String]). On the other hand, they return variousatypes:String,Day, andString, respectively.Regarding your third question, I could also have defined the functions so that they would only have taken the values they'd need to validate. That would better fit Postel's law, so I should probably have done that...
As for the last question, I was just following the 'spec' implied by the original forum question.