ploeh blog danish software design
Reactive functor
IObservable<T> is (also) a functor.
This article is an instalment in an article series about functors. While the previous articles showed, in great detail, how to turn various classes into functors, this article mostly serves as a place-holder. The purpose is only to point out that you don't have to create all functors yourself. Sometimes, they come as part of a reusable library.
Rx is such a library, and IObservable<T> is a functor. (It's also a monad, but this is not a monad tutorial; it's a functor tutorial.) Reactive Extensions define a Select method for IObservable<T>, so if source is an IObservable<int>, you can translate it to IObservable<string> like this:
IObservable<string> dest = source.Select(i => i.ToString());
Since the Select method is, indeed, called Select and has the signature
public static IObservable<TResult> Select<TSource, TResult>( this IObservable<TSource> source, Func<TSource, TResult> selector)
you can also use C#'s query syntax:
IObservable<string> dest = from i in source select i.ToString();
In both of the above examples, I've explicitly declared the type of dest instead of using the var keyword. There's no practical reason to do this; I only did it to make the type clear to you.
First functor law #
The Select method obeys the first functor law. As usual, it's proper computer-science work to actually prove that, but you can write some tests to demonstrate the first functor law for the IObservable<T> interface. In this article, you'll see a few parametrised tests written with xUnit.net. Here's one that demonstrates that the first functor law holds:
[Theory] [InlineData(-101)] [InlineData(-1)] [InlineData(0)] [InlineData(1)] [InlineData(42)] [InlineData(1337)] public async Task ObservableObeysFirstFunctorLaw(int value) { var sut = new[] { value }.ToObservable(); IObservable<int> projected = sut.Select(x => x); var actual = await projected.FirstAsync(); Assert.Equal(value, actual); }
Here, I chose to implement the identity function as an anonymous lambda expression. In contrast, in a previous article, I explicitly declared a function variable and called it id. Those two ways to express the identity function are equivalent.
As always, I'd like to emphasise that this test doesn't prove that IObservable<T> obeys the first functor law. It only demonstrates that the law holds for those six examples.
Second functor law #
Like the above example, you can also write a parametrised test that demonstrates that IObservable<T> obeys the second functor law:
[Theory] [InlineData(-101)] [InlineData(-1)] [InlineData(0)] [InlineData(1)] [InlineData(42)] [InlineData(1337)] public async Task ObservableObeysSecondFunctorLaw(int value) { string g(int i) => i.ToString(); string f(string s) => new string(s.Reverse().ToArray()); var sut = new[] { value }.ToObservable(); IObservable<string> projected = sut.Select(i => f(g(i))); var actual = await projected.FirstAsync(); var expected = await sut.Select(g).Select(f).FirstAsync(); Assert.Equal(expected, actual); }
This test defines two local functions, f and g. Instead of explicitly declaring the functions as Func variables, this test uses a (relatively) new C# feature called local functions.
Again, while the test doesn't prove anything, it demonstrates that for the six test cases, it doesn't matter if you project the observable in one or two steps.
Summary #
The point of this article is mostly that functors are commonplace. While you may discover them in your own code, they may also come in a reusable library. If you already know C# LINQ based off IEnumerable<T>, much of Rx will be easy for you to learn. After all, it's the same abstraction, and familiar abstractions make code readable.
Next: The Identity functor.
A Visitor functor
Some Visitors can be functors. Another functor example for object-oriented programmers.
This article is an instalment in an article series about functors. In the previous article, you saw how to implement a generalised tree as a functor. In this article, you'll see another functor example, which will also be an application of the Visitor design pattern.
The Visitor design pattern is often described in such a way that it's based on mutation; the Visit and Accept methods in those descriptions typically return void. You can, however, also implement immutable variations. This blog already contains an older example of this.
Visitor #
In this article, you'll see how to implement a full binary tree using the Visitor design pattern. You can make the tree generic, so that each node can contain values of any generic type.
public interface IBinaryTree<T> { TResult Accept<TResult>(IBinaryTreeVisitor<T, TResult> visitor); }
As promised, this interface implies an immutable variant where the Accept method doesn't mutate the input Visitor, but rather returns a new value. You can learn how you arrive at this particular generic method signature in my article Visitor as a sum type.
A full binary tree is a tree where each node has either zero or two children. This means that a Visitor must have two methods, one for each case:
public interface IBinaryTreeVisitor<T, TResult> { TResult Visit(Node<T> node); TResult Visit(Leaf<T> leaf); }
The IBinaryTreeVisitor<T, TResult> interface introduces two new concrete classes: Node<T> and Leaf<T>. A leaf node is a node with zero children:
public sealed class Leaf<T> : IBinaryTree<T> { public T Item { get; } public Leaf(T item) { if (item == null) throw new ArgumentNullException(nameof(item)); Item = item; } public TResult Accept<TResult>(IBinaryTreeVisitor<T, TResult> visitor) { if (visitor == null) throw new ArgumentNullException(nameof(visitor)); return visitor.Visit(this); } public override bool Equals(object obj) { if (!(obj is Leaf<T> other)) return false; return Equals(Item, other.Item); } public override int GetHashCode() { return Item.GetHashCode(); } }
While a leaf node has no children, it still contains an Item of the generic type T. A leaf node still counts as a binary tree, so it implements the IBinaryTree<T> interface. Complying with the Visitor design pattern, its Accept method is implemented using double dispatch. Thereby, any visitor knows that it's now visiting a concrete Leaf<T> object.
Likewise, a node is a (sub)tree:
public sealed class Node<T> : IBinaryTree<T> { public T Item { get; } public IBinaryTree<T> Left { get; } public IBinaryTree<T> Right { get; } public Node(T item, IBinaryTree<T> left, IBinaryTree<T> right) { if (item == null) throw new ArgumentNullException(nameof(item)); if (left == null) throw new ArgumentNullException(nameof(left)); if (right == null) throw new ArgumentNullException(nameof(right)); Item = item; Left = left; Right = right; } public TResult Accept<TResult>(IBinaryTreeVisitor<T, TResult> visitor) { if (visitor == null) throw new ArgumentNullException(nameof(visitor)); return visitor.Visit(this); } public override bool Equals(object obj) { if (!(obj is Node<T> other)) return false; return Equals(Item, other.Item) && Equals(Left, other.Left) && Equals(Right, other.Right); } public override int GetHashCode() { return Item.GetHashCode() ^ Left.GetHashCode() ^ Right.GetHashCode(); } }
In addition to an Item, a Node<T> object also contains a Left and a Right sub-tree. Notice that the Accept method is literally identical to Leaf<T>.Accept. Its behaviour differs, though, because this has a different type.
A couple of static helper methods makes it a bit easier to create binary tree objects:
public static class BinaryTree { public static IBinaryTree<T> Leaf<T>(T item) { return new Leaf<T>(item); } public static IBinaryTree<T> Create<T>( T item, IBinaryTree<T> left, IBinaryTree<T> right) { return new Node<T>(item, left, right); } }
The main convenience of these two methods is that C# (limited) type inference enables you to create tree objects without explicitly typing out the generic type argument every time. You'll soon see an example of creating a binary tree of integers.
Functor #
Since IBinaryTree<T> is a generic type, you should consider whether it's a functor. Given the overall topic of this article, you'd hardly be surprised that it is.
In the previous two functor examples (Maybe and Tree), the Select methods were instance methods. On the other hand, the .NET Base Class Library implements IEnumerable<T>.Select as an extension method. You can do the same with this binary tree Visitor:
public static IBinaryTree<TResult> Select<TResult, T>( this IBinaryTree<T> tree, Func<T, TResult> selector) { if (tree == null) throw new ArgumentNullException(nameof(tree)); if (selector == null) throw new ArgumentNullException(nameof(selector)); var visitor = new SelectBinaryTreeVisitor<T, TResult>(selector); return tree.Accept(visitor); }
This Select method has the right signature for turning IBinaryTree<T> into a functor. It starts by creating a new instance of a private helper class called SelectBinaryTreeVisitor<T, TResult>. Notice that this class has two generic type arguments: the source type T and the destination type TResult. It also contains selector, so that it knows what to do with each Item it encounters.
SelectBinaryTreeVisitor<T, TResult> is a Visitor, so you pass it to the tree object's Accept method. The Accept method returns a variable that you can directly return, because, as you'll see below, the return type of SelectBinaryTreeVisitor<T, TResult>'s Visit methods is IBinaryTree<TResult>.
SelectBinaryTreeVisitor<T, TResult> is a private helper class, and is the most complex functor implementation you've seen so far. The Visitor design pattern solves a specific problem, but it was never the simplest of design patterns.
private class SelectBinaryTreeVisitor<T, TResult> : IBinaryTreeVisitor<T, IBinaryTree<TResult>> { private readonly Func<T, TResult> selector; public SelectBinaryTreeVisitor(Func<T, TResult> selector) { if (selector == null) throw new ArgumentNullException(nameof(selector)); this.selector = selector; } public IBinaryTree<TResult> Visit(Leaf<T> leaf) { var mappedItem = selector(leaf.Item); return Leaf(mappedItem); } public IBinaryTree<TResult> Visit(Node<T> node) { var mappedItem = selector(node.Item); var mappedLeft = node.Left.Accept(this); var mappedRight = node.Right.Accept(this); return Create(mappedItem, mappedLeft, mappedRight); } }
Since the class implements IBinaryTreeVisitor<T, IBinaryTree<TResult>>, it must implement the two Visit overloads. The overload for Leaf<T> is simple: use the selector to map the Item, and use the Leaf convenience method to return a new Leaf<TResult> containing the mapped item. Notice that while SelectBinaryTreeVisitor<T, TResult> looks like it has a generic 'return' type argument of TResult, it implements IBinaryTreeVisitor<T, IBinaryTree<TResult>>, which means that the return type of each Visit method must be IBinaryTree<TResult>, and that matches Leaf<TResult>.
The overload for a Node<T> object looks twice as big, but it's still simple. Like the leaf overload, it uses selector to map the Item, but in addition to that, it must also recursively map the Left and Right sub-trees. It does this by passing itself, in its role as a Visitor, to the left and right nodes' Accept methods. This returns mapped sub-trees that can be used to create a new mapped tree, using the Create convenience method.
Usage #
While the implementation of such a Visitor is cumbersome, it's easy enough to use.
var source = BinaryTree.Create(42, BinaryTree.Create(1337, BinaryTree.Leaf(0), BinaryTree.Leaf(-22)), BinaryTree.Leaf(100));
You can translate this binary tree of integers to a tree of strings using method call syntax:
IBinaryTree<string> dest = source.Select(i => i.ToString());
or by using query syntax:
IBinaryTree<string> dest = from i in source select i.ToString();
In both of these examples, I've explicitly declared the type of dest instead of using the var keyword. There's no practical reason to do this; I only did it to make the type clear to you.
Haskell #
Why would anyone ever do something so complicated as this?
The answer to such a question is, I believe, that it's only complicated in some programming languages. In Haskell, all of the above can be reduce to a single type declaration:
data BinaryTree a = Node a (BinaryTree a) (BinaryTree a) | Leaf a deriving (Show, Eq, Functor)
Notice that the Haskell compiler can automatically derive an implementation of the Functor typeclass, although that does require the DeriveFunctor language extension.
This may explain why binary trees aren't part of object-oriented programmers' normal tool box, whereas they are more commonplace in functional programming.
While not strictly required, in order to keep the examples equivalent, you can define these two aliases:
leaf :: a -> BinaryTree a leaf = Leaf create :: a -> BinaryTree a -> BinaryTree a -> BinaryTree a create = Node
This enables you to create a binary tree like this:
source :: BinaryTree Int source = create 42 ( create 1337 ( leaf 0) ( leaf (-22))) ( leaf 100)
As usual you can map the tree using the fmap function:
dest :: BinaryTree String dest = fmap show source
or by using infix notation:
dest :: BinaryTree String dest = show <$> source
The <$> operator is an alias for fmap.
F# #
As usual, F# lies somewhere between the extremes of C# and Haskell, although it's closer to Haskell in simplicity. The type declaration is similar:
type BinaryTree<'a> = | Node of ('a * BinaryTree<'a> * BinaryTree<'a>) | Leaf of 'a
Unlike Haskell, however, F# doesn't have any built-in functor awareness, so you'll have to implement the map function yourself:
// ('a -> 'b) -> BinaryTree<'a> -> BinaryTree<'b> let rec map f = function | Node (x, left, right) -> Node (f x, map f left, map f right) | Leaf x -> Leaf (f x)
Notice that you have to use the rec keyword in order to make map recursive. Instead of having to create a new helper class, and all the byzantine interactions required by the Visitor design pattern, the implementation uses simple pattern matching to achieve the same goal. In the Node case, it uses f to translate x, and recursively calls itself on left and right. In the Leaf case, it simply returns a new Leaf value with x translated by f.
Create helper functions to keep all three examples aligned:
// 'a -> BinaryTree<'a> let leaf = Leaf // 'a -> BinaryTree<'a> -> BinaryTree<'a> -> BinaryTree<'a> let create x left right = Node (x, left, right)
You can now create a binary tree of integers:
// BinaryTree<int> let source = BinaryTree.create 42 ( BinaryTree.create 1337 ( BinaryTree.leaf 0) ( BinaryTree.leaf -22)) ( BinaryTree.leaf 100)
which you can translate like this:
// BinaryTree<string> let dest = source |> BinaryTree.map string
Here, all of the above functions are defined in a module named BinaryTree.
First functor law #
The Select method obeys the first functor law. As usual, it's proper computer-science work to actually prove that, but you can write some tests to demonstrate the first functor law for the IBinaryTree<T> interface. In this article, you'll see a few parametrised tests written with xUnit.net. First, you can define some reusable trees as test input:
public static IEnumerable<object[]> Trees { get { yield return new[] { BinaryTree.Leaf(0) }; yield return new[] { BinaryTree.Create(-3, BinaryTree.Leaf(2), BinaryTree.Leaf(99)) }; yield return new[] { BinaryTree.Create(42, BinaryTree.Create(1337, BinaryTree.Leaf(0), BinaryTree.Leaf(-22)), BinaryTree.Leaf(100)) }; yield return new[] { BinaryTree.Create(-927, BinaryTree.Leaf(2), BinaryTree.Create(211, BinaryTree.Leaf(88), BinaryTree.Leaf(132))) }; yield return new[] { BinaryTree.Create(111, BinaryTree.Create(-336, BinaryTree.Leaf(113), BinaryTree.Leaf(-432)), BinaryTree.Create(1299, BinaryTree.Leaf(-32), BinaryTree.Leaf(773))) }; } }
This is just a collection of five small binary trees that can be used as input for parametrised tests. The first tree is only a single node - the simplest tree you can make with the IBinaryTree<T> API.
You can use this static property as a source of input for parametrised tests. Here's one that demonstrates that the first functor law holds:
[Theory, MemberData(nameof(Trees))] public void FirstFunctorLaw(IBinaryTree<int> tree) { Assert.Equal(tree, tree.Select(x => x)); }
Here, I chose to implement the identity function as an anonymous lambda expression. In contrast, in a previous article, I explicitly declared a function variable and called it id. Those two ways to express the identity function are equivalent.
As always, I'd like to emphasise that this test doesn't prove that IBinaryTree<T> obeys the first functor law. It only demonstrates that the law holds for those five examples.
Second functor law #
Like the above example, you can also write a parametrised test that demonstrates that IBinaryTree<T> obeys the second functor law. You can reuse the Trees test case source for that test:
[Theory, MemberData(nameof(Trees))] public void SecondFunctorLaw(IBinaryTree<int> tree) { string g(int i) => i.ToString(); bool f(string s) => s.Length % 2 == 0; Assert.Equal(tree.Select(g).Select(f), tree.Select(i => f(g(i)))); }
This test defines two local functions, f and g. Instead of explicitly declaring the functions as Func variables, this test uses a (relatively) new C# feature called local functions.
Again, while the test doesn't prove anything, it demonstrates that for the five test cases, it doesn't matter if you project the tree in one or two steps.
Summary #
Statically typed functional languages like F# and Haskell enable you to define sum types: types that encode a selection of mutually exclusive cases. Combined with pattern matching, it's easy to deal with values that can be one of several non-polymorphic cases. Object-oriented languages like C# or Java don't have good support for this type of data structure. Object-oriented programmers often resort to using type hierarchies, but this requires down-casting in order to work. It also comes with the disadvantage that with type hierarchies, the hierarchy is extensible, which means that as an implementer, you never know if you've handled all sub-types. The Visitor design pattern is a way to model sum types in object-oriented programming, although it tends to be verbose.
Nevertheless, if you have a generic type that models a set of mutually exclusive cases, it just may be a functor. In Haskell, you can make such a type a Functor with a mere declaration. In C#, you have to write considerable amounts of code.
Next: Reactive functor.
A Tree functor
A generalised tree object as a functor. Another functor example for object-oriented programmers.
This article is an instalment in an article series about functors. In a previous article, you saw how to implement the Maybe functor in C#. In this article, you'll get another functor example: a generalised tree (also known as a rose tree).
As opposed to a binary tree, any node in a generalised tree can have an arbitrary number of children, including none.
Implementation #
The following Tree<T> class can contain objects of the generic type T. Being generic, it's a candidate for a functor, and it does, in fact, turn out to be one:
public sealed class Tree<T> : IReadOnlyCollection<Tree<T>> { private readonly IReadOnlyCollection<Tree<T>> children; public T Item { get; } public Tree(T item, IReadOnlyCollection<Tree<T>> children) { if (item == null) throw new ArgumentNullException(nameof(item)); if (children == null) throw new ArgumentNullException(nameof(children)); Item = item; this.children = children; } public Tree<TResult> Select<TResult>(Func<T, TResult> selector) { var mappedItem = selector(Item); var mappedChildren = new List<Tree<TResult>>(); foreach (var t in children) mappedChildren.Add(t.Select(selector)); return new Tree<TResult>(mappedItem, mappedChildren); } public int Count { get { return children.Count; } } public IEnumerator<Tree<T>> GetEnumerator() { return children.GetEnumerator(); } IEnumerator IEnumerable.GetEnumerator() { return children.GetEnumerator(); } public override bool Equals(object obj) { if (!(obj is Tree<T> other)) return false; return Equals(Item, other.Item) && Enumerable.SequenceEqual(this, other); } public override int GetHashCode() { return Item.GetHashCode() ^ children.GetHashCode(); } }
As is usually the case, you can implement a tree in more than one way. Here, I chose an approach where Tree<T> contains an Item and is a collection of (sub)trees. Notice that the definition is recursive: in addition to its Item, each Tree<T> object also contains a finite collection of other trees. You create leaf nodes with empty collections.
This variation uses finite collections (IReadOnlyCollection<T>), but you could also enable infinite trees by instead using potentially infinite sequences (IEnumerable<T>). This would slightly complicate the implementation of the Select method, though, so I decided to leave that as an exercise to the reader.
The Select method first translates the contained Item using the selector function, and then recursively calls itself for each sub-tree in children. This method has the desired signature, and furthermore obeys the functor laws, as you'll see later in the article. Tree<T> is a functor.
Usage #
While you can create trees directly with the Tree<T> constructor, a few static helper methods makes it smoother:
public static class Tree { public static Tree<T> Leaf<T>(T item) { return new Tree<T>(item, new Tree<T>[0]); } public static Tree<T> Create<T>(T item, params Tree<T>[] children) { return new Tree<T>(item, children); } }
This enables you to create a tree like this:
var source = Tree.Create(42, Tree.Create(1337, Tree.Leaf(-3)), Tree.Create(7, Tree.Leaf(-99), Tree.Leaf(100), Tree.Leaf(0)));
This is a tree containing integers. You can translate it to a tree containing strings like this:
Tree<string> dest = source.Select(i => i.ToString());
or like this:
Tree<string> dest = from i in source select i.ToString();
In both of these examples, I've explicitly declared the type of dest instead of using the var keyword. There's no practical reason to do this; I only did it to make the type clear to you.
Haskell #
Haskell has a more explicit model of functors, and the language features to support it. The Haskell equivalent to the above Tree<T> class is literally one line of code:
data Tree a = Tree a [Tree a] deriving (Show, Eq, Functor)
Notice that the Haskell compiler can automatically derive an implementation of the Functor typeclass, although that does require the DeriveFunctor language extension.
You can expend a few more lines of code for utility functions, so that it looks like you're actually programming:
leaf :: a -> Tree a leaf x = Tree x [] create :: a -> [Tree a] -> Tree a create = Tree
These functions correspond to the static methods on the above Tree class. With them, you can now create a tree:
source :: Tree Int source = create 42 [ create 1337 [ leaf (-3)], create 7 [ leaf (-99), leaf 100, leaf 0]]
You can translate such a tree of integers to a tree of strings with the fmap function:
dest :: Tree String dest = fmap show source
or with the infix operator:
dest :: Tree String dest = show <$> source
The <$> operator is an alias for fmap.
F# #
In F#, the type definition has the same structure as in Haskell:
type Tree<'a> = Tree of ('a * Tree<'a> list)
Unlike Haskell, however, F# doesn't have any built-in functor awareness, so you'll have to implement the map function yourself:
// ('a -> 'b) -> Tree<'a> -> Tree<'b> let rec map f (Tree (x, children)) = let mappedX = f x let mappedChildren = children |> List.map (map f) Tree (mappedX, mappedChildren)
Notice that you have to use the rec keyword in order to make map recursive. The implementation is similar to the C# code: first use f to map the contained item, and then recursively map the children.
To keep all three examples equivalent, you can also define utility functions:
// 'a -> Tree<'a> let leaf x = Tree (x, List.empty) // 'a -> Tree<'a> list -> Tree<'a> let create x children = Tree (x, children)
This enables you to create a tree like this:
// Tree<int> let source = Tree.create 42 [ Tree.create 1337 [ Tree.leaf -3] Tree.create 7 [ Tree.leaf -99 Tree.leaf 100 Tree.leaf 0]]
which you can translate like this:
// Tree<string> let dest = source |> Tree.map string
Here, all of the above functions are defined in a module named Tree.
First functor law #
The Select method obeys the first functor law. As usual, it's proper computer-science work to actually prove that, but you can write some tests to demonstrate the first functor law for the Tree<T> class. In this article, you'll see a few parametrised tests written with xUnit.net. First, you can define some reusable trees as test input:
public static IEnumerable<object[]> Trees { get { yield return new[] { Tree.Leaf(42) }; yield return new[] { Tree.Create(-32, Tree.Leaf(0)) }; yield return new[] { Tree.Create(99, Tree.Leaf(90), Tree.Leaf(2)) }; yield return new[] { Tree.Create(99, Tree.Leaf(90), Tree.Create(2, Tree.Leaf(-3))) }; yield return new[] { Tree.Create(42, Tree.Create(1337, Tree.Leaf(-3)), Tree.Create(7, Tree.Leaf(-99), Tree.Leaf(100), Tree.Leaf(0))) }; } }
This is just a collection of five small trees that can be used as input for parametrised tests. The first tree is only a single node - the simplest tree you can make with the Tree<T> class.
You can use this static property as a source of input for parametrised tests. Here's one that demonstrates that the first functor law holds:
[Theory, MemberData(nameof(Trees))] public void FirstFunctorLaw(Tree<int> tree) { Assert.Equal(tree, tree.Select(x => x)); }
Here, I chose to implement the identity function as an anonymous lambda expression. In contrast, in the previous article, I explicitly declared a function variable and called it id. Those two ways to express the identity function are equivalent.
As always, I'd like to emphasise that this test doesn't prove that Tree<T> obeys the first functor law. It only demonstrates that the law holds for those five examples.
Second functor law #
Like the above example, you can also write a parametrised test that demonstrates that Tree<T> obeys the second functor law. You can reuse the Trees test case source for that test:
[Theory, MemberData(nameof(Trees))] public void SecondFunctorLaw(Tree<int> tree) { string g(int i) => i.ToString(); bool f(string s) => s.Length % 2 == 0; Assert.Equal(tree.Select(g).Select(f), tree.Select(i => f(g(i)))); }
This test defines two local functions, f and g. Instead of explicitly declaring the functions as Func variables, this test uses a (relatively) new C# feature called local functions.
Again, while the test doesn't prove anything, it demonstrates that for the five test cases, it doesn't matter if you project the tree in one or two steps.
Summary #
This was the second example of a functor implemented in a statically typed object-oriented language, but contrasted with implementations in statically typed functional languages. The concept of a functor translates without much loss of fidelity, but you'll have to write more verbose code. A language like C# isn't optimised for functors or their like; Haskell and F# are.
The purpose of this article series is to show enough examples of functors that you should start to see a pattern. Keep in mind, though, that a functor isn't a design pattern. It's a mathematical concept.
Next: A rose tree functor.
Flattening arrow code using a stack of monads
Flatten arrow code with a stack of monads. A horrible example in C#.
In the previous article, you saw how to refactor an injected dependency to a Visitor that implements a free monad. One remaining problem is that some of the code tends towards the Arrow anti-pattern. In this article, you'll see how elegantly you can deal with this in Haskell, how it translates to slightly more verbose F# code, but how, even though it does translate all the way to C#, it stops being nice along the way.
All code for this article is available on GitHub.
Arrow code #
This is the problematic code:
public IReservationsProgram<int?> TryAccept(Reservation reservation) { return ReservationsProgram .IsReservationInFuture(reservation) .SelectMany(isInFuture => { if (!isInFuture) return new Pure<int?>(null); return ReservationsProgram .ReadReservations(reservation.Date) .SelectMany(reservations => { var reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return new Pure<int?>(null); reservation.IsAccepted = true; return ReservationsProgram .Create(reservation) .Select(x => new int?(x)); }); }); }
Perhaps it doesn't look that bad, but I think that that's mostly a result of the original example being as simple as it is. After all, the original example code started out like this:
public int? TryAccept(Reservation reservation) { if (!ReservationsRepository.IsReservationInFuture(reservation)) return null; var reservedSeats = ReservationsRepository .ReadReservations(reservation.Date) .Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return null; reservation.IsAccepted = true; return ReservationsRepository.Create(reservation); }
The cyclomatic complexity of this method could be as low as 3, so if this was real production code, there'd be no reason to refactor it. As with most of my articles, however, you have to think of this example problem as a stand-in for something more complicated.
If you take a second look at the top version (which is actually the later version), I hope you'll agree that the change has harmed the code. In general, it's more noisy, and it shows a clear tendency towards the dreaded Arrow anti-pattern. Again, it may not look that bad here, but if you imagine that we're looking at a stand-in for a much worse problem, I hope you can see how this could quickly become unsustainable.
Part of the problem is that while C# has some syntactic sugar for monads, you can't branch inside a query expression, so instead it seems as though you're stuck with such nested closures.
First F# attempt #
F#, on the other hand, doesn't have that limitation. In F#, you can branch inside of computation expressions, so would that address the problem? Unfortunately, that's not the whole story. Here's an attempt at writing equivalent code in F#, using a custom reservations computation expression:
// int -> Reservation -> ReservationsProgram<int option> let tryAccept capacity reservation = reservations { let! isInFuture = isReservationInFuture reservation if not isInFuture then return None else let! reservations = readReservations reservation.Date let reservedSeats = List.sumBy (fun r -> r.Quantity) reservations if (capacity < reservedSeats + reservation.Quantity) then return None else let! reservationId = create { reservation with IsAccepted = true } return Some reservationId }
While this is, in my opinion, more readable than the C# code, it doesn't successfully address the Arrow anti-pattern. While it's perfectly possible to branch (that is: use if, then, and else) inside a computation expression, we run into another problem. In statement-based languages like C# and Java, you can use Guard Clauses to return early, as the original, pretty C# example demonstrates. In expression-based languages like F# and Haskell, on the other hand, any if branch must have a corresponding else branch, and both branches must return a value of the same type. This restriction forces the above F# code into the same Arrow shape as the problematic C# code.
Languages like F# and Haskell would be poor languages, though, if they didn't have ways to address problems like this one.
Flattening with MaybeT #
While it already feels unpleasant to write F# code like the above, writing similar code in Haskell would be figuratively painful. In Haskell, however, you essentially just change the return type of your function, pull in some standard library functions, and before you know it, you have nice flat code, with nary an Arrow in sight:
tryAccept :: Int -> Reservation -> MaybeT ReservationsProgram Int tryAccept capacity reservation = do guard =<< isReservationInFuture reservation reservations <- readReservations $ reservationDate reservation let reservedSeats = sum $ reservationQuantity <$> reservations guard $ reservedSeats + reservationQuantity reservation <= capacity create $ reservation { reservationIsAccepted = True }
One of the notable traits of Haskell is that, because of its high-level abstractions, changing the type of an expression can change its behaviour. In this case, I decided to add a MaybeT to the ReservationsProgram Int return type. This means that not only does the following code take place inside the ReservationsProgram free monad, it takes place inside a stack of monads. In this case, the stack consists of Maybe and ReservationsProgram.
What this means is that you can use the built-in guard function to short-circuit the program if the guards fail. Yes, these are literally guard clauses!
Not only does this address the Arrow anti-pattern, it completely flattens the code so that the happy path is emphasised.
Stacking monads in F# #
While Haskell comes with built-in monad transformers that enable you to declaratively stack monads, you'll have to do it manually in F#. It's still possible, though. All it takes to stack ReservationsProgram and option is something like this:
// ('a -> ReservationsProgram<'b option>) -> ReservationsProgram<'a option> -> // ReservationsProgram<'b option> let bind f x = reservations { let! x' = x match x' with | Some x'' -> return! f x'' | None -> return None } type ReservationsOptionBuilder () = member this.Bind (x, f) = bind f x member this.Return x = Pure (Some x) member this.ReturnFrom x = x member this.Zero () = Pure (Some ()) let reservationsOption = ReservationsOptionBuilder ()
This stack of monads specifically handles the combination where a ReservationsProgram contains an option value. It considers the continuation value x' produced by the previous step in a ReservationsProgram, and only continues with f if the value is a Some value. Just like option normally works, it short-circuits further processing if the value is a None value.
While F# doesn't have a general-purpose guard function, you can easily write one for this particular stack of monads:
// bool -> ReservationsProgram<unit option> let guard = function | true -> Pure (Some ()) | false -> Pure None
This function takes a Boolean value as input, and returns Pure (Some ()) when the value is true, and Pure None otherwise. While this seems weird at first glance, this is essentially what Haskell's guard does in the above code listing. The point is that Pure None short-circuits further processing, while Pure (Some ()) allows the program to continue, as per the above bind function.
You can now write a flattened version of tryAccept
// int -> Reservation -> ReservationsProgram<int option> let tryAccept capacity reservation = reservationsOption { do! ReservationsOption.bind guard <| isReservationInFuture reservation let! reservations = readReservations reservation.Date let reservedSeats = List.sumBy (fun r -> r.Quantity) reservations do! guard (reservedSeats + reservation.Quantity <= capacity) return! create { reservation with IsAccepted = true } }
Notice that the type of the function doesn't change. It still returns a ReservationsProgram<int option>, but the implementation is different. Instead of explicitly dealing with branching in a reservations computation expression, it implicitly deals with it in the composed reservationsOption computation expression.
Using the specialised guard function doesn't look as pretty as in Haskell, but it gets the job done.
Maybe as a Visitor #
Can you do the same in C#? Yes, sort of, but it'll be ugly.
As a first step, you'll need a Maybe monad, as this isn't a built-in type in C#. While I'd typically prefer a simpler implementation, since we're already looking at Church-encoded sum types, let's take the Church-encoded Maybe implementation, and refactor it to a Visitor. The IMaybe<T> interface is simply this:
public interface IMaybe<T> { TResult Accept<TResult>(IMaybeVisitor<T, TResult> visitor); }
The Visitor is defined like this:
public interface IMaybeVisitor<T, TResult> { TResult VisitNothing { get; } TResult VisitJust(T just); }
This is, hopefully, not terribly surprising. There's two cases: just and nothing, and only the just case has a value associated. While I'm not going to walk you through all the details, this version of IMaybe<T> is still a monad:
public static IMaybe<TResult> SelectMany<T, TResult>( this IMaybe<T> source, Func<T, IMaybe<TResult>> selector) { return source.Accept(new SelectManyMaybeVisitor<T, TResult>(selector)); }
If you want to see how SelectManyMaybeVisitor<T, TResult> is implemented, you can see it in the code repository, but otherwise, it's also a good exercise to see if you can puzzle it out yourself.
Stacking Reservations and Maybe #
You already have the IReservationsProgram<T> and IMaybe<T> monads. Now you just need to stack them, just like the above F# code:
public static IReservationsProgram<IMaybe<TResult>> SelectMany<T, TResult>( this IReservationsProgram<IMaybe<T>> source, Func<T, IReservationsProgram<IMaybe<TResult>>> selector) { return source.SelectMany(x => x.Accept(new SelectManyMaybeVisitor<T, TResult>(selector))); } private class SelectManyMaybeVisitor<T, TResult> : IMaybeVisitor<T, IReservationsProgram<IMaybe<TResult>>> { private readonly Func<T, IReservationsProgram<IMaybe<TResult>>> selector; public SelectManyMaybeVisitor(Func<T, IReservationsProgram<IMaybe<TResult>>> selector) { this.selector = selector; } public IReservationsProgram<IMaybe<TResult>> VisitNothing { get { return new Pure<IMaybe<TResult>>(new Nothing<TResult>()); } } public IReservationsProgram<IMaybe<TResult>> VisitJust(T just) { return this.selector(just); } }
Just like in the F# code, you can write the code inside of the IReservationsProgram<T> monad. To do that, you call SelectMany on source. The x in that lambda expression is a IMaybe<T> value, so in order to be able to proceed, you'll have to call its Accept method and pass it a Visitor.
The overall signature of the outer SelectMany method is fixed. This is, after all, the monadic bind function, so you know that the return type must be IReservationsProgram<IMaybe<TResult>>. Therefore, this must be the second type argument of the Visitor that you pass to Accept, so the Visitor must have the type IMaybeVisitor<T, IReservationsProgram<IMaybe<TResult>>>. From there, it's 'just' a matter of figuring out how to implement VisitNothing and VisitJust.
In the VisitNothing case, you simply return a new Nothing<TResult>(), but wrapped in a Pure value, so that it becomes an IReservationsProgram<IMaybe<TResult>>, rather than just an IMaybe<TResult>.
In the VisitJust case, you'll need the injected selector, which you can simply call with the input argument and return the result.
In order to support query expressions, you'll also need this special SelectMany overload:
public static IReservationsProgram<IMaybe<TResult>> SelectMany<T, U, TResult>( this IReservationsProgram<IMaybe<T>> source, Func<T, IReservationsProgram<IMaybe<U>>> k, Func<T, U, TResult> s) { return source .SelectMany(x => k(x) .SelectMany(y => new Pure<IMaybe<TResult>>(new Just<TResult>(s(x, y))))); }
This is merely a weird C# technical detail, so I'm not going to tire you with this. It's not interesting.
Guard #
Like the above F# code, you can define a specialised Guard method:
public static IReservationsProgram<IMaybe<Unit>> Guard(bool b) { if (b) return new Pure<IMaybe<Unit>>(new Just<Unit>(Unit.Instance)); else return new Pure<IMaybe<Unit>>(new Nothing<Unit>()); }
It does the same as its F# counterpart, only is it more verbose, and it required me to define a unit type, because C# doesn't have one:
public class Unit { public readonly static Unit Instance = new Unit(); private Unit() { } }
This is simply a Singleton that carries no data. It's like void, but can act as a generic return type, which is what we need here.
Do #
Finally, in order to be able to set IsAccepted to true and make it look like a function, you can add a Do method:
public static IReservationsProgram<IMaybe<Unit>> Do(Action action) { action(); return new Pure<IMaybe<Unit>>(new Just<Unit>(Unit.Instance)); }
This is a nasty piece of impure code, but it'll get the job done. It'd also be possible to refactor to a make the Reservation class immutable, but for this proof of concept code, that's not necessary. It'll be ugly regardless.
The point of the method is to enable method chaining in the Fluent style, even while you're mutating state. In general, I'd like to warn against doing something like this, because the entire point of functional programming is to avoid mutating state. It does allow us, however, to reproduce the original behaviour in the top of the article, which also mutates the reservation argument.
Method chaining #
You can now write TryAccept as an IReservationsProgram<IMaybe<int>> method, instead of IReservationsProgram<int?>. In other words, you replace the int? (Nullable<int>) with IMaybe<int>. This enables you write the entire program as a 'flat' composition, by chaining calls to SelectMany and Select:
public IReservationsProgram<IMaybe<int>> TryAccept(Reservation reservation) { return ReservationsProgram.IsReservationInFuture(reservation) .SelectMany(isInFuture => ReservationsProgram.Guard(isInFuture)) .SelectMany((Unit _) => ReservationsProgram.ReadReservations(reservation.Date)) .Select(reservations => reservations.Sum(r => r.Quantity)) .SelectMany(reservedSeats => ReservationsProgram.Guard(reservedSeats + reservation.Quantity <= Capacity)) .SelectMany((Unit _) => ReservationsProgram.Do(() => { reservation.IsAccepted = true; })) .SelectMany((Unit _) => ReservationsProgram.Create(reservation)); }
You start with ReservationsProgram.IsReservationInFuture and continue with SelectMany off of its return value. Inside SelectMany, you then call ReservationsProgram.Guard in order to short-circuit if isInFuture is false. In fact, that step can be reduced to SelectMany(ReservationsProgram.Guard), using method group syntax.
While Guard returns a program containing Unit, you can still continue with SelectMany to call ReservationsProgram.ReadReservations.
I'm not going to walk you through the rest of this code, but it works.
Query syntax #
If you can write an entire program by chaining SelectMany and Select, chances are you can write it using C# query syntax as well. This turns out to be the case:
public IReservationsProgram<IMaybe<int>> TryAccept(Reservation reservation) { return from isInFuture in ReservationsProgram.IsReservationInFuture(reservation) from _ in ReservationsProgram.Guard(isInFuture) from reservations in ReservationsProgram.ReadReservations(reservation.Date) let reservedSeats = reservations.Sum(r => r.Quantity) from __ in ReservationsProgram.Guard(reservedSeats + reservation.Quantity <= Capacity) from ___ in ReservationsProgram.Do(() => { reservation.IsAccepted = true; }) from id in ReservationsProgram.Create(reservation) select id; }
This is simply the 'sugared' version of the previous code. It's a little more succinct, but whether it's better is subjective at best. I think you'd be challenged to find anyone who'd consider this idiomatic C# code.
It gets the job done, though. It actually works!
To be clear, I'm not particularly impressed with the readability of this. I love the Haskell version, but the C# translation isn't my cup of tea.
Conclusion #
When I go to meetups and conferences, I often get the chance to talk to people who have read my articles or seen my talks on functional programming. I often get the question whether it's possible to use some of the wonderful F# and Haskell concepts in C#. This article answers such questions. Yes, it's possible, but what's the point?
Such code is brittle, because you're dancing on the edge of what C# can do. I had to accept some compromises just to get this proof-of-concept code to work. To add spite to injury, the code is not as readable as idiomatic C#, and it taps into concepts that most C# developers wouldn't be familiar with.
I'd expect most C# programmers to consider a code base like this unreadable. In the amount of time it takes to understand and learn the underlying concepts of monads and their syntactic sugar, one can learn a proper functional programming language like F#. Don't try to make C# do something it wasn't designed to do; just use a functional programming language; you can learn that sooner than you'll be able to make sense of this Frankenstein's monster shown here.
Dependency Injection revisited
Replace Dependency Injection with a Visitor
In a previous article, you saw how you can model any sum type as a Visitor. Does that mean, then, that you can model a free monad as a Visitor?
Yes, it does.
In the F# free monad recipe, you saw how to refactor any injected, interface-based dependency to a free monad. Since a free monad is nothing but a recursive sum type, this means that you now have the tools at your disposal to refactor your injected dependencies to a Visitor.
To be clear, this is an article exploring the boundaries of what's possible with a language like C#. It's not intended to be an endorsement of a particular way to organise code. A conference talk recording that covers the same example also exists.
Dependency Injection example #
I'll walk you through how to do this. We'll start with an example, which, as usual, is about developing an online restaurant reservations system. The code base you'll see here implements the business logic that decides whether or not to accept a reservation request. All code from this article is available on GitHub.
In order to make the example illustrative, but still manageable, we'll look at a single dependency, defined like this:
public interface IReservationsRepository { // This method doesn't belong on a Repository interface. It ought to be // on some sort of ITimeProvider interface, or an extension method // thereof, but in order to keep the example refactorings as simple as // possible, it'll go here for demo purposes. bool IsReservationInFuture(Reservation reservation); IReadOnlyCollection<Reservation> ReadReservations(DateTimeOffset date); int Create(Reservation reservation); }
As the code comment explains, the IsReservationInFuture method doesn't belong on this IReservationsRepository interface. A dedicated 'time provider' dependency would be more appropriate, but as you'll see when you read on, refactoring just one interface to a free monad Visitor is already complicated. Doing it twice would just repeat the process while adding little additional clarity.
Apart from IsReservationInFuture, the IReservationsRepository declares ReadReservations for querying the Repository for existing reservations, and Create for adding a new reservation to the Repository. Notice that the Create method violates the Command Query Separation principle. While better alternatives exist, I decided to design the present example like this because it better illustrates how data could flow through a system.
The only consumer of the interface that we're going to consider is this MaîtreD class:
public class MaîtreD { public MaîtreD(int capacity, IReservationsRepository reservationsRepository) { Capacity = capacity; ReservationsRepository = reservationsRepository; } public int? TryAccept(Reservation reservation) { if (!ReservationsRepository.IsReservationInFuture(reservation)) return null; var reservedSeats = ReservationsRepository .ReadReservations(reservation.Date) .Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return null; reservation.IsAccepted = true; return ReservationsRepository.Create(reservation); } public int Capacity { get; } public IReservationsRepository ReservationsRepository { get; } }
This is straightforward example code. First, it queries whether the reservation is in the past, because it makes no sense accepting a reservation in the past.
If it gets past that hurdle, the TryAccept method then queries the injected ReservationsRepository for the reservations already recorded on that date, and calculates the sum of the quantities. This produces reservedSeats - the number of already reserved seats. If the restaurant's Capacity (a Primitive Dependency) is less than the already reserved seats, plus the requested quantity, the method again rejects the reservation. This time, the reason is that there's insufficient remaining capacity to accept it.
Finally, if the reservation makes it past all the guards, IsAccepted is set to true, and the reservation is added to the Repository. Recall that Create returns the ID of the new reservation (presumably a database ID), so that ID is returned from the method. In all other cases, the method returns null. The return type of TryAccept is int? (Nullable<int>), so the int value returned from Create is implicitly converted to int?; the compiler does that.
Testability #
My original motivation for learning about Dependency Injection was that I did Test-Driven Development. Dependency Injection enables you to make automated tests deterministic by replacing common sources of non-determinism with Test Doubles. This is, predictably, also the case here:
[Theory, BookingApiTestConventions] public void TryAcceptReturnsReservationIdInHappyPathScenario( [Frozen]Mock<IReservationsRepository> td, Reservation reservation, IReadOnlyCollection<Reservation> reservations, MaîtreD sut, int excessCapacity, int expected) { td.Setup(r => r.IsReservationInFuture(reservation)).Returns(true); td .Setup(r => r.ReadReservations(reservation.Date)) .Returns(reservations); td.Setup(r => r.Create(reservation)).Returns(expected); var reservedSeats = reservations.Sum(r => r.Quantity); reservation.IsAccepted = false; sut = sut.WithCapacity( reservedSeats + reservation.Quantity + excessCapacity); var actual = sut.TryAccept(reservation); Assert.Equal(expected, actual); Assert.True(reservation.IsAccepted); }
This tests exercises the happy path scenario where the reservation is in the future, and there is enough remaining capacity to accept the request. It uses xUnit.net and Moq with AutoFixture gluing it all together.
Database implementation #
It's nice to be able to test the business logic, but ultimately, you'll need your application to be able to store reservations in some sort of persistent storage like a relational database. That's easy, too. Just implement IReservationsRepository:
public class SqlReservationsRepository : IReservationsRepository { public SqlReservationsRepository(string connectionString) { this.ConnectionString = connectionString; } public string ConnectionString { get; } public bool IsReservationInFuture(Reservation reservation) { return DateTimeOffset.Now < reservation.Date; } public IReadOnlyCollection<Reservation> ReadReservations( DateTimeOffset date) { return this.ReadReservations( date.Date, date.Date.AddDays(1).AddTicks(-1)); } private IReadOnlyCollection<Reservation> ReadReservations( DateTimeOffset min, DateTimeOffset max) { var result = new List<Reservation>(); using (var conn = new SqlConnection(this.ConnectionString)) using (var cmd = new SqlCommand(readByRangeSql, conn)) { cmd.Parameters.Add(new SqlParameter("@MinDate", min)); cmd.Parameters.Add(new SqlParameter("@MaxDate", max)); conn.Open(); using (var rdr = cmd.ExecuteReader()) { while (rdr.Read()) result.Add( new Reservation { Date = (DateTimeOffset)rdr["Date"], Name = (string)rdr["Name"], Email = (string)rdr["Email"], Quantity = (int)rdr["Quantity"] }); } } return result; } private const string readByRangeSql = @" SELECT [Date], [Name], [Email], [Quantity] FROM [dbo].[Reservations] WHERE YEAR(@MinDate) <= YEAR([Date]) AND MONTH(@MinDate) <= MONTH([Date]) AND DAY(@MinDate) <= DAY([Date]) AND YEAR([Date]) <= YEAR(@MaxDate) AND MONTH([Date]) <= MONTH(@MaxDate) AND DAY([Date]) <= DAY(@MaxDate)"; public int Create(Reservation reservation) { using (var conn = new SqlConnection(ConnectionString)) using (var cmd = new SqlCommand(createReservationSql, conn)) { cmd.Parameters.Add( new SqlParameter("@Date", reservation.Date)); cmd.Parameters.Add( new SqlParameter("@Name", reservation.Name)); cmd.Parameters.Add( new SqlParameter("@Email", reservation.Email)); cmd.Parameters.Add( new SqlParameter("@Quantity", reservation.Quantity)); conn.Open(); return cmd.ExecuteNonQuery(); } } private const string createReservationSql = @" INSERT INTO [dbo].[Reservations] ([Date], [Name], [Email], [Quantity]) VALUES (@Date, @Name, @Email, @Quantity)"; }
As has been my position for years, I find it easier to write database implementations using .NET's original ADO.NET API than fighting with an ORM.
Free monad in F# #
In order to refactor IReservationsRepository to a free monad, it's illustrative to first see how it would look in F#. This step is by no means required, but it offers another perspective of the translation that you have to perform. According to the F# free monad recipe, you can represent the IReservationsRepository interface with a sum type that describes the instruction set of the API:
type ReservationsInstruction<'a> = | IsReservationInFuture of (Reservation * (bool -> 'a)) | ReadReservations of (DateTimeOffset * (Reservation list -> 'a)) | Create of (Reservation * (int -> 'a))
Each case corresponds to a method from the original interface, and each contains a tuple. The first element of the tuple should contain the input to the method, so the first element of IsReservationInFuture is a Reservation value, the first element of ReadReservations is a DateTimeOffset, and the first element of Create is a Reservation, just like IsReservationInFuture.
The second tuple element is a continuation. This is a function an interpreter must call once it's produced the value required to continue. This corresponds to the output value from the interface methods, so the input to the continuation associated with IsReservationInFuture is a Boolean value, and so on.
The rest of the F# code example follows the recipe to the letter, so it's not important to list it here. You're welcome to look in the Git repository, if you'd like to see the details.
Church-encoded instruction set #
From Church encodings we know that we can represent a sum type as an interface with a single Match method. The instruction set is a functor, so it has a generic type argument:
public interface IReservationsInstruction<T>
The Match method must take an argument for each case in the sum type. In the above F# code, you can see that there's three cases, corresponding to the three methods in the original IReservationsRepository interface.
Furthermore, we know from the previous articles on Church encodings that the Match method must be generic, and return a value of its generic type argument:
TResult Match<TResult>(
Third, each argument (i.e. each case from the sum type you're encoding) must have this form:
Func<something, TResult> name,
where something is the type of the data associated with the case, and name is the name of the case.
The names are easy: they're isReservationInFuture, readReservations, and create, but what are the types associated with each case?
The F# free monad recipe gives the answer, which is why I chose to include the above F# code. For instance, the type associated with the IsReservationInFuture case is Reservation * (bool -> 'a). That's a tuple, where the first element is a Reservation 'object', and the second element is a function.
Take it slow for the first case, then. A tuple where the first element is a Reservation has the type:
Tuple<Reservation, function-type>
where function-type is the type of the continuation function. In F#, that type was bool -> 'a, which means a function that takes a bool as input, and returns a value of the generic type 'a as output. In our Church-encoded C# code, we call that type T, so you need a function from bool to T; that is: Func<bool, T>. If you plug that into the above tuple type, you get:
Tuple<Reservation, Func<bool, T>>
Again, you can plug that type into the something place-holder further up, to find the type of the input argument that corresponds to the isReservationInFuture case:
Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture
Doing this for the two other cases finally reveals the entire Match method:
public interface IReservationsInstruction<T> { TResult Match<TResult>( Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture, Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> readReservations, Func<Tuple<Reservation, Func<int, T>>, TResult> create); }
That's a worthy candidate for the Ugliest C# method signature of 2018 award, I admit, but it's just an intermediate step. This is how the sausage is made.
Implementations of the instruction set #
The IReservationsInstruction<T> interface defines an API. You'll need classes that implement the interface in order to do something useful. As you've seen multiple times in the articles series about Church encodings, you must add an implementation per case. Starting from the top:
public class IsReservationInFuture<T> : IReservationsInstruction<T> { private readonly Tuple<Reservation, Func<bool, T>> t; public IsReservationInFuture(Tuple<Reservation, Func<bool, T>> t) { this.t = t; } public TResult Match<TResult>( Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture, Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> readReservations, Func<Tuple<Reservation, Func<int, T>>, TResult> create) { return isReservationInFuture(this.t); } }
This class simply adapts an 'object' of the type Tuple<Reservation, Func<bool, T>> to the IReservationsInstruction<T> interface. Importantly, it unconditionally calls the Match method's isReservationInFuture argument, while ignoring readReservations and create. This is consistent with the previous incarnations of Church-encodings you've seen. It's an automatable process. You implement the two other cases in the same way:
public class ReadReservations<T> : IReservationsInstruction<T> { private readonly Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>> t; public ReadReservations(Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>> t) { this.t = t; } public TResult Match<TResult>( Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture, Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> readReservations, Func<Tuple<Reservation, Func<int, T>>, TResult> create) { return readReservations(this.t); } }
and
public class Create<T> : IReservationsInstruction<T> { private readonly Tuple<Reservation, Func<int, T>> t; public Create(Tuple<Reservation, Func<int, T>> t) { this.t = t; } public TResult Match<TResult>( Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture, Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> readReservations, Func<Tuple<Reservation, Func<int, T>>, TResult> create) { return create(this.t); } }
If you find the class names odd, then that's a fair criticism. I agree that Create isn't the most object-oriented class name. At this point, though, the design is hardly object-oriented, even though the code in use is C#. You can deal with the names later.
Functor #
The IReservationsInstruction<T> interface is generic, and as expected, it's a functor:
public static IReservationsInstruction<TResult> Select<T, TResult>( this IReservationsInstruction<T> source, Func<T, TResult> selector) { return source.Match<IReservationsInstruction<TResult>>( isReservationInFuture: t => new IsReservationInFuture<TResult>( new Tuple<Reservation, Func<bool, TResult>>( t.Item1, b => selector(t.Item2(b)))), readReservations: t => new ReadReservations<TResult>( new Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, TResult>>( t.Item1, d => selector(t.Item2(d)))), create: t => new Create<TResult>( new Tuple<Reservation, Func<int, TResult>>( t.Item1, r => selector(t.Item2(r))))); }
Yes, this is horrendous. The F# code is neater:
let private mapI f = function | IsReservationInFuture (x, next) -> IsReservationInFuture (x, next >> f) | ReadReservations (x, next) -> ReadReservations (x, next >> f) | Create (x, next) -> Create (x, next >> f)
Again, this is an intermediary step. Things will get better.
Church-encoded free monad #
Since IReservationsInstruction<T> is a functor, you can package it as a free monad. This entails creating a wrapper 'program' type for it. This is another sum type, in F# written like this:
type ReservationsProgram<'a> = | Free of ReservationsInstruction<ReservationsProgram<'a>> | Pure of 'a
The direct translation to Church-encoded C#, then, is to a Match method with two arguments:
public interface IReservationsProgram<T> { TResult Match<TResult>( Func<IReservationsInstruction<IReservationsProgram<T>> ,TResult> free, Func<T, TResult> pure); }
While the free case looks intimidating, you arrive at it through the same automatic process as already described.
The pure case is implemented by this trivial class:
public class Pure<T> : IReservationsProgram<T> { private readonly T x; public Pure(T x) { this.x = x; } public TResult Match<TResult>( Func<IReservationsInstruction<IReservationsProgram<T>>, TResult> free, Func<T, TResult> pure) { return pure(this.x); } }
The free case is slightly, but not much, more complex:
public class Free<T> : IReservationsProgram<T> { private readonly IReservationsInstruction<IReservationsProgram<T>> i; public Free(IReservationsInstruction<IReservationsProgram<T>> i) { this.i = i; } public TResult Match<TResult>( Func<IReservationsInstruction<IReservationsProgram<T>>, TResult> free, Func<T, TResult> pure) { return free(this.i); } }
Both of them, true to the plan we're following, call their respective method arguments with the objects that they adapt.
Monad #
In C#, the typical monadic bind function is idiomatically called SelectMany, and for various reasons, you need two overloads:
public static IReservationsProgram<TResult> SelectMany<T, TResult>( this IReservationsProgram<T> source, Func<T, IReservationsProgram<TResult>> selector) { return source.Match( free: i => new Free<TResult>(i.Select(p => p.SelectMany(selector))), pure: x => selector(x)); } public static IReservationsProgram<TResult> SelectMany<T, U, TResult>( this IReservationsProgram<T> source, Func<T, IReservationsProgram<U>> k, Func<T, U, TResult> s) { return source .SelectMany(x => k(x) .SelectMany(y => new Pure<TResult>(s(x, y)))); }
The bottom of the two overloads is required by C# if you want to be able to support various query syntax language constructs. The top overload utilises Match to dispatch between pure and free. Again, the pure case is easy, because you simply call selector with x, and return its result.
The free case is more complicated. While i.Select is the Select method defined for IReservationsInstruction<T>, p.SelectMany is a recursive call to the method itself.
That's a fly in the ointment, as C# doesn't handle recursion as well as F# or Haskell. It'll work fine as long as you don't blow the stack by producing huge programs that have to be interpreted.
Lifts #
Following the free monad recipe, you'll need to lift each of the instruction set cases to the 'program' type. The following are plain helper methods:
public static IReservationsProgram<bool> IsReservationInFuture(Reservation reservation) { return new Free<bool>( new IsReservationInFuture<IReservationsProgram<bool>>( new Tuple<Reservation, Func<bool, IReservationsProgram<bool>>>( reservation, x => new Pure<bool>(x)))); } public static IReservationsProgram<IReadOnlyCollection<Reservation>> ReadReservations( DateTimeOffset date) { return new Free<IReadOnlyCollection<Reservation>>( new ReadReservations<IReservationsProgram<IReadOnlyCollection<Reservation>>>( new Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, IReservationsProgram<IReadOnlyCollection<Reservation>>>>( date, x => new Pure<IReadOnlyCollection<Reservation>>(x)))); } public static IReservationsProgram<int> Create(Reservation reservation) { return new Free<int>( new Create<IReservationsProgram<int>>( new Tuple<Reservation, Func<int, IReservationsProgram<int>>>( reservation, x => new Pure<int>(x)))); }
Again, the (unfortunately required) type information makes this unreadable, but in fact, not much happens. In F#, the same lift functions are three one-liners:
let isReservationInFuture r = Free (IsReservationInFuture (r, Pure)) let readReservations d = Free (ReadReservations (d, Pure)) let create r = Free (Create (r, Pure))
These helper methods serve the sole purpose of making it easier to write client code that produces IReservationsProgram<T> 'objects' (they're actually abstract syntax trees).
MaîtreD #
You now have all the building blocks that enable you to refactor MaîtreD.TryAccept to return an IReservationsProgram<int?>:
public class MaîtreD : IMaîtreD { public MaîtreD(int capacity) { Capacity = capacity; } public IReservationsProgram<int?> TryAccept(Reservation reservation) { return ReservationsProgram .IsReservationInFuture(reservation) .SelectMany(isInFuture => { if (!isInFuture) return new Pure<int?>(null); return ReservationsProgram .ReadReservations(reservation.Date) .SelectMany(reservations => { var reservedSeats = reservations.Sum(r => r.Quantity); if (Capacity < reservedSeats + reservation.Quantity) return new Pure<int?>(null); reservation.IsAccepted = true; return ReservationsProgram .Create(reservation) .Select(x => new int?(x)); }); }); } public int Capacity { get; } }
This is hardly as pretty as the original version that used Dependency Injection, but you should notice an interesting effect: by returning a free monad, you get rid of the injected dependency. While the code still depends on Capacity, that's just a read-only number.
Through the so-called query syntax, C# offers some syntactic sugar for monadic composition, similar to F#'s computation expressions or Haskell's do notation. Where its utility ends, though, is exactly where you need it. Unfortunately, it doesn't support branching (the use of if statements and such) inside of from x in xs expressions, so while we've supplied the requisite SelectMany methods for IReservationsProgram<T>, you can't use them.
Instead, you have to resort to branching inside of each continuation, which, unfortunately, pulls you towards arrow code.
The TryAccept method starts by calling the IsReservationInFuture helper method (defined above), which returns an IReservationsProgram<bool> object. You can't easily pull the bool value out of the container, but you can use SelectMany to define what happens next.
If the reservations is in the future, an interpreter should call the continuation with true, and otherwise, with false. Thus, you can branch on that Boolean value for the next step. If the reservations turned out to be in the past, the return value ought to be null, but you have to package that in an IReservationsProgram<int?>. The correct way to do that is to wrap it in a Pure object.
If the reservation, on the other hand, turned out to be in the future, the program can continue. It proceeds to call the ReadReservations helper method, and again uses SelectMany to define what happens next. An interpreter will supply reservations (presumably read from an actual database), and the code inside the continuation decides what to do next. In the case of insufficient remaining capacity, you return another null wrapped in Pure, but if you decide to accept the reservation, you can finally call the Create helper method and return its return value. Here, however, C#'s implicit conversion no longer works, so you have to explicitly use Select to turn the int into an int?.
Interpreters #
You can still unit test the code by supplying a test-specific interpreter, but in the interest of keeping this article to essentials, I'll refer you to the code repository if you want to see how the tests look at this point.
You're probably more interested in seeing how an interpreter actually interacts with a real database, like the above SqlReservationsRepository class did. The scenario is still the same, only the specifics have changed. Instead of implementing an interface, you'll now have to interpret an IReservationsProgram<int?>. How do you do that?
You do it like you'd traverse any other Church-encoded sum type: use the Match method and supply a handler for each of the cases:
public static T Interpret<T>( this IReservationsProgram<T> program, string connectionString) { return program.Match( pure: x => x, free: i => i.Match( isReservationInFuture: t => t.Item2(IsReservationInFuture(t.Item1)) .Interpret(connectionString), readReservations: t => t.Item2(ReadReservations(t.Item1, connectionString)) .Interpret(connectionString), create: t => t.Item2(Create(t.Item1, connectionString)) .Interpret(connectionString))); }
Since a free monad is a nested, recursive sum type, you'll first have to supply handlers for the pure and free cases. The pure case is, as always, trivial. This is where you finally encounter a leaf node in the abstract syntax tree you're traversing. This is where you get to return the final value of the program.
In the free case, on the other hand, you'll need to handle an IReservationsInstruction<IReservationsProgram<T>> value, which is another Church-encoded sum type. It looks daunting, but is an entirely automatic refactoring: just call Match on that object as well, and supply a handler for each of the cases.
Recall that each of the cases of IReservationsInstruction<T> contains a tuple. The first element (t.Item1) is a value to be used as an input argument for the interpreter. The second element (t.Item2) is a function. Notice that in all three cases, this interpreter calls a helper method with t.Item1 and then calls the continuation t.Item2 with the return value from the helper method; e.g. t.Item2(IsReservationInFuture(t.Item1)). All three continuation functions return a new IReservationsProgram<T>, representing the next step in the program, so you'll have to recursively call Interpret again.
The IsReservationInFuture helper method is simple:
public static bool IsReservationInFuture(Reservation reservation) { return DateTimeOffset.Now < reservation.Date; }
Notice that this is an entirely normal static helper method that every C# programmer should know how to write. You're now back on familiar territory. The same goes for the two other helper methods ReadReservations and Create. They're slightly refactored versions of the above SqlReservationsRepository methods, so I'm not going to repeat them here. Again, you're welcome to look at the details in the code repository.
Refactor instruction arguments to Parameter Object #
As you know from another article, you can refactor any Church-encoded sum type to a Visitor. If you want to do it step-wise, you start by introducing a Parameter Object, as suggested by Refactoring. There's two sum types in play in this code base, but you can arbitrarily choose to start with the instruction set. Instead of taking three method arguments, change the Match method so that it takes only a single argument:
public interface IReservationsInstruction<T> { TResult Match<TResult>( ReservationsInstructionParameters<T, TResult> parameters); }
The new Parameter Object looks like this:
public class ReservationsInstructionParameters<T, TResult> { public ReservationsInstructionParameters( Func<Tuple<Reservation, Func<bool, T>>, TResult> isReservationInFuture, Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> readReservations, Func<Tuple<Reservation, Func<int, T>>, TResult> create) { this.IsReservationInFuture = isReservationInFuture; this.ReadReservations = readReservations; this.Create = create; } public Func<Tuple<Reservation, Func<bool, T>>, TResult> IsReservationInFuture { get; } public Func<Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>>, TResult> ReadReservations { get; } public Func<Tuple<Reservation, Func<int, T>>, TResult> Create { get; } }
This change clearly just moves things around, so nothing much is yet gained. You'll need to adjust other parts of the code in order to pass an instance of this Parameter Object to the Match method, but that's trivial and automatable work, so I'll skip showing it.
If you've noticed that the ReservationsInstructionParameters<T, TResult> Parameter Object is nothing but a container of three functions, you may not be impressed, but from Object isomorphisms we know that a tuple (or record) of functions is isomorphic to an object, thereby nicely putting everything in place for the next change.
Refactor instruction set Parameter Object to an interface #
Instead of a record of three functions, refactor the Parameter Object to an interface with three members:
public interface IReservationsInstructionParameters<T, TResult> { TResult IsReservationInFuture(Tuple<Reservation, Func<bool, T>> t); TResult ReadReservations(Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>> t); TResult Create(Tuple<Reservation, Func<int, T>> t); }
Each function is now a method on the interface. Still not perfect, but better. Again, you have to make all sort of adjustments to code that interacts with the Match method. This is the most laborious refactoring, because in every place where before you could simply pass lambda expressions, you now have to introduce explicit classes that implement the interface.
For example, the database interpreter now has to look like this:
public static T Interpret<T>( this IReservationsProgram<T> program, string connectionString) { return program.Match( pure: x => x, free: i => i.Match( new InterpretReservationsInstructionParameters<T>( connectionString))); }
So far, we've only started refactoring the instruction set, so you still need to handle IReservationsProgram<T> values by supplying two lambda expressions to its Match method. When handling the instruction i, however, you must now supply an implementation of the new IReservationsInstructionParameters<T, TResult> interface.
You can do that by creating a new private, nested class:
private class InterpretReservationsInstructionParameters<T> : IReservationsInstructionParameters<IReservationsProgram<T>, T>
As an example, this class implements the ReadReservations method like this:
public T ReadReservations( Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, IReservationsProgram<T>>> t) { var reservations = ReadReservations( t.Item1.Date, t.Item1.Date.AddDays(1).AddTicks(-1)); return t.Item2(reservations).Interpret(connectionString); } private IReadOnlyCollection<Reservation> ReadReservations( DateTimeOffset min, DateTimeOffset max)
The method first calls a helper method also called ReadReservations to read the reservations from the database. That helper method is a perfectly normal C# method that queries a database. Its implementation is equivalent to the above SqlReservationsRepository.ReadReservations implementation, so while I've included its signature in the above code listing, there's no need to repeat the method body here.
Keep in mind that t is the horribly typed tuple declared as the method argument, so t.Item1 is just a DateTimeOffset value that you can pass as argument(s) to the ReadReservations helper method.
The helper method returns reservations, which is an IReadOnlyCollection<Reservation>. You can now (as before) call the continuation function t.Item2 with that object. The continuation returns a new IReservationsProgram<T> that you'll then have to recursively handle by calling Interpret again. This is just like before the refactoring.
Rename instruction set API #
You're simply following the refactoring steps outlined in Visitor as a sum type, so now you can rename the types involved with the instruction set to follow the naming conventions of the Visitor design pattern:
public interface IReservationsInstructionVisitor<T, TResult> { TResult VisitIsReservationInFuture(Tuple<Reservation, Func<bool, T>> t); TResult VisitReadReservations(Tuple<DateTimeOffset, Func<IReadOnlyCollection<Reservation>, T>> t); TResult VisitCreate(Tuple<Reservation, Func<int, T>> t); }
This is the interface previously named IReservationsInstructionParameters<T, TResult> renamed, and with the word Visit affixed. Likewise, you can also make similar changes to the IReservationsInstruction<T> interface:
public interface IReservationsInstruction<T> { TResult Accept<TResult>(IReservationsInstructionVisitor<T, TResult> visitor); }
These changes are simple rename refactorings, so while they affect much other code, I'm not going to list it all.
Make program API a Visitor #
Following the same refactoring steps, you can also turn IReservationsProgram<T> into an application of the Visitor design pattern:
public interface IReservationsProgram<T> { TResult Accept<TResult>(IReservationsProgramVisitor<T, TResult> visitor); }
You simply rename the Match method to Accept, and call the object passed to it visitor. The Visitor itself is defined like this:
public interface IReservationsProgramVisitor<T, TResult> { TResult VisitFree(IReservationsInstruction<IReservationsProgram<T>> i); TResult VisitPure(T x); }
While these steps conclude the refactoring steps outlined in the previously mentioned article on how to turn a Church-encoded sum type into a Visitor, the resulting code can still benefit from further clean-up.
Refactor tuple argument to argument list #
If you consider the current definition of IReservationsInstructionVisitor<T, TResult> (see above), you'll notice that each method takes a single argument in the shape of a tuple. From Argument list isomorphisms you know that you can refactor such a method into a method that takes a normal argument list:
public interface IReservationsInstructionVisitor<T, TResult> { TResult VisitIsReservationInFuture( Reservation reservation, Func<bool, T> continuation); TResult VisitReadReservations( DateTimeOffset date, Func<IReadOnlyCollection<Reservation>, T> continuation); TResult VisitCreate( Reservation reservation, Func<int, T> continuation); }
Each of these methods now take an input argument (e.g. a Reservation or a DateTimeOffset) and a continuation function. This already improves the API.
SQL Visitor #
In an attempt to make things look proper object-oriented, then, the journey is complete. Instead of a SqlReservationsRepository, you instead need a SqlReservationsProgramVisitor<T>:
public class SqlReservationsProgramVisitor<T> : IReservationsProgramVisitor<T, T>, IReservationsInstructionVisitor<IReservationsProgram<T>, T> { private readonly string connectionString; public SqlReservationsProgramVisitor(string connectionString) { this.connectionString = connectionString; } public T VisitPure(T x) { return x; } public T VisitFree(IReservationsInstruction<IReservationsProgram<T>> i) { return i.Accept(this); } public T VisitIsReservationInFuture( Reservation reservation, Func<bool, IReservationsProgram<T>> continuation) { var isInFuture = DateTimeOffset.Now < reservation.Date; return continuation(isInFuture).Accept(this); } public T VisitReadReservations( DateTimeOffset date, Func<IReadOnlyCollection<Reservation>, IReservationsProgram<T>> continuation) { var reservations = ReadReservations( date.Date, date.Date.AddDays(1).AddTicks(-1)); return continuation(reservations).Accept(this); } private IReadOnlyCollection<Reservation> ReadReservations( DateTimeOffset min, DateTimeOffset max) { var result = new List<Reservation>(); using (var conn = new SqlConnection(connectionString)) using (var cmd = new SqlCommand(readByRangeSql, conn)) { cmd.Parameters.Add(new SqlParameter("@MinDate", min)); cmd.Parameters.Add(new SqlParameter("@MaxDate", max)); conn.Open(); using (var rdr = cmd.ExecuteReader()) { while (rdr.Read()) result.Add( new Reservation { Date = (DateTimeOffset)rdr["Date"], Name = (string)rdr["Name"], Email = (string)rdr["Email"], Quantity = (int)rdr["Quantity"] }); } } return result; } private const string readByRangeSql = @" SELECT [Date], [Name], [Email], [Quantity] FROM [dbo].[Reservations] WHERE YEAR(@MinDate) <= YEAR([Date]) AND MONTH(@MinDate) <= MONTH([Date]) AND DAY(@MinDate) <= DAY([Date]) AND YEAR([Date]) <= YEAR(@MaxDate) AND MONTH([Date]) <= MONTH(@MaxDate) AND DAY([Date]) <= DAY(@MaxDate)"; public T VisitCreate( Reservation reservation, Func<int, IReservationsProgram<T>> continuation) { return continuation(Create(reservation)).Accept(this); } private int Create(Reservation reservation) { using (var conn = new SqlConnection(connectionString)) using (var cmd = new SqlCommand(createReservationSql, conn)) { cmd.Parameters.Add( new SqlParameter("@Date", reservation.Date)); cmd.Parameters.Add( new SqlParameter("@Name", reservation.Name)); cmd.Parameters.Add( new SqlParameter("@Email", reservation.Email)); cmd.Parameters.Add( new SqlParameter("@Quantity", reservation.Quantity)); conn.Open(); return cmd.ExecuteNonQuery(); } } private const string createReservationSql = @" INSERT INTO [dbo].[Reservations] ([Date], [Name], [Email], [Quantity]) VALUES (@Date, @Name, @Email, @Quantity)"; }
Most of this code is similar to the SqlReservationsRepository from the beginning of the article. The IReservationsRepository interface no longer exists; instead this Visitor implements two interfaces: IReservationsProgramVisitor<T, T> and IReservationsInstructionVisitor<IReservationsProgram<T>, T>. A free monad recursively interacts with itself by going back and forth between an 'instruction' and the overall 'program'. Implementing both interfaces in a single class makes it much easier to transition between these two views, as you no longer have to pass e.g. the connectionString around between various objects.
This also means that instead of having to rely on an extension method in order to be able to continue, notice that each method can now continue by calling Accept(this).
Instead of injecting IReservationsRepository into objects, you can call methods that return IReservationsProgram<T> objects and then interpret them using the above SqlReservationsProgramVisitor<T>. For example, you could call TryAccept with a Reservation object:
var p = maîtreD.TryAccept(reservation);
The p variable is an IReservationsProgram<int?> object, where the int? represents a potential reservation ID. At this point, p is a 'program', and you can 'run' it by asking it to accept a Visitor:
var id = p.Accept(new SqlReservationsProgramVisitor<int?>(connectionString));
When Accept returns, id (an int?) has a value, or is null, according to the exact details of reservation and the state of the database.
Testability #
Is this design still testable? Yes, indeed, the overall free monad design is pure, and thereby inherently testable. Instead of using a dynamic mock library like Moq, you can add a test-specific implementation of the free monad Visitor to your unit testing code base:
public class StubReservationsVisitor<T> : IReservationsProgramVisitor<T, T>, IReservationsInstructionVisitor<IReservationsProgram<T>, T> { private readonly bool isInFuture; private readonly IReadOnlyCollection<Reservation> reservations; private readonly int id; public StubReservationsVisitor( bool isInFuture, IReadOnlyCollection<Reservation> reservations, int id) { this.isInFuture = isInFuture; this.reservations = reservations; this.id = id; } public T VisitPure(T x) { return x; } public T VisitFree(IReservationsInstruction<IReservationsProgram<T>> i) { return i.Accept(this); } public T VisitIsReservationInFuture( Reservation reservation, Func<bool, IReservationsProgram<T>> continuation) { return continuation(isInFuture).Accept(this); } public T VisitReadReservations( DateTimeOffset date, Func<IReadOnlyCollection<Reservation>, IReservationsProgram<T>> continuation) { return continuation(reservations).Accept(this); } public T VisitCreate( Reservation reservation, Func<int, IReservationsProgram<T>> continuation) { return continuation(id).Accept(this); } }
As a true Stub, this implementation ignores the input values and returns pre-configured values. When VisitIsReservationInFuture is called, for example, the implementation ignores the reservation argument and instead 'returns' the isInFuture class field by calling continuation(isInFuture).
You can exercise the happy-path test case from the beginning of this article as a unit test using this Stub Visitor:
[Theory, BookingApiTestConventions] public void TryAcceptReturnsReservationIdInHappyPathScenario( Reservation reservation, IReadOnlyCollection<Reservation> reservations, MaîtreD sut, int excessCapacity, int expected) { var reservedSeats = reservations.Sum(r => r.Quantity); reservation.IsAccepted = false; sut = sut.WithCapacity( reservedSeats + reservation.Quantity + excessCapacity); var actual = sut.TryAccept(reservation); Assert.Equal( expected, actual.Accept(new StubReservationsVisitor<int?>(true, reservations, expected))); Assert.True(reservation.IsAccepted); }
This test still uses AutoFixture to create objects such as reservation, reservations, and so on, but instead of relying on dynamic mocks injected into the sut, it uses the StubReservationsVisitor<T> class to interpret the return value from TryAccept.
Arrow code #
From an external perspective, as a user of MaîtreD.TryAccept, the API looks exotic, but to a degree, fairly object-oriented, with its implementation of the Visitor design pattern. Looking at the above internal implementation of the method, however, reveals the most problematic part of this entire exercise. The code doesn't look nice.
Not only do we have nested closures, but it also looks like the dreaded Arrow Code anti-pattern. Partially, the problem is that while C# has some support for monadic syntactic sugar, in the form of query expressions, you can't branch inside a query expression. That's not the whole problem, though. Even in F#, with a computation expression, the equivalent code would look like this:
let tryAccept capacity reservation = reservations { let! isInFuture = isReservationInFuture reservation if not isInFuture then return None else let! reservations = readReservations reservation.Date let reservedSeats = List.sumBy (fun r -> r.Quantity) reservations if (capacity < reservedSeats + reservation.Quantity) then return None else let! reservationId = create { reservation with IsAccepted = true } return Some reservationId }
While this looks smoother, the code still exhibits the arrow shape. There are ways to address that problem, but that's a topic for the next article.
Conclusion #
Even in C#, you can refactor from Dependency Injection to a free monad, implemented as a Visitor. Should you, though?
As a rule of thumb, no, I don't think it's a good idea. Free monads are worth considering in Haskell where they are much closer to being 'free', in the sense that there's little programming overhead involved with defining and using them. Already when you translate a free monad to F# do you discover how much boilerplate programming is involved. Still, due to F#'s computation expressions, a free monad may occasionally be worth considering. Both in implementation and at call sites, you can make the API easy to use.
In C#, you run into its lack of support for branching inside monadic composition. Not only does a free monad look non-idiomatic in C#, but writing the 'programs' without good syntactic sugar for monads make this alternative even less compelling. To make matters worse, the boilerplate code you have to write in C# is positively ugly. As this article is a result of an experiment, I admit that I have no production experience with free monads as Visitors in C#. Still, due to the lack of type inference in crucial parts, I'd venture the guess that the implementation would also prove to be frustratingly refactor-resistant.
Perhaps, one day, you'll run into an edge case where you have a dependency that could benefit from being refactored to a Visitor, but in general, I'd presume that Dependency Injection in C# is the lesser of two evils. Still, I think it's interesting, and illustrative, that it's possible to refactor an injected dependency to a free monad - even in C#!
Angular addition monoid
Geometric angles can be added together. Angular addition forms a monoid.
This article is part of a series about monoids. In short, a monoid is an associative binary operation with a neutral element (also known as identity).
In geometry, an angle is a measure of how two crossing lines relate to each other. In mathematics, angles are usually represented in radians, but in daily use, they're mostly measured in degrees between 0 and 360.
Angular addition #
You can always draw an angle within a circle. Here's a 45° angle:

If you add another 90° angle to that, you get a 135° angle:

What do you get if you add 90° to 315°?

Well, you get 45°, of course!
There's only 360° in a circle, so overflow is handled, in this case, by subtracting 360°. In general, however, angular addition is nothing but modulo 360 addition.
Angle struct #
You can model a geometric angle as a struct. Here's a simple example:
public struct Angle { private readonly decimal degrees; private Angle(decimal degrees) { this.degrees = degrees % 360m; if (this.degrees < 0) this.degrees += 360m; } public static Angle FromDegrees(decimal degrees) { return new Angle(degrees); } public static Angle FromRadians(double radians) { return new Angle((decimal)((180D / Math.PI) * radians)); } public Angle Add(Angle other) { return new Angle(this.degrees + other.degrees); } public readonly static Angle Identity = new Angle(0); public override bool Equals(object obj) { if (obj is Angle) return ((Angle)obj).degrees == this.degrees; return base.Equals(obj); } public override int GetHashCode() { return this.degrees.GetHashCode(); } public static bool operator ==(Angle x, Angle y) { return x.Equals(y); } public static bool operator !=(Angle x, Angle y) { return !x.Equals(y); } }
Notice the Add method, which is a binary operation; it's an instance method on Angle, takes another Angle as input, and returns an Angle value.
Associativity #
Not only is Add a binary operation; it's also associative. Here's an example:
var x = Angle.FromDegrees(135); var y = Angle.FromDegrees(180); var z = Angle.FromDegrees(300); var left = x.Add(y).Add(z); var right = x.Add(y.Add(z));
Notice that left first evaluates x.Add(y), which is 315°; then it adds 300°, which is 615°, but normalises to 255°. On the other hand, right first evaluates y.Add(z), which is 480°, but normalises to 120°. It then adds those 120° to x, for a final result of 255°. Since left and right are both 255°, this illustrates that Add is associative.
Obviously, this is only a single example, so it's no proof. While still not a proof, you can demonstrate the associativity property with more confidence by writing a property-based test. Here's one using FsCheck and xUnit.net:
[Property(QuietOnSuccess = true)] public void AddIsAssociative(Angle x, Angle y, Angle z) { Assert.Equal( x.Add(y).Add(z), x.Add(y.Add(z))); }
By default, FsCheck generates 100 test cases, but even when I experimentally change the configuration to run 100,000 test cases, they all pass. For full disclosure, however, I'll admit that I defined the data generators to only use NormalFloat for the radian values, and only decimal values with up to 10 decimal places. If you try to use entirely unconstrained floating points, you'll see test failures caused by rounding errors.
Changing the data generator is one way to address rounding errors. Another way is to add a bit of fuzzy tolerance to the assertion. In any case, though, the Add operation is associative. That rounding errors occur is an implementation detail of floating point arithmetic.
Identity #
The above code listing defines a value called Identity:
public readonly static Angle Identity = new Angle(0);
As an Angle, I want my Add and Identity members to obey the monoid laws so that I can be a monoid.
As an example, both left and right should be true in the following:
var x = Angle.FromDegrees(370); var left = x == Angle.Identity.Add(x); var right = x == x.Add(Angle.Identity);
That does, indeed, turn out to be the case.
Again, you can generalise using FsCheck:
[Property(QuietOnSuccess = true)] public void AddHasIdentity(Angle x) { Assert.Equal(x, Angle.Identity.Add(x)); Assert.Equal(x, x.Add(Angle.Identity)); }
Once more, a reservation identical to the one given above must be given when it comes to floating point arithmetic.
Conclusion #
The Add method is an associative, binary operation with identity; it's a monoid.
As far as I can tell, any modulo-based addition is a monoid, but while, say, modulo 37 addition probably doesn't have any practical application, modulo 360 addition does, because it's how you do angular addition.
Typing and testing problem 23
Yet another reflection on the relationship between types and tests, this time with a simple example.
The debate about dynamic typing versus static typing still goes on. If it ever gets resolved, I suppose it'll be in the far future. Until then, one's position is bound to be determined mostly by experience and belief. I openly admit that I prefer statically typed languages like F# and Haskell.
As I've previously touched on, I can't help seeing types as a slider. The more to the right you pull it, the stronger the type system. The more to the left you pull it, the more you'll need automated tests to give you a sense of confidence in your code.
In this article, I'll share an small revelation recently given to me.
Problem 23 #
Somewhere, a Stack Overflow user was going through Ninety-Nine Haskell Problems, and asked how to unit test problem 23.
The problem is elementary:
"Extract a given number of randomly selected elements from a list."Here's an example of the intended use:
λ> rndSelect "abcdefgh" 3 "fag"
The first argument to rndSelect is the candidates from which to pick elements; in this case the letters a to h. The second argument is the number of values to select; in this case the number 3.
Test plan #
How does one test a function like that? Clearly, when randomness is involved, you'll need some way to regulate the randomness in order to make tests deterministic. With my blinders on, I assumed that this was the main problem, so I answered with the following plan for a few properties:
- The length of the returned list should be equal to the input length.
- All elements in the returned list should be elements of the list of candidates.
In response to this plan, the user chi commented on my second suggestion:
"I think this it is a consequence of the free theorem. If so, no need to test for that!"Sometimes, I find it difficult to shake my object-oriented TDD-influenced way of thinking, but chi is right. Here's why:
Parametric polymorphism #
.NET, including C# and F#, has a platform feature called generics. Haskell has generics as well, although normally, that language feature is called parametric polymorphism. What I had in mind was a set of parametrically polymorphic functions with these types:
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a] rndSelect :: Integral i => [a] -> i -> IO [a]
Notice that both functions return lists of a values, where a is a type variable (in C#, you'd call it a generic type argument). It could be Integer, String, Day, or a custom domain type you'd added to the code base two minutes earlier.
Given a completely unrestricted type variable, Haskell has no way of creating values. How could it, logically?
In C#, you can write default(T), which tends to mostly produce null references. Haskell doesn't have null, so with that option cut off, how would it be able to produce values of arbitrary types? It can't.
When returning a list of a values, the only option open to a parametric polymorphic function is to pick values from its input arguments. For both rndGenSelect and rndSelect, there's only a single source of a values, so there's no reason to test that the functions return values from those lists of candidates. It's the only thing it can do. That's the free theorem for that function.
It'd been an entirely different story if the function had had concrete types. If, for example, the function had had the type RandomGen g => g -> String -> Int -> String, I could have written a function like this one:
rndGenSelect' :: RandomGen g => g -> String -> Int -> String rndGenSelect' _ _ count = replicate count 's'
Because the type of elements is known at compile-time, we can pick an arbitrary Char value ('s'). This is possible because we know the type, and therefore can come up with a strategy to hard-code known values of that type. When the type argument is unknown, this is no longer possible. To paraphrase Robert C. Martin, as the types get more generic, the tests become more redundant.
Taming randomness #
Before we look at automated testing, let's consider how to turn randomness into deterministic behaviour. This is (seemingly) always a problem with unit testing when the desired behaviour contains randomness, because tests should be deterministic. Once again, however, it turns out that functional design is intrinsically testable. Since Haskell design favours pure functions, the core of System.Random is deterministic.
This is, in fact, not much different from C#, where the Random class encapsulates an algorithm that computes a series of random-looking values based on an initial seed value. If you give it the same seed, it'll produce the same sequence of random-looking numbers. Haskell works the same way.
This led me to a design with a 'core' function that does all the work, and a 'wrapper' function that only adds one extra feature: randomness.
Starting my design with types, I wanted a function with this type:
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a]
This is the type that I've already discussed above. Because of the free theorem, we already know that the returned list can only contain values selected from the input list. In other words, there's no need to test for that.
This function takes a RandomGen argument, which is a type class of pure functions. RandomGen itself is pure; the source of randomness comes from how it's produced. More on that later. This, however, should enable me to write deterministic tests.
Properties #
Before we start adding deterministic tests, let's see how far we can get with property-based testing. First, designing with types, I need to implement the function so that it compiles. This is the simplest implementation I could think of:
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a] rndGenSelect _ xs _ = [head xs]
This implementation is both incorrect and unsafe, but it compiles. In TDD fashion, then, I found it appropriate to add a test - in this case a QuickCheck property:
lenProp :: Integral i => Int -> [a] -> NonNegative i -> Bool lenProp seed xs (NonNegative i) = i == genericLength (rndGenSelect (mkStdGen seed) xs i)
This little piece of test code is the only surviving property from my original test plan. It states that for any non-negative count, the list returned from rndGenSelect should have the requested length.
Writing this property, however, quickly forced me to deal with the case where the count is negative. It's easy to forget about edge cases when your function is nothing but a pie in the sky, but QuickCheck (and property-based testing in general) is really effective at grounding you in reality. Even with a language like Haskell, I still find the fast feedback loop from tests helpful.
The original exercise specification doesn't mention what should happen if the count is negative, so after short deliberation, I decide to write another property:
negLenProp :: Integral i => Int -> [a] -> Positive i -> Bool negLenProp seed xs (Positive i) = 0 == genericLength (rndGenSelect (mkStdGen seed) xs (-i))
This property simply states that for all negative counts, the returned list should be empty.
Both of these properties obviously fail, because of the incorrect implementation.
The simplest implementation I could think of that passes both properties is this:
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a] rndGenSelect _ xs count = genericReplicate count (head xs)
At this point, I don't see how TDD or property-based testing can help me move forward. The remaining work required is to add randomness to the mix. In this case, I'll need to use the RandomGen argument to produce random values, but since I don't know how its algorithm works, then even if I had a seed value known at compile-time, I wouldn't be able to predict which values it'd produce.
Selecting random indices #
I admit that I don't know how to write the next test a priori. I do know, however, that if I implement what's missing, I have a deterministic function, and I can use it to write regression test. In other words, I'll reverse direction and write the code first, and then the test. What a novel idea.
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a] rndGenSelect rnd xs count = let indices = genericTake count $ randomRs (0, length xs - 1) rnd in fmap (xs !!) indices
This function first uses randomRs to produce an infinite list of values. These values are indices because they all fall between 0 and length xs - 1. In other words, they are indices into xs.
While the list is infinite, it's lazily evaluated, so infinity itself isn't a problem. We only need count elements, though, so we can simply take the first count elements.
Finally, the function maps over the list of indices, and for each index value, selects the element at that position.
I could inline indices in the return expression, like this:
rndGenSelect :: (RandomGen g, Integral i) => g -> [a] -> i -> [a] rndGenSelect rnd xs count = fmap (xs !!) $ genericTake count $ randomRs (0, length xs - 1) rnd
I find that more obscure than the first alternative, though, but both versions pass the properties and do what they're supposed to do.
Regression testing #
How do I know that my code works? Well, that's always difficult with code that contains randomness, but you can load the function into GHCi and perform some sanity testing:
λ> rndGenSelect (mkStdGen 42) "foo" 3 "ofo" λ> rndGenSelect (mkStdGen 1337) "bar" 10 "rabbaarrra" λ> rndGenSelect (mkStdGen (-197221)) ['a'..'z'] 5 "ntfnc"
That looks, I suppose, random enough... What's more important is that this is completely repeatable. This means that I can write parametrised tests that protect against regressions:
"rndGenSelect of chars returns correct result" ~: do (seed, xs, count, expected) <- [ ( 42, "foo", 3, "ofo"), ( 1337, "bar", 10, "rabbaarrra"), (-197221, ['a'..'z'], 5, "ntfnc") ] let rnd = mkStdGen seed let actual = rndGenSelect rnd xs count return $ expected ~=? actual
These tests don't drive the design, but they prevent regressions. If, at a later time, I, or someone else, inadvertently revert rndGenSelect to genericReplicate count (head xs), these tests will fail.
Humble function #
The original problem statement is to write a function without an explicit RandomGen argument. In the spirit of xUnit Test Patterns' Humble Object pattern, we can now click all our pieces together to a function that does what is required:
rndSelect :: Integral i => [a] -> i -> IO [a] rndSelect xs count = do rnd <- newStdGen return $ rndGenSelect rnd xs count
The only thing of interest here is that the function is impure, because it uses newStdGen to produce a random RandomGen value. It then delegates all work to rndGenSelect, which is covered by tests.
As you can see, this function does not exhibit repeatable behaviour:
λ> rndSelect "abcdefgh" 3 "add" λ> rndSelect "abcdefgh" 3 "daf"
This should, I think, address the original problem statement.
All source code for this article is available on GitHub.
Summary #
The first time I encountered parametric polymorphism was when C# got generics in 2005. Back then it was mostly explained as a mechanism to avoid boxing, although it also seriously reduced the amount of boilerplate code you'd have to write in order to have type-safe collections. In many years, I mostly understood C# generics as a language feature aimed at efficiency and programmer productivity.
It wasn't until I started to program in F#, with its stronger type inference, that it began to dawn on me that parametric polymorphism could also be a design tool. Making a function more generic tightens its contract, so to speak. The more generic a function becomes, the less wriggle room does it have. This may sound like a disadvantage to a programmer, but it's a boon to a code reader. When you, as a reader, encounter a parametrically polymorphic function, you already know that there are things that function can't do. Such functions come with invariants, or 'theorems', for free.
Terse operators make business code more readable
Sometimes, terse operators can make code more readable. An article for all, even people who don't read Haskell code.
The Haskell programming language has a reputation for being terse to the point of being unreadable. That reputation isn't undeserved, but to counter, other languages exist that are verbose to the point of being unreadable.
Particularly, idiomatic Haskell code involves abstruse operators like ., $, <$>, >>=, <*>, <>, and so on. Not only do such operators look scary, but when I started writing Haskell code, it also bothered me that I didn't know how to pronounce these operators. I don't know how you read code, but my brain often tries to 'talk' about the code, silently, inside my head, and when it encounters something like =<<, it tends to stumble.
At least, it used to. These days, my brain has accepted that in many cases, Haskell operators are a little like punctuation marks. When I read a piece of prose, my brain doesn't insist on 'saying' comma, semicolon, question mark, period, etcetera. Such symbols assist reading, and often adjust the meaning of a text, but aren't to be read explicitly as themselves.
I'm beginning to realise that Haskell operators work like that; sometimes, they fade into the background and assist reading.
As a word of caution, don't take this analogy literally. Each Haskell operator means something specific, and they aren't interchangeable. Additionally, Haskell enables you to add your own custom operators, and I'm not sure that e.g. lens operators like .~ or %~ make code more readable.
A simple business code example #
Forgetting about the lens operators, though, consider a piece of business code like this:
tryAccept :: Int -> Reservation -> MaybeT ReservationsProgram Int tryAccept capacity reservation = do guard =<< isReservationInFuture reservation reservations <- readReservations $ reservationDate reservation let reservedSeats = sum $ reservationQuantity <$> reservations guard $ reservedSeats + reservationQuantity reservation <= capacity create $ reservation { reservationIsAccepted = True }
Please read on, even if you don't read Haskell code. I'm not going to walk you through the details of how the operators work. That's not the point of this article. The point is how the operators enable you to focus on the overall picture of what's going on. The full source code is available on GitHub.
To establish a bit of context, this function determines whether or not to accept a restaurant reservation. Even if you've never read Haskell code before, see if you can get a sense of what's going on.
First, there's a guard which seems to involve whether or not the reservation is in the future. Second, there seems to be some calculations involving reservations, reserved seats, culminating in another guard. Third, the function seems to create a reservation by setting reservationIsAccepted to True.
Granted, it probably helps if you know that both = and <- bind the left-hand symbol to the expression on the right side. Additionally, after all this talk about special Haskell operators, it may not be immediately apparent that + is the perfectly normal addition operator, and <= is the well-known less-than-or-equal relational operator. What if we keep those operators, and mask the rest with a white rectangle symbol (▯)?
tryAccept :: Int -> Reservation -> MaybeT ReservationsProgram Int tryAccept capacity reservation = do guard ▯ isReservationInFuture reservation reservations <- readReservations ▯ reservationDate reservation let reservedSeats = sum ▯ reservationQuantity ▯ reservations guard ▯ reservedSeats + reservationQuantity reservation <= capacity create ▯ reservation { reservationIsAccepted = True }
Finally, you also ought to know that while Haskell code is read from top to bottom, you tend to read each expression from right to left. Armed with this knowledge, and by masking the operators, the business logic begins to stand out.
First, it examines whether the reservation is in the future, and it does a guard of that. Again, I don't wish to make any claims that the code is magically self-documenting, because if you don't know what guard does, you don't know if this expression guards against the reservation being in the future, or if, conversely, it ensures that the reservation is in the future. It does the latter.
Second, it conjures up some reservations from somewhere, by first getting the reservationDate from reservation, and then passing that value to readReservations (expressions are read from right to left).
Moving on, it then calculates reservedSeats by starting with reservations, somehow extracting the reservationQuantity from those, and taking the sum. Since we've masked the operators, you can't tell exactly what's going on, but the gist is, hopefully, clear.
The middle block of code concludes with another guard, this time ensuring that the reservedSeats plus the reservationQuantity is less than or equal to the capacity.
Finally, the function sets reservationIsAccepted to True and calls create.
What I find compelling about this is that the terseness of the Haskell operators enables you, a code reader, to scan the code to first understand the big picture.
Guards #
Additionally, some common motifs begin to stand out. For example, there are two guard expressions. Because the operators are terse, the similarities stand out better. Let's juxtapose them:
guard ▯ isReservationInFuture reservation guard ▯ reservedSeats + reservationQuantity reservation <= capacity
It seems clear that the same sort of thing is going on in both cases. There's a guard ensuring that a Boolean condition is satisfied. If you, however, reconsider the actual code, you'll see that the white rectangle hides two different operators:
guard =<< isReservationInFuture reservation guard $ reservedSeats + reservationQuantity reservation <= capacity
The reason for this is that it has to, because otherwise it wouldn't compile. isReservationInFuture reservation has the type MaybeT ReservationsProgram Bool. There's a Boolean value hidden in there, but it's buried inside a container. Using =<< enables you to pull out the Boolean value and pass it to guard.
In the second guard expression, reservedSeats + reservationQuantity reservation <= capacity is a 'naked' Boolean expression, so in this case you can use the $ operator to pass it to guard.
Haskellers may wonder why I chose =<< instead of the more common >>= operator in the first of the two guard expressions. I could have, but then the expression would have been this:
isReservationInFuture reservation >>= guard
The resulting behaviour is the same, but I think this obscures how the two guard expressions are variations on the same motif.
The use of operators enables you to express code in such a way that motifs stand out. In contrast, I tried writing the same business functionality in F#, but it didn't come out as readable (in my opinion):
// int -> Reservation -> ReservationsProgram<int option> let tryAccept capacity reservation = reservationsOption { do! ReservationsOption.bind guard <| isReservationInFuture reservation let! reservations = readReservations reservation.Date let reservedSeats = List.sumBy (fun r -> r.Quantity) reservations do! guard (reservedSeats + reservation.Quantity <= capacity) return! create { reservation with IsAccepted = true } }
While you can also define custom operators in F#, it's rarely a good idea, for various reasons that, at its core, are related to how F# isn't Haskell. The lack of 'glue' operators in F#, though, obliged me to instead use the more verbose ReservationsOption.bind. This adds noise to the degree that the guard function disappears in the middle of the expression. The motif is fainter.
Piping #
Another motif in Haskell code is piping. This is known from F# as well, where piping is normally done from left to right using the |> operator. You can, as the above example shows, also use the right-to-left pipe operator <|. In Haskell, expressions are idiomatically composed from right to left, often with the $ operator, or, when using point-free style, with the . operator.
Once you realise that expressions compose from right to left, a masked expression like sum ▯ reservationQuantity ▯ reservations begins to look like a pipeline: start with reservations, somehow pipe them to reservationQuantity, and finally pipe the result of doing that to sum. That's actually not quite what happens, but I think that this compellingly communicates the overall idea: start with some reservations, consider their quantities, and calculate the sum of those.
Another way to write that expression would be:
let reservedSeats = sum (fmap reservationQuantity reservations)
This implements the same behaviour as sum $ reservationQuantity <$> reservations, but once you get used to it, I like the operator-based alternative better. The operators fade into the background, enabling the flow of data to stand out better.
Conclusion #
Haskell operators constitute the glue that enables you to compose expressions together. Often, you need to vary how expressions are composed together, because the types are slightly different. Picking an appropriate operator that composes particular expressions enables you to perform the composition with a high signal-to-noise ratio.
Once you get used to reading Haskell code, the operators can fade into the background in well-factored code, just like punctuation marks assist you when you read prose. As always, this is no silver bullet. I've seen plenty of examples of obscure Haskell code as well, and copious use of operators is a fast way to obfuscate code.
Use; punctuation? marks with. taste!
Visitor as a sum type
The Visitor design pattern is isomorphic to sum types.
This article is part of a series of articles about specific design patterns and their category theory counterparts. In it, you'll see how the Visitor design pattern is equivalent to a sum type.
Sum types #
I think that the most important advantage of a statically typed programming language is that it gives you immediate feedback on your design and implementation work. Granted, that your code compiles may not be enough to instil confidence that you've done the right thing, but it's obvious that when your code doesn't compile, you still have work to do.
A static type system enables you to catch some programming errors at compile time. It prevents you from making obvious mistakes like trying to divide a GUID by a date. Some type systems don't offer much more help than that, while others are more articulate; I think that type systems inhabit a continuous spectrum of capabilities, although that, too, is a simplification.
An often-touted advantage of programming languages like F#, OCaml, and Haskell is that they, in the words of Yaron Minsky, enable you to make illegal states unrepresentable. The way these languages differ from languages like C# and Java is that they have algebraic data types.
In short, algebraic data types distinguish between product types and sum types. All statically typed language I've seen have product types, which you can think of as combinations of data. Objects with more than a single class fields would be product types.
Sum types (also known as discriminated unions), on the other hand, are types that express mutually exclusive alternatives. Object-oriented programmers might mistake such a statement for sub-classing, but the difference is that object-oriented sub-classing creates a potentially infinite hierarchy of subtypes, while a sum type is statically constrained to a finite number of mutually exclusive cases. This is often useful.
In this article, you'll see that a sum type is isomorphic to a corresponding Visitor.
Church-encoded payment types #
In a previous article, you saw how to Church-encode a domain-specific sum type. That article, again, demonstrated how to rewrite a domain-specific F# discriminated union as a C# API. The F# type was this PaymentType sum type:
type PaymentType = | Individual of PaymentService | Parent of PaymentService | Child of originalTransactionKey : string * paymentService : PaymentService
Using Church-encoding in C#, you can arrive at this interface that models the same business problem:
public interface IPaymentType { T Match<T>( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child); }
In order to use the API, the compiler obligates you to handle all three mutually exclusive cases defined by the three arguments to the Match method. Refer to the previous article for more details and code examples. All the C# code is also available on GitHub.
While the C# code works, I think it'd be a fair criticism to say that it doesn't feel object-oriented. Particularly the use of function delegates (Func<PaymentService, T>, etcetera) seems off. These days, C# is a multi-paradigmatic language, and function delegates have been around since 2007, so it's a perfectly fine C# design. Still, if we're trying to understand how object-oriented programming relates to fundamental programming abstractions, it behoves us to consider a more classic form of object-orientation.
Introduce Parameter Object #
Through a series of refactorings you can transform the Church-encoded IPaymentType interface to a Visitor. The first step is to use Refactoring's Introduce Parameter Object to turn the three method arguments of Match into a single object:
public class PaymentTypeParameters<T> { public PaymentTypeParameters( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child) { Individual = individual; Parent = parent; Child = child; } public Func<PaymentService, T> Individual { get; } public Func<PaymentService, T> Parent { get; } public Func<ChildPaymentService, T> Child { get; } }
The modified IPaymentType interface then looks like this:
public interface IPaymentType { T Match<T>(PaymentTypeParameters<T> parameters); }
Clearly, this change means that you must also adjust each implementation of IPaymentType accordingly. Here's the Match method of Individual:
public T Match<T>(PaymentTypeParameters<T> parameters) { return parameters.Individual(paymentService); }
The two other implementations (Parent and Child) change in the same way; the modifications are trivial, so I'm not going to show them here, but all the code is available as a single commit.
Likewise, client code that uses the API needs adjustment, like the ToJson method:
public static PaymentJsonModel ToJson(this IPaymentType payment) { return payment.Match( new PaymentTypeParameters<PaymentJsonModel>( individual : ps => new PaymentJsonModel { Name = ps.Name, Action = ps.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Nothing<string>() }, parent : ps => new PaymentJsonModel { Name = ps.Name, Action = ps.Action, StartRecurrent = new ChurchTrue(), TransactionKey = new Nothing<string>() }, child : cps => new PaymentJsonModel { Name = cps.PaymentService.Name, Action = cps.PaymentService.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Just<string>(cps.OriginalTransactionKey) })); }
From argument list isomorphisms we know that an argument list is isomorphic to a Parameter Object, so this step should come as no surprise. We also know that the reverse translation (from Parameter Object to argument list) is possible.
Add Run prefix #
I think it looks a little strange that the functions comprising PaymentTypeParameters<T> are named Individual, Parent, and Child. Functions do something, so they ought to be named with verbs. This turns out only to be an intermediary step, but I'll add the prefix Run to all three:
public class PaymentTypeParameters<T> { public PaymentTypeParameters( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child) { RunIndividual = individual; RunParent = parent; RunChild = child; } public Func<PaymentService, T> RunIndividual { get; } public Func<PaymentService, T> RunParent { get; } public Func<ChildPaymentService, T> RunChild { get; } }
This doesn't change the structure of the code in any way, but sets it up for the next step.
Refactor to interface #
The definition of PaymentTypeParameters<T> still doesn't look object-oriented. While it's formally an object, it's an object that composes three function delegates. We've managed to move the function delegates around, but we haven't managed to get rid of them. From object isomorphisms, however, we know that tuples of functions are isomorphic to objects, and that's essentially what we have here. In this particular case, there's no implementation code in PaymentTypeParameters<T> itself - it's nothing but a group of three functions. You can refactor that class to an interface:
public interface IPaymentTypeParameters<T> { T RunIndividual(PaymentService individual); T RunParent(PaymentService parent); T RunChild(ChildPaymentService child); }
The implementations of Individual, Parent, and Child don't change; only the signature of Match changes slightly:
public interface IPaymentType { T Match<T>(IPaymentTypeParameters<T> parameters); }
Since this change removes the function delegates, it requires client code to change:
public static PaymentJsonModel ToJson(this IPaymentType payment) { return payment.Match(new PaymentTypeToJsonParameters()); } private class PaymentTypeToJsonParameters : IPaymentTypeParameters<PaymentJsonModel> { public PaymentJsonModel RunIndividual(PaymentService individual) { return new PaymentJsonModel { Name = individual.Name, Action = individual.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Nothing<string>() }; } public PaymentJsonModel RunParent(PaymentService parent) { return new PaymentJsonModel { Name = parent.Name, Action = parent.Action, StartRecurrent = new ChurchTrue(), TransactionKey = new Nothing<string>() }; } public PaymentJsonModel RunChild(ChildPaymentService child) { return new PaymentJsonModel { Name = child.PaymentService.Name, Action = child.PaymentService.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Just<string>(child.OriginalTransactionKey) }; } }
The ToJson method now has to delegate to a private class that implements IPaymentTypeParameters<PaymentJsonModel>. In Java and F# you'd be able to pass an object expression, but in C# you have to create an explicit class for the purpose. The implementations of the three methods of the interface still correspond to the three functions the previous incarnations of the code used.
Rename to Visitor #
At this point, the Visitor pattern's structure is already in place. The only remaining step is to rename the various parts of the API so that this becomes clear. You can start by renaming the IPaymentTypeParameters<T> interface to IPaymentTypeVisitor<T>:
public interface IPaymentTypeVisitor<T> { T VisitIndividual(PaymentService individual); T VisitParent(PaymentService parent); T VisitChild(ChildPaymentService child); }
Notice that I've also renamed the methods from RunIndividual, RunParent, and RunChild to VisitIndividual, VisitParent, and VisitChild.
Likewise, you can rename the Match method to Accept:
public interface IPaymentType { T Accept<T>(IPaymentTypeVisitor<T> visitor); }
In Design Patterns, the Visitor design pattern is only described in such a way that both Accept and Visit methods have void return types, but from unit isomorphisms we know that this is equivalent to returning unit. Thus, setting T in the above API to a suitable unit type (like the one defined in F#), you arrive at the canonical Visitor pattern. The generic version here is simply a generalisation.
For the sake of completeness, client code now looks like this:
public static PaymentJsonModel ToJson(this IPaymentType payment) { return payment.Accept(new PaymentTypeToJsonVisitor()); } private class PaymentTypeToJsonVisitor : IPaymentTypeVisitor<PaymentJsonModel> { public PaymentJsonModel VisitIndividual(PaymentService individual) { return new PaymentJsonModel { Name = individual.Name, Action = individual.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Nothing<string>() }; } public PaymentJsonModel VisitParent(PaymentService parent) { return new PaymentJsonModel { Name = parent.Name, Action = parent.Action, StartRecurrent = new ChurchTrue(), TransactionKey = new Nothing<string>() }; } public PaymentJsonModel VisitChild(ChildPaymentService child) { return new PaymentJsonModel { Name = child.PaymentService.Name, Action = child.PaymentService.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Just<string>(child.OriginalTransactionKey) }; } }
You can refactor all the other Church encoding examples I've shown you to Visitor implementations. It doesn't always make the code more readable, but it's possible.
From Visitor to sum types #
In this article, I've shown how to refactor from a Church-encoded sum type to a Visitor, using the following refactoring steps:
- Introduce Parameter Object
- (Rename Method (by adding a
Runprefix)) - Refactor to interface
- Rename to Visitor terminology
- Refactor the Visitor interface to a Parameter Object that composes functions
- Refactor the Parameter Object to an argument list
- Rename types and members as desired
Summary #
Algebraic data types enable you to make illegal states unrepresentable. Most programming languages have product types, so it's the lack of sum types that seems to make the difference between languages like C# and Java on the one side, and languages like F#, OCaml, or Haskell on the other side.
You can, however, achieve the same objective with object-oriented design. The Visitor design pattern is equivalent to sum types, so everything you can express with a sum type in, say, F#, you can express with a Visitor in C#.
That's not to say that these two representations are equal in readability or maintainability. F# and Haskell sum types are declarative types that usually only take up a few lines of code. Visitor, on the other hand, is a small object hierarchy; it's a more verbose way to express the idea that a type is defined by mutually exclusive and heterogeneous cases. I know which of these alternatives I prefer, but if I were caught in an object-oriented code base, it's nice to know that it's still possible to model a domain with algebraic data types.
Comments
I think that it's important to remember the type of abstractions you highlight by showing that the Vistor design pattern is the same as sum types. I appreciate this post.
When I read up on Entity component system, I found it interesting how the pattern arrived from the need to be able to control memory. Perhaps the somewhat odd form of the Visitor pattern has arrived from the same limitations in some common languages? Perhaps there are other constructs that can be expressed more clearly using more modern patterns?
Oskar, thank you for writing. I didn't know about entity component system.
This very article series tries to identify various design patterns and how they relate to more fundamental constructs. Most likely you're already aware of that, so perhaps you meant something else by your questions. If you did, however, I can't glean what.
I was not aware of that article series. The answer I'm looking for seems to be the identified subset.
Church-encoded payment types
How to translate a domain-specific sum type into a Church-encoded C# API. An article for object-oriented developers.
This article is part of a series of articles about Church encoding. In the previous articles, you've seen how to implement Boolean logic without Boolean primitives, as well as how to model natural numbers, how to implement a Maybe container, and how to implement an Either container. Common to all four examples is that they're based on sum types with exactly two mutually exclusive cases.
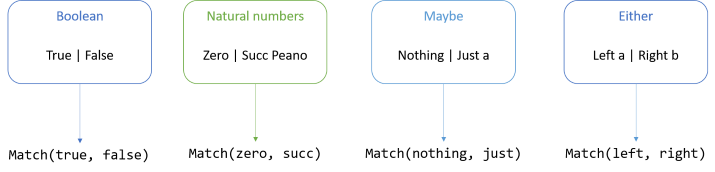
You may already have noticed that all three translate to Match methods that take two arguments. The translation is so mechanical that you could automate it. Each case in a sum type becomes an argument in a Match method. In this article, you'll see an example of a domain-specific sum type with three cases, translated to Church-encoding.
A payment type model in F# #
In a previous article I described a particular business problem that was elegantly addressed with a discriminated union (sum type) in F#:
type PaymentService = { Name : string; Action : string } type PaymentType = | Individual of PaymentService | Parent of PaymentService | Child of originalTransactionKey : string * paymentService : PaymentService
In short, this model enables you to model various payments against a third-party payment service. An individual payment is, as the name implies, a single payment. A parent payment can be used to authorise a series of recurring, automated payments, for example to pay for a subscription. A child payment is one of those recurring payments; it must have a parent payment to authorise it, as automation means that no user interaction takes place.
One task that is easily addressed with the above PaymentType discriminated union is that you can translate the data to JSON in a type-safe manner. The compiler will tell you whether or not you've handled all three cases.
Auxiliary C# classes #
You can Church-encode PaymentType just like Boolean values, natural numbers, Maybe, and Either. Before you do that, however, you need to define the input types involved in each case. These are normal classes, although I prefer to make them immutable:
public class PaymentService { public PaymentService(string name, string action) { this.Name = name; this.Action = action; } public string Name { get; } public string Action { get; } } public class ChildPaymentService { public ChildPaymentService( string originalTransactionKey, PaymentService paymentService) { this.OriginalTransactionKey = originalTransactionKey; this.PaymentService = paymentService; } public string OriginalTransactionKey { get; } public PaymentService PaymentService { get; } }
These are straightforward translations of the F# PaymentService record type, and the tuple associated with the Child case. In a real code base, I'd override Equals for both classes in order to turn them into proper Value Objects, but in order to keep the size of the code down, I omitted doing that here.
Church-encoded payment type #
You can now translate the PaymentType F# discriminated union to a Church-encoded API in C#, starting with the interface:
public interface IPaymentType { T Match<T>( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child); }
Since there's three cases in the sum type, that turns into a Match method with three arguments, each corresponding to one of the cases. As was also the case for the previous articles' INaturalNumber, IMaybe<T>, and IEither<L, R> interfaces, the data associated with each case is modelled as a function from the data to the generic return type T.
Again, following the recipe implied by the previous examples, you should now add a concrete implementation of the IPaymentType interface for each case. It's natural to start with the first argument to the Match method, individual:
public class Individual : IPaymentType { private readonly PaymentService paymentService; public Individual(PaymentService paymentService) { this.paymentService = paymentService; } public T Match<T>( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child) { return individual(paymentService); } }
The Individual class adapts a PaymentService value, which it passes as the argument to the individual function argument when Match is called. As you've seen in the previous articles, a particular implementation uses only one of the method arguments, so the two other arguments, parent and child, are simply ignored.
The parent implementation is almost identical:
public class Parent : IPaymentType { private readonly PaymentService paymentService; public Parent(PaymentService paymentService) { this.paymentService = paymentService; } public T Match<T>( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child) { return parent(paymentService); } }
The Parent class also adapts a PaymentService value that it passes to a function when Match is called. The only difference is that it calls the parent function instead of the individual function argument.
The third case is handled by the following Child class:
public class Child : IPaymentType { private readonly ChildPaymentService childPaymentService; public Child(ChildPaymentService childPaymentService) { this.childPaymentService = childPaymentService; } public T Match<T>( Func<PaymentService, T> individual, Func<PaymentService, T> parent, Func<ChildPaymentService, T> child) { return child(childPaymentService); } }
While the two other classes both adapt a PaymentService value, a Child object instead composes a ChildPaymentService value. When Match is called, it calls the child function argument with the composed value.
Using the IPaymentType API #
One important feature that I originally had to implement was to translate a payment type value into a JSON document. For the purposes of this example, imagine that you can model the desired JSON document using this Data Transfer Object:
public class PaymentJsonModel { public string Name { get; set; } public string Action { get; set; } public IChurchBoolean StartRecurrent { get; set; } public IMaybe<string> TransactionKey { get; set; } }
This is a mutable object because most .NET serialisation APIs require that the class in question has a parameterless constructor and writeable properties. Notice, however, that in order to demonstrate that all this code still doesn't rely on any primitive Boolean operators and such, the class' properties are defined as IChurchBoolean and IMaybe<string> values, as well as regular string values.
Writing a method that translates any IPaymentType object into a PaymentJsonModel object is now straightforward:
public static PaymentJsonModel ToJson(this IPaymentType payment) { return payment.Match( individual : ps => new PaymentJsonModel { Name = ps.Name, Action = ps.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Nothing<string>() }, parent : ps => new PaymentJsonModel { Name = ps.Name, Action = ps.Action, StartRecurrent = new ChurchTrue(), TransactionKey = new Nothing<string>() }, child : cps => new PaymentJsonModel { Name = cps.PaymentService.Name, Action = cps.PaymentService.Action, StartRecurrent = new ChurchFalse(), TransactionKey = new Just<string>(cps.OriginalTransactionKey) }); }
Because the Match method takes three arguments, you have to supply a 'handler' function for each of them, and they all have to have the same return type. In this case they all return a new PaymentJsonModel object, so that requirement is fulfilled. All three lambda expressions simply copy over Name and Action, but they differ in the values they assign to StartRecurrent and TransactionKey.
Tests #
In order to show you that it all works, here's a few examples I wrote as xUnit.net tests:
[Fact] public void IndividualToJsonReturnsCorrectResult() { var sut = new Individual(new PaymentService("MasterCard", "Pay")); var actual = sut.ToJson(); Assert.Equal("MasterCard", actual.Name); Assert.Equal("Pay", actual.Action); Assert.False(actual.StartRecurrent.ToBool()); Assert.True(actual.TransactionKey.IsNothing().ToBool()); } [Fact] public void ParentToJsonReturnsCorrectResult() { var sut = new Parent(new PaymentService("MasterCard", "Pay")); var actual = sut.ToJson(); Assert.Equal("MasterCard", actual.Name); Assert.Equal("Pay", actual.Action); Assert.True(actual.StartRecurrent.ToBool()); Assert.True(actual.TransactionKey.IsNothing().ToBool()); } [Fact] public void ChildToJsonReturnsCorrectResult() { var sut = new Child( new ChildPaymentService( "12345", new PaymentService("MasterCard", "Pay"))); var actual = sut.ToJson(); Assert.Equal("MasterCard", actual.Name); Assert.Equal("Pay", actual.Action); Assert.False(actual.StartRecurrent.ToBool()); Assert.Equal("12345", actual.TransactionKey.Match("", x => x)); }
All three tests pass.
Summary #
The major advantage of sum types in statically typed languages is that you can make illegal states unrepresentable (a maxim attributed to Yaron Minsky). Specifically, in the business example of payment types shown here, I need to be able to express that only three out of four combinations of start recurrent and original transaction key is legal. Specifically, I needed to express that the combination of start recurrent = true and the presence of a transaction key is illegal. Making such an illegal state unrepresentable is easy with a sum type, but as this article has shown, you can achieve the same goal in C#.
With the API shown here, there's only three possible states (Individual, Child, and Parent). Notice that all three classes hide their data as private class fields, so the only way to extract that data is to call Match. The compiler will make sure that you handle all three cases, because you must supply a function for all three method arguments.
The code shown in this article is available on GitHub.
This article concludes the little series on how to use Church-encoding in C# to create sum types. You may, however, think that it doesn't really feel object-oriented, with its heavy reliance on function arguments (e.g. Func<PaymentService, T>). It turns out, though, that with only a few refactorings, you'll come to the realisation that what you've seen here is isomorphic to a classic design pattern. Read on!
Next: Church-encoded rose tree.

Comments
Roman, thank you for writing. For no particularly good reason. I tend to automatically disregard
undefined, since it's basically one kind of bottom in Haskell.But I admit that that's not a bulletproof reason, since the actual function, at that point in the article, is still partial.
So honestly, the best answer is that I wrote "the simplest implementation I could think of" because I didn't think of
undefined.