ploeh blog danish software design
What to test and not to test
Should you unit test everything? Hardly surprising, the answer is that It Depends™. This article outlines some of the circumstances you might consider.
Some years ago, I, somewhat to my own surprise, found myself on the wrong side of a controversy about whether one should test trivial code. The context was a discussion about Test-Driven Development (TDD), and for reasons that I still stand behind today, I argued that you should test all code, including trivial code, such as property getters.
Most of the 'TDD community' reacted quite negatively to that article, some in not-so-nice ways. Some people reacted, I believe, based on their dislike of the conclusion, without responding to my arguments. Others, however, gave reasoned rebuttals. When people like Derick Bailey and Mark Rendle disagree with me, in a reasoned matter, even, I consider that a good reason to revisit my thinking.
Could I have been wrong? That certainly wouldn't be the first time, but even re-reading the article today, I find my logic sound. Yet, I've substantially nuanced my position since then.
It took me some time to understand how I could disagree so radically with people I respect. It didn't take me five years, though, but while I've been at peace with the apparent conflict for years, I've never written a coherent description of my current understanding of this problem space. This article is my attempt to remedy that omission.
Context matters #
Whenever you consult an expert about how to address a problem, you'll invariably get the answer that it depends. I'd suggest that if you don't get that answer, the person is probably not an expert, after all. A useful expert will also be able to tell you on what 'it' depends.
In an abstract sense, what 'it' depends on is the context.
I wrote my original piece from a particular context. Part of that context is explicitly present in the article, but another part is entirely implicit. People read the article from within their own contexts, which in many cases turned out to be incongruent with mine. No wonder people disagreed.
Watching the wildlife #
My context at that time was that I had some success with AutoFixture, an open source library, which is what I consider wildlife software. Once you've released a version of the software, you have no control of where it's installed, or how it's used.
This means that backwards compatibility becomes important. If I broke something, I would inconvenience the users of my software. Making sure that compatibility didn't break became one of my highest priorities. I used unit tests for regression tests, and I did, indeed, test the entire public API of AutoFixture, to make sure that no breaking changes were introduced.
That was my implicit context. Read in that light, my dogmatic insistence on testing everything hopefully makes a little more sense.
Does that mean that my conclusion transfers to other circumstances? No, of course it doesn't. If you're developing and maintaining zoo software, breaking changes are of less concern. From that perspective, my article could easily look like the creation of an unhinged mind.
The purpose of tests #
In order to figure out what to test, and what not to test, you should ask yourself the question: what's the purpose of testing?
At first glance, that may seem like an inane question, but there's actually more than one purpose of a unit test. When doing TDD, the purpose of a test is to provide feedback about the API you're developing. A unit test is the first client of the production API. If a test is difficult to write, the production API is difficult to use. More on TDD later, though.
You may say that another purpose of automated tests is that they prevent errors. That's not the case, though. Automated tests prevent regressions.
If you wrote the correct test, your test suite may also help to prevent errors, but a unit test is only as good as the programmer who wrote it. You could have made a mistake when you wrote the test. Or perhaps you misunderstood the specification of what you were trying to implement. Why do you even trust tests?
The cost of regressions #
Why do you want to prevent regressions? Because they're costly?
Based on the little risk management I know about, you operate with two dimensions of risk: the impact of an event, should it occur, and the probability that the event occurs.
Should we all be worried that an asteroid will hit the Earth and wipe out most life? The impact of such an event is truly catastrophic, yet the probability is diminishingly small, so the risk is insignificant. The risk of going for a drive in a car is much higher.
How do you reduce risk? You either decrease the probability that the adverse event will happen, or you reduce the impact of it, should it happen.
Steve Freeman once wrote a nice article about the distinction between fail-safe software, and software that could safely fail. Unfortunately, that article seems to have disappeared from the internet. The point, however, was that with unit tests, we attempt to make our software fail-safe. The unit tests act as a gate that prevents bad versions of the software from being released. That's not a bad strategy for managing risk, but only half of the strategies available.
For example, Continuous Delivery describes how you can use Canary Releases and automated rollbacks to reduce the impact of errors. That's what Steve Freeman called safe fail.
I apologise for this detour around risk management, but I think that it's important that you make an explicit decision about automated testing. You can use unit tests to prevent regressions. What's the impact of an error in production, though?
This depends on the type of software you're developing. When considering alternatives, I often envision the various options as inhabiting a continuum:

For some types of software, an error 'in production' could be fatal. This would be the case for guidance software for Voyager 1, 2, other guidance software, software for medical devices, and so on. If you deploy a defect to Voyager 2, you've probably lost the craft for ever.
(I'd be surprised if the Voyager guidance software is actually covered by unit tests, but I'd expect that other quality assurance checks are in place. For comparison, the space shuttle software development process has been appraised at CMMI level 5.)
On the other side of the continuum, as a software developer, you probably write small ad-hoc development tools for your own use. For example, a few years ago I did a lot of REST API development, and many of the APIs I worked with required OAuth authentication. I wrote a little command-line program that I could use to log on to an internal system and exchange that to a token. I don't think that I wrote any tests for that program. If there were problems with it, I'd just open the source code and fix the problem. Errors were cheap in that situation.
Most software probably falls somewhere in the middle of those extremes. The cost of errors in wildlife software is probably higher than it is for zoo software, but most software can get by with less coverage than everything.
Cyclomatic complexity #
How do you know that your software works? You test it. If you want to automate your testing efforts, you write unit tests... but a unit test suite is software. How do you know that your tests work? Is it going to be turtles all the way down?
I think that we can trust tests for other reasons, but one of them is that each test case exercises a deterministic path through a unit that supports many paths of execution.
In other words, each unit test is an example of a singular execution path. Tests, then, should have a cyclomatic complexity of 1. In other words, you write (test) code with a cyclomatic complexity of 1 in order to test code with a higher cyclomatic complexity.
Should you test code that has a cyclomatic complexity of 1?
What would be the point of that? Why would you write a unit test with a cyclomatic complexity of 1 to test a piece of code with a cyclomatic complexity of 1? Wouldn't you just be adding more code?
From the perspective of trusting the code, there's no reason to trust such a test more than the code that it exercises. In that light, I think it makes sense to not write that test.
To be clear, there could be other reasons to test code with a cyclomatic complexity of 1. One reason, that I pointed out in my original article, is that you don't know if the simple piece of code will stay simple. Another reason is to prevent regressions. A common metaphor for unit testing is double-entry bookkeeping. If you write the unit test in a different way than the implementation, the two views on that behaviour may keep each other in check. You could do that with triangulation using parametrised tests, or perhaps with property-based testing.
I tend to use a heuristic where the farther to the left I am on the above continuum, the more I'm inclined to skip testing of simple functionality. Code with a cyclomatic complexity of 1 falls into that bucket.
TDD #
Let's return our attention to TDD. The previous paragraphs have mostly discussed automated tests as a way to prevent regressions. TDD gives us an entirely different motivation for writing tests: the tests provide feedback on the design of our production code.
Viewed like this, the tests themselves are only artefacts of the TDD process. It's usually a good idea to keep them around after the standard red-green-refactor cycle, because they serve double-duty as regression tests.
Should you test-drive everything? If you're inexperienced with TDD, you get the best exercise by test-driving as much as possible. This still doesn't have to mean that you must write a an explicit test case for each class member. That's what both Mark Rendle and Derick Bailey pointed out. It's often enough if the tests somehow exercise those members.
Revisiting my old article, my mistake was that I conflated TDD with regression testing. My motivation for writing an explicit test case for each member, no matter how trivial, was to preserve backwards compatibility. It really had nothing to do with TDD.
When in doubt #
Despite all other rules of thumb I've so far listed, I'll suggest a few exceptions.
Even if a piece of code theoretically has a cyclomatic complexity of 1, if you're in doubt of how it works, then write a test.
If you have a defect in production, then reproduce that defect with one or more tests, even if the code in question is 'trivial'. Obviously, it wasn't trivial after all, if it caused a bug in production.
Pragmatism #
When you're learning something new, you're typically struggling with even the most basic concepts. That's just how learning works. In that phase of learning, it often pays to follow explicit rules. A way to think about this is the Dreyfus model of skill acquisition. Once you gain some experience, you can start deviating from the rules. We could call this pragmatism.
I often discuss TDD with people who plead for pragmatism. Those people have typically practised TDD for years, if not decades. So have I, and, believe it or not, I'm often quite pragmatic when I practice TDD 'for real'. This is, however, a prerogative of experience.
You can only be pragmatic if you know how to be dogmatic.I use the concept of dogmatism as an antonym to pragmatism. I view pragmatism in programming as the choice of practical solutions over theoretical principles. It's a choice, which means that you must be aware of alternatives.
If you don't know the (principled) alternative, there's no choice.
When you're learning something new, you're still not aware of how to do things according to principle. That's natural. I find myself in that situation all the time. If you keep at it, though, eventually you'll have gained enough experience that you can make actual choices.
This applies to TDD as well. When you're still learning TDD, stick to the principles, particularly when it's inconvenient. Once you've done TDD for a few years, you've earned the right to be pragmatic.
Conclusion #
Which parts of your code base should you (unit) test? It Depends™.
It depends on why you are unit testing, and on the cost of defects in production, and probably many other things I didn't think of.
What's the purpose of tests? Are you using TDD to get feedback on your API design ideas? Or is the main purpose of tests to prevent regressions? Your answers to such questions should guide your decisions on how much to test.
Recently, I've mostly been writing about topics related to computer science, such as the relationships between various branches of mathematics to computation. In such realms, laws apply, and answers tend to be either right or wrong. A piece like this article is different.
This is fundamentally a deeply subjective essay. It's based on my experience with writing automated tests in various circumstances since 2003. I've tried to be as explicit about my context as possible, but I've most likely failed to identify one or more implicit assumptions or biases. I do, therefore, encourage comments.
I wrote this commentary because people keep asking me about how much to test, and when. I suppose it's because they wish to learn from me, and I'm happy to share what I know, to the best of my ability. I have much to learn myself, though, so read this only as the partial, flawed, personal answer that it is.
Applicative validation
Validate input in applicative style for superior readability and composability.
This article is an instalment in an article series about applicative functors. It demonstrates how applicative style can be used to compose small validation functions to a larger validation function in such a way that no validation messages are lost, and the composition remains readable.
All example code in this article is given in Haskell. No F# translation is offered, because Scott Wlaschin has an equivalent example covering input validation in F#.
JSON validation #
In my Pluralsight course about a functional architecture in F#, you can see an example of an on-line restaurant reservation system. I often return to that example scenario, so for regular readers of this blog, it should be known territory. For newcomers, imagine that you've been asked to develop an HTTP-based API that accepts JSON documents containing restaurant reservations. Such a JSON document could look like this:
{
"date": "2017-06-27 18:30:00+02:00",
"name": "Mark Seemann",
"email": "mark@example.com",
"quantity": 4
}
It contains the date and time of the (requested) reservation, the email address and name of the person making the reservation, as well as the number of people who will be dining. Particularly, notice that the date and time is represented as a string value (specifically, in ISO 8601 format), since JSON has no built-in date and time data type.
In Haskell, you can represent such a JSON document using a type like this:
data ReservationJson = ReservationJson { jsonDate :: String, jsonQuantity :: Double, jsonName :: String, jsonEmail :: String } deriving (Eq, Show, Read, Generic)
Haskell's strength is in its type system, so you should prefer to model a reservation using a strong type:
data Reservation = Reservation { reservationDate :: ZonedTime, reservationQuantity :: Int, reservationName :: String, reservationEmail :: String } deriving (Show, Read)
Instead of modelling the date and time as a string, you model it as a ZonedTime value. Additionally, you should model quantity as an integer, since a floating point value doesn't make much sense.
While you can always translate a Reservation value to a ReservationJson value, the converse doesn't hold. There are ReservationJson values that you can't translate to Reservation. Such ReservationJson values are invalid.
You should write code to validate and translate ReservationJson values to Reservation values, if possible.
Specialised validations #
The ReservationJson type is a complex type, because it's composed of multiple (four) elements of different types. You can easily define at least three validation rules that ought to hold:
- You should be able to convert the
jsonDatevalue to aZonedTimevalue. jsonQuantitymust be a positive integer.jsonEmailshould look believably like an email address.
In Haskell, people often use Either for validation, but instead of using Either directly, I'll introduce a specialised Validation type:
newtype Validation e r = Validation (Either e r) deriving (Eq, Show, Functor)
You'll notice that this is simply a redefinition of Either. Haskell can automatically derive its Functor instance with the DeriveFunctor language extension.
My motivation for introducing a new type is that the way that Either is Applicative is not quite how I'd like it to be. Introducing a newtype enables you to change how a type behaves. More on that later. First, you can implement the three individual validation functions.
Date validation #
If the JSON date value is an ISO 8601-formatted string, then you can parse it as a ZonedTime. In that case, you should return the Right case of Validation. If you can't parse the string into a ZonedTime value, you should return a Left value containing a helpful error message.
validateDate :: String -> Validation [String] ZonedTime validateDate candidate = case readMaybe candidate of Just d -> Validation $ Right d Nothing -> Validation $ Left ["Not a date."]
This function uses readMaybe from Text.Read to attempt to parse the candidate String. When readMaybe can read the String value, it returns a Just value with the parsed value inside; otherwise, it returns Nothing. The function pattern-matches on those two cases and returns the appropriate value in each case.
Notice that errors are represented as a list of String values, although this particular function only returns a single message in its list of error messages. The reason for that is that you should be able to collect multiple validation issues for a complex value such as ReservationJson, and keeping track of errors in a list makes that possible.
Haskell golfers may argue that this implementation is overly verbose, and it could, for instance, instead be written as:
validateDate = Validation . maybe (Left ["Not a date."]) Right . readMaybe
which is true, but not as readable. Both versions get the job done, though, as these GCHi-based ad-hoc tests demonstrate:
λ> validateDate "2017/27/06 18:30:00 UTC+2" Validation (Left ["Not a date."]) λ> validateDate "2017-06-27 18:30:00+02:00" Validation (Right 2017-06-27 18:30:00 +0200)
That takes care of parsing dates. On to the next validation function.
Quantity validation #
JSON numbers aren't guaranteed to be integers, so it's possible that even a well-formed Reservation JSON document could contain a quantity property of 9.7, -11.9463, or similar. When handling restaurant reservations, however, it only makes sense to handle positive integers. Even 0 is useless in this context. Thus, validation must check for two conditions, so in principle, you could write two separate functions for that. In order to keep the example simple, though, I've included both tests in the same function:
validateQuantity :: Double -> Validation [String] Int validateQuantity candidate = if isInt candidate && candidate > 0 then Validation $ Right $ round candidate else Validation $ Left ["Not a positive integer."] where isInt x = x == fromInteger (round x)
If candidate is both an integer, and greater than zero, then validateQuantity returns Right; otherwise, it returns a Left value containing an error message. Like validateDate, you can easily test validateQuantity in GHCi:
λ> validateQuantity 4 Validation (Right 4) λ> validateQuantity (-1) Validation (Left ["Not a positive integer."]) λ> validateQuantity 2.32 Validation (Left ["Not a positive integer."])
Perhaps you can think of rules for names, but I can't, so we'll leave the name be and move on to validating email addresses.
Email validation #
It's notoriously difficult to validate SMTP addresses, so you shouldn't even try. It seems fairly safe to assume, however, that an email address must contain at least one @ character, so that's going to be all the validation you have to implement:
validateEmail :: String -> Validation [String] String validateEmail candidate = if '@' `elem` candidate then Validation $ Right candidate else Validation $ Left ["Not an email address."]
Straightforward. Try it out in GHCI:
λ> validateEmail "foo" Validation (Left ["Not an email address."]) λ> validateEmail "foo@example.org" Validation (Right "foo@example.org")
Indeed, that works.
Applicative composition #
What you really should be doing is to validate a ReservationJson value. You have the three validation rules implemented, so now you have to compose them. There is, however, a catch: you must evaluate all rules, and return a list of all the errors you encountered. That's probably going to be a better user experience for a user.
That's the reason you can't use Either. While it's Applicative, it doesn't behave like you'd like it to behave in this scenario. Particularly, the problem is that it throws away all but the first Left value it finds:
λ> Right (,,) <*> Right 42 <*> Left "foo" <*> Left "bar" Left "foo"
Notice how Left "bar" is ignored.
With the new type Validation based on Either, you can now define how it behaves as an applicative functor:
instance Monoid m => Applicative (Validation m) where pure = Validation . pure Validation (Left x) <*> Validation (Left y) = Validation (Left (mappend x y)) Validation f <*> Validation r = Validation (f <*> r)
This instance is restricted to Monoid Left types. It has special behaviour for the case where both expressions passed to <*> are Left values. In that case, it uses mappend (from Monoid) to 'add' the two Left values together in a new Left value.
For all other cases, this instance of Applicative delegates to the behaviour defined for Either. It also uses pure from Either to implement its own pure function.
Lists ([]) form a monoid, and since all the above validation functions return lists of errors, it means that you can compose them using this definition of Applicative:
validateReservation :: ReservationJson -> Validation [String] Reservation validateReservation candidate = pure Reservation <*> vDate <*> vQuantity <*> vName <*> vEmail where vDate = validateDate $ jsonDate candidate vQuantity = validateQuantity $ jsonQuantity candidate vName = pure $ jsonName candidate vEmail = validateEmail $ jsonEmail candidate
The candidate is a ReservationJson value, but each of the validation functions work on either String or Double, so you'll have to use the ReservationJson type's access functions (jsonDate, jsonQuantity, and so on) to pull the relevant values out of it. Once you have those, you can pass them as arguments to the appropriate validation function.
Since there's no rule for jsonName, you can use pure to create a Validation value. All four resulting values (vDate, vQuantity, vName, and vEmail) are Validation [String] values; only their Right types differ.
The Reservation record constructor is a function of the type ZonedTime -> Int -> String -> String -> Reservation, so when you arrange the four v* values correctly between the <*> operator, you have the desired composition.
Try it in GHCi:
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" 4 "Jane Doe" "j@example.com"
Validation (Right (Reservation {
reservationDate = 2017-06-30 19:00:00 +0200,
reservationQuantity = 4,
reservationName = "Jane Doe",
reservationEmail = "j@example.com"}))
λ> validateReservation $ ReservationJson "2017/14/12 6pm" 4.1 "Jane Doe" "jane.example.com"
Validation (Left ["Not a date.","Not a positive integer.","Not an email address."])
λ> validateReservation $ ReservationJson "2017-06-30 19:00:00+02:00" (-3) "Jane Doe" "j@example.com"
Validation (Left ["Not a positive integer."])
The first ReservationJson value passed to validateReservation is valid, so the return value is a Right value.
The next ReservationJson value is about as wrong as it can be, so three different error messages are returned in a Left value. This demonstrates that Validation doesn't give up the first time it encounters a Left value, but rather collects them all.
The third example demonstrates that even a single invalid value (in this case a negative quantity) is enough to make the entire input invalid, but as expected, there's only a single error message.
Summary #
Validation may be the poster child of applicative functors, but it is a convenient way to solve the problem. In this article you saw how to validate a complex data type, collecting and reporting on all problems, if any.
In order to collect all errors, instead of immediately short-circuiting on the first error, you have to deviate from the standard Either implementation of <*>. If you go back to read Scott Wlaschin's article, you should be aware that it specifically implements its applicative functor in that way, instead of the normal behaviour of Either.
More applicative functors exist. This article series has, I think, room for more examples.
The Maybe applicative functor
An introduction to the Maybe applicative functor for object-oriented programmers.
This article is an instalment in an article series about applicative functors. Previously, in a related series, you got an introduction to Maybe as a functor. Not all functors are applicative, but some are, and Maybe is one of them (like list).
In this article, you'll see how to make a C# Maybe class applicative. While I'm going to start with F# and Haskell, you can skip to the C# section if you'd like.
F# #
A few years ago, I did the Roman numerals kata in F#. This is an exercise where you have to convert between normal base 10 integers and Roman numerals. Conversions can fail in both directions, because Roman numerals don't support negative numbers, zero, or numbers greater than 3,999, and Roman numerals represented as strings could be malformed.
Some Roman numbers are written in a subtractive style, e.g. "IV" means subtract 1 (I) from 5 (V). It's easy enough to subtract two numbers, but because parsing isn't guaranteed to succeed, I didn't have two numbers; I had two number options (recall that in F#, Maybe is called option).
How do you subtract one int option from another int option?
Both of these values could be Some, or they could be None. What should happen in each case? With Maybe, only four combinations are possible, so you can put them in a table:
Some x |
None |
|
|---|---|---|
Some y |
Some (x - y) |
None |
None |
None |
None |
Some cases should you return a Some case with the result of the subtraction; in all other cases, you should return None.
You can do this with regular pattern matching, but it's hardly the most elegant solution:
// int option let difference = match minuend, subtrahend with | Some m, Some s -> Some (m - s) | _ -> None
You could attempt to solve this with a specialised helper function like this:
module Option = // ('a -> 'b -> 'c) -> 'a option -> 'b option -> 'c option let map2 f xo yo = match xo, yo with | Some x, Some y -> Some (f x y) | _ -> None
which you could use like this:
let difference = Option.map2 (-) minuend subtrahend
It doesn't, however, generalise well... What if you need to operate on three option values, instead of two? Or four? Should you add map3 and map4 functions as well?
Making option an applicative functor addresses that problem. Here's one possible implementation of <*>:
// ('a -> 'b) option -> 'a option -> 'b option let (<*>) fo xo = match fo, xo with | Some f, Some x -> Some (f x) | _ -> None
This enables you two write the subtraction like this:
let difference = Some (-) <*> minuend <*> subtrahend
For a detailed explanation on how that works, see the previous explanation for lists; it works the same way for Maybe as it does for List.
In the end, however, I didn't think that this was the most readable code, so in the Roman numeral exercise, I chose to use a computation expression instead.
Haskell #
In Haskell, Maybe is already Applicative as part of the language. Without further ado, you can simply write:
difference = pure (-) <*> minuend <*> subtrahend
As is the case with the F# code, I don't consider this the most readable way to express the subtraction of two integers. In F#, I ultimately decided to use a computation expression. In Haskell, that's equivalent to using do notation:
difference :: Maybe Integer difference = do m <- minuend s <- subtrahend return $ m - s
While more verbose, I think it's clearer that one number is being subtracted from another number.
This works for Maybe because not only is Maybe Applicative, it's also a Monad. It's its monadness that enables the do notation. Not all applicative functors are monads, but Maybe is.
C# #
In a previous article you saw how to implement the Maybe functor in C#. You can extend it so that it also becomes an applicative functor:
public static Maybe<TResult> Apply<T, TResult>( this Maybe<Func<T, TResult>> selector, Maybe<T> source) { if (selector.HasItem && source.HasItem) return new Maybe<TResult>(selector.Item(source.Item)); else return new Maybe<TResult>(); } public static Maybe<Func<T2, TResult>> Apply<T1, T2, TResult>( this Maybe<Func<T1, T2, TResult>> selector, Maybe<T1> source) { if (selector.HasItem && source.HasItem) { Func<T2, TResult> g = x => selector.Item(source.Item, x); return new Maybe<Func<T2, TResult>>(g); } else return new Maybe<Func<T2, TResult>>(); }
As was the case for making sequences applicative in C#, you need overloads of the Apply method, because C#'s type inference is inadequate for this task.
If you have two Maybe<int> values, minuend and subtrahend, you can now perform the subtraction:
Func<int, int, int> subtract = (x, y) => x - y; Maybe<int> difference = subtract.ToMaybe().Apply(minuend).Apply(subtrahend);
Like in F# and Haskell, applicative style is hardly the most readable way to express subtraction. It'd be nice if you could write it like Haskell's do notation. You can, but to do that, you must make Maybe a monad, and this isn't a monad tutorial. Mike Hadlow has a good monad tutorial for C# developers, the gist of which is that you must implement SelectMany in order to turn your generic type into a monad. For now, I'll leave this as an exercise for you, but if you add an appropriate SelectMany method, you'd be able to write the subtraction like this:
Maybe<int> difference = from m in minuend from s in subtrahend select m - s;
Again, I think this is more readable, but it does require that the type in question is a monad, and not all applicative functors are (but Maybe is).
Summary #
This article demonstrates that lists or sequences aren't the only applicative functors. Maybe is also an applicative functor, but more exist. The next article will give you another example.
Next: Applicative validation.
Applicative combinations of functions
Applicative lists and sequences enable you to create combinations of functions as well as values.
This article is an instalment in an article series about applicative functors. In the previous article, you saw how you can use applicative lists and sequences to generate combinations of values; specifically, the example demonstrated how to generate various password character combinations.
People often create passwords by using a common word as basis, and then turn characters into upper- or lower case. Someone feeling particularly tech-savvy may replace certain characters with digits, in an imitation of 1337. While this isn't secure, let's look at how to create various combinations of transformations using applicative lists and sequences.
List of functions #
In the previous article, I mentioned that there was a feature of applicative lists that I had, so far, deliberately ignored.
If you consider an example like this:
let passwordCombinations = [sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"] <*> ["a"; "4"] <*> ["ssw"] <*> ["o"; "0"] <*> ["rd"] <*> [""; "!"]
you may have already noticed that while the left side of the <*> operator is a list of functions, it contains only a single function. What happens if you supply more than a single function?
You get a combination of each function and each list element.
Assume that you have three functions to convert characters:
module Char = // char -> char let toUpper c = System.Char.ToUpperInvariant c // char -> char let toLower c = System.Char.ToLowerInvariant c // Not even trying to be complete: // char -> char let to1337 = function | 'a' | 'A' -> '4' | 'b' -> '6' | 'E' -> '3' | 'H' -> '#' | 'i' -> '!' | 'l' -> '1' | 'o' | 'O' -> '0' | 't' -> '+' | c -> c
All three are functions that convert one char value to another, although many values could pass through without being modified. Since they all have the same type, you can create a list of them:
> List.map String.map [Char.toUpper; Char.toLower; Char.to1337] <*> ["Hello"; "World"];; val it : string list = ["HELLO"; "WORLD"; "hello"; "world"; "#e110"; "W0r1d"]
There's a bit to unpack there. Recall that all three functions in the Char module have the same type: char -> char. Making a list of them gives you a (char -> char) list, but you really need a (string -> string) list. Fortunately, the built-in String.map function takes a char -> char function and uses it to map each char values in a string. Thus, List.map String.map [Char.toUpper; Char.toLower; Char.to1337] gives you a (string -> string) list.
When you apply (<*>) that list of functions with a list of string values, you get all possible combinations of each function used with each string. Both "Hello" and "World" are converted to upper case, lower case, and 1337.
Combinations of functions #
Perhaps you're happy with the above combinations, but can we do better? As an example, you'll notice that to1337 only converts an upper-case 'E' to '3', but ignores a lower-case 'e'. What if you also want the combination where 'e' is first converted to upper case, and then to 1337? You'd like that, but you still want to retain the combinations where each of these transformations are applied without the other.
Fear not; functions are values, so you can combine them as well!
In the previous article, did you notice how you could model the presence or absence of a particular value? Specifically, the last character in the potential password could be '!', but '!' could also be omitted.
Consider, again, the expression for all password combinations:
let passwordCombinations = [sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"] <*> ["a"; "4"] <*> ["ssw"] <*> ["o"; "0"] <*> ["rd"] <*> [""; "!"]
Notice that the last list contains two options: "!" and the empty string (""). You can read about this in another article series, but character strings are monoids, and one of the characteristics of monoids is that they have an identity element - a 'neutral' element, if you will. For strings, it's ""; you can append or prepend the empty string as much as you'd like, but it's not going to change the other string.
If you have a set of functions of the type 'a -> 'a, then the built-in function id is the identity element. You can compose any 'a -> 'a function with id, and it's not going to change the other function.
Since functions are values, then, you can create combinations of functions:
// (char -> char) list let maps = [fun f g h -> f >> g >> h] <*> [Char.toUpper; id] <*> [Char.toLower; id] <*> [Char.to1337; id]
Here, maps is a list of functions, but it's not only three functions as in the above example. It's eight functions:
> List.length maps;; val it : int = 8
The above applicative composition of maps combines three lists of functions. Each list presents two alternatives: a function (e.g. Char.toUpper), and id. In other words, a choice between doing something, and doing nothing. The lambda expression fun f g h -> f >> g >> h takes three (curried) arguments, and returns the composition of calling f, then passing the result of that to g, and again passing the result of that to h. f is either Char.toUpper or id, g is either Char.toLower or id, and h is either Char.to1337 or id. That's eight possible combinations.
Combine eight functions with two string values, and you get sixteen alternatives back:
> List.map String.map maps <*> ["Hello"; "World"];; val it : string list = ["he110"; "w0r1d"; "hello"; "world"; "#3LL0"; "W0RLD"; "HELLO"; "WORLD"; "he110"; "w0r1d"; "hello"; "world"; "#e110"; "W0r1d"; "Hello"; "World"]
Notice, for example, how one of the suggested alternatives is "#3LL0". Previously, there was no translation from 'e' to '3', but now there is, via Char.toUpper >> id >> Char.to1337.
Some of the combinations are redundant. For example, "hello" is generated twice, by Char.toUpper >> Char.toLower >> id and id >> Char.toLower >> id, respectively. You can reduce the output with List.distinct:
> List.map String.map maps <*> ["Hello"; "World"] |> List.distinct;; val it : string list = ["he110"; "w0r1d"; "hello"; "world"; "#3LL0"; "W0RLD"; "HELLO"; "WORLD"; "#e110"; "W0r1d"; "Hello"; "World"]
You can write equivalent code in Haskell, but it's so similar to the F# code that there's no reason to show it.
Translation to C# #
Using the Apply extension methods from the previous article, you can translate the above code to C#.
While you can use the .NET Base Class Library's Char.ToUpperInvariant and Char.ToLowerInvariant methods as is, you'll need to supply a to1337 function. You can write it as a named static method, but you can also write it as a delegate:
Func<char, char> to1337 = c => { switch (c) { case 'A': case 'a': return '4'; case 'b': return '6'; case 'E': return '3'; case 'H': return '#'; case 'i': return '!'; case 'l': return '1'; case 'o': case 'O': return '0'; case 't': return '+'; default: return c; } };
You're also going to need an id function:
Func<char, char> id = c => c;
In order to compose three functions to one, you can write something like this:
Func<Func<char, char>, Func<char, char>, Func<char, char>, Func<char, char>> compose3 = (f, g, h) => x => h(g(f(x)));
That's going to be a contender for some of the most obscure C# code I've written in a while. By the double use of =>, you can tell that it's a delegate that returns a delegate. That's not even the worst part: check out the type of the thing! In reality, nothing happens here that doesn't also happen in the above F# code, but it's an example of the superiority of Hindley–Milner type inference: in F#, you don't have to explicitly type out the type.
With a function to compose three other functions, you can now apply the three alternative functions:
IEnumerable<Func<char, char>> maps = new[] { compose3 } .Apply(new[] { Char.ToUpperInvariant, id }) .Apply(new[] { Char.ToLowerInvariant, id }) .Apply(new[] { to1337, id });
Now you have a sequence of functions that translate char values to char values. What you really need, though, is a sequence of functions that translate string values to string values.
The F# core library defines the built-in String.map function, but as far as I can tell, there's no equivalent method in the .NET Base Class Library. Therefore, you must implement it yourself:
Func<Func<char, char>, Func<string, string>> stringMap = f => (string s) => new string(s.Select(f).ToArray());
This is a function that takes a Func<char, char> as input and returns a Func<string, string>. Again, the type declaration isn't the prettiest.
You can now apply maps to some string values, using the Apply extension method:
IEnumerable<string> hellos = maps.Select(stringMap).Apply(new[] { "Hello", "World" });
This produces exactly the same output as the above F# example, even in the same order.
Applicative functors are elegant in F# and Haskell, but awkward in a language like C# - mostly because of its inferior type inference engine.
Summary #
Previous articles demonstrated how applicative lists can be used to compose several lists into a list that contains all possible combinations. In this article you saw how this also extends to combinations of functions.
The last three articles (including the present) focus on lists as applicative functors, but lists aren't the only type of applicative functor. In the next articles, you'll encounter some other applicative functors.
An applicative password list
How to use the applicative functor capabilities of lists to create a password list, with examples that object-oriented programmers can understand.
This article is an instalment in an article series about applicative functors. In the previous article, you saw how to use Haskell and F# lists as applicative functors to generate combinations of values. In this article, you'll see a similar example, but this time, there will also be a C# example.
Guess the password variation #
Years ago, I worked in an organisation that (among other things) produced much demo software. Often, the demo software would include a demonstration of the security features of a product, which meant that, as a user evaluating the software, you had to log in with a user name and password. In order to keep things simple, the password was usually Passw0rd!, or some variation thereof.
(Keep in mind that this was demoware. Password strength wasn't a concern. We explicitly wanted the password to be easy to guess, so that users evaluating the software had a chance to test how log in worked. This was long before social login and the like.)
We had more than one package of demoware, and over the years, variations of the standard password had snuck in. Sometimes it'd be all lower-case; sometimes it'd use 4 instead of a, and so on. As the years went on, the number of possible permutations grew.
Recently, I had a similar problem, but for security reasons, I don't want to divulge what it was. Let's just pretend that I had to guess one of those old demo passwords.
There weren't that many possible variations, but just enough that I couldn't keep them systematically in my head.
- The first letter could be upper or lower case.
- The second letter could be a or 4.
- The o could be replaced with a zero (0).
- The password could end with an exclamation mark (!), but it might also be omitted.
> let (<*>) fs l = fs |> List.collect (fun f -> l |> List.map f);;
val ( <*> ) : fs:('a -> 'b) list -> l:'a list -> 'b list
> [sprintf "%s%s%s%s%s%s"]
<*> ["P"; "p"] <*> ["a"; "4"] <*> ["ssw"] <*> ["o"; "0"] <*> ["rd"] <*> [""; "!"];;
val it : string list =
["Password"; "Password!"; "Passw0rd"; "Passw0rd!"; "P4ssword"; "P4ssword!";
"P4ssw0rd"; "P4ssw0rd!"; "password"; "password!"; "passw0rd"; "passw0rd!";
"p4ssword"; "p4ssword!"; "p4ssw0rd"; "p4ssw0rd!"]
This produces a list of all the possible password combinations according to the above rules. Since there weren't that many, I could start trying each from the start, until I found the correct variation.
The first list contains a single function. Due to the way sprintf works, sprintf "%s%s%s%s%s%s" is a function that takes six (curried) string arguments, and returns a string. The number 6 is no coincidence, because you'll notice that the <*> operator is used six times.
There's no reason to repeat the exegesis from the previous article, but briefly:
sprintf "%s%s%s%s%s%s"has the typestring -> string -> string -> string -> string -> string -> string.[sprintf "%s%s%s%s%s%s"]has the type(string -> string -> string -> string -> string -> string -> string) list.[sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"]has the type(string -> string -> string -> string -> string -> string) list.[sprintf "%s%s%s%s%s%s"] <*> ["P"; "p"] <*> ["a"; "4"]has the type(string -> string -> string -> string -> string) list.- ...and so on.
<*>, an argument is removed from the resulting function contained in the returned list. When you've applied six lists with the <*> operator, the return value is no longer a list of functions, but a list of values.
Clearly, then, that's no coincidence. I deliberately shaped the initial function to take six arguments, so that it would match the six segments I wanted to model.
Perhaps the most interesting quality of applicative functors is that you can compose an arbitrary number of objects, as long as you have a function to match the number of arguments.
Haskell #
This time I started with F#, but in Haskell, <*> is a built-in operator, so obviously this also works there:
passwordCombinations :: [String] passwordCombinations = [printf "%s%s%s%s%s%s"] <*> ["P", "p"] <*> ["a", "4"] <*> ["ssw"] <*> ["o", "0"] <*> ["rd"] <*> ["", "!"]
The output is the same as the above F# code.
C# #
While you can translate the concept of lists as an applicative functor to C#, this is where you start testing the limits of the language; or perhaps I've simply forgotten too much C# to do it full justice.
Instead of making linked lists an applicative functor, let's consider a type closer to the spirit of the C# language: IEnumerable<T>. The following code attempts to turn IEnumerable<T> into an applicative functor.
Consider the above F# implementation of <*> (explained in the previous article). It uses List.collect to flatten what would otherwise had been a list of lists. List.collect has the type ('a -> 'b list) -> 'a list -> 'b list. The corresponding method for IEnumerable<T> already exists in the .NET Base Class Library; it's called SelectMany. (Incidentally, this is also the monadic bind function, but this is still not a monad tutorial.)
For an applicative functor, we need a method that takes a sequence of functions, and a sequence of values, and produces a sequence of return values. You can translate the above F# function to this C# extension method:
public static IEnumerable<TResult> Apply<T, TResult>( this IEnumerable<Func<T, TResult>> selectors, IEnumerable<T> source) { return selectors.SelectMany(source.Select); }
That's a single line of code! That's not so bad. What's the problem?
So far there's no problem. You can, for example, write code like this:
Func<string, int> sl = s => s.Length; var lengths = new[] { sl }.Apply(new[] { "foo", "bar", "baz" });
This will return a sequence of the numbers 3, 3, 3. That seems, however, like quite a convoluted way of getting the lengths of some strings. A normal Select method would have sufficed.
Is it possible to repeat the above password enumeration in C#? In order to do that, you need a function that takes six string arguments and returns a string:
Func<string, string, string, string, string, string, string> concat = (x, y, z, æ, ø, å) => x + y + z + æ + ø + å;
With programmers' penchant to start with the variable name x, and continue with y and z, most people will have a problem with six variables - but not us Danes! Fortunately, we've officially added three extra letters to our alphabet for this very purpose! So with that small problem out of the way, you can now attempt to reproduce the above F# code:
var combinations = new[] { concat } .Apply(new[] { "P", "p" }) .Apply(new[] { "a", "4" }) .Apply(new[] { "ssw" }) .Apply(new[] { "o", "0" }) .Apply(new[] { "rd" }) .Apply(new[] { "", "!" });
That looks promising, but there's one problem: it doesn't compile.
The problem is that concat is a function that takes six arguments, and the above Apply method expects selectors to be functions that take exactly one argument.
Alas, while it's not pretty, you can attempt to address the problem with an overload:
public static IEnumerable<Func<T2, T3, T4, T5, T6, TResult>> Apply<T1, T2, T3, T4, T5, T6, TResult>( this IEnumerable<Func<T1, T2, T3, T4, T5, T6, TResult>> selectors, IEnumerable<T1> source) { return selectors.SelectMany(f => source.Select(x => { Func<T2, T3, T4, T5, T6, TResult> g = (y, z, æ, ø, å) => f(x, y, z, æ, ø, å); return g; })); }
This overload of Apply takes selectors of arity six, and return a sequence of functions with arity five.
Does it work now, then?
Unfortunately, it still doesn't compile, because new[] { concat }.Apply(new[] { "P", "p" }) has the type IEnumerable<Func<string, string, string, string, string, string>>, and no overload of Apply exists that supports selectors with arity five.
You'll have to add such an overload as well:
public static IEnumerable<Func<T2, T3, T4, T5, TResult>> Apply<T1, T2, T3, T4, T5, TResult>( this IEnumerable<Func<T1, T2, T3, T4, T5, TResult>> selectors, IEnumerable<T1> source) { return selectors.SelectMany(f => source.Select(x => { Func<T2, T3, T4, T5, TResult> g = (y, z, æ, ø) => f(x, y, z, æ, ø); return g; })); }
You can probably see where this is going. This overload returns a sequence of functions with arity four, so you'll have to add an Apply overload for such functions as well, plus for functions with arity three and two. Once you've done that, the above fluent chain of Apply method calls work, and you get a sequence containing all the password variations.
> new[] { concat } . .Apply(new[] { "P", "p" }) . .Apply(new[] { "a", "4" }) . .Apply(new[] { "ssw" }) . .Apply(new[] { "o", "0" }) . .Apply(new[] { "rd" }) . .Apply(new[] { "", "!" }) string[16] { "Password", "Password!", "Passw0rd", "Passw0rd!", "P4ssword", "P4ssword!", "P4ssw0rd", "P4ssw0rd!", "password", "password!", "passw0rd", "passw0rd!", "p4ssword", "p4ssword!", "p4ssw0rd", "p4ssw0rd!" }
In F# and Haskell, the compiler automatically figures out the return type of each application, due to a combination of currying and Hindley–Milner type inference. Perhaps I've allowed my C# skills to atrophy, but I don't think there's an easy resolution to this problem in C#.
Obviously, you can always write a reusable library with Apply overloads that support up to some absurd arity. Once those methods are written, they're unlikely to change. Still, it seems to me that we're pushing the envelope.
Summary #
In this article, you saw how to turn C# sequences into an applicative functor. While possible, there are some bumps in the road.
There's still an aspect of using lists and sequences as applicative functors that I've been deliberately ignoring so far. The next article covers that. After that, we'll take a break from lists and look at some other applicative functors.
Comments
In F# and Haskell, the compiler automatically figures out the return type of each application, due to a combination of currying and Hindley–Milner type inference. Perhaps I've allowed my C# skills to atrophy, but I don't think there's an easy resolution to this problem in C#.
I think the difference is that all functions in F# and Haskell are automatically curried, but nothing is automatically curreid in C#. If you explicitly curry concat, then the code complies and works as expected. Here is one way to achieve that.
var combinations = new[] { LanguageExt.Prelude.curry(concat) } .Apply(new[] { "P", "p" }) .Apply(new[] { "a", "4" }) .Apply(new[] { "ssw" }) .Apply(new[] { "o", "0" }) .Apply(new[] { "rd" }) .Apply(new[] { "", "!" });
In this example, I curried concat using curry from the NuGet package LanguageExt. It is a base class library for functional programming in C#.
So you don't need many overloads of your Apply for varrying numbers of type parameters. You just need many overloads of curry.
Tyson, thank you for writing. Yes, you're right that it's the lack of default currying that makes this sort of style less than ideal in C#. This seems to be clearly demonstrated by your example.
Full deck
An introduction to applicative functors in Haskell, with a translation to F#.
This article is an instalment in an article series about applicative functors. While (non-applicative) functors can be translated to an object-oriented language like C# in a straightforward manner, applicative functors are more entrenched in functional languages like Haskell. This article introduces the concept with a motivating example in Haskell, and also shows a translation to F#. In the next article, you'll also see how to implement an applicative functor in C#.
Deck of cards in Haskell #
Imagine that you want to model a card game. In order to do so, you start by defining data types for suits, faces, and cards:
data Suit = Diamonds | Hearts | Clubs | Spades deriving (Show, Eq, Enum, Bounded) data Face = Two | Three | Four | Five | Six | Seven | Eight | Nine | Ten | Jack | Queen | King | Ace deriving (Show, Eq, Enum, Bounded) data Card = Card { face :: Face, suit :: Suit } deriving (Show, Eq)
Since both Suit and Face are instances of the Enum and Bounded typeclasses, you can easily enumerate them:
allFaces :: [Face] allFaces = [minBound .. maxBound] allSuits :: [Suit] allSuits = [minBound .. maxBound]
For example, allSuits enumerates all four Suit values:
λ> allSuits [Diamonds,Hearts,Clubs,Spades]
Notice, by the way, how the code for allFaces and allSuits is identical. The behaviour, however, is different, because the types are different.
While you can enumerate suits and faces, how do you create a full deck of cards?
A full deck of cards should contain one card of every possible combination of suit and face. Here's one way to do it, taking advantage of lists being applicative functors:
fullDeck :: [Card] fullDeck = pure Card <*> allFaces <*> allSuits
This will give you all the possible cards. Here are the first six:
λ> forM_ (take 6 fullDeck) print
Card {face = Two, suit = Diamonds}
Card {face = Two, suit = Hearts}
Card {face = Two, suit = Clubs}
Card {face = Two, suit = Spades}
Card {face = Three, suit = Diamonds}
Card {face = Three, suit = Hearts}
How does it work? Let's break it down, starting from left:
λ> :type Card Card :: Face -> Suit -> Card λ> :type pure Card pure Card :: Applicative f => f (Face -> Suit -> Card) λ> :type pure Card <*> allFaces pure Card <*> allFaces :: [Suit -> Card] λ> :type pure Card <*> allFaces <*> allSuits pure Card <*> allFaces <*> allSuits :: [Card]
From the top, Card is a function that takes a Face value and a Suit value and returns a Card value. Object-oriented programmers can think of it as a constructor.
Next, pure Card is the Card function, elevated to an applicative functor. At this point, the compiler hasn't decided which particular applicative functor it is; it could be any applicative functor. Specifically, it turns out to be the list type ([]), which means that pure Card has the type [Face -> Suit -> Card]. That is: it's a list of functions, but a list of only a single function. At this point, however, this is still premature. The type doesn't materialise until we apply the second expression.
The type of allFaces is clearly [Face]. Since the <*> operator has the type Applicative f => f (a -> b) -> f a -> f b, the expression on the left must be the same functor as the expression on the right. The list type ([]) is an applicative functor, and because allFaces is a list, then pure Card must also be a list, in the expression pure Card <*> allFaces. In other words, in the definition of <*>, you can substitute f with [], and a with Face. The interim result is [Face -> b] -> [Face] -> [b]. What is b, then?
You already know that pure Card has the type [Face -> Suit -> Card], so b must be Suit -> Card. That's the reason that pure Card <*> allFaces has the type [Suit -> Card]. It's a list of functions. This means that you can use <*> a second time, this time with allSuits, which has the type [Suit].
Using the same line of reasoning as before, you can substitute Suit for a in the type of <*>, and you get [Suit -> b] -> [Suit] -> [b]. What is b now? From the previous step, you know that the expression on the left has the type [Suit -> Card], so b must be Card. That's why the entire expression has the type [Card].
Deck of cards in F# #
You can translate the above Haskell code to F#. The first step is to make F# lists applicative. F# also supports custom operators, so you can add a function called <*>:
// ('a -> 'b) list -> 'a list -> 'b list let (<*>) fs l = fs |> List.collect (fun f -> l |> List.map f)
This implementation iterates over all the functions in fs; for each function, it maps the list l with that function. Had you done that with a normal List.map, this would have returned a list of lists, but by using List.collect, you flatten the list.
It's worth noting that this isn't the only way you could have implemented <*>, but this is the implementation that behaves like the Haskell function. An alternative implementation could have been this:
// ('a -> 'b) list -> 'a list -> 'b list let (<*>) fs = List.collect (fun x -> fs |> List.map (fun f -> f x))
This variation has the same type as the first example, and still returns all combinations, but the order is different. In the following of this article, as well as in subsequent articles, I'll use the first version.
Here's the playing cards example translated to F#:
type Suit = Diamonds | Hearts | Clubs | Spades type Face = | Two | Three | Four | Five | Six | Seven | Eight | Nine | Ten | Jack | Queen | King | Ace type Card = { Face: Face; Suit : Suit } // Face list let allFaces = [ Two; Three; Four; Five; Six; Seven; Eight; Nine; Ten; Jack; Queen; King; Ace] // Suit list let allSuits = [Diamonds; Hearts; Clubs; Spades] // Card list let fullDeck = [fun f s -> { Face = f; Suit = s }] <*> allFaces <*> allSuits
The F# code is slightly more verbose than the Haskell code, because you have to repeat all the cases for Suit and Face. You can't enumerate them automatically, like you can in Haskell.
It didn't make much sense to me to attempt to define a pure function, so instead I simply inserted a single lambda expression in a list, using the normal square-bracket syntax. F# doesn't have constructors for record types, so you have to pass a lambda expression, whereas in Haskell, you could simply use the Card function.
The result is the same, though:
> fullDeck |> List.take 6 |> List.iter (printfn "%A");;
{Face = Two; Suit = Diamonds;}
{Face = Two; Suit = Hearts;}
{Face = Two; Suit = Clubs;}
{Face = Two; Suit = Spades;}
{Face = Three; Suit = Diamonds;}
{Face = Three; Suit = Hearts;}
While the mechanics of applicative functors translate well to F#, it leaves you with at least one problem. If you add the above operator <*>, you've now 'used up' that operator for lists. While you can define an operator of the same name for e.g. option, you'd have to put them in separate modules or namespaces in order to prevent them from colliding. This also means that you can't easily use them together.
For that reason, I wouldn't consider this the most idiomatic way to create a full deck of cards in F#. Normally, I'd do this instead:
// Card list let fullDeck = [ for suit in allSuits do for face in allFaces do yield { Face = face; Suit = suit } ]
This alternative syntax takes advantage of F#'s 'extended list comprehension' syntax. FWIW, you could have done something similar in Haskell:
fullDeck :: [Card] fullDeck = [Card f s | f <- allFaces, s <- allSuits]
List comprehension, however, is (as the name implies) specific to lists, whereas an applicative functor is a more general concept.
Summary #
This article introduced you to lists as an applicative functor, using the motivating example of having to populate a full deck of cards with all possible combinations of suits and faces.
The next article in the series shows another list example. The F# and Haskell code will be similar to the code in the present article, but the next article will also include a translation to C#.
Next: An applicative password list.
Applicative functors
An applicative functor is a useful abstraction. While typically associated with functional programming, applicative functors can be conjured into existence in C# as well.
This article series is part of a larger series of articles about functors, applicatives, and other mappable containers.
In a former article series, you learned about functors, and how they also exist in object-oriented design. Perhaps the utility of this still eludes you, although, if you've ever had experience with LINQ in C#, you should realise that the abstraction is invaluable. Functors are abundant; applicative functors not quite so much. On the other hand, applicative functors enable you to do more.
I find it helpful to think of applicative functors as an abstraction that enable you to express combinations of things.
In the functor article series, I mostly focused on the mechanics of implementation. In this article series, I think that you'll find it helpful to slightly change the perspective. In these articles, I'll show you various motivating examples of how applicative functors are useful.
- Full deck
- An applicative password list
- Applicative combinations of functions
- The Maybe applicative functor
- Applicative validation
- The Test Data Generator applicative functor
- Danish CPR numbers in F#
- The Lazy applicative functor
- Applicative monoids
A Haskell perspective #
A normal functor maps objects in an 'elevated world' (like C#'s IEnumerable<T> or IObservable<T>) using a function in the 'normal world'. As a variation, an applicative functor maps objects in an 'elevated world' using functions from the same 'elevated world'.
In Haskell, an applicative functor is defined like this:
class Functor f => Applicative f where pure :: a -> f a (<*>) :: f (a -> b) -> f a -> f b
This is a simplification; there's more to the Applicative typeclass than this, but this should highlight the essence. What it says is that an applicative functor must already be a Functor. It could be any sort of Functor, like [] (linked list), Maybe, Either, and so on. Since Functor is an abstraction, it's called f.
The definition furthermore says that in order for a functor to be applicative, two functions must exist: pure and <*> ('apply').
pure is easy to understand. It simply 'elevates' a 'normal' value to a functor value. For example, you can elevate the number 42 to a list value by putting it in a list with a single element: [42]. Or you can elevate "foo" to Maybe by containing it in the Just case: Just "foo". That is, literally, what pure does for [] (list) and Maybe.
The <*> operator applies an 'elevated' function to an 'elevated' value. When f is [], this literally means that you have a list of functions that you have to apply to a list of values. Perhaps you can already see what I meant by combinations of things.
This sounds abstract, but follow the above list of links in order to see several examples.
An F# perspective #
Applicative functors aren't explicitly modelled in F#, but they're easy enough to add if you need them. F# doesn't have typeclasses, so implementing applicative functors tend to be more on a case-by-case basis.
If you need list to be applicative, pure should have the type 'a -> 'a list, and <*> should have the type ('a -> 'b) list -> 'a list -> 'b list. At this point, you already run into the problem that pure is a reserved keyword in F#, so you'll have to find another name, or simply ignore that function.
If you need option to be applicative, <*> should have the type ('a -> 'b) option -> 'a option -> 'b option. Now you run into your second problem, because which function is <*>? The one for list, or the one for option? It can't be both, so you'll have to resort to all sorts of hygiene to prevent these two versions of the same operator from clashing. This somewhat limits its usefulness.
Again, refer to the above list of linked articles for concrete examples.
A C# perspective #
Applicative functors push the limits of what you can express in C#, but the equivalent to <*> would be a method with this signature:
public static Functor<TResult> Apply<T, TResult>( this Functor<Func<T, TResult>> selector, Functor<T> source)
Here, the class Functor<T> is a place-holder for a proper functor class. A concrete example could be for IEnumerable<T>:
public static IEnumerable<TResult> Apply<T, TResult>( this IEnumerable<Func<T, TResult>> selectors, IEnumerable<T> source)
As you can see, here you somehow have to figure out how to combine a sequence of functions with a sequence of values.
In some of the examples in the above list of linked articles, you'll see how this will stretch the capability of C#.
Summary #
This article only attempts to provide an overview of applicative functors, while examples are given in linked articles. I find it helpful to think of applicative functors as an abstraction that enables you to model arbitrary combinations of objects. This is a core feature in Haskell, occasionally useful in F#, and somewhat alien to C#.
Next: Full deck.
Asynchronous functors
Asynchronous computations form functors. An article for object-oriented programmers.
This article is an instalment in an article series about functors. The previous article covered the Lazy functor. In this article, you'll learn about closely related functors: .NET Tasks and F# asynchronous workflows.
A word of warning is in order. .NET Tasks aren't referentially transparent, whereas F# asynchronous computations are. You could argue, then, that .NET Tasks aren't proper functors, but you mostly observe the difference when you perform impure operations. As a general observation, when impure operations are allowed, the conclusions of this overall article series are precarious. We can't radically change how the .NET languages work, so we'll have to soldier on, pretending that impure operations are delegated to other parts of our system. Under this undue assumption, we can pretend that Task<T> forms a functor.
Task functor #
You can write an idiomatic Select extension method for Task<T> like this:
public async static Task<TResult> Select<T, TResult>( this Task<T> source, Func<T, TResult> selector) { var x = await source; return selector(x); }
With this extension method in scope, you can compose asynchronous computations like this:
Task<int> x = // ... Task<string> y = x.Select(i => i.ToString());
Or, if you prefer query syntax:
Task<int> x = // ... Task<string> y = from i in x select i.ToString();
In both cases, you start with a Task<int> which you map into a Task<string>. Perhaps you've noticed that these two examples closely resemble the equivalent Lazy functor examples. The resemblance isn't coincidental. The same abstraction is in use in both places. This is the functor abstraction. That's what this article series is all about, after all.
The difference between the Task functor and the Lazy functor is that lazy computations don't run until forced. Tasks, on the other hand, typically start running in the background when created. Thus, when you finally await the value, you may actually not have to wait for it. This does, however, depend on how you created the initial task.
First functor law for Task #
The Select method obeys the first functor law. As usual in this article series, actually proving that this is the case belongs to the realm of computer science. Instead of proving that the law holds, you can use property-based testing to demonstrate that it does. The following example shows a single property written with FsCheck 2.11.0 and xUnit.net 2.4.0.
[Property(QuietOnSuccess = true)] public void TaskObeysFirstFunctorLaw(int i) { var left = Task.FromResult(i); var right = Task.FromResult(i).Select(x => x); Assert.Equal(left.Result, right.Result); }
This property accesses the Result property of the Tasks involved. This is typically not the preferred way to pull the value of Tasks, but I decided to do it like this since FsCheck 2.4.0 doesn't support asynchronous properties.
Even though you may feel that a property-based test gives you more confidence than a few hard-coded examples, such a test is nothing but a demonstration of the first functor law. It's no proof, and it only demonstrates that the law holds for Task<int>, not that it holds for Task<string>, Task<Product>, etcetera.
Second functor law for Task #
As is the case with the first functor law, you can also use a property to demonstrate that the second functor law holds:
[Property(QuietOnSuccess = true)] public void TaskObeysSecondFunctorLaw( Func<string, byte> f, Func<int, string> g, int i) { var left = Task.FromResult(i).Select(g).Select(f); var right = Task.FromResult(i).Select(x => f(g(x))); Assert.Equal(left.Result, right.Result); }
Again the same admonitions apply: that property is no proof. It does show, however, that given two functions, f and g, it doesn't matter if you map a Task in one or two steps. The output is the same in both cases.
Async functor #
F# had asynchronous workflows long before C#, so it uses a slightly different model, supported by separate types. Instead of Task<T>, F# relies on a generic type called Async<'T>. It's still a functor, since you can trivially implement a map function for it:
module Async = // 'a -> Async<'a> let fromValue x = async { return x } // ('a -> 'b) -> Async<'a> -> Async<'b> let map f x = async { let! x' = x return f x' }
The map function uses the async computation expression to access the value being computed asynchronously. You can use a let! binding to await the value computed in x, and then use the function f to translate that value. The return keyword turns the result into a new Async value.
With the map function, you can write code like this:
let (x : Async<int>) = // ... let (y : Async<string>) = x |> Async.map string
Once you've composed an asynchronous workflow to your liking, you can run it to compute the value in which you're interested:
> Async.RunSynchronously y;; val it : string = "42"
This is the main difference between F# asynchronous workflows and .NET Tasks. You have to explicitly run an asynchronous workflows, whereas Tasks are usually, implicitly, already running in the background.
First functor law for Async #
The Async.map function obeys the first functor law. Like above, you can use FsCheck to demonstrate how that works:
[<Property(QuietOnSuccess = true)>] let ``Async obeys first functor law`` (i : int) = let left = Async.fromValue i let right = Async.fromValue i |> Async.map id Async.RunSynchronously left =! Async.RunSynchronously right
In addition to FsCheck and xUnit.net, this property also uses Unquote 4.0.0 for the assertion. The =! operator is an assertion that the left-hand side must equal the right-hand side. If it doesn't, then the operator throws a descriptive exception.
Second functor law for Async #
As is the case with the first functor law, you can also use a property to demonstrate that the second functor law holds:
[<Property(QuietOnSuccess = true)>] let ``Async obeys second functor law`` (f : string -> byte) g (i : int) = let left = Async.fromValue i |> Async.map g |> Async.map f let right = Async.fromValue i |> Async.map (g >> f) Async.RunSynchronously left =! Async.RunSynchronously right
As usual, the second functor law states that given two arbitrary (but pure) functions f and g, it doesn't matter if you map an asynchronous workflow in one or two steps. There could be a difference in performance, but the functor laws don't concern themselves with the time dimension.
Both of the above properties use the Async.fromValue helper function to create Async values. Perhaps you consider it cheating that it immediately produces a value, but you can add a delay if you want to pretend that actual asynchronous computation takes place. It'll make the tests run slower, but otherwise will not affect the outcome.
Task and Async isomorphism #
The reason I've covered both Task<T> and Async<'a> in the same article is that they're equivalent. You can translate a Task to an asynchronous workflow, or the other way around.
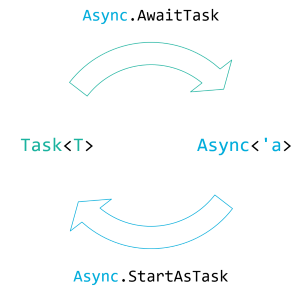
There's performance implications of going back and forth between Task<T> and Async<'a>, but there's no loss of information. You can, therefore, consider these to representations of asynchronous computations isomorphic.
Summary #
Whether you do asynchronous programming with Task<T> or Async<'a>, asynchronous computations form functors. This enables you to piecemeal compose asynchronous workflows.
Next: The Const functor.
Comments
As a general observation, when impure operations are allowed, the conclusions of this overall article series are precarious. We can't radically change how the .NET languages work, so we'll have to soldier on, pretending that impure operations are delegated to other parts of our system. Under this undue assumption, we can pretend that Task<T> forms a functor.
I am with you. I also want to be pragmatic here and treat Task<T> as a functor. It is definitely better than the alternative.
At the same time, I want to know what prevents Task<T> from actually being a functor so that I can compensate when needed.
A word of warning is in order. .NET Tasks aren't referentially transparent, whereas F# asynchronous computations are. You could argue, then, that .NET Tasks aren't proper functors, but you mostly observe the difference when you perform impure operations.
Can you elaborate about this? Why is Task<T> not referentially transparent? Why is the situation worse with impure operations? What issue remains when restricting to pure functions? Is this related to how the stack trace is closely related to how many times await appears in the code?
Tyson, thank you for writing. That .NET tasks aren't referentially transparent is a result of memoisation, as Diogo Castro pointed out to me.
The coming article about Task asynchronous programming as an IO surrogate will also discuss this topic.
Ha! So funny. It is the same caching behavior that I pointed out in this comment. I wish I had known about Diogo's comment. I could have just linked there.
You could argue, then, that .NET Tasks aren't proper functors, but you mostly observe the difference when you perform impure operations.
I am still not completely following though. Are you saying that this caching behavior prevents .NET Tasks from satisfying one of the functor laws? If so, is it the identity law or the composition law? If it is the composition law, what are the two functions that demonstate the failure? Even when allowing impure functions, I can't think of an example. However, I will keep thinking about this and comment again if I find an example.
Tyson, I am, in general trying to avoid claiming that any of this applies in the presence of impurity. Take something as trivial as Select(i => new Random().Next(i)), for Task or any other 'functor'. It's not even going to evaluate to the same outcome between two runs.
I think I understand your hesitation now regarding impurity. I also think I can argue that the existence of impure functions in C# does not prevent Task<T> from being a functor.
Before I give that argument and we consider if it works, I want to make sure there isn't a simpler issue only involving pure functions the prevents Task<T> from being a functor.
You could argue, then, that .NET Tasks aren't proper functors, but you mostly observe the difference when you perform impure operations.
Your use of "mostly" makes me think that you believe there is a counterexample only involving pure functions that shows Task<T> is not a functor. Do I correctly understanding what you meant by that sentence? If so, can you share that counterexample? If not, can you elaborate so that I can better understand what you meant.
Tyson, I wrote this article two years ago. I can't recall if I had anything specific in mind, or if it was just a throwaway phrase. Even if I had a specific counter-example in mind, I might have been wrong, just like the consensus is about Fermat's last theorem.
If you can produce an example, however, you'd prove me right 😀
Typing is not a programming bottleneck
Some developers seem to think that typing is a major bottleneck while programming. It's not.
I sometimes give programming advice to people. They approach me with a software design problem, and, to the best of my ability, I suggest a remedy. Despite my best intentions, my suggestions sometimes meet resistance. One common reaction is that my suggestion isn't idiomatic, but recently, another type of criticism seems to be on the rise.
The code that I suggest is too verbose. It involves too much typing.
I'll use this article to reflect on that criticism.
The purpose of code #
Before we get into the details of the issue, I'd like to start with the big picture. What's the purpose of code?
I've discussed this extensively in my Clean Coders video on Humane Code. In short, the purpose of source code is to communicate the workings of a piece of software to the next programmer who comes along. This could easily include your future self.
Perhaps you disagree with that proposition. Perhaps you think that the purpose of source code is to produce working software. It's that, too, but that's not its only purpose. If that was the only purpose, you might as well write the software in machine code.
Why do we have high-level programming languages like C#, Java, JavaScript, Ruby, Python, F#, Visual Basic, Haskell, heck - even C++?
As far as I can tell, it's because programmers are all human, and humans have limited cognitive capacity. We can't keep track of hundreds, or thousands, of global variables, or the states of dozens of complex resources. We need tools that help us structure and understand complex systems so that they're broken down into (more) manageable chunks. High-level languages help us do that.
The purpose of source code is to be understood. You read source code much more that you write. I'm not aware of any scientific studies, but I think most programmers will agree that over the lifetime of a code base, any line of code will be read orders of magnitude more often that it's edited.
Typing speed #
How many lines of code do you produce during a productive working day?
To be honest, I can't even answer that question myself. I've never measured it, since I consider it to be irrelevant. The Mythical Man-Month gives the number as 10, but let's be generous and pretend it's ten times that. This clearly depends on lots of factors, such as the language in which you're writing, the state of the code base, and so on. You'd tend to write more lines in a pristine greenfield code base, whereas you'll write fewer lines of code in a complicated legacy code base.
How many characters is a line of code? Let's say it's 80 characters, because that's the maximum width code ought to have. I realise that many people write wider lines, but on the other hand, most developers (fortunately) use indentation, so as a counter-weight, code often has some blank space to the left as well. This is all back-of-the-envelope calculations anyway.
When I worked in a Microsoft product group, we typically planned that a productive, 'full' day of coding was five hours. Even on productive days, the rest was used in meetings, administration, breaks, and so on.
If you write code for five hours, and produce 100 lines of code, at 80 characters per line, that's 8,000 characters. Your IDE is likely to help you with statement completion and such, but for the sake of argument, let's pretend that you have to type it all in.
8,000 characters in five hours is 1,600 characters per hour, or 27 characters per minute.
I'm not a particularly fast typist, but I can type ten times faster than that.
Typing isn't a bottleneck.
Is more code worse? #
I tend to get drawn into these discussions from time to time, but good programming has little to do with how fast you can produce lines of code.
To be clear, I entirely accept that statement completion, refactoring support, and such are, in general, benign features. While I spend most of my programming time thinking and reading, I also tend to write code in bursts. The average count of lines per hour may not be great, but that's because averages smooth out the hills and the valleys of my activity.
Still, increasingly frequent objection to some of my suggestions is that what I suggest implies 'too much' code. Recently, for example, I had to defend the merits of the Fluent Builder pattern that I suggest in my DI-Friendly Library article.
As another example, consider two alternatives for modelling a restaurant reservation. First, here's a terse option:
public class Reservation { public DateTimeOffset Date { get; set; } public string Email { get; set; } public string Name { get; set; } public int Quantity { get; set; } public bool IsAccepted { get; set; } }
Here's a longer alternative:
public sealed class Reservation { public Reservation( DateTimeOffset date, string name, string email, int quantity) : this(date, name, email, quantity, false) { } private Reservation( DateTimeOffset date, string name, string email, int quantity, bool isAccepted) { Date = date; Name = name; Email = email; Quantity = quantity; IsAccepted = isAccepted; } public DateTimeOffset Date { get; } public string Name { get; } public string Email { get; } public int Quantity { get; } public bool IsAccepted { get; } public Reservation WithDate(DateTimeOffset newDate) { return new Reservation(newDate, Name, Email, Quantity, IsAccepted); } public Reservation WithName(string newName) { return new Reservation(Date, newName, Email, Quantity, IsAccepted); } public Reservation WithEmail(string newEmail) { return new Reservation(Date, Name, newEmail, Quantity, IsAccepted); } public Reservation WithQuantity(int newQuantity) { return new Reservation(Date, Name, Email, newQuantity, IsAccepted); } public Reservation Accept() { return new Reservation(Date, Name, Email, Quantity, true); } public override bool Equals(object obj) { if (!(obj is Reservation other)) return false; return Equals(Date, other.Date) && Equals(Name, other.Name) && Equals(Email, other.Email) && Equals(Quantity, other.Quantity) && Equals(IsAccepted, other.IsAccepted); } public override int GetHashCode() { return Date.GetHashCode() ^ Name.GetHashCode() ^ Email.GetHashCode() ^ Quantity.GetHashCode() ^ IsAccepted.GetHashCode(); } }
Which alternative is better? The short version is eight lines of code, including the curly brackets. The longer version is 78 lines of code. That's ten times as much.
I prefer the longer version. While it takes longer to type, it comes with several benefits. The main benefit is that because it's immutable, it can have structural equality. This makes it trivial to compare objects, which, for example, is something you do all the time in unit test assertions. Another benefit is that such Value Objects make better domain models. The above Reservation Value Object only shows the slightest sign of emerging domain logic in the Accept method, but once you start modelling like this, such objects seem to attract more domain behaviour.
Maintenance burden #
Perhaps you're now convinced that typing speed may not be the bottleneck, but you still feel that you don't like the verbose Reservation alternative. More code could be an increased maintenance burden.
Consider those With[...] methods, such as WithName, WithQuantity, and so on. Once you make objects immutable, such copy-and-update methods become indispensable. They enable you to change a single property of an object, while keeping all other values intact:
> var r = new Reservation(DateTimeOffset.Now, "Foo", "foo@example.com", 3); > r.WithQuantity(4) Reservation { Date=[11.09.2018 19:19:29 +02:00], Email="foo@example.com", IsAccepted=false, Name="Foo", Quantity=4 }
While convenient, such methods can increase the maintenance burden. If you realise that you need to change the name of one of the properties, you'll have to remember to also change the name of the copy-and-update method. For example, if you change Quantity to NumberOfGuests, you'll have to also remember to rename WithQuantity to WithNumberOfGuests.
I'm not sure that I'm ready to concede that this is a prohibitive strain on the sustainability of a code base, but I do grant that it's a nuisance. This is one of the many reasons that I prefer to use programming languages better equipped for such domain modelling. In F#, for example, a record type similar to the above immutable Reservation class would be a one-liner:
type Reservation =
{ Date : DateTimeOffset; Name : string; Email : string; Quantity : int; IsAccepted : bool }
Such a declarative approach to types produces an immutable record with the same capabilities as the 78 lines of C# code.
That's a different story, though. There's little correlation between the size of code, and how 'good' it is. Sometimes, less code is better; sometimes, more code is better.
Summary #
I'll dispense with the usual Edsger Dijkstra and Bill Gates quotes on lines of code. The point that lines of code is a useless metric in software development has been made already. My point is a corollary. Apparently, it has to be explicitly stated: Programmer productivity has nothing to do with typing speed.
Unless you're disabled in some way, you can type fast enough to be a productive programmer. Typing isn't a programming bottleneck.
Comments
Watch a bad typist code. (It's easier with coding-heavy tutorial videos). It usually go as: type four or five characters, backspace, make a correction, type another six characters, backspace, make another fix, type a few more character, etc.
They rarely get more than 10 keystrokes out before have to stop and go back. This reeks havoc with your cognitive flow, and makes it much harder to get into the "groove" of coding. Once you can type fluidly, you can concetrate on the code itself, rather than the mechanics of entering it.
Moreover, in many cases, too much verbosity might only lead to more defects (unless you're a strong advocate of TDD et similia)
That said, one thing that I really liked about your article is the version of the Builder pattern you've implemented in the Reservation class. I love immutability in my classes and I often use the Builder pattern implemented as a inner class, just to be able to access the private cTor.
One thing that I don't like with your approach is that in case you have a bit parameter list in your cTor (as you do in the example), the consumers are forced to create a "dummy" instance and then call the WithXXX() methods on it when possible. I guess it could be solved adding a static readonly Empty property on the Reservation class that can be used as a starting point.
Anyways thank you for sharing this!
James, thank you for writing. I agree that being able to type out your thoughts as fast as possible lowers the barrier between your brain and whatever medium you're working in. I had something similar in mind when I wrote
"I also tend to write code in bursts. The average count of lines per hour may not be great, but that's because averages smooth out the hills and the valleys of my activity."I do, however, have mounting concerns about what you call the groove of coding. Flow state is generally characterised by a lack of reflection that I have often found to be counter-productive. These days, when programming, I deliberately use the Pomodoro technique - not to motivate me to code, but to force me to take breaks. Uncountable are the times I've had an important realisation about my work as soon as I'm away from the keyboard. These insights never seem to come to me when I'm in flow.
Perhaps you're now convinced that typing speed may not be the bottleneck, but you still feel that you don't like the verbose
Reservationalternative. More code could be an increased maintenance burden. Consider thoseWith[...]methods, such asWithName,WithQuantity, and so on. Once you make objects immutable, such copy-and-update methods become indispensable.
You could create a more generic With method that would enable modifying any property. Here is an alternative design of the Reservation class including such a method. It is untested, so it might not work properly in every case.
public sealed class Reservation
{
public Reservation(
DateTimeOffset date,
string name,
string email,
int quantity) :
this(date, name, email, quantity, false)
{
}
private Reservation(
DateTimeOffset date,
string name,
string email,
int quantity,
bool isAccepted)
{
Date = date;
Name = name;
Email = email;
Quantity = quantity;
IsAccepted = isAccepted;
}
private Reservation()
{
}
public DateTimeOffset Date { get; private set; }
public string Name { get; private set; }
public string Email { get; private set; }
public int Quantity { get; private set; }
public bool IsAccepted { get; private set; }
public Reservation With(string propertyName, object value)
{
if (propertyName == null)
{
throw new ArgumentNullException(nameof(propertyName));
}
var property = typeof(Reservation).GetProperty(propertyName);
if (property == null)
{
throw new ArgumentException($"Property ${propertyName} does not exist.");
}
if (!IsAssignable(property, value))
{
throw new ArgumentException($"Value ${value} is not assignable to property ${propertyName}");
}
var result = new Reservation();
foreach (var prop in typeof(Reservation).GetProperties())
{
prop.SetValue(result, prop.Name == propertyName ? value : prop.GetValue(this));
}
return result;
}
public Reservation Accept()
{
return new Reservation(Date, Name, Email, Quantity, true);
}
public override bool Equals(object obj)
{
if (!(obj is Reservation other))
return false;
return Equals(Date, other.Date)
&& Equals(Name, other.Name)
&& Equals(Email, other.Email)
&& Equals(Quantity, other.Quantity)
&& Equals(IsAccepted, other.IsAccepted);
}
public override int GetHashCode()
{
return
Date.GetHashCode() ^
Name.GetHashCode() ^
Email.GetHashCode() ^
Quantity.GetHashCode() ^
IsAccepted.GetHashCode();
}
private static bool IsAssignable(PropertyInfo property, object value)
{
if (value == null && property.PropertyType.IsValueType &&
Nullable.GetUnderlyingType(property.PropertyType) == null)
{
return false;
}
return value == null || property.PropertyType.IsAssignableFrom(value.GetType());
}
}
Of course this design is not type-safe and we are throwing exceptions whenever the types of property and value don't match. Property names can be passed using nameof which will provide compile-time feedback. I believe it would be possible to write a code analyzer that would help calling the With method by raising compilation errors whenever the types don't match. The With method could be even designed as an extension method on object and distributed in a Nuget package with the anayler alongside it.
The Lazy functor
Lazy evaluation forms a functor. An article for object-oriented programmers.
This article is an instalment in an article series about functors. Previous articles have covered Maybe, rose trees, and other functors. This article provides another example.
Most programming languages are eagerly evaluated. Sometimes, however, you'd like to defer execution of an expensive operation. On .NET, you can use Lazy<T> to achieve that goal. This generic type, like so many others, forms a functor.
Functor #
You can implement an idiomatic Select extension method for Lazy<T> like this:
public static Lazy<TResult> Select<T, TResult>( this Lazy<T> source, Func<T, TResult> selector) { return new Lazy<TResult>(() => selector(source.Value)); }
This would, for example, enable you to write code like this:
Lazy<int> x = // ... Lazy<string> y = x.Select(i => i.ToString());
Or, using query syntax:
Lazy<int> x = // ... Lazy<string> y = from i in x select i.ToString();
You can add more steps to such a pipeline of lazy computation until you finally decide to force evaluation with the Value property.
Notice that while the Select method looks like it might force evaluation as well, by accessing the Value property, this happens inside a new lazily evaluated lambda expression. Thus, all steps in a Lazy pipeline are deferred until evaluation is forced.
First functor law #
The Select method obeys the first functor law. As usual in this article series, actually proving that this is the case belongs in the realm of computer science. Instead of proving that the law holds, you can demonstrate that it does using property-based testing. The following example shows a single property written with FsCheck 2.11.0 and xUnit.net 2.4.0.
[Property(QuietOnSuccess = true)] public void LazyObeysFirstFunctorLaw(int i) { var left = Lazy.FromValue(i); var right = Lazy.FromValue(i).Select(x => x); Assert.Equal(left.Value, right.Value); }
Even though you may feel that a property-based test gives you more confidence than a few hard-coded examples, such a test is nothing but a demonstration of the first functor law. It's no proof, and it only demonstrates that the law holds for Lazy<int>, not that it holds for Lazy<string>, Lazy<Address>, etcetera.
Both this property and the next uses this little static helper method:
public static Lazy<T> FromValue<T>(T value) { return new Lazy<T>(() => value); }
This helper method is only a convenience. You can put in a delay if you want to pretend that actual lazy evaluation takes place. It'll make the tests run slower, but otherwise will not affect the outcome.
Second functor law #
As is the case with the first functor law, you can also use a property to demonstrate that the second functor law holds:
[Property(QuietOnSuccess = true)] public void LazyObeysSecondFunctorLaw( Func<string, byte> f, Func<int, string> g, int i) { var left = Lazy.FromValue(i).Select(g).Select(f); var right = Lazy.FromValue(i).Select(x => f(g(x))); Assert.Equal(left.Value, right.Value); }
Again the same admonitions apply: that property is no proof. It does show, however, that given two functions, f and g, it doesn't matter if you map a Lazy computation in one or two steps. The output is the same in both cases.
F# #
F# has built-in language support for lazy evaluations, but surprisingly doesn't supply a map function. You can, however, easily implement such a function yourself:
module Lazy = // ('a -> 'b) -> Lazy<'a> -> Lazy<'b> let map f (x : Lazy<'a>) = lazy f x.Value
This enables you to write code like this:
let (x : Lazy<int>) = // ... let (y : Lazy<string>) = x |> Lazy.map string
The F# language feature is based on the same Lazy<T> class that you can use from C# (and Visual Basic .NET), so the behaviour is the same as described above. The functor laws hold for the Lazy.map function just like it holds for the above Select method.
Haskell #
Unlinke C#, F#, and most other programming languages, Haskell is lazily evaluated. All values, whether scalar or complex, are lazy by default. For that reason, there's no explicit Lazy type in Haskell.
Haskell values are, in themselves, not functors, but you can put any value into the Identity functor. Since all values are already lazy, you could view Identity as Haskell's Lazy functor.
The equivalence is only partial, however. .NET Lazy objects are small state machines. Before you've forced evaluation, they carry around the expression to be evaluated. Once you've evaluated the value once, Lazy objects effectively replace the lazy expression with its result. Thus, the next time you access the Value property, you immediately receive the result.
Haskell's lazily evaluated values are different. Since they're immutable, they don't 'change state' like that. On the other hand, sometimes the Haskell compiler can identify optimisations that it can apply to make lazily evaluated values more efficient. In other cases, you may have to apply more explicit memoisation.
Summary #
In languages with eager evaluation (which is most of them), you can model deferred execution as a functor. This enables you to compose lazily evaluated expressions piecemeal.
Next: Asynchronous functors.

Comments
I think we agreed that the issue is not C#'s weak type inference but its lack of default function currying? My guess is that you wrote this quoted part of this article before my comment on your previous article.
Tyson, thank you for writing.
Yes, June 27, 2017, in fact...You're correct that this particular issue is related to the uncurried nature of C# methods.
I do, however, maintain that C#'s type inference capabilities are weaker than F#'s or Haskell's. To be clear, I view this as the result of priorities. I don't think that the people who designed and wrote the C# compiler are less skilled than the designers of F# or Haskell. The C# compiler has to solve many other problems, such as for example overload resolution, which is a language feature in direct opposition to currying. The C# compiler is excellent at overload resolution, a task with which the F# compiler sometimes struggle (and is not even a language feature in Haskell).
Your comment is, however, a reminder that I should consider how I phrase such notions in the future. Thank you for pointing that out. As I'm publishing and get feedback, I constantly learn new things. I'm always grateful when someone like you take the time to educate me.
I'll see if I can improve in the future. I do, however, still have a backlog of articles I wrote months, or even more than a year, ago, so it's possible that more errors escape my attention when I proof read them before publication. If that happens, I'll appreciate more corrections.
Thank you very much for your kind reply. I agree with everything you said.
I will expand my comment a bit to give a clearer picture of my understanding.
First, very little is "needed"; most things are merely sufficient. In particular, we don't need to overload your
Applymethod to achieve your goal. As I mentioned before, it sufficies to have a singleApplymethod and instead create overloads of a function calledcurrythat explicitly curries a given function. Furthermore, I think there is a sense in which this latter approach to overcome the lack of default currying is somehow minimal or most abstract or most general.Second, compared to languages like F# or Haskell, type inference is definitely weaker in C#. This issue was also present (in a subtle way) in your previous article, but I decided to largely ignore it in order to keep my comment more focused. In your previous article, you expliciltly defined the local variable
In particular, you explicitly told the C# compiler that the type of all of these six variable isconcatlike thisstring. That part was necessary; the type inference in C# is not strong enough to innfer (possibily in some use ofconcat) that the types could bestring.Suppose instead of defining
Again, I think there is a sense in which this explicit way to specify non-inferable types is somehow minimal or most abstract or most general.concatas a local variable (withFunc<string, string, string, string, string, string, string>as its type) you had defined it as a member method on a class. Then its type in C# is some kind "method group". The method group of a method essentially corresponds to the set of methods containing itself and its overloads. Then in order to passconcatintocurry, there needs to be a type conversion (or cast) from its method group toFunc<string, string, string, string, string, string, string>. This is also something that the C# system cannot do, and so Language Ext has overloads of a function calledfunto do this explicitly. Using it on our hypothetical member functionconcatwould look likeMy impression is that there is some low hanging fruit here for strengthing the type inference of the C# compiler. If a method group correpsonds to a singleton set (and that method has no
reforoutarguments), then I would think it would be straight forward to consider an implicit cast from the method group to the correspondingFuncorActiondelegate.